Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems

Abstract

This paper presents fractional order fixed-time nonsingular terminal sliding mode control for stabilization and synchronization of fractional order chaotic systems with uncertainties and disturbances. First, a novel fractional order terminal sliding mode surface is proposed to guarantee the fixed-time convergence of system states along the sliding surface. Second, a nonsingular terminal sliding mode controller is designed to force the system states to reach the sliding surface within fixed-time and remain on it forever. Furthermore, the fractional Lyapunov stability theory is used to prove the fixed-time stability and the robustness of the proposed control scheme and estimate the upper bound of convergence time. Next, the proposed control scheme is applied to the synchronization of two nonidentical fractional order Liu chaotic systems and chaos suppression of fractional order power system. Simulation results verify the effectiveness of the proposed control scheme. Finally, some application issues about the proposed scheme are discussed.

1 Introduction

Fractional calculus, with more than 300 years of history, is a generalization of ordinary differentiation and integration to arbitrary (noninteger) order. For many years, fractional calculus is considered as a sole mathematical and theoretical science with nearly no applications [1]. Nevertheless, in recent years, great attention has been paid to the applications of fractional calculus in engineering and physical systems. One of the most striking applications is the fractional order controller. Additionally, it has been found that many practical systems, including electrical circuit [2, 3], DC–DC converter [4], power system [5], permanent magnet synchronous motor [6], can be elegantly described and accurately modeled with the help of fractional calculus. Furthermore, many fractional order differential systems, such as fractional order Rossler system [7], fractional order Lorenz system [8], fractional order Duffing system [9], fractional order Liu system [10], fractional order Chua circuit [11], exhibit chaotic behavior.

Chaos is a complex dynamical phenomenon, which has been found in many nonlinear systems. A chaotic system is a deterministic nonlinear system with several special features including sensitiveness to initial condition, strange attractors, ergodicity, and irregular motion. Recently, dynamical behaviors of chaos system have been well studied. In [12,13,14], the ultimate bound and positively invariant set were investigated for Lorenz chaotic system using Lyapunov stability theory combined with comparison principle. In [15], hyperchaos was generated from Lorenz system. In [16], double-scroll and four-scroll strange attractors were generated from memristor. In [17], the stability theory of fractional order systems was applied to analyze the condition that ensures a fractional order system is chaotic and study linear coupling method to achieve synchronization. On the one hand, chaos is an undesirable phenomenon for many practical systems and effective control scheme is needed to suppress it. On the other hand, since Pecora and Carroll [18] proved that chaotic systems could be synchronized, great efforts have been made to study various chaos synchronization methods [19,20,21,22] and chaos synchronization has found many engineering applications, such as secure communication [23], power quality detection [24], fault protection [25]. Due to the existence of chaos in many fractional order real systems and many practical applications in engineering, stabilization and synchronization of fractional order chaotic systems have become a hot topic in recent years. Many control schemes have been proposed for the stabilization and synchronization of fractional order chaotic systems. An active sliding mode control scheme was presented to synchronize fractional order chaotic systems in [26]. In [27], an adaptive feedback controller was designed for the synchronization of two coupled fractional order chaotic systems. In [28] and [29], the ultimate bound and positively invariant set of chaotic system were used to determine desired linear feedback gain for global complete chaos synchronization, which shows great potential to be applied into the synchronization of fractional order chaotic systems. Lin and Lee [30] addressed time delay uncertain fractional order chaotic system synchronization problem via adaptive fuzzy sliding mode control. Chen et al. [31] applied fuzzy control to study synchronization and anti-synchronization problem for fractional order chaotic systems with uncertain stochastic parameters. In [32], a novel adaptive fuzzy control method was proposed to achieve H-inf synchronization of fractional order chaotic systems. Based on passive control theory, Wu et al. [33] investigated synchronization problem for fractional order hyperchaotic system. In [34], LMI-based control scheme was proposed to stabilize a class of fractional order chaotic systems. Fuzzy state feedback [35] and fuzzy output feedback [36] were proposed to stabilize uncertain fractional order chaotic systems.

However, all the aforementioned control methods can only achieve asymptotical synchronization and stabilization, which means that exact convergence cannot be achieved within finite time. In addition, the convergence time of these control methods cannot be estimated in advance. From a practical point of view, it is more advisable to realize stabilization and synchronization within a prescribed time, especially for those applications that require exact convergence and have severe settling time constraint. Finite time control can achieve high-precision convergence within finite time. Besides, finite time stability has better disturbance rejection property and stronger robustness against uncertainties. Therefore, finite time fractional order chaotic system synchronization and stabilization have attracted great attention. In [37], nonsingular terminal sliding mode control was introduced to achieve finite time fractional order chaos synchronization and control. Aghababa [38] presented a chatter-free terminal sliding mode controller to control uncertain fractional order chaotic system in finite time. Robust finite time fractional controller was presented in [39] to stabilize uncertain fractional order chaotic systems. Hierarchical terminal sliding mode control was proposed for synchronization and control of fractional order chaotic systems in [40]. Using frequency distributed model, Wang et al. [41] investigated robust finite time control of fractional order chaotic systems. It is worth noting that the convergence time of finite time control scheme depends on initial condition. However, for many practical applications, it is always hard to obtain accurate information of initial condition, which makes it difficult to estimate the convergence time. In addition, the convergence time of finite time control becomes infinite if the initial condition tends to infinity.

Fixed-time control [42] is proposed to overcome the drawback of finite time control. Different from finite time control, fixed-time control can guarantee exact convergence within finite time upper bounded by a constant independent of initial condition. Due to this appealing feature, fixed-time control has been applied to power system stable control [43, 44] and multi-agent system consensus [45,46,47,48,49,50]. However, to the best of our knowledge, there is no literature reporting the fractional order fixed-time control scheme. In fact, fractional calculus provides a new way for the controller design. In comparison with integer order controller, fractional order controller provides greater facilitates to improve robustness and control performance [51]. Additionally, fractional order controller can help dynamical systems gain more stability [52].

Motivated by aforementioned discussion, this paper presents fractional order fixed-time nonsingular terminal sliding mode control for chaos synchronization and stabilization. We first propose a novel fractional order terminal sliding mode surface which can guarantee fixed-time convergence of system states along the sliding surface. Then, a nonsingular terminal sliding mode control law is designed to force the system states to reach the proposed sliding surface within fixed-time and stay on it forever. The main contributions of this paper can be summarized as the following three aspects. First, fixed-time control is first presented to the synchronization and stabilization of fractional order chaotic systems. Second, fractional order fixed-time control scheme is first proposed, which combines the advantages of fixed-time control and fractional order control. Third, the proposed terminal sliding mode control does not include singularity term, thereby eliminating singularity, while the existing fixed-time nonsingular terminal sliding mode controls [43, 46, 50] contain singularity term and they used nonlinear function or saturation function to overcome singularity, which complicates the controller design and prolongs the convergence time.

The rest of this paper is organized as follows. Section 2 reviews preliminary knowledge necessary throughout the paper, and Sect. 3 formulates the problem. Main results of this paper are presented in Sect. 4, and simulation results verifying the effectiveness of proposed controller are given in Sect. 5. Some application issues about the proposed scheme are discussed in Sect. 6. Finally, the conclusion is drawn in Sect. 7.

2 Preliminary

In this section, we first present some basic definitions of fractional calculus and fixed-time stability and then introduce some useful lemmas which are necessary for controller design.

2.1 Fractional calculus

Definition 1

[53] The $\alpha$th-order Riemann–Liouville fractional derivative of function f(t) is given by:

$$\begin{aligned} {}_{t_{0}}D^{\alpha }_{t}f(t)= & {} \frac{\mathrm{d}^{\alpha }f(t)}{\mathrm{d}t^{\alpha }}\nonumber \\= & {} \frac{1}{{\varGamma }(m-\alpha )}\frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}}\int _{t_{0}}^{t}\frac{f(\tau )}{(t-\tau )^{\alpha -m+1}}\mathrm{d}\tau \end{aligned}$$

(1)

where $m-1<\alpha \le m$, $m\in N$ and ${\varGamma }(\cdot )$ is the Gamma function.

Definition 2

[53] The definition of the $\alpha$th-order Riemann–Liouville fractional integration is:

$$\begin{aligned} {}_{t_{0}}I_{t}^{\alpha }f(t)=\frac{1}{{\varGamma }(\alpha )}\int _{t_{0}}^{t}\frac{f(\tau )}{(t-\tau )^{1-\alpha }}\mathrm{d}\tau \end{aligned}$$

(2)

where $t_{0}$ is the initial time.

Definition 3

[53] The $\alpha$th-order Caputo fractional derivative of function f(t) is defined as:

$$\begin{aligned}&{}_{t_{0}}D_{t}^{\alpha }f(t)\nonumber \\&=\left\{ \begin{array}{ll}&{}\frac{1}{{\varGamma }(m-\alpha )}\int _{t_{0}}^{t}\frac{f^{(m)}(\tau )}{(t-\tau )^{\alpha -m+1}}\mathrm{d}\tau ,\quad m-1<\alpha <m\\ &{}\frac{\mathrm{d}^{m}f(t)}{\mathrm{d}t^{m}},\quad \alpha =m \end{array}\right. \nonumber \\ \end{aligned}$$

(3)

where m is the smallest integer number larger than or equal to $\alpha$.

Property 1

[53] The following equality holds for both the Caputo derivative and the Riemann–Liouville derivative:

$$\begin{aligned} {}^{\mathrm{RL,C}}_{t_{0}}D^{\alpha }_{t}\left( {}^{\mathrm{RL,C}}_{t_{0}}D^{-\beta }_{t}f(t)\right) ={}^{\mathrm{RL,C}}_{t_{0}}D^{\alpha -\beta }_{t}f(t) \end{aligned}$$

(4)

where $\alpha \ge \beta \ge 0$. Here, the superscript “RL” denotes the Riemann–Liouville derivative and “C” denotes the Caputo derivative.

Lemma 1

[54] Let $x=0$ be an equilibrium point of the following nonautonomous fractional order system:

$$\begin{aligned} D^{\alpha }x=f(x,t) \end{aligned}$$

(5)

where $\alpha \in (0,1)$ and f(x, t) satisfies the Lipschitz condition with Lipschitz constant $l>0$. Suppose that there exists a Lyapunov function V(t, x(t)) that satisfies:

$$\begin{aligned}&\alpha _{1}\Vert x\Vert ^{\alpha }\le V(t,x(t))\le \alpha _{2}\Vert x\Vert \end{aligned}$$

(6)

$$\begin{aligned}&\dot{V}(t,x)\le -\alpha _{3}\Vert x\Vert \end{aligned}$$

(7)

where $\alpha _{1}, \alpha _{2}, \alpha _{3}$ and $\alpha$ are positive constants. Then the equilibrium point of the system (5) is Mittag–Leffler stable, which also implies asymptotical stable.

Remark 1

Lemma 1 reveals an important property that the commonly used Lyapunov function in the form of $V=1/2x^{2}$ do not satisfy the condition (6). Therefore, alternative Lyapunov function is needed to analyze the stability of fractional order systems.

In the rest of this paper, the Caputo definition of fractional derivative and integration is employed. To simplify this notation, $D^{\alpha }$ is utilized to denote the Caputo fractional derivative of order $\alpha$.

2.2 Fixed-time stability

Consider the following differential equation system:

$$\begin{aligned} \dot{x}(t)=f(x(t)),\quad x(0)=x_{0}. \end{aligned}$$

(8)

where $x\in R^{n}$ and $f: R^{n}\rightarrow R^{n}$ is a nonlinear function. Suppose that the origin is an equilibrium point of (8).

Definition 4

[48, 55] The origin of system (8) is a finite time stable equilibrium if the origin is Lyapunov stable and there exists a function $T: R^{n}\mapsto R^{+}$, called the settling time function, such that for every $x_{0}\in R^{n}$, the solution $x(t,x_{0})$ of system (8) satisfies $\displaystyle {\lim _{t\rightarrow T(x_{0})}}x(t,x_{0})$ $=0$.

Definition 5

[42] The origin of system (8) is said to be fixed-time stable equilibrium point if it is globally finite time stable with bounded convergence time $T(x_{0})$, that is, there exists a bounded positive constant $T_{\max }$ such that $T(x_{0})<T_{\max }$ satisfies.

Lemma 2

[49] Consider the following system:

$$\begin{aligned} \dot{y}=-\alpha y^{\frac{m}{n}}-\beta y^{\frac{p}{q}},~~y(0)=y_{0} \end{aligned}$$

(9)

where $\alpha ,\beta >0$, m, n, p, q are positive odd integers satisfying $m>n$ and $p<q$. Then, the equilibrium point of system (9) is fixed-time stable and the settling time is upper bounded by:

$$\begin{aligned} T<\frac{1}{\alpha }\frac{n}{m-n}+\frac{1}{\beta }\frac{q}{q-p} \end{aligned}$$

(10)

2.3 Mathematical Lemmas

Lemma 3

[56] For any nonnegative real numbers $\xi _{1},\xi _{2},$ $\ldots ,\xi _{N}$ and $0<p\le 1$, the following inequality holds:

$$\begin{aligned} \sum ^{N}_{i=1}\xi ^{p}_{i}\ge \left( \sum ^{N}_{i=1}\xi _{i}\right) ^{p} \end{aligned}$$

(11)

Lemma 4

[56] For any nonnegative real numbers $\xi _{1},\xi _{2},\ldots ,\xi _{N}$ and $p>1$, the following inequality holds:

$$\begin{aligned} \sum ^{N}_{i=1}\xi ^{p}_{i}\ge N^{1-p}\left( \sum ^{N}_{i=1}\xi _{i}\right) ^{p} \end{aligned}$$

(12)

3 Problem formulation

Consider the following N-dimensional nonautonomous fractional order chaotic system with uncertainties and external disturbances:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&D^{\alpha }x_{1}=f_{1}(X,t)+\Delta f_{1}(X,t)+d_{1}^{f}(t)+u_{1},\\&D^{\alpha }x_{2}=f_{2}(X,t)+\Delta f_{2}(X,t)+d_{2}^{f}(t)+u_{2},\\&\ldots \\&D^{\alpha }x_{N}=f_{N}(X,t)+\Delta f_{N}(X,t)+d_{N}^{f}(t)+u_{N}\\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(13)

where $\alpha \in (0,1)$ is the fractional order of the system, $X(t)=[x_{1},x_{2},\ldots ,x_{N}]^\mathrm{T}\in R^{N}$ is the state vector, $f_{i}(X,t)\in R$, $i=1,2,\ldots ,N$ is a known nonlinear function of X and t, $\Delta f_{i}(X,t)\in R$ and $d_{i}^{f}(t)\in R$, $i=1,2,\ldots ,N$ are uncertainties and external disturbances of the system, and $u_{i}$ is the control input.

Assumption 1

The uncertainties $\Delta f_{i}(X,t)$ and external disturbances $d_{i}^{f}(t)$ are bounded, that is, there exist positive constants $\varepsilon _{i}, \mu _{i}$, such that $|\Delta f_{i}(X,t)|\le \varepsilon _{i}$, $|d_{i}^{f}(t)|\le \mu _{i}$ .

The fixed-time chaos synchronization problem can be formulated as designing fractional order fixed-time nonsingular terminal sliding mode control $u_{i}$ for slave system (13) such that its trajectories can track the trajectories of the following master system within finite time upper bounded by a constant independent of initial values

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&D^{\alpha } y_{1}=g_{1}(Y,t)+\Delta g_{1}(Y,t)+d_{1}^{g}(t),\\&D^{\alpha } y_{2}=g_{2}(Y,t)+\Delta g_{2}(Y,t)+d_{2}^{g}(t),\\&\ldots \\&D^{\alpha } y_{N}=g_{N}(Y,t)+\Delta g_{N}(Y,t)+d_{N}^{g}(t)\\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(14)

where $\alpha \in (0,1)$ is the fractional order of the system, $Y(t)=[y_{1},y_{2},\ldots ,y_{N}]^\mathrm{T}\in R^{N}$ is the state vector, $g_{i}(Y,t)\in R$, $i=1,2,\ldots ,N$ is a known nonlinear function of Y and t, $\Delta g_{i}(Y,t)\in R$ and $d_{i}^{g}(t)\in R$, $i=1,2,\ldots ,N$ are uncertainties and external disturbances of the system.

Assumption 2

The uncertainties $\Delta g_{i}(Y,t)$ and external disturbances $d_{i}^{g}(t)$ are bounded, that is, there exist positive constants $\gamma _{i}, \eta _{i}$, such that $|\Delta g_{i}(Y,t)|\le \gamma _{i}$, $|d_{i}^{g}(t)|\le \eta _{i}$.

Remark 2

It is hard to obtain the exact values for external disturbances and uncertainties in many practical systems. However, the upper bound of external disturbances and uncertainties can be exactly estimated, for example, using adaptive techniques presented in [57, 58]. Further, the states of chaotic attractors are bounded [59]. Therefore, Assumptions 1 and 2 are reasonable and accurate.

Subtracting (13) from (14) and defining $E(t)=Y(t)-X(t)=[y_{1}-x_{1},y_{2}-x_{2},\ldots ,y_{N}-x_{N}]^\mathrm{T}$, we have:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&D^{\alpha } e_{1}=g_{1}(Y,t)+\Delta g_{1}(Y,t)+d_{1}^{g}(t)\\&~~~~~~~~~~\quad -(f_{1}(X,t)+\Delta f_{1}(X,t)+d_{1}^{f}(t)+u_{1}),\\&D^{\alpha } e_{2}=g_{2}(Y,t)+\Delta g_{2}(Y,t)+d_{2}^{g}(t)\\&~~~~~~~~~~\quad -(f_{2}(X,t)+\Delta f_{2}(X,t)+d_{2}^{f}(t)+u_{2}),\\&...\\&D^{\alpha } e_{N}=g_{N}(Y,t)+\Delta g_{N}(Y,t)+d_{N}^{g}(t)\\&~~~~~~~~~~\quad -(f_{N}(X,t)+\Delta f_{N}(X,t)+d_{N}^{f}(t)+u_{N})\\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(15)

Now, the fixed-time chaos synchronization problem is transformed into the fixed-time stabilization problem for error system (15).

The fixed-time chaos control problem can be formulated as designing fractional order fixed-time nonsingular terminal sliding mode control $u_{i}$ such that chaotic system (13) can be stabilized within finite time upper bounded by a constant independent of initial values.

4 Main results

In this section, we will develop a novel fractional order fixed-time nonsingular terminal sliding mode control to stabilize the synchronization error system (15) and the chaotic system (13).

The sliding surface can be constructed as:

$$\begin{aligned} s_{i}{=}D^{\alpha -1}e_{i}+D^{\alpha -2}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}{+}\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \end{aligned}$$

(16)

where $\beta _{1}$, $\lambda _{1}$ are positive constants, $m_{1}, n_{1}, p_{1}, q_{1}$ are positive odd integers that satisfy $m_{1}>n_{1}$, $p_{1}<q_{1}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

The control input is designed as:

$$\begin{aligned} u_{i}= & {} g_{i}(Y,t){-}f_{i}(X,t){+}\left( \varepsilon _{i}{+}\gamma _{i}{+}\mu _{i}{+}\eta _{i}\right) \mathrm{sign}\left( s_{i}\right) \nonumber \\&+ D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \nonumber \\&+ \beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}+\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}} \end{aligned}$$

(17)

where $\beta _{2}, \lambda _{2}$ are positive constants, $m_{2}, n_{2}, p_{2}, q_{2}$ are positive odd integers that satisfy $m_{2}>n_{2}$, $p_{2}<q_{2}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

Theorem 1

Consider the synchronization error system (15) with uncertainties and external disturbances satisfying Assumptions 1–2. If this system is controlled under control input (17), its trajectories will converge to the sliding surface within finite time upper bounded by:

$$\begin{aligned} T_{1}<\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}} \end{aligned}$$

(18)

Proof

Consider the following Lyapunov function candidate:

$$\begin{aligned} V_{1}=\sum _{i=1}^{N}\left| s_{i}\right| \end{aligned}$$

(19)

Taking time derivative of Lyapunov function $V_{1}(t)$ along the sliding surface (16) yields:

$$\begin{aligned} \dot{V_{1}}= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \dot{s_{i}}\nonumber \\= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \left( D^{\alpha }e_{i}+D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}\right. \right. \nonumber \\&\left. \left. +\,\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \right) \end{aligned}$$

(20)

Substituting error system dynamics (15) into (20), one has:

$$\begin{aligned} \dot{V_{1}}= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \left( g_{i}(Y,t){+}\Delta g_{i}(Y,t){+}d_{i}^{g}(t){-}f_{i}(X,t)\right. \nonumber \\&-\,\Delta f_{i}(X,t)-d_{i}^{f}(t){-}u_{i}{+}D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}\right. \nonumber \\&\left. \left. +\,\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \right) \end{aligned}$$

(21)

Substituting control input (17) into (21), we have:

$$\begin{aligned} \dot{V_{1}}= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \left( g_{i}(Y,t)+\Delta g_{i}(Y,t)+d_{i}^{g}(t)\right. \nonumber \\&-\,f_{i}(X,t)-\Delta f_{i}(X,t)-d_{i}^{f}(t)-\left( g_{i}(Y,t)\right. \nonumber \\&-\,f_{i}(X,t)+D^{\alpha -1}(\beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}})\nonumber \\&+\,\left( \varepsilon _{i}+\gamma _{i}+\mu _{i}+\eta _{i}\right) \mathrm{sign}\left( s_{i}\right) +\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}\nonumber \\&\left. +\,\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}\right) +D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}\right. \nonumber \\&\left. \left. +\,\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \right) \nonumber \\= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \left( -\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}-\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}\right) \nonumber \\&-\,\left( \varepsilon _{i}+\gamma _{i}+\mu _{i}+\eta _{i}\right) +\mathrm{sign}\left( s_{i}\right) \left( g_{i}(Y,t)+\Delta g_{i}(Y,t)\right. \nonumber \\&+\,\,d_{i}^{g}(t)-f_{i}(X,t)-\,\Delta f_{i}(X,t)-d_{i}^{f}(t)\nonumber \\&\left. -\,\,g_{i}(Y,t)+f_{i}(X,t)\right) \end{aligned}$$

(22)

Use Lemmas 3–4 and Assumptions 1–2, and (22) becomes:

$$\begin{aligned} \dot{V_{1}}\le & {} \sum _{i=1}^{N}-\beta _{2}\left| s_{i}\right| ^{m_{2}/n_{2}}-\lambda _{2}\left| s_{i}\right| ^{p_{2}/q_{2}}-\left( \varepsilon _{i}+\gamma _{i}+\mu _{i}+\eta _{i}\right. \nonumber \\&\left. -\,\left| \Delta g_{i}(Y,t)\right| -\left| d_{i}^{g}(t)\right| -\left| \Delta f_{i}(X,t)\right| -\left| d_{i}^{f}(t)\right| \right) \nonumber \\\le & {} \,-N^{1-m_{2}/n_{2}}\beta _{2}\left( \sum _{i=1}^{N}\left| s_{i}\right| \right) ^{m_{2}/n_{2}}-\lambda _{2}\left( \sum _{i=1}^{N}\left| s_{i}\right| \right) ^{p_{2}/q_{2}}\nonumber \\= & {} -N^{1-m_{2}/n_{2}}\beta _{2}V_{1}^{m_{2}/n_{2}}-\lambda _{2}V_{1}^{p_{2}/q_{2}} \end{aligned}$$

(23)

Therefore, according to Lemma 1, the system states will converge to the sliding surface asymptotically. Furthermore, based on Lemma 2, we can prove fixed-time convergence and the convergence time is upper bounded by (18). The proof is completed. $\square$

When the error state is on the sliding surface, its dynamics satisfies:

$$\begin{aligned} D^{\alpha -1}e_{i}=-D^{\alpha -2}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \end{aligned}$$

(24)

Theorem 2

Consider the sliding mode dynamics (24). The error state variables will converge to the origin within finite time upper bounded by:

$$\begin{aligned} T_{2}<\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned}$$

(25)

Proof

Select the Lyapunov function candidate as follows:

$$\begin{aligned} V_{2}(t)=\sum _{i=1}^{N}\left| e_{i}(t)\right| \end{aligned}$$

(26)

Using Lemmas 3–4 and Property 1, the time derivative of Lyapunov function $V_{2}(t)$ can be derived as:

$$\begin{aligned} \dot{V}_{2}(t)= & {} \sum _{i=1}^{N}\dot{e}_{i}(t)\mathrm{sign}\left( e_{i}(t)\right) \nonumber \\= & {} \sum _{i=1}^{N}\left( D^{2-\alpha }\left( D^{\alpha -1}e_{i}(t)\right) \right) \mathrm{sign}(e_{i}(t))\nonumber \\= & {} \sum _{i=1}^{N}\left( \mathrm{sign}\left( e_{i}(t)\right) \right) \left( D^{2-\alpha }\left( -D^{\alpha -2}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}\right. \right. \right. \nonumber \\&\left. \left. \left. +\,\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \right) \right) \nonumber \\= & {} \sum _{i=1}^{N}\left( -\left( \beta _{1}\left| e_{i}\right| ^{m_{1}/n_{1}}+\lambda _{1}\left| e_{i}\right| ^{p_{1}/q_{1}}\right) \right) \nonumber \\&\le -N^{1-m_{1}/n_{1}}\beta _{1}\left( \sum _{i=1}^{N}\left| e_{i}\right| \right) ^{m_{1}/n_{1}}-\lambda _{1}\left( \sum _{i=1}^{N}\left| e_{i}\right| \right) ^{p_{1}/q_{1}}\nonumber \\= & {} -N^{1-m_{1}/n_{1}}\beta _{1}V_{2}^{m_{1}/n_{1}}-\lambda _{1}V_{2}^{p_{1}/q_{1}} \end{aligned}$$

(27)

Therefore, according to Lemma 1, the system states will converge to zero asymptotically. Furthermore, based on Lemma 2, we can prove fixed-time stability of the system and the convergence time is upper bounded by (25). The proof is completed. $\square$

From Theorems 1–2, we have the following result:

Theorem 3

For the synchronization error system (15) with uncertainties and external disturbances satisfying Assumptions 1–2, if the control input is designed as (17), the error system will converge to zero within finite time upper bounded by:

$$\begin{aligned} \begin{aligned} T<\,&\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}}\\&+\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned} \end{aligned}$$

(28)

Proof

The proof process includes fixed-time convergence to sliding surface and fixed-time stabilization along the sliding surface. Theorem 1 has proved fixed-time convergence to sliding surface, and Theorem 2 has proved fixed-time stabilization along the sliding surface. Therefore, from Theorems 1–2, we have that Theorem 3 holds. $\square$

The proposed control scheme is extended to address fixed-time fractional order chaotic system stabilization problem, and we have the following result:

Theorem 4

Consider the stabilization problem of the fractional order chaotic system (13) with uncertainties and external disturbances satisfying Assumption 1. If the system (13) is controlled by control law (29), then the system can be stabilized within finite time upper bounded by (30).

$$\begin{aligned}&\begin{aligned} u_{i}(t)=&-f_{i}(X,t)-D^{\alpha -1}(\beta _{1}\mathrm{sig}(x_{i})^{m_{1}/n_{1}}\\&+\lambda _{1}\mathrm{sig}(x_{i})^{p_{1}/q_{1}})-\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}\\&-\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}-\left( \varepsilon _{i}+\mu _{i}\right) \mathrm{sign}\left( s_{i}\right) \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned}&\begin{aligned} T<&\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}}\\&+\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned} \end{aligned}$$

(30)

where $\beta _{1}, \lambda _{1}, \beta _{2}, \lambda _{2}$ are positive constants, $m_{1}, n_{1}, p_{1}, q_{1},$ $m_{2}, n_{2}, p_{2}, q_{2}$ are positive odd integers that satisfy $m_{1}>n_{1}, p_{1}<q_{1} , m_{2}>n_{2}, p_{2}<q_{2}$, $s_{i}$ is the sliding surface which has the following form:

$$\begin{aligned} s_{i}=D^{\alpha -1}x_{i}+D^{\alpha -2}\left( \beta _{1}\mathrm{sig}(x_{i})^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}(x_{i})^{p_{1}/q_{1}}\right) \end{aligned}$$

(31)

Proof

The proof process is similar to that of Theorem 3 and is omitted here. $\square$

Remark 3

As mentioned in remark 1 and reported in [37,38,39,40,41], nonsmooth Lyapunov functions can be adopted to analyze the stability of fractional order systems.

Remark 4

The existing control and synchronization schemes can achieve asymptotical and finite time convergence. Asymptotical convergence implies that exact convergence cannot be achieved within finite time and finite time convergence implies exact convergence can be guaranteed within finite time dependent on initial condition. In fact, for many practical applications, it is always hard to obtain accurate information of initial condition, which makes it difficult to estimate the convergence time. Therefore, the existing control and synchronization schemes are unsuitable to be applied into some practical fractional order chaotic systems that require exact convergence and have severe settling time constraint, such as secure communication and system emergency control. The proposed control scheme can achieve exact stabilization and synchronization within finite time upper bounded by a constant independent of initial condition and the upper bound is only determined by design parameters. We can tune the design parameters to satisfy the requirement of convergence time.

Remark 5

Singularity is one of the main drawbacks of the terminal sliding mode control. The existing fixed-time nonsingular terminal sliding mode controls [43, 46, 50] contain singularity term, and they used nonlinear function or saturation function to overcome singularity, which complicates the controller design and prolongs the convergence time. In this paper, fractional order control is combined with fixed-time control, which eliminates singularity term and improves the performance of the fixed-time control.

Remark 6

The proposed control scheme combines the advantages of fractional order control and fixed-time control and has fast and exact convergence property as well as nonsingular control input.

Remark 7

There are many results on the sliding mode control of chaotic system, for example, see [26, 30, 37,38,39,40,41] and references therein. However, these control schemes can either achieve asymptotical stabilization, or guarantee finite time stabilization but the upper bound of convergence time depends on initial condition. In comparison with these control schemes, the contributions of this paper can be summarized as the following four aspects. First, a novel fractional order terminal sliding mode surface is proposed, which can guarantee fixed-time convergence of system states along the sliding surface. Second, a new nonsingular terminal sliding mode control law is designed, which forces the system states to reach the proposed sliding surface within fixed-time and stay on it forever. Third, the proposed terminal sliding mode control scheme does not include singularity term, thereby eliminating singularity. Fourth, the proposed control scheme can ensure exact system stabilization within finite time upper bounded by a constant independent of initial condition and the upper bound is only determined by design parameters. We can tune the design parameters to satisfy the requirement of convergence time.

Remark 8

In this paper, we propose fractional order fixed-time nonsingular terminal sliding mode control to synchronize and stabilize fractional order chaotic systems with uncertainties and disturbances. In [37, 38] and [40], terminal sliding mode control was derived to stabilize fractional order chaotic systems within finite time. However, the convergence time of these control schemes is dependent on initial condition. In this paper, fixed-time control is extended to the synchronization and stabilization of fractional order chaotic systems and as shown in Theorem 3 and Theorem 4, the convergence time of the proposed control is upper bounded by a constant independent of initial condition but only dependent on controller design parameters. This advantage facilitates controller design and convergence time estimation. In [43, 46] and [50], fixed-time terminal sliding mode control was presented. However, the presented control schemes contain singularity term and they used nonlinear function or saturation function to overcome singularity, which complicates the controller design and prolongs the convergence time. In addition, these control schemes are only suitable to control integer order systems and it is hard to extend these results to fractional order systems. In this paper, fractional order fixed-time control is proposed, which can be applied to stabilize and synchronize fractional order systems. Besides, the proposed control scheme does not include singularity term, thereby overcoming singularity problem without complicating controller design and sacrificing convergence time.

Remark 9

Since the control law contains discontinuous sign function, it may induce chattering phenomenon. To eliminate chattering, discontinuous sign function can be replaced by continuous saturation function.

5 Simulation results

In this section, two illustrative examples are presented to demonstrate the effectiveness and applicability of the proposed control scheme.

5.1 Fixed-time synchronization of fractional order Liu hyperchaotic systems

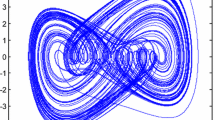
This example is employed to verify the effectiveness of the proposed control scheme in synchronization of fractional order chaotic systems. Let us consider fractional order Liu hyperchaotic system (32) as master system and different structural fractional order Liu hyperchaotic system (33) as slave system. The systems are taken from [60].

Master system:

$$\begin{aligned} \left\{ \begin{aligned} D^{q}y_{1}&=a\left( y_{2}-y_{1}\right) +y_{4}+\Delta g_{1}(Y,t)+d_{1}^{g}(t)\\ D^{q}y_{2}&=by_{1}+ky_{1}y_{3}-y_{4}+\Delta g_{2}(Y,t)+d_{2}^{g}(t)\\ D^{q}y_{3}&=-hy_{1}^{2}-cy_{3}-y_{4}+\Delta g_{3}(Y,t)+d_{3}^{g}(t)\\ D^{q}y_{4}&=ey_{1}+\Delta g_{4}(Y,t)+d_{4}^{g}(t) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(32)

Slave system:

$$\begin{aligned} \left\{ \begin{aligned} D^{q}x_{1}&=a\left( x_{2}-x_{1}\right) +\Delta f_{1}(X,t)+d_{1}^{f}(t)\\ D^{q}x_{2}&=bx_{1}-kx_{1}x_{3}+x_{4}+\Delta f_{2}(X,t)+d_{2}^{f}(t)\\ D^{q}x_{3}&=hx_{1}^{2}-cx_{3}+x_{4}+\Delta f_{3}(X,t)+d_{3}^{f}(t)\\ D^{q}x_{4}&=-ex_{2}+\Delta f_{4}(X,t)+d_{4}^{f}(t) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(33)

The parameters for the systems are selected as $a=10$, $b=40$, $k=10$, $c=2.5$, $h=4$, $e=2.5$, and the uncertainties and external disturbances are selected as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\Delta g_{1}(Y,t)=0.25 \mathrm{cos}(6t)y_{1},\ d_{1}^{g}(t)=-0.15\mathrm{sin}(t),\\&\Delta g_{2}(Y,t)=-0.2\mathrm{cos}(2t)y_{2},\ d_{2}^{g}(t)=0.1\mathrm{sin}(3t),\\&\Delta g_{3}(Y,t)=0.15\mathrm{sin}(3t)y_{3},\ d_{3}^{g}(t)=0.2\mathrm{cos}(5t),\\&\Delta g_{4}(Y,t)=-0.2\mathrm{cos}(t)y_{4},\ d_{4}^{g}(t)=-0.15\mathrm{cos}(t),\\&\Delta f_{1}(X,t)=-0.25\mathrm{sin}(4t)x_{1},\ d_{1}^{f}(t)=0.1\mathrm{sin}(7t),\\&\Delta f_{2}(X,t)=0.1\mathrm{cos}(t)x_{2},\ d_{2}^{f}(t)=0.15\mathrm{cos}(3t),\\&\Delta f_{3}(X,t){=}0.25\mathrm{sin}(4t)x_{3},\ d_{3}^{f}(t){=}-0.15\mathrm{sin}(5t),\\&\Delta f_{4}(X,t)=-0.15\mathrm{sin}(t)x_{4},\ d_{4}^{f}(t)=0.2\mathrm{cos}(2t) \end{aligned} \right. \end{aligned} \end{aligned}$$

(34)

According to [60], the existence of chaos in the fractional order Liu hyperchaotic systems (32) and (33) can be guaranteed if the fractional order q is set to 0.82. In our simulation, the fractional order is selected as $q=0.82$ and the initial conditions are chosen as $(x_{1}(0), x_{2}(0), x_{3}(0), x_{4}(0))$ $=(0.6, 0.7, 0.3, 0.4), (y_{1}(0),$

Fig. 1

Phase portraits of master system

Fig. 2

Phase portraits of slave system

$y_{2}(0), y_{3}(0), y_{4}(0))=(0.5, 0.5,$ 0.2, 0.5). The dynamics of the master and slave systems shows chaotic behavior, as shown in Figs. 1–2. The presented control scheme is applied to achieve synchronization and the controller parameters are selected as $\beta _{1}=\beta _{2}=10$, $\lambda _{1}=\lambda _{2}=10$, $p_{1}=p_{2}=5$, $q_{1}=q_{2}=9$, $n_{1}=n_{2}=5$, $m_{1}=m_{2}=9$, $\Delta _{1}=3.3$, $\Delta _{2}=3.2$, $\Delta _{3}=3.7$, $\Delta _{4}=4.1$ ($\Delta _{i}=\varepsilon _{i}+\mu _{i}+\gamma _{i}+\eta _{i}$ , $i=1,\ldots ,4$). The results are shown in Figs. 3, 4 and 5. As shown in Fig. 3, the system states of the slave system will track the trajectories of the master system within 0.16s and Fig. 4 shows that the synchronization error $e_{i}=y_{i}-x_{i}$ will converge to zero within 0.16s. According to theorem 3, the upper bound of convergence time can be estimated as $T<1.2079$. The results verify the effectiveness of the proposed control scheme and the correctness of the theoretical results. The curves of control input are given in Fig. 5. From Fig. 5, no harmful chattering is observed and the singularity problem has been overcome effectively.

Fig. 3

Time response of master system and slave system

Fig. 4

Time response of synchronization error

In order to demonstrate the superiority of the proposed control strategy, the proposed control scheme is compared with the existing terminal sliding mode control results. The control scheme proposed in [37] is borrowed as a typical example of the existing terminal sliding mode control schemes to make a comparison. To make a fair comparison, the simulated conditions for the two controllers are chosen to be the same. Both control schemes are employed to synchronize the fractional order hyperchaotic systems (32) and (33). Figure 6 compares the settling time of both control schemes under different initial synchronization errors. As shown in Fig. 6, the settling time of the control scheme proposed in [37] grows unboundedly as the initial synchronization errors grow, while the convergence time of the control scheme proposed in this paper is bounded by a constant with the increment of the initial synchronization errors. In addition, the control scheme proposed in this paper can synchronize the fractional order chaotic systems faster than the method presented in [37]. The results verify the superiority of the proposed control scheme in fractional order chaotic system synchronization.

Fig. 5

Curves of control input

Fig. 6

Convergence time versus the logarithm of norm of initial synchronization errors

5.2 Fixed-time synchronization between fractional order hyperchaotic Chen system and fractional order hyperchaotic Lorenz system

The proposed control scheme can also be applied to other fractional order hyperchaotic systems. In this case, we consider fixed-time synchronization of two different fractional order hyperchaotic systems. Let us consider fractional order Chen system (35) as master system and fractional order Lorenz system (36) as slave system.

Master system:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} D^{q}y_{1}&=a\left( y_{2}-y_{1}\right) +y_{4}+\Delta g_{1}(Y,t)+d_{1}^{g}(t)\\ D^{q}y_{2}&=by_{1}+cy_{2}-y_{1}y_{3}+\Delta g_{2}(Y,t)+d_{2}^{g}(t)\\ D^{q}y_{3}&=y_{1}y_{2}-dy_{3}+\Delta g_{3}(Y,t)+d_{3}^{g}(t)\\ D^{q}y_{4}&=y_{2}y_{3}+ry_{4}+\Delta g_{4}(Y,t)+d_{4}^{g}(t) \end{aligned} \right. \end{aligned} \end{aligned}$$

(35)

Slave system:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} D^{q}x_{1}&=a_{1}\left( x_{2}-x_{1}\right) +x_{4}+\Delta f_{1}(X,t)+d_{1}^{f}(t)\\ D^{q}x_{2}&=b_{1}x_{1}-x_{2}-x_{1}x_{3}+\Delta f_{2}(X,t)+d_{2}^{f}(t)\\ D^{q}x_{3}&=x_{1}x_{2}-c_{1}x_{3}+\Delta f_{3}(X,t)+d_{3}^{f}(t)\\ D^{q}x_{4}&=-x_{2}x_{3}-r_{1}x_{4}+\Delta f_{4}(X,t)+d_{4}^{f}(t) \end{aligned} \right. \end{aligned} \end{aligned}$$

(36)

The uncertainties and external disturbances are selected as (37). When the parameters for the systems are selected as $a=35$, $b=7$, $c=12$, $d=3$, $r=0.5$, $a_{1}=10$, $b_{1}=28$, $c_{1}=8/3$, $r_{1}=1$, $q=0.98$ and the initial conditions are chosen as $(x_{1}(0), x_{2}(0), x_{3}(0), x_{4}(0))=(2,-2,4,1)$, $(y_{1}(0), y_{2}(0), y_{3}(0), y_{4}(0))=(3,-4,2,2)$, master system (35) and slave system (36) show hyperchaotic behavior, which is shown in Figs. 7 and 8, respectively.

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&\Delta g_{1}(Y,t)=0.15\mathrm{cos}(6t)y_{1},\ d_{1}^{g}(t)=-0.2\mathrm{sin}(t),\\&\Delta g_{2}(Y,t)=-0.25\mathrm{cos}(2t)y_{2},\ d_{2}^{g}(t)=0.1\mathrm{sin}(3t),\\&\Delta g_{3}(Y,t)=0.1\mathrm{sin}(3t)y_{3},\ d_{3}^{g}(t)=0.2\mathrm{cos}(5t),\\&\Delta g_{4}(Y,t)=0,\ d_{4}^{g}(t)=-0.25\mathrm{cos}(t),\\&\Delta f_{1}(X,t)=-0.15\mathrm{sin}(4t)x_{1},\ d_{1}^{f}(t)=0.2\mathrm{sin}(7t),\\&\Delta f_{2}(X,t)=0.15\mathrm{cos}(t)x_{2},\ d_{2}^{f}(t)=0.1\mathrm{cos}(3t),\\&\Delta f_{3}(X,t)=0.15\mathrm{sin}(4t)x_{3},\ d_{3}^{f}(t)=-0.25\mathrm{sin}(5t),\\&\Delta f_{4}(X,t)=-0.25\mathrm{sin}(t)x_{4},\ d_{4}^{f}(t)=0.2\mathrm{cos}(2t) \end{aligned} \right. \end{aligned} \end{aligned}$$

(37)

The presented control scheme is applied to achieve synchronization, and the controller parameters are selected as $\beta _{1}=\beta _{2}=6$, $\lambda _{1}=\lambda _{2}=6$, $p_{1}=p_{2}=5$, $q_{1}=q_{2}=9$, $n_{1}=n_{2}=5$, $m_{1}=m_{2}=9$, $\Delta _{1}=6.65$, $\Delta _{2}=9.23$, $\Delta _{3}=9.27$, $\Delta _{4}=28.75$($\Delta _{i}=\varepsilon _{i}+\mu _{i}+\gamma _{i}+\eta _{i}$ , $i=1,\ldots ,4$). The results are shown in Figs. 9 and 10. As shown in Fig. 9, the system states of the slave system will track the trajectories of the master system within 0.5s and Fig. 10 shows that the synchronization error $e_{i}=y_{i}-x_{i}$ will converge to zero within 0.5s. According to Theorem 3, the upper bound of convergence time can be estimated as $T<2.0131$. The results verify the proposed control scheme can synchronize two different fractional order hyperchaotic systems within fixed-time.

Fig. 7

Hyperchaotic attractor of master system

Fig. 8

Hyperchaotic attractor of slave system

Fig. 9

Time response of master system and slave system

Fig. 10

Time response of synchronization error

5.3 Application to chaos suppression for fractional order power system

In this example, the proposed control scheme is applied to suppress chaotic oscillation in fractional order interconnected power system to demonstrate its effectiveness in the stabilization of fractional order chaotic systems. In power system, the occurrence of chaos can shrink the region of stability [61], lead to angle divergence and voltage collapse [62, 63], and even end up with a catastrophic blackout. Almost all the studies about chaotic dynamic of the power system, such as [64,65,66,67,68,69], are concerned with integer order model, and there is little literature reporting fractional order modeling and control design for the power system. However, fractional order modeling can give a more accurate description about actual physical and applied systems and the fractional order interconnected power system model shown in Fig. 11 can be described as:

$$\begin{aligned} \left\{ \begin{aligned}D^{q}\delta&=\omega \\ D^{q}\omega&=-\frac{1}{H}P_\mathrm{max}\mathrm{sin}(\delta ){-}\frac{D}{H}\omega {+}\frac{1}{H}P_{m}{+}\frac{1}{H}P_{e}\mathrm{cos}(\beta t) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(38)

Fig. 11

Single line diagram of interconnected power system: 1 and 2 denote equivalent generators; 3 and 4 represent transformers; 5, 6, and 7 are considered as circuit breakers and tie line between two areas, respectively; 8 is local load

Fig. 12

Phase portraits of the studied power system

where q is fractional order, $\delta =\delta _{1}-\delta _{2}$ and $\omega =\omega _{1}-\omega _{2}$ are relative angle and angular frequency between equivalent generators in two areas, H and D are rotational inertia and damping coefficient of equivalent generators; $P_{m}$ is the mechanical power of equivalent generators and $P_{e}$ is the amplitude of power disturbance. Denote $\alpha =P_\mathrm{max}/H$, $\gamma =D/H$, $\rho =P_{m}/H$, $\mu =P_{e}/H$ and the parameters value are selected as $\alpha =1$, $\gamma =0.02$, $\rho =0.2$, $\mu =0.2593$, $\beta =1$. The fractional order is selected as $q=0.98$ to ensure the existence of chaos in fractional order interconnected power system (38) [70]. The initial conditions are chosen as $(\delta (0),\omega (0))=(0.43,0.1)$, and the power system exhibits chaotic behavior as depicted in Figs. 12 and 13. Fig. 12 shows that the system is in chaotic state. As shown in Fig. 13, the power system experiences irregular and aperiodic morbid angle and frequency oscillation, which indicates that the synchronous generators lose synchronism and the power system undergoes severe frequency swings arising from power disturbance. Now, the power system is in extremis and it will result in catastrophic blackout if no effective measurement is taken to suppress chaos. The presented control scheme is carried out to suppress chaos in power system and the controlled power system can be described as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}D^{q}\delta&=\omega +u_{1} \\ D^{q}\omega&=-\frac{1}{H}P_\mathrm{max}\mathrm{sin}(\delta )-\frac{D}{H}\omega +\frac{1}{H}P_{m}\\&~~~+\frac{1}{H}P_{e}\mathrm{cos}(\beta t)+u_{2} \end{aligned} \right. \end{aligned} \end{aligned}$$

(39)

The controller parameters are selected to be $\beta _{1}=\beta _{2}=8$, $\lambda _{1}=\lambda _{2}=8$, $p_{1}=p_{2}=7$, $q_{1}=q_{2}=11$, $n_{1}=n_{2}=7$, $m_{1}=m_{2}=11$, $\Delta _{1}=0$, $\Delta _{2}=0.46$. The results are shown in Figs. 14 and 15. Figure 14 shows that the chaotic oscillation has been suppressed completely and the system states converge to zero within 0.28 s. According to Theorem 4, the upper bound of convergence time can be computed as $T<1.3376$. The results validate that the proposed control scheme can effectively suppress chaos in power system within fixed-time. Curves of control input are shown in Fig. 15. Fig. 15 shows that there is no harmful chattering in control input and singularity problem has been overcome effectively.

Fig. 13

Time response of the studied power system without control

For comparison, the terminal sliding mode control proposed in [37] is also implemented to stabilize the fractional order interconnected power system (38). The settling time of the control scheme proposed in this paper and the control scheme proposed in [37] under different initial stabilization errors is shown in Fig. 16. Fig. 16 shows that with the increment of initial stabilization errors, the settling time of the control scheme proposed in [37] grows unboundedly, while the convergence time of the control scheme proposed in this paper is bounded by a constant. In addition, the convergence time of the control scheme proposed in this paper is shorter than that of the method presented in [37]. The results verify the superiority of the proposed control scheme in fractional order chaotic system stabilization.

Fig. 14

Time response of the studied power system under proposed control

Fig. 15

Curves of control input

Fig. 16

Convergence time versus the logarithm of norm of initial stabilization errors

6 Discussion about the applications of the proposed scheme

Some other chaotic systems also exist in real world, such as neural network. In recent years, neural network has attracted great attention from researchers due to its wide applications in signal and image processing [71], automatic control [72], pattern recognition [73], and so on. Since Arena et al. [74] firstly investigated bifurcation and chaos in fractional order neural networks, many important and interesting results have been obtained for fractional order chaotic neural network. Besides, many chaotic systems have time delay. In this section, the application of the proposed scheme to the synchronization and stabilization of fractional order time-delayed chaotic neural network systems is taken as an example to demonstrate that the proposed scheme can be applied to other chaotic systems and time-delayed chaotic systems.

Consider a class of fractional order neural networks whose dynamics can be described by:

$$\begin{aligned} D^{\alpha }x_{i}(t)= & {} -d_{i}x_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}(x_{j}(t))\nonumber \\&+\sum _{j=1}^{N}b_{ij}g_{j}\left( x_{j}\left( t-\tau _{j}\right) \right) +I_{i} \end{aligned}$$

(40)

where $i={1,2,\ldots ,N}$, N is the number of neurons in neural network, $x_{i}$ is the state of the i-th neuron, $f_{j}(x_{j}(t))$ and $g_{j}(x_{j}(t-\tau _{j}))$ correspond to activation functions of the j-th neuron, $a_{ij}$ and $b_{ij}$ represent the connection weight and the time delay connection weight, respectively, $\tau _{j}$ denotes time delay along the axon of the j-th unit from the i-th unit, $d_{i}>0$ is the rate with which the i-th neuron will reset its potential to the resting state when disconnected from the network, $I_{i}$ is an external input. The initial condition for system (40) is $x_{i}(t)=\phi _{i}(t), t\in [-\tau ,0]$, where $\tau =\mathrm{max}\{\tau _{j}\}$.

In this paper, we consider system (40) as master system and the following system as slave system:

$$\begin{aligned} \begin{aligned} D^{\alpha }y_{i}(t)=&-d_{i}y_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}(y_{j}(t))\\&+\sum _{j=1}^{N}b_{ij}g_{j}\left( y_{j}\left( t-\tau _{j}\right) \right) +I_{i}+u_{i} \end{aligned} \end{aligned}$$

(41)

where $u_{i}$ is control input and the meanings of other parameters are the same as system (40). The initial condition for system (41) is $y_{i}(t)=\psi _{i}(t), t\in [-\tau ,0]$, where $\tau =\mathrm{max}\{\tau _{j}\}$.

In order to achieve fixed-time chaos synchronization, we need the following assumption for delayed systems (40) and (41).

Assumption 3

The activation functions $f_{j}$ and $g_{j}$ satisfy Lipschitz conditions, that is, there exist positive constants $L_{j}$ and $N_{j}$, such that $|f_{j}(x_{j})-f_{j}(y_{j})|\le L_{j}|x_{j}-y_{j}|$, $|g_{j}(x_{j})-g_{j}(y_{j})|\le N_{j}|x_{j}-y_{j}|$.

Denote synchronization error $e_{i}=y_{i}-x_{i}$ and its dynamics can be expressed as:

$$\begin{aligned} D^{\alpha }e_{i}(t)= & {} -d_{i}e_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}\left( e_{j}(t)\right) \nonumber \\&+\sum _{j=1}^{N}b_{ij}g_{j}\left( e_{j}\left( t-\tau _{j}\right) \right) +u_{i} \end{aligned}$$

(42)

where $f_{j}(e_{j}(t))=f_{j}(y_{j})-f_{j}(x_{j})$, $g_{j}(e_{j}(t-\tau _{j}))=g_{j}(y_{j}(t-\tau _{j}))-g_{j}(x_{j}(t-\tau _{j}))$.

The sliding surface can be constructed as:

$$\begin{aligned} s_{i}=D^{\alpha -1}e_{i}+D^{\alpha -2}(\beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}})\nonumber \\ \end{aligned}$$

(43)

where $\beta _{1}$, $\lambda _{1}$ are positive constants, $m_{1}, n_{1}, p_{1}, q_{1}$ are positive odd integers that satisfy $m_{1}>n_{1}$, $p_{1}<q_{1}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

The control input can be designed as:

$$\begin{aligned} u_{i}= & {} -\eta _{i}\mathrm{sign}\left( s_{i}(t)\right) \left| e_{i}\right| -\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}\nonumber \\&-\,\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}\nonumber \\&-\,D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \nonumber \\&-\,\delta _{i}\mathrm{sign}\left( s_{i}(t)\right) \left| e_{i}\left( t-\tau _{i}\right) \right| \end{aligned}$$

(44)

where $\beta _{2}, \lambda _{2}$ are positive constants, $\eta _{i}$ and $\delta _{i}$ are positive constants determined later, $m_{2}, n_{2}, p_{2}, q_{2}$ are positive odd integers that satisfy $m_{2}>n_{2}$, $p_{2}<q_{2}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

Theorem 5

Consider the synchronization error system (42) under Assumption 3. If this system is controlled under control input (44), its trajectories will converge to the sliding surface (43) within finite time upper bounded by:

$$\begin{aligned} T_{3}<\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}} \end{aligned}$$

(45)

Proof

Consider the following Lyapunov function candidate:

$$\begin{aligned} V_{3}=\sum _{i=1}^{N}\left| s_{i}\right| \end{aligned}$$

(46)

The time derivative of Lyapunov function $V_{3}(t)$ can be derived as:

$$\begin{aligned} \dot{V_{3}}= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \dot{s_{i}}\nonumber \\= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) (D^{\alpha }e_{i}+D^{\alpha -1}(\beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}\nonumber \\&+\,\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}})) \end{aligned}$$

(47)

Substituting error system dynamics (42) and control input (44) into (47), one has:

$$\begin{aligned} \dot{V_{3}}= & {} \sum _{i=1}^{N}\mathrm{sign}\left( s_{i}\right) \left( -d_{i}e_{i}+\sum _{j=1}^{N}a_{ij}f_{j}\left( e_{j}(t)\right) \right. \nonumber \\&+\sum _{j=1}^{N}b_{ij}g_{j}\left( e_{j}\left( t-\tau _{j}\right) \right) +u_{i}\nonumber \\&\left. +\,D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \right) \nonumber \\= & {} -\sum _{i=1}^{N}d_{i}e_{i}\mathrm{sign}\left( s_{i}\right) +\sum _{i=1}^{N}\sum _{j=1}^{N}a_{ij}f_{j}\left( e_{j}(t)\right) \mathrm{sign}\left( s_{i}\right) \nonumber \\&+\sum _{i=1}^{N}\sum _{j=1}^{N}b_{ij}g_{j}\left( e_{j}\left( t-\tau _{j}\right) \right) \mathrm{sign}\left( s_{i}\right) -\sum _{i=1}^{N}\eta _{i}\left| e_{i}\right| \nonumber \\&-\,\sum _{i=1}^{N}\beta _{2}\left| s_{i}\right| ^{m_{2}/n_{2}}-\sum _{i=1}^{N}\lambda _{2}\left| s_{i}\right| ^{p_{2}/q_{2}}\nonumber \\&-\,\sum _{i=1}^{N}\delta _{i}\left| e_{i}\left( t-\tau _{i}\right) \right| \end{aligned}$$

(48)

Employing Assumption 3, (48) becomes:

$$\begin{aligned} \dot{V_{3}}\le & {} \sum _{i=1}^{N}d_{i}\left| e_{i}\right| +\sum _{i=1}^{N}\sum _{j=1}^{N}\left| a_{ij}\right| L_{j}\left| e_{j}(t)\right| \nonumber \\&+\sum _{i=1}^{N}\sum _{j=1}^{N}\left| b_{ij}\right| N_{j}\left| e_{j}\left( t-\tau _{j}\right) \right| -\sum _{i=1}^{N}\eta _{i}\left| e_{i}\right| \nonumber \\&-\sum _{i=1}^{N}\beta _{2}\left| s_{i}\right| ^{m_{2}/n_{2}}-\sum _{i=1}^{N}\lambda _{2}\left| s_{i}\right| ^{p_{2}/q_{2}}\nonumber \\&-\sum _{i=1}^{N}\delta _{i}\left| e_{i}\left( t-\tau _{i}\right) \right| \nonumber \\= & {} -\sum _{i=1}^{N}(\eta _{i}-d_{i}-\sum _{j=1}^{N}\left| a_{ji}\right| L_{i})\left| e_{i}(t)\right| \nonumber \\&-\sum _{i=1}^{N}\beta _{2}\left| s_{i}\right| ^{m_{2}/n_{2}}\nonumber \\&-\sum _{i=1}^{N}\left( \delta _{i}-\sum _{j=1}^{N}\left| b_{ji}\right| N_{i}\right) \left| e_{i}\left( t-\tau _{i}\right) \right| \nonumber \\&-\sum _{i=1}^{N}\lambda _{2}\left| s_{i}\right| ^{p_{2}/q_{2}} \end{aligned}$$

(49)

Choosing $\eta _{i}\ge d_{i}+\sum _{j=1}^{N}|a_{ji}|L_{i}$ and $\delta _{i}\ge \sum _{j=1}^{N}|b_{ji}|N_{i}$, and using Lemmas 3–4, we have

$$\begin{aligned} \begin{aligned} \dot{V_{3}}&\le \sum _{i=1}^{N}-\beta _{2}\left| s_{i}\right| ^{m_{2}/n_{2}}-\lambda _{2}\left| s_{i}\right| ^{p_{2}/q_{2}}\\&\le -N^{1-m_{2}/n_{2}}\beta _{2}\left( \sum _{i=1}^{N}\left| s_{i}\right| \right) ^{m_{2}/n_{2}}\\&\,\quad -\lambda _{2}\left( \sum _{i=1}^{N}\left| s_{i}\right| \right) ^{p_{2}/q_{2}}\\&=-N^{1-m_{2}/n_{2}}\beta _{2}V_{3}^{m_{2}/n_{2}}-\lambda _{2}V_{3}^{p_{2}/q_{2}} \end{aligned} \end{aligned}$$

(50)

Therefore, according to Lemma 1, the system states will converge to the sliding surface asymptotically. Furthermore, based on Lemma 2, we can prove fixed-time convergence and the convergence time is upper bounded by (45). The proof is completed. $\square$

When the error state is on the sliding surface, its dynamics satisfies:

$$\begin{aligned} D^{\alpha -1}e_{i}{=}-D^{\alpha -2}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}{+}\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \nonumber \\ \end{aligned}$$

(51)

Theorem 6

Consider the sliding mode dynamics (51). The error state variables will converge to the origin within finite time upper bounded by:

$$\begin{aligned} T_{4}<\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned}$$

(52)

Proof

Similar to the proof process of Theorem 2, we can prove Theorem 6 hold and detailed proof process is omitted here. $\square$s

From Theorems 5 and 6, we have the following result:

Theorem 7

For the synchronization error system (42) under Assumption 3, if the control input is designed as (44), the error system will converge to zero within finite time upper bounded by:

$$\begin{aligned} \begin{aligned} T<&\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}}\\&+\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned} \end{aligned}$$

(53)

The proposed control scheme is extended to address fixed-time fractional order chaotic neural network system stabilization problem. Suppose $y_{i}^{*}$ is an equilibrium point of system (41). Denote the stabilization error $e_{i}=y_{i}(t)-y_{i}^{*}$ and its dynamics satisfies:

$$\begin{aligned} \begin{aligned} D^{\alpha }e_{i}(t)=&-d_{i}e_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}(e_{j}(t))\\&+\sum _{j=1}^{N}b_{ij}g_{j}\left( e_{j}\left( t-\tau _{j}\right) \right) +u_{i} \end{aligned} \end{aligned}$$

(54)

where $f_{j}(e_{j}(t))=f_{j}(y_{j})-f_{j}(y_{j}^{*})$, $g_{j}(e_{j}(t-\tau _{j}))=g_{j}(y_{j}(t-\tau _{j}))-g_{j}(y_{j}^{*})$.

Construct the sliding surface (43) and the controller can be designed as:

$$\begin{aligned} \begin{aligned} u_{i}=&-\eta _{i}\mathrm{sign}\left( s_{i}(t)\right) \left| e_{i}\right| -\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}\\&-\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}\\&-D^{\alpha -1}(\beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}})\\&-\delta _{i}\mathrm{sign}\left( s_{i}(t)\right) \left| e_{i}\left( t-\tau _{i}\right) \right| \end{aligned} \end{aligned}$$

(55)

where $\beta _{2}, \lambda _{2}$ are positive constants, $\eta _{i}$ and $\delta _{i}$ are positive constants that satisfy $\eta _{i}\ge d_{i}+\sum _{j=1}^{N}|a_{ji}|L_{i}$ and $\delta _{i}\ge \sum _{j=1}^{N}|b_{ji}|N_{i}$, $m_{2}, n_{2}, p_{2}, q_{2}$ are positive odd integers that satisfy $m_{2}>n_{2}$, $p_{2}<q_{2}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

Similar to Theorem 4 and Theorem 7, we have the following result.

Theorem 8

Consider the stabilization problem of the fractional order chaotic neural network system (41) under Assumption 3. If the system (41) is controlled by control law (55), then the system can be stabilized within finite time upper bounded by:

$$\begin{aligned} \begin{aligned} T<&\frac{1}{N^{1-m_{2}/n_{2}}\beta _{2}}\frac{n_{2}}{m_{2}-n_{2}}+\frac{1}{\lambda _{2}}\frac{q_{2}}{q_{2}-p_{2}}\\&+\frac{1}{N^{1-m_{1}/n_{1}}\beta _{1}}\frac{n_{1}}{m_{1}-n_{1}}+\frac{1}{\lambda _{1}}\frac{q_{1}}{q_{1}-p_{1}} \end{aligned} \end{aligned}$$

(56)

Remark 10

If the time-varying delay strength $b_{ij}=0$, mater system (40) and slave system (41) become fractional order neural networks without time delay and can be described as:

$$\begin{aligned} D^{\alpha }x_{i}(t)= & {} -d_{i}x_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}\left( x_{j}(t)\right) +I_{i} \end{aligned}$$

(57)

$$\begin{aligned} D^{\alpha }y_{i}(t)= & {} -d_{i}y_{i}(t)+\sum _{j=1}^{N}a_{ij}f_{j}\left( y_{j}(t)\right) +I_{i}+u_{i}\nonumber \\ \end{aligned}$$

(58)

Construct sliding surface (43) and the controller can be designed as:

$$\begin{aligned} u_{i}= & {} -\eta _{i}\mathrm{sign}\left( s_{i}(t)\right) \left| e_{i}\right| -\beta _{2}\mathrm{sig}\left( s_{i}\right) ^{m_{2}/n_{2}}\nonumber \\&-\,\lambda _{2}\mathrm{sig}\left( s_{i}\right) ^{p_{2}/q_{2}}\nonumber \\&-\,D^{\alpha -1}\left( \beta _{1}\mathrm{sig}\left( e_{i}\right) ^{m_{1}/n_{1}}+\lambda _{1}\mathrm{sig}\left( e_{i}\right) ^{p_{1}/q_{1}}\right) \end{aligned}$$

(59)

where $\beta _{2}, \lambda _{2}$ are positive constants, $\eta _{i}$ is a positive constant that satisfies $\eta _{i}\ge d_{i}+\sum _{j=1}^{N}|a_{ji}|L_{i}$, $m_{2}, n_{2}, p_{2}, q_{2}$ are positive odd integers that satisfy $m_{2}>n_{2}$, $p_{2}<q_{2}$, $\mathrm{sig}(\cdot )^{\alpha }=|\cdot |^{\alpha }\mathrm{sign}(\cdot )$, and $\mathrm{sign}(\cdot )$ is signum function.

Fig. 17

Phase portraits of master system

Control input (59) can achieve fixed-time synchronization for systems (57) and (58) and fixed-time stabilization for system (58). Moreover, $e_{i}=y_{i}-x_{i}$ for synchronization and $e_{i}=y_{i}-y_{i}^{*}$ for stabilization.

Remark 11

Information about the neuron states is required to design control input (44), (55) and (59). However, for most cases, only partial information about neuron states of large scale neural networks can be obtained. Fortunately, references [75] and [76] provide state estimators to estimate the neuron states through available measurements.

Numerical simulations are conducted to verify the effectiveness of the proposed scheme. In our simulation, fractional order Hopfield neural networks are considered and the system parameters are selected as $d_{1}=d_{2}=1$, $a_{11}=2$, $a_{12}=0.3$, $a_{21}=5$, $a_{22}=3$, $b_{11}=-2$, $b_{12}=0.2$, $b_{21}=0.3$, $b_{22}=-2.5$, $I_{1}=I_{2}=0$, $\tau _{1}=\tau _{2}=1$, $f_{j}(x_{j})=g_{j}(x_{j})={ tanh}(x_{j})$. It is not difficult to check that Assumption 3 holds with $L_{j}=N_{j}=1$. If the fractional order $\alpha$ is set to 0.92 and the initial conditions are chosen as $(x_{1}(s),x_{2}(s))=(0.4,0.6)$, for $s\in [-1,0]$ and $(y_{1}(s),y_{2}(s))=(-0.4,-2)$, for $s\in [-1,0]$, master system (40) and slave system (41) exhibit chaotic behavior, which is shown in Figs. 17 and 18, respectively. The proposed scheme is applied to synchronize fractional order chaotic neural networks (40) and (41). The controller parameters are selected as $\eta _{1}=8$, $\eta _{2}=4.3$, $\beta _{1}=\beta _{2}=12$, $\lambda _{1}=\lambda _{2}=12$, $p_{1}=p_{2}=5$, $q_{1}=q_{2}=9$, $n_{1}=n_{2}=5$, $m_{1}=m_{2}=9$, $\delta _{1}=2.3$ and $\delta _{2}=2.7$. Time response of system (40) and system (41) under control input (44) are presented in Fig. 19. As shown in Fig. 19, the system states of the slave system will track the trajectories of the master system within 0.18 s. Next, the proposed scheme is applied to stabilize fractional order chaotic neural network (41) with the same controller parameters and the results are shown in Fig. 20. Fig. 20 shows that the system will stabilize to its equilibrium point $(y_{1}^{*},y_{2}^{*})=(0,0)$ within 0.16 s. All the results verify the effectiveness of the proposed scheme in synchronization and stabilization of fractional order chaotic neural networks with time delay.

Fig. 18

Phase portraits of slave system

Fig. 19

Time response of master system and slave system under control input (44)

Fig. 20

Time response of system (41) under control input (55)

7 Conclusion

In this paper, fractional order fixed-time nonsingular terminal sliding mode control scheme is proposed to stabilize and synchronize fractional order chaotic systems with uncertainties and external disturbances. A novel fractional order terminal sliding surface is first proposed to guarantee fixed-time convergence of system states along the sliding surface, and then, a nonsingular terminal sliding mode control is designed to force the system state to reach the sliding surface within fixed-time and remain on it forever. The fixed-time stability and robustness of the proposed control scheme are proved using fractional Lyapunov stability theory, and the upper bound of convergence time is also estimated. Finally, the simulation results confirm the estimated convergence time bound and demonstrate that the proposed control scheme can achieve chaos synchronization and suppress chaotic oscillation in fractional order power system within fixed-time. It is worth noting that the proposed control scheme can be extended to synchronize and stabilize other chaotic systems and time-delayed chaotic systems.