1 Introduction

Internet refers to the current world’s largest, open and specific Internet connected by many networks, which has developed into the world’s largest computer network covering the whole world. With the rapid development of society, the Internet has been widely applied in various areas such as economics, industry, agriculture, medical and health care, and information processing. We can say that the competition of all aspects of life in the future depends on the Internet to a great extent. Over the past several decades, many competitive web site models of the Internet and some phenomena related to World Wide Web have emerged up. For example, Smith et al. [1] referred to the electronic delivery of web pages. Brynjolfsson and Smith [2] investigated the comparison issue of Internet and conventional retailers, Bakos and Brynjolfsson [3] discussed the bundling and competition on the Internet, Varian [4] analyzed the versioning information goods. In detail, we refer the readers to [5,6,7,8,9, 58,59,60,61,62,63]. The emergence of the Internet brings out great changes in our daily economic life. Thus, the maintenance of web site can provide better information to user to make plans for the future. Therefore, the research on competitive web site models has important theoretical value and practical significance.

Based on the Lotka–Volterra competition systems, the competitive web site model can be described as follows:

$$\begin{aligned} \frac{\mathrm{d}u_i(t)}{\mathrm{d}t}=u_i(t)\left( a_ib_i-a_iu_i(t)-\sum _{i\ne j}c_{ij}u_j\right) , \end{aligned}$$
(1.1)

where \(u_i\) is the fraction of the market which is a customer of site i, \(a_i\ge 0\) is the growth rate which measures the capacity of site i to grow, \(b_i\in [0,1]\) is the maximum capacity which is related to the saturation value of \(u_i\) (the maximum value \(u_i\) can reach) and \(c_{ij}\ge 0\) is the competition rate between sites i and j. For the sake of simplicity, we assume that \(b_i=1\). If we assume that the market has three competitors, then system (1.1) takes the following form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \dot{u}_1(t)=u_1(t)\left[ a_1-a_1u_1(t)-c_{12}u_2(t)-c_{13}u_3(t)\right] ,\\ \displaystyle \dot{u}_2(t)=u_2(t)\left[ a_2-a_2u_2(t)-c_{21}u_1(t)-c_{23}u_3(t)\right] ,\\ \displaystyle \dot{u}_3(t)=u_3(t)\left[ a_3-a_3u_3(t)-c_{31}u_1(t)-c_{32}u_2(t)\right] . \end{array}\right. \nonumber \\ \end{aligned}$$
(1.2)

Considering that the first web site has self-feedback time delay and for the simplification, Xiao and Cao [10] assumed that \(a_1=a_2=a_3=a, c_{12}=c_{13}=c_{21}=c_{23}=c_{31}=c_{32}=c\) and obtained the following delayed competitive web site model:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle \dot{u}_1(t)=u_1(t)\left[ a-au_1(t-\varrho )-cu_2(t)-cu_3(t)\right] ,\\ \displaystyle \dot{u}_2(t)=u_2(t)\left[ a-au_2(t)-cu_1(t)-cu_3(t)\right] ,\\ \displaystyle \dot{u}_3(t)=u_3(t)\left[ a-au_3(t)-cu_1(t)-cu_2(t)\right] , \end{array}\right. \nonumber \\ \end{aligned}$$
(1.3)

where \(\varrho \) is time delay. By regarding the time delay \(\varrho \) as bifurcation parameter, Xiao and Cao [10] considered the stability and the existence of Hopf bifurcation of (1.3). Applying the normal form theorem and center manifold reduction, the direction, the stability and the period of bifurcating periodic solutions are determined.

During the past few decades, fractional calculus, which is a generalization of traditional ordinary differentiation and integration to random order (non-integer) [11,12,13,14,15,16,17,18,19], has attracted much attention by numerous scholars due to its potential applications in various disciplines such as electroanalytical chemistry, viscoelasticity, robotics, bioengineering, and control and medicine issues [20, 51,52,53,54,55,56,57]. Moreover, a good deal of phenomena in objective world can be modeled by fractional-order differential equations since fractional-order differential equations have memory and hereditary properties of various materials and processes. So it is more reasonable to establish the fractional-order differential equations to describe the practical problems.

Hopf bifurcation and its control issue are important dynamical behavior of delayed differential equations (integer-order and fractional-order). During the past several decades, Hopf bifurcation phenomena of integer-order delayed differential equations have been widely investigated. But the research on the Hopf bifurcation of fractional-order differential equations is rare. Based on these considerations, Zhao et al. [21] established the following fractional-order delayed competitive web site model:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^{p_1}{u}_1(t)=u_1(t)\left[ a-au_1(t-\varrho )-cu_2(t)-cu_3(t)\right] ,\\ \displaystyle D^{p_2}{u}_2(t)=u_2(t)\left[ a-au_2(t)-cu_1(t)-cu_3(t)\right] ,\\ \displaystyle D^{p_3}{u}_3(t)=u_3(t)\left[ a-au_3(t)-cu_1(t)-cu_2(t)\right] , \end{array}\right. \nonumber \\ \end{aligned}$$
(1.4)

where \(p_i\in (0,1] (i=1,2,3)\). By choosing the time delay as bifurcation parameter, Zhao et al. [21] considered the stability and the existence of Hopf bifurcation of (1.4). Meanwhile, they investigated the bifurcation control issue of Hopf bifurcation of (1.4) by applying the nonlinear time delay feedback control method.

Here we would like to mention that in real Internet, customers of different web sites have time lag due to the finite reaction times and propagation speeds of signals. This case occurs in many web sites such as Baidu net and Sina net. Thus, different customers of the same site have self-feedback time delay. So we introduce the following fractional-order delayed competitive web site model:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^{p_1}{u}_1(t)=u_1(t)\left[ a_1-a_1u_1(t-\varrho )-c_{12}u_2(t)-c_{13}u_3(t)\right] ,\\ \displaystyle D^{p_2}{u}_2(t)=u_2(t)\left[ a_2-a_2u_2(t-\varrho )-c_{21}u_1(t)-c_{23}u_3(t)\right] ,\\ \displaystyle D^{p_3}{u}_3(t)=u_3(t)\left[ a_3-a_3u_3(t-\varrho )-c_{31}u_1(t)-c_{32}u_2(t)\right] . \end{array}\right. \nonumber \\ \end{aligned}$$
(1.5)

where \(p_i\in (0,1] (i=1,2,3)\). All other coefficients have the same meaning as those in (1.2). Different from the work of Zhao et al. [21], the characteristic equation of model (1.5) which has three delays is more complex, and the time delay feedback technique is more simple than those in Zhao et al. [21].

The advantage of the new model (1.5) mainly lies in the following two aspects: (i) model (1.5) is more realistic than (1.4) due to the fact that it considers that the three web sites have self-feedback delays; (ii) model (1.5) reveals the memory and hereditary properties of all variables of web sites and it can better reflect the real situation of the operation process of web sites.

The key objective of this article is to consider two problems: (1) the stability and the existence of Hopf bifurcation of system (1.5) and (2) applying the time delay feedback control method to control bifurcation of system (1.5). In addition, we point out that fractional-order delayed competitive web site model can characterize the memory and hereditary properties of web site activities and the research on Hopf bifurcation can help site maintainers handle their business strategies.

In order to establish our results, we make the following assumption:

(P1) The following inequality

$$\begin{aligned} \det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] \ne 0 \end{aligned}$$

holds.

The highlights of this paper include the following aspects:

  • We generalize integer-order delayed competitive web site model to new fractional-order version.

  • A set of sufficient conditions to ensure the stability and the existence of Hopf bifurcation of fractional-order delayed competitive web site model are established. The study shows that the delay and fractional order have an important effect on the stability and the existence of Hopf bifurcation of involved systems.

  • To the best of our knowledge, few authors have dealt with the Hopf bifurcation of fractional-order delayed competitive web site model. The theoretical findings of this article will be an enrichment and development to Hopf bifurcation theory of fractional-order delayed differential equations and complete the previous publications.

  • The method of this article will provide a good reference to investigate some other fractional-order delayed differential models.

The remainder of this article is planned as follows: In Sect. 2, several vital notations and elementary results on fractional calculus are prepared. In Sect. 3, the sufficient criteria to ensure the stability and the existence of Hopf bifurcation of considered system are presented. In Sect. 4, Hopf bifurcation is controlled by applying the linear time delay feedback approach. Two examples with their numerical simulations are given to illustrate the obtained main results in Sect. 5. Finally, a simple conclusion is presented.

Remark 1.1

Since the Caputo fractional-order derivative only requires initial conditions given in terms of inter-order derivatives which represent well-understand nature of physical situations. Then it can better characterize the real-world problems. Thus, we adopt the Caputo fractional-order derivative in this paper.

2 Preliminary results

In this segment, some basic definitions and lemmas of fractional calculus are listed.

Definition 2.1

[22] The fractional integral of order \(\sigma \) for a function \(g(\eta )\) is defined as follows:

$$\begin{aligned} I^\sigma g(\eta )=\frac{1}{\Gamma (\sigma )} \int _{\eta _0}^{\eta }(\eta -s)^{\sigma -1}g(s)\mathrm{d}s, \end{aligned}$$

where \(\eta \ge \eta _0, \sigma >0, \Gamma (.)\) denotes the Gamma function \(\Gamma (s)=\int _0^\infty \eta ^{s-1}e^{-\eta }d\eta .\)

Definition 2.2

[22] The Caputo fractional-order derivative of order \(\sigma \) for a function \(g(\eta )\in ([\eta _0,\infty ),R)\) is defined as follows:

$$\begin{aligned} D^\sigma g(\eta )=\frac{1}{\Gamma (n-\sigma )} \int _{\eta _0}^{\eta }\frac{ g^{(n)}(s)}{(\eta -s)^{\sigma -n+1}}\mathrm{d}s, \end{aligned}$$

where \(\eta \ge \eta _0\) and n is a positive integer such that \(n-1\le \sigma <n.\) In particular, when \(0<\sigma <1\),

$$\begin{aligned} D^\sigma g(\eta )=\frac{1}{\Gamma (1-\sigma )} \int _{\eta _0}^{\eta }\frac{ g^{'}(s)}{(\eta -s)^{\sigma }}\mathrm{d}s. \end{aligned}$$

Lemma 2.1

[23] Consider the following autonomous system \(D^\sigma u=Au, u(0)=u_0\) where \(0<\sigma <1, u\in R^n, A\in R^{n\times n}.\) Let \(\lambda _i(i=1,2,\ldots ,n)\) be the root of the characteristic equation of \(D^\sigma u=Au\). Then system \(D^\sigma u=Au\) is asymptotically stable if and only if \(|\text{ arg }(\lambda _i)| >\frac{\sigma \pi }{2} (i=1,2,\ldots ,n)\). In this case, each component of the states decays toward 0 like \(t^{-\sigma }\). Also, this system is stable if and only if \(|\text{ arg }(\lambda _i)| >\frac{\sigma \pi }{2} (i=1,2,\ldots ,n)\) and those critical eigenvalues that satisfy \(|\text{ arg }(\lambda _i)| =\frac{\sigma \pi }{2} (i=1,2,\ldots ,n)\) have geometric multiplicity one.

Lemma 2.2

[11] For the given fractional-order delayed differential equation with Caputo derivative: \(D^\sigma v(t)=C_1v(t)+C_2v(t-\tau )\), where \(v(t)=\phi (t), t\in [-\tau ,0], \sigma \in (0,1], v\in R^n, C_1,C_2\in R^{n\times n}, \tau \in R^{+(n\times n)}\). Then, the characteristic equation of the system is \(\det |s^\sigma I-C_1-C_2e^{-s\tau }|=0.\) If all the roots of the characteristic equation of the system have negative real roots; then, the zero solution of the system is asymptotically stable.

3 Stability and Hopf bifurcation for fractional-order delayed model (1.5)

In this segment, we will investigate the stability and the existence of Hopf bifurcation for model (1.5). Under the condition (P1), system (1.5) has a unique equilibrium point \(u^*=(u_{1}^*, u_{2}^*, u_{3}^*)\), where

$$\begin{aligned} u_{1}^*= & {} \frac{ \det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }{\det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }, \nonumber \\ u_{2}^*= & {} \frac{ \det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }{ \det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }, \nonumber \\ u_{3}^*= & {} \frac{\det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }{ \det \left[ \begin{array}{ccc} a_1 &{} c_{12} &{} c_{13} \\ c_{21} &{} a_2 &{} c_{23} \\ c_{31} &{} c_{32} &{} a_3 \\ \end{array} \right] }. \end{aligned}$$
(3.1)

The linearization of system (1.5) near the equilibrium point \(u^*=(u_{1}^*, u_{2}^*, u_{3}^*)\) takes the form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^{p_1}{u}_1(t)=-u_1^*c_{12}u_2(t)-u_1^*c_{13}u_3(t)-u_1^*a_1u_1(t-\varrho ),\\ \displaystyle D^{p_2}{u}_2(t)=-u_2^*c_{21}u_1(t)-u_2^*c_{23}u_3(t)-u_2^*a_2u_2(t-\varrho ),\\ \displaystyle D^{p_3}{u}_3(t)=-u_3^*c_{31}u_1(t)-u_3^*c_{32}u_2(t)-u_3^*a_3u_3(t-\varrho ). \end{array}\right. \nonumber \\ \end{aligned}$$
(3.2)

The characteristic equation of (3.2) is

$$\begin{aligned} \det \left[ \begin{array}{ccc} s^{p_1}+u_1^*a_1e^{-s\varrho } &{} u_1^*c_{12} &{} u_1^*c_{13} \\ u_2^*c_{21} &{} s^{p_2}+u_2^*a_2e^{-s\varrho } &{} u_2^*c_{23} \\ u_3^*c_{31} &{} u_3^*c_{32} &{} s^{p_3}+u_3^*a_3e^{-s\varrho } \\ \end{array} \right] =0\nonumber \\ \end{aligned}$$
(3.3)

which leads to

$$\begin{aligned} B_0(s)e^{-3s\varrho }+B_1(s)e^{-2s\varrho }{+}B_2(s)e^{-s\varrho }+B_3(s){=}0,\nonumber \\ \end{aligned}$$
(3.4)

where \(B_0(s),B_1(s),B_2(s),B_3(s)\) can be seen in “Appendix A”. Multiplying \(e^{s\varrho }\) on both sides of (3.4), we get

$$\begin{aligned} B_0e^{-2s\varrho }+B_1(s)e^{-s\varrho }+B_2(s)+B_3(s)e^{s\varrho }=0.\nonumber \\ \end{aligned}$$
(3.5)

Let \(s=i\theta =\theta \left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2}\right) (\theta >0)\) be a root of (3.5). Then

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle B_0\cos 2\theta \varrho +(B_{1R}(\theta )+B_{3R}(\theta ))\cos \theta \varrho +(B_{1I}(\theta )\\ \quad -B_{3I}(\theta ))\sin \theta \varrho +B_{2R}(\theta )=0,\\ \displaystyle B_0\sin 2\theta \varrho -(B_{1I}(\theta )+B_{3I}(\theta ))\cos \theta \varrho +(B_{1R}(\theta )\\ \quad -B_{3R}(\theta ))\sin \theta \varrho -B_{2I}(\theta )=0, \end{array}\right. \nonumber \\ \end{aligned}$$
(3.6)

where \(B_{iR}(\theta ), B_{iI}(\theta )(i=1,2,3)\) are the real parts and the imaginary parts of \(B_i(i\theta )\) (see “Appendix B”). In view of \(\sin \theta \varrho =\pm \sqrt{1-\cos ^2\theta \varrho }\), it follows from the first equation of (3.6) that

$$\begin{aligned}&2B_0\cos ^2\theta \varrho +(B_{1R}(\theta )+B_{3R}(\theta ))\cos \theta \varrho \pm (B_{1I}(\theta ) \nonumber \\&\quad -\,B_{3I}(\theta ))\sqrt{1-\cos ^2\theta \varrho }+B_{2R}(\theta )-B_0=0\nonumber \\ \end{aligned}$$
(3.7)

which leads to

$$\begin{aligned}&\alpha _4\cos ^4\theta \varrho +\alpha _3\cos ^3\theta \varrho \nonumber \\&\quad +\,\alpha _2\cos ^2\theta \varrho +\alpha _1\cos \theta \varrho +\alpha _0=0, \end{aligned}$$
(3.8)

where \(\alpha _i(i=0,1,2,3,4,5)\) can be seen in “Appendix C”.

We suppose that (3.8) has roots; then, we can get the expression of \(\cos \theta \varrho \). Assume that \(\cos \theta \varrho =g_1(\theta )\), where \(g_1(\theta )\) is a continuous function with respect to \(\theta \). By the first equation of (3.6), we can easily get the expression \(\sin \theta \varrho \), say \(\sin \theta \varrho =g_2(\theta )\), where \(g_2(\theta )\) is a continuous function with respect to \(\theta \). Then

$$\begin{aligned} g_1^2(\theta )+g_2^2(\theta )=1. \end{aligned}$$
(3.9)

In view of \(\cos \theta \varrho =g_1(\theta )\), we have

$$\begin{aligned} \varrho ^{(j)}=\frac{1}{\theta }[\arccos g_1(\theta )+2j\pi ],\quad j=0,1,2,\ldots .\nonumber \\ \end{aligned}$$
(3.10)

Suppose that (3.9) has at least one positive real root. Let

$$\begin{aligned} \varrho _0=\min \{\varrho ^{(j)}\}, \quad j=0,1,2,\ldots , \theta _0=\theta |_{\varrho =\varrho _0}.\nonumber \\ \end{aligned}$$
(3.11)

In order to establish the main results of this article, we give a necessary assumption as follows:

  1. (P2)

    \(\beta _0>0, \beta _2\beta _1-\beta _0>0\), where \(\beta _i(i=0,1,2)\) can be seen in “Appendix D”.

  2. (P3)

    \(G_1H_1+G_2H_2>0,\) where \(G_i, H_i(i=1,2)\) can be seen in “Appendix E”.

Lemma 3.1

If \(\varrho =0\) and (P2) is satisfied, then system (1.5) is asymptotically stable.

Proof

If \(\varrho =0\), then (3.5) takes the form:

$$\begin{aligned} \lambda ^{3}+\beta _2\lambda ^2+\beta _1\lambda +\beta _0=0. \end{aligned}$$
(3.12)

It follows from (P2) that all the roots \(\lambda _i\) of (3.12) satisfy \(|\text{ arg }(\lambda _i)|>\frac{p_i\pi }{2} (i=1,2,3)\). By Lemma 2.2, we can conclude that system (1.5) with \(\varrho =0\) is asymptotically stable. This ends the proof of Lemma 3.1. \(\square \)

Lemma 3.2

Let \(s(\varrho )=\mu (\varrho )+i\theta (\varrho )\) be the root of (3.5) at \(\varrho =\varrho _0\) satisfying \( \mu (\varrho _0)=0, \theta (\varrho _0)=\theta _{0}\), then \(Re\left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] \Big |_{\varrho =\varrho _{0}, \theta =\theta _{0}}>0\).

Proof

Differentiating (3.5) with respect to \(\varrho \) leads to

$$\begin{aligned} \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}=\frac{A_1(s)}{A_2(s)}-\frac{\varrho }{s}, \end{aligned}$$
(3.13)

where

$$\begin{aligned} A_1(s)= & {} e^{-s\varrho }\left( u_1^*u_2^*a_1a_2p_3s^{p_3-1}+u_2^*u_3^*a_2a_3p_1s^{p_1-1} \right. \\&\left. +\,u_1^*u_3^*a_1a_3p_2s^{p_2-1}\right) \\&+u_2^*a_2(p_1+p_3)s^{p_1+p_3-1}\\&+u_1^*a_1(p_2+p_3)s^{p_2+p_3-1} \\&+\,u_3^*a_3(p_1+p_2)s^{p_1+p_2-1}\\&+\,e^{s\varrho }\left[ (p_1+p_2+p_3)s^{p_1+p_2+p_3-1} \right. \\&-\,u_1^*u_3^*c_{13}c_{31}p_2s^{p_2-1}-u_1^*u_2^*c_{12}c_{21}p_3s^{p_3-1} \\&\left. -\,u_2^*u_3^*c_{23}c_{32}p_1s^{p_1-1}\right] ,\\ A_2(s)= & {} 2B_0se^{-2s\varrho }+e^{-s\varrho }s (u_1^*u_2^*a_1a_2s^{p_3} \\&+\,u_2^*u_3^*a_2a_3s^{p_1}+u_1^*u_3^*a_1a_3s^{p_2})-se^{s\varrho }. \end{aligned}$$

Then

$$\begin{aligned}&\text{ Re }\left\{ \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}\right\} \Bigg |_{\varrho =\varrho _{0}, \theta =\theta _{0}}=\text{ Re }\left\{ \frac{A_1(s)}{A_2(s)}\right\} \Bigg |_{\varrho =\varrho _{0}, \theta =\theta _{0}} \nonumber \\&\quad =\frac{G_1H_1+G_2H_2}{H_1^2+H_2^2}. \end{aligned}$$
(3.14)

It follows from (P3) that

$$\begin{aligned} \text{ Re }\left\{ \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}\right\} \Bigg |_{\varrho =\varrho _{0}, \theta =\theta _{0}}>0. \end{aligned}$$
(3.15)

This ends the proof of Lemma 3.2.

Based on the discussion above and Lemmas 3.1 and 3.2, one has the following result.

Theorem 3.1

Under the conditions (P1–P3). (a) If \(\varrho \in [0,\varrho _0)\), then the equilibrium point \((u_{1}^*,u_{2}^*, u_{3}^*)\) of system (1.5) is globally asymptotically stable; (b) if \(\varrho =\varrho _{0}\), then a Hopf bifurcation of system (1.5) occurs near the equilibrium point \((u_{1}^*,u_{2}^*, u_{3}^*)\).

4 Bifurcation control of fractional-order delayed model (1.5)

Over the past few decades, many time delay feedback methods are applied to control the Hopf bifurcation of integer-order models. However, the time delay feedback controllers are very rare in controlling Hopf bifurcation of fractional-order models. To make up the deficiency, we design a time delay feedback controller [24] which takes the form:

$$\begin{aligned} \mathrm{d}(t)=-\kappa _1[u_1(t-\varrho )-u_1(t)], \end{aligned}$$
(4.1)

where \(\kappa _1\) is feedback gain coefficient. We add the time delay feedback controller to the first equation of system (1.5), then (1.5) takes the form:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle D^{p_1}{u}_1(t)&{}=u_1(t)\big [a_1-a_1u_1(t-\varrho )-c_{12}u_2(t)\\ &{}\quad -c_{13}u_3(t)\big ]+d(t),\\ \displaystyle D^{p_2}{u}_2(t)&{}=u_2(t)\big [a_2-a_2u_2(t-\varrho )-c_{21}u_1(t)\\ &{}\quad -c_{23}u_3(t)\big ],\\ \displaystyle D^{p_3}{u}_3(t)&{}=u_3(t)\big [a_3-a_3u_3(t-\varrho )-c_{31}u_1(t)\\ &{}\quad -c_{32}u_2(t)\big ]. \end{array}\right. \nonumber \\ \end{aligned}$$
(4.2)

The linearization of system (4.2) near the equilibrium point \(u^*=(u_{1}^*, u_{2}^*, u_{3}^*)\) takes the form:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle D^{p_1}{u}_1(t)&{}=\kappa _1u_1(t)-u_1^*c_{12}u_2(t)-u_1^*c_{13}u_3(t)\\ &{}\quad -(u_1^*a_1+\kappa _1)u_1(t-\varrho ), \\ \displaystyle D^{p_2}{u}_2(t)&{}=-u_2^*c_{21}u_1(t)-u_2^*c_{23}u_3(t)\\ &{}\quad -u_2^*a_2u_2(t-\varrho ), \\ \displaystyle D^{p_3}{u}_3(t)&{}=-u_3^*c_{31}u_1(t)-u_3^*c_{32}u_2(t)\\ &{}\quad -u_3^*a_3u_3(t-\varrho ). \end{array}\right. \nonumber \\ \end{aligned}$$
(4.3)

The characteristic equation of (4.3) is

$$\begin{aligned}&\det \left[ \begin{array}{ccc} s^{p_1}-\kappa _1+(u_1^*a_1+\kappa _1)e^{-s\varrho } &{} u_1^*c_{12} &{} u_1^*c_{13} \\ u_2^*c_{21} &{} s^{p_2}+u_2^*a_2e^{-s\varrho } &{} u_2^*c_{23} \\ u_3^*c_{31} &{} u_3^*c_{32} &{} s^{p_3}+u_3^*a_3e^{-s\varrho } \\ \end{array} \right] \nonumber \\&\quad =0 \end{aligned}$$
(4.4)

which leads to

$$\begin{aligned} M_0e^{-3s\varrho }+M_1(s)e^{-2s\varrho }+M_2(s)e^{-s\varrho }+M_3(s){=}0,\nonumber \\ \end{aligned}$$
(4.5)

where \(M_i(s)(i=0,1,2,3)\) can be seen in “Appendix F”. Multiplying \(e^{s\varrho }\) on both sides of (4.5), we get

$$\begin{aligned} M_0e^{-2s\varrho }+M_1(s)e^{-s\varrho }+M_2(s)+M_3(s)e^{s\varrho }=0.\nonumber \\ \end{aligned}$$
(4.6)

Let \(s=i\theta =\theta \left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2}\right) \) be a root of (4.6). Then

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle M_0\cos 2\theta \varrho +(M_{1R}(\theta )+M_{3R}(\theta ))\cos \theta \varrho \\ \quad +(M_{1I}(\theta )-M_{3I}(\theta ))\sin \theta \varrho +M_{2R}(\theta )=0,\\ \displaystyle M_0\sin 2\theta \varrho -(M_{1I}(\theta )+M_{3I}(\theta ))\cos \theta \varrho \\ \quad +(M_{1R}(\theta )-M_{3R}(\theta ))\sin \theta \varrho -M_{2I}(\theta )=0, \end{array}\right. \nonumber \\ \end{aligned}$$
(4.7)

where \(M_{iR}(\theta ), M_{iI}(\theta )(i=1,2,3)\) are the real parts and the imaginary parts of \(M_i(i\theta )\) (see “Appendix G”). In view of \(\sin \theta \varrho =\pm \sqrt{1-\cos ^2\theta \varrho }\), then it follows from the first equation of (4.7) that

$$\begin{aligned}&2M_0\cos ^2\theta \varrho +(M_{1R}(\theta ){+}M_{3R}(\theta ))\cos \theta \varrho \,{\pm }\,(M_{1I}(\theta ) \nonumber \\&\quad -\,M_{3I}(\theta ))\sqrt{1-\cos ^2\theta \varrho }+\,M_{2R}(\theta )-M_0=0\nonumber \\ \end{aligned}$$
(4.8)

which leads to

$$\begin{aligned} \gamma _4\cos ^4\theta \varrho+ & {} \gamma _3\cos ^3\theta \varrho +\gamma _2\cos ^2\theta \varrho \nonumber \\+ & {} \gamma _1\cos \theta \varrho +\gamma _0=0, \end{aligned}$$
(4.9)

where \(\gamma _i(i=0,1,2,3,4)\) can be seen in “Appendix H”. We suppose that (4.9) has roots; then, we can get the expression of \(\cos \theta \varrho \). Assume that \(\cos \theta \varrho =h_1(\theta )\), where \(h_1(\theta )\) is a continuous function with respect to \(\theta \). By the first equation of (4.7), we can get easily the expression \(\sin \theta \varrho \), say \(\sin \theta \varrho =h_2(\theta )\), where \(h_2(\theta )\) is a continuous function with respect to \(\theta \). Then

$$\begin{aligned} h_1^2(\theta )+h_2^2(\theta )=1. \end{aligned}$$
(4.10)

In view of \(\cos \theta \varrho =h_1(\theta )\), we have

$$\begin{aligned} \varrho ^{(l)}=\frac{1}{\theta }[\arccos h_1(\theta )+2l\pi ],\quad l=0,1,2,\ldots .\nonumber \\ \end{aligned}$$
(4.11)

Suppose that (4.10) has at least one positive real root. Let

$$\begin{aligned} \varrho _{0*}=\min \{\varrho ^{(l)}\},\quad l=0,1,2,\ldots , \theta _{0*}=\theta |_{\varrho =\varrho _{0*}}.\nonumber \\ \end{aligned}$$
(4.12)

In order to establish the main results of this article, we give a necessary assumption as follows:

  1. (P4)

    \(\delta _0>0, \delta _2\delta _1-\delta _0>0\), where \(\delta _i(i=0,1,2)\) can be seen in “Appendix I”.

  2. (P5)

    \(P_1Q_1+P_2Q_2>0,\) where \(P_i,Q_i(i=1,2)\) can be seen in “Appendix J”.

Lemma 4.1

If \(\varrho =0\) and (P4) is satisfied, then system (4.2) is asymptotically stable.

Proof

If \(\varrho =0\), then (4.5) takes the form:

$$\begin{aligned} \lambda ^{3}+\delta _2\lambda ^2+\delta _1\lambda +\delta _0=0. \end{aligned}$$
(4.13)

It follows from (P4) that all the roots \(\lambda _i\) of (4.13) satisfy \(|\text{ arg }(\lambda _i)|>\frac{p_i\pi }{2} (i=1,2,3)\). By Lemma 2.2, we can conclude that system (4.2) with \(\varrho =0\) is asymptotically stable. This ends the proof of Lemma 4.1. \(\square \)

Lemma 4.2

Let \(s(\varrho )=\mu (\varrho )+i\theta (\varrho )\) be the root of (4.6) at \(\varrho =\varrho _{0*}\) satisfying \( \mu (\varrho _{0*})=0, \theta (\varrho _{0*})=\theta _{0*}\); then, \(Re\left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] \Big |_{\varrho =\varrho _{0*}, \theta =\theta _{0*}}>0\).

Fig. 1
figure 1figure 1

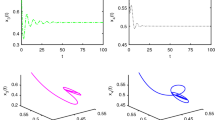
\(\varrho =1.36<\varrho _0= 1.4836.\) The equilibrium point (0.7413, 0.6739, 0.8101) of system (5.1) is asymptotically stable

Full size image
Fig. 2
figure 2figure 2

\(\varrho =1.59>\varrho _0= 1.4836.\) Hopf bifurcation of system (5.1) occurs from the equilibrium point (0.7413, 0.6739, 0.8101)

Full size image

Proof

Differentiating (4.6) with respect to \(\varrho \) leads to

$$\begin{aligned} \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}=\frac{L_1(s)}{L_2(s)}-\frac{\varrho }{s}, \end{aligned}$$
(4.14)

where

$$\begin{aligned} L_1(s)= & {} e^{-s\varrho }\left( u_1^*u_2^*a_1a_2p_3s^{p_3-1} \right. \\&\left. +\,u_2^*u_3^*a_2a_3p_1s^{p_1-1}+u_1^*u_3^*a_1a_3p_2s^{p_2-1}\right) \\&+\,u_2^*a_2(p_1+p_3)s^{p_1+p_3-1}\\&+\,u_1^*a_1(p_2+p_3)s^{p_2+p_3-1} \\&+\,u_3^*a_3(p_1+p_2)s^{p_1+p_2-1}\\&+\,e^{s\varrho }\left[ (p_1+p_2+p_3)s^{p_1+p_2+p_3-1} \right. \\&-\,u_1^*u_3^*c_{13}c_{31}p_2s^{p_2-1}-u_1^*u_2^*c_{12}c_{21}p_3s^{p_3-1} \\&\left. -\,u_2^*u_3^*c_{23}c_{32}p_1s^{p_1-1}\right] \\&+\,u_3a-3k_1p-2s^{p_2-1}e^{-s\varrho }\\&+\, k_1(p_2+p_3)s^{p_2+p_3-1} \\&-\,k_1u_2^*a_2p_3s^{p_3-1}-k_1u_3^*a_3p_2s^{p_2-1} \\&-\,k_1(p_2+p_3)s^{p_2+p_3-1}e^{s\varrho },\\ L_2(s)= & {} 2B_0se^{-2s\varrho }+e^{-s\varrho }s \left( u_1^*u_2^*a_1a_2s^{p_3}\right. \\&+\,u_2^*u_3^*a_2a_3s^{p_1} \\&+\,u_1^*u_3^*a_1a_3s^{p_2})-se^{s\varrho }\\&\left. +\,e^{-s\varrho }u_3^*a_3k_1(s^{p_2}-u_2^*a_2\right) \\&-\,e^{s\varrho }\left[ -k_1s^{p_2+p_3}+k_1u_2^*u_3^*c_{23}c_{32}\right] . \end{aligned}$$

Then

$$\begin{aligned}&\text{ Re }\left\{ \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}\right\} \Bigg |_{\varrho =\varrho _{0*}, \theta =\theta _{0*}}=\text{ Re }\left\{ \frac{L_1(s)}{L_2(s)}\right\} \Bigg |_{\varrho =\varrho _{0*}, \theta =\theta _{0*}} \nonumber \\&\quad =\frac{P_1Q_1+P_2Q_2}{Q_1^2+Q_2^2}. \end{aligned}$$
(4.15)

It follows from (P5) that

$$\begin{aligned} \text{ Re }\left\{ \left[ \frac{\mathrm{d}s}{\mathrm{d}\varrho }\right] ^{-1}\right\} \Bigg |_{\varrho =\varrho _{0*}, \theta =\theta _{0*}}>0. \end{aligned}$$
(4.16)

This ends the proof of Lemma 4.2. \(\square \)

Based on the discussion above and Lemmas 4.1 and 4.2, one has the following result.

Theorem 4.1

Under the conditions (P1),(P4) and (P5). (a) If \(\varrho \in [0,\varrho _{0*})\), then the equilibrium point \((u_{1}^*,u_{2}^*, u_{3}^*)\) of system (4.2) is globally asymptotically stable; (b) if \(\varrho =\varrho _{0*}\), then a Hopf bifurcation of system (4.2) occurs near the equilibrium point \((u_{1}^*,u_{2}^*, u_{3}^*)\).

Table 1 Impact of fractional order \(p_1\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\) of (5.1)
Full size table
Fig. 3
figure 3

Relation graph of fractional order \(p_1\) and bifurcation point \(\varrho _0\) of system (5.1)

Full size image

Remark 4.1

In [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], the authors investigated the Hopf bifurcation problems of integer-order delayed systems. In this article, we consider the stability and Hopf bifurcation of fractional-order delayed competition model of Internet. All the derived results of [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39] cannot be applied to (1.5) to obtain the stability and the existence of Hopf bifurcation for (1.5). In [10], Xiao and Cao discussed the Hopf bifurcation of delayed competitive web sites model, but they did not analyze the fractional-order case. Thus, we think that the obtained results are completely innovative, and our investigation on the stability and the existence of Hopf bifurcation for (1.5) also complements the earlier publications.

Remark 4.2

Xu and Zhang [40] and Yang et al. [41] dealt with the control of Hopf bifurcation for integer-order delayed systems by applying linear time delay feedback control. They did not discuss the control of Hopf bifurcation for fractional-order systems. Based on this viewpoint, the results of this article supplement the works of Xu and Zhang [40] and Yang et al. [41].

Remark 4.3

Xiao et al. [42] analyzed the control of Hopf bifurcation in fractional-order system by designing the fractional-order PD controller. Huang et al. [43] focused on the bifurcation control of fractional-order system by designing hybrid controller. In this article, we handle the bifurcation control of fractional-order model by designing a linear time delay feedback controller, which is a more simple control strategy than those in [42, 43], and this controller can be easily designed.

Table 2 Impact of fractional order \(p_2\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\) of (5.1)
Full size table
Table 3 Impact of fractional order \(p_3\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\) of (5.1)
Full size table

Remark 4.4

Zhao et al. [21] designed a feedback controller with square term and cubic term. In this paper, we design a feedback controller without square term and cubic term. The feedback controller of this paper is simpler than that of [21]. In addition, we can also design some non-delayed controllers to control the Hopf bifurcation. We will leave this topic be our future direction.

Fig. 4
figure 4figure 4

\(\varrho =2.3<\varrho _{0*}= 2.4551.\) The equilibrium point (0.7413, 0.6739, 0.8101). of system (5.2) is asymptotically stable

Full size image
Fig. 5
figure 5figure 5

\(\varrho =2.82>\varrho _{0*}= 2.4551.\) Hopf bifurcation of system (5.2) occurs from the equilibrium point (0.7413, 0.6739, 0.8101)

Full size image

5 Examples

Example 5.1

Consider the following fractional-order system:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^{p_1}{u}_1(t)=u_1(t)\left[ 1.2-1.2u_1(t-\varrho )-0.1u_2(t)-0.3u_3(t)\right] ,\\ \displaystyle D^{p_2}{u}_2(t)=u_2(t)\left[ 1.2-1.2u_2(t-\varrho )-0.2u_1(t)-0.3u_3(t)\right] ,\\ \displaystyle D^{p_3}{u}_3(t)=u_3(t)\left[ 1.1-1.1u_3(t-\varrho )-0.1u_1(t)-0.2u_2(t)\right] . \end{array}\right. \nonumber \\ \end{aligned}$$
(5.1)

Obviously, system (5.1) has a unique equilibrium point (0.7413, 0.6739, 0.8101). Let \(p_1=0.85,p_2=0.77, p_3=0.91\). Then the critical frequency \(\theta _0=0.8093\) and the bifurcation point \(\varrho _0= 1.4836\). Then all the conditions (P1–P3) of Theorem 3.1 hold true. Figure 1 reveals that the equilibrium point (0.7413, 0.6739, 0.8101) of system (5.1) is locally asymptotically stable for \(\varrho \in [0, \varrho _0)\). Figure 2 implies that system (5.1) loses its stability and that Hopf bifurcation occurs for \(\varrho \in [\varrho _0,+\infty )\). Next, we investigate the impact of different fractional order on Hopf bifurcation of system (5.1). Let \(p_2=0.77,p_3=0.91\); then, the Hopf bifurcation appears in advance as \(p_1\) increases. Table 1 illustrates the relation of fractional order \(p_1\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\). Figure 3 shows the relation of fractional order \(p_1\) and bifurcation point \(\varrho _0.\) Let \(p_1=0.85,p_3=0.91\); then, the Hopf bifurcation occurs in advance as \(p_2\) increases. Table 2 illustrates the relation of fractional order \(p_2\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\). Let \(p_1=0.85,p_2=0.77\); then, the Hopf bifurcation emerges in advance as \(p_3\) increases. Table 3 illustrates the relation of fractional order \(p_3\) on the critical frequency \(\theta _0\) and bifurcation point \(\varrho _0\).

Example 5.2

Consider the following fractional-order controlled system:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^{p_1}{u}_1(t)=u_1(t)\left[ 1.2-1.2u_1(t-\varrho )-0.1u_2(t)-0.3u_3(t)\right] \\ \qquad \qquad \qquad +\,\kappa _1[u_1(t-\varrho )-u_1(t)],\\ \displaystyle D^{p_2}{u}_2(t)=u_2(t)\left[ 1.2-1.2u_2(t-\varrho )-0.2u_1(t)-0.3u_3(t)\right] ,\\ \displaystyle D^{p_3}{u}_3(t)=u_3(t)\left[ 1.1-1.1u_3(t-\varrho )-0.1u_1(t)-0.2u_2(t)\right] . \end{array}\right. \nonumber \\ \end{aligned}$$
(5.2)

Obviously, system (5.2) has a unique equilibrium point (0.7413, 0.6739, 0.8101). Let \(p_1=0.85,p_2=0.77, p_3=0.91\) and \(\kappa _1=0.2\). Then the critical frequency \(\theta _{0*}=1.6023\) and the bifurcation point \(\varrho _{0*}= 2.4551\). Then all the assumptions (P1), (P4) and (P5) of Theorem 4.1 hold true. Figure 4 shows that the equilibrium point (0.7413, 0.6739, 0.8101) of system (5.2) is locally asymptotically stable for \(\varrho \in [0, \varrho _{0*})\). Figure 5 implies that system (5.2) loses its stability and that Hopf bifurcation appears for \(\varrho \in [\varrho _{0*},+\infty )\). Clearly, the order can delay the onset of Hopf bifurcation [compared with uncontrolled system (5.1)].

6 Conclusions

In recent years, the Hopf bifurcation and its control issue have attracted great attention by many scholars (see [44,45,46,47,48,49,50]). In the present paper, we mainly focus on two themes: (1) We proposed a new fractional-order delayed competitive web site model. By choosing the time delay as bifurcation parameter, we establish a set of sufficient conditions to ensure the stability and the existence of Hopf bifurcation of the new fractional-order delayed competitive web site model. The research shows that both time delay and the fractional order have important effects on the bifurcation behavior of the considered model. (2) We deal with the bifurcation control issue of fractional-order delayed competitive web site model by designing a simple time delay feedback controller. Some new sufficient conditions to ensure the stability and the existence of Hopf bifurcation of fractional-order controlled fractional-order delayed competitive web site model are given. The investigation reveals that one can delay the onset of Hopf bifurcation by adjusting the fractional-order, time delay and feedback gain coefficients. The derived results have important theoretical guiding significance in maintaining the stability of web site of Internet. In addition, the analysis method on Hopf bifurcation and Hopf bifurcation control can also be applied to investigate bifurcation or chaotic control problems in many fields such as engineering and physics. Here we mention that three web sites have different self-feedback time delays. Thus, the effect of different delays on the stability and Hopf bifurcation of competitive web site models of the Internet will be our future research direction.