1 Introduction

Nonlinear vibrations of circular cylindrical shells made of linearly elastic materials received large attention in the literature. Reviews were written by Amabili and Païdoussis [1] and Alijani and Amabili [2]. Particularly relevant are the studies of Chen and Babcock [3], Batista and Goncalves [4], Amabili, Pellicano and Païdoussis [5], Amabili [6,7,8], Pellicano [9], Jansen [10], Ribeiro [11], Amabili, Balasubramanian and Ferrari [12]. They studied the presence of a second mode, identical to the one directly excited by an external force but orthogonal to it, in a narrow frequency range close to the resonance due to a one-to-one internal resonance. The effect of a contained liquid, giving additional inertia through the so-called virtual mass, was also investigated in references [4,5,6,7,8]. Experimental results were reported in [4, 7, 12] together with the corresponding numerical simulations.

The mechanics and dynamics of hyperelastic shells have received much less attention in the literature. Nonlinear vibrations of a hyperelastic anisotropic circular cylindrical shell were addressed by Breslavsky, Amabili and Legrand [13]. Amabili [14] and Amabili et al. [15] introduced a nonlinear higher-order shell theory for incompressible biological hyperelastic materials.

Soft shells are used in a wide range of engineering applications, such as vascular prostheses and soft robots. When repairing the aorta, surgeons often use tubes made of polyethylene terephthalate fabric as aortic prostheses; they are usually referred as Dacron grafts, where Dacron is a commercial name of the fabric. They have an overall circular cylindrical shape and present corrugations along the axial direction. Due to the corrugations, they are flexible in axial direction, but they are stiff to pressure load in circumferential direction. However, the fabric is not capable of carrying significant compression without buckling. Aortic prostheses have been studied statically and dynamically because of their clinical relevance [16,17,18,19]. However, no vibration study is available in the literature for Dacron shells and for soft shells made by fabrics, despite they are loaded by pulsatile pressure in applications. The investigation of large-amplitude vibrations, which are vibrations with amplitude of the order of the fabric thickness, is of particular interest for a soft shell since this amplitude can be easily achieved under relatively small excitation. The complication arising for fabric shells is that fibers carry only small compressive loads. Also, internal pressurization helps to avoid fiber compression only for moderate vibration amplitude since the Dacron fabric is stiff to tensile loads. Therefore, it presents small pre-stretch due to pressurization, which is easily reverted into compression during a large vibration cycle. This behavior of fabric introduces complex nonlinearities in the system dynamics.

In the present study, vibration experiments are carried out on a slightly corrugated circular cylindrical shell made of Dacron fabric. The shell is liquid-filled, it is pressurized by a liquid column that applies a pressure of 100 mmHg, and the two edges are clamped to fix supports. Forced vibrations of the shell are experimentally studied in the linear (small amplitude) and in the geometrically nonlinear (large amplitude) regime. The large-amplitude vibrations of the liquid-filled shell are characterized by a strong softening behavior that cannot be captured by any quadratic nonlinear stiffness. Since compressed fibers do not carry load, a piecewise linear stiffness with viscous damping is thus introduced in a reduced-order model, which is used to identify the nonlinear stiffness and damping from the experimental data. The accurate evaluation of nonlinear stiffness and damping may be used to improve the design of deformable shells subjected to dynamic loading.

2 Experimental setup

A circular cylindrical shell with axial corrugations and made by polyethylene terephthalate fabric is studied. The dimensions are given in Table 1, and a photograph is shown in Fig. 1. This is a prosthetic tube for aortic repair named Hemashield Platinum woven double velour straight graft by Maquet (model 175428P). The shell is constituted by woven Dacron fabric, which is straight and stiff in the circumferential direction, while it features a constant-pitch wavy corrugation in the longitudinal direction to allow axial flexibility. An axial pre-stretch increases the stiffness of the shell against unwanted bending responses to internal pressure. The woven fabric is strongly anisotropic and presents direction-dependent hyperelastic and viscoelastic material behavior, investigated experimentally in [17,18,19]. The woven Dacron fabric is pre-impregnated by stabilized bovine collagen, to reduce the permeability of the fabric to human blood, thus reducing hemorrhaging during surgery.

Table 1 Dimensions of the Dacron shell
Full size table
Fig. 1
figure 1

Dacron circular cylindrical shell. The axial direction x and the circumferential direction y are indicated. The corrugations in axial direction are visible

Full size image

The shell is subjected to internal pressure applied by the contained liquid. This liquid is constituted by a mixture of glycerol and physiological saline solution for medical usage, which approximates the viscosity and the density of blood in dynamic experiments. The characteristics of the liquid are given in Table 2. The temperature was kept constant at 37° Celsius by means of an electric heater, because of the effect of temperature on the viscosity of the liquid. While collaged-impregnated Dacron is impervious to blood, because of the presence of large cells and because of coagulation, it is permeable to the water–glycerin mixture. Therefore, a thin (0.046 mm) latex membrane was inserted inside the graft to prevent leaking. The stiffness and mass of the membrane are negligible with respect to those of the shell and to the virtual mass of the liquid participating in the shell dynamics.

Table 2 Parameters of the blood-equivalent liquid
Full size table

The two edges of the shell are clamped to fixed supports, and a liquid column applies an internal pressure of 100 mmHg. In particular, a stiff metal frame, insensitive to the vibrations of the shell, was designed and manufactured from heavyweight stainless-steel plates and bolts. The frame is constituted by two disks that feature a 28-mm shoulder and a ½” hydraulic threaded hole at the center. The shell is slipped at the two ends onto the centering shoulders and glued in place, so that fixed boundary conditions are constituted. The hydraulic ports on the plates of the frame allow the connection to tubes at both edges. The two plates can be positioned at adjustable distance by means of threaded rods and fixing nuts, thus allowing the desired axial stretch of the shell. The threaded-rod construction allows for an optimal accessibility of the shell to excitation and measurement sensors.

The shell is connected at the top to a 3/4” ID Tygon tubing that serves as a liquid column. Liquid is added to the column until a height of 1.360 m is reached with respect to the center of the shell. This liquid column creates the desired pressure of 100 mmHg. A large ID Tygon tubing was chosen to minimize possible liquid oscillation in the column as a consequence of the shell vibrations. A second soft shell, closed at one end and axially unconstrained, was placed below the tested shell to function as an expansion chamber, so that the volume change inside the shell during vibrations would not result in an oscillation of the liquid column. To understand the role of gravity and of the consequent pressure gradient inside the shell, tests were performed with both horizontal and vertical shell by turning the metallic frame. The experimental setup in vertical configuration is shown in Fig. 2.

Fig. 2
figure 2

Experimental setup: a, shell; b, water column; c, expansion chamber

Full size image

Forced vibration experiments were performed under force excitation. The force was generated by a Bruel and Kjaer model 4810 eletrodynamic exciter. Since the Dacron shell is lightweight, a miniature piezoelectric force transducer (Bruel and Kjaer model 8203) was interposed between the exciter and the shell; in this case, it was connected to the exciter, so that no added mass was attached to the shell. A harmonic wire acted as a stinger connecting the force transducer to a small and very thin metal disk glued to the shell. The function of the small disk was to avoid local buckling of the fabric at the point of application of the force. The force excitation was placed at distance of 25 mm from one support of the shell, to reduce the interaction between the shell and the exciter during large-amplitude vibrations. The excitation system is shown in Fig. 3.

Fig. 3
figure 3

Excitation system. a, electrodynamic exciter; b, force transducer; c, wire stinger

Full size image

3 Experiments

3.1 Linear vibrations

Vibrations of amplitude significantly smaller than the fabric thickness of the shell are within a linear regime. Preliminary analysis revealed that the shell coupled to the liquid presents a rich dynamic response below 200 Hz. Thus, the bandwidth of the experiments was limited to this value. A Polytec PSV-400 scanning laser Doppler vibrometer was used to measure the vibration. The scanning capability allows the vibrometer to measure a large number of points without contact and to obtain a good spatial resolution. A displacement decoder was used with the vibrometer, so that displacement signals were measured (accuracy 1 nm).

Linear vibrations were studied by modal analysis. A pseudo-random excitation in the bandwidth up to 200 Hz was used, and 130 points on the surface of the shell were measured. The signals were acquired by a Siemens/LMS modal analysis system for data processing with Difa Scadas III front-end, using DC inputs to avoid low-frequency frequency filtering. In particular, the PolyMax modal estimator of the Test.Lab software was used for the estimation of the H1 frequency response function (FRF), and for the identification of natural frequencies, damping ratios and natural modes. Modal analysis was performed for the liquid-filled shell at 100 mmHg pressure in both horizontal and vertical configurations. The comparison between the two experiments allows to understand the effects of gravity. For both cases, natural frequencies and damping ratios are given in Table 3 for the first six modes. The fundamental mode in the vertical configuration has natural frequency of 35.9 Hz, damping ratio 4.91%, and it presents an axisymmetric shape with one longitudinal half-wave. Frequencies and damping ratios are similar in the two configurations under exam. The horizontal configuration appears to be slightly stiffer (higher frequencies), due to the more uniform pressure along the shell, and the fundamental mode is slightly less damped. The synthesized sum of the measured frequency response functions in the vertical configuration is shown in Fig. 4a, b for amplitude and phase. The peaks in Fig. 4a correspond to the natural frequencies presented in Table 3. The experimentally identified natural mode shapes are presented in Fig. 5 for the vertical configuration. As previously observed, the fundamental mode presents an axisymmetric shape with one longitudinal half-wave. The inertia of the contained liquid has a very significant effect on the shell in the studied setup [20].

Table 3 Natural frequencies and damping ratios identified by experimental modal analysis in the vertical and horizontal configurations
Full size table
Fig. 4
figure 4

Synthesized sum of the measured frequency response functions in the vertical configuration. a Amplitude; b phase

Full size image
Fig. 5
figure 5

Natural mode shapes of vibration of the vertical shell. The first mode is axisymmetric with one longitudinal half-wave

Full size image

3.2 Nonlinear vibrations

Vibrations of amplitude of the order of the fabric thickness of the shell, or larger, are associated with a nonlinear behavior of the system. Experiments to measure the large-amplitude vibrations were performed forcing the shell with a harmonic excitation in the frequency neighborhood of the fundamental natural frequency. In the absence of internal resonances, by exciting sinusoidally around the fundamental frequency, the response of the system is dominated by the fundamental mode shape. Therefore, it is sufficient to point the laser beam at an antinode of the fundamental mode shape to measure the response. For the fundamental mode, the antinode is at half-length of the shell. Since the fundamental mode is axisymmetric, any measurement point along the central circumference is equivalent. The chosen point was located at 180° with respect to the excitation point. The frequency of the harmonic excitation changes by steps of 0.1 Hz during experiments. The force excitation and the response are recorded in the time domain at the sampling frequency of 3200 Hz. At each frequency step, the first 10 periods are discarded to get rid of any transient; afterward, the vibration is measured. The amplitude of the excitation is kept constant (with a tolerance of +- 0.01 dB) by the closed-loop control when the excitation frequency is changed. The control is implemented in the LMS Test.Lab software and Difa Scadas III front-end, which receives the signal from the miniaturized force sensor. Since the vibration response of the shell depends on the excitation in nonlinear (large-amplitude) regime, it is necessary to apply the stepped—sine excitation at various levels of constant forcing amplitude, ranging from the linear (small amplitude) to the nonlinear regime. Nonlinear tests were performed for the liquid-filled shell at a pressure of 100 mmHg in horizontal configuration.

Figure 6 shows the vibration amplitude versus the excitation frequency for seven forcing amplitudes between 0.01 N and 0.55 N. The level 0.01 N can be considered in the linear regime. The nonlinear behavior is strongly softening, as the peak frequency decreases with the forcing amplitude: the peak frequency reduces almost 30% in the present range of force levels. For a forcing amplitude of 0.55 N, a maximum vibration amplitude of 1.26 mm is reached. This value is much larger than the shell thickness. The experimental curves, however, do not feature any jump associated with the strong nonlinearity. It can be observed that the backbone curve, which joins the peaks of the curves at different force levels in Fig. 6, starts inclined to the left with respect to the vertical.

Fig. 6
figure 6

Experimental frequency–amplitude responses to different harmonic excitations of the soft shell in the horizontal configuration under an internal pressure of 100 mmHg. The black dashed line represents the backbone curve joining the peaks of the vibration response. Force levels 0.01 N, 0.05 N, 0.15 N, 0.25 N, 0.35 N, 0.45 N, 0.55 N

Full size image

4 Identification of nonlinear stiffness and damping

Since no complex nonlinear dynamics is observed, a single-degree-of-freedom reduced-order model is used for the system identification, where x represents the modal displacement coordinate associated with the fundamental mode shape. The results presented in Fig. 6 are not compatible with a model of the nonlinear elastic restoring force of the liquid-filled shell given by the following polynomial

$$ k\,x + k_{2} x^{2} + k_{3} x^{3}, $$
(1)

for any value of the stiffness coefficients \( k \), \( k_{2} \) and \( k_{3} \). In fact, the modified Duffing equation resulting from the stiffness expressed by Eq. (1) and with viscous damping is unable to fit the experimental results and predicts a completely different backbone curve for any possible combination of the values \( k \), \( k_{2} \) and \( k_{3} \). However, the nonlinearity given by Eq. (1) is the one resulting from geometric nonlinearity of linearly elastic shells [14]. In order to find the correct nonlinear stiffness representation, it is necessary to consider that during large-amplitude vibrations the shell undergoes harmonic elongation and reduction in the diameter with respect to the initial value under pressurization. As a consequence of the internal pressurization and consequent stretching, if the vibration amplitude is small enough, fibers in circumferential direction do not undergo to compression. However, if the amplitude overcomes this limit, compression of the fabric is reached at some point during the vibration cycle, and the corresponding stiffness is largely reduced.

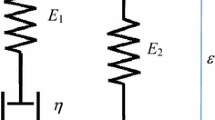
In order to introduce the different stiffness of fabric during the expansion and contraction phase of the vibration cycle, a different nonlinear stiffness model is applied with an idea originated from bilinear stiffness. Viscous damping is introduced and represents the global effect of different contributions: dissipation at the shell boundaries, viscoelasticity of the tube and liquid-structure interaction. The equation of motion of the single-degree-of-freedom model with nonlinear stiffness and viscous damping is given by

$$ m{\kern 1pt} \ddot{x}(t) + c{\kern 1pt} \dot{x}(t) + k{\kern 1pt} f(x) = F\cos (\omega \,t), $$
(2)

where \( f(x) \) is the displacement-dependent nonlinear stiffness function, F is the harmonic force excitation, \( \omega \) is the excitation frequency (rad/s), m, c and k are the modal mass, damping and stiffness parameters of the system. Equation (2) is transformed in the following form

$$ x^{\prime\prime}(\tau) + 2\zeta \,x^{\prime}(\tau) + \,f(x) = \lambda \sin ({\varOmega}\,\tau), $$
(3)

where \( {\lambda =}F/m\,\omega_{n}^{2} \) is the excitation parameter, \( {\varOmega} = \omega/\omega_{n} \) is the frequency ratio, \( \tau = t\,\omega_{n} \) is the non-dimensional time, \( \omega_{n} \) is the natural frequency (rad/s), \( \zeta \) is the damping ratio and \( x^{\prime} = \text{d} x/\text{d} \tau \). The nonlinear stiffness \( f(x) \), which is nonlinear only for negative values of x corresponding to compression of fibers, can be approximated with a piecewise linear stiffness function, which is plotted in Fig. 7. There are three (I, II, III) line segments shown in Fig. 7, just for illustration of the method. In general, an appropriate number of line segments can be chosen to describe the stiffness function \( f(x) \) with accuracy. In the present case, eight segments are used; they have equations

Fig. 7
figure 7

Piecewise linear function \( f(x) \). The switching points x1 and x2 and the stiffness parameters μ1 and μ2 are also defined

Full size image
$$ \begin{array}{*{20}c} {{\text{I}}:} & {f(x) = x,\quad x \ge - x_{1},} & {(4{\text{a}})} \\ {{\text{II}}:} & {f(x) = \mu_{1} x - (1 - \mu_{1})\,x_{1},\quad - x_{1} > x \ge - x_{2}} & {(4{\text{b}})} \\ {} & \vdots & {} \\ {{\text{VII}}:} & {f(x) = \mu_{6} x - (1 - \mu_{1})\,x_{1} - \sum\limits_{i = 1}^{5} {(\mu_{i} - \mu_{i + 1})\,x_{i + 1}},\quad - x_{6} > x \ge - x_{7}} & {(4{\text{c}})} \\ {{\text{VIII}}:} & {f(x) = \mu_{7} x - (1 - \mu_{1})\,x_{1} - \sum\limits_{i = 1}^{6} {(\mu_{i} - \mu_{i + 1})\,x_{i + 1}},\quad - x_{7} > x} & {(4{\text{d}})} \\ \end{array} $$

where xi are the switch distances and μi are the stiffness parameters that are given in Table 4; they are obtained by an iterative minimization of the distance (least squares) among the experimental points and the numerical response obtained from Eq. (3). It is clear that, as the number of segments grows, \( f(x) \) approaches a continuous function representing the nonlinear stiffness. Figure 8 shows the function obtained with the values in Table 4. The function is linear for positive values of x (expansion) and piecewise linear progressively reduces its value for negative x (contraction).

Table 4 Parameters of the stiffness function \( f(x) \)
Full size table
Fig. 8
figure 8

Stiffness function \( f(x) \) of the soft shell identified by the nonlinear vibration experiments on the fundamental mode; the seven switching points are indicated

Full size image

The second-order ordinary differential Eq. (3) is numerically integrated in the software AUTO [21] for continuation and bifurcation analysis of nonlinear ordinary differential equations by using collocation method.

Figure 9 shows the comparison of experimental and numerical results in the frequency domain for the 7 excitation levels: 0.01, 0.05, 0.15, 0.25, 0.35, 0.45 and 0.55 N. The measured and identified vibration amplitudes are very close in all the frequency range around the fundamental mode of the system. The stiffness parameters given in Table 4 are used in the numerical model. The stiffness for negative x values is only 20% of the original value when x is smaller than -0.7 mm. During the identification of the stiffness parameters by least squares procedure, also the damping ratio is estimated at each force level. The damping ratios are given in Table 5 and grow with the excitation.

Fig. 9
figure 9

Comparison of experimental and numerical results, presented as vibration amplitude (mm) versus non-dimensional excitation frequency Ω, for the nonlinear forced vibration response of the soft shell; force levels 0.01 N, 0.05 N, 0.15 N, 0.25 N, 0.35 N, 0.45 N, 0.55 N. open circle, experimental point; line, numerical simulation

Full size image
Table 5 Identified damping ratios at different harmonic force levels
Full size table

The experimental and numerical time responses for harmonic excitation of 0.55 N and frequency ratio Ω = 0.732, i.e., at the peak of the response in Fig. 9, are compared in Fig. 10. They show that the reduced-order model capture with accuracy the system nonlinear dynamics also in the time domain. The small difference is due to higher harmonics present in the experimental excitations near the resonance as a consequence of the interaction between the stinger and the vibrations of the shell. It is significant to observe that the positive (outwards) vibration amplitude is smaller than the negative (inwards), which is typical of softening systems. This clarifies that the amplitude reported in Fig. 9 is the average between the vibrations inwards and outwards the shell.

Fig. 10
figure 10

Time response for harmonic excitation of 0.55 N and frequency ratio Ω = 0.732 (at the peak of the response amplitude). Blue line, experimental results; red line, numerical results. (Color figure online)

Full size image

It is interesting to plot the damping ratios obtained for different values of the maximum vibration amplitudes of each one of the seven curves in Fig. 9. This produces Fig. 11, which shows a linear increase in the damping ratio with the maximum vibration amplitude. Both the identified experimental values and the linear regression (R = 0.989) are shown. This linear increase is attributed to the predominant hydrodynamic damping, which is related to the fluid–structure interaction, with respect to viscoelastic dissipation of the shell. In fact, a damping associated with viscoelastic dissipation takes the cubic nonlinear expression [22,23,24,25] \( c\,\dot{x}(t) + c_{n} x^{2} (t)\,\dot{x}(t) \) while hydrodynamic damping can be formulated as [26, 27] \( c\,\dot{x}(t) + c_{n} \left| {\dot{x}(t)} \right|\dot{x}(t) \), where \( c_{n} \) is the nonlinear damping coefficient. The latter expression gives a linear increase in the equivalent linear damping ratio with the vibration amplitude, while the cubic nonlinear damping presents an increase more than linear. The linear viscous damping contribution is here \( c\,\dot{x}(t) \), where c would be the value identified for the smallest excitation (0.01 N).

Fig. 11
figure 11

Damping ratio versus maximum vibration amplitude (for each curve in Fig. 9). Filled circle, identified experimental damping ratio; line, linear regression (R = 0.989)

Full size image

5 Conclusions

Nonlinear dynamics of fluid-filled and pressurized soft shells is a subject of significant interest at the present time, but still largely unexplored. Experiments on large-amplitude forced vibrations of a shell made of polyethylene terephthalate fabric show nonlinear stiffness and nonlinear damping that are a combined effect of the structural viscoelasticity and fluid–structure interaction, as observed for large human vessels [28]. The present experimental results shed light on the system’s nonlinear dynamics and allow to identify a reduced-order model with a single degree of freedom that is capable of capturing the response with very good accuracy. The nonlinear stiffness, due to the reduced load capacity during the part of the vibration cycle that compresses the fabric, is well described by a piecewise linear function with eight segments for negative displacement, while it is linear for positive displacement. Due to the relatively large number of segments, the piecewise liner function approximates well a continuous function, which progressively loses stiffness for negative displacements; it remains with only 20% of its initial value for the maximum vibration amplitude reached in the experiments. The damping ratio increases 2.75 times from the small-amplitude vibrations to a maximum amplitude of 1.26 mm. This is a very significant increase that highlights the necessity to introduce nonlinear damping to model shell structures.