1 Introduction

Large-amplitude vibrations have been deeply investigated in the last few decades and still present a lot of opportunities for ground-breaking research. Most of the published studies deal only with geometric nonlinearities, which are due to the large amplitude of vibration with respect to a characteristic dimension of the structure (e.g. the plate thickness), while the strains are still small enough to allow application of linear elasticity. This simplification is not appropriate for very flexible biological structures, like arteries, where large strains are observed during the heart beating cycle. In this case, the stress–strain relationships are nonlinear and can be described by hyperelasticity.

In case of nonlinear vibrations, the present knowledge allows us to create sophisticated structural models that produce very accurate mass and stiffness representations, which retain the geometric, and eventual material, nonlinearity. The resulting problem is described by a set of second-order, nonlinearly coupled, ordinary differential equations. These systems can present softening or hardening nonlinearity, and the resonance has a frequency shift of a few or some per cent. Cases of internal resonances and very complex nonlinear dynamics can arise. Depending on the geometry and material of the structure, and eventually on the presence of a coupled multi-field problem like fluid–structure interaction, the modelling operation can be straightforward or challenging and can have a different degree of approximation. But it can be successfully implemented. However, in a vibration problem, this is not enough. The vibration amplitude is mainly controlled by the mass and the stiffness away from resonances, and it is fully controlled by damping at resonance. Here, the fundamental role of the energy dissipated during a vibration cycle comes into play. In case of small-amplitude vibrations, the problem is linear and damping must be determined by experiments for that specific structure and boundary conditions. In fact, dissipation at the boundaries and joints between different components can be larger than the energy lost during the deformation of the material. The last contribution can be evaluated by applying viscoelastic constitutive equations, while the other contributions are quite difficult to model and can be very different from an application to another.

Recently published experimental data for plates and shells [1, 2] clearly show a strong and nonlinear dependence of the damping value from the maximum vibration amplitude reached in a cycle. This dependence takes a completely different level with respect to frequency shift of resonances due to nonlinearity, which is commonly of 10–25% at most for shells and plates. The experiments show that, in case of damping, a value over six times larger must be expected for vibration of thin plates when the vibration amplitude is about twice the thickness. This is a huge change!

Experiments in reference [1] have been performed on plates made of different materials, with different boundary conditions and sizes of the order of one metre wide and up to 3.3 mm thickness; results show similar trend. Plates are hardening-type systems. But the case of a curved panel, which is a softening system, is also shown in [1], and a significant damping increase with the vibration amplitude has been observed also in this case. It is interesting to observe that all the experiments reported in references [1, 2] have been obtained for small strains and linearly elastic materials. Therefore, the change in damping cannot be attributed to material nonlinearities.

A similar increase in damping has been observed for sheets of 2D materials. In particular, graphene circular membranes of thickness 5 nm and radius \(2.5\,\upmu \hbox {m}\) have been experimentally tested [3]; the results show hardening nonlinearity and a similar behaviour of the damping versus the peak vibration amplitude, but at a different space and timescale.

2 Literature review

Phenomenological nonlinear damping terms have been added in a few studies [4,5,6] to the modified Duffing equation (second-order differential equation with linear, quadratic and cubic stiffness terms), representing a single-degree-of-freedom nonlinear system. For example, in addition to the linear viscous damping term, Zaitsev et al. [6] added two cubic damping terms: the first one given by the velocity multiplied by the squared displacement and the second one proportional to the cube of the velocity. However, the nature of the damping is not investigated in [4, 5]. In reference [6], it is claimed that nonlinear damping can be, in part, closely related to material behaviour with a linear dissipation law that operates within a geometrically nonlinear regime. A model based on the Kelvin–Voigt viscoelastic model was developed, but it was not capable of reproducing the experimental results, showing that dissipation is not well described by this viscoelastic model [6]. Amabili [7] and Balasubramanian et al. [8] derived rigorously linear, quadratic and cubic dissipation terms by using the Kelvin–Voigt viscoelastic model for metal and rubber plates, which were discretized with reduced-order models retaining up to 54 degrees of freedom. Comparison to experimental results in [8] was performed, indicating that the nonlinear damping model developed was not capable of reproducing the experimental results. The Kelvin–Voigt viscoelastic model was also used by Xia and Lukaziewicz [9, 10] for modelling free and forced nonlinear vibrations of sandwich rectangular plates with simply supported moveable edges. They treated the two external layers as elastic and the core as viscoelastic. The numerical solution was obtained by direct integration of the equations of motion by Runge–Kutta method. Nonlinear damping terms appeared in the equations of motion due to the viscoelastic model.

A forced spherical pendulum has been experimentally and numerically investigated in [11] by Gottlieb and Habib, where a nonlinear damping with linear, quadratic and cubic terms was introduced. The damping coefficients were obtained by fitting the experimental results. A cubic damping, in addition to the linear term, has been proposed in [12] for carbon nanotubes and graphene sheets and [13] for nanomechanical and micromechanical resonators, without a derivation. Jeong et al. [14] studied a microcantilever–nanotube system with linear and cubic damping. The nonlinear damping was geometrically obtained from the specific arrangement of two viscous dashpots forming an angle between their axes. De et al. [15] introduced a dissipation mechanism due to the interaction of the time-varying strain field in a \(\hbox {MoS}_{2}\) single-layer resonator with its thermal phonons by using molecular dynamics. They found that the energy dissipated has \(4\mathrm{th}\) and higher-order terms in the transverse vibration amplitude.

Elliot et al. [16] observed many cases of nonlinear damping for system that they modelled with linear stiffness and nonlinear damping forces, which were assumed to be proportional to the \(n\hbox {th}\) power of the velocity.

A nonlinear viscoelastic model based on a single integral formulation with four kernels and nonlinear terms has been introduced for vibration of sandwich plates by Mahmoudkhani and Haddadpour [17] and Mahmoudkhani et al. [18]. No verification of its suitability to represent experimental data at different excitation levels has been attempted.

The fractional derivative has been introduced to model viscoelasticity with success [19] since it allows to build accurate viscoelastic material models with very few mechanical elements [20]. Pérez Zerpa et al. [21] applied a few linear viscoelastic material models with a fractional viscoelastic element to study the dynamic response of arterial walls. The fractional standard linear solid, the fractional generalized Maxwell model with two arms and the fractional Kelvin–Voigt material model were considered. Spanos and Manara [22] introduced a linear fractional viscoelastic damper to study the geometrically nonlinear vibrations of beams. Rossihkin and Shitikova [23] used the Riemann–Liouville fractional derivative to describe linear viscoelasticity of a rectangular plate undergoing geometrically nonlinear free damped vibrations. The use of the fractional derivative to derive nonlinear damping has not been attempted yet.

The present study derives, for the first time, the nonlinear damping from a fractional viscoelastic standard solid model by introducing geometric nonlinearity in both the springs. The damping model obtained is nonlinear, and its frequency dependence can be tuned by the fractional derivative to match the material behaviour. At the same time, the dynamic storage stiffness of the system versus frequency is also modelled. The solution is obtained for a nonlinear single-degree-of-freedom system by harmonic balance. Numerical results are compared to experimental forced vibration responses measured for large-amplitude vibrations of a rectangular plate (hardening system), a circular cylindrical panel (softening system) and a clamped rod made of zirconium alloy (weak hardening system). Sets of experiments have been obtained at different harmonic excitation levels. Experimental results present a very large damping increase with the peak vibration amplitude, and the model is capable of reproducing them with great accuracy.

3 Viscoelastic model

A continuous system, e.g. a beam, a plate or a curved panel, is assumed to be discretized with a single-degree-of-freedom nonlinear equation of motion; no internal resonances are present. The model can be very accurate if a suitable algorithm is used to obtain the reduced-order problem [2, 24]. The material is assumed to be linearly viscoelastic and the nonlinearity is of geometric type.

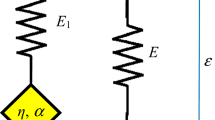
Figure 1 shows a viscoelastic standard linear solid material model [25,26,27]. The left side of the model is composed by a spring in series with a dashpot (they give the Maxwell model), while the right branch of the model is simply a spring. The two branches work in parallel. This classic viscoelastic model is extended here, for the first time, to take into account geometric nonlinearities in the two springs in order to derive rigorously the expression of nonlinear damping.

Fig. 1
figure 1

Standard linear solid model

Full size image

Figure 2 presents a single-degree-of-freedom forced vibration system based on an extended version of the standard linear solid model, in which the two springs are geometrically nonlinear. This material model can be named geometrically nonlinear standard solid. The spring on the right-side of Fig. 2 represents the geometrically nonlinear stiffness of the system. In fact, for very slow deformation, this is the only spring subjected to strain, due to the presence of the dashpot below the spring on the left side of the model. Instead, this second spring represents, together with the dashpot, the viscoelastic characteristic of the system. For this reason, this second spring has linear and nonlinear stiffness that are different from those of the previous spring, and must be characterized to satisfy the damping, or the relaxation and creep, of the system.

Fig. 2
figure 2

Single-degree-of-freedom system with geometrically nonlinear standard solid material model

Full size image

In order to further improve the viscoelastic model, the damper is replaced by a spring-pot [19] element described by fractional derivative, as shown in Fig. 3. The spring-pot shows an intermediate behaviour between a linear spring and a linear dashpot, according to the order of the fraction derivative. In the limit case of fractional order one, it gives the system previously presented in Fig. 2. The model proposed has the feature to be geometrically nonlinear, but it retains material linearity.

Fig. 3
figure 3

Single-degree-of-freedom system with geometrically nonlinear fractional solid material model

Full size image

The constitutive equation of the fractional standard linear solid model can be written as [21, 25]

$$\begin{aligned} \left( {E_1 +E_2 } \right) \frac{\hbox {d}^{\alpha }\varepsilon }{\hbox {d}t^{\alpha }}+\frac{E_2 }{\tau _r^\alpha }\varepsilon =\frac{\hbox {d}^{\alpha }\sigma }{\hbox {d}t^{\alpha }}+\frac{\sigma }{\tau _r^\alpha }, \end{aligned}$$
(1)

where \(\sigma \) is the stress, \(\varepsilon \) is the strain, \(E_1 \) and \(E_2 \) are the stiffness moduli of the two springs in Fig. 1, t is time, \(\alpha \) is the order of the fractional derivative with \(0<\alpha \le 1\), \(\tau _r =\eta /E_1 \) is the relaxation time constant, which is a characteristic of the viscoelastic material, and \(\eta \) is the viscosity coefficient of the dashpot. In Eq. (1), \(D_t^\alpha =\hbox {d}^{\alpha }/\hbox {d}t^{\alpha }\) is the fractional derivative operator of order \(\alpha \). Before introducing the mathematical description of the fractional derivative, it is assumed that the system dynamic response x(t) is a periodic forced vibration that can be represented by (i) a constant component, (ii) a fundamental harmonic component of frequency \(\omega \) identical to the excitation frequency and (iii) its super-harmonics. In nonlinear vibrations, it means that quasi-periodic and chaotic dynamics cannot be represented by this description. This means that it is assumed that no complex nonlinear mechanics is observed in the system. Under this hypothesis, the vibration response can be expanded in the complex Fourier series [28]

$$\begin{aligned} x(t)=\sum _{n=-\infty }^\infty {a_n e^{i 2 n \pi t/T}}, \end{aligned}$$
(2)

where

$$\begin{aligned} a_n =\frac{1}{T}\int \limits _0^T {x(t) e^{-i 2 n \pi t/T}} \hbox {d}t, \end{aligned}$$
(3)

i is the imaginary unit and T is the period. It is assumed that the zero-order value \(a_{0}\) of periodic functions has zero fractional derivative. The fractional derivative of order 0 < \(\alpha \, < 1\), based on the Weyl integro-differential operator, is defined as [29]

$$\begin{aligned} D_t^\alpha x(t)=\frac{\hbox {d}^{\alpha }x(t)}{\hbox {d}t^{\alpha }}=\sum _{n=-\infty }^\infty {(i 2 n \pi /T)^{\alpha } a_n e^{i 2 n \pi t/T}}. \end{aligned}$$
(4)

As previously stated, Eq. (4) is not the only definition available of fractional derivative. The most used are probably the Reimann–Louisville left- and right-hand formulations [29, 30], the Caputo [30] and the Grunwald–Letnikov one [30, 31], which is particularly suitable for numerical implementation. It is interesting to observe that different definitions of fractional derivative lead out to expressions that are not equivalent. For example, according to the Reimann–Louisville formulation, the fractional derivative of a periodic function is non-periodic, which makes it not convenient in dealing with harmonic functions. However, the definition of the Weyl fractional integral is in complete agreement with the Riemann–Liouville definition of the fractional derivative with the lower bound of the integral being \(-\infty \) [29].

For \(x(t)=\sin (\omega t)\), where \(\omega =2\pi /T\), the Weyl fractional derivative of order \(\alpha \) gives

$$\begin{aligned} D_t^\alpha \sin (\omega t)= & {} \omega ^{\alpha }\left[ \cos \left( {\alpha \frac{\pi }{2}} \right) \sin (\omega t)\right. \nonumber \\&\left. +\,\sin \left( {\alpha \frac{\pi }{2}} \right) \cos (\omega t) \right] . \end{aligned}$$
(5)

For \(\alpha = 1\), the classical first derivative is obtained, while \(\alpha = 0\) gives the original function.

After this mathematical parenthesis on the fractional derivative, Eq. (1) can be rewritten as

$$\begin{aligned} \sigma +\tau _r^\alpha \frac{\hbox {d}^{\alpha }\sigma }{\hbox {d}t^{\alpha }}=E_2 \left( {\varepsilon +\tau _r^\alpha \frac{\hbox {d}^{\alpha }\varepsilon }{\hbox {d}t^{\alpha }}} \right) +E_1 \tau _r^\alpha \frac{\hbox {d}^{\alpha }\varepsilon }{\hbox {d}t^{\alpha }}. \end{aligned}$$
(6)

The stiffness moduli \(E_1\) and \(E_2\) can be generalized to be nonlinear functions of the strain in order to take into account geometric nonlinearity.

Assuming that the continuous system could be discretized into the single-degree-of-freedom system represented in Fig. 3, where the two springs are nonlinear and provide elastic forces given by \(k_1 x+k_2 x^{2}+k_3 x^{3}\) and \(\tilde{k}_1 x+\tilde{k}_2 x^{2}+\tilde{k}_3 x^{3}\), respectively, then the constitutive Eq. (6) can be rewritten as

$$\begin{aligned} F+\tau _r^\alpha \frac{\hbox {d}^{\alpha }F}{\hbox {d}t^{\alpha }}= & {} k_1 x+k_2 x^{2}+k_3 x^{3}\nonumber \\&+\,\tau _r^\alpha \frac{\hbox {d}^{\alpha }}{\hbox {d}t^{\alpha }}(k_1 x+k_2 x^{2}+k_3 x^{3})\nonumber \\&+\,\tau _r^\alpha \frac{\hbox {d}^{\alpha }}{\hbox {d}t^{\alpha }}(\tilde{k}_1 x+\tilde{k}_2 x^{2}+\tilde{k}_3 x^{3}), \end{aligned}$$
(7)

where F is the viscoelastic force acting on the mass, \(\tau _r =c/\tilde{k}_1 , c\) is the damping coefficient of the spring-pot, x is the displacement of the mass, \(k_{1}\) and \(\tilde{k}_1 \) are the linear coefficients of the two springs, \(k_{2}\) and \(\tilde{k}_2 \) are the quadratic coefficients and \(k_{3}\) and \(\tilde{k}_3 \) are the cubic coefficients. Here, it must be stressed that, while \(k_{1}\), \(k_{2}\) and \(k_{3}\) are the geometrically nonlinear stiffness coefficients, \(\tilde{k}_1 , \tilde{k}_2 \) and \(\tilde{k}_3 \) are geometrically nonlinear viscoelastic coefficients having the same units of their stiffness counterparts but different values. Equation (7) is a fractional differential equation, and its solution gives the dynamic viscoelastic force F(t) acting on the mass.

In case of forced harmonic excitation of frequency \(\omega \) and modal amplitude \(\tilde{f},\) the equation of motion for the system can be written as

$$\begin{aligned} m \ddot{x}+F(t)=\tilde{f} \sin (\omega t+\phi ), \end{aligned}$$
(8)

where m is the modal mass of the system and \(\phi \) is a phase angle.

4 Harmonic balance solution

Assuming the vibration displacement x to be expressed as

$$\begin{aligned} x(t)=a_0 +a_1 \sin (\omega t)+\cdots , \end{aligned}$$
(9)

the solution of the ordinary nonlinear differential equation (7) can be expressed as

$$\begin{aligned} F(t)=f_0 +f_{1s} \sin (\omega t)+f_{1c} \cos (\omega t)+\cdots , \end{aligned}$$
(10)

where \(a_0 , a_1 , f_0 , f_{1s} , f_{1c} \) are coefficients to be determined. Higher harmonics and sub-harmonics of the excitation frequency \(\omega \) are neglected in Eqs. (9 and 10). Since the first-order harmonic is generally larger than other harmonics and is the one measured with great accuracy in the experiments, in the following analysis just the constant terms (zero-order) and the first-order harmonic are considered; additional harmonics can be obtained in similar way.

The following elementary trigonometric transformations are used in the derivations

$$\begin{aligned} \sin ^{2}(\omega t)= & {} \frac{1}{2}-\frac{1}{2}\cos (2\omega t), \end{aligned}$$
(11)
$$\begin{aligned} \sin ^{3}(\omega t)= & {} \frac{3}{4}\sin (\omega t)-\frac{1}{4}\sin (3\omega t). \end{aligned}$$
(12)

The following expressions are obtained from Eq. (9) making use of (5), (11) and (12)

$$\begin{aligned}&x^{2}=a_0^2 +2a_0 a_1 \sin (\omega t)+a_1^2 /2, \end{aligned}$$
(13)
$$\begin{aligned}&x^{3}=a_0^3 +(3/2) a_0 a_1^2 \nonumber \\&\quad +\,3 a_0^2 a_1 \sin (\omega t)+(3/4) a_1^3 \sin (\omega t), \end{aligned}$$
(14)
$$\begin{aligned}&D_t^\alpha x(t)=\omega ^{\alpha }a_1 \left[ \cos (\alpha \pi /2)\sin (\omega t)\right. \nonumber \\&\quad \left. +\,\sin (\alpha \pi /2)\cos (\omega t) \right] , \end{aligned}$$
(15)
$$\begin{aligned}&D_t^\alpha x^{2}(t)=\omega ^{\alpha }2a_0 a_1 \left[ \cos (\alpha \pi /2)\sin (\omega t)\right. \nonumber \\&\quad \left. +\,\sin (\alpha \pi /2)\cos (\omega t) \right] , \end{aligned}$$
(16)
$$\begin{aligned}&D_t^\alpha x^{3}(t)=\omega ^{\alpha }\left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) \left[ \cos (\alpha \pi /2)\sin (\omega t)\right. \nonumber \\&\quad \left. +\,\sin (\alpha \pi /2)\cos (\omega t) \right] . \end{aligned}$$
(17)

The zero-order terms, once inserted in Eq. (7), give the following algebraic equation

$$\begin{aligned} f_0 =k_1 a_0 +k_2 \left( {a_0^2 +a_1^2 /2} \right) +k_3 \left( {a_0^3 +3 a_0 a_1^2 /2} \right) , \end{aligned}$$
(18)

since it has been assumed that the fractional derivative of constant terms is zero.

The terms multiplied by \(\sin (\omega t)\) give the expression

$$\begin{aligned}&f_{1s} \left[ {1+\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)} \right] -f_{1c} \tau _r^\alpha \omega ^{\alpha }\sin (\alpha \pi /2)\nonumber \\&\quad =k_1 a_1 +k_2 2a_0 a_1 +k_3 \left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) \nonumber \\&\qquad +\,\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)\left[ (k_1 +\tilde{k}_1 )a_1\right. \nonumber \\&\qquad +(k_2 +\tilde{k}_2 )2a_0 a_1 \nonumber \\&\qquad +\,(\left. {k_3 +\tilde{k}_3 )\left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] . \end{aligned}$$
(19)

The terms multiplied by \(\cos (\omega t)\) are governed by the equation

$$\begin{aligned}&f_{1c} \left[ {1+\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)} \right] +f_{1s} \tau _r^\alpha \omega ^{\alpha }\sin (\alpha \pi /2)\nonumber \\&\quad =\tau _r^\alpha \omega ^{\alpha }\sin (\alpha \pi /2)\left[ {(k_1 +\tilde{k}_1 )a_1 +(k_2 +\tilde{k}_2 )2a_0 a_1 } \right. \nonumber \\&\qquad +\,(\left. {k_3 +\tilde{k}_3 )\left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] . \end{aligned}$$
(20)

The solution of the linear algebraic equations (19) and (20) is

$$\begin{aligned} f_{1s}= & {} \frac{A}{1+\tau _r^{2\alpha } \omega ^{2\alpha }+2\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)}, \end{aligned}$$
(21)
$$\begin{aligned} f_{1c}= & {} \frac{B}{1+\tau _r^{2\alpha } \omega ^{2\alpha }+2\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)}, \end{aligned}$$
(22)

where

$$\begin{aligned} A= & {} k_1 a_1 +k_2 2a_0 a_1 +k_3 \left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) \nonumber \\&+\,\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)\left[ (2k_1 +\tilde{k}_1 )a_1\right. \nonumber \\&+(2k_2 +\tilde{k}_2 )2a_0 a_1 \nonumber \\&+\,(\left. {2k_3 +\tilde{k}_3 )\left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] \nonumber \\&+\,\tau _r^{2\alpha } \omega ^{2\alpha }\left[ {(k_1 +\tilde{k}_1 )a_1 +(k_2 +\tilde{k}_2 )2a_0 a_1 } \right. \nonumber \\&+\,(\left. {k_3 +\tilde{k}_3 )\left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] , \end{aligned}$$
(23)
$$\begin{aligned} B= & {} \tau _r^\alpha \omega ^{\alpha }\sin (\alpha \pi /2)\left[ {\tilde{k}_1 a_1 +\tilde{k}_2 2a_0 a_1 } \right. \nonumber \\&+\,\left. {\tilde{k}_3 \left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] . \end{aligned}$$
(24)

It is interesting to observe that Eq. (21) gives the force in phase with the displacement x, i.e. the elastic response of the material, which is a function of the frequency according to the present viscoelastic model. For some materials like metals, this effect can be very small. On the other side, Eq. (22) gives the damping force, which is 90 degrees out-of-phase with respect to the displacement. Equations (21) and (22) are inserted into Eq. (10), which is finally introduced in the equation of motion (8). The right-hand term in Eq. (8) can be rewritten as

$$\begin{aligned} \tilde{f}\sin (\omega t+\phi )=\tilde{f}\left[ {\cos \phi \sin (\omega t)+\sin \phi \cos (\omega t)} \right] . \end{aligned}$$
(25)

The zero-order terms inserted in Eq. (8) give the following algebraic equation

$$\begin{aligned} k_1 a_0 +k_2 \left( {a_0^2 +a_1^2 /2} \right) +k_3 \left( {a_0^3 +3 a_0 a_1^2 /2} \right) =0. \end{aligned}$$
(26)

The terms multiplied by \(\sin (\omega t)\) give the expression

$$\begin{aligned} -m \omega ^{2}a_1 +f_{1s} =\tilde{f}\cos \phi , \end{aligned}$$
(27)

where the symbol \(f_{1s}\) stays for the long expression given in Eq. (21) once (23) is substituted in it. The terms multiplied by \(\cos (\omega t)\) are governed by the equation

$$\begin{aligned} f_{1c} =\tilde{f}\sin \phi , \end{aligned}$$
(28)

where \(f_{1c}\) is obtained by Eq. (22) once (24) is substituted in it. Equations (26–28) form a set of three nonlinear transcendental equations that can be solved numerically. In order to simplify considerably the numerical solution of the equations, it is convenient to set \(y=\cos \phi , z=\sin \phi \) and to add the \(4\mathrm{th}\) equation \(y^{2}+z^{2}=1\). This transformation allows to find the roots of polynomial equations in the unknowns \(a_0 , a_1 , y\hbox { and }z\); the phase angle is then obtained as \(\phi =\cos ^{-1}y\).

Linear and nonlinear damping terms appear in Eq. (28). Equation (24) shows that the two nonlinear damping terms depend on the geometric viscoelastic coefficients \(\tilde{k}_2\) and \(\tilde{k}_3\), but they do not depend on the nonlinear stiffness \(k_2\) and \(k_3\). The quadratic damping term reduces the linear damping, while the cubic ones increase it. Damping is also frequency dependent. The presence of viscoelasticity changes the natural frequency of the system since it changes the stiffness, even if the effect can be very small for many materials, specifically, for those respecting the relationship \(\tau _r^\alpha \omega ^{\alpha }<<1\). In the narrow frequency region around the resonance, the denominator in Eqs. (21) and (22) is almost constant, as well the quantity \(\omega ^{\alpha }\).

The amplitude of the damping force \(f_{1c}\) can be written as

$$\begin{aligned} f_{1c} =\gamma \left[ {\tilde{k}_1 a_1 +\tilde{k}_2 2a_0 a_1 } \right. +\left. {\tilde{k}_3 \left( {3 a_0^2 a_1 +(3/4) a_1^3 } \right) } \right] , \end{aligned}$$
(29)

where \(\gamma \) is a damping coefficient given by

$$\begin{aligned} \gamma =\frac{\tau _r^\alpha \omega ^{\alpha }\sin (\alpha \pi /2)}{1+\tau _r^{2\alpha } \omega ^{2\alpha }+2\tau _r^\alpha \omega ^{\alpha }\cos (\alpha \pi /2)}. \end{aligned}$$
(30)

For \(\alpha =1\), Eq. (30) simplifies into

$$\begin{aligned} \gamma =\frac{\tau _r \omega }{1+\tau _r^2 \omega ^{2}}. \end{aligned}$$
(31)

In case of small damping, i.e. for \(\tau _r \omega<<1\), Eq. (31) gives \(\gamma \simeq \tau _r \omega \). Equation (29) is a nonlinear expression involving the amplitudes of the zero-order (mean value) \(a_{0}\) and the first-order harmonic \(a_{1}\) of the vibration displacement x. In general, \(a_{0}\) is smaller than \(a_{1}\).

In case of systems with only linear and cubic stiffness, the zero-order displacement \(a_{0} = 0\). Then, for \(\alpha =1\), the damping force \(F_{D}\) is obtained by Eq. (29) multiplied by \(\cos (\omega t)\); taking Eqs. (9) and (13) into account, it gives

$$\begin{aligned} F_D (t)=\frac{\tau _r }{1+\tau _r^2 \omega ^{2}}\left[ {\tilde{k}_1 \dot{x}} \right. +(3/2) \left. {\tilde{k}_3 x^{2}\dot{x}} \right] . \end{aligned}$$
(32)

Therefore, the nonlinear damping term is of the type \(x^{2}\dot{x}\), which agrees with the expression phenomenologically introduced in references [12, 13]; the same term was also obtained in the specific configuration of two inclined linear dashpots in [14].

The formulation (29) is more complicated than (32) and must be used for systems that present also quadratic stiffness. Equation (29) is the first general and accurate derivation of nonlinear damping for vibration of a geometrically nonlinear system. In fact, previous derivations based on the Kelvin–Voigt viscoelastic model were not capable of reproducing the experimental results, as previously discussed. This approach is valid for continuous systems discretized with a single degree of freedom and can be extended to systems discretized with any number of degrees of freedom.

It is convenient to rewrite the system parameters in the following form:

$$\begin{aligned}&\frac{k_1 }{m}=\omega _n^2 , \quad \frac{k_2 }{m}=\beta _2 \frac{k_1 }{h}, \quad \frac{k_3 }{m}=\beta _3 \frac{k_1 }{h^{2}}, \end{aligned}$$
(33a--c)
$$\begin{aligned}&\tau _r=\frac{1}{\omega _n }\left[ {\frac{2 \zeta }{\sin (\alpha \pi /2)}} \right] ^{1/\alpha }, \end{aligned}$$
(33d)
$$\begin{aligned} \tilde{k}_1&=k_1 , \quad \frac{\tilde{k}_2 }{m}=\tilde{\beta }_2 \frac{k_1 }{h}, \quad \frac{\tilde{k}_3 }{m}=\tilde{\beta }_3 \frac{k_1 }{h^{2}}, \end{aligned}$$
(33e--g)

where \(\omega _n =\sqrt{k/m}\) is the natural frequency, used to non-dimensionalize the excitation frequency \(\omega ; \beta _2, \beta _3, \tilde{\beta }_2, \tilde{\beta }_3 \) are the non-dimensional nonlinear stiffness parameters of the two nonlinear springs, \(\zeta \) is the damping ratio, which is traditionally used in linear viscous damping models, and h is a characteristic dimension of the system used to non-dimensionalize the vibration amplitude x and its zero-order and first-order harmonic \(a_{0}\) and \(a_{1}\); for plates and shells, h is the thickness. It is observed that the introduction of the damping ratio in the expression of the relaxation time, see Eq. (33d), allows to link a traditional viscoelastic parameter, \(\tau _r \), to a coefficient, \(\zeta \), commonly used by the vibration community. Equation (33e) is introduced just for convenience, but a different value of \(\tilde{k}_1 \) can be assumed with the only consequence that Eq. (33d) must be modified accordingly.

5 Experimental results

Three mechanical systems are considered: (i) a hardening type constituted by a stainless steel rectangular plate; (ii) a softening type, given by a stainless steel circular cylindrical panel; (iii) a hollow rod in zirconium alloy, which is an example of weak hardening system.

5.1 Hardening system: rectangular plate

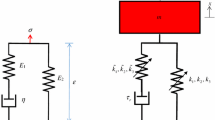
Experiments have been conducted on an almost squared, AISI 304 stainless steel plate (see Fig. 4) with the following dimensions and material properties: in-plane dimensions \(a = 0.25\,\hbox { m}\) and \(b = 0.24\,\hbox { m}\), thickness \(h = 0.0005\,\hbox { m}\), Young’s modulus \(E = 193 \times 10^{9}\) Pa, mass density \(\rho = 8000\,\hbox {kg/m}^{3}\) and Poisson ratio \(\nu = 0.29\). The thin plate was bolted to an AISI 410 stainless steel rectangular frame. The boundary conditions are almost those of a clamped plate, with blocked displacements in the three directions at the plate edges and rotation constrained by rotational springs of very high rotational stiffness. The experimental set-up of the nonlinear vibration measurement is illustrated in Fig. 4. The plate has been subjected to harmonic excitation, increasing or decreasing the excitation frequency by very small steps in the spectral neighbourhood of the lowest natural frequency to characterize the nonlinear vibration responses. The excitation has been provided by an electrodynamical exciter (shaker), model B&K 4810. A piezoelectric miniature force transducer B&K 8203, of the weight of 3.2 g, has been applied to the plate at \(a/5\hbox { and }4b/5\) to measure the force excitation and has been connected to the shaker with a stinger. The plate response has been measured by using a laser Doppler vibrometer Polytec (sensor head OFV-505 and controller OFV-5000) in order to have non-contact measurement with no introduction of additional inertia. The laser beam has been pointed to the centre of the plate during nonlinear tests since the goal was to investigate the nonlinear vibration of the fundamental mode, which has maximum displacement at that location. The natural frequency of the fundamental mode is 72.45 Hz, and the mode shape has a half-wave in both the in-plane directions, with zero displacements at the edges. The closed-loop control used in the experiments keeps constant the amplitude of the harmonic excitation force, after filtering the signal from the load cell in order to use only the harmonic component with the given excitation frequency. Experiments have been performed increasing and decreasing the excitation frequency (up and down); the frequency step used in this case is 0.05 Hz, 16 periods have been measured with 128 points per period, and 40 periods have been waited before data acquisition every time that the frequency is changed.

Fig. 4
figure 4

Schematic of the nonlinear vibration measurement set-up: a laser Doppler vibrometer with displacement and velocity decoders is used to read out the vibration of the structure at an antinode M. As an example of structure, the tested rectangular plate is shown, with indication of the excitation point E and the measurement point M. The vibration and the force input signals are received by an analog–digital converter (front-end) connected to a computer. The converter is capable of producing the excitation signal through a closed-loop control, drawn on the side, where the feedback comes from the load cell signal Q(t) measuring the harmonic force excitation provided to the structure at that specific excitation frequency. The excitation signal v(t) produced by the controller goes to a power amplifier and becomes V(t); then, it drives the suspended electrodynamic exciter (shaker), which is mechanically connected to the tested structure through a stinger and the piezoelectric miniature load cell. The excitation force F(t) is applied by the exciter to the structure, and it is measured by the load cell, which closes the loop providing the signal Q(t). The software installed on the computer allows to analyse the different harmonics contained in the signal or to identify complex nonlinear dynamics. It finally produces the frequency–amplitude curves for the zero-order and first-order harmonic at different excitation forces

Full size image

Figure 5 shows the first-order harmonic of the forced vibrations (displacement, directly measured by using the laser Doppler vibrometer with displacement decoder, divided by the plate thickness h; measurement position at the centre of the plate) of the plate in vertical position in the spectral neighbourhood of the fundamental natural frequency, versus the non-dimensional excitation frequency \(\omega /\omega _{n}\), for four different harmonic excitation force levels: 0.1, 0.3, 0.7 and 0.9 N. Experiments are compared to numerical simulations. Results show a clear hardening-type nonlinearity with an increase of about 10% of the resonance frequency for vibration amplitude around 1.5 times the plate thickness. This nonlinear behaviour is reduced with respect to the one of a perfectly flat plate that presents a frequency increase of about 30% for vibration amplitude around 1.5 times the plate thickness [32]. The reason of the reduced nonlinearity is due to the initial geometric imperfections, which have been measured [32]. The hysteresis between the two curves obtained increasing and decreasing the excitation frequency is clearly visible for all the five excitation levels. Sudden increments (jumps) of the vibration amplitude are observed, as expected for hardening-type nonlinear systems in case of small damping.

Fig. 5
figure 5

Nonlinear vibrations of rectangular plate (hardening system) versus excitation frequency for different harmonic excitation forces; first-order harmonic. Comparison of experiments (small dots) and numerical simulations (circles)

Full size image

5.2 Softening system: circular cylindrical panel

Tests have been carried on a stainless steel circular cylindrical panel, with the following dimensions and material properties: length 0.199 m, radius 2 m, opening angle \(=\) 0.066 rad, thickness \(h =\)  0.0003 m, \(E = \) 195 \(\times 10^{9}\) Pa, \(\rho =\) 7800 \(\hbox {kg/m}^{3}\) and \(\nu =\)  0.3. This is a shallow shell and the fundamental mode presents one half-wave in both in-plane directions. The panel was inserted into a heavy rectangular steel frame made of several thick parts, having V-grooves designed to hold the panel and to avoid transverse (radial) displacements at the edges. Practically all the in-plane displacements normal to the edges were allowed at the edges; in-plane displacements parallel to the edges were elastically constrained by silicon inserted in the supporting grooves. The experimental set-up is similar to the one of the rectangular plate described in Sect. 5.1. The excitation point has been chosen at 1/4 of the length and 1/3 of the curvilinear width.

Fig. 6
figure 6

Forced nonlinear vibrations of the circular cylindrical panel (softening system) versus excitation frequency for different harmonic excitation forces. Comparison of experiments (small dots) and numerical simulations (circles) for the first-order harmonic

Full size image

Figure 6 shows the measured and calculated vibration displacement for the first-order harmonic versus the excitation frequency in the neighbourhood of the fundamental mode for five different force levels: 0.01, 0.05, 0.1, 0.15 and 0.2 N. The 0.01 N level gives a good evaluation of the natural frequency, identified at 95.2 Hz. The hysteresis between the two curves obtained for the same harmonic excitation force (one increasing the frequency, the other decreasing it) is clearly visible for the three larger excitation levels (0.1, 0.15 and 0.2 N). Jumps of the vibration amplitude are observed when increasing and decreasing the excitation frequency; these indicate softening-type nonlinearity.

5.3 Weak hardening system: hollow rod in zirconium alloy

A hollow rod of annular section made of zirconium alloy has been experimentally studied. It is 0.9 m long with external and internal diameters of 9.50 and 8.28 mm, respectively, giving a wall thickness of 0.61 mm; \(E =\)  98 \(\times 10^{9}\) Pa, \(\rho =\)  6450 \(\hbox {kg/m}^{3}\) and \(\nu =\)  0.37. The boundary conditions were designed to be very close to perfectly clamped ends, allowing to manually release axial stresses in case of temperature variations. The excitation point has been chosen 50 mm away from one end, in order to reduce the interaction between the vibrating rod and the electrodynamic exciter. The fundamental mode of vibration has a natural frequency of 33.79 Hz and very low damping. Nonlinear vibration tests have been conducted in the frequency neighbourhood of this mode at several different levels of harmonic excitation. The maximum vibration amplitudes of the first-order harmonic observed in a cycle are presented in Fig. 7 for harmonic forces of 0.1, 0.15, 0.2 and 0.35 N versus the excitation frequency. Both experiments and numerical simulations are presented. They show a very weak hardening behaviour, since the change in the natural frequency is less than 1% for vibration amplitudes up to 3.6 times the wall thickness \(h=\)  0.61 mm, which is used to non-dimensionalize the vibration amplitude.

Fig. 7
figure 7

Nonlinear vibrations of the clamped zirconium rod (hardening system) versus excitation frequency for different harmonic excitation forces; first-order harmonic. Comparison of experiments (small dots) and numerical simulations (circles)

Full size image

6 Comparison of numerical and experimental results

Calculations have been done for order of the fractional derivative \(\alpha = 1\). In fact, for the three studied cases, the damping is low and results calculated for different order of the fractional derivative are practically coincident; therefore, it is convenient to apply the classical first derivative. The system parameters used in the numerical simulations are given in Table 1 for the three cases. The presence of quadratic stiffness for the plate, in addition to the linear and the cubic stiffness, is a consequence of the initial geometric imperfections. The damping parameters \(\zeta , \tilde{\beta }_2 \) and \(\tilde{\beta }_3 \) are identified from the experiments. The stiffness and mass parameters \(\omega _n,\, \beta _2 \hbox { and }\beta _3 \) can be obtained by modelling the system [1, 32, 33] or can be identified by experimental data without any necessity of developing a model. A very good agreement of the full model and the identified stiffness parameters has been shown for plates and shells [2]. The identification procedure of stiffness has been previously reported [2].

Table 1 System parameters for the rectangular plate, the circular cylindrical panel and clamped rod cases; derivative of order \(\alpha = 1\)
Full size table

Figure 5 shows the comparison of the numerical and experimental results for the plate. The same system parameters are used to simulate the different five excitation levels. The comparison is very good and shows that the nonlinear damping is perfectly capable of reproducing the experimental results. In case of linear viscous damping model, the damping ratio values identified from the experiments are given in Table 2. Therefore, the damping increases 6.4 times with the vibration amplitude in this case. Despite the large variation of the linear damping necessary to model the dynamic response, the nonlinear damping is fully representing it. The nonlinear damping is completely described by the two parameters \(\zeta \) and \(\tilde{\beta }_3\). Differently from the stiffness, the dissipation parameters cannot be modelled with the present knowledge and must be identified from experiments. It is important to observe that these two are not material parameters, but geometrically nonlinear characteristics of the whole structure and its material.

Table 2 Equivalent damping ratio in case of linear viscous damping for the rectangular plate
Full size table

An excellent agreement between experimental and numerical results is obtained also for the curved panel. The comparison is illustrated in Fig. 6. In case of linear viscous damping model, the damping ratio values identified from the experiments are given in Table 3. The damping increases 1.6 times with the vibration amplitude in this case. The dissipation is described by only two parameters: \(\zeta \) and \(\tilde{\beta }_3 \), while \(\tilde{\beta }_2 \) is null also in this case.

Table 3 Equivalent damping ratio in case of linear viscous damping for the circular cylindrical panel
Full size table

The clamped rod is the last example that is presented here for validation of the theory; in fact, experiments have been conducted on three of the most classical continuous systems in order to show the validity of the formulation. The comparison of the experimental results to those obtained by the identified one-degree-of-freedom model is presented in Fig. 7. Also in this case the agreement is satisfactory. There is a narrow frequency region after the resonance where some additional nonlinear phenomena are observed that are not captured by the model (it would require more degrees of freedom to model it), but this is a small difference. Table 4 shows the damping ratio values identified from the experiments. The damping is doubled in this case between the linear case and the larger excitation level investigated. Also in this case, it has been observed that the quadratic nonlinear damping parameter \(\tilde{\beta }_2 \) is null.

Table 4 Equivalent damping ratio in case of linear viscous damping for the clamped zirconium rod
Full size table

7 Numerical results in case of medium damping

Since the three experimentally studied cases have damping ratio below 0.01, the effect of the fractional derivative on the vibration response is insignificant. For this reason, additional calculations have been done for the plate by changing the damping ratio to \(\zeta = 0.03\), i.e. increasing it by 13 times with respect to the experimental case previously shown. A harmonic force excitation of 15 N has been applied. The relaxation time is obtained from Eq. (33d). The forced vibration response versus frequency is shown in Fig. 8 for three values of the order of fractional derivative: \(\alpha =\)  1, 0.8, 0.6. Numerical results show that the order of the fractional derivative changes the qualitative behaviour of the vibration response. In particular, the frequency of the peak of the vibration amplitude is moved to the right by decreasing the value of \(\alpha \); at the same time, the curve becomes steeper on the right side of the peak. Therefore, the order of fractional derivative is a further viscoelastic parameter to be identified in case of nonlinear vibrations of systems with medium and large damping ratio; this is the case of structures made of rubber, fabrics or biological materials.

Fig. 8
figure 8

Nonlinear vibrations of the hardening system (rectangular plate) for largely increased damping \(\zeta \) = 0.03 versus excitation frequency for different orders of the fractional derivative; plot of the first-order harmonic; excitation 15 N; o, \(\alpha =\)  1; *, \(\alpha = \) 0.8; \(\Delta \), \(\alpha =\) 0.6

Full size image

8 Conclusions

This study derives for the first time the correct nonlinear damping. In particular, geometrically nonlinear viscoelasticity is applied to the fractional linear solid model. Identification of the nonlinear damping parameters from experimental cases shows that the nonlinear dissipation force is cubic of the type \(x^{2}\dot{x}\) for systems with only cubic stiffness, while the zero-order displacement also appears in the case of quadratic stiffness giving rise to a more complicated expression. Even if the formulation allows for a quadratic nonlinear damping term, the corresponding coefficient has been identified to be zero in the cases investigated. However, this term could appear in the study of more complicated problems with additional degrees of freedom, as those arising for internal resonances. The approach introduced is valid for continuous systems discretized with a single degree of freedom; it can be extended to systems discretized with any number of degrees of freedom.