An analytical approach for the vibration behavior of viscoelastic cylindrical shells under internal moving pressure

Abstract

In the current paper, the vibrational behavior of viscoelastic cylindrical shells under moving internal pressure is studied, analytically. The viscoelastic behavior is considered as viscoelastic in shear and elastic in the bulk. The equations of motion are extracted based on the classical shell theory by applying Hamilton’s principle. These equations which are a system of coupled partial differential equations are solved by employing a closed form mathematic method, and the natural frequencies, the critical velocity, and response due to moving pressure are determined. Moreover, the effects of different geometric and viscoelastic parameters on the results are studied. The results are compared with the finite element analysis and the results available in the literature.

1 Introduction

Moving loads have a significant effect on dynamic stresses in the structures and cause them to vibrate, especially at high velocities. Therefore, the moving load on the structures has become one of the notified problems in engineering. Transmitted fluid in a tube, and the air flow on aircraft parts or a car body are some of the practical cases. Also, the material properties are an important issue which has noticeable effects on the responses of structures due to this excitation. In most studies of structures in recent years, the material has been assumed elastic while the main of materials has time-dependent characteristics, and they are in the viscoelastic field. Jones and Bhuta [1] determined the response of an elastic cylindrical shell under a moving ring load with constant velocity, using Duhamel integrals by considering the classical shell theory (CST). Huang [2,3,4] studied the effects of moving pressure on an infinitely long viscoelastic cylindrical shell with a material that obeys the solid linear standard (SLS) model. The Williams modal acceleration method was applied to reduce the governing equations to a set of quasi-static equations. Datta et al. [5] investigated the dynamic response of pipelines to moving loads. The pipeline was modeled as an elastic thin shell. A thin layer of viscoelastic material was assumed to separate the pipe from the ground. It was indicated that the viscoelastic layer does not influence the pipe response. Singh et al. [6] studied the dynamic response of a buried orthotropic infinite cylindrical shell subjected to a radial load which moves along the shell axis. Huang and Hsu [7] investigated the resonance of a rotating elastic cylindrical shell under harmonic moving loads using the Love–Timoshenko theory. Panneton et al. [8] evaluated the vibration and sound radiation of an elastic cylindrical shell excited by a circumferentially moving load. They identified the critical velocity numerically. Singh et al. [9] determined the non-axisymmetric dynamic behavior of fluid-filled orthotropic cylindrical shells under a load which was moving along the shell axis. The shell was considered thick. Barkanov et al. [10] determined the transient response of sandwich beams, plates, and shells with viscoelastic layers subjected to impulse loading by applying the finite element (FE) method. The dynamic stability of elastic cylindrical shells under periodic axial load was analyzed by Pellicano and Amabili [11]. The geometric nonlinearity was considered using Donnell’s shallow shell theory. The results were obtained using a numerical method based on the Galerkin procedure. Sheng and Wang [12] investigated the dynamic behavior of functionally graded (FG) cylindrical shells with piezoelectric layers subjected to moving loads numerically. The governing equations were determined using the first-order shear deformation theory (FSDT), Hamilton’s principle, and the Maxwell equation. Pellicano [13] studied the dynamic stability of elastic cylindrical shells subjected to compressive static and periodic axial loads. The nonlinearity of the system was modeled by applying the Sanders–Koiter theory. The nonlinear partial differential equations were reduced to a set of ordinary differential equations using the Lagrange equations. Sofiyev [14] presented an analytical procedure to study the dynamic behavior of an infinitely long, FGM cylindrical shell subjected to combined action of the axial tension and internal constant moving compressive pressure. Sofiyev et al. [15] investigated the dynamic behavior of an infinitely long, non-homogenous orthotropic cylindrical shell resting on an elastic foundation under combined axial tension and internal moving compressive pressure. The effects of some parameters such as the Pasternak foundations and materials distribution were studied parametrically. Malekzadeh and Heydarpour [16] presented the transient thermo-elastic analysis of FG cylindrical shells subjected to moving pressure and heat flux. A combination of differential quadrature (DQ) and FE methods was employed to discretize the governing equations in the spatial domain. Wang et al. [17] studied the nonlinear vibration of an elastic cylindrical shell subjected to a harmonic excitation moving in a circular path. The equations were solved by applying Galerkin’s method. Lee and Seok [18] investigated the dynamic behavior of an elastic hollow thick cylinder under a dual traveling force applied to the inner surface. The governing equations were solved by employing the Frobenius method. Tahami et al. [19] investigated the optimum designs of FG carbon nanotube-reinforced pipes conveying fluid which were under a moving load, by applying a harmony search algorithm. The dynamic displacement of the system was determined based on the DQ method. Thomas and Roy [20] studied the vibrational behavior of functionally graded carbon nanotube (FG-CNT)-reinforced composite shells based on Mindlin’s hypothesis. It was concluded that the carbon nanotube (CNT) distribution and the volume fraction of the CNT have a remarkable effect on the vibrational behavior of the structure. Eftekhari [21] presented a numerical method based on a DQ methodology which was used for a vibration analysis of variable thickness circular arches subjected to a moving point load. Askari and Esmailzadeh [22] studied nonlinear and linear vibrations of fluid conveying CNT considering thermal effects and a nonlinear Winkler–Pasternak foundation. The governing equations were derived using the nonlocal Euler–Bernoulli beam theory. The nonlinear differential equations were solved by applying Galerkin’s procedure. Tahami et al. [23] studied the dynamic response of FG-CNT-reinforced pipes conveying fluid subjected to accelerated moving load. The material properties of the pipe were temperature dependent, and the DQ method and Newmark’s time integration scheme were applied to obtain the dynamic response of the system. Lu et al. [24] investigated the dynamic behavior of an infinite circular tunnel subjected to moving loads. According to Biot’s theory, the Helmholtz equations were derived and the response was determined using the Fourier transform method. Norouzi and Alibeigloo [25] presented a static analysis of a viscoelastic cylindrical panel made of FGM, under transverse uniform pressure using three-dimensional elasticity theory. For simply supported boundary conditions, an analytical solution based on the state space method and Fourier expansion was presented, and for other boundary conditions, a semi-analytical method using DQ method has been applied. Akbari et al. [26] investigated the dynamic response of an FG viscoelastic cylinder under thermo-mechanical loads. The meshless local Petrov–Galerkin method was applied to extract the result. A numerical investigation of geometrically nonlinear forced vibration of a cantilever shell was presented by Avramov and Malyshev [27]. The dynamic responses were determined numerically using a combination of the shooting technique and the continuation algorithm. Sofiyev presented a solution for the dynamic stability of heterogeneous orthotropic viscoelastic [28] and FGM [29] cylindrical shells under an axial load and determined the critical time. He studied the effect of different parameters on the stability of the system. Also, he [30] prepared a complete literature review on the vibration and buckling problems of FG and composite conical shells. Mirzaei and Ramezani [31] studied the transient elasto-dynamic response of cylindrical shells subjected to internal moving pressure by applying an analytical solution. The shell was thick, and the effects of transverse shear and rotary inertia were considered. Arazm et al. [32] presented an analytical method to analyse the dynamic behavior of FG shells subjected to moving internal pressure. The effect of z/R was not considered in their work. Sadeghi and Alibeigloo [33] studied the free vibrational behavior of a viscoelastic cylindrical shell using the theory of elasticity. The viscoelastic material has been assumed to obey the Boltzmann model, and the time-dependent modulus of elasticity was modeled by employing Prony series. The governing equations of motion have been solved analytically using the state space technique and Fourier series. Sofiyev et al. [34] analyzed the free vibration and the dynamic stability of FG viscoelastic plates subjected to a compressive load and resting on the Winkler and Pasternak elastic foundations. The equations were extracted by employing the concepts of Boltzmann and Volterra integral, and they have been solved using the Galerkin and Laplace methods.

In the analysis of shells under moving load, most of the researchers investigated elastic shells. In this paper, the governing equations of motion for a viscoelastic cylindrical shell subjected to an internal moving pressure are extracted by assuming the CST as the displacement field and applying Hamilton’s principle. In the formulation, the following features are considered:

• (i) The shear and bulk behavior of the materials are separated. The shear behavior is defined with the SLS model, and the bulk behavior is assumed as elastic.

• (ii) The effect of z/R is considered in the formulation. So, the stresses resultants are calculated with more precession.

• (iii) The shell has a finite length.

The governing equations which are a system of coupled partial differential equations are solved analytically, and the frequencies, critical velocity, and the response due to moving pressure are determined. By performing a parametric study, the effects of different viscoelastic parameters on the results are studied.

2 Governing equations

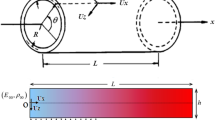
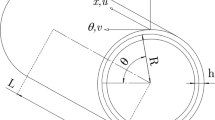
The location of each point on the cross section of a shell in the cylindrical coordinate system can be defined by three parameters r, x, and $\theta$ as Fig. 1. The origin of the coordinate system is on the middle surface. We have $r=R_{0}+z$; where $R_{0}$ is the middle surface radius and z is a through thickness variable, which is measured from the middle surface of the shell. The geometry of the shell is shown in Fig. 1.

Fig. 1

Geometry of the cylindrical shell

The displacement field for axisymmetric conditions is defined by employing classical shell theory as follows [32]:

$$\begin{aligned} u(x,z,t)=u_{0} (x,t)-z\frac{\partial \,w_{0} (x,\,t)}{\partial \,x};v=0\,;w(x,z,t)=w_{0} (x,t). \end{aligned}$$

(1)

u, v, and w are displacement components in x, $\theta$, and z directions, respectively; $u_{0}$ and $w_{0}$ are the middle surface displacements which are unknown functions of x and t, and t is time. According to Eq. (1), the radial displacement of each layer is the same or it is independent of z. For the linear kinematic relations, the nonzero strains are the following [35]:

$$\begin{aligned} e_{x} =\frac{\partial \,u}{\partial \,x}=\frac{\partial \,u_{0} }{\partial \,x}-z\frac{\partial ^{2}w_{0} }{\partial \,x^{2}};\,\,\,e_{\theta } =\frac{w}{r}=\frac{w_{0} }{R_{0} +z}. \end{aligned}$$

(2)

The constitutive equations according to Hooke’s law are [35]:

$$\begin{aligned} \sigma _{x} =b_{0} (e_{x} +e_{\theta } )+2Ge_{x};\,\,\sigma _{\theta } \;=b_{0} (e_{x} +e_{\theta } )+2Ge_{\theta };\,b_{0} =K-\frac{2G}{3} \end{aligned}$$

(3)

where K and G are the bulk and shear modulus, respectively. Due to $\varepsilon _{z}= 0$, the value of $\sigma _{\mathrm {z}}$ has not effect on the strain energy. The strain energy U, kinetic energy T, and the external work W are the following [36]:

$$\begin{aligned} U= & {} \frac{1}{2}\iiint {(\sigma _{x} \varepsilon _{x} +\sigma _{\theta } \varepsilon _{\theta } )\text {d}V};\,\,\text {d}V=(R_{0} +z)\cdot \text {d}z\cdot \text {d}\theta \cdot \text {d}x, \end{aligned}$$

(4.1)

$$\begin{aligned} T= & {} \frac{1}{2}\iiint {\rho \left[ {\left( {\frac{\partial u_{x} }{\partial t}} \right) ^{2}+\left( {\frac{\partial u_{z} }{\partial t}} \right) ^{2}} \right] \text {d}V}\;\;\,;\;\;-h/2\le z\le h/2;\;\;0\le \theta \le 2\pi ;\;\;0\le x\le L, \end{aligned}$$

(4.2)

$$\begin{aligned} W= & {} \iint \limits _s {\left( {f_{x} u_{x} +f_{z} u_{z} } \right) }ds;\quad ds=\left( R_{0} -\frac{h}{2}\right) \text {d}\theta .\text {d}x;\,\,f_{z} =P;\,f_{x} =0 \end{aligned}$$

(4.3)

Fig. 2

SLS model

where $f_{x}$ and $f_{z}$ are the traction components in x and z directions, respectively, and P is the internal pressure distribution. The stress resultants are defined as follows:

$$\begin{aligned} N_{x} {=}\int _{h/2}^{-h/2} {\sigma _{x} \left( 1+\frac{z}{R_{0} }\right) } \,\text {d}z;M_{x} {=}\int _{h/2}^{-h/2} {\sigma _{x} \left( 1+\frac{z}{R_{0} }\right) \,} z\,\text {d}z;\,\,N_{\theta } {=}\int _{h/2}^{-h/2} {\sigma _{\theta } \,} \text {d}z;\,M_{\theta } {=}\int _{h/2}^{-h/2} {\sigma _{\theta \,} z\,} \text {d}z.\nonumber \\ \end{aligned}$$

(5)

The Hamilton principle states that:

$$\begin{aligned} \delta \int \limits _{t_{1} }^{t_{2} } {(T-U+W)\text {d}t} =0. \end{aligned}$$

(6)

By substituting Eqs. (1)–(5) into Hamilton’s equation [(Eq. (6)], the equations of motion in terms of stress resultants are derived as follows:

$$\begin{aligned}&R_{0} \frac{\partial N_{x} }{\partial \,x}-\rho R_{0} h\frac{\partial ^{2}u_{0} }{\partial \,t^{2}}+\frac{\rho h^{3}}{12}\frac{\partial ^{3}w_{0} }{\partial \,x\partial \,t^{2}}=0, \end{aligned}$$

(7.1)

$$\begin{aligned}&R_{0} \frac{\partial ^{2}M_{x} }{\partial \,x^{2}}-N_{\theta } -\frac{\rho h^{3}}{12}\frac{\partial ^{3}u_{0} }{\partial \,x\partial \,t^{2}}-\rho R_{0} h\frac{\partial ^{2}w_{0} }{\partial \,t^{2}}+\frac{\rho R_{0} h^{3}}{12}\frac{\partial ^{4}w_{0} }{\partial \,x^{2}\partial \,t^{2}}+P\left( R_{0} -\frac{h}{2}\right) =0. \end{aligned}$$

(7.2)

By substituting Eqs. (2), (3) into Eq. (5), the stress resultants are determined in terms of displacements:

$$\begin{aligned} N_{x}= & {} b_{1} h\frac{\partial \,u_{0} }{\partial \,x}-\frac{b_{1} h^{3}}{12R}\frac{\partial ^{2}w_{0} }{\partial \,x^{2}}+\frac{b_{0} h}{R}w_{0};\,\,M_{x} =\frac{b_{1} h^{3}}{12}\left( \frac{1}{R}\frac{\partial \,u_{0} }{\partial \,x}-\frac{\partial ^{2}w_{0} }{\partial \,x^{2}}\right) , \end{aligned}$$

(8.1)

$$\begin{aligned} N_{\theta }= & {} b_{0} h\frac{\partial \,u_{0} }{\partial x}+b_{1} \alpha _{0} \,w_{0};\,\,b_{1} =K+\frac{4}{3}G;\quad \alpha _{0} =\int _{-h/2}^{h/2} {\frac{\text {d}z}{R_{0} +z}}. \end{aligned}$$

(8.2)

In this paper, the Zener or SLS model is employed to model the characteristics of a viscoelastic material (Fig. 2).

As it is seen in Fig. 2, the SLS model contains a Kelvin element parallel with a spring. This model can predict the creep as well as the relaxation behaviors of materials. For this model, $K=K_{0}$, $G=\frac{G_{1} G_{2} +\eta G_{1} D}{G_{1} +G_{2} +\eta D}$, and $D=\frac{\partial }{\partial t}$ [37]. By substituting these parameters and Eq. (8.1) into Eq. (6), the equations of motion in terms of displacements are extracted in the general following form:

$$\begin{aligned} L_{1} [u_{0} (x,t),w_{0} (x,t)]=0;\,\,L_{2} [u_{0} (x,t),w_{0} (x,t),P]=0.\,\, \end{aligned}$$

(9)

$L_{1}$ and $L_{2}$ are differential operators. The explicit form of these equations in dimensionless form is reported later. Equations (9) are a system of two linear coupled partial differential equations. The boundary conditions are determined from Hamilton’s principle as follows:

$$\begin{aligned} RN_{x} \left. {\delta u_{0} } \right| _{0}^{L}= & {} 0\rightarrow N_{x} =0\,\,\,\,\,\text{ OR }\,\,\,\,u_{0} =0\,\,\,\,\,\,\,\,\,\,\,\text{ at }\,\,x=0,L,\; \nonumber \\ \left. {R\frac{\partial M_{x} }{\partial x}\delta w_{0} } \right| _{0}^{L}= & {} 0\rightarrow \frac{\partial M_{x} }{\partial x}\;=0\,\,\,\,\text{ OR }\,\,\;w_{0} =0\,\,\,\text{ at }\,\,x=0,L, \nonumber \\ RM_{x} \left. {\delta \frac{\partial w_{0} }{\partial x}} \right| _{0}^{L}= & {} 0\rightarrow M_{x} =0\,\,\,\,\text{ OR }\,\,\,\,\frac{\partial w_{0} }{\partial x}=0\,\,\,\text{ at }\,\,x=0,L. \end{aligned}$$

(10.1)

As special cases, the following boundary conditions have been used in the modal analysis in this text:

$$\begin{aligned} \mathrm{Clamped}:\,\,\,\,u_{0}= & {} 0\,,\,\,w_{0} =0,\,\frac{\partial w_{0} }{\partial x}=0;\,\,\,\,\mathrm{Simple}:\,\,\,w_{0} =0,\,\,\,N_{x} =0,\,M_{x} =0, \nonumber \\ \mathrm{Free}\,:\,\,N_{x}= & {} 0,\,M_{x} =0,\,\,\,\frac{\partial M_{x} }{\partial x}\;=0 \end{aligned}$$

(10.2)

3 Analytical solution

In this paper, to prepare a more convenient report of the results, the equations are converted into dimensionless form. For this purpose, the following dimensionless parameters are defined:

$$\begin{aligned} x^{*}= & {} \frac{x}{L};\;\;t^{*}=\frac{t}{t_{0} };\;\;h^{*}=\frac{h}{h_{0} };\;\;R^{*}=\frac{R_{0} }{R_{0}^{\prime }};\;\;w^{*}=\frac{w_{0} }{h_{0} };\;\;u^{*}=\frac{u_{0} }{h_{0} };\;\beta =\frac{\tau }{t_{0} };\;\;e=\frac{\rho }{K_{0} }\left( {\frac{h_{0} }{t_{0} }} \right) ^{2}, \nonumber \\ \;\varepsilon= & {} \frac{h_{0} }{L};\;\;P^{*}=\frac{P}{K_{0} };\,\,\;\;Z_{2} =\frac{R_{0}^{\prime }}{h_{0} }\,\,;\,\,R_{0}^{\prime }=R_{0};\,\,t_{0} =L\sqrt{\rho /K{ }_{0}} \end{aligned}$$

(11)

where $h_{0}$, $R_{0}$, and $t_{0}$ are thickness, radius, and time characteristics, respectively; and (*) stands for a dimensionless quantity. By applying the above dimensionless parameters into Eq. (9), the dimensionless form of the equations of motion is determined as Eq. (12.1),

$$\begin{aligned}&-\,\varepsilon ^{3}\frac{h^{{*}{2}}}{12}\frac{\partial ^{3}}{\partial x^{{*}{3}}}L_{6} [a_{10},a_{11},\,w^{*}]+\varepsilon ^{2}R^{*}Z_{2} \frac{\partial ^{2}}{\partial x^{{*}{2}}}L_{6} [a_{10},a_{11} ,\,u^{*}]-e\;R^{*}Z_{2} \frac{\partial ^{2}}{\partial t^{{*}{2}}}L_{6} [\beta G_{1}^{*},G_{0}^{*},\,u^{*}] \nonumber \\&\quad +\,\varepsilon \frac{\partial }{\partial x^{*}} \left( e\frac{h^{{*}{2}}}{12}\frac{\partial ^{2}}{\partial t^{{*}{2}}}L_{6} [\beta G_{1}^{*},G_{0}^{*},\,w^{*}]-L_{6} [a_{3},a_{2},\,w^{*}]\right) =0; \nonumber \\&\quad \,L_{6} [a,b,v_{1} ]=a\frac{\partial v_{1} }{\partial t^{*}}+b.v_{1};\,a_{10} =\beta \left( \frac{4}{3}+G_{1}^{*} \right) ;\;a_{11} =\frac{4}{3}+G_{0}^{*} \;;\,\,a_{2}=\frac{2}{3} \nonumber \\&\quad -\,G_{0}^{*} ;\;\;a_{3} =\beta \left( \frac{2}{3}-G_{1}^{*} \right) ; \end{aligned}$$

(12.1)

$$\begin{aligned}&\varepsilon ^{4}\frac{Z_{2} R^{*}h^{{*}{2}}}{12}\frac{\partial ^{4}}{\partial x^{{*}{4}}}L_{6} [a_{10},a_{11},w^{*}]+\varepsilon ^{3}\frac{h^{{*}{2}}}{12}\frac{\partial ^{3}}{\partial x^{{*}{3}}}L_{6} [a_{10} ,a_{11},u^{*}]-eR^{*}Z_{2} \frac{\partial ^{2}}{\partial t^{{*}{2}}}L_{6} [\beta G_{1}^{*},G_{0}^{*} ,w^{*}] \nonumber \\&\quad +\,\varepsilon ^{2}\frac{eZ_{2} R^{*}h^{{*}{2}}}{12}\frac{\partial ^{4}}{\partial x^{{*}{2}}\partial t^{{*}{2}}}L_{6} [\beta G_{1}^{*},G_{0}^{*},w^{*}]+\varepsilon \frac{\partial }{\partial x^{*}} \left( -e\frac{h^{{*}{2}}}{12}\frac{\partial ^{2}}{\partial t^{{*}{2}}}L_{6} [\beta G_{1}^{*},G_{0}^{*},u^{*}]+L_{6} [a_{3} ,a_{2},u^{*}]\right) \nonumber \\&\quad -\,\frac{1}{h^{*}}(\alpha _{0}^{*}L_{6} [a_{10},a_{11} ,w^{*}]+L_{6} [\beta G_{1}^{*},G_{0}^{*},P^{*}]\left( \frac{h^{*}}{2}-Z_{2} R^{*})\right) =0;\,\alpha _{0}^{*}=\int _{-h/2}^{h/2} {\frac{\text {d}z}{R_{0} +z}} \nonumber \\&\quad =\ln \frac{2R^{*}+Z_{2}.h^{*}}{2R^{*}-Z_{2} .h^{*}}. \end{aligned}$$

(12.2)

3.1 Modal analysis

For the free vibrations analysis, the load P is neglected. The solution will be considered as $\{u^{*}{,w}^{*}\}=\{V(x^{*})\}_{\mathrm {2*1}}\hbox {exp}(i\omega t^{*})$, where $\omega$ is the dimensionless natural frequency, and by substituting into Eq. (12.1), it gives the following equation:

$$\begin{aligned}&\left[ {B_{5} } \right] \frac{d^{4}V}{\text {d}x^{{*}{4}}}+\left[ {B_{4} } \right] \frac{d^{3}V}{\text {d}x^{{*}{3}}}+\left[ {B_{3} } \right] \frac{d^{2}V}{\text {d}x^{{*}{2}}}+\left[ {B_{2} } \right] \frac{\text {d}V}{\text {d}x^{*}}+\left[ {B_{1} } \right] =\left\{ 0 \right\} _{2*1} \nonumber \\&\quad \left[ {B_{1} } \right] =\left[ {B_{6} } \right] +i\left( {\omega \left[ {B_{7} } \right] -\omega ^{3}\left[ {B_{9} } \right] } \right) -\omega ^{2}\left[ {B_{8} } \right] +\left[ {B_{0} } \right] \end{aligned}$$

(13)

where $[B_{j}]$, $j= 0,1,\ldots ,9$ are the coefficient matrices. Equations (13) are a system of ordinary differential equations, and the solution can be considered as $\{V(x^{*})\}=\{ A\}$ exp$(\beta x^{*})$, where $\{A\}_{{2*1}}$ is the eigenvector and $\beta$ is the eigenvalue. By substituting $\{ V(x^*)\}$ into Eq. (13), a system of algebraic equations as $[{ax}]_{{2*2}}\{A\}_{{2*1}}=\{0\}$ is obtained. For nonzero solution, the determinant of [ax] is equated to zero which results in a relation between $\beta$, and $\omega$. It is an equation of order six with respect to $\beta$. It has six roots, and for each root, an eigenvector $\{A\}$ can be determined. These eigenvalues and eigenvectors are functions of $\omega$. So, the general solution of Eq. (13) is the following:

$$\begin{aligned} \left\{ V \right\} =\sum \limits _{j=1}^6 {C_{j} } \left\{ A \right\} _{j} \,\exp (\beta _{j} x^{*}) \end{aligned}$$

(14)

where $C_{j}$ are constant and will be determined from the boundary conditions. By applying the boundary conditions at $x^{{*}}= 0,1$, six algebraic equations are obtained in terms of $C_{j}$, $j= 1..6$. The general forms of these equations are as $[{bx}]_{{6*6}}\{C\} _{{6*1}} =\{ 0\}$. For nonzero solution, we set det $([{bx}])= 0$. It is a complicated algebraic equation, and its solutions are the frequencies $\omega$. We used the bisection method to solve this equation.

3.2 Forced vibrations analysis

To determine the response of the shell to the moving load, the displacements are considered as in Eqs. (15),

$$\begin{aligned} u(x^{*},t^{*})=\sum \limits _{n=1}^\infty {fu_{n} (t^{*})\cos (n\pi x^{*})}&\,;w(x^{*},t^{*})=\sum \limits _{n=1}^\infty {fw_{n} (t^{*})\sin (n\pi x^{*})}. \; \end{aligned}$$

(15)

In these equations, $\hbox {sin}(n\pi x^{*})$ and $\cos (n\pi x^{*})$ are the mode shapes that satisfy the simply supported boundary conditions at $x^{*}= 0$,1. By substituting Eq. (15) into Eq. (12.1), and applying the half-range expansion of the Fourier series, two coupled ordinary differential equations [(Eq. (16)] are obtained where $p_{1n}$ and $p_{2n}$ are in terms of $f_{1n}(t^{*})$, $f_{2n}(t^{*})$, and their derivatives,

$$\begin{aligned} \sum \limits _{n=1}^\infty {p_{1n} \sin (n\pi x^{*})}= & {} 0\;;\;\sum \limits _{n=1}^\infty {p_{2n} \cos (n\pi x^{*})} =Q^{*};\,\,Q^{*}=\,L_{6} [\beta G_{1}^{*},G_{0}^{*} ,P^{*}]\left( Z_{2} R^{*}-\frac{h^{*}}{2}\right) \nonumber \\ p_{1n}= & {} \sum \limits _{j=0}^3 \left( a_{1j} \frac{d^{j}fu_{n} }{\text {d}t^{*j}} +b_{1j} \frac{d^{j}fw_{n} }{\text {d}t^{*j}}\right) ;\,\,p_{2n} =\sum \limits _{j=0}^3 \left( a_{2j} \frac{d^{j}fu_{n} }{\text {d}t^{*j}}+b_{2j} \frac{d^{j}fw_{n} }{\text {d}t^{*j}}\right) .\quad \end{aligned}$$

(16)

The pressure distribution is $P=P_{\mathrm {0}}$(1-H(x-v.t)) where $P_{\mathrm {0}}$ is the pressure intensity, v is the velocity of the wave front, and H is the Heaviside step function. We assume that the pressure moves with a constant velocity v. So, the applied pressure for the points behind of the wave front is $P_{\mathrm {0}}$ ($x< {vt}$) and after it, the pressure is zero ($x> {vt}$). It is clear that when $t_{d}=L/v$, the wave front is at the end of the shell. $t_{d}$ is called the departure time. When ${t> t}_{d}$, the entire of the shell is subjected to the constant pressure $P_{{0}}$. Therefore, we divide the solution into two parts:

(a) Before departure of the wave front from the shell $({t< t}_{d})$, Eq. (15) results in:

$$\begin{aligned} \sum \limits _{n=1}^\infty {p_{1n} \sin (n\pi x^{*})}= & {} 0\rightarrow \;p_{1n} =0\,\,;\,v^{*}=\frac{v}{L/t_{0} }, \nonumber \\ \sum \limits _{n=1}^\infty {p_{2n} \cos (n\pi x^{*})}= & {} Q^{*}\rightarrow p_{2n} =2\int \limits _0^{v^{*}t^{*}} {Q^{*}\text {d}x^{*}}. \end{aligned}$$

(17)

$v^{*}$ is the dimensionless velocity. Note that in this region after $x^{*} > v^{*}t^{*}$ the pressure value is zero.

(b) After departure of the wave front from the shell $({t> t}_{d})$, from Eq. (15) we have:

$$\begin{aligned} \sum \limits _{n=1}^\infty {p_{1n} \sin (n\pi x^{*})} =0\rightarrow \;p_{1n} =0;\,\,\;\sum \limits _{n=1}^\infty {p_{2n} \cos (n\pi x^{*})} =Q^{*}\rightarrow p_{2n} =2\int \limits _0^1 {Q^{*}\text {d}x^{*}}. \end{aligned}$$

(18)

Equations (17), (18) are two systems of ordinary differential equations with constant coefficients. Each equation contains two coupled equations with time derivative of order-three. One can use the elementary theory of differential equations for the solution. The solution of Eq. (17) has six constants which are determined from the initial conditions at $t^{*}= 0$. We assume that the function, the first time derivative, and its second derivative are zero. So, the constants can be determined. The solution in this part is designated with the vector $\{y_{\mathrm {1}}\}$. The solution of Eq. (18) is determined like that of Eq. (17). If we call the solution of Eq. (18) as $\{y_{{2}}\}$, the constants can estimated from the initial condition at $t^{*}=t_{d}/t_{0}$. It is the dimensionless time at the departure of the wave front from the shell. $\{y_{{1}}\}$, $\{y_{{2}}\}$ and their first and second derivatives must have the same at this time (continuity conditions). Note that, if we rewrite the solution as the rational form, their denominators are functions of $v^{*}$. The values of $v^{*}$ which result in the zero value for the denominators are called the critical velocities. In other word, the critical velocity can produce a large amplitude for response. For each quantity of n, the response and the corresponding critical velocity are determined. In order to find the required number of terms of convergence [(in Eqs. (17), (18)], the critical velocity in each step is compared with the new obtained critical velocities.

4 Numerical solution

ANSYSFE software was employed for the modal analysis of the cylindrical shells. PLANE182, which is an element with four nodes and two translational degrees of freedom at each node, in axisymmetric mode was used to determine the axisymmetric frequencies and mode shapes.

5 Sensitivity analysis

According to the presented formulation, a mathematical code has been prepared on Maple 15 mathematical environment to study the effects of different parameters on the vibration behaviors of viscoelastic shells. The boundary conditions are designated with two letters in this text. The first letter is the boundary condition at $x^{*}= 0$, and the second relates to $x^{*}=1$. S, C, and F stand of the simple, clamped, and free conditions, respectively. So, S–F defines the simply supported boundary condition at $x^{*}= 0$ and free at $x^{*}= 1$. The characteristics of the shell are listed in Table 1, and all the results are according to this Table, and S–S boundary conditions except those are mentioned.

Table 1 Characteristics of the shell

Table 2 reports the axisymmetric natural frequency for an elastic cylindrical shell for various length-to-middle radius ratio $(L/R_{0})$, and the middle radius-to-thickness ratio $(R_{0}/h)$ that attains from the current method, FE, and the formula presented by Amabili [38]. Amabili extracted the equation of motion from Donnell’s theory with canceling the nonlinear terms. It is concluded that the results of the presented method are closer to the FE in comparison with the Amabili results. Also, it can be seen that by increasing $L/R_{0}$ the natural frequency decreases. By substituting $\tau = 0$, the presented results can be obtained for the elastic case. Also, the following equations are used for the elastic case [39, 40]:

$$\begin{aligned} K_{0} =\frac{2}{3}G_{s} \frac{1+\nu }{1-2\nu };E=2G_{s} (1+\nu );\,\,G_{s} =\frac{G_{1} G_{2} }{G_{1} +G_{2} }. \end{aligned}$$

(19)

Table 2 Comparison of axisymmetric natural frequency (Hz) of S–S elastic shell for different values of the aspect ratio. $(R_{0}= 0.16)$ m

Figure 3 shows the effects of viscoelastic modulus and viscosity coefficient on the first natural frequency of viscoelastic cylindrical shells with C–C boundary conditions. It is seen that, by increasing $G_{1}$, the natural frequency increases. As a result, increasing $G_{2}$ just in the interval [1.0E4, 1.0E10] can increase the natural frequency for input data (Table 1). Moreover, the viscosity coefficient $\eta$ affects the natural frequency in the range $\eta < 1.0\hbox {E}5$, and by increasing $\eta$ the natural frequency increases.

Fig. 3

Natural frequency of viscoelastic cylindrical C–C shell versus $G_{{1}}$, $G_{{2}}$, and $\eta$

Table 3 shows the fundamental natural frequency of a viscoelastic cylindrical shell for different boundary conditions. It is seen that C–C has the highest natural frequency as one would expect. Note that for F–F the first natural frequency is zero (rigid body motion), and Table 3 reports the first bending frequency.

The critical velocity $(V_\mathrm{cr})$ of elastic cylindrical shells is reported in Table 4 for different formulations. Ruzzene and Baz [41] used the FE method according to the Donnell–Mushtari theory, and the other references [14, 32, 42] used the CST theory without considering the effect of $z/R_{0}$. The maximum difference percentage is about 10% which may be due to consideration of the effect of $z/R_{0}$ in the current formulation. Moreover, the results presented by the current method for thick shells are closer to the results of Ruzzene and Baz [41], with respect to the other references which do not consider the effect of $z/R_{0}$.

Table 3 Effect of boundary conditions on the first natural frequency (Hz) of a viscoelastic shell

Table 4 Critical velocity $(V_\mathrm{cr})$–m/s for elastic cylindrical shells $(L/R_{0}= 10$, $E= 210$ GPa, $\rho = 7800$${\mathrm{kg}/m}^{3}$, $\nu = 0.33$)

Table 5 shows the effects of viscoelastic modulus and viscosity coefficient on the critical velocity for a viscoelastic cylindrical shell. It can be concluded that by increasing the viscoelastic modulus and viscosity coefficient the critical velocity increases. As it is seen, the effect of $G_{1}$ is more significant than $G_{2}$ and $\eta$. The critical velocity has a significant increase in the ranges [2.74E4,2.74E5] and [2.45E6,2.45E7] of $\eta$ and $G_{2}$, respectively, and in the other ranges its increase is not considerable. In other word, by increasing $G_{2}$ and $\eta$, the Kelvin part of the viscoelastic model acts as a rigid body. Figure 4 shows the effect of $R_{0}$/h and L/$R_{0}$ on the critical velocity. It is seen that the small values of L/$R_{0}$ can affect the critical velocity, but for longer shells it does not have significant effects on the critical velocity, and the shell is similar to a long pipe. In the studied range, for $L/R_{{0}}> 3$ one can nearly assume that the shell is long but by increasing $R_{0}$/h the critical velocity decreases.

Table 5 Effects of viscoelastic modulus and viscosity coefficient on the critical velocity of a viscoelastic shell

Fig. 4

Effects of aspect ratio on critical velocity

Table 6 presents a comparison of the radial displacements of the middle point of the elastic cylindrical shells by the current method, FE, and the FSDT [43] for the static condition. The current method results are the solution of Eq. (7.1) when $\partial /\partial t= 0$ and $P(\textit{x,t})=P_{{0}}$. By increasing the thickness, the difference between the results with respect to the FE increases. In the FSDT solution, the radial displacement is considered as a function of z and x, while in the current method the radial displacement is just a function of x parameter, and so the FSDT results are closer than to the FE with respect to the current formulation.

Table 6 Dimensionless radial displacements of the middle point ($x^{*}= 0.5$, $z =-\,h/2$) for different thicknesses of elastic cylindrical shells by the current method, FSDT [43], and FE ($E= 200$ GPa, $\nu = 0.3$, $P = 0.3$ GPa, $R_{O }= 0.16$ m, $L= 1\,\hbox {m}$)

Figure 5 shows the distribution of the dimensionless radial displacements of a viscoelastic cylindrical shell versus dimensionless length $(x^{*})$ and dimensionless time $(t^{*})$. It can be seen that, by moving the load along the longitudinal direction, the radial displacement gradually increases. By increasing the departure time, the dimensionless radial displacement increases significantly. Moreover, it is observed that as the moving load arrives at the end of the cylinder, and after the departure of the load, the cylinder vibrates about its static deflection.

Fig. 5

a Dimensionless radial response versus dimensionless length at different departure times ($v^{{*}} =1.91$). b Dimensionless radial response versus dimensionless time at different locations ($v^{{*}} =1.91$)

Fig. 6

Dimensionless radial and axial response of viscoelastic cylindrical shell versus dimensionless length for different viscoelastic moduli $G_{\mathrm {1}}$ ($t^*=t_{d}/t_{0})$

Fig. 7

Dimensionless radial and axial response of a viscoelastic cylindrical shell versus dimensionless length for different viscoelastic moduli $G_{\mathrm {2}}$ ($t^*=t_{d}/t_{0})$

Figure 6 shows the effects of the viscoelastic modulus $G_{1}$ on the response of the shell subjected to moving load. It is observed that by increasing the viscoelastic modulus $G_{1}$, in contrast to the natural frequency and critical velocity the response amplitude decreases. The effect of $G_{1}$ on the axial displacement is less than the radial one. In addition, it is seen that by increasing $G_{1}$ the behavior of the viscoelastic shell under moving load approaches to the first mode shape for S–S boundary conditions. The effect of viscoelastic modulus $G_{2}$ on the response is shown in Fig. 7. It is seen, just like the effect of $G_{1}$, by increasing $G_{2}$, the response amplitude decreases unlike the critical velocity, but the effect of $G_{2}$ in the range of [2.45E6,2.45E7] is remarkable, and for $G_{\mathrm {2}}> = 2.45\hbox {E}6$, a significant decrement is observed in the response. Fig. 8 shows the effect of the viscosity coefficient $\eta$ on the response. Just like the viscoelastic modulus, by increasing $\eta$, the response amplitude decreases as expected. Moreover, it is seen that the response has the largest variations in the range of [2.74E4, 2.74E5]. As it is explained formerly, using Eq. (19), one can find the equivalent elastic case for the viscoelastic shells. Figure 9 shows the response of a viscoelastic and equivalent elastic case on the response. It is seen that, by taking into consideration viscous behavior of the material, the radial displacement is decreased, unlike the axial displacement.

Fig. 8

Dimensionless response of a viscoelastic cylindrical shell under versus dimensionless lengths for different viscosity coefficients $\eta$ ($t^*=t_{d}/t_{0})$

Fig. 9

Dimensionless response of a viscoelastic and elastic cylindrical shell under moving load versus dimensionless length $(t^*=t_{d}/t_{0})$

6 Conclusions

An analytical formulation based on the classical shell theory has been presented for the dynamic analysis of a viscoelastic cylindrical shell under moving internal pressure. The behavior of the shell was assumed viscoelastic in shear and incompressible in bulk. The governing equations were solved for free and forced vibrations. The presented method can be used for elastic materials, too. Some of the most important points mentioned in the results for the studied range of input data are the following:

• Although the results have been presented for a moving pressure, the presented procedure can be used for other pressure distributions.

• By increasing $G_{1}$, $G_{2}$, and $\eta$ the natural frequency increases. But $G_{2}$ just in the interval [1.0E4, 1.0E10] has effects on the natural frequency. Moreover, the viscosity coefficient $\eta$ affects the natural frequency in the range $\eta < 1.0\hbox {E}5$.

• The critical velocity increases by increasing $G_{1}$, $G_{2}$, and $\eta$, unlike the response amplitude. The results have the most variations in the ranges [2.74E4, 2.74E5] and [2.45E6, 2.45E7] of $\eta$ and $G_{2}$, respectively and in the other ranges, the changes are not considerable.

• The small values of L/$R_{0}$ can affect the critical velocity, but for long shells it is not a significant effect to calculate the critical velocity, and the shell acts as a long pipe. As a result, for $L/R_{\mathrm {0}}> 3$ one can nearly assume that the shell is long.

• By increasing $R_{0}$/h, the critical velocity decreases, and this ratio does not have any considerable effect on the natural frequency.

• As the load moves along the longitudinal direction, the radial displacement gradually increases, and by increasing the departure time, the dimensionless radial displacement increases significantly.

• By taking into account the viscoelastic behavior, the radial displacement is decreased, in opposite of the axial displacement.