Mechanisms of strange nonchaotic attractors in a nonsmooth system with border-collision bifurcations

Abstract

It is not very clear to understand genesis and mechanisms for the creation of strange nonchaotic attractors (SNAs) due to the nonsmooth bifurcations in the nonsmooth systems. A quasiperiodically forced piecewise Logistic system is shown to exhibit many types of routes to the creation of SNAs. We point out that the truncation of border-collision torus-doubling bifurcation can lead to different types of SNAs. We identify and describe the Heagy–Hammel routes, fractalization route and intermittent routes after the two coexisting tori collide at the border and the doubled torus is interrupted in this system. It has been shown that there exist two critical tongue-type regions in the parameter space, where the different mechanisms for the birth of SNAs are investigated. These SNAs are identified by the Lyapunov exponents and the phase sensitivity exponents. Different types of SNAs are also characterized by the singular-continuous spectrum, Fourier transform, rational approximations, distribution of finite-time Lyapunov exponents and recurrence analysis.

1 Introduction

Strange nonchaotic attractors (SNAs) are found as typical attractors in quasiperiodically forced nonlinear systems. SNAs are geometrically strange and the largest nontrivial Lyapunov exponent is negative, which do not depend on initial conditions sensitively and imply nonchaotic dynamics [1,2,3]. SNAs were firstly discovered by Grebogi et al. [4] and since then extensively investigated by theoretical analysis [5,6,7] and experimental verification [8,9,10] in dynamical systems. In particular, the investigations on their mechanisms and routes have attracted great interests by a large number of numerical studies. For example, Heagy–Hammel routes [11], fractal routes [12,13,14], symmetry breaking [15], intermittent routes [16,17,18], crisis route [19,20,21,22], blowout bifurcation [23] and a bubbling route [24]. In 2015, the existence of strange nonchaotic stars has also been demonstrated in spaces, which further illustrates the strange nonchaotic phenomenon [25]. It has important practical application in field such as secure communication [26,27,28], spin dynamics of an anisotropic magnetic particle [29] and climate dynamics [30]. Therefore the existence (or genesis) of SNAs in more dynamical systems has been a subject of intense further interest.

It is known that the different types of bifurcations are useful for understanding the mechanism and genesis of SNAs [31, 32]. A common observation is that the truncation of period-doubling can creates SNAs [33]. The truncation of the doubled torus is usually caused by the following routes. In the Heagy–Hammel route, the doubled torus collided with its unstable parent and the period-2$^{k}$ torus created a SNA [11]. In the fractalization route, the doubled torus became wrinkled and forms a SNA [12,13,14]. In type-I intermittency route, the torus-doubling bifurcation is tamed by a subharmonic bifurcation so that the torus attractor gives rises to a SNA [34]. Besides torus-doubling bifurcation, other types of bifurcations are used to analyze the mechanism for the creation of SNAs. When the torus loses its transverse stability and blowout bifurcation occurs, a SNA is created and it exhibits on-off intermittency [23]. A quasiperiodic analog of a saddle-node bifurcation leads to SNAs through the intermittent route [16]. This type of bifurcation is also called nonsmooth saddle-node bifurcation of tori, which is widely investigated theoretically and numerically in skew product maps [5, 31]. In nature, strange nonchaotic attractors through nonsmooth saddle-node bifurcation can also be observed by analyzing the phase oscillator model of glacial-interglacial cycles [31].

In most all the above studies, the SNAs and the mechanism for bifurcation usually have been explored in smooth systems. It is well known that nonsmooth dynamical systems display some special types of bifurcations and a wealth of complex dynamical phenomena [35,36,37,38,39,40,41]. In recent years, the strange nonchaotic dynamics has been understood by exploring the nonsmooth systems. In nonsmooth Chua’s oscillators, some new routes to SNAs have been identified, e.g., multilayered bubbling route [42], formation and merging of bubbles route [43]. In vibro-impact systems, it is shown that the coexistence of SNAs can also be observed and a new intermittency accompanied by symmetry restoring bifurcation occurs in the vibro-impact system [44]. The SNAs can also be observed near a codimension three bifurcation, and the mechanism for the creation of SNA is also explored by the collision of doubled torus with some unstable period orbits [45]. It is natural to ask whether there exists a relation between the creation of SNAs and nonsmooth bifurcations. As a specific feature and anomalous bifurcation in nonsmooth systems, nonsmooth bifurcations may lead to the unexpected change due to the collision of some invariant set [36,37,38,39]. The main goal of this paper is to investigate the border-collision bifurcation of tori and the creation of SNAs. In the present work, we consider a quasiperiodically driven piecewise Logistic system and show the genesis and mechanisms for the creation of SNAs due to the truncation of border-collision torus-doubling bifurcation (namely, two coexisting tori do not continue to merge or collide at the border). We identify different types of SNAs and focus on the two critical tongue-type regimes in the parameter space. These types of SNAs are described by the Lyapunov exponents, phase sensitivity exponents, singular-continuous spectrums, distribution of finite-time Lyapunov exponents, rational approximations and recurrence analysis.

This paper is organized as follow. In Sect. 2, we shall introduce the quasiperiodically forced model and show how to identify the SNAs by the Lyapunov exponents and phase sensitivity exponents. In Sect. 3, we describe the dynamical regimes (SNAs, Tori and Chaos) and discuss the general mechanism for the creation of SNAs. In Sect. 4, we investigate different types of SNAs and give some examples, describing three typical routes by some measures after the border-collision bifurcations of tori are interrupted. In Sect. 5, we conclude with a summary.

2 The forced piecewise Logistic system

The piecewise Logistic system often is used as a representative model for analyzing nonsmooth bifurcations. The model of system is defined as follows [46]:

$$\begin{aligned}&x_{n+1} =f\left( {x_n ,a} \right) \nonumber \\&\quad =\left\{ {\begin{array}{ll} f_l \left( {x_n ,a} \right) =ax_n \left( {1-x_n } \right) &{} \hbox {if} \, {x_n <1/2} \\ f_c \left( {x_n } \right) =1/2&{} \hbox {if} \, {x_n =1/2} \\ f_r \left( {x_n ,a} \right) =ax_n \left( {x_n -1} \right) +1&{} \hbox {if} \, {x_n >1/2} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(1)

where $x\in$[0,1], $a\in$[0,4]. For all parameter values except for $a=1$, the system function f is discontinuous at the point $x=1/2$. In order to investigate the mechanisms for the creation of SNAs, we add an additional quasiperiodic forcing:

$$\begin{aligned}&x_{n+1} =f\left( {x_n ,a,\varepsilon ,\phi _n } \right) \nonumber \\&\quad =\left\{ {\begin{array}{ll} f_l \left( {x_n ,a,\varepsilon ,\phi _n } \right) \\ \quad =\left( {a+\varepsilon \cos 2\pi \phi _n } \right) x_n \left( {1-x_n } \right) &{} \hbox {if} \, {x_n <1/2} \\ f_c \left( {x_n } \right) =1/2 &{} \hbox {if} \, {x_n =1/2} \\ f_r \left( {x_n ,a,\varepsilon ,\phi _n } \right) \\ \quad =\left( {a+\varepsilon \cos 2\pi \phi _n } \right) x_n \left( {x_n -1} \right) +1 &{} \hbox {if} \, {x_n >1/2} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(2)

$$\begin{aligned}&\phi _{n+1} =\phi _n +\omega \left( {\bmod 1} \right) \end{aligned}$$

(3)

where $x\in$[0,1],$\phi \in S^{1}$, the nonlinearity parameter of the system $\omega$ and $\varepsilon$ represent the frequency and amplitude of the quasiperiodic forcing, respectively. The frequency is set to be the reciprocal of the golden mean, $\omega =(\sqrt{5}-1)/2$. In order to describe the strange nonchaotic dynamics of system (2), (3), it is useful to characterize the SNAs through both the Lyapunov exponents $\lambda _x$, which is given by

$$\begin{aligned} \lambda _x =\mathop {\lim }\limits _{N\rightarrow \infty } \frac{1}{N}\sum _{i=1}^N {\ln \left| {\frac{\partial f}{\partial x_i }} \right| } \end{aligned}$$

(4)

and the phase sensitivity exponent which can be obtained by the phase sensitivity function $\Gamma _N$ [47]. On a SNA, the function $\Gamma _N$ grows with the length of the orbit N, as a power, i.e., $\Gamma _N \sim N^{\mu }$, where $\mu$ is the phase sensitivity exponent [47].

$$\begin{aligned}&\Gamma _N \left( {a,\varepsilon } \right) =\mathop {\min }\limits _{x_0 ,\phi _0 } \left( {\mathop {\max }\limits _{0\le n\le N} \left| {\frac{\partial x_n }{\partial \phi }} \right| } \right) \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial x_n }{\partial \phi }=\left\{ {\begin{array}{ll} \left[ {-2\pi \varepsilon \sin \left( {2\pi \phi _n } \right) } \right] \left( {x_n -x_n^2 } \right) \\ \quad +\left[ {a+\varepsilon \cos \left( {2\pi \phi _n } \right) } \right] \left( {1-2x_n } \right) \frac{\partial x_n }{\partial \phi } &{} \hbox {if} \, x_n <\frac{1}{2} \\ 0&{} \hbox {if} \, x_n =\frac{1}{2} \\ \left[ {-2\pi \varepsilon \sin \left( {2\pi \phi _n } \right) } \right] \left( {x_n^2 -x_n } \right) \\ \quad +\left[ {a+\varepsilon \cos \left( {2\pi \phi _n } \right) } \right] \left( {2x_n -1} \right) \frac{\partial x_n }{\partial \phi } &{} \hbox {if} \, {x_n >\frac{1}{2}}\\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(6)

Fig. 1

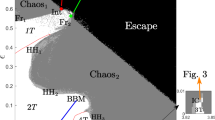
Phase diagrams in the $\left( {a-\varepsilon } \right)$ parameter plane for Eqs. (2), (3). Regular, chaotic, SNAs and divergence regions are shown in white, gray, light gray and black, respectively. For the regular attractors, a torus and its doubled tori are denoted by 1T, 2T, 4T and 8T, respectively. The black curves (L1, L3 and L5) are codimension two bifurcation curves on quasiperiodic analog of pitchfork bifurcation. The red curves (L2, L4 and L6) are codimension two bifurcation curves on the border-collision bifurcation of coexisting tori. (Fr), (Int) and (HH) correspond to different routes, where SNAs are created through the fractalizations, intermittencies and Heagy–Hammel, respectively. The crisis of SNAs is denoted by (Cr). (Color figure online)

Fig. 2

Six typical phase diagrams before and after border-collision bifurcations of tori for three critical points ($\alpha ,\beta ,\gamma$ in Fig. 1)

3 SNAs and general mechanism

Figure 1 shows two phase diagrams in the $a-\varepsilon$ plane. Each phase diagram is characterized by both the Lyapunov exponent $\lambda _x$ in the x-direction and the phase sensitivity exponent $\mu$. The torus attractors have negative Lyapunov exponents ($\lambda _x )$ and zero phase sensitivity exponent, where regions are denoted by nT and shown in white. Different tori are denoted by 1T, 2T, 4T and 8T. The largest nonzero (nontrivial) Lyapunov exponent is denoted by $\lambda _{\max }$. Chaotic attractors have positive Lyapunov exponents ($\lambda _{\max }>$0) and chaotic regions are shown in gray. Between the regular and chaotic regions, SNAs have negative Lyapunov exponent $\lambda _{\max }$ and positive phase sensitivity, which are shown in light gray. The escape regimes are shown in black. Three codimension two bifurcation curves (L1, L3 and L5) show quasiperiodic analog of pitchfork bifurcations and they are shown in black. Three red curves (L2, L4 and L6) denote the codimension two border-collision bifurcations of coexisting tori. The regimes between the black curves and red curves are coexisting tori attractors and three regimes are denoted C-1T (coexisting 1T torus), C-2T (coexisting 2T torus) and C-4T (coexisting 4T torus), respectively. Box in Fig. 1b illustrates that the 2T tori attractors are originated from the border-collision bifurcations of coexisting 1T torus attractors. Two typical tongue-type regimes are denoted by Tongue I and Tongue II. (Fr), (Int) and (HH) correspond to the regimes where SNAs are created through the fractalizations, intermittencies and Heagy–Hammel routes, respectively. The crisis of SNAs is denoted by (Cr). For lower $\varepsilon$ and any a value, the system exhibits many border-collision torus-doubling bifurcations and the truncation of bifurcations occurs. In Fig. 1a, the truncation of 8T tori can be observed and the SNAs are created. On increasing external forcing $\varepsilon$, the 4T tori are interrupted and the SNAs are created, where there exists a typical tongue I and the boundaries of tongue I exhibit different types of transitions to chaos via SNAs, namely intermittency (Int), fractalization (Fr) and Heagy–Hammel (HH). As $\varepsilon$ is increased further (Fig. 1b), the doubled 2T tori do not continue to collide at the border and 2T tori are interrupted, where there is also a tongue-type region (Tongue II) and several types of mechanisms for creation of SNAs, namely 2T tori fractalization (2T-Fr), 2T tori intermittency (2T-Int) and Heagy–Hammel (HH). In the tongue I regions, the SNAs present a crisis and escape to infinity. Figure 1b shows these types of SNAs and some critical points (A, B, C, D, E and F). The routes A (or a) is typical Heagy–Hammel route to the SNAs. The routes B and E are illustrated the crisis of chaotic attractors. The routes C and D show the crisis of SNAs. In the following, we will focus on the creation of SNAs in more details, omitting the transition and evolution of SNAs.

Fig. 3

Lyapunov exponent diagram in Eqs. (2), (3) for $\varepsilon =0.001$

In order to discover border-collision bifurcations of coexisting tori, Fig. 2 gives six typical phase diagrams before and after border-collision bifurcations for three critical points ($\alpha$, $\beta$, $\gamma$ in Fig. 1). Figure 2a shows two coexisting 4T torus (red and blue) for $\varepsilon =0.025$ and $a=3.4797$. Two coexisting 4T torus approach the border $x=0.5$ simultaneously before the border-collision torus-doubling bifurcation. Figure 2b shows that an 8T torus attractor is created after the border-collision torus-doubling bifurcation for $\varepsilon =0.025$ and $a=3.4798$. Figure 2c shows that two coexisting 2T torus attractor (red and blue) will collide at the border $x=0.5$ before the border-collision torus-doubling bifurcation for $\varepsilon =0.150, a=3.1187$. After border-collision torus-doubling bifurcation, Fig. 2d shows that a 4T torus attractor is created for $\varepsilon =0.150, a=3.1188$. Figure 2e shows that two coexisting 1T torus attractors (red and blue) will collide at the border $x=0.5$ for the $\varepsilon =0.600, a=1.6896$. A 2T torus is created by the border-collision torus-doubling bifurcation of coexisting 1T torus (Fig. 2e). In order to discover further the mechanism for the creation of SNAs, the truncation of border-collision torus-doubling bifurcation is investigated by the Lyapunov exponent $\lambda _x$ as a representative example $\varepsilon =0.001$ shown in Fig. 3. The diagram of the Lyapunov exponent (Fig. 3) shows the obvious properties with $\lambda _x =0$ at the quasiperiodic analog of pitchfork bifurcation point and $\lambda _x \rightarrow -\infty$ at border-collision torus-doubling bifurcation point. It is noted that the bifurcation is different from the classical torus-doubling bifurcation scenario. For the classical torus-doubling bifurcation, the largest Lyapunov exponent is zero at the bifurcation point. However, the Lyapunov exponent $\lambda _x$ tend to infinity ($-\infty )$ at the border-collision torus-doubling bifurcation point. Here, the quasiperiodic analog of pitchfork bifurcation can lead to coexisting attractors except for the torus-doubling bifurcation in a small parameter plane, where the largest Lyapunov exponent is zero. The truncation of doubled torus implies that the attractors are created before their Lyapunov exponents tend to zero from infinity ($-\infty )$. Therefore, it is necessary for the birth of SNAs with negative Lyapunov exponent $\lambda _x$. Figure 4 shows that the SNAs are created by the truncation of border-collision torus-doubling bifurcation for $\varepsilon =0.001$ as an example. The doubled tori (2T$\rightarrow \,$4T$\rightarrow$8T$\rightarrow$16T$\rightarrow$SNA) are shown in Figs. 4a–e, respectively. Figure 4f shows the phase sensitivity functions for the 16T torus and the SNA, which the largest Lyapunov exponent $\lambda _x$ approximately equals to − 0.007 and the phase sensitivity exponent $\mu$ approximately equals to 0.886.

Fig. 4

SNAs are created by truncation of border-collision torus-doubling bifurcation for $\varepsilon =0.001$a A 2T torus for $a=3.100$; b A 4T torus for $a=3.250$; c A 8T torus for $a=3.520$; d A 16T torus for $a=3.550$; e A SNA for $a=3.569$; f Two phase sensitivity functions for $a=3.550$ (16T) and $a=3.569$ (SNA)

4 Strange nonchaotic dynamics after the truncation of border-collision bifurcations of tori

4.1 Methods on characteristics of SNAs

One of the characteristics of the SNAs through different mechanisms is the difference in the distribution $P(t,\lambda )$of finite-time or local Lyapunov exponents because a typical trajectory on a SNA actually possesses positive Lyapunov exponents in finite-time intervals [1, 33, 48]. The finite-time or local Lyapunov exponents depend on the initial conditions. In fact, $P(t,\lambda )$corresponds to counting the normalized number of times any one of the $\lambda$ appears for fixed time t. In the limit of large t, this distribution will collapse to a $\delta$ function $P(N,\lambda )\rightarrow \delta (\Lambda -\lambda )$. The variance $\upsigma$ of $\Lambda$ is also a useful method to describe the transition from tori to SNAs [33, 48]. In our numerical calculations, $\Lambda$ and its variance are typically computed from a sample of 50 estimations of step length $N=10^{5}$. Namely, we take the distribution $P(50,\lambda )$ as an example. To quantify further the distribution of finite-time Lyapunov exponents, we use the fraction of positive local Lyapunov exponents $F_+ (N)$ (the fraction of exponents lying above $\lambda =0$, and here the total number of exponents is 10000) to describe the SNA. For more details on the computation of $P(N,\lambda )$,$\upsigma$,$\Lambda$ and $F_+ (N)$, see the references, e.g., [1, 33, 38].

To detect the transition from quasiperiodic motion to SNAs, Ngamga et.al introduced four measures which are based on the time needed by the system to recur to a neighborhood of a previous point of the trajectory [49, 50]. Here, we used the variance $\upsigma _{\mathrm{MRT}}$ of the mean recurrence time to detect the onset of SNAs. From the previous results, the maximal Lyapunov exponents and their variances cannot detect the onset of SNAs by the gradual fractalization route [33, 48]. However, this measure $\upsigma _{\mathrm{MRT}}$ is able to detect the onset of SNAs in the Heagy–Hammel route, intermittency route and the fractalization of a torus. In order to visualize these recurrences of a given trajectory $\left\{ {\mathbf {x}_i } \right\} _{i=1}^N$, one needs to compute an $N\times N$matrix:

$$\begin{aligned} R_{i,j} =\Theta (\delta -\left\| {\mathbf {x}_i -\mathbf {x}_j } \right\| ),\quad {i,j=1,\ldots ,N} \end{aligned}$$

(7)

where $\mathbf {x}_i \in R^{n}$,$\delta$ is a predefined threshold, $\Theta (\cdot )$ is the Heaviside function, and $\left\| \cdot \right\|$ denotes a norm (here the maximum norm).

From the recurrence plots [49,50,51], we evaluate the frequency distribution $P^{\delta }(\omega )$ of the lengths $\omega$ of the white vertical lines. We compute the mean recurrence time $T_{\mathrm{MRT}}$ from the distribution.

$$\begin{aligned} T_{\mathrm{MRT}} =\sum _{\omega =1}^N {\omega P(\omega )/\sum _{\omega =1}^N {P(\omega )} } , \end{aligned}$$

(8)

The variance $\upsigma _{\mathrm{MRT}}$ of $T_{\mathrm{MRT}}$ is evaluated by dividing the trajectory into ksegments:

$$\begin{aligned} \upsigma _{\mathrm{MRT}} =\sum _{l=1}^k {(T_{\mathrm{MRT}} (l)-\bar{{T}}_{\mathrm{MRT}} } )^{2}/k, \end{aligned}$$

(9)

where $\bar{{T}}_{\mathrm{MRT}}$ is the mean value of $T_{\mathrm{MRT}}$. Here, we used $\upsigma _{\mathrm{MRT}}$ to describe the transition from the torus to SNA. In our numerical calculations, we use the threshold $\delta =0.08, l=100$ and $N=1000$ for each segment.

To verify the strangeness of the attractor, we examine the spectral characteristics of the attractor. The singular-continuous spectrum technique has been used to verify the SNAs effectively in some dynamical systems [1, 23, 24]. Compute the following Fourier sum:

$$\begin{aligned} X\left( {\Omega ,T} \right) =\mathop {\sum }\limits ^T_{n=1} {x_n e^{i2\pi n\Omega }} , \end{aligned}$$

(10)

where $\Omega$ is proportional to the ratio of two incommensurate frequencies of the quasiperiodic driving. It was demonstrated that for strange nonchaotic attractors, the following scaling relation $\left| {X(\Omega ,N)} \right| ^{2}{\sim }N^{\beta }$ holds and, for SNAs the scaling exponent satisfies $1<\beta <2$. In addition, the SNAs can also studied by the method of a rational approximation, which is based on the fact that the irrational number can be approximated by an appropriate rational. For the golden mean irrational, the adjusting rational can be obtained from the continued fraction representation of $\omega$, they have the form $\omega _k ={F_{k-1} }/{F_k }$, where $F_k =1,1,2,3,5,8,\ldots$ are the Fibonacci numbers. The irrational rotation number turns out to be the limit: $\omega =\lim _{k\rightarrow \infty } \omega _k$. We study the strange nonchaotic behavior of systems where the irrational frequency $\omega$ is replaced by its rational approximate $\omega _k$.

4.2 Different mechanisms

In this section, we will describe some different routes to creation of SNAs after the coexisting tori collide at the border and they are interrupted. Different methods are used to describe the SNAs. The details are as follows.

4.2.1 Heagy–Hammel route

Now we consider the strange nonchaotic dynamics by varying the value of $\varepsilon$ and a so that the mechanism for the birth of SNAs is described in detail. A very interesting pattern is the truncation of doubled torus and the existence of the unstable parent torus, which the route is called Heagy–Hammel (HH) route. The obvious property of HH routes is that a period-$2^{n}$torus gets wrinkled and collides with the unstable period-$2^{n-1}$ torus, bifurcating into a strange nonchaotic attractor. We identify this type of route in the typical two regions. The first region is within the range of ${\varepsilon } , {0.310}<{\varepsilon }<0.510$, and a values $3.260<a<3.430$. The second region is within the range of $\varepsilon$, 0.033$<\varepsilon<$0.075, and a values 3.500$<a<$3.540. Obviously, when the black curves keep close to the terminus, two larger regions (light gray in Fig. 1) marked by A and A’ show the abundance of SNAs due to the HH routes. It is similar to that of the previous one in the neighborhood of endpoint of the black curve. Here, the truncation of border-collision bifurcation of tori can also generate the SNAs by the HH routes.

Fig. 5

Heagy–Hammel mechanism for $\varepsilon =0.35$: a crucial transition point $a_\mathrm{HH} \approx 3.2734$ can be observed. a the maximal Lyapunov exponent $\lambda _x$ as a function of a; b the variance ($\upsigma )$ of the local Lyapunov exponents as a function of a and small changes in torus and large changes in SNA. Abrupt increase at the transition point; c recurrence analysis: variance of the mean recurrence time $T_{\mathrm{MRT}}$ from a distribution

We examine the HH transition from torus to SNA by the Lyapunov exponent and recurrence time measure $\upsigma _{\mathrm{MRT}}$. The first property has been confirmed through the calculation of the maximal Lyapunov exponent and its variance. For the first example, we fix the parameter $\varepsilon$ at $\varepsilon =0.350$ and vary a. Figure 5a is a plot of the maximal Lyapunov exponent as a function of a and Fig. 5b is a plot of the variances $\upsigma$ of the local Lyapunov exponent as a function of a. At this transition, abrupt changes in the Lyapunov exponent as well as its variance show the characteristic signature of the Heagy–Hammel route to SNA. It is examined that the transition (in a sufficiently small neighborhood of the critical value $a_\mathrm{HH} \approx 3.2734$) is clearly revealed by the Lyapunov exponent, which varies smoothly in the torus region ($a<a_\mathrm{HH} )$ while it varies irregularly in the SNA region ($a>a_\mathrm{HH} )$. We can identify this transition point by examining the variance $\upsigma$ of the Lyapunov exponent in Fig. 5b, in which the fluctuation is small in the torus region while it is large in the SNA region. Secondary, we are able to find a threshold $a_\mathrm{HH}$ which lead to a good detection of the transition to SNAs by the recurrence time measure $\upsigma _{\mathrm{MRT}}$ (See Fig. 5c). We present two examples: a torus before the transition ($a<a_\mathrm{HH} )$ and a SNA after the transition ($a>a_\mathrm{HH} )$. For example, the attractor is a 4T quasiperiodic attractor in Fig. 6a ($a=3.201$), and the attractor exhibits four smooth curves. As a is increased to $a=3.276$, the 4T torus attractor does not continue to bifurcate and the four tori become extremely wrinkled because the wrinkled torus collide with the unstable 2T torus (red curves) shown in Fig. 6b. For this case, the attractor exhibits a fractal property but does not depend on the initial conditions sensitively (the maximal Lyapunov exponent is negative, $\lambda _{\max } \approx -\,0.001$) and it is indeed a strange nonchaotic attractor.

Fig. 6

Attractors through Heagy–Hammel route of 4T torus for $\varepsilon =0.350$. a A 4T torus for $a=3.201$; b A SNA for $a=3.276$

In addition, in order to distinguish the quasiperiodic attractor and the strange nonchaotic attractor, we can examine the attractor by the phase sensitivity function $\Gamma _N$ and the distribution of finite-time exponents $P(50,\lambda )$. We calculate the phase sensitivity exponent $\mu \approx 2.229$ and show this geometrically strange property for this SNA. Figure 7a shows that the phase sensitivity function $\Gamma _N$ of the SNA grows unboundedly with the power-law relation$\Gamma _N \sim N^{\mu }$, $\mu \approx 2.229$ and the torus attractor is bounded. Figure 7b is the distribution for $P(50,\lambda )$across the transition discussed above, namely on the torus (in blue) and the corresponding SNA (in red). A feature is that the distribution $P(50,\lambda )$ picks up a tail which extends into the $\lambda >0$ region when the attractor is a SNA. This tail directly correlates with the enhanced fluctuation in the Lyapunov exponent and its variance on SNAs (see Fig. 5a, b). On the HH SNA, the actual shapes of the distribution on the torus and the SNA are different. Furthermore, we use the fraction of positive local Lyapunov exponents $F_+ (N)$ (the fraction of exponents lying above $\lambda =0$) to describe the SNA. It has been found that on the HH SNA, the quantity shows the large N behavior $F_+ (N)\sim \exp (-\gamma N)$. The exponent $\gamma$is dependent strongly on the parameters of the system. For example, a resulting exponential decay with $\gamma \approx -\,0.004$ for $F_+ (N)$ has been observed in Fig. 7c. We note that the spectrum of this SNA is singular-continuous (Fig. 7d). To provide more solid evidence for the singular-continuous nature of the spectrum, we compute the time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$. This behavior is shown in Fig. 7e, where we observe a relatively robust power-law behavior with $\beta \approx 1.3$. Finally, we study the SNA ($a=3.276$) by a rational approximation, where the irrational frequency $\omega$ is replaced by its rational approximate $\omega _k =610/987$ (Fig. 7f). It can be seen that Figs. 6b and 7f exhibits a similar fractal property.

For the second example, we fix the parameter $\varepsilon$ at $\varepsilon =0.050$ and vary a. For $a=3.520$, the 8T torus attractor become wrinkle (Fig. 8a) and the 8T torus attractor is originated from the border-collision bifurcations of coexisting 4T torus attractors (Fig. 1a). As the parameter a is increased to $a=3.524$, the attractor has also fractal structure but is not chaotic ($\lambda _{\max } \approx -\,0.019$), see Fig. 8b. It is similar to the above case, which the 8T torus collides with the unstable 4T torus and a SNA is created. In order to distinguish the quasiperiodic attractor and the strange nonchaotic attractor, we can examine the phase sensitivity function $\Gamma _N$ for every attractor. For 8T torus attractor, the phase function $\Gamma _N$ is bounded and the phase sensitivity exponent is zero. For $a=3.524$, the phase function $\Gamma _N$ grows unboundedly with the power-low relation with $\mu \approx 1.197$, see Fig. 8c. We also investigate the power spectrum for the SNA and find that it exhibits the singular-continuous nature of the spectrum (Fig. 8d). For the time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$, we observe a relatively robust power-law behavior with $\beta \approx 1.15$ shown in Fig. 8e. These properties provide more solid evidences for this SNA. Similarly, we use a rational approximation $\omega _k =987/1597$ to describe the SNA (Fig. 8f). It can be seen that the approximated attractor (Fig. 8f) exhibits a similar nature like Fig. 8b. We have done a lot of numerical experiments and found that the HH mechanisms in Fig. 1 are common and this type of SNAs can exhibit some similar properties.

Fig. 7

Heagy–Hammel route for $\varepsilon =0.350$. a phase sensitivity functions; b distribution of finite-time Lyapunov exponents. A torus for $a=3.201$ (blue) and a SNA for $a=3.276$ (red); c variation of $F_+ (N)$ for the SNA ($a=3.276$), showing an exponential decay; d power spectrum of the SNA for $a=3.276$; e Singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.3}$; f A rational approximation to a SNA ($a=3.276$). (Color figure online)

Fig. 8

Heagy–Hammel route of 8T torus for $\varepsilon =0.050$. a A 4T torus for $a=3.520$; b A SNA for $a=3.524$; c phase sensitivity functions; d power spectrum of the SNA for $a=3.524$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.15}$; f a rational approximation to a SNA ($a=3.524$)

4.2.2 Fractalization route

Fractalization route is both the most common and the most intriguing transition to SNAs, which the quasiperiodic torus suddenly gets increasingly wrinkled and loses its original smoothness with the change of parameters, which does not collide with the unstable orbits. Such a route has been identified in a larger parameter region within the range of $\varepsilon$ values, $0.540<\varepsilon < 1.380$, and a values, 2.620$<a<$3.160. For clarity, we only give a magnified window near the tongue II region in Fig. 1b (e.g., the arrow F shows a typical fractalization route). In this regime, the 2T tori are originated from the truncation of border-collision bifurcations of coexisting 1T tori attractors. However, the 2T torus attractors do not continue to bifurcate. Here, a 2T torus gradually becomes fractal and forms a SNA.

Fig. 9

Fractalization mechanism for fixed $\varepsilon =0.6$. a The maximal Lyapunov exponent $\lambda _x$ as a function of a and no significant changes; b the variance ($\upsigma )$ of the local Lyapunov exponents as a function of a and no significant changes; c recurrence analysis: variance of the mean recurrence time $T_{\mathrm{MRT}}$ from a distribution. A crucial transition point $a_F \approx 3.0295$ can be observed

Now we examine the fractalization transition from torus to SNA by the Lyapunov exponent and recurrence time measure $\upsigma _{\mathrm{MRT}}$. For example, we fix the parameter $\varepsilon$ at $\varepsilon =0.600$ and vary a. In the gradual fractalization route, the Lyapunov exponent and the variance $\upsigma$ of the Lyapunov exponent vary only slowly, as shown in Fig. 9a, and there are no significant changes in its variance (see Fig. 9b). We cannot identify this transition point by examining the largest Lyapunov exponent and the variance $\upsigma$. The fractalization appears as a gradual change in the structure of the attractor, and it is difficult to detect a precise bifurcation. However, there is a drastic jump followed by irregular fluctuations of the recurrence time measure $\upsigma _{\mathrm{MRT}}$ at the critical value of the bifurcation parameter $a_F \approx 3.0295$. It can be seen that the attractor varies slightly in the torus region ($a<a_F )$ and at the critical value there is a drastic jump, after which, some oscillations varies irregularly in the SNA region ($a>a_F )$. In the torus region ($a<a_F )$, an example is given as a 2T quasiperiodic attractor (Fig. 10a) for $a =2.970$. In the SNA region ($a>a_F )$, we take $a=3.050$ (Fig. 10b) as an example, which the attractor loses the smoothness and becomes a SNA with the largest Lyapunov exponent $\lambda _{\max } \approx -\,0.106$. As the parameter a is increased to $a=3.100$ (Fig. 10c), the attractor looks like a chaotic attractor, but it is also indeed a SNA with negative Lyapunov exponent $\lambda _{\max } \approx -\,0.002$.

Fig. 10

Attractors through fractalization routes of 2T torus for $\varepsilon =0.600$. a A 2T torus for $a=2.970$; b a SNA for $a=3.050$; c a SNA for $a=3.100$

Fig. 11

Fractalization routes of 2T torus for $\varepsilon =0.600$. a Phase sensitivity functions; b distribution of finite-time Lyapunov exponents. A torus (blue) and a SNA (red); c variation of $F_+ (N)$ for the SNA($a=3.1$), showing an exponential decay; d power spectrum of the SNA for $a=3.1$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.25}$; f a rational approximation to a SNA ($a=3.1$). (Color figure online)

Fig. 12

Fractalization routes of 4T torus for $\varepsilon =0.250$. a a 4T torus for $a=3.250$; b a SNA for $a=3.265$; c phase sensitivity functions; d power spectrum of the SNA for $a=3.265$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.25}$; f a rational approximation to a SNA ($a=3.265$)

Fig. 13

Fractalization routes of 8T torus for $\varepsilon =0.010$. a A 8T torus for $a=3.540$; b a SNA for $a=3.552$; c phase sensitivity functions; d power spectrum of the SNA for $a=3.552$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.25}$; f a rational approximation to a SNA ($a=3.552$)

Furthermore, in order to identify the quasiperiodic attractor and the strange nonchaotic attractor, we can also examine the attractor by the phase sensitivity function $\Gamma _N$ and the distribution of finite-time exponents $P(N,\lambda )$. We calculate two phase sensitivity exponents $\mu \approx 0.904$ (for $a=3.050$ in Fig. 10b) and $\mu \approx 2.929$ ($a=3.100$ in Fig. 10c), showing this geometrically strange property. Figure 11a shows that the phase sensitivity function $\Gamma _N$ of the attractor ($a=3.100$) grows unboundedly with the power-law relation $\Gamma _N \sim N^{\mu }$, $\mu \approx 2.929$ and the torus attractor ($a=2.97$) is bounded. Figure 11b is the distribution for $P(50,\lambda )$across the transition discussed above, namely on the tori (in blue) and the corresponding SNA ($a=3.100$, in red). On the fractalized SNA, the distribution shifts continuously to larger positive Lyapunov exponents, but the shape remains the same for torus regions as well as SNA regions, while on the HH routes, the shapes of the distribution on the torus and the SNA are different. These positive local Lyapunov exponents directly correlate with the change of Lyapunov exponents on SNAs (see Fig. 9a, b, no obvious changes). Furthermore, we also use the fraction of positive local Lyapunov exponents $F_+ (N)$ to describe the SNA ($a=3.100$). It has been found that on the fractalized SNA, the quantity shows the large N behavior $F_+ (N)\sim \exp (-\gamma N)$. The exponent $\gamma$are also dependent strongly on the parameters of the system. For example, a resulting exponential decay with $\gamma \approx -\,0.018$ ($a=3.100$) for $F_+ (N)$ has been observed in Fig. 11c. We have also investigate that the spectrum of this SNA ($a=3.100$) is singular-continuous (Fig. 11d). Simultaneously, we compute the time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$, which is shown a relatively robust power-law behavior with $\beta \approx 1.25$ in Fig. 11e. Finally, we study the SNA ($a=3.1$) by a rational approximation, where the irrational frequency $\omega$ is replaced by its rational approximate $\omega _k =2584/4181$ (Fig. 11f). It can be seen that Figs. 10c and 11f exhibits a similar fractal property.

Fig. 14

Type-I intermittency mechanism for fixed $a=3.29$: A crucial transition point $\varepsilon _I \approx 0.55519496$ can be observed. a The maximal Lyapunov exponent $\lambda _x$ as a function of $\varepsilon$; b the variance ($\upsigma )$ as a function of $\varepsilon$ and small changes in torus and large changes in SNA; Abrupt changes at the transition point; c recurrence analysis: Variance of the mean recurrence time $T_{\mathrm{MRT}}$ from a distribution

Fig. 15

Attractors through type-I intermittent route of 2T torus for $a=3.290$. a A 2T torus for $\varepsilon =0.555193$; b a SNA for $\varepsilon =0.555196$

Fig. 16

Type-I intermittent route of 2T torus for $a=3.290$. a Two phase sensitivity functions; b Distribution of finite-time Lyapunov exponents. A torus (blue) and a SNA (red) for three routes; c variation of $F_+ (N)$ for the SNA, showing a power-law decay with $\beta \approx 0.28$; d power spectrum of the SNA for $\varepsilon =0.555196$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.75}$; f a rational approximation to a SNA ($\varepsilon =0.555196$). (Color figure online)

Fig. 17

Type-I intermittent route of 4T torus for $a=3.450$. a A 4T torus for $\varepsilon =0.162$; b a SNA for $\varepsilon =0.163$; c phase sensitivity functions; d power spectrum of the SNA for $\varepsilon =0.163$; e singular-continuous spectrum analysis: $\log _{10} |X(\Omega ,T)|^{2}$ versus $\log _{10} ^{T}$. We have $|X(\Omega ,T)|^{2}\sim T^{1.38}$; f a rational approximation to a SNA ($\varepsilon =0.163$)

We have also investigated 4T torus fractalization and 8T torus fractalization shown in Fig. 1a. The fractalization of 4T torus occurs between the red curve L$_{4}$ and black curve L$_{5}$, where 4T tori are originated from the truncation of border-collision bifurcations of coexisting 2T torus attractors. For example, we fix the parameter $\varepsilon$ at $\varepsilon =0.250$ and vary a. For $a=3.250$, a 4T torus attractor begins to get wrinkled (Fig. 12a) and the attractor becomes extremely wrinkled (Fig. 12b) for $a=3.265$. We examine the phase sensitivity function $\Gamma _N$ and the largest Lyapunov exponent ($\lambda _{\max } \approx -\,0.003$) for the attractor ($a=3.265$). The $\Gamma _N$ grows unboundedly with the power-low relation $\Gamma _N \sim N^{\mu }$, $\mu \approx 1.580$ (Fig. 12c). Figure 12d shows that the spectrum of the SNA is singular-continuous. The time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$ is also a relatively robust power-law behavior with $\beta \approx 1.25$ in Fig. 12e. The SNA is also obtained by a rational approximate $\omega _k =4181/6765$ (Fig. 12f).

The fractalization of 8T torus appears in the right region of red curve L$_{6}$, where 8T tori are originated from the truncation of border-collision bifurcations of coexisting 4T torus attractors. For example, we fix $\varepsilon$ at $\varepsilon =0.010$ and vary a. For $a=3.540$, a 8T torus exhibits the quasiperiodic motion with zero phase sensitivity exponent (Fig. 13a, c). As the parameter a is increased to $a=3.552$, the fractalization of 8T occurs and $\Gamma _N$ grows unboundedly with the power-low relation $\Gamma _N \sim N^{\mu }$, $\mu \approx 0.682$ (Fig. 13b, c). However, the attractor has negative Lyapunov exponent $\lambda _{\max } \approx -\,0.007$, and it is indeed a strange nonchaotic attractor. Figure 13d shows a singular-continuous spectrum for the SNA. The time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$ is also a relatively robust power-law behavior with $\beta \approx 1.25$ in Fig. 13e. The SNA is also obtained by a rational approximate $\omega _k =4181/6765$ (Fig. 13f). Therefore, the truncation of border-collision torus-doubling bifurcation (L$_{2}$, L$_{4}$ and L$_{6})$ can lead to the fractalization of different tori (2T, 4T and 8T).

4.2.3 Intermittent route

The predominant routes that lie in the upper regimes of tongues (tongue I and tongue II) are type-I intermittent routes. The first region of this route has been identified within the range of a, 3.320$<a<$3.510 and on increasing the value of $\varepsilon$, 0.150$<\varepsilon<$0.180, as shown in Fig. 1a. In this region, the type-I intermittency of 4T torus is created by the quasiperiodic analog of saddle-node bifurcation, which the 4T torus is originated from the truncation of the border-collision bifurcations of coexisting 2T torus attractors (L$_{4}$ is the bifurcation curve). The second region of the intermittent route has also been identified within the range of a, 3.11$<a<$3.42 and on increasing the value of $\varepsilon$, 0.53$<\varepsilon<$0.58, which the type-I intermittency of 2T torus is created by the quasiperiodic analog of saddle-node bifurcation. In this region, the 2T torus is originated from the truncation of the border-collision bifurcations of coexisting 1T torus attractors (L$_{2}$ is the bifurcation curve).

Now we examine the intermittent transition from torus to SNA by the Lyapunov exponent and recurrence time measure $\upsigma _{\mathrm{MRT}}$. For Type-I intermittent routes, these methods can find a bifurcation point. To understand more about this route, we consider the specific parameter value $a=3.290$ and vary $\varepsilon$ in the tongue II region (e.g., the route H). The first property has been confirmed through the calculation of the maximal Lyapunov exponent and its variance. Figure 14a, b are two plots of the maximal Lyapunov exponent and the variances $\upsigma$ as a function of $\varepsilon$. At this transition, two abrupt changes at the same bifurcation point in the Lyapunov exponent as well as its variance show the characteristic signature of the Type-I intermittency route to SNA. A crucial transition point $\varepsilon _0 \approx 0.555195$ can be observed. Unlike the case of fractalization routes, there is no distinctive abrupt signature in the $\lambda _x$ and $\upsigma$. When we examined the transition in a sufficiently small neighborhood of $\varepsilon _0$, it is clearly revealed: on the torus, $\lambda _x$ and $\upsigma$ vary smoothly, but on the SNA, the variations are rather irregular and the crossover between these two behaviors is abrupt. It is also possible to identify the precise transition point $\varepsilon _I \approx 0.55519496$ from the examination of recurrence time measure $\upsigma _{\mathrm{MRT}}$, shown in Fig. 14c: in the torus region, $\varepsilon <\varepsilon _I$, the fluctuations in $\upsigma _{\mathrm{MRT}}$ are very small, while for $\varepsilon >\varepsilon _I$, the fluctuations are large and depend irregularly on the function of the control parameter $\varepsilon$. Here, we give two representative attractors before and after the transition. For example, the attractor is a 2T quasiperiodic attractor ($\varepsilon =0.555193$, Fig. 15a). As $\varepsilon$ is increased to $\varepsilon =0.555196$, the 2T torus attractor exhibits intermittency and its Lyapunov exponent is$\lambda _{\max } \approx -\,0.003$ (Fig. 15b).

Next we describe the SNA (Fig. 15b) by the different methods. Figures 16a, b show the phase sensitivity function $\Gamma _N$ and the distribution of finite-time exponents $P(N,\lambda )$ for the torus ($\varepsilon =0.555193$) and the SNA ($\varepsilon =0.555196$). The phase sensitivity function $\Gamma _N$ grows unboundedly with the power-law relation $\Gamma _N \sim N^{\mu }$, $\mu \approx 3.274$ and the torus attractor is bounded. Figure 16b is the distribution for $P(50,\lambda )$across the transition discussed above, namely on the tori (in blue) and corresponding SNAs (in red). One of the most obvious features is that the distribution $P(50,\lambda )$ picks up a tail which extends into the $\lambda >0$ region when the attractor is a SNA. This tail directly correlates with the enhanced fluctuation in the Lyapunov exponents on SNAs (see Figs. 14a, b). One remarkable feature of intermittent SNAs is that the positive tail in the distribution decays very slowly. To quantify further the distribution of finite-time Lyapunov exponents, we have shown that on the intermittent SNA, these quantities show the large N behavior $F_+ (N)\sim N^{-\beta }$, here $\beta \approx 0.28$ ($\varepsilon =0.555196$) in Fig. 16c, while for the fractalized or HH SNAs, the approach is exponentially fast, $F_+ (N)\sim \exp (-\gamma N)$. It is investigated that the spectrum of this SNA ($\varepsilon =0.555196$) is singular-continuous (Fig. 16d) and the time-dependent Fourier transform $\left| {X(\Omega ,N)} \right|$ is shown a relatively robust power-law behavior with $\beta \approx 1.75$ in Fig. 16e. Finally, we study the SNA by a rational approximation$\omega _k =1597/2584$ (Fig. 16f), which exhibits a similar fractal property.

For another example, we consider the parameter value $a=3.450$ and vary $\varepsilon$ in the tongue I region (e.g., the route d in Fig. 1a). For $\varepsilon =0.162$, the attractor is a 4T torus attractor (Fig. 17a) with zero phase sensitivity exponent. As $\varepsilon$ is increased to $\varepsilon =0.163$, the 4T torus attractor exhibits the intermittent signature, but it is nonchaotic because its Lyapunov exponent $\lambda _{\max } \approx -\,0.021$ is negative (Fig. 17b). It is found that the phase sensitivity function $\Gamma _N \sim N^{\mu }$ grows unboundedly with the power-law $\mu \approx 3.178$ (Fig. 17c), and thus, it is indeed a SNA. It is also investigated that the spectrum of this SNA is singular-continuous (Fig. 17d) and $\left| {X(\Omega ,N)} \right|$ is shown a relatively robust power-law behavior with $\beta \approx 1.38$ in Fig. 17e. Finally, we study the SNA by a rational approximation$\omega _k =6765/10946$ (Fig. 17f), which exhibits intermittency like Fig. 15b. Usually, the regions of SNAs are rare by the type-I intermittency and the SNAs easily become the chaotic attractors (gray region in Fig. 1). There exists a narrow region (e.g., the route C and the route D), where the SNAs are also created by the type-I intermittency and the SNAs disappear suddenly due to the boundary crisis of SNAs but not the boundary crisis of chaotic attractors (e.g., the route B and the route E in Fig. 1).

5 Conclusions

While the SNAs have been studied for more than three decades, one interesting topic focused on the bifurcation and the creation of SNAs, which most works have paid attention to the smooth systems in different fields. In this paper, we have investigated the relation between the border-collision bifurcations of tori and the creation of SNAs in the nonsmooth system. We found that the coexisting torus attractors (1T torus, 2T torus and 4T torus) collided at the border and a finite sequence of torus-doubling appeared in a quasiperiodically driven system with nonsmooth factors, which was called the truncation of border-collision torus-doubling bifurcation. It was the first to demonstrate that the truncation of border-collision bifurcation of tori can generate strange nonchaotic dynamics. We have identified the different types of SNAs through different routes and mechanisms in a nonsmooth system, namely the quasiperiodically driven piecewise Logistic map. This system is a representative model for quasiperiodically driven border-collision period-doubling system. These SNAs have been identified in a two parameter ($a-\varepsilon )$ phase diagram and the SNAs are abundant.

In order to distinguish different mechanisms for the creation of SNAs, we have described Heagy–Hammel routes (e.g., 4T torus and 8T torus), gradual fractalization (e.g., 2T torus, 4T torus and 8T torus) and type-I intermittency (2T torus and 4T torus), whose routes are explored through the truncation of border-collision bifurcations of tori. In particular, we found that the routes to strange nonchaotic dynamics are more diverse in two tongue-type regions. Besides the above routes, the crisis of SNAs occurs in the tongue-type regime. We have presented a number of examples and described different routes and mechanisms. To distinguish the type of attractors and verify the SNAs, we have examined the maximal Lyapunov exponent and phase sensitivity exponent. For three routes (Heagy–Hammel, Type-I intermittency and fractalization), we detect the transitions from quasiperiodic motions to SNAs by different measures (the maximal Lyapunov exponent, the variance of local Lyapunov exponents and the recurrence time variance measure). Three types of SNAs are also characterized by the singular-continuous spectrum, Fourier transform and the rational approximation. We expect that these results are common in more nonsmooth systems.