Bifurcations of Chaotic Attractors in a Piecewise Smooth Lorenz-Type System

Abstract

We study the dynamics of a piecewise-smooth system of differential equations for which the existence of a strange Lorenz-type attractor had been rigorously proved previously and bifurcation mechanisms of its birth had been obtained. In this work we discuss the destruction of this attractor due to the appearance of sliding motions in its structure. Using qualitative and numerical methods, we study a complex sequence of attractor bifurcations that leaves in the system a globally stable limit cycle. We show that this sequence is based on C-bifurcations and bifurcations of multi-loop homoclinic trajectories.

1 Introduction

This paper pays tribute to pioneering contributions of Yu.I. Neimark to the dynamical systems theory. The well-known D-partition method can be considered as one of the first fundamental contributions of Neimark to the local bifurcation and stability theory. Another significant Neimark’s result is the bifurcation of the birth of a torus or a complex nonwandering set out of a periodic motion when its stability changes. This is the Neimark–Saker bifurcation well-known to specialists [1]. The theory of piecewise smooth (relay) systems, initiated by Neimark in the 1950–1960s [2, 3], is still being successfully developed up to the present time [4, 5]. This work can be considered as a further development of bifurcation theory of piecewise smooth dynamical systems.

Piecewise linear and piecewise smooth systems have been widely used in the theory of dynamical systems in various contexts and applications [4, 6–8]. Their potential advantage over their nonlinear counterparts is that one can obtain explicit solutions in given regions of the system’s phase space and “glue” solutions at the boundaries of these regions.

Piecewise smooth dynamic systems [4–6] are broadly used in practice as relay systems, automatic control systems, and switching systems [9–12]. An interesting example of such a piecewise smooth system is a biomechanical model of the balance of a pedestrian walking over a bridge [13], where switching between two systems [14] corresponds to the transfer of the pedestrian weight from one foot to another. The trajectory of such a piecewise-smooth system is determined by two glued solutions of integrable subsystems, which makes it possible to obtain exact forms of periodic pedestrian movement [15].

Piecewise smooth dynamical systems can be used to construct flows that possess basic properties of chaotic nonlinear systems and allow rigorous analytical investigation. In a recent paper [16], we proposed a new approach to constructing piecewise smooth models that replace nonlinear non-integrable chaotic systems. These models have qualitatively the same bifurcation structure and allow one to analytically prove the existence of strange attractors and characterize their bifurcations.

This approach was applied to the well-known Lorenz system [17], instead of which we constructed a piecewise smooth linear system as its simplest counterpart. For this system, we have given a rigorous proof of the existence of a singular-hyperbolic attractor and explicitly described bifurcations leading to its birth. The resulting bifurcations and attractors qualitatively coincide with the bifurcation scenario and the structure of the Lorenz attractor, studied in detail by qualitatively-numerical methods [18–20]. It is known from numerical studies that the Lorenz attractor collapses when the invariant foliation is lost [19, 21] as a result of subsequent complex bifurcations. Due to its complexity, the exact bifurcation mechanism of the Lorenz attractor disappearance has not yet been rigorously studied.

In this paper we address this problem, i.e., we study the bifurcation scenario of the death of a singular-hyperbolic attractor, not in the Lorentz system but rather in its counterpart, the model from [16]. This destruction begins with the destruction of the invariant foliation and, after an infinite sequence of bifurcations, ends with the birth of a unique stable limit cycle.

The paper is organized as follows. Section 2 describes the proposed piecewise smooth linear model, Section 3 gives a description of sliding movements, Section 4 presents the main result [16], and Section 5 provides a numerical analysis of the destruction of a strange attractor.

2 Model Description

We consider a piecewise smooth system glued from three-dimensional linear subsystems A_s, A_l, and A_r:

$$\begin{array}{l}{A}_{s}\,:\,\begin{array}{l}\dot{x}=x,\\ \dot{y}=-\alpha y,\\ \dot{z}=-\nu z,\end{array}\quad (x,y,z)\in {G}_{s},\\ {A}_{l}\,:\,\begin{array}{l}\dot{x}=-\lambda (x+1)+\omega (z-b),\\ \dot{y}=-\delta (y+1),\\ \dot{z}=-\omega (x+1)-\lambda (z-b),\end{array}\quad (x,y,z)\in {G}_{l},\\ {A}_{r}\,:\,\begin{array}{l}\dot{x}=-\lambda (x-1)-\omega (z-b),\\ \dot{y}=-\delta (y-1),\\ \dot{z}=\omega (x-1)-\lambda (z-b),\end{array}\quad (x,y,z)\in {G}_{r},\end{array}$$

(1)

where α, δ, ν, ω, λ, and b are positive parameters. These subsystems are defined on the following phase space partition G_s, G_l, and G_r, respectively:

$$\begin{array}{l}{G}_{s}:| x| <1,\quad y\in {{\mathbb{R}}}^{1},\quad z<b,\\ {G}_{l}:\left\{\begin{array}{l}x\leqslant -1\quad {\rm{for}}\quad z\leqslant b\\ x\leqslant -1\quad {\rm{for}}\quad z>b\quad {\rm{and}}\quad y\geqslant 0\\ x<1\quad {\rm{for}}\quad z>b\quad {\rm{and}}\quad y<0,\end{array}\right.\\ {G}_{r}:\left\{\begin{array}{l}x\geqslant 1\quad {\rm{for}}\quad z\leqslant b\\ x\geqslant 1\quad {\rm{for}}\quad z>b\quad {\rm{and}}\quad y<0\\ x>-1\quad {\rm{for}}\quad z>b\quad {\rm{and}}\quad y\geqslant 0.\end{array}\right.\end{array}$$

(2)

We denote the vector fields of subsystems A_s, A_l, and A_r by F_s, F_l, and F_r respectively in the form of the system $\dot{X}={F}_{i}(X)$ with index i = (s, l, r) and vector X = (x, y, z).

This system qualitatively reproduces the main properties of the Lorenz system [17]. Similar to the Lorentz system, it has three equilibrium states and remains invariant with respect to the substitution (x, y, z) → ( − x, − y, z).

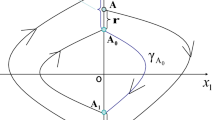
Linear subsystem A_s controls the dynamics of system (1) in the region G_s. This system has the saddle equilibrium state O_s at the origin, so we will call G_s the saddle region. Subsystems A_r,l are defined in regions G_r,l and have symmetric equilibria e_r,l = {±1,±1, b}, respectively. These equilibria are stable three-dimensional foci in subsystems A_r,l. In the complete system, these equilibria become glued and therefore can change their stability. Note that gluing lines ${w}_{l}=\{x=-1,z=b,y\in {{\mathbb{R}}}^{1}\}$ and ${w}_{r}=\{x=1,z=b,y\in {{\mathbb{R}}}^{1}\}$ are stable manifolds of foci e_l and e_r respectively (see Fig. 1). We will call G_r and G_l the right and left focal regions.

Fig. 1

Constructing the piecewise smooth system (1). The phase space is divided into three regions: G_s, G_l, and G_r (not shown in the figure). The saddle region G_s is formed by the vertical half-planes S_1,2 and the horizontal surface D. Focal regions G_l and G_r are separated by the saddle region and the vertical Z-shaped border Z_s. The saddle O_s has the two-dimensional stable manifold W^s and the one-dimensional unstable manifold (${W}_{1}^{u}$ and ${W}_{2}^{u}$ are its right and left branches, respectively). Segments w_l and w_r belong to stable manifolds of foci e_l and e_r, respectively.

The saddle region G_s is bounded by the right and left vertical half-planes ${S}_{1}=\{x=1,y\in {{\mathbb{R}}}^{1},\,z < b\}$ and ${S}_{2}=\{x=-1,\,y\in {{\mathbb{R}}}^{1},\,z < b\}$ (see Fig. 1). Region G_s is also bounded from above by a part of the plane $D=\{| x| \leqslant 1,\,y\in {{\mathbb{R}}}^{1},\,z=b\}$ (the dark gray horizontal plane in Fig. 1). Below the plane D, focal regions G_l and G_r are located to the left and right of the vertical half-planes S₂ and S₁ respectively. Above the plane D, the focal regions are separated by the Z-shaped border Z_s (see Fig. 1).

The saddle O_s has a two-dimensional stable manifold defined in the saddle region as ${W}_{saddle}^{s}=\{x=0,\,y\in {{\mathbb{R}}}^{1},\,z < b\}$ (the central vertical plane in Fig. 1) and a one-dimensional unstable manifold defined in the saddle region as ${W}_{1saddle}^{u}=\{0 < x < 1,\,y=z=0\}$ and ${W}_{2saddle}^{u}=\{-1 < x < 0,\,y=z=0\}$. These manifolds and their extensions along the trajectories of systems A_r,l in the focal regions form global saddle manifolds W^s, ${W}_{1}^{u}$ and ${W}_{2}^{u}$ of saddle O_s in the full phase space of system (1).

We assume that the following condition holds:

$$\frac{1}{2}<\nu <1<\alpha .$$

(3)

The part of inequality (3) with ν < 1 means that the saddle value of O_s is positive. Due to the inequality 1 < α, the plane W^lead = ((x, z) ∈ G_s, y = 0) is a part of the leading manifold, which is similar to the Lorenz system.

3 Sliding Motions

System (1) is dissipative, that is, its phase space has an absorbing region G such that any trajectory with a starting point in the region ${{\mathbb{R}}}^{3}\setminus G$ falls into the region G and remains there forever. This region is defined by the following inequalities [16]:

$$G=\left\{\begin{array}{ll}| y| \leqslant 1&\\ 0\leqslant z\leqslant 2b&{\rm{for}}\,| x| \leqslant 1\\ {V}_{l}\leqslant {b}^{2}&{\rm{for}}\,x<-1\\ {V}_{r}\leqslant {b}^{2}&{\rm{for}}\,x>1,\end{array}\right.$$

(4)

where V_l,r = (x ± 1)² + (z − b)². Obviously, all trajectories of system (1) are contained in this region. The system (1) has two surfaces of stable sliding motions ${S}_{1}^{+}=\{x=1,\,z>{b}^{+}=b+\frac{2\lambda }{\omega },\,y<0\}$ and ${S}_{2}^{+}=\{x=-1,\,z>{b}^{+}=b+\frac{2\lambda }{\omega },\,y>0\}$. On surfaces ${S}_{1}^{+}$ and ${S}_{2}^{+}$, the vector field of the system A_l is oriented towards increasing x, and system A_r is oriented towards decreasing x (vector fields of systems A_l and A_r join each other on these surfaces). The sliding motions on these surfaces can be defined by two-dimensional systems obtained by means of an extension method due to A.F. Filippov [22] that is similar to an extension method due to Neimark [2]. In the considered case, this extension takes the form

$$\dot{X}=\alpha {F}_{r}(X)+(1-\alpha ){F}_{l}(X).$$

(5)

Here, the coefficient α is defined by the scalar product

$$(\alpha {F}_{r}(X)+(1-\alpha ){F}_{l}(X),\bigtriangledown s)=0,$$

(6)

where the gradient of the function s(X), which defines the surface of the sliding motions s(X) = 0, represents the vector ▽s(1, 0, 0). Now (1), (2), (5), (6) together imply that the system of sliding motions has the form

$$\begin{array}{l}\dot{y}=-\delta y+\frac{\lambda \delta }{\omega (z-b)-\lambda },\\ \dot{z}=-\omega -\lambda (z-b)-\frac{\lambda \omega }{\omega (z-b)-\lambda }.\end{array}$$

(7)

System (7) describes simple dynamics of the sliding movements. Since in (7)${\left.\dot{z}\right|}_{{S}_{1,2}^{+}}<0$, the coordinate z decreases and every trajectory leaves ${S}_{1,2}^{+}$ through the break lines z = b⁺. Depending on the parameters of system (1), the role of the sliding motions in the dynamics of system (1) may be different. We consider two main cases.

4 Attractors without Sliding Movements

The work [16] proves that in the parameter region

$$\begin{array}{cc}\delta >{\delta }_{cr}=\frac{\omega \,\,\mathrm{ln}\,\,2}{\pi },\\ b<{b}_{cr}=2\sqrt{1+\frac{{\lambda }^{2}}{{\omega }^{2}}}\exp \left\{\frac{\lambda }{\omega }\left({\rm{arctan}}\frac{\omega }{\lambda }+\pi \right)\right\}\end{array}$$

(8)

attractors of system (1) do not contain sliding motions.

Theorem [16] 1. In the parameter region

$${b}_{het}={\gamma }_{het}\exp \frac{3\pi \lambda }{2\omega }\leqslant b<{\nu }^{-1}\exp \frac{3\pi \lambda }{2\omega },$$

where γ_het(ν) is the inverse function of the function $\nu =1+\frac{\mathrm{ln}\,\,2-\mathrm{ln}\gamma }{\mathrm{ln}(\gamma -1)}$, there exists a strange chaotic Lorenz-type attractor, born as a result of a heteroclinic bifurcation at b = b_het and coexisting with two stable foci e_l and e_r.

2. Surface

$${b}_{AH}={\nu }^{-1}\exp \frac{3\pi \lambda }{2\omega }$$

corresponds to an Andronov–Hopf-like bifurcation where two symmetric saddle cycles merge into stable equilibrium states e_l and e_r.

3. In the parameter region

$${b}_{AH}\leqslant b\leqslant {b}_{cr}$$

(9)

the strange singular-hyperbolic attractor is the only attractor of system (1) (see Fig. 2).

Fig. 2

Lorenz type attractor existing in system (1) with parameter values b = 3.8, α = 2, ν = 0.75, δ = 0.588, ω = 2 and λ = 0.294 from the region (9). Trajectories of this attractor are glued from the trajectories of the saddle system A_s (shown in black) and trajectories of the focal systems A_l,r (shown in gray).

5 Attractors Containing Sliding Motions

For b > b_cr, trajectories of the attractor of system (1) can fall on the surface of sliding motions. Moreover, any periodic orbit containing a section of sliding movements becomes stable. The fact is that the instability of periodic motions in the system is determined by the direction of the axis x (see system A_s in (1)). The X-axis is perpendicular to the plane of the sliding motions, along which trajectories fall on them non-asymptotically. Thus, the instability along the saddle orbits is compensated by the superstability of the sliding planes. If trajectories of the nonwandering set of the system do not fall on the surface of sliding motions, they continue to remain saddle trajectories, the same as for b < b_cr in the case of the singular-hyperbolic attractor. The possibility of the existence of attractors containing both stable trajectories with sliding motions and saddle trajectories complicates the solution of the problem of the destruction of the strange attractor and necessitates the use of qualitative–numerical methods. In the numerical study of system (1) that we carry out below, we pay attention to the following possible effects.

• 1. The stabilization of saddle trajectories falling on the plane of sliding motions, i.e., the effect of the appearance of stable orbits. For a small deviation of the parameter b from the critical value μ = 1 − b_cr/b > 0, μ ≪ 1, stable orbits have large periods, and their basins of attraction are so small that they are difficult to find even numerically. Thus, for small μ > 0 the attractor ceases to be singular-hyperbolic and becomes the so-called quasi-strange attractor [23].

• 2. The bifurcation of the birth of a stable cycle from the homoclinic orbit of a saddle with a positive saddle value. This effect is unexpected, because in the case of smooth or even piecewise smooth continuous systems, the cycle must be born unstable.

• 3. The possibility of a C-bifurcation [11], where two symmetric stable cycles of the same period are born from a stable limit cycle, and the cycle itself, leaving the surface of sliding movements, becomes a saddle cycle. In smooth systems, a counterpart of such a bifurcation is a pitchfork bifurcation of codimension two occurring in symmetric systems where two stable cycles of the same period are born from a limit cycle that loses stability through the multiplier m =+1. Further, for simplicity, such a C-bifurcation in system (1) will be called a pitchfork bifurcation.

5.1 Bifurcations of Attractors Containing Sliding Motions

The sequence of bifurcations in the parameter region b > b_cr for whose points the attractor contains sliding motions is more convenient to consider as the parameter b decreases, starting with large values of b ≈ 300.

Figure 3 shows a bifurcation diagram of system (1). For any given value of parameter b along the Y-axis, intersection points of the steady movements of the system with the section plane D are indicated. The horizontal lines near lines x = ±1 are an extreme trace of limit cycles.

Fig. 3

Bifurcation diagram of system (1) for α = 2, ω = 2, δ = 0.588, λ = 0.294. The Y-coordinates show intersection points of the steady motions of the system (1) with the section plane D.

Figure 3a shows a bifurcation diagram constructed for the entire range of values of the parameter b ∈ [0, 300]. For b > 283 the diagram contains only traces of a globally stable period-two limit cycle (see Fig. 4a).

Fig. 4

The first sequence of changing the phase patterns of system (1) when decreasing the parameter b. (a) For b = 300 the system has a globally stable period-two limit cycle enveloping the stable one-dimensional manifolds w_l,r of foci e_l,r once. (b) For b = 270 two stable limit cycles of the same period coexist. (c) For b = 143.07 these limit cycles merge into a homoclinic butterfly and, with a further decrease in the parameter, form a globally stable limit cycle of a double period. (d) Phase portrait of this four-loop cycle for b = 40. The cycle trajectory goes around each of the manifolds w_l,r twice. Other parameters: α = 2, ω = 2, δ = 0.588, λ = 0.294.

The vertical dashed line at b = 283 corresponds to the first C-bifurcation of the cycle doubling. At this point, two curves extend from the extreme traces. Together with the horizontal lines, they correspond to the traces of two stable limit cycles born as a result of the pitchfork bifurcation (see Fig. 4b).

The vertical dashed line at b = 143 marks the first homoclinic bifurcation, where two stable cycles merge into the line (x = 0, ∣y∣ < 1, z = b) on the stable saddle manifold W^s and form a homoclinic butterfly (see Fig. 4c). This corresponds to the intersection of the curves at the point (b = 143, x = 0).

With a further decrease in b, the homoclinic butterfly is destroyed and a globally stable limit cycle of a double period is born (see Fig. 4d). All four curves of the bifurcation diagram on the interval b ∈ (29, 143) are the traces of this cycle until the next pitchfork bifurcation occurs at b = 29.

Figures 3b and 3c are enlarged fragments of Fig. 3a. Figure 3b shows the second pair of bifurcations: “pitchfork (b = 29)—homoclinic butterfly bifurcation (b = 21).”

With a further decrease in the parameter b, bifurcation pairs “pitchfork—homoclinic butterfly” are repeated, doubling the period (round-trip) of the stable cycles (see Fig. 5). These pairs accumulate at b → b_cr, forming a sequence that serves as the skeleton of a bifurcation set. Figure 3c shows that every interval (b_k+1, b_k), where b_k is the previous and b_k+1 is the next pitchfork bifurcation, contains a chaotic window. The bifurcation set in chaotic windows becomes more complex as k increases. Apparently, this is due to the fact that the sections of sliding motions on nonwandering paths decrease with increasing k, i.e., when approaching the the existence region of a strange attractor.

Fig. 5

Example of a homoclinic butterfly formed by two symmetrical multi-loop homoclinic orbits for b = 4.075. Other parameters: α = 2, ω = 2, δ = 0.588, λ = 0.294.

The area to the left of the vertical dashed line b_cr = 3.95 in Fig. 3c corresponds to a singular-hyperbolic attractor. We noted that, according to the well-known scenario of transition to chaos in Lorenz-like smooth flows with a negative saddle value [24, 25], with an increase in the bifurcation parameter the period of stable limit cycles through the cascade of bifurcations of homoclinic orbits doubles.

A significant difference in the scenario obtained in this paper is that the saddle value of system (1) is positive. However, the cycles originating from homoclinic orbits, unlike the case of smooth systems [26], are stable due to the presence of sliding motions. In addition, in the case under consideration there are windows of chaotic motions along with windows of stable periodic orbits.

6 Conclusion

In this paper, we have conducted a qualitatively–numerical study of a complex bifurcation set corresponding to the destruction of a singular-hyperbolic attractor in a piecewise smooth system, which is a counterpart of the well-known Lorenz system. This destruction is due to the appearance of sliding motions in the structure of the attractor. The bifurcation set is a sequence of patterns that converges to a critical value of the parameter corresponding to the beginning of the destruction of the strange attractor. The bifurcation patterns are based on C-bifurcations, where doublings of multi-period limit cycles occur, and the system undergoes bifurcations of multi-loop homoclinic orbits leading to the birth of stable limit cycles with a double period. These patterns contain chaotic windows whose structure becomes more complex along the sequence. The nontrivial task of a rigorous analysis for a complex bifurcation transition from a stable limit cycle to a strange attractor, briefly described in the present work, requires the construction of point mappings that take into account sliding motions and is beyond the scope of this paper.

7 Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation, project no. 0729-2020-0036, the Russian Science Foundation, project no. 19-12-00367 (numerics; to V.N.B. and N.V.B), and the US National Science Foundation, grant no. DMS-1909924 (to I.V.B.).