1 Introduction

Nonlinear systems with quasiperiodic forcing exhibit different dynamical behaviors [1,2,3,4,5]. In general, quasiperiodic forcing means that the dynamics of the system are more complex and the corresponding invariant sets are tori, rather than fixed points, periodic orbits, and limit cycles. In 1984 Grebogi et al. [6] discovered a special class of invariant sets in a nonlinear oscillator with two incommensurate frequencies, known as strange nonchaotic attractors (SNAs). The strangeness refers to the geometry or shape of SNAs is similar to chaotic attractors, that is, SNAs have complex fractal structures but are nonchaotic. The nonchaos means that the maximum Lyapunov exponent of the dynamics is nonpositive, which is an important feature that distinguishes SNAs from chaotic attractors.

SNAs typically appear between quasiperiodic and chaotic attractors, and scholars have done a large number of works in mathematics, numerical simulation, and experimental observation. Romeiras and Ott [7] uncovered SNAs in the damped pendulum equation under two-frequency excitation and pointed out that SNAs have unique spectral characteristics. Feudel et al. [8] discussed the correlation between the appearance of SNAs and the destruction of invariant torus attractors in a quasiperiodic forcing circle map. Ditto et al. [9] observed SNAs in the magnetoelastic ribbon experiment. Since it is difficult to confirm that the maximum Lyapunov exponent of the system is nonpositive in the experiment, Ditto et al. verified the nonchaotic characteristics of SNAs with the help of Fourier amplitude spectrum and information dimension measurements. Furthermore, the existence of SNAs is proved in the discrete Schrödinger equation with quasiperiodic potential [10]. Most of the studies show that the emergence of SNAs depends on quasiperiodic excitation applied to the system. However, some experts [11,12,13] show that quasiperiodic excitation is not a necessary condition for the appearance of SNAs. SNAs can occur in some systems with noise and periodic excitation, even in the absence of external excitation and variable stars [14, 15].

How to verify the strange property of SNAs and what is the generation mechanism of SNAs are both interesting questions. Some quantitative methods can be used to characterize strange property, such as phase sensitivity function [16], rational approximation [17], and singular continuous spectra [18]. The common evolution routes of SNAs include the torus-doubling [19], Heagy and Hammel [20], fractal [21], and intermittency routes [22, 23]. In addition, the unconventional routes are identified, such as interior crisis [24], bubble [25], merging bubble [26], symmetry breaking [27], and double grazing bifurcation routes [28], and so on [29,30,31,32].

The research on SNAs has mainly focused on forced smooth dynamical systems, and relatively few results have been known for nonsmooth ones. Zhang and Shen [33] studied a class of interval maps with square root singularity for quasiperiodic excitation, and showed that torus attractors lose their smoothness through grazing bifurcation, and eventually evolve into SNAs. Li et al. [34] found that SNAs appear between two parameter regions with chaotic motion in a two-degree-freedom quasiperiodically forced vibro-impact system, and further explored the multistability in the system. SNAs usually exist in a very small parameter region in that systems, so distinguishing SNAs from quasiperiodic and chaotic attractors is a difficult problem. However, Zhao and Zhang [35] investigated that the border collision bifurcation in a quasiperiodic forcing nonsmooth map can lead to the birth of SNAs, and the region with SNAs accounts for about 40% of the given parameter region.

The concept of crises in dynamical systems was introduced by Grebogi et al. in [36, 37]. Crises were originally used to describe the phenomenon of sudden qualitative changes of attractor structure caused by collisions between chaotic attractors and unstable orbits. Pal et al. [38] noticed large amplitude events in nonlinear damping pendulum caused by interior crisis. Transient or intermittent behavior associated with crises can be well characterized with the help of critical exponents [39,40,41], and crises are also found in some quasiperiodic and stochastic excitation systems [42,43,44].

In our previous work [45], the torus-doubling, fractal and type-I intermittency routes to SNAs are identified in a quasiperiodically forced piecewise smooth system. The goal of the present work is to identify SNAs due to interior crisis, metamorphoses of basin boundaries, double crises, and discontinuous quasiperiodic orbits in the system. The paper is arranged as follows: we briefly introduce a system that possesses SNAs in different regions of the parameter plane in Sect. 2. In Sect. 3, we study the four evolution routes of SNAs and describe the associated mechanisms. We conclude our results in Sect. 4.

2 The quasiperiodically forced piecewise smooth system

Unimodal maps with one break point are a typical class of nonsmooth systems. Sushko et al. [46] considered the following piecewise smooth system and described the border-collision bifurcations, chaos, and multistability of the system.

$$\begin{aligned} x\rightarrow & {} f(x)\nonumber \\= & {} \left\{ \begin{array}{lr} x_{n+1}=r x_n, &{}\quad 0 \le x<{\bar{x}}, \\ x_{n+1}=a x_n\left( 1-x_n\right) , &{}\quad {\bar{x}} \le x \le 1, \end{array} \quad {\bar{x}}{=}1-\frac{r}{a},\right. \nonumber \\ \end{aligned}$$
(1)

where \(a>3\) and \(1<r<a\).

To enrich the birth and mechanism of SNAs in nonsmooth systems, we consider map (1) under quasiperiodic perturbations, that is

$$\begin{aligned} (x, \theta ) \rightarrow&f(x, \theta )\nonumber \\ =&{\left\{ \begin{array}{ll}x_{n+1}=\left( r+\varepsilon \cos 2 \pi \theta _n\right) x_n, \qquad 0 \le x_n<{\bar{x}} \\ x_{n+1}=\left( a+\varepsilon \cos 2 \pi \theta _n\right) x_n\left( 1-x_n\right) , \\ \qquad \qquad \quad \qquad \qquad \quad \qquad \qquad \qquad {\bar{x}} \le x_n \le 1, \\ \theta _{n+1}=\theta _n+\omega (\bmod 1), \end{array}\right. } \nonumber \\ \end{aligned}$$
(2)

where \(\varepsilon \) is the amplitude, \(\omega \) is the frequency and is taken as an irrational number (usually the golden mean ratio, \(\omega =(\sqrt{5}-1)/2\)). Successive iterations of \(\theta \) densely cover the \(\theta \)-axis, so the dynamics of the system is ergodic in the \(\theta \)-axis. Furthermore, if a quasiperiodic forcing is applied to the system (1), then the periodic orbits become quasiperiodic tori in the system (2).

The system is an irrational shift in the \(\theta \)-axis, so the Lyapunov exponent in the x direction determines whether the system is chaotic or not.

$$\begin{aligned} \lambda _x=\lim _{n \rightarrow \infty } \frac{\ln \left| \frac{\partial x_n}{\partial x_0}\right| }{n}=\lim _{n \rightarrow \infty } \frac{1}{n} \sum _{k=0}^{n-1} \ln \left| \frac{\partial f\left( x_k, \theta _k\right) }{\partial x_k}\right| . \nonumber \\ \end{aligned}$$
(3)

The strange property of attractors can be verified by the phase sensitivity function, which elaborates the sensitive dependence of the attractor with respect to the phase under quasiperiodic forcing. The recurrence relation can be obtained from system (2) as follows

$$\begin{aligned} \frac{\partial x_{n+1}}{\partial \theta }= {\left\{ \begin{array}{ll} -2 \pi \varepsilon x_n \sin 2 \pi \theta _n+\left( r+\varepsilon \cos 2 \pi \theta _n\right) \frac{\partial x_n}{\partial \theta }, \\ \qquad \qquad \quad \qquad \qquad \qquad \qquad \ 0 \le x_n \le {\bar{x}}, \\ -2 \pi \varepsilon x_n\left( 1-x_n\right) \sin 2 \pi \theta _n\\ \quad +\left( a+\varepsilon \cos 2 \pi \theta _n\right) \left( 1-2 x_n\right) \frac{\partial x_n}{\partial \theta }, \\ \qquad \qquad \qquad \quad \qquad \qquad \qquad \quad {\bar{x}} \le x_n \le 1.\end{array}\right. } \end{aligned}$$
(4)

Therefore, starting from any initial derivative \(\frac{\partial x_0}{\partial \theta }\), we can obtain the derivatives at all points of the trajectory

$$\begin{aligned} \frac{\partial x_N}{\partial \theta }= {\left\{ \begin{array}{ll}\sum _{k=1}^N-2 \pi \varepsilon x_{k-1} \sin 2 \pi \theta _{k-1} R_{N-k}\left( x_k, \theta _k\right) \\ \quad +R_N\left( x_0, \theta _0\right) \frac{\partial x_0}{\partial \theta }, \qquad \qquad 0 \le x_n \le {\bar{x}}, \\ \sum _{k=1}^N-2 \pi \varepsilon x_{k-1}\left( 1-x_{k-1}\right) \sin 2 \pi \theta _{k-1} \\ \quad R_{N-k}\left( x_k, \theta _k\right) +R_N\left( x_0, \theta _0\right) \frac{\partial x_0}{\partial \theta }, \\ \qquad \qquad \quad \qquad \qquad \qquad \qquad \qquad {\bar{x}} \le x_n \le 1,\end{array}\right. } \end{aligned}$$
(5)

where

$$\begin{aligned}&R_M\left( x_m, \theta _m\right) \nonumber \\&\quad = {\left\{ \begin{array}{ll} \prod _{i=1}^M r+\varepsilon \cos 2 \pi \theta _{m+i}, \qquad \qquad \qquad 0 \le x_n \le {\bar{x}}, \\ \prod _{i=1}^M\left( a+\varepsilon \cos 2 \pi \theta _{m+i}\right) \left( 1-2 x_{m+i}\right) , \\ \qquad \qquad \quad \qquad \qquad \qquad \qquad \qquad \qquad \ {\bar{x}} \le x_n \le 1.\end{array}\right. } \end{aligned}$$
(6)

If an attractor is nonchaotic, then the Lyapunov exponent of the system will be nonpositive, and \(R_N(x_0, \theta _0) \frac{\partial x_0}{\partial \theta }\) will tend to 0 as \(N \rightarrow \infty \). Thus, Eq. (5) can be approximately expressed as follows

$$\begin{aligned} \frac{\partial x_N}{\partial \theta } \approx {\left\{ \begin{array}{ll}\sum _{k=1}^N -2 \pi \varepsilon x_{k-1} \sin 2 \pi \theta _{k-1} R_{N-k}\left( x_k, \theta _k\right) , \\ \qquad \qquad \quad \qquad \qquad \qquad \qquad \qquad \qquad 0 \le x_n \le {\bar{x}}, \\ \sum _{k=1}^N -2 \pi \varepsilon x_{k-1}\left( 1-x_{k-1}\right) \sin 2 \pi \theta _{k-1}\\ \quad R_{N-k}\left( x_k, \theta _k\right) , \qquad \qquad \qquad \qquad {\bar{x}} \le x_n \le 1.\end{array}\right. } \end{aligned}$$
(7)

The phase sensitivity function in Ref. [16] is defined as

$$\begin{aligned} \tau _N=\min _{x_0, \theta _0}\left( \max _{0 \le n \le N}\left| \frac{\partial x_n}{\partial \theta }\right| \right) . \end{aligned}$$
(8)

If \(\tau _N\) tends to infinity as the number of iterations increases, then the attractor is nonsmooth and has no differentiability, which means that the attractor is strange. In addition, there is a power-law relationship between \(\tau _N\) and \(N^\mu \), i.e., \(\tau _N \sim N^\mu \), where \(\mu \) is regarded as the phase sensitivity exponent.

Fig. 1
figure 1

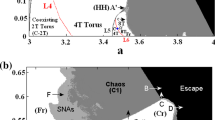
The dynamical transition in the \((\textrm{a}, \varepsilon )\) plane with fixed parameter as \(r=3.2\). Quasiperiodic attractors, SNAs, chaotic attractors, and escape regions are shown in white, light gray, gray, and black, respectively. \(1\,\textrm{T}, 2\,\textrm{T}\), and \(4\,\textrm{T}\) denote the quasiperiodic tori resulting from the torus-doubling bifurcations. Fr, HH, and Int indicate that the birth of SNAs is through fractal, Heagy–Hammel, and intermittent routes, respectively. 3T denotes the triple torus. The birth of SNAs due to interior crisis and basin boundary metamorphosis are denoted by IC and BBM

Full size image
Fig. 2
figure 2

The dynamical transition in the (a, r) plane with fixed parameter as \(\varepsilon =0.3\). Dc and \(\textrm{HH}\) denote that the birth of SNAs is through the discontinuous route and the Heagy–Hammel route, respectively. (Color figure online)

Full size image

In general, SNAs exist in the dynamical transition region where the attractors change from regular to chaotic. For different parameter planes in Figs. 1 and 2, the types of attractors can be distinguished by the Lyapunov exponent \(\lambda _x\) and the phase sensitivity exponent \(\mu \) of the system (2). The torus attractors are denoted by nT, which a negative Lyapunov exponent and a zero phase sensitivity shown in white. However, SNAs correspond to negative Lyapunov exponent and positive phase sensitivity exponent, which are shown in light gray. In contrast, the Lyapunov exponent and the phase sensitivity exponent of the chaotic attractors are both positive, shown in gray. The escape regions are shown in black. 1T, 2T, and 4T are generated by the torus-doubling bifurcations. Fr, HH, and Int represent torus attractors evolving into SNAs through the fractal, Heagy–Hammel, and intermittent routes, respectively. Moreover, some typical bifurcation points are shown in Tables 1 and 2.

In Fig. 1, a and \(\varepsilon \) are taken as control parameters, and \(r=3.2\) is fixed. We consider that quasiperiodic attractors become SNAs due to interior crises (IC) and basin boundary metamorphism (BBM). In addition, there is a bubble-like region between the intermittent route (Int) and the fractal route (\(\textrm{Fr}2\)), where the double crises phenomenon occurs.

In Fig. 2, take a and r as control parameters and fix \(\varepsilon =0.3\). We find that quasiperiodic orbits along the blue bifurcation curve exhibit breaks and discontinuities, and further evolve into SNAs, which we call it the discontinuous route (Dc). In contrast, along the green bifurcation curve quasiperiodic attractors evolve into SNAs by the Heagy–Hammel route.

3 The birth of SNAs

3.1 The interior crisis route

The appearance of an interior crisis corresponds to the collision of the attractor with a chaotic saddle or, equivalently, with the basin boundaries of a suitable iterate of the system [24, 37]. For system (2), when an interior crisis occurs, there are two remarkable features: (1) the size of the attractor suddenly changes. (2) The number of attractors suddenly change. In the period-3 window indicated by the arrow of Fig. 1, we analyze the dynamical transition from \(3\,\textrm{T}\) quasiperiodic attractors to chaotic attractors, involving the interior crisis phenomenon and the appearance of SNAs.

Table 1 Typical bifurcation points for \(r=3.2\) in the \((a,\varepsilon )\)-plane
Full size table

We take the parameters \(r=3.2, a=3.83\), and the amplitude \(\varepsilon \) as the control parameter. From Fig. 3a, b, we uncover that the 3T quasiperiodic attractor gradually loses smoothness and evolves into an SNA with three branches. When \(\varepsilon \) continues to increase, the system gradually approaches the critical value of the interior crisis. When \(\varepsilon =0.00595\), the interior crisis occurs and the size and the number of the attractor suddenly change, that is, the SNA composed of three branches evolves into an SNA with only one branch. The gaps between the previous three-branch SNA are filled by orbit points belonging to the one-branch SNA, as shown in Fig. 3c. When the amplitude \(\varepsilon =0.0068\), the system enters a chaotic motion, see Fig. 3d. The evolution of the attractor is summarized as follows

$$\begin{aligned}{} & {} 3\,\textrm{T}\,\text {quasiperiodic\,attractor}\rightarrow \text {three-branch\,SNA} \nonumber \\{} & {} \quad \xrightarrow {\textit{IC}} \text {one-branch\,SNA} \rightarrow \text {chaotic\,attractor}. \end{aligned}$$

In general, an interior crisis is used to describe a transition from chaos to chaos. However, we find that the attractors before and after the interior crisis are nonchaotic in the system (2). There is a saddle-node bifurcation at the beginning of the period-3 window, resulting in two invariant curves with three branches, one of which is stable and the other unstable. If we consider three iterations of the system (2), then the map will have three 1T quasiperiodic attractors coexisting, which corresponds to 3T quasiperiodic attractor of the system (2). We choose an initial condition grid in the \((\theta , x)\) plane to compute the basins of attraction of each attractor and visualize the structure of these basins. The parts of the basin of attraction that are slightly less than and very close to the interior crisis value are shown in Figs. 4a, b, respectively. The blue region represents the basin of attraction of the middle attractor, while the yellow region represents the basin of attraction of the other two attractors that are not plotted. Thus, the interior crisis phenomenon can be revealed by the collision of three coexisting attractors with the boundaries of the basin of attraction. In other words, the interior crisis can be described by the boundary crisis of three coexisting attractors.

Table 2 Typical bifurcation points for \(\varepsilon =0.3\) in the (a, r)-plane
Full size table

The temporal behavior beyond the interior crisis can be described as crisis-induced intermittency [39]. The trajectory of the third iteration of the system (2) spends a long time in the vicinity of one of these former three attractors (i.e., the upper, middle, or lower attractor), Then suddenly it bursts out of this region, approaching also the other two attractors. As a result, the trajectory visits irregularly the three former attractors existing before the interior crisis as time goes to infinity. The characteristic time \(\langle \sigma \rangle \) is defined as the average over a trajectory of a long time between bursts out of the region of the original attractor. The time interval between two adjacent bursts appears to be random. However, when the amplitude \(\varepsilon \) approaches the critical value \(\varepsilon _c\) at which the crisis occurs, its average \(\langle \sigma \rangle \) has a scaling law [39],

$$\begin{aligned} \langle \sigma \rangle \sim (\varepsilon -\varepsilon _c)^{-\gamma }, \end{aligned}$$
(9)

where \(\gamma \) is the critical exponent. Determining this power-law scaling behavior is quite difficult because the scaling region of the critical exponent is very small. We take the critical value \(\varepsilon _c=0.00595\) and take the logarithm of the computed data. It is concluded that the critical exponent \(\gamma =0.4827\), and the power-law relationship is shown in Fig. 5.

Fig. 3
figure 3

For \(r=3.2, a=3.83\), the phase diagram in the \((\theta , x)\) plane

Full size image
Fig. 4
figure 4

For \(r=3.2\) and \(a=3.83\), visualization of SNA due to interior crisis. The blue region represents the basin of attraction of the plotted attractor, and the yellow region represents the basin of attraction belonging to the other two attractors, which are outside the part of the state space shown. (Color figure online)

Full size image

We can confirm that the attractor corresponding to Fig. 3c is nonchaotic by calculating the Lyapunov exponent in the x-direction \((\lambda _x=-0.0566<0)\), see Fig. 6a. For strangeness verification, we use the phase sensitivity function \(\tau _N\). When the attractor is strange, \(\tau _N\) will grow rapidly with the increase in the number of iterations N. Taking the quasiperiodic attractors and SNAs in Fig. 3a, c as examples, the maximum derivative value of the state variable with respect to phase \(\theta \) and the phase sensitivity exponent \(\mu \) are calculated, respectively. For quasiperiodic attractor \((\varepsilon =0.0051)\), as the number of iterations N increases, the value of the phase sensitivity function does not increase and tends to a bounded value, and the phase sensitivity exponent \(\mu \approx 0\), which indicates that the attractor is smooth. When the attractor is an SNA \((\varepsilon =0.00595)\), we find that the phase sensitivity function will increase rapidly with the increase of the number of iterations N. Under this parameter, the phase sensitivity exponent \(\mu =10.97\), which indicates that the attractor is nonsmooth (strange), as shown in Fig. 6b.

3.2 The basin boundary metamorphosis route

The boundary of the basin of attraction also changes abruptly when the system (2) passes a certain set of critical parameters. In particular, basin boundaries can change from smooth to fractal, which is called basin boundary metamorphosis (BBM) [47]. This transition can be observed in the parameter plane in Fig. 1, which lies in a small strip between quasiperiodic and chaotic motion, namely, the BBM region. A common route is that dual-frequency quasiperiodic attractors become SNAs through torus-doubling bifurcations. The birth of SNAs in this case is due to the collision between the doubling torus and its unstable parent torus, which causes a period \(2^k\)-torus to become a \(2^{k-1}\)-banded SNA. However, we describe a new scenario in which the basin boundary metamorphosis causes the dual-frequency quasiperiodic attractor to become an SNA, and the torus-doubling sequence is interrupted.

Fig. 5
figure 5

For \(r=3.2\) and \(a=3.83\), the power-law scaling behavior for crisis-induced intermittency

Full size image
Fig. 6
figure 6

For \(r=3.2\) and \(a=3.83\), the Lyapunov exponent in the x variable and the phase sensitivity functions

Full size image

To describe the basin boundary metamorphosis route, we take \(r=3.2, a=3.45\) and consider \(\varepsilon \) as a control variable. When \(\varepsilon =0.12\), the system exhibits a smooth \(2\,\textrm{T}\) quasiperiodic attractor, as shown in Fig. 7a. The basin of attraction for the second iteration of the system is also smooth under this parameter, see Fig. 7b. When \(\varepsilon \) further increases to 0.14, the 2T quasiperiodic attractor remains smooth, but its corresponding basin boundary changes abruptly. At the same time, the basin of attraction of one attractor embeds some isolated “islands” in the two dimensional section. Figure 7d shows the basin boundary metamorphosis, where the “islands” are still rather small and scattered in the basin of attraction of the other attractor. As \(\varepsilon \) increases to 0.162, the previously smooth quasiperiodic attractor appears wrinkled, which is seen as a prelude to the birth of SNAs. The basin of attraction in Fig. 7f is already far beyond the critical value of basin boundary metamorphosis, and the “island” becomes large and shows the feature of a fractal basin.

Fig. 7
figure 7

For \(r=3.2\) and \(a=3.45\), the phase diagram in the \((\theta , x)\) plane and the basins of attraction

Full size image

The power spectrum (Fourier amplitude spectrum) plays an important role in analyzing the motion state of nonlinear systems. It can be divided into two types: continuous spectrum and discrete spectrum. The discrete spectrum generally corresponds to periodic and quasiperiodic motion, while the power spectrum of chaotic and random motion shows a continuous spectrum. Since SNAs appear in the transition region from quasiperiodic attractors to chaotic attractors, the power spectrum of SNAs is a special spectrum between discrete and continuous spectrum. The special spectrum has multiple \(\delta \)-peaks and is called a singular continuous spectrum [18]. Figure 8 shows that the power spectrum of SNA is different from that of a quasiperiodic attractor, so the strange property of SNAs can be verified by the power spectrum. The Fourier transform is defined as follows:

$$\begin{aligned} S(\omega , N)=\sum _{n=1}^N x_n e^{i 2 \pi m \omega }, \end{aligned}$$
(10)

and the power spectrum of the attractor is defined as [18]

$$\begin{aligned} P_\omega =\lim _{N \rightarrow \infty }|S(\omega , N) / N|^2. \end{aligned}$$
(11)
Fig. 8
figure 8

For \(r=3.2\) and \(a=3.45\), the power spectrum. a Quasiperiodic attractor, b SNA

Full size image

3.3 The discontinuous route

We find that not only continuous quasiperiodic orbits but also discontinuous the quasiperiodic orbits exist in the system (2). When \(a=3.2\) and \(\varepsilon =0.3\), as the parameter r gradually decreases, there will be discontinuous quasiperiodic attractors in a region before the appearance of SNAs. Along the blue curve in Fig. 2, quasiperiodic attractors can evolve into SNAs through discontinuous route. For \(r=1.72\), there are two smooth invariant curves in the \((\theta ,x)\) plane, which are 2T quasiperiodic attractor, as shown in Fig. 9a. When \(r=1.7182\), the 2T quasiperiodic attractor shows a few discontinuous points. From the local magnification in Fig. 9b, it can be observed that the quasiperiodic attractor shows discontinuities and jumps in the phase plane. Decreasing the parameter r to 1.718, the geometry of the invariant curves is similar to the two dashed lines, which are manifested by the appearance of an increasing number of discontinuous points in the quasiperiodic orbit, see Fig. 9c. When \(r=1.715\), the discontinuous quasiperiodic attractor has a single branch in some regions and two branches in other regions, but the region with two branches is much larger than the region with one branch, as shown in Fig. 9d. The branches refers to the situation where one value of \(\theta \) corresponding to two different values of x. As the parameter r decreases to 1.64, the jump phenomenon of the quasiperiodic attractor becomes more obvious, the region with a single branch gradually becomes larger, and the region with two branches only exists at the joining point of the orbit, as shown in Fig. 9e. When \(r=1.626\), the discontinuous 1T quasiperiodic attractor becomes an SNA, and Lyapunov exponent of the system \((\lambda _x=-0.0514<0)\) is shown in Fig. 9h. The strangeness of the SNA is verified by the phase sensitivity function. When \(r=1.594\), the SNA eventually evolves into a chaotic attractor \((\lambda _x=0.0478>0)\), see Fig. 9g.

There are obvious differences between discontinuous and H–H routes in Fig. 2. For the H–H route (along the green curve), the double torus resulting from the torus-doubling bifurcation collides with its unstable parent torus (single torus), causing a 2T quasiperiodic attractor to become an SNA, namely, \( 1T \rightarrow 2T \rightarrow \text{ SNA }\). For the discontinuous route (along the blue curve), the number of quasiperiodic attractors does not increase but decreases. The quasiperiodic orbits appear to break and jump, which causes the 2T quasiperiodic attractor to become the discontinuous 1T quasiperiodic attractor and eventually evolve into an SNA, namely, \(2T \rightarrow 1T \rightarrow \text{ SNA }\).

Fig. 9
figure 9

For \(a=3.2\) and \(\varepsilon =0.3\), the phase diagram in the \((\theta , x)\) plane. (Color figure online)

Full size image

3.4 The double bifurcation route

Boundary crisis describes a sudden change in the dynamical behavior of a system, which can lead not only to the appearance but also to the disappearance of attractors. Its mechanism is based on the collision between the attractor and the boundary of its own basin of attraction. However, many systems have a second attractor in addition to the physically relevant attractor. In this case, these systems have finite effectiveness, and once a boundary crisis occurs and all trajectories escape to infinity, the system will be in a divergent state.

The black region in Fig. 1 represents attractor escape to the attractor at infinity. The boundary of the black region is given by the boundary crisis of the attractors. The boundary line is either a boundary crisis of chaotic attractors (along the gray region) or a boundary crisis of quasiperiodic attractors and SNAs (along the light gray region). For chaotic attractors, the boundary line of the boundary crisis is a straight line, while for regular attractors, the boundary crisis line seems to form a bubble-like region in the two-dimensional projection, i.e., \((a, \varepsilon ) \in [3.3,3.5] \times [0.4,0.6].\) We are more interested in the mechanism of SNAs by boundary crisis, and the formation mechanism of this bubble region has been described in Refs. [48, 49].

Fig. 10
figure 10

For \(r=3.2\), visualization of boundary crises. The yellow region represents the basin of attraction of the plotted attractors, and the blue region represents the escape of the attractors at infinity. a \(a=3.35\) and \(\varepsilon =0.63\), b \(a=3.43\) and \(\varepsilon =0.57\). (Color figure online)

Full size image

Let us now consider two different types of boundary crises. The first one is that the transition from gray to black regions corresponds to a standard boundary crisis, namely, Chaos \(\rightarrow \) Escape. When the parameters approach the boundary crisis, a chaotic attractor is about to collide with the boundary of its basin of attraction, see Fig. 10a. It is worth noting that the boundary of the basin of attraction is smooth curves. In other words, this boundary crisis is caused by the collision of the chaotic attractor with the smooth basin boundary. In sharp contrast, quasiperiodic attractors and SNAs in bubble-like region transition directly escape, and there is no chaos in between, namely, regular \(\rightarrow \) escape. In this case, the attractor is a smooth torus before the boundary crisis, but we find that the basin of attraction is fractal. Thus, the second type of boundary crisis corresponds to the collision of the smooth attractor with the boundary of the fractal basin, see Fig. 10b.

To distinguish between these two different types of boundary crises, we consider the intersection points between the two different boundary crisis lines. There are two such intersection points where one on the left of the bubble and the other on the right. These two points are known as double crisis points in the parameter space [50]. Such a double crisis is characterized by a simultaneous occurrence of a boundary crisis, where the attractor touches its basin boundary and an interior crisis, where the size of the attractor suddenly changes. In addition, basin boundary metamorphosis occurring in the bulging small bubble region, that is, the basin boundary gradually evolves from smooth to fractal.

Fig. 11
figure 11

For \(r=3.2\) and \(\varepsilon =0.592\), visualization near the intermittent transition in the double bifurcations route. a \(a=3.4\), b \(a=3.3999\), c the Lyapunov exponent corresponding to the banded SNA

Full size image

Next, we discuss the birth of SNAs around the double bifurcation. The smooth quasiperiodic attractor evolves into a banded SNA near the intermittent transition on the left. Although the approximate shape of the quasiperiodic attractor still exists, there are a large number of disordered points near the attractor, which exhibits intermittent characteristics, see Fig. 11b. In this scenario, the torus doubling sequence is interrupted by subharmonic bifurcation, and thus the type-III intermittence leads to the birth of the SNAs [51]. However, the quasiperiodic attractor evolves into an extremely wrinkled SNA near the boundary crisis point, see Fig. 12b. The birth of SNAs is not associated with the bifurcation phenomenon in the system. Neither the number of attractors nor the dynamical properties of the system change substantially. It is only because of the existence of quasiperiodic forcing that the geometry of the attractor changes and evolves into an invariant set with a fractal structure. Furthermore, if the parameters are slightly changed around the critical values of the double bifurcation, the attractors may escape.

Fig. 12
figure 12

For \(r=3.2\) and \(\varepsilon =0.558\), visualization near the boundary crisis point in the double bifurcations route. a \(a=3.41\), b \(a=3.445\), c the yellow region represents the basin of attraction of the plotted SNA, and the blue region represents the escape region. (Color figure online)

Full size image

4 Conclusion

In this work, we consider a piecewise smooth system with quasiperiodic forcing. The global dynamics of the system are discussed in different two-parameter planes. There are four routes to SNAs in this system, including interior crisis, basin boundary metamorphosis, discontinuous, and double bifurcation routes. For the first case, we find that the size and number of attractors suddenly change due to the interior crisis, so that an SNA with three branches suddenly becomes a whole SNA and exhibits crisis-induced intermittency. We characterize this intermittent behavior effectively by the critical exponent. The second scenario is that when the system parameters pass through a certain critical value, the boundary of the basin of attraction will undergo a sudden change. Especially, the basin boundaries gradually change from smooth to fractal. We refer to this change as metamorphoses of basin boundaries and point out that collisions between attractors and their fractal basin boundaries lead to the birth of SNAs. The third is that the 2T quasiperiodic attractor will obviously break and jump with the change of the control parameters, and evolve into a discontinuous 1T quasiperiodic attractor, and finally become an SNA. The last one is that the system has a double bifurcation in a bubble-like region, which is characterized by an intermittent transition for the left point, where the size of the attractor suddenly changes and thus forms the banded SNA, and a boundary crisis for the right point, where the extremely wrinkle SNA suddenly disappears.