Two-parameter bifurcation analysis of limit cycles of a simplified railway wheelset model

Abstract

The effect of the nonlinear terms on bifurcation behaviors of limit cycles of a simplified railway wheelset model is investigated. At first, the stable equilibrium state loses its stability via a Hopf bifurcation. The bifurcation curve is divided into a supercritical branch and a subcritical one by a generalized Hopf point, which plays a key role in determining the occurrence of flange contact and derailment of high-speed railway vehicles, and the occurrence of this critical situation is an important decision-making criteria for design parameters. Secondly, bifurcations of limit cycles are discussed by comparing the bifurcation behavior of cycles for two different nonlinear parameters. Unlike local Hopf bifurcation analysis based on a single bifurcation parameter in most papers, global bifurcation analysis of limit cycles based on two bifurcation parameters is investigated, simultaneously. It is shown that changing nonlinear parameter terms can affect bifurcation types of cycles and division of parameter domains. In particular, near the branch points of cycles, two symmetrical limit cycles are created by a pitchfork bifurcation and then two symmetrical cycles both undergo a period-doubling bifurcation to form two stable period-two cycles. Around the resonant points, period orbits can make several turns, whose number of turns corresponds to the ratio of resonance. Thirdly, near the Neimark–Sacker bifurcation of cycles, a stable torus is created by a supercritical Neimark–Sacker bifurcation, which shows that the orbit of the model exhibits modulated oscillations with two frequencies near the limit cycle. These results demonstrate that nonlinear parameter terms can produce very complex global bifurcation phenomena and make obvious effects on possible hunting motions even though a simple railway wheelset model is concerned.

1 Introduction

A wheelset is the basic unit of a railway vehicle. The interaction between wheels and rails involves both complex geometry of wheel treads and rail heads and nonconservative forces generated by the relative motion in the contact area [1], which can control the wear of wheels and rails, the vehicle ride performance and running safety. So developing analytical or numerical models of wheelset motion and describing the motion of a rolling wheelset incorporated in a vehicle have been receiving increasing attention from many researchers in the fields of mechanical manufacturing, vibration control engineering and applied mathematics [1,2,3,4,5]. Hunting motion is a common phenomenon in railway vehicles which is characterized by lateral oscillations of the wheel flanges banging from one rail to the other. In general, a railway vehicle is stable at low speeds and will undergo a decaying oscillation to return to the center of the track following a disturbance of the vehicle [1]. While when the running speed exceeds some critical value, the oscillations following a disturbance grow and eventually lead to a limit cycle oscillation or a hunting motion, which can be explained by the Hopf bifurcation mechanism of the nonlinear dynamics theory. Hence, more recent studies have utilized bifurcation theory to investigate the hunting motion of rail vehicles.

In [6], the authors studied the Hopf bifurcation for a motion model with flange contact and nonlinear yaw dampers and discussed the amplitude and frequency of the bifurcated limit cycle based on the Bogoliubov averaging method. Their results indicated that the nonlinearities in the primary suspension and flange contact contribute significantly to the hunting behavior. Sedighi et al. [7] presented an investigation on the Hopf bifurcation of railway bogie behavior in the presence of nonlinearities which are yaw damping forces in longitudinal suspension system and the friction creepage model of the wheel/rail contact including clearance. By using the Bogoliubov averaging method, a relation between the limit cycle amplitude and parameters of the system was introduced. It was shown that in contrary to lateral damping, yaw stiffness has a major effect on hunting velocity and can be regarded as an important design parameter. The Hopf bifurcation behavior of a vehicle dynamic model including a semi-carbody and a bogie was discussed in [8] based on the center manifold theorem and the normal form theory. The influence of parameter variation on the Hopf normal form coefficient $\text {Re}c_1(0)$ was studied, and numerical shooting method was used to verify their theoretical results.

In [9], a lateral mathematical model of a railway wheelset with two degrees of freedom was discussed. Therein the Poincaré method and normal forms have been used to derive the symbolic expression of the first-order fine focus, which can also be used to determine the Hopf bifurcation type. In addition, the influence of different parameters on the critical velocity was also investigated. It was shown that with the increase in the yaw damper, secondary longitudinal or lateral stiffness, the Hopf bifurcation value increases, which is opposite to the effect of the creep coefficient. In [10], the Hopf bifurcation behavior of a railway bogie was analyzed, and the effect of the yaw damper and wheel tread shape on the Hopf bifurcation type was also discussed. In [11], a simplified wheelset dynamic model

$$\begin{aligned}&\left\{ \begin{array}{l} {\displaystyle \frac{\mathrm{d}^2y}{\mathrm{d}t^2}=-\displaystyle \frac{2\kappa _y}{mv} \frac{\mathrm{d}y}{\mathrm{d}t}- \displaystyle \frac{k_x}{m}\left( 1-\frac{l_0}{l}\right) y+\frac{2\kappa _y}{m}\psi },\\ {\displaystyle \frac{\mathrm{d}^2\psi }{\mathrm{d}t^2}=-\displaystyle \frac{2d_0^2\kappa _x}{Iv} \frac{\mathrm{d}\psi }{\mathrm{d}t}-\displaystyle \frac{2d_0\kappa _x\gamma _e}{Ir_0} y-\displaystyle \frac{k_xd_1^2}{I}\psi }, \end{array} \right. \end{aligned}$$

(1)

was discussed by Yabuno et al., where the lateral and longitudinal creepages were considered and the creep force in each direction was linearly proportional to the creepage and the restoring force was implemented by the longitudinal spring stiffness. y is a lateral displacement, and $\psi$ is a yawing motion variable. The physical significance and values of the parameters in Eq. (1) are listed in Table 1 except the forward speed v. Wherein the authors proposed a stabilization control method for the hunting motion by reducing the unsymmetrical effect of the stiffness matrix and showed that under this control no hunting motion occurs at any finite speed.

Table 1 The values and physical meanings of the parameters in Eq. (1)

Fig. 1

a The mechanical model of wheelset with elastic joints. b Configuration of the wheelset and rails. The description and values of the symbols are listed in Table 1. These two figures are selected from [15]

However, as is indicated in some papers [12,13,14,15], the creepage–creep force relationship in realistic wheelset model is nonlinear and damped according to the Coulomb friction law and Vermeulen and Johnson creep theory. When the left and right contact angles differ or the flange contact occurs, the gravitational stiffness force can not be neglected which arises from the variation of the normal reaction between wheels and rails with lateral displacement [13]. According to the center manifold theory [16, 17] and bifurcation theory of limit cycles, to analyze the Hopf bifurcation type and bifurcation structure of cycles, the third-order terms in the wheelset model must be considered. In addition, the factors of kinematics of the contact points and the mechanical suspension can also estimated by nonlinear terms.

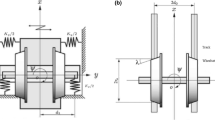
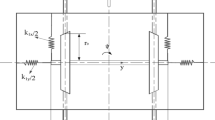
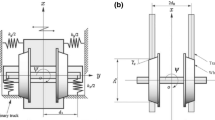
Based on the above analysis, a nonlinear wheelset motion model is discussed here, which is obtained by adding nonlinear cubic terms after the model (1) and reserving the original linear terms and parameters. Figure 1a, b shows the mechanical model of wheelset with elastic joints and nomenclature symbols relative to the wheelset and rails. All parts in Fig. 1 except the springs are assumed to be stiff and the springs have a linear characteristic.

By dimensionless transformations $y=d_0y^*, t=t^*/\omega _\psi$ and $v=d_0\omega _\psi v^*$ as described in [15], the following model

$$\begin{aligned}&\left\{ \begin{array}{l} \ddot{y}^*+\frac{d_{11}}{v^*}\dot{y}^*+(k_{11}+k_{a11})y^*+k_{12}\psi +\alpha _{yyy}{y^*}^3\\ \quad +\,\alpha _{yy\psi }{y^*}^2\psi +\alpha _{y\psi \psi }y^*\psi ^2+\alpha _{\psi \psi \psi }\psi ^3=0,\\ \end{array}\right. \nonumber \\&\left\{ \begin{array}{l} \ddot{\psi }+\frac{d_{22}}{v^*}\dot{\psi }+k_{21}y^*+k_{22}\psi +\beta _{yyy}{y^*}^3\\ \quad +\,\beta _{yy\psi }{y^*}^2\psi +\beta _{y\psi \psi }y^*\psi ^2+\beta _{\psi \psi \psi }\psi ^3=0, \end{array}\right. \end{aligned}$$

(2)

is obtained. The relationship of coefficients of (1) and (2) is given as following

$$\begin{aligned}&d_{11}=\frac{2\kappa _y}{md_0\omega _\psi ^2}, \quad d_{22}=\frac{2\kappa _xd_0}{I\omega _\psi ^2}, \\&v^*=\frac{v}{d_0\omega _\psi },\quad k_{11}= \frac{k_x(1-l_0/l)}{m\omega _\psi ^2} , \\&k_{a11}=\frac{k_y}{m\omega _\psi ^2},\quad k_{22}=\frac{k_x d_1^2}{I\omega _\psi ^2},\\&k_{12}=\frac{-2\kappa _y}{md_0\omega _\psi ^2} ,\quad k_{21}=\frac{2d_0^2\kappa _x\gamma _e}{Ir_0\omega _\psi ^2}. \end{aligned}$$

These cubic terms as described above are the nonlinear effects, including kinematics of the contact points, creepage–creep force and mechanical suspension. $v^*$ expresses a dimensionless running speed, and $k_{a11}$ is regarded as a dimensionless lateral suspension stiffness.

With the change of variables

$$\begin{aligned} y_1=y^*,\quad y_2=\dot{y}^*,\quad y_3=\psi ,\quad y_4=\dot{\psi }, \end{aligned}$$

then (2) turns into

$$\begin{aligned} { \left( \begin{array}{cc} \dot{y}_1\\ \dot{y}_2\\ \dot{y}_3\\ \dot{y}_4\\ \end{array}\right) } ={ \left( \begin{array}{cc} y_2\\ -\frac{d_{11}}{v^*}y_2\!-\!(k_{11}+k_{a11})y_1\!-\!k_{12}y_3\!-\!\alpha _{yyy}y_1^3\!-\!\alpha _{yy\psi }y_1^2y_3\!-\!\alpha _{y\psi \psi }y_1y_3^2\!-\!\alpha _{\psi \psi \psi }y_3^3\\ y_4 \\ -\frac{d_{22}}{v^*}y_4-k_{21}y_1-k_{22}y_3-\beta _{yyy}y_1^3-\beta _{yy\psi }y_1^2y_3-\beta _{y\psi \psi }y_1y_3^2-\beta _{\psi \psi \psi }y_3^3\\ \end{array}\right) }. \end{aligned}$$

(3)

For this model, the authors [15] investigated nonlinear characteristics of the bifurcation at the critical speed and clarified the effect of the lateral linear stiffness on the nonlinear stability against disturbance. However, for this model there are a lot of questions not to be solved in [15]. For example, these values of $\alpha _{yyy}, \ldots ,\beta _{y\psi \psi }$, and $\beta _{\psi \psi \psi }$ are not stated and the analysis of Hopf bifurcation is not quiet clear. The effect of these nonlinear coefficients on bifurcation structure of equilibria and cycles has not been discussed yet. Bifurcation curves of cycles and resonant points are not given or found. As far as we know, bifurcation structure of cycles for any wheelset model has not been discussed yet in present papers. Based on the above analysis, in this paper we mainly discuss the number and stability of equilibria and then indicate that the boundary of attraction region is a Hopf bifurcation curve, which is divided into a supercritical branch and a subcritical one by a generalized Hopf point. Next, bifurcations of cycles including the generalize Hopf bifurcation, limit point bifurcation, pitchfork bifurcation and Neimark–Sacker bifurcation have been investigated and exhibited by numerical simulations. At last, the effect of the nonlinear coefficient $\alpha _{yyy}$ on bifurcation structure of cycles has been discussed by comparing bifurcation diagrams for two different values of $\alpha _{yyy}$.

2 Bifurcations of equilibria

Now we discuss the number and stability of equilibria for the model (3).

2.1 The number and stability of equilibria

Obviously, an equilibrium $Y_{0}=(y_{10},y_{20},y_{30},y_{40} )$ of (3) should satisfy the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} y_{20}=y_{40}=0,\\ (k_{11}+k_{a11})y_{10}+k_{12}y_{30}+\alpha _{yyy}y_{10}^3 +\alpha _{yy\psi }y_{10}^2y_{30}\\ \quad +\,\alpha _{y\psi \psi }y_{10}y_{30}^2 +\alpha _{\psi \psi \psi }y_{30}^3=0,\\ k_{21}y_{10}+k_{22}y_{30}+\beta _{yyy}y_{10}^3 +\beta _{yy\psi }y_{10}^2y_{30}\\ \quad +\,\beta _{y\psi \psi }y_{10}y_{30}^2+\beta _{\psi \psi \psi }y_{30}^3=0. \end{array}\right. \end{aligned}$$

(4)

Table 2 Values of the parameters in Eq. (2)

The Jacobian matrix of (3) evaluated at $Y_{0}$ is given by

$$\begin{aligned} {A_{Y_0}=\begin{pmatrix} 0&{} 1 &{} 0 &{} 0 \\ \delta _1 &{} -\frac{d_{11}}{v^*} &{} \delta _2 &{} 0 \\ 0&{} 0&{} 0&{} 1 \\ \delta _3 &{} 0&{} \delta _4 &{} -\frac{d_{22}}{v^*}\\ \end{pmatrix}}, \end{aligned}$$

where

$$\begin{aligned} \delta _1= & {} -(k_{11}+k_{a11})-3\alpha _{yyy}y_{10}^2-2\alpha _{yy\psi }y_{10}y_{30}\\&-\alpha _{y\psi \psi }y_{30}^2, \\ \delta _2= & {} -k_{12}-\alpha _{yy\psi }y_{10}^2-2\alpha _{y\psi \psi }y_{10}y_{30}-3\alpha _{\psi \psi \psi }y_{30}^2,\\ \delta _3= & {} -k_{21}-3\beta _{yyy}y_{10}^2-2\beta _{yy\psi }y_{10}y_{30}-\beta _{y\psi \psi }y_{30}^2, \\ \delta _4= & {} -k_{22}-\beta _{yy\psi }y_{10}^2-2\beta _{y\psi \psi }y_{10}y_{30}-3\beta _{\psi \psi \psi }y_{30}^2. \end{aligned}$$

Since there are so many parameters, it will be difficult to determine the characteristics of equilibria when all the parameters are changed. Here $k_{a11}$ is chosen as a bifurcation parameter and all the other parameters are fixed as listed in Table 2. Obviously, the origin O(0, 0, 0, 0) is a trivial solution to Eq. (4), while nontrivial solutions to Eq. (4) about the parameter $k_{a11}$ is too complicated to be given analytically. So the characteristics of equilibria are discussed by the method of numerical simulations. Geometrical demonstrations of the last two equations of Eq. (4) are exhibited in Fig. 2a–c for the different intervals of $k_{a11}$. The red surface corresponds to the second equation, and the green one corresponds to the last. The intersection lines of two surfaces constitute equilibrium curves of the model (3). Wherein it is shown that the number of equilibria is changing with the parameter $k_{a11}$.

Now we discuss stability types and bifurcation behaviors of equilibria. The following numerical simulations are carried out by the software package Matcont [18]. Based on the eigenvalues of $A_{Y_0}$, stability types and bifurcation points of equilibria are displayed in Fig. 3a. The dash magenta lines denote unstable equilibria, and the solid blue line denotes the stable origin O. The labels BP, H and $\text {LP}_{1,2}$ are the branch point, the Hopf bifurcation point and limit point bifurcation points, through which the interval of $k_{a11}$ is divided into four parts. In different part, the equilibria have different features. Combining Fig. 2 with Fig. 3a, about the characteristics of equilibria we get the following conclusion:

Proposition 1

If $k_{a11}$ is regarded as a bifurcation parameter and all the other parameters are fixed as listed in Table 2, then we have:

• (a) when $k_{a11}< -2.899$, there only exists an unstable equilibrium O;

• (b) when $-2.899<k_{a11}<-1.365546$, there exist two pairs of unstable equilibria and an unstable equilibrium O;

• (c) when $-1.365546<k_{a11}<0.7$, there exists a pair of unstable equilibria and an unstable equilibrium O;

• (d) when $k_{a11}>0.7$, there exists a pair of unstable equilibria and a stable equilibrium O.

2.2 Stable parameter domain of the origin O

From the above analysis, it is shown that although there exist several equilibria, the origin O is the only stable equilibrium, which can be achieved when the lateral stiffness parameter $k_{a11}$ exceeds some critical value. A stable equilibrium state O for $k_{a11}=1$ is exhibited in Fig. 3b.

In the following, we will give a stable parameter domain of the origin O based on two bifurcation parameters and then discuss what kind of bifurcation will be encountered when the origin O loses its stability. Here $k_{a11}$ and $v^*$ are chosen as two bifurcation parameters, and $k_{11}, k_{12}, k_{21}, k_{22},$ $d_{11}$ and $d_{22}$ are chosen as those in Table 2. By the Hartman–Grobman theorem [16] and bifurcation conditions of equilibria [17], it is shown that local stability and bifurcation curves of the origin O can not be affected by the values of $\alpha _{yyy}, \ldots , \beta _{y\psi \psi }$, and $\beta _{\psi \psi \psi }$, which means that these parameters can be arbitrarily selected. In order to conveniently numerically simulate, $\alpha _{yyy}, \ldots , \beta _{y\psi \psi }$, and $\beta _{\psi \psi \psi }$ are also chosen as those in Table 2. Now based on the Hurwitz criterion, we can choose appropriate parameter values of $k_{a11}$ and $v^*$ such that the origin O is locally asymptotically stable. A stable parameter domain for the origin O is exhibited in Fig. 4a.

2.3 Hopf bifurcation of the origin O

In this subsection, we will give the analytic expression of the boundary in Fig. 4a and discuss what kind of bifurcation will be encountered when the parameters cross the boundary. The Jacobian matrix $A_{Y_0}$ evaluated at the origin is given as

$$\begin{aligned} {A_{0}=\begin{pmatrix} 0&{} 1 &{} 0 &{} 0 \\ -\,k_{11}\!-\!k_{a11} &{} -\,\frac{d_{11}}{v^*} &{} -\,k_{12} &{} 0 \\ 0&{} 0&{} 0&{} 1 \\ -\,k_{21}&{} 0&{} -\,k_{22} &{} -\,\frac{d_{22}}{v^*}\\ \end{pmatrix}}. \end{aligned}$$

It is well known that if the model (3) undergoes a Hopf bifurcation at the origin O, the Jacobian matrix $A_0$ will have a simple pair of conjugated purely imaginary eigenvalues $\lambda _{1,2}$ and the other two eigenvalues $\lambda _{3,4}$ have no zero real parts. So the Hopf bifurcation curve $C_\mathrm{H}$ should satisfy the following relationship

$$\begin{aligned} C_\mathrm{H}:\left\{ \begin{array}{ll} k_{12}\!=k^*_{12}=\!\frac{-\,d_{11}d_{22}\left[ (k_{11}+k_{a11})d^2_{22}+(k_{11}+k_{22}+k_{a11})d_{11}d_{22}+(k_{11}\!-\!k_{22}+k_{a11})^2v^{*2}+d^2 _{11} k_{22} \right] }{k_{21}v^{*2}(d_{11}+d_{22})^2},\\ \gamma \triangleq \frac{d_{11}k_{22}+d_{22} k_{11}+d_{22}k_{a11} }{d_{11}+d_{22}}>0. \end{array}\right. \end{aligned}$$

(5)

When (5) holds, a pair of conjugated imaginary eigenvalues $\lambda _{1,2}(k^*_{12})=\pm i\omega$ appears and $\omega =\sqrt{\gamma }$. To determine the nondegeneracy of the Hopf bifurcation and predict the direction of the bifurcated limit cycle, we deduce the normal form along the line $C_\mathrm{H}$ and compute the first Lyapunov coefficient $l_1$ to decide the stability of the cycle.

For given $k_{12}=k^*_{12}$, look for complex eigenvectors q and p, respectively, corresponding to $\lambda _1(k^*_{12})=i\omega$ and $\lambda _2(k^*_{12})=-i\omega$ such that

$$\begin{aligned} A_0q=i\omega q, \quad A^\mathrm{T}_0 p=-i\omega p \quad \text {and} \quad \langle p,q\rangle =1, \end{aligned}$$

where $A^\mathrm{T}_0$ is the transposed matrix of $A_0$ and $\langle p, q\rangle =\sum _{i=1}^{4}\overline{p}_{i}q_{i}$ is the standard scalar product in $C^4$. It is easy to verify that the following vectors can do the job, with

$$\begin{aligned}&q= \begin{pmatrix} \frac{d_{22}(k_{11}-k_{22}+k_{a11})}{k_{21}(d_{11}+d_{22})}-i\frac{d_{22}\omega }{k_{21}v^*} \\ \frac{d_{22}\omega ^2}{k_{21}v^*}+i\frac{d_{22}\omega (k_{11}-k_{22}+k_{a11})}{k_{21}(d_{11}+d_{22})} \\ 1\\ i\omega \\ \end{pmatrix}, \\&p= {\tfrac{1}{\tau }} \begin{pmatrix} \frac{d_{11}}{v^*}-i\omega \\ 1\\ \frac{d_{11}k_{22}}{k_{21}v^*} +i\omega d_{11}\left( \frac{d_{22}}{k_{21}v^{*2}}+ \frac{k_{11}-k_{22}+k_{a11}}{k_{21}(d_{11}+d_{22})}\right) \\ -\frac{d_{11}(k_{11}-k_{22}+k_{a11})}{k_{21}(d_{11}+d_{22})}+i\frac{d_{11}\omega }{k_{21}v^*}\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}&\tau =2\omega \left[ \frac{\omega (d_{11}+d_{22})}{k_{21}v^* } +i\left( \frac{d_{11}d_{22}}{k_{21}v^{*2}}\right. \right. \\&\left. \left. \quad +\frac{(d_{11}-d_{22})(k_{11}-k_{22}+k_{a11})}{k_{21}(d_{11}+d_{22})}\right) \right] . \end{aligned}$$

Let $y=(y_1,y_2,y_3,y_4)^\mathrm{T}$ and for y we perform the following coordinate transformation

$$\begin{aligned} \left\{ \begin{array}{l} z=\langle p,y\rangle ,\\ u=y-\langle p,y\rangle q-\langle \bar{p},y\rangle \bar{q}. \end{array}\right. \end{aligned}$$

(6)

In the coordinates of (6), then the vector $y=zq+\bar{z} \bar{q}+u$, where $z\in C^1, u\in R^4$, and

$$\begin{aligned}&zq+\bar{z} \bar{q}\in \text {Span}\{\text {Re} q, \text {Im}q\},~~\\&u\in \text {Span}\{ y|A_0y=\lambda _i y, i=3,4\}. \end{aligned}$$

Substituting y into (3), we get

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}=i\omega z+A_{21}z^2\bar{z}+\cdot \cdot \cdot ,\\ \dot{u}=A_0u+\cdot \cdot \cdot , \end{array}\right. \end{aligned}$$

(7)

where $A_{21}$ is listed in “Appendix.” The omitted terms are the rest of third-order polynomials and above about $z,\bar{z}$ and y in the complex field, which hardly plays any role in determining the Hopf bifurcation type, thus they are omitted here.

In view of no quadratic terms in Eq. (3), the center manifold has the form $u=V(z,\bar{z})=O(|z|^3)$. Therefore, the restriction of (7) to the center manifold has the form

$$\begin{aligned} \dot{z}=i\omega z+A_{21}z^2\bar{z}+\cdot \cdot \cdot . \end{aligned}$$

(8)

The first Lyapunov coefficient $l_1$ [17] along the line $C_\mathrm{H}$ has the representation

$$\begin{aligned} l_1(k^*_{12})={\tfrac{1}{\omega }}\text {Re}(A_{21}). \end{aligned}$$

The transversality condition along the line $C_\mathrm{H}$ has the form

$$\begin{aligned} d_1(k^*_{12})={\tfrac{\partial }{\partial k_{12}}}\text {Re}\left( \lambda _1(k^*_{12})\right) . \end{aligned}$$

According to the Hopf bifurcation theory in [17], we get the following result:

Proposition 2

If $l_1(k^*_{12}) \ne 0$ and $d_1(k^*_{12})\ne 0$, the model (3) will undergo a Hopf bifurcation at $k_{12}=k^*_{12}$. Moreover, when $l_1(k^*_{12})>0$, the bifurcation is subcritical and an unstable limit cycle appears for $k_{12}<k^*_{12}$; when $l_1(k^*_{12})<0$, the bifurcation is supercritical and a stable limit cycle appears for $k_{12}>k^*_{12}$.

In order to verify this result by numerical simulations, $k_{a11}$ and $v^*$ are chosen as free variables and the other parameters are chosen as those in Table 2. The curve $C_\mathrm{H}$ can be specially given as follows

$$\begin{aligned}&1.61891{v^*}^2k_{a11}^2-0.68658k_{a11}{v^*}^2-2.18721{v^*}^2\\&\quad +\,43.0653k_{a11}+6.68925=0, \end{aligned}$$

whose geometric shape is coincided with the boundary of the yellow domain in Fig. 4a. When parameters $k_{a11}$ and $v^*$ are chosen on the line $C_\mathrm{H}$, the Jacobian matrix $A_0$ has a pair of conjugate imaginary eigenvalues. Thence the origin O loses its stability through a Hopf bifurcation. In order to judge the Hopf bifurcation supercritical or subcritical, we need to compute the first Lyapunov coefficient $l_1$ along the line $C_\mathrm{H}$. The expression of $l_1(k_{a11},v^*)$ is given in “Appendix.” By computation, it is shown that the Hopf bifurcation curve $C_\mathrm{H}$ is divided into two branches $H^+$ and $H^-$. The upper branch $H^+$ corresponds to the positive first Lyapunov coefficients, and the lower branch $H^-$ corresponds to the negative ones. Thus, for a given $k_{a11}$ the system (3) exhibits different bifurcation types when the parameter $v^*$ crosses the branches $H^+$ and $H^-$. Since the stability of the bifurcated cycles depends on the sign of $l_1$ rather than its magnitude, for the sake of simplification, the following Lyapunov coefficients computed by Matcont are standardized but with the same signs as the expression of $l_1(k_{a11},v^*)$.

Figure 4b shows a bifurcation diagram for $k_{a11}=0.7$. It is shown that with the increase of $v^*$, the equilibrium O loses its stability through a Hopf bifurcation and an unstable limit cycle is bifurcated from $v^*=4.432839$, which just corresponds to the point $\text {P}_1$ in Fig. 4a. The unstability can be verified by the positive first Lyapunov coefficient $l_1=0.8630817$, so the upper branch $H^+$ is a subcritical Hopf bifurcation curve.

Figure 4c shows that for $k_{a11}=0.05774$, the equilibrium O also experiences a Hopf bifurcation at $v^*=2.032378$, and the distinction is that a stable limit cycle is bifurcated from $v^*=2.032378$, which corresponds to the point $\text {P}_2$ in Fig. 4a. The negative first Lyapunov coefficient $l_1=-0.1888022$ indicates that the bifurcated limit cycle is stable, so the lower branch $H^-$ is a supercritical Hopf bifurcation curve.

Fig. 2

Equilibrium curves are constituted of the intersection lines of two surfaces. a One intersecting line for $-\,5<k_{a11}<-2.899$; b five intersecting lines for $-2.899<k_{a11}<-1.365546$; c three intersecting lines for $-1.365546<k_{a11}<2$

Fig. 3

a Bifurcations and stability of equilibria with the variation of $k_{a11}$. The solid blue line denotes the stable origin O, and the dash magenta lines correspond to unstable equilibria. Bifurcation points $\text {LP}_{1,2}$ for $k_{a11}=-2.899$, BP for $k_{a11}=-1.365546$ and H for $k_{a11}= 0.7$. b A phase diagram of a stable equilibrium O for $(k_{a11},v^*)=(1,4.4328)$. (Color figure online)

2.4 Generalized Hopf bifurcation of the origin O

The dividing point GH in Fig. 4a is a generalized Hopf point, at which the first Lyapunov coefficient $l_1=0$ and the second Lyapunov coefficient $l_2=-\,0.7331651 \ne 0$. So the model will undergo a generalized Hopf bifurcation at the point GH, and a parametric portrait is exhibited in Fig. 4d. Therein two limit cycles with opposite stability will generate and a nondegenerate limit point bifurcation curve of cycles T will also appear, whose expression is given as following

$$\begin{aligned} v^*= 6.291k_{a11}^3-7.273k_{a11}^2+4.238k_{a11}+1.88, \end{aligned}$$

on which two limit cycles collide to form a semistable cycle. Next we will choose different parameter points in Fig. 4d to exhibit the corresponding four phase diagrams in Fig. 5.

• 1. When a parameter pair $(k_{a11},v^*)=(0.15,3.1)$ is chosen in region $\textcircled {1}$, corresponding to the point A in Fig. 4d, there exists a stable limit cycle and an unstable equilibrium O, which is shown in Fig. 5a.

• 2. When a point B for $(k_{a11},v^*)=(0.4,3.1)$ is chosen in region $\textcircled {2}$ in Fig. 4d, there exist two limit cycles with opposite stability. The outer one (red) is stable and the inner one (magenta) is unstable, which is shown in Fig. 5b. Wherein the black and the green trajectories tending to the red cycle show that the outer cycle is stable. The blue trajectory from the position

  

  approaching to the equilibrium O verifies that the inner magenta cycle is unstable.

• 3. When a point D for $(k_{a11},v^*)=(0.2,2)$ is chosen in region $\textcircled {3}$, there is only a stable equilibrium O, which is shown in Fig. 5c.

• 4. When a point C for $(k_{a11}, v^*)=(-\,0.0951, 1.106685)$ is chosen on the line T, a semistable cycle appears and it is stable from the outside and unstable from the inside, which is verified by two trajectories with different initial values. From Fig. 5d, we find the outer trajectory approaches the limit cycle (red) and the inner one is away from it.

By comparing the properties of Fig. 5, it is shown that the region $\textcircled {2}$ in Fig. 4d is a bistable domain. When a perturbance near the equilibrium O is small, then the wheelset will undergo a decaying oscillation to return to the center of the track. When the perturbance near the equilibrium O is large enough to exceed the unstable cycle shown in Fig. 5b, then the stable hunting motion takes place in the railway vehicle.

Fig. 4

a The shaded area is a stable parameter domain of the origin O. The generalized Hopf point GH for $(k_{a11},v^*)=( 0.113035, 2.269349)$ divides the Hopf bifurcation curve into $H^+$ and $H^-$, corresponding to a Hopf bifurcation with the positive and the negative first Lyapunov coefficient, respectively. $P_1(0.7,4.432839)$ and $P_2(0.05774,2.032378)$ are two representative points on each branch. b When $k_{a11}=0.7$ and $v^*$ varies from the bottom up, the origin O is stable (solid red line) at first and then becomes unstable (dash blue line). A family of unstable limit cycles bifurcates from the point $H_1$, whose coordinates just correspond to the point $P_1$ in a. c When $k_{a11}=0.05774$ and $v^*$ increases, the equilibrium O loses its stability and a family of stable limit cycles bifurcates from $H_2$ ($v^*= 2.032378$), which corresponds to the point $P_2$ in a. d A larger version of some neighborhood of the point GH in a, T is a limit point bifurcation curve of cycles. The domain is divided into three parts $\textcircled {1}$, $\textcircled {2}$ and $\textcircled {3}$ by curves $H^-$, $H^+$ and T. C(0.5, 2.965725) is a typical point on T, and A(0.15, 3.1), B(0.4, 3.1) and D(0.2, 2) are representative points in each region, respectively. (Color figure online)

Fig. 5

Phase diagrams of the model (3) for different parameters in Fig. 4d. a For $(k_{a11},v^*)=(0.15,3.1)$ in region $\textcircled {1}$, there is only a stable limit cycle. b For $(k_{a11},v^*)=(0.4,3.1)$ in region $\textcircled {2}$, there are two limit cycles with opposite stability. The outer cycle (red) is stable, and the inner one (magenta) is unstable. The mark

is the position for initial values $(-\,0.05,0.055,0.03,0.04)$. c For $(k_{a11},v^*)=(0.2,2)$ in region $\textcircled {3}$, there is only a stable equilibrium for optional initial values. d For $(k_{a11}, v^*)=(0.5,2.965725)$ on the line T, there exists a semistable cycle, which is stable from the outside and unstable from the inside. (Color figure online)

3 Bifurcations of the cycles from the point $H_1$

From the above analysis, it is shown that the Hopf bifurcation curve of the equilibrium O is independent of the nonlinear coefficients $\alpha _{yyy}, \ldots , \beta _{y\psi \psi }$, and $\beta _{\psi \psi \psi }$. In the following, it is shown that bifurcation curves of cycles will be affected by them. Now we study the effect of $\alpha _{yyy}$ on the bifurcation structure of cycles and the effect of the other parameters is discussed similarly and omitted here. Here we choose two different values of $\alpha _{yyy}$ to compare the bifurcation structure of cycles and the other parameter values remain unchanged. $k_{a11}$ and $v^*$ are also regarded as bifurcation parameters.

3.1 Bifurcation structure of cycles for $\alpha _{yyy}=1.1$

Figure 4b shows that when $k_{a11}=0.7$, a family of unstable limit cycles is bifurcated from the point $H_1$ by an subcritical Hopf bifurcation. Next, we will discuss bifurcation behaviors of the cycles resulted from $H_1$ with the variation of $v^*$. From Fig. 6a, we find that as $v^*$ decreases, a family of unstable limit cycles (magenta) bifurcates from $H_1$ and then a cycle limit point labeled by LPC$_1$ is encountered at $v^*=3.267744$, which means that the limit cycle manifold has a fold here. When $v^*$ begins to increase, a series of stable limit cycles (blue) exists till a Neimark–Sacker bifurcation point labeled by NS$_{1}$ is encountered at $v^*=14.10666$. The negative normal form coefficient − 0.0041129 indicates that a stable torus bifurcates from the limit cycle NS$_{1}$.

Fig. 6

a Bifurcation structure of the cycles bifurcated from $H_1$, the magenta lines denote unstable limit cycles and the blue ones indicate stable cycles. The red line LPC$_1$ and the green line NS$_1$ are a cycle limit point and a Neimark–Sacker bifurcation point, respectively. b The green line $\mathrm{NS}^c$ is a Neimark–Sacker bifurcation curve of cycles, and the red line T is a limit point bifurcation curve of cycles. $Q_1$ and $Q_2$ are two typical points on the two lines, which just correspond to the bifurcation points in a. The explanation of $H^\pm$ and GH is the same as that in Fig. 4d. R3 for $(k_{a11},v^*)=( 0.5134421, 11.87089)$ and R4 for $(k_{a11},v^*)=(0.1134707, 8.931515)$ are a 1:3 resonance and a 1:4 resonance point, respectively. c A stable torus for $(k_{a11},v^*)=(0.13,10)$ above the line $\mathrm{NS}^c$ in b. d A period-three cycle for the point R3. e A period-four cycle for the point R4. f A period-six cycle for $(k_{a11},v^*)=(0.25,19)$. (Color figure online)

Figure 6a shows a bifurcation diagram of cycles for $k_{a11}=0.7$. It is well known that bifurcation values of $v^*$ will be changed with the variation of $k_{a11}$. So the Neimark–Sacker bifurcation curve and the limit point bifurcation curve of cycles are shown in Fig. 6b. The points $Q_1$ and $Q_2$ on the bifurcation curves just correspond to the bifurcation points in Fig. 6a. By comparing Fig. 6b with Fig. 4d, it is shown that the curve T in Fig. 4d is the limit point bifurcation curve of cycles, and the Neimark–Sacker bifurcation curve of cycles $\mathrm{NS}^c$ is above the Hopf bifurcation curve $H^\pm$. Figure 4d shows that when parameters are chosen in region $\textcircled {1}$, there exists a stable limit cycle. Figure 6b shows that with the increase of $v^*$ the stable limit cycle loses its stability through a Neimark–Sacker bifurcation and a two dimensional torus will arise for parameters above the line $\hbox {NS}^c$. Negative normal form coefficients along the line $\hbox {NS}^c$ indicate that the Neimark–Sacker bifurcation is supercritical and the torus is stable. A phase diagram of a stable torus for $(k_{a11}, v^*)=(0.13,10)$ is shown in Fig. 6c.

In Fig. 6b, on the line $\mathrm{NS}^c$ there exist two resonant points. One is 1:3 resonance point R3, at which the cycle has a pair of Floquet multipliers $\mu _{1,2}=e^{\pm \frac{2\pi }{3}i}$. When parameters $(k_{a11},v^*)$ are chosen near the 1:3 resonance point, a period-three cycle appears which can make three turns before closure. A typical phase diagram for the point R3 is displayed in Fig. 6d. The other is 1:4 resonance point R4, at which the cycle has a pair of Floquet multipliers $\mu _{1,2}=e^{\pm \frac{\pi }{2}i}$. When parameters $(k_{a11},v^*)$ are chosen near the 1:4 resonance point, there exists a period-four cycle and a typical phase diagram for the point R4 is displayed in Fig. 6e. From the above analysis, we find that when parameters are chosen near the line $\mathrm{NS}^c$, a stable torus or a period-three or period-four cycle is created. While when parameters are chosen a little far from the line $\mathrm{NS}^c$, some new bifurcation phenomena arise, which is irrelevant to the Neimark–Sacker bifurcation of cycles. For example, a period-six cycle appears for $(k_{a11},v^*)=(0.25,19)$, which is exhibited in Fig. 6f.

Fig. 7

a Bifurcation structure of cycles for $k_{a11}=0.7$ and $\alpha _{yyy}=0.4$. The magenta lines and the blue ones denote unstable cycles and stable limit cycles, respectively. The red lines correspond to bifurcation points of cycles. Cycle limit point LPC$_2$ for $v^*=2.42781$, cycle branch point BPC$_1$ (BPC$_2$) for $v^*=6.671552$ ($v^*=10.35964$) and Neimark–Sacker point NS$_2$ for $v^*=19.68055$. b Bifurcation structure of the cycles from $H_1$ in three-dimensional space. The explanation of labels is the same as that in a. c Bifurcation curves and bifurcation points for $\alpha _{yyy}=0.4$. The meaning of $T'$ and GH$'$ for $(k_{a11},v^*)=( -\,0.05231, 1.43756)$ is the same as that of T and GH, respectively. $\hbox {BPC}^\pm$ is a branch point bifurcation curve. The green line $\mathrm{NS}_1^\pm$ is a Neimark–Sacker bifurcation curve, which is divided into a supercritical branch $\mathrm{NS}_1^-$ and a subcritical branch $\mathrm{NS}_1^+$ by CH, while the magenta lines $\mathrm{NS}_2^\pm$ are neutral saddle cycle curves. R1 for $(k_{a11},v^*)=( 0.62932, 16.46944)$ is a 1:1 resonance point, and R4$'$ for $(k_{a11},v^*)=( 0.78959, 26.8305)$ is another 1:4 resonance point. CH for $(k_{a11},v^*)=( 0.75306, 23.255)$ is a Chenciner point of cycles. d A period-doubling bifurcation segment of a branch of symmetrical cycles from BPC$_3$ for $(k_{a11},v^*)=( 0.3,3.798801)$. PD for $(k_{a11},v^*)=( 0.3, 4.896602)$ is a period-doubling bifurcation point of cycles. (Color figure online)

Fig. 8

Phase diagrams for different parameter regions in Fig. 7c. a A stable period orbit for $(k_{a11},v^*)=(-\,0.08,3.5)$, which is between $H^-$ and $\mathrm{NS}_2^-$ and on the left of the line 1. b A pair of stable symmetrical cycles for $(k_{a11},v^*)=(0.3,3.9)$. c A pair of period-two cycles for $(k_{a11},v^*)=(0.3,5)$, which is resulted from a period-doubling bifurcation of the symmetrical cycles. d A period-six orbit for $(k_{a11},v^*)=(0.65,16)$ near R1 and above $\hbox {BPC}^+$. e A stable torus for $(k_{a11},v^*)=(0.758,24.54)$ above $\mathrm{NS}_1^-$ and on the right of line 4. f A period-four orbit for $(k_{a11},v^*)=(0.789,26.7)$ near R$'$4. (Color figure online)

3.2 Bifurcation structure of cycles for $\alpha _{yyy}=0.4$

For $\alpha _{yyy}=0.4$, we also discuss bifurcations of the cycles resulted from the point $H_1$. From Fig. 7a, we find that with the decrease in $v^*$, a cycle limit point arises at $v^*=2.42781$ labeled by LPC$_2$, through which the unstable limit cycles (magenta) turn into stable ones (blue). When $v^*$ increases, the stable limit cycles undergo a pitchfork bifurcation at a cycle branch point $v^*=6.671552$ labeled by BPC$_1$ and then become unstable ones shown in magenta lines. A pair of symmetrical stable limit cycles bifurcates from BPC$_1$ and continues until another point BPC$_2$ is encountered. As $v^*$ further increases, the magenta unstable limit cycles become stable ones (blue). Then the stable limit cycles lose their stabilities again through a Neimark–Sacker bifurcation at $v^*=19.68055$ labeled by NS$_2$, at which a positive normal form coefficient 0.00086345 indicates that an unstable torus is created. A stereoscopic bifurcation diagram in three-dimensional space for $v^* \in [2,12]$ is displayed in Fig. 7b.

Bifurcation curves of cycles for $\alpha _{yyy}=0.4$ are exhibited in Fig. 7c, which is contrasted with Fig. 6b for $\alpha _{yyy}=1.1$. By comparing Fig. 7c with Fig. 6b, it is shown that the Hopf bifurcation curve $H^\pm$ cannot be affected by the value of $\alpha _{yyy}$, while bifurcation curves of cycles can be affected by it. In Fig. 6b, when parameters are chosen between $H^\pm$ and $\mathrm{NS}^c$, there exists a stable limit cycle, which loses its stability through a supercritical Neimark–Sacker bifurcation when parameters cross the line $\mathrm{NS}^c$ from bottom to up. While the bifurcation structure in Fig. 7c is more complicated compared with Fig. 6b. Figure 7c shows that besides a 1:4 resonance point R4$'$, there also exists a 1:1 resonance point R1, at which the limit cycle has a pair of Floquet multipliers $\mu _{1,2}=1$ and from which a branch point curve of cycles $\text {BPC}^\pm$ bifurcates. In addition, the Neimark–Sacker curve $\mathrm{NS}_{1,2}^\mp$ is divided into a supercritical branch $\mathrm{NS}_1^-$, a subcritical branch $\mathrm{NS}_1^+$ and a neutral saddle cycle branch $\mathrm{NS}_2^+$ by R1 and CH. Labels of curves and bifurcation points are explained in the caption of Fig. 7c. Now we analyze bifurcation behaviors of limit cycles when a parameter point is chosen in different domains of Fig. 7c.

$\mathbf 1'$ When parameters are chosen between $H^-$ and $\mathrm{NS}_2^-$ and on the left of the line 1, there exists a stable limit cycle, which is generated by a supercritical Hopf bifurcation of the origin O. A phase diagram for $(k_{a11},v^*)=(-\,0.08,3.5)$ is exhibited in Fig. 8a. As $v^*$ increases and crosses the neutral saddle cycle curve $\mathrm{NS}_2^-$, the stable limit cycle becomes unstable.

$\mathbf 2'$ For parameters between the line 1 and the line 2, like the case in Fig. 6b, the unstable limit cycles resulted from $H^+$ undergo a limit point bifurcation at $T'$ and then turn into stable cycles, which are always present till the line $\text {BPC}^-$ is encountered. When $v^*$ crosses the line $\text {BPC}^-$, the stable limit cycles lose stabilities and a pair of symmetrical stable cycles appears. A phase diagram of a pair of symmetrical limit cycles for $(k_{a11},v^*)=(0.3,3.9)$ is exhibited in Fig. 8b. In fact, when $v^*$ continues to increase, two symmetrical limit cycles will both experience a series of bifurcations at the same value of $v^*$, such as the period-doubling bifurcation, the limit point bifurcation and the Neimark–Sacker bifurcation. If the integrated bifurcation diagram of two symmetrical limit cycles is exhibited in a figure, the bifurcation structure is too complicated to be viewed clearly. So a period-doubling bifurcation fragment of a branch of symmetrical cycles is displayed in Fig. 7d, which shows that the symmetrical limit cycles bifurcated from BPC$_3$ lose stabilities through a period-doubling bifurcation and a pair of period-two cycles is resulted from the point PD. A phase diagram of two period-two cycles for $(k_{a11},v^*)=(0.3,5)$ is exhibited in Fig. 8c. As $v^*$ further increases, the Neimark–Sacker bifurcation and the limit point bifurcation will take place in the symmetrical cycles, which is not analyzed in detail here.

$\mathbf 3'$ When parameters lie between the line 2 and the line 3, unlike the case $\mathbf 2'$, two branch point curves of cycles $\hbox {BPC}^-$ and $\hbox {BCP}^+$ will be encountered. Between them a pair of symmetrical stable limit cycles coexists with an unstable limit cycle, whose phase diagram is similar to Fig. 8b. When $v^*$ exceeds the line $\hbox {BCP}^+$, the symmetrical limit cycles disappear and the unstable limit cycle turns into a stable one. And then the stable limit cycle loses its stability through a subcritical Neimark–Sacker bifurcation when $v^*$ crosses $\mathrm{NS}_1^+$ from bottom to top. The bifurcation diagram in Fig. 7a belongs to this case. In addition, it is worth pointing out that when $v^*$ increases and approaches to the point R1, an Arnold tongue structure will root at some point on $\mathrm{NS}_1^+$. Long-periodic or quasi-periodic orbits, homoclinic tangencies or chaotic motion maybe appear. The complete picture includes other bifurcations and seems to be unknown, which is confirmed in [17]. A period-six orbit for $(k_{a11},v^*)=(0.65,16)$ near R1 is shown in Fig. 8d.

$\mathbf 4'$ When a parameter point is chosen between the line 3 and the line 4, the branch points of cycles disappear and the stable limit cycles resulted from $T'$ continue till the line $\mathrm{NS}_1^+$ is encountered, where the stable limit cycles lose stabilities through a subcritical Neimark–Sacker bifurcation and an unstable torus is created.

$\mathbf 5'$ For parameters on the right of line 4, the bifurcation behavior is similar to the case $\mathbf 4'$ except that the Neimark–Sacker bifurcation is supercritical. A stable torus is created when $v^*$ crosses the line $\mathrm{NS}_1^-$ from bottom to top, which is displayed in Fig. 8e. A Chenciner bifurcation point CH divides the green Neimark–Sacker bifurcation curve $\mathrm{NS}_1$ into a supercritical branch $\mathrm{NS}_1^-$ and a subcritical branch $\mathrm{NS}_1^+$. It should be noted that there is a resonance point R4$'$ on the line $\mathrm{NS}_1^-$. When a parameter point is chosen near the point R4$'$, a period-four cycle will appear and a phase diagram for $(k_{a11},v^*)=(0.789,26.7)$ is shown in Fig. 8f.

From the above analysis, it is shown that changing the value of $\alpha _{yyy}$ will affect the location of bifurcation curves of cycles, thus affecting the distribution of bifurcation parameter regions, while it will not affect the location of bifurcation curves of the equilibrium O.

4 Conclusions

In this paper, at first, a stable parameter domain of the equilibrium O of a simplified railway wheelset model is given, by which it is shown that the equilibrium O loses its stability through a supercritical or subcritical Hopf bifurcation. Next, bifurcation behaviors of the cycles resulted from $H_1$ have been discussed. With the variation of $v^*$, the limit cycle point, the cycle branch point or the Neimark–Sacker bifurcation point will be encountered, whose existence is dependent on the nonlinear coefficients $\alpha _{yyy}, \ldots , \beta _{y\psi \psi }$,and $\beta _{\psi \psi \psi }$. As a typical case study, the effect of $\alpha _{yyy}$ has been studied, which shows that changing the value of $\alpha _{yyy}$ can affect the location and existence of bifurcation curves of cycles as well as the distribution of bifurcation parameter regions. In the case for $\alpha _{yyy}=0.4$, two different resonant points and cycle branch points will be encountered, near which two symmetrical cycles or a cycle with several turns arise. It shows that if the motion of running wheels deviates from the central position, the running wheels will oscillate along the left or the right cycle or along the cycle combining with several oscillations. In addition, as the variation of $v^*$, a stable torus can be created by a supercritical Neimark–Sacker bifurcation of cycles, which can be distinguished from the subcritical Neimark–Sacker bifurcation by a Chenciner point.

Although some bifurcations of limit cycles have been discussed in this paper based on two bifurcation parameters $k_{a11}$ and $v^*$ for a simplified railway wheelset model, there are still a lot of questions not to be solved. For example, what kinds of global bifurcation phenomena will happen if many more parameters are considered? If there exist homoclinic or heteroclinic tangencies or even chaotic motions, what are their mechanisms of hunting motion and what are their bifurcation structures near the resonance points? These questions have not fully been understood so far, which will be our future work.

Appendix

$$\begin{aligned} A_{21}= & {} -\frac{3d^3_{22}}{\bar{\tau } k^3_{21}}\left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}+i\frac{\omega }{v^*}\right) \\&\times \left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}-i\frac{\omega }{v^*} \right) ^2\alpha _{yyy}\\&-\,\frac{d^2_{22}}{\bar{\tau } k^2_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2}+\frac{\omega ^2}{v^{*2}}\right. \\&\left. -\,i\frac{2\omega (k_{11}-k_{22}+k_{a11})}{(d_{11}+d_{22})v^{*}}\right) \alpha _{yy\psi }\\&-\,\frac{d_{22}}{\bar{\tau } k_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})}{d_{11}+d_{22}}-i\frac{\omega }{v^{*}}\right) \alpha _{y\psi \psi }\\&-\frac{3}{\bar{\tau }}\alpha _{\psi \psi \psi }\\&+\,\frac{3 d_{11}d^3_{22}\left( (k_{11}-k_{22}+k_{a11})^2v^{*2}+\omega ^2(d_{11}+d_{22})^2\right) ^2}{ \tau (k_{21}v^{*})^4(d_{11}+d_{22})^4 }\beta _{yyy}\\&+\,\frac{d_{11}d^2_{22}}{\bar{\tau } k^3_{21}}\left( \frac{(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2} +\frac{\omega ^2}{v^{*2}}\right) \\&\times \left( \frac{3(k_{11}-k_{22}+k_{a11})}{d_{11}+d_{22}}+i\frac{\omega }{v^{*}}\right) \beta _{yy\psi }\\&+\,\frac{d_{11}d_{22}}{\bar{\tau } k^2_{21}}\left( \frac{3(k_{11}-k_{22}+k_{a11})^2}{(d_{11}+d_{22})^2}\right. \\&\left. +\,\frac{\omega ^2}{v^{*2}}+ i\frac{2\omega (k_{11}-k_{22}+k_{a11})}{(d_{11}+d_{22})v^{*}}\right) \beta _{y\psi \psi }\\&+\,\frac{3d_{11}}{\bar{\tau } k_{21}}\left( \frac{k_{11}-k_{22}+k_{a11}}{d_{11}+d_{22}}+i\frac{\omega }{v^{*}}\right) \beta _{\psi \psi \psi }, \end{aligned}$$

$$\begin{aligned}&l_{1}(k_{a11},v^*)=\left[ \left( 2265k^5_{a11}-2379.1k^4_{a11} +789.17k^3_{a11}\right. \right. \\&\quad \qquad \qquad \qquad \left. \left. -\,46.093k^2_{a11}-30.711k_{a11}+0.8893\right) v^{*4}\right. \\&+\,\left( 120{,}500k^4_{a11}-51{,}814k^3_{a11}-6779.5k^2_{a11}\right. \\&\left. +1550.7k_{a11}+140.13\right) v^{*2}\\&+\,\left( 0.6474k_{a11}+0.1006\right) ^{\frac{3}{2}} \left( 0.399+2.5689k_{a11}\right) v^{*}\\&+\,1{,}602{,}800k^3_{a11}+305{,}210k^2_{a11}\\&-\,\left. 21{,}188k_{a11}-4648.3\right] \!{\big /} \!\left\{ \!\left[ \left( k^3_{a11}-0.2688k^2_{a11}\right. \right. \right. \\&\left. \left. \left. -\,0.021k_{a11}+0.007\right) v^{*5}+\left( 98.661k_{a11}\right. \right. \right. \\&+\,\left. \left. \left. 9.4776+242.36k_{a11}^2\right) v^{*3}\right. \right. \\&\left. \left. +\,\left( 157.15+1011.8k_{a11}\right) v^{*}\right] \sqrt{0.6474k_{a11}+0.1006}\right\} . \end{aligned}$$