1 Introduction

Vehicle system dynamics is an interesting topic in railway engineering, since Klingel [1] performed a purely kinematic analysis of the hunting motion of a single wheelset on a tangential track in 1883. There are many works on the nonlinear stability of vehicle systems in the early stages. Carter [2] constructed a theoretical model of wheel-rail contact force, which is crucial for deriving the dynamic behavior of railway wheelsets. Wickens [3] analyzed the nonlinear stability of railway bogie with profiled wheels instead of pure conical wheels. Huilgol [4] introduced the bifurcation analysis in nonlinear dynamics to the problem of railway vehicle dynamics, creating a new trend in railway engineering research. True and Kaas-Petersen [5] found that the bifurcation of periodic motion is subcritical and the critical speed must be found by an investigation of the existence of multiple attractors. Yabuno et al. [6] investigated the influence of lateral linear stiffness on the nonlinear characteristics of the hunting phenomenon of railway wheelsets. Zhang et al. [7] considered the nonlinear relationship between creepage and creep force when studying the lateral dynamics of a railway wheelset suspended under a moving vehicle with linear springs and dry friction dampers. They also analyzed the effect of the wheel tread conicity on the Hopf bifurcation through numerical simulations. Gao et al. [8] studied the symmetric/asymmetric bifurcations and chaos of a bogie system under a nonlinear wheel-rail contact relation.

In the practical problem, the wheel-rail contact geometry has an important influence on the running dynamics and operating safety of railway vehicles [9]. It directly affects the wheelset performance of the curve passing and the running stability of high-speed vehicles [10]. The equivalent conicity is an indicator for characterizing the wheel-rail contact geometry, and it is one of the important parameters in the wheel-rail contact geometry relationship [11]. Cooperrider et al. [12] proposed a kind of computation method for determining the nonlinear contact restraint condition of wheel-rail, after that the equivalent conicity has been widely used as a key index in the railway industry. In [13], many scholars discussed the equivalent conicity method for the stability evaluation of rail vehicles, and this kind of method is very useful to many railway engineers in practical application, while it has to be noted that the equivalent conicity concept is a purely heuristic engineering concept because it still lacks a strict mathematical basis. Internationally, the equivalent conicity value at 3 mm of the wheelset lateral displacement is used to evaluate the wheel-rail contact relationship, which is called the nominal equivalent conicity [14].

With the in-depth works of the equivalent conicity, scholars found that the nominal equivalent conicity value cannot fully describe the nonlinear characteristics of the wheel-rail contact geometry relationship in the railway [15,16,17,18]. Polach [15] pointed out that the same nominal equivalent conicity corresponds to several different equivalent conicity curves. Even if the wheel-rail contact geometry has the same nominal equivalent conicity, the dynamic behavior of the vehicle systems is different. Therefore, Polach [16, 17] put forward a new nonlinearity parameter (NP) to describe the geometric contact nonlinearity with the slope of the equivalent conicity curve. In further work, Polach [19] pointed out that as the vehicle travel distance increases, the equivalent conicity increases and the NP of the wheel and rail decreases. Since the NP only represents the equivalent conicity slope between the two points around 3 mm of the wheelset lateral displacement, a nonlinear factor for evaluating the nonlinearity of equivalent conicity is proposed in [20]. It is calculated by multiplying the standard deviation of the equivalent conicity between 1–6 mm of the wheelset lateral displacement by the direction of the slope of the equivalent conicity curve. Moreover, the stability of the vehicle systems is evaluated in more detail through the Hopf bifurcation analysis in [16, 17, 20]. If the slope of the equivalent conicity curve is negative (positive) at 3 mm of the wheelset lateral displacement, the Hopf bifurcation is supercritical (subcritical) [16, 17]. Similarly, if the nonlinear factor presented in [20] is positive (negative), the Hopf bifurcation is supercritical (subcritical). However, neither of these two papers [16, 17, 20] determined the relationship between equivalent conicity and the Hopf bifurcation type through bifurcation theory and rigorous mathematical proof. This paper intends to deduce the expression of the first Lyapunov coefficient by calculating the normal form of the Hopf bifurcation, so as to judge whether the Hopf bifurcation is supercritical or subcritical.

In this paper, different types of equivalent conicity are fitted smoothly to analyze the influence of equivalent conicity difference on the vehicle dynamic behavior when the lateral displacement of the wheelset is less than 3 mm. To study the mechanism of equivalent conicity type affecting the Hopf bifurcation characteristics, the expression of the first Lyapunov coefficient is calculated by the bifurcation theory. If the second-order derivative of the equivalent conicity function with respect to the lateral displacement of the wheelset at the equilibrium is positive (negative), the Hopf bifurcation of the wheelset system is subcritical (supercritical). The conclusion is consistent with the existing simulation results of the real wheel-rail relationship in references [16, 17, 20]. Moreover, the codimension-1 and codimension-2 bifurcations of limit cycles produced by the Hopf bifurcation are analyzed, such as the fold bifurcation, the period-doubling bifurcation, the cusp bifurcation and the fold-flip bifurcation. The effect of these bifurcations on the hunting motion of the wheelset system is discussed, which provides a theoretical reference for improving the running stability of vehicles.

This paper is arranged as follows. Section 1 is an introduction of previous work done by other researchers, and a presentation of the aim of this work. In Sect. 2, a simplified wheelset model with a nonlinear smooth equivalent conicity function is established. Taking the running speed as a single bifurcation parameter, the stability and Hopf bifurcation of the trivial equilibrium are investigated in Sect. 3. Moreover, the first Lyapunov coefficient of the Hopf bifurcation is calculated by the normal form theory. Two different types of the equivalent conicity curves are introduced in Sect. 4, and the effects of their differences on bifurcation speed and Hopf bifurcation characteristics are studied, respectively. In Sect. 5, the codimension-1 and codimension-2 bifurcations of the limit cycles are investigated simultaneously. The numerical simulations are mainly carried out by the software package MATCONT [21]. A conclusion section comes at the end.

Fig. 1
figure 1

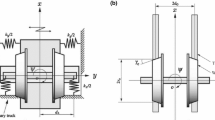
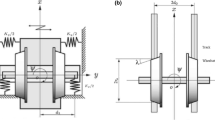
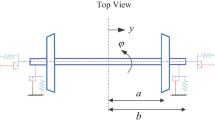
Wheelset model diagram [22]

Full size image

2 Wheelset model

Consider the following linear wheelset model [22]:

$$\begin{aligned} m\ddot{y} + \left( {{k_{1y}} + \frac{{W\lambda }}{b}} \right) y + \frac{{2{f_{22}}}}{v}\dot{y} - 2{f_{22}}\psi&=0,\nonumber \\ J\ddot{\psi }+ \frac{{2{f_{11}}b\lambda }}{{{r_0}}}y + \left( {{k_{1x}}{L^2} - Wb\lambda } \right) \psi + \frac{{2{f_{11}}{b^2}}}{v}{\dot{\psi }}&= 0, \end{aligned}$$
(1)

where y and \(\psi \) denote the lateral displacement and the yaw motion of the wheelset, m and J represent the mass and the moment of inertia of the wheelset, \(k_{1x}\) and \(k_{1y}\) represent the primary longitudinal stiffness and lateral stiffness, respectively. b and L are the half distance of wheel rolling cycles, half of the lateral spacing of primary suspension, respectively. W, \(\lambda \), \(r_0\), v, \(f_{11}\) and \(f_{22}\) denote the axle load, equivalent conicity, wheel rolling radius, running speed, and the longitudinal and lateral creep force coefficients, respectively. Figure 1 is a schematic diagram of the wheelset model [22].

Because the value of the equivalent conicity \(\lambda \) is affected by the lateral displacement of the wheelset y, a nonlinear function \(\lambda (y)\) is introduced to represent the equivalent conicity curve. The equivalent conicity curves in this paper are smoothly fitted by the measured data of the equivalent conicity varying with the lateral displacement of the wheelset, which is to qualitatively study the bifurcation at the trivial equilibrium and limit cycles.

Replacing the equivalent conicity \(\lambda \) in Eq. (1) with the nonlinear equivalent conicity function \(\lambda (y)\), Eq. (1) becomes

$$\begin{aligned} m\ddot{y} + \left( {{k_{1y}} + \frac{{W{\lambda (y)} }}{b}} \right) y + \frac{{2{f_{22}}}}{v}\dot{y} - 2{f_{22}}\psi&= 0,\nonumber \\ J\ddot{\psi }+ \frac{{2{f_{11}}b{\lambda (y)} }}{{{r_0}}}y + \left( {{k_{1x}}{L^2} - Wb{\lambda (y)} } \right) \psi + \frac{{2{f_{11}}{b^2}}}{v}{\dot{\psi }}&= 0. \end{aligned}$$
(2)

With the change of variables

$$\begin{aligned} {x_1} = {y},{x_2} = {{\dot{y}}},{x_3} = {\psi },{x_4} = {{{\dot{\psi }} }}, \end{aligned}$$

the Eq. (2) turns into

$$\begin{aligned} {{\dot{x}}_1}&= {x_2},\nonumber \\ {{\dot{x}}_2}&= - \Bigg ( {k_{1y}}{x_1} + \frac{{W\lambda ({x_1}){x_1}}}{b} + \frac{{2{f_{22}}}}{v}{x_2} \nonumber \\&\quad - 2{f_{22}}{x_3} \Bigg )/m,\nonumber \\ {{\dot{x}}_3}&= {x_4},\nonumber \\ {{\dot{x}}_4}&= - \left( \frac{{2{f_{11}}b\lambda ({x_1}){x_1}}}{{{r_0}}} + {k_{1x}}{L^2}{x_3} \right. \nonumber \\&\quad -\left. Wb\lambda ({x_1}){x_3} + \frac{{2{f_{11}}{b^2}}}{v}{x_4} \right) /J. \end{aligned}$$
(3)

3 Hopf bifurcation of the equilibrium

In this section, the parameter v is chosen as a single bifurcation parameter.

3.1 Stability of the trivial equilibrium O

The Jacobian matrix of the Eq. (3) evaluated at the trivial equilibrium O is

$$\begin{aligned} {A_0} = \left( {\begin{array}{*{20}{c}} 0&{}1&{}0&{}0\\ { - {a_1} - {a_2}\lambda (0)}&{}{ - \frac{{{a_3}}}{v}}&{}{{a_3}}&{}0\\ 0&{}0&{}0&{}1\\ { - {a_4}\lambda (0)}&{}0&{}{ - {a_5} + {a_6}\lambda (0)}&{}{ - \frac{{{a_7}}}{v}} \end{array}} \right) , \end{aligned}$$
(4)

where

$$\begin{aligned} {a_1}&= \frac{{{k_{1y}}}}{m},{a_2} = \frac{W}{{mb}},{a_3} = \frac{{2{f_{22}}}}{m},{a_4} = \frac{{2{f_{11}}b}}{{{r_0}J}},\\ {a_5}&= \frac{{{k_{1x}}{L^2}}}{J},{a_6} = \frac{{Wb}}{J},{a_7} = \frac{{2{f_{11}}{b^2}}}{J}. \end{aligned}$$

The characteristic polynomial corresponding to the Jacobian matrix \({A_0}\) is

$$\begin{aligned} P(\mu ) = {c_0}{\mu ^4} + {c_1}{\mu ^3} + {c_2}{\mu ^2} + {c_3}\mu + {c_4}, \end{aligned}$$
(5)

where

$$\begin{aligned} c_{0}&= 1, c_{1} = \frac{{(a_{3} + a_{7})}}{v},\\ c_{2}&= (a_{2} - a_{6})\lambda (0) + a_{1} + a_{5} + \frac{{a_{3}a_{7}}}{{{v^2}}},\\ {c_3}&= \frac{{({a_2}{a_7} - {a_3}{a_6})\lambda (0) + {a_1}{a_7} + {a_3}{a_5}}}{v},\\ {c_4}&= - {a_2}{a_6}{[\lambda (0)]^2} + ({a_2}{a_5} - {a_1}{a_6} + {a_3}{a_4})\lambda (0)\\&\quad + {a_1}{a_5}. \end{aligned}$$

The stability of the equilibrium O can be described by the following proposition.

Proposition 1

If the characteristic polynomial \(P(\mu )\) has two pairs of complex roots \({\mu _{1,2}} = {\alpha _1} \pm i{\omega _1},{\mu _{3,4}} = {\alpha _2} \pm i{\omega _2}\), and \({\alpha _1} < {\alpha _2}, {\omega _i} > 0,{\alpha _i},{\omega _i} \in R(i = 1,2)\), then there are the following results:

  • Case 1: If \({\alpha _2}< 0\), the equilibrium O of the wheelset system (3) is asymptotically stable;

  • Case 2: If \({\alpha _2} = 0\), the equilibrium O of the wheelset system (3) is at a critical condition between stability and instability;

  • Case 3: If \({\alpha _2}> 0\), the equilibrium O of the wheelset system (3) is unstable.

3.2 Hopf bifurcation of the equilibrium O

If the wheelset system (3) undergoes a Hopf bifurcation at the equilibrium O, the Jacobian matrix \({A_0}\) will have a simple pair of conjugated purely imaginary eigenvalues and the other eigenvalues have negative real parts. The conditions that there is a pair of pure imaginary roots in the four eigenvalues of the Eq. (5) and the real parts of the other two roots are negative are as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} {c_i} > 0 (i = 1,2,3,4),\\ {\varDelta _3} = 0, \end{array}} \right. \end{aligned}$$
(6)

where \({\varDelta _3}\) is the Hurwitz determinant.

Because every coefficient of the polynomial \(P(\mu )\) is a positive real number, the first condition of Eq. (6) is satisfied. Let \({\varDelta _3} = 0\), the bifurcation speed of the wheelset system satisfies the following equation:

$$\begin{aligned} {\varDelta _3}&= \left| {\begin{array}{ccc} {{c_1}}&{}{{c_0}}&{}0\\ {{c_3}}&{}{{c_2}}&{}{{c_1}}\\ 0&{}{{c_4}}&{}{{c_3}} \end{array}} \right| = \frac{1}{{{v^4}}}((({({a_2} + {a_6})^2}{[\lambda (0)]^2}\nonumber \\&\quad + 2\lambda (0)(({a_2} + {a_6})({a_1} - {a_5}) \nonumber \\&\quad - {a_3}{a_4}) + {({a_1} - {a_5})^2}){a_7} - \lambda (0)a_3^2{a_4} \nonumber \\&\quad - {a_4}\lambda (0)a_7^2){a_3}{v^2} + (({a_5} - {a_6}\lambda (0)){a_3} \nonumber \\&\quad + {a_7}({a_2}\lambda (0) + {a_1}))({a_3} + {a_7}){a_7}{a_3})=0. \end{aligned}$$
(7)

So the equation for the bifurcation speed \(v_b\) of the wheelset system is

$$\begin{aligned} {v_b} = \sqrt{ - \frac{{(({a_5} - {a_6}\lambda (0)){a_3} + {a_7}({a_2}\lambda (0) + {a_1}))({a_3} + {a_7}){a_7}{a_3}}}{{(({{({a_2} + {a_6})}^2}{{[\lambda (0)]}^2} + 2\lambda (0)(({a_2} + {a_6})({a_1} - {a_5}) - {a_3}{a_4}) + {{({a_1} - {a_5})}^2}){a_7} - \lambda (0)a_3^2{a_4} - {a_4}\lambda (0)a_7^2){a_3}}}}. \end{aligned}$$
(8)

When the running speed v reaches the bifurcation speed \(v_b\), the wheelset system (3) undergoes Hopf bifurcation and there are a pair of pure imaginary roots \(\pm i\omega _0\), where \({\omega _0} = \sqrt{\frac{{{c_3}}}{{{c_1}}}} = \sqrt{\frac{{({a_5} - \lambda (0){a_6}){a_3} + ({a_1} + \lambda (0){a_2}){a_7}}}{{{a_3} + {a_7}}}} \). Furthermore, it is easy to find that the bifurcation speed \(v_b\) is only related to \(\lambda (0)\) when other parameters are fixed.

To determine whether the Hopf bifurcation is subcritical or supercritical, the normal form of the Hopf bifurcation is deduced and the expression of the first Lyapunov coefficient \(l_1\) is computed.

At the bifurcation point \(v=v_b\), the wheelset system (3) is Taylor expanded at the equilibrium O and the Eq. (3) can be written as

$$\begin{aligned} \dot{x}=A_0(v_b) x+F(x). \end{aligned}$$
(9)

The nonlinear term of the system is represented as the following form:

$$\begin{aligned} F(x) = \frac{1}{{2!}}B(x,x) + \frac{1}{{3!}}C(x,x,x) + O( {| x|^4}), \end{aligned}$$
(10)

where B(x, x) and C(x, x, x) are multilinear functions of \(x = {({x_1},{x_2},{x_3},{x_4})^T} \in {R^4}\), respectively. The expressions can be described as follows

$$\begin{aligned} {B_i}(\xi ,\eta )&= {\left. {\sum \limits _{j,k = 1}^4 {\frac{{{\partial ^2}{F_i}(x)}}{{\partial {x_j}\partial {x_k}}}} } \right| _{x = 0}}{\xi _j}{\eta _k},\nonumber \\&\quad (i = 1,2,3,4), \end{aligned}$$
(11)
$$\begin{aligned} {C_i}(\xi ,\eta ,\varsigma )&= {\left. {\sum \limits _{j,k,l = 1}^4 {\frac{{{\partial ^3}{F_i}(x)}}{{\partial {x_j}\partial {x_k}\partial {x_l}}}} } \right| _{x = 0}}{\xi _j}{\eta _k}{\varsigma _l},\nonumber \\&\quad (i = 1,2,3,4). \end{aligned}$$
(12)

According to Eqs. (11) and (12), the following expressions can be obtained:

$$\begin{aligned}&B(\xi ,\eta ) = \left( {\begin{array}{c} 0\\ { - 2{a_2}{\xi _1}{\eta _1}\left( {{{\left. {\frac{d}{{d{x_1}}}\lambda \left( {{x_1}} \right) } \right| }_{{x_1} = 0}}} \right) }\\ 0\\ {\left( { - 2{a_4}{\xi _1}{\eta _1} + {a_6}\left( {{\xi _1}{\eta _3} + {\xi _3}{\eta _1}} \right) } \right) \left( {{{\left. {\frac{d}{{d{x_1}}}\lambda \left( {{x_1}} \right) } \right| }_{{x_1} = 0}}} \right) } \end{array}} \right) , \end{aligned}$$
(13)
$$\begin{aligned}&C(\xi ,\eta ,\varsigma ) = \left( {\begin{array}{c} 0\\ { - 3{a_2}{\xi _1}{\eta _1}{\varsigma _1}\left( {{{\left. {\frac{{{d^2}}}{{dx_1^2}}\lambda \left( {{x_1}} \right) } \right| }_{{x_1} = 0}}} \right) }\\ 0\\ {\left( { - 3{a_4}{\xi _1}{\eta _1}{\varsigma _1} + {a_6}({\xi _1}{\eta _1}{\varsigma _3} + {\xi _1}{\eta _3}{\varsigma _1} + {\xi _3}{\eta _1}{\varsigma _1})} \right) \left( {{{\left. {\frac{{{d^2}}}{{dx_1^2}}\lambda \left( {{x_1}} \right) } \right| }_{{x_1} = 0}}} \right) } \end{array}} \right) . \end{aligned}$$
(14)

Suppose that the eigenvectors \(q_0\) and \(p_0\) satisfy \(A_0(v_b)q_0 = i\omega _0 q_0\) and \({A_0^T}(v_b)p_0 = - i\omega _0 p_0\), respectively, where

$$\begin{aligned} q_0&= \left( {\begin{array}{c} 1\\ {i{\omega _0}}\\ {\frac{{\lambda (0){a_2} - \omega _0^2 + {a_1}}}{{a3}} + \frac{{i{\omega _0}}}{v}}\\ { - \frac{{\omega _0^2}}{v} + i{\omega _0}\left( {\frac{{\lambda (0){a_2} - \omega _0^2 + {a_1}}}{{{a_3}}}} \right) } \end{array}} \right) , \end{aligned}$$
(15)
$$\begin{aligned} p_0&= \left( {\begin{array}{c} {\frac{{ - \lambda (0){a_6} - \omega _0^2 + {a_5}}}{v} - \frac{{{a_7}\omega _0^2}}{{v{a_3}}} + i{\omega _0}(\frac{{\lambda (0){a_6} + \omega _0^2 - {a_5}}}{{{a_3}}} - \frac{{{a_7}}}{{{v^2}}})}\\ {\frac{{ - \lambda (0){a_6} - \omega _0^2 + {a_5}}}{{{a_3}}} - \frac{{i{\omega _0}{a_7}}}{{v{a_3}}}}\\ {\frac{{{a_7}}}{v} - i{\omega _0}}\\ 1 \end{array}} \right) . \end{aligned}$$
(16)

Let \(k=\left\langle {{p_0},{q_0}} \right\rangle \), \(q=q_0\) and \({p = \frac{1}{k}{p_0}}\), then p and q satisfy the normalization \(\left\langle {p,q} \right\rangle = 1\).

Introducing complex variables z, the system (9) can be written as

$$\begin{aligned} \dot{z}=\mu (v_b) z+g(z, \bar{z}, v_b), \end{aligned}$$
(17)

where \(g = O({\left| z \right| ^2})\) is a smooth function of \((z, \bar{z}, v_b), x\) and z satisfy the following relationship

$$\begin{aligned} x=z q+\bar{z} \bar{q} \end{aligned}$$
(18)

After a series of complicated deductions [23], the system (17) can be transformed into an equation containing only three terms of resonance, which can be written as follows:

$$\begin{aligned} \dot{z}=i\omega z+c_{1}(v_b) z^{2} \bar{z}+O\left( |z|^{4}\right) , \end{aligned}$$
(19)

where

$$\begin{aligned} c_{1}\left( v_{b}\right)&=\frac{1}{2}\langle p, C(q, q, \bar{q})\rangle \nonumber \\&\quad -2\left\langle p, B\left( q, A_{0}^{-1}\left( v_{b}\right) B(q, \bar{q})\right) \right\rangle \nonumber \\&\quad +\left\langle p, B\left( \bar{q},\left( 2 i \omega _{0} I_{4}-A_{0}\left( v_{b}\right) \right) \right) ^{-1} B(q, q))\right\rangle , \end{aligned}$$
(20)

and \(I_4\) is a \(4 \times 4\) identity matrix.

The first Lyapunov coefficient \(l_1\) has the representation:

$$\begin{aligned} {l_1}\left( {{v_b}} \right)&= \frac{1}{\omega }{\mathrm{Re}} \left( {{c_1}\left( {{v_c}} \right) } \right) \nonumber \\&= \frac{1}{{2\omega }}{\mathrm{Re}} \left( \langle p,C(q,q,{\bar{q}})\rangle \right. \nonumber \\&\left. \quad - 2\left\langle p,B\left( {q,A_0^{ -1}( {v_c})B(q,{\bar{q}})} \right) \right\rangle \right. \nonumber \\&\left. { + \left\langle {p,B{{\left( {{\bar{q}},\left( {2i{\omega _0}{I_4} - {A_0}\left( {{v_c}} \right) } \right) } \right) }^{ - 1}}B(q,q))} \right\rangle } \right) . \end{aligned}$$
(21)

The transversality condition coefficient of the Hopf bifurcation has the form:

$$\begin{aligned} {d_1}({v_b}) = \frac{\partial }{{\partial v}}{\mathrm{Re}} ({\mu _3}({v_b})). \end{aligned}$$
(22)

According to the Hopf bifurcation theory in [23, 24], the following result is obtained.

Proposition 2

If \({l_1}({v_b})\ne 0\) and \({d_1}({v_b})\ne 0\), the wheelset system (3) undergoes a Hopf bifurcation at \(v=v_b\). When \({l_1}({v_b})>0\), the subcritical Hopf bifurcation occurs in the system (3) and produces a series of unstable limit cycles. Conversely, when \({l_1}({v_b})<0\), the Hopf bifurcation is supercritical and a series of stable limit cycles appear.

Fig. 2
figure 2

Nonlinear equivalent conicity function curves of different types. a Equivalent conicity curves of “Type A”. b Equivalent conicity curves of “Type B”

Full size image
Table 1 Values of the parameters in this paper [22]
Full size table

4 Influence of the nonlinear equivalent conicity on the dynamic behavior

The same nominal equivalent conicity corresponds to different equivalent conicity curves, which show different dynamic behavior and bifurcation characteristics. These equivalent conicity curves are generally divided into two types, called “Type A” and “Type B” [15]. Especially when the lateral displacement of the wheelset is less than 3 mm, these two types have significant differences. According to the raw data of the two types of equivalent conicity, the nonlinear functions of the equivalent conicity with respect to the lateral displacement of the wheelset are fitted using the Gaussian function in the software package Curve Fitting Tool of MATLAB.

For “Type A”:

$$\begin{aligned} {\lambda _{A_{1}}}({x_1})&= 0.3378\exp \left( - {\left( \frac{{{x_1} - 0.003387}}{{0.00253}}\right) ^2}\right) \nonumber \\&\quad + 0.3378\exp \left( - {\left( \frac{{{x_1} + 0.003387}}{{0.00253}}\right) ^2}\right) . \end{aligned}$$
(23)

The raw data (black dots) and the nonlinear equivalent conicity function curve (black dash line) of the “Type A” are shown in Fig. 2a. The nonlinear function \(\lambda _{A}(x_1)\) fits very well with the measured data. The sum of squares of error is \(\mathrm{SSE} = 0.001076\), the coefficient of determination is R-square = 0.9968, the adjusted R-square = 0.9965, and the root mean squared error is \(\mathrm{RMSE} = 0.004423\).

For “Type B”:

$$\begin{aligned} {\lambda _{B_{1}}}({x_1})&= 0.4982\exp \left( - {\left( \frac{{{x_1}}}{{0.0009375}}\right) ^2}\right) \nonumber \\&\quad + 0.3153\exp \left( - {\left( \frac{{{x_1}}}{{0.009965}}\right) ^2}\right) . \end{aligned}$$
(24)

The raw data (black dots) and the nonlinear equivalent conicity function curve (black dash line) of the “Type B” are shown in Fig. 2b. The nonlinear function \(\lambda _{B}(x_1)\) fits very well with the measured data. The sum of squares of error is \(\mathrm{SSE} = 0.005135\), the coefficient of determination is R-\(\mathrm{square} = 0.9974\), the adjusted R-\(\mathrm{square} = 0.9971\), and the root mean squared error is \(\mathrm{RMSE} = 0.009663\).

As can be clearly seen from Fig. 2, the change of the equivalent conicity of “Type A” is monotonically increasing when the lateral displacement of the wheelset is between 1–3 mm, while the “Type B” is monotonically decreasing.

4.1 Influence of the nonlinear equivalent conicity on the bifurcation speed

Although with the equal nominal equivalent conicity, the bifurcation speed is not necessarily the same. How different nonlinear equivalent conicity curves affect bifurcation speed is explained in this subsection.

From Eq. (8), it can be known that the value of the bifurcation speed \(v_b\) is only related to the value of \(\lambda (0)\) when the other parameters are fixed as the values in Table 1. Several equivalent conicity functions of “Type A” and “Type B” with the same nominal equivalent conicity and different values of \(\lambda (0)\) are established, which are presented in Fig. 2. These equivalent conicity functions are substituted into Eq. (3), and the corresponding bifurcation speeds are calculated, respectively. The numerical results are shown in Table 2, and the following conclusions can be drawn:

  1. (1)

    The larger value of \(\lambda (0)\), the smaller the bifurcation speed \(v_b\). That is to say, for the equivalent conicity curve of “Type A”, the smaller the change rate of the curve with the lateral displacement of wheelset \(x_1\), the smaller the bifurcation speed. While for “Type B”, the greater the change rate, the larger the bifurcation speed. Hence, the running speed can be safely increased by controlling the change rate of the equivalent conicity \(\lambda \) with the lateral displacement of the wheelset \(x_1\).

  2. (2)

    The bifurcation speed corresponding to the equivalent conicity curve of “Type A” is larger than that of “Type B”. Since the equivalent conicity curve of “Type A” is monotonically increasing and the curve of “Type B” is monotonically decreasing as the lateral displacement of the wheelset is less than 3 mm, and the nominal equivalent conicity of “Type A” and “Type B” is equal, the value of \(\lambda (0)\) of “Type A” must be less than that of “Type B”. Therefore, the bifurcation speed corresponding to the equivalent conicity curve of “Type A” must be larger than that of “Type B”.

Table 2 The variation of \(v_b\) with different \(\lambda (0)\)
Full size table

4.2 Influence of the equivalent conicity type on the Hopf Bifurcation type

In this subsection, the bifurcation mechanism of the effect of equivalent conicity curve on Hopf bifurcation type is studied by calculating the expression of the first Lyapunov coefficient.

When the lateral displacement of the wheelset is less than 3 mm, according to the corresponding nonlinear equivalent conicity functions, the first-order derivative of the equivalent conicity function with respect to the lateral displacement of the wheelset \(\lambda (x_1)\) at the wheelset lateral displacement of 0 is equal to 0, i.e., \(\left( {{{\left. {\frac{d}{{d{x_1}}}\lambda ({x_1})} \right| }_{{x_1} = 0}}} \right) = 0\). Thus, \(B(\xi ,\eta )\) in the Eq. (14) becomes zero. It should be noted that this condition only holds for wheel profiles with symmetric wear.

Through the above calculation and analysis, the expression of the first Lyapunov coefficient in the Eq. (21) becomes

$$\begin{aligned} {l_1}({v_c})&= \frac{1}{{2\omega _0 }}{\mathrm{Re}} \left( {\left\langle {p,C(q,q,{\bar{q}})} \right\rangle } \right) \nonumber \\&= \frac{1}{{2{\omega _0}}}{\mathrm{Re}} \left( \left( {\frac{{{d^2}}}{{dx_1^2}}\lambda ({x_1})\left| {_{{x_1} = 0}} \right. } \right) \right. \nonumber \\&\quad \left. \frac{1}{{{\bar{k}}}}( - 3{a_2}{{{\bar{p}}}_2} - 3{a_4} + {a_6}({{{\bar{q}}}_3} + 2{q_3})) \right) \nonumber \\&= \frac{1}{{2{\omega _0}}}\left( {\frac{{{d^2}}}{{dx_1^2}}\lambda ({x_1})\left| {_{{x_1} = 0}} \right. } \right) {\mathrm{Re}}\nonumber \\&\quad \left( {\frac{1}{{{\bar{k}}}}( - 3{a_2}{{{\bar{p}}}_2} - 3{a_4} + {a_6}({{{\bar{q}}}_3} + 2{q_3}))} \right) . \end{aligned}$$
(25)

Let \({\mathrm{Re}} \left( {\frac{1}{{{\bar{k}}}}( - 3{a_2}{{{\bar{p}}}_2} - 3{a_4} + {a_6}({{{\bar{q}}}_3} + 2{q_3}))} \right) \) in the Eq. (25) be \({\mathrm{Re}} \left( \alpha \right) \). Substitute the basic parameters of wheelset parameters in Table 1 to \({\mathrm{Re}} \left( \alpha \right) \) and obtain that

$$\begin{aligned} {\mathrm{Re}} ( \alpha )=\frac{{ - 0.003486(\lambda (0) - \mathrm{{96}}\mathrm{{.829302}})(\lambda (0) - \mathrm{{4902}}\mathrm{{.748623}})(\lambda (0) - \mathrm{{0}}\mathrm{{.011}})(\lambda (0) - \mathrm{{4442}}\mathrm{{.058}})}}{{(\lambda (0) + \mathrm{{1}}\mathrm{{.002252}})(\lambda (0) - \mathrm{{0}}\mathrm{{.008106}})({{[\lambda (0)]}^2} - \mathrm{{8471}}\mathrm{{.3874}}\lambda (0) + 17949181.25)}}. \end{aligned}$$

As is well known, the value of the equivalent conicity is generally greater than 0, then \({\mathrm{Re}} ( \alpha )\) in Eq. (25) is positive. Hence, the sign of the first Lyapunov coefficient \({l_1}({v_c})\) is determined by the sign of \(\left( {\frac{{{d^2}}}{{dx_1^2}}\lambda ({x_1})\left| {_{{x_1} = 0}} \right. } \right) \) and the following proposition is obtained:

Fig. 3
figure 3

The limit cycles produced from the Hopf bifurcations of the wheelset system (3). a A subcritical Hopf bifurcation point \(H^-\) and the unstable limit cycles marked by red dotted lines. b A supercritical Hopf bifurcation point \(H^+\) and the stable limit cycles marked by blue dash lines. (Color figure online)

Full size image

Proposition 3

The sign of the first Lyapunov coefficient \({l_1}({v_c})\) is determined by the sign of \(\left( {\frac{{{d^2}}}{{dx_1^2}}\lambda ({x_1})\left| {_{{x_1} = 0}} \right. } \right) \). The value of \(\left( {\frac{{{d^2}}}{{dx_1^2}}\lambda _A ({x_1})\left| {_{{x_1} = 0}} \right. } \right) \) of the equivalent conicity function of “Type A” is positive. On the contrary, for “Type B”, \(\left( {\frac{{{d^2}}}{{dx_1^2}}\lambda _B ({x_1})\left| {_{{x_1} = 0}} \right. } \right) <0\). Therefore, if the nonlinear equivalent conicity curve belongs to “Type A” (or “Type B”), the wheelset system (3) will occur a subcritical (or supercritical) Hopf bifurcation and produces a series of unstable (or stable) limit cycles.

Proposition 3 is consistent with the simulation results of the real wheel-rail relationship presented in [16, 17, 20]. The conclusion can also be verified by numerical simulations. Fixing the values of parameters as those in Table 1 and selecting two different types of equivalent conicity functions, the Hopf bifurcation types are compared. Substituting the function \({\lambda _{A_1}}({x_1})\) into the wheelset system (3), the subcritical Hopf bifurcation occurs at \(v=257.1674614\,\mathrm{km/h}\) with the first Lyapunov coefficient \(l_1=3852.916>0\). As is seen from Fig. 3a, a family of unstable limit cycles arises from the subcritical Hopf bifurcation point \(H^-\). Similarly, taking the function \({\lambda _{B_4}}({x_1})\) into the Eq. (3), the supercritical Hopf bifurcation with the first Lyapunov coefficient \(l_1=-3979.408<0\) undergoes at \(v=91.53065099\,\mathrm{km/h}\) and produces a series of stable limit cycles, which is shown in Fig. 3b.

5 Bifurcations of the limit cycles

In the previous sections, the nonlinear equivalent conicity functions are fitted within 3 mm of the lateral displacement of the wheelset. And the wheel-rail contact force is not considered for eliminating the influence of other nonlinear factors on the dynamic behavior of the wheelset. In this section, the high codimension bifurcations of the limit cycles are analyzed as the lateral displacement of the wheelset is extended to 8 mm. Meanwhile, the lateral wheel-rail contact force \(F_T={\delta _1}x_1^3+{\delta _2}x_1^5\) (\({\delta _1}=-1.6 \times 10^{11}\), \({\delta _2}=1.6 \times 10^{15}\)) [22, 25] is also taken into account in the wheelset system (3). Here, the lateral displacement of the wheel set \(0\,\mathrm{m} \le |y| \le 0.008\,\mathrm{m}\) is considered to avoid of flange contact. Then, Eq. (3) becomes:

$$\begin{aligned} \dot{x}_{1}&=x_{2} \nonumber \\ \dot{x}_{2}&=-\left( k_{1 y} x_{1}+\frac{W \lambda \left( x_{1}\right) x_{1}}{b}+\frac{2 f_{22}}{v} x_{2}\right. \nonumber \\&\left. \quad -2 f_{22} x_{3}+\delta _{1} x_{1}^{3}+\delta _{2} x_{1}^{5}\right) / m \nonumber \\ \dot{x}_{3}&=x_{4} \nonumber \\ \dot{x}_{4}&=-\left( \frac{2 f_{11} b \lambda \left( x_{1}\right) x_{1}}{r_{0}}+k_{1 x} L^{2} x_{3}\right. \nonumber \\&\left. \quad -W b \lambda \left( x_{1}\right) x_{3}+\frac{2 f_{11} b^{2}}{v} x_{4}\right) / J \end{aligned}$$
(26)

Taking the equivalent conicity curve of “Type B” (corresponding to a certain type of high-speed train in China) as an example and the corresponding nonlinear function is as follows:

$$\begin{aligned} {\lambda _B}\left( {{x_1}} \right)&= 1010 \exp \left( { - {{\left( {\frac{{{x_1} - 0.01299}}{{0.001849}}} \right) }^2}} \right) \nonumber \\&\quad + 10.92 \exp \left( { - {{\left( {\frac{{{x_1} + 0.01006}}{{0.00141}}} \right) }^2}} \right) \nonumber \\&\quad + 0.138 \exp \left( { - {{\left( {\frac{{{x_1} - 0.0001089}}{{0.0009091}}} \right) }^2}} \right) \nonumber \\&\quad + 0.08916 \exp \left( { - {{\left( {\frac{{{x_1} + 0.0001739}}{{0.001229}}} \right) }^2}} \right) \nonumber \\&\quad - 0.01263 \exp \left( { - {{\left( {\frac{{{x_1} - 0.0006772}}{{0.0004752}}} \right) }^2}} \right) \nonumber \\&\quad + 0.3839 \exp \left( { - {{\left( {\frac{{{x_1} + 14.08}}{{16.76}}} \right) }^2}} \right) \nonumber \\&\quad + 0.107 \exp \left( { - {{\left( {\frac{{{x_1} - 0.00253}}{{0.005892}}} \right) }^2}} \right) \nonumber \\&\quad + 0.07366 \exp \left( { - {{\left( {\frac{{{x_1} + 0.004705}}{{0.003604}}} \right) }^2}} \right) . \end{aligned}$$
(27)

The raw data (black dots) and the nonlinear equivalent conicity curve (blue dash line) are shown in Fig. 4. The nonlinear function \(\lambda _{B}(x_1)\) fits very well with the measured data. The sum of squares of error is \(\mathrm{SSE} = 0.004308\), the coefficient of determination is R-\(\mathrm{square} = 0.9977\), the adjusted R-\(\mathrm{square} = 0.9972\), and the root mean squared error is \(\mathrm{RMSE} = 0.006017\).

Fig. 4
figure 4

The nonlinear function of the equivalent conicity as the lateral displacement of the wheelset is extended to 8 mm. (Color figure online)

Full size image
Fig. 5
figure 5

The bifurcation process of the limit cycles produced from the Hopf bifurcation of the wheelset system (3). a Two-dimensional bifurcation diagram. b Three-dimensional bifurcation diagram. The lines labeled by LPC (red) and PD (green), respectively, denote the fold bifurcation and period-doubling bifurcation of the cycles. The solid blue lines represent the stable limit cycles, and the dashed red lines represent the unstable limit cycles. (Color figure online)

Full size image

Substituting Eq. (27) into Eq. (26). When the running speed v is the single bifurcation parameter and the other parameters are fixed to the values in Table 1, the wheelset system undergoes a supercritical Hopf bifurcation with the first Lyapunov coefficient \(l_1=-3217.91052<0\) at \(v=115.62088\,\mathrm{km/h}\). The Hopf bifurcation produces a family of stable limit cycles, which is represented by the solid blue lines in Fig. 5a. The codimension-1 and codimension-2 bifurcations of the limit cycles will be analyzed separately in the following subsections. The critical normal form coefficients of the bifurcations are uniformly represented by c [23], which is computed by the bifurcation software package MATCONT.

5.1 Codimension-1 bifurcations

In this subsection, the codimension-1 bifurcations of the limit cycles are studied by applying the continuation method in the bifurcation software package MATCONT. The initial stepsize is set as 0.01, the minimum stepsize to compute the next point on the curve is 1e−05, and the maximum stepsize is 1. The tolerance of coordinates is set as 1e−06, the tolerance of function values is 1e−06, and the tolerance of test functions is 1e−05.

The bifurcation route of the stable limit cycle is: \({\textit{SLC}} {\mathop {\longrightarrow }\limits ^{{\textit{LPC}}_{1}}} {\textit{ULC}} {\mathop {\longrightarrow }\limits ^{{\textit{LPC}}_{2}}} {\textit{SLC}} {\mathop {\longrightarrow }\limits ^{P D_{1}}} {\textit{ULC}} {\mathop {\longrightarrow }\limits ^{{\textit{PD}}_{2}}} {\textit{SLC}}\), which is shown in Fig. 5a. \({\textit{SLC}}\) and \({\textit{ULC}}\) denote the stable and unstable limit cycles, respectively. When the running speed reaches \(143.04812\,\mathrm{km/h}\), the stable limit cycles (blue dash lines) undergo a fold (limit point) bifurcation (labeled by \({\textit{LPC}}_1\)) with the normal form coefficient: \(c=21.4342652>0\). From the Hopf bifurcation point \(H^+\) to the fold bifurcation \({\textit{LPC}}_1\), the elapsed time is 14.8 s. Then, the stable limit cycles become unstable (red dotted lines) and the bifurcation direction becomes opposite. As the running speed decreases, another fold bifurcation of the limit cycles (labeled by \({\textit{LPC}}_2\)) with the normal form coefficient: \(c=-16.3026378<0\) occurs at \(v=135.36798\,\mathrm{km/h}\), which changes the stability and bifurcation direction of the limit cycles once again. The elapsed time of this process is 7.7 s. At the fold bifurcation point, the limit cycle has the Floquet multipliers \(\mu _1= 1\). After the fold bifurcation \({\textit{LPC}}_2\), the limit cycles become stable and the running speed continues to increase. Then, the limit cycles occur period-doubling (flip) bifurcations, which labeled by \({\textit{PD}}_1\) at \(v=143.57394\,\mathrm{km/h}\) with the normal form coefficient: \(c=-1.52566855<0\) and \({\textit{PD}}_2\) at \(v=147.79299\,\mathrm{km/h}\) with the normal form coefficient: \(c=-2.78736433<0\). The time elapsed for the occurrence of these two period-doubling bifurcations is 11.7 s and 2 s, respectively. At the period-doubling bifurcation point, the limit cycle has the Floquet multipliers \(\mu _1= -1\). To represent the bifurcation route stereoscopically, the bifurcation diagram on the three-dimensional plane is given in Fig. 5b.

Fig. 6
figure 6

Two-parameter bifurcation curves of limit cycles about the parameters v and \(f_{11}\). The blue curve is the Hopf bifurcation curve of the equilibrium O. The red curve is the fold bifurcation curve of the limit cycles, and the green curve is the period-doubling bifurcation curve of the limit cycles. (Color figure online)

Full size image
Fig. 7
figure 7

a Phase diagram of the limit cycles at \((v,f_{11})=(140,1.5)\) in the region surrounded by the curves \(T_1^+\), \(T_2^-\) and \(T_3^+\). b Phase diagram of the period-2 limit cycle at \((v,f_{11})=(143.574,1.5232)\) on the period-doubling bifurcation curve. c Waveform corresponding to a. d Waveform corresponding to b. (Color figure online)

Full size image

5.2 Codimension-2 bifurcations

To study the codimension-2 bifurcations of the limit cycles, the bifurcation curves of limit cycles about the parameters v and \(f_{11}\) are drawn in Fig. 6. The computation in this subsection also uses the bifurcation software package MATCONT. The initial stepsize is set to 0.01, the minimum stepsize to compute the next point on the curve is 1e−05, the maximum stepsize is 0.1. The stepsize displayed as 0.1 during curve drawing. The tolerance of coordinates is set as 1e−06, the tolerance of function values is 1e−06, the tolerance of test functions is 1e−05.

The red curve denotes the fold bifurcation curve of limit cycles, on which there exist two cusp bifurcation points: \({\textit{CPC}}_1\) at \((v,f_{11})=(148.2688,1.2313122)\) with the normal form coefficient \(c=-39.9195291\) and \({\textit{CPC}}_2\) at \((v,f_{11})=(123.62071,1.6752247)\) with the normal form coefficient \(c=115.854142\). From the bifurcation point \({\textit{CPC}}_1\) to \({\textit{CPC}}_2\), the elapsed time is 102.4 s. These two cusp bifurcation points divide the fold bifurcation curve into three parts: the supercritical fold bifurcation curve \(T_1^+\), the subcritical fold bifurcation \(T_2^-\) and the supercritical fold bifurcation \(T_3^+\). The phase diagram of the limit cycles in the area surrounded by the three curves (\(T_1^+\), \(T_2^-\), \(T_3^+\)) is given in Fig. 7a. There exist two stable limit cycles and an unstable limit cycle. The amplitudes of these limit cycles are shown in Fig. 7c. Since the limit cycle with the maximum amplitude is stable, the lateral displacement of the wheelset will not exceed 6 mm.

The green line represents the period-doubling bifurcation curve of limit cycles, on which there are two fold-flip bifurcation points: \({\textit{LPPD}}_1\) at \((v,f_{11})=(187.72301,0.67217205)\) and \({\textit{LPPD}}_2\) at \((v,f_{11})=(111.68838,0.29160552)\). The elapsed time between these two fold-flip bifurcation points is 314 s. At the fold-flip bifurcation point, the limit cycle has the Floquet multipliers \(\mu _{1,2} =\pm 1\). In addition, the limit cycle of period-2 at \((v,f_{11})=(143.574,1.5232)\) on the period-doubling bifurcation curve is presented in Fig. 7b and the corresponding waveform is given in Fig. 7d.

6 Conclusions

This paper investigates the bifurcations in a simplified and smoothed model of a rolling wheelset. It mainly focuses on the influence of different nonlinear smooth equivalent conicity functions on the bifurcation characteristics. The stability and the Hopf bifurcation of the trivial equilibrium O are analyzed qualitatively. The normal form of the Hopf bifurcation is calculated, and the expression for the first Lyapunov coefficient is obtained by the normal form theory.

When the lateral displacement of the wheelset is less than 3 mm, two different types of nonlinear smooth equivalent conicity curves “Type A” and “Type B” are considered to study the effect of their differences on the bifurcation speed and the Hopf bifurcation characteristics. The analytical results show that the bifurcation speed corresponding to the equivalent conicity of “Type B” is lower than that of “Type A”. In addition, the sign of the first Lyapunov coefficient is determined by the sign of the second-order derivative of the nonlinear equivalent conicity function with respect to the lateral displacement of the wheelset at the equilibrium O. The equivalent conicity of “Type A” corresponds to the subcritical Hopf bifurcation, and “Type B” corresponds to the supercritical Hopf bifurcation. These theoretical analysis results are consistent with the existing simulation results of the real wheel-rail relationship.

The bifurcations of the limit cycles produced by the Hopf bifurcation are studied when the lateral displacement of the wheelset is extended to 8 mm. Choosing the running speed v as the single bifurcation parameter, fold bifurcations and period-doubling bifurcations of the limit cycles are found. If the running speed v and the longitudinal creep coefficient \(f_{11}\) are considered as two bifurcation parameters, cusp bifurcations and fold-flip bifurcations will occur. These bifurcations affect the stability and the amplitude variation of the limit cycles, which affects the amplitude of the hunting motion and the safety of train operation.

There are still many problems unsolved. The period-doubling bifurcation process is a typical route leading to chaos, that is, it can be considered a way to enter chaos from the period window. However, the period-doubling bifurcation in this paper does not induce chaos, and there is no symmetry breaking phenomenon, which may be because the lateral displacement of the wheelset is so small. Moreover, this paper only considers the equivalent conicity curves of the wheel profiles with symmetric wear, what will happen for wheel profiles with asymmetric wear? These problems will be studied theoretically in future work.