Hopf–Hopf bifurcation analysis based on resonance and non-resonance in a simplified railway wheelset model

Abstract

This paper mainly investigates the dynamics of the non-resonant and near-resonant Hopf–Hopf bifurcations caused by the interaction of the lateral and yaw motion in a simplified railway wheelset model, which involves local and global dynamical scenarios, respectively. This study aims to clarify the resonances due to the wheelset instability. Firstly, the ratio of longitudinal suspension stiffness and the square of natural frequency in yawing direction denoted as the parameter $k_{22}$ has an important impact on the transitions of distinct Hopf–Hopf bifurcations, and the ratio of the oscillation frequencies $\omega _1$/$\omega _2$ at the Hopf–Hopf singularity point will reduce with the decrease in $k_{22}$ within a certain range. Secondly, the absence of strong resonance under the non-resonant condition indicates that the operation wheelset will not produce the maximum oscillation amplitude triggered by the resonance point, and several torus solutions arisen from the wheelset are obtained by numerical simulation. Thirdly, five near-resonant Hopf–Hopf bifurcations reveal that the global dynamical scenario becomes much more complex than other cases as $k_{22}$ decreases. In particular, near the 1:4 resonant Hopf–Hopf interaction occurs when $\omega _1$/$\omega _2$ is close to 1:4, which has the most marked effect on wheelset hunting motions and resonances. Finally, the cyclic bifurcation behaviors under the near-resonant conditions indicate the coexistence of multiple limit cycles, and the loop of equilibria and limit cycles detected between two Hopf bifurcation points reveals that the wheelset will perform a cyclical motion in lateral and yaw direction. These results show that the change in frequency ratio induced by the intersection of the lateral and yaw motion of the unbalanced wheelset will greatly affect the hunting motions and resonances of railway vehicles. Therefore, appropriately increasing the value of $k_{22}$ is helpful to maintain the vehicle stability.

1 Introduction

The single wheelset is an indispensable component in the process of railway vehicle regular operation. Due to nonconservative contact force, the interaction of the wheelset and track tread is accompanied by the resonance of a flutter-type self-excited oscillation when the vehicle experiences a hunting motion [9]. As a result of the complex vibration surrounding of a railway vehicle, in addition to vertical line vibration, there are longitudinal, lateral, pitch, roll, and yaw angular vibrations, which are all factors that affect the passenger amenity as well as the safety and stability of operation. Resonance is a common phenomenon in railway vehicles, which is characterized by the lowest natural frequency of the carbody in the frequency range of hunting motions [5]. There are some interactions between the wheelset and the primary suspension, the primary suspension and bogie frame, as well as the bogie frame and motor, which enable vibration to be transmitted among them. When the operating speed exceeds some critical value, or the vehicle changes track or departures and arrivals, the oscillations following a disturbance grow and eventually result in a limit cycle oscillation, which increase the risk of the hunting motions and resonances of railway vehicles.

It is found that two pairs of pure imaginary eigenvalues at $\pm i\omega _1$ and $\pm i\omega _2$ will emerge in a four-dimensional wheelset system under the certain parameters, the frequencies of lateral and yaw motion of the wheelset intersect to form a specific ratio $\omega _1$/$\omega _2$, which will produce rich dynamics accompanied by the superposition of multiple resonances. The strong resonance arises on the Neimark–Sacker bifurcation born at the Hopf–Hopf singularity point, hence the resonances induced by the interaction between the self-excited oscillation modes can be interpreted in the framework of the Hopf–Hopf bifurcation [1, 2].

Supercritical and subcritical Hopf bifurcation phenomena were found to exist in two types of China high-speed vehicle systems [3]. These factors affecting the optimal fixed frequency of the bogie motor suspension system were investigated in [4], such as the primary and secondary suspension as well as the wheel-rail contact conditions, it was shown that proper design with the natural frequency of the traction motor far away from the frequency of the kinematic bogie oscillation is attractive to refrain motor resonance. In [5], since the unstable frequency of the bogie frame hunting motion can be controlled far lower than the frequency of the flexible carbody, the method of suspending a dynamic vibration absorber on the bogie frame to change its unstable frequency can prevent the bogie from riding at the resonant frequency of the flexible carbody and ensure that the carbody elastic vibration can be effectively controlled.

Owing to some common properties among oscillation simulators, the clear ideas and effective methods provided by a simple four-dimensional circuit model motivate us to investigate the simplified wheelset dynamic system. Revel et al. [6] explored a simple electric oscillation simulator, the main structure of the Hopf–Hopf bifurcation near 1:2 resonance is that the 1:1 and 1:2 strong resonance points emerging on two Neimark–Sacker bifurcation branches are connected by several lower-codimension singularity points. In [7], the local and global dynamics near the 2:3 resonant Hopf–Hopf bifurcation triggered by the interaction between the electric oscillation models were discussed. Several truncated normal forms including “simple” and “difficult” cases of the non-resonant Hopf–Hopf bifurcation were investigated in a coupled circuit [8], the presence of different frequency components for the quasi-periodic solutions of the two-dimensional (2D) torus and the three-dimensional (3D) torus was confirmed.

When a four-dimensional original system is converted to a truncated amplitude system, the corresponding relation between the equilibria was discussed in [1]. Among them, a trivial equilibrium $e_0$ with $r_1 =r_2 = 0$ of the truncated amplitude system corresponds to the equilibrium at the origin of the original system. Possible equilibria in the changeless coordinate axes of the truncated amplitude system with $r_1 = 0$ or $r_2 = 0$, called $e_1$ and $e_2$, respectively, correspond to limit cycles of the original system. Moreover, a nontrivial equilibrium $e_3$ with $r_{1,2} > 0$ of the truncated amplitude system yields a 2D torus of the original system. Finally, if a limit cycle is present in the truncated amplitude system, then the original system has a 3D torus.

Fig. 1

a The schematic of wheelset with elastic joints. b Configuration of the wheelset and rails. The description and values of the symbols are listed in Table 1. These graphics are from [10]

The 1/10 scale vehicle model proposed in Yabuno et al. [9] is for theoretical and experimental research, the details of the wheelset model for the contact conditions and of the experimental derivation for the correlative parameters were shown in [9]. The nonlinear characteristics of the bifurcation based on critical velocity and the influence of the lateral linear stiffness on the nonlinear stability against disturbance were clarified in [10]. The modified wheelset model based on equivalent conicity date was investigated in [11], which showed that the feasible coexistence of stable and unstable limit cycles induced by the cyclic fold bifurcation was accompanied by the hunting motions. Two-parameter bifurcation based on two distinct nonlinear coefficients in a simplified wheelset model was explored in [12], which indicated that the variety of nonlinear coefficient can lead to a global bifurcation phenomenon. In addition, the number of turns of the periodic orbit near the strong resonance point corresponds to the resonance ratio. However, there are still several unsolved issues, for example, the global dynamics scenarios related to the resonances have not been taken into account in the wheelset model.

There are two ways for us to study the Hopf–Hopf bifurcation in a three-parameter space, one is to determine a pair of continuity parameter values $d_{11}$ and $k_{11}$ of the near-resonance Hopf–Hopf bifurcation based on the relationship between two frequency ratio and the third parameter $k_{22}$, and the other is to constantly vary the third parameter value to hunt for a pair of continuity parameter values when the near-resonance Hopf–Hopf bifurcation emerges.

In this paper, the focus is centered on Hopf–Hopf bifurcation scenarios of the simplified wheelset model to provide distinct numerical insights resulted from changes in oscillation frequency ratio. Firstly, the parameter $k_{22}$ is of great significance to the transitions of distinct Hopf–Hopf interactions, and the result shows that the ratio of the oscillation frequencies $\omega _1$/$\omega _2$ at the Hopf–Hopf singularity point will reduce with the decrease in $k_{22}$ within a certain range. Secondly, under the non-resonant condition, the absence of strong resonance on the two Neimark–Sacker branches indicates that the running wheelset will not produce the maximum oscillation amplitude induced by the resonance point. The torus solutions including unstable 2D torus, stable 3D torus and stable 2D torus emanated from the wheelset are obtained by numerical simulation. Thirdly, five global bifurcation phenomena such as near the 1:1, 2:3, 1:2, 1:3 and 1:4 resonant Hopf–Hopf bifurcations show that the dynamical scenario becomes more complex as $k_{22}$ decreases. In particular, the case near 1:4 resonance has the most prominent influence on wheelset hunting motions and resonances. At last, under the near-resonant conditions, the cyclic bifurcation structures reveal the coexistence of multiple limit cycles arisen from the wheelset. It is worth noting that the loop of equilibria and limit cycles detected between two Hopf bifurcation points indicates that the wheelset will develop a cyclical motion in lateral and yaw direction.

The paper is organized as follows. In Sect. 2, a simplified wheelset model is described. A local bifurcation analysis is performed on a non-resonant Hopf–Hopf bifurcation in Sect. 3. In Sect. 4, five near-resonant Hopf–Hopf bifurcations and the corresponding cyclic bifurcation structures are presented. Finally, Sect. 5 summarizes some conclusions.

Table 1 Values of the parameters in Eq. (1)

Table 2 Values of the parameters in Eq. (2)

2 The simplified railway wheelset model

In our study of Hopf–Hopf bifurcation, we shall review a two-dimensional system of the simplified railway wheelset model discussed by Yabuno et al. [9], as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d^2y}{dt^2}=-\frac{2\kappa _y}{mv}\frac{dy}{dt}-\frac{k_x}{m}\left( 1-\frac{l_0}{l}\right) y+\frac{2\kappa _y}{m}\psi ,\\ \frac{d^2\psi }{dt^2}=-\frac{2d^2_0\kappa _x}{Iv}\frac{d\psi }{dt}-\frac{2d_0\kappa _x\gamma _e}{Ir_0}y-\frac{k_xd^2_1}{I}\psi . \end{array} \right. \end{aligned}$$

(1)

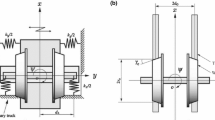
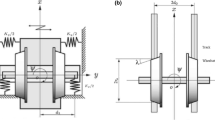
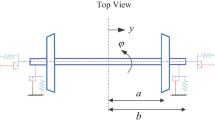
The lateral displacement and yaw motion variable are presented by y and $\psi$, respectively. The mechanical model as well as symbols of the wheelset and track are shown in Fig. 1. An illustration is supplied and several physical notations as well as the corresponding parameter values are labeled in Table 1.

According to the center manifold theory and bifurcation theory of limit cycles [1, 2], the cubic and odd nonlinear terms decide the occurrence of hunting motion induced by Hopf bifurcation. In order to analyze the Hopf bifurcation type and bifurcation structure of cycles, the third-order terms in the wheelset model must be considered. The dimensionless transformations $y = d_0y^*$, $t = t^*/\omega _{\psi }$ and $\upsilon = d_0\omega _{\psi }\upsilon ^*$ are used to derive a nonlinear wheelset motion model described in [9]

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{y}^*+\frac{d_{11}}{\upsilon ^*}{\dot{y}}^*+(k_{11}+k_{a11})y^*+k_{12}\psi +\alpha _{yyy}y^{*3}\\ \quad +\alpha _{yy\psi }y^{*2}\psi +\alpha _{y\psi \psi }y^*\psi ^2+\alpha _{\psi \psi \psi }\psi ^3=0,\\ \ddot{\psi }+\frac{d_{22}}{\upsilon ^*}{\dot{\psi }}+k_{21}y^*+k_{22}\psi +\beta _{yyy}y^{*3}\\ \quad +\beta _{yy\psi }y^{*2}\psi +\beta _{y\psi \psi }y^*\psi ^2+\beta _{\psi \psi \psi }\psi ^3=0. \end{array} \right. \end{aligned}$$

(2)

These eight nonlinear coefficients, $\alpha _{yyy},\ldots ,\alpha _{\psi \psi \psi }$, are given in some References [9, 10, 13,14,15]. These cubic nonlinear terms include factors such as the nonlinear effects owing to kinematics of the contact points, mechanical suspension, and creepage-creep forces determined by Kalker’s theory. In addition, the elements of Eq. (2) are represented as follows:

$$\begin{aligned} d_{11}&=\displaystyle \frac{2\kappa _y}{md_0\omega ^2_{\psi }},\quad d_{22}=\displaystyle \frac{2\kappa _xd_0}{I\omega ^2_{\psi }},\quad k_{21}=\displaystyle \frac{2d^2_0\kappa _x\gamma _e}{Ir_0\omega ^2_{\psi }},\\ v^*&=\displaystyle \frac{\upsilon }{d_0\omega _{\psi }},\\ k_{12}&=\displaystyle \frac{-2\kappa _y}{md_0\omega ^2_{\psi }},\quad k_{22}=\displaystyle \frac{k_xd^2_1}{I\omega ^2_{\psi }},\quad k_{a11}=\displaystyle \frac{k_y}{m\omega ^2_{\psi }},\\ k_{11}&=\displaystyle \frac{k_x(1-l_0/l)}{m\omega ^2_{\psi }}. \end{aligned}$$

where $v^*$ is the dimensionless running speed of vehicle, $d_{11}$ is the ratio of the creep coefficient in lateral and the primary spring stiffness of longitudinal, $k_{11}$ is the ratio of the primary spring stiffness of lateral and the primary spring stiffness of longitudinal, and $k_{22}$ is the ratio of the longitudinal suspension stiffness and the square of natural frequency in yawing direction. These dimensionless coefficients are shown in Table 2.

With the change of variables $(y_1, y_2, y_3, y_4)^T=(y^*,\dot{y^*}, \psi , {\dot{\psi }})^T$, then (2) turns into

$$\begin{aligned} \dot{y_1}&=y_2,\nonumber \\ \dot{y_2}&=-\frac{d_{11}}{\upsilon ^*}y_2-(k_{11}+k_{a11})y_1-k_{12}y_3-\alpha _{yyy}y_1^3\nonumber \\&\quad - \alpha _{yy\psi }y_1^2y_3-\alpha _{y\psi \psi }y_1y_3^2-\alpha _{\psi \psi \psi }y_3^3,\nonumber \\ \dot{y_3}&=y_4,\nonumber \\ \dot{y_4}&=-\frac{d_{22}}{\upsilon ^*}y_4-k_{21}y_1-k_{22}y_3-\beta _{yyy}y_1^3\nonumber \\&\quad - \beta _{yy\psi }y_1^2y_3-\beta _{y\psi \psi }y_1y_3^2-\beta _{\psi \psi \psi }y_3^3. \end{aligned}$$

(3)

The Jacobian matrix of (3) evaluated at the equilibrium $(y^*_1,y^*_2,y^*_3,y^*_4)^T$ $=$ $(0,0,0,0)^T$ is given by

$$\begin{aligned} R= \left( \begin{array}{cccc} 0&{}1&{}0&{}0\\ -k_{11}-k_{a11}&{}-\frac{d_{11}}{\upsilon ^*}&{}-k_{12}&{}0\\ 0&{}0&{}0&{}1\\ -k_{21}&{}0&{}-k_{22}&{}-\frac{d_{22}}{\upsilon ^*}\\ \end{array}\right) \end{aligned}$$

and the characteristic polynomial $P(\uplambda )$ is

$$\begin{aligned} P(\uplambda )=q_0\uplambda ^4+q_1\uplambda ^3+q_2\uplambda ^2+q_3\uplambda +q_4. \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} q_0=1\\ q_1=\frac{1}{{\upsilon ^*}}(d_{11}+d_{22})\\ q_2=\frac{1}{{\upsilon ^*}^2}d_{11}d_{22}+k_{11}+k_{22}+k_{a11}\\ q_3=\frac{1}{\upsilon ^*}(d_{11}k_{22}+d_{22}(k_{11}+k_{a11}))\\ q_4=k_{22}(k_{11}+k_{a11})-k_{12}k_{21}\\ \end{array} \end{aligned}$$

(4)

A novel Hopf–Hopf bifurcation criterion was proposed in [16]. According to the generalization of Orlando’s formula [17]

$$\begin{aligned} \varDelta _{n-1}=(-1)^{n(n-1)/2}q^{n-1}_0\prod _{1\le i<j\le n}^{1,\ldots ,n}(\uplambda _i+\uplambda _j) \end{aligned}$$

where

$$\begin{aligned} \varDelta _{n-1}= \left| \begin{array}{ccc} q_1 &{} 1&{}0 \\ q_3 &{} q_2&{}q_1 \\ 0 &{} q_4&{}q_3 \end{array}\right| =q_1q_2q_3-q^2_1q_4-q^2_3,\\\mathrm{for}\quad n=4. \end{aligned}$$

the $\uplambda _i$ and $\uplambda _j$ are the roots of the polynomial $P(\uplambda )$.

The non-resonant Hopf–Hopf bifurcation or resonant Hopf–Hopf bifurcation of system (2) occurs at $(d^*_{11},k^*_{11})$ if and only if the following conditions (H1), (H2) and (H3) or (H1), (H2) and (H4) hold, respectively:

• (H1) Eigenvalue assignment: $q_1=0,\, q_3=0, \,q_2>0, \,q_4>0, \,q^2_2-4q_4>0.$

• (H2) Transversality condition:

  $$\begin{aligned} \displaystyle \frac{\partial ^2(q_1q_2q_3-q^2_1q_4-q^2_3)}{\partial d^2_{11}}\bigg |_{(d_{11},k_{11})=(d^*_{11},k^*_{11})}&\ne 0 ,\\ \displaystyle \frac{\partial ^2(q_1q_2q_3-q^2_1q_4-q^2_3)}{\partial k^2_{11}}\bigg |_{(d_{11},k_{11})=(d^*_{11},k^*_{11})}&\ne 0. \end{aligned}$$

• (H3) Non-resonance condition:

  $\sqrt{\displaystyle \frac{q_2-\sqrt{q^2_2-4q_4}}{2}} \bigg /\sqrt{\displaystyle \frac{q_2+\sqrt{q^2_2-4q_4}}{2}} \ne \displaystyle \frac{m}{n},$ where m and n are relatively prime, such that $m+n\le 5$.

• (H4) Resonance condition:

  $\sqrt{\displaystyle \frac{q_2-\sqrt{q^2_2-4q_4}}{2}}\bigg /\sqrt{\displaystyle \frac{q_2+\sqrt{q^2_2-4q_4}}{2}}=\displaystyle \frac{m}{n},$ where m and n are relatively prime, such that $m+n \le 5$.

3 Local dynamical analysis

In the principal bifurcation parameter space ($d_{11}$, $k_{11}$, $k_{22}$), the mathematical model related to the simplified railway wheelset model (3) undergoes a Hopf–Hopf bifurcation along the curve defined by

$$\begin{aligned} {\textit{HH}}=&\left\{ (d_{11}, k_{11}, k_{22}):d_{11}=-d_{22} , k_{11}\right. \nonumber \\&\left. =k_{22}-k_{a11} , k_{22}\le \frac{k_{12}k_{21}{\upsilon ^*}^2}{d^2_{22}}+\frac{d^2_{22}}{4{\upsilon ^*}^2}\right\} . \end{aligned}$$

(5)

The ratio of two frequencies $\omega _1$ and $\omega _2$ at the Hopf–Hopf singularity points is revealed in Fig. 2a, and the Hopf–Hopf singularity points regarding six distinct $k_{22}$ are shown in Fig. 2b. For simplicity, these singularity points are denoted from top to bottom as HH$_{1:1}$, HH$_{2:3}$, HH$_{1:2}$, HH$_{{\textit{non}}}$, HH$_{1:3}$, HH$_{1:4}$ throughout the paper. Two “independent” Hopf bifurcation curves H$_1$ and H$_2$ exist on every curve in Fig. 2b caused by two distinct pairs of conjugated purely imaginary eigenvalues pass transversally through the imaginary axis, the corresponding frequencies are $\omega _1$ and $\omega _2$, respectively.

Fig. 2

a The ratio of frequencies $\omega _1$ and $\omega _2$ on the Hopf–Hopf curve as a function of $k_{22}$. b Hopf curves with five distinctive values of $k_{22}$ ($k_{22} = 3.322$, 1.78, 1.332, 1.084 and 1.01) in the parameter plane $(d_{11}, k_{11})$

The four-dimensional normal form of the wheelset model can be reduced to a two-dimensional amplitude system given by [1, 18]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\xi _1}=\xi _1(\mu _1+\xi _1-\theta \xi _2+\varTheta \xi ^2_2)\\ \dot{\xi _2}=\xi _2(\mu _2+\delta \xi _1-\xi _2+\varDelta \xi ^2_1) \end{array} \right. \end{aligned}$$

(6)

where the state variables $\xi _{1,2}$ represent the amplitude of the emerging limit cycles, $\xi _1=p_{11}\rho _1,\xi _2=p_{22}\rho _2$, $p_{11}$ and $p_{22}$ are real coefficients, $\mu _{1,2}$ are the bifurcation parameters.

All the continuations were implemented with MATCONT [19]. Computing the coefficients of the truncated normal form of the Hopf–Hopf bifurcation with MATCONT results in $p_{11}\cdot p_{22}=-1,\theta =-2,\delta =-2,\varTheta =603.568,\varDelta =-406.0986$. Note that the truncated normal form excludes resonance conditions of m/n. The parametric portrait belongs to the “difficult” case VI and the dynamics presented by the phase portraits can be translated to the wheelset model, as depicted in Fig. 3.

Fig. 3

a Parametric portraits associated with the truncated normal form of the Hopf–Hopf bifurcation for $p_{11}\cdot p_{22} < 0$ ($k_{22}= 1.2$). b Phase diagram of region ①−⑧ in a

The point $e_0$ of the amplitude system Eq.(6) is the equilibrium point at the origin of system Eq.(3), the equilibria $e_1$ and $e_2$ are the limit cycles born at the Hopf curves H$_1$ and H$_2$ in Fig. 3a, respectively, which are formally the same as in the “simple” case and coincide with the coordinate axes. The nontrivial equilibrium $e_3$ collides with $e_1$ and $e_2$ at the Neimark–Sacker curves TR$_1$ and TR$_2$, respectively, but $e_3$ undergoes a Hopf bifurcation, the emerging limit cycle vanishes at a heteroclinic bifurcation, which are not shown in Fig. 3a since the implemented algorithms on the numerical continuation package do not calculate bifurcation of torus [20].

Fig. 4

(I) Unstable 2D torus present in region ⑤. (II) Stable 3D torus located in region ⑥. (III) Stable 2D torus related to regions ⑦

The associated phase diagrams [1] near the non-resonant Hopf–Hopf singularity point HH$_{{\textit{non}}}$ at $d^*_{11}$ = 2.26 and $k^*_{11} = 0.50$ (detected at $k_{22}= 1.2$) are presented in Fig. 3b. In region ②, the equilibrium $e_0$ is unstable and it is the only local limit set. In region ③, the unstable limit cycle produced by the Hopf bifurcation H$_2$ coexists with equilibrium $e_0$. Within region ④, another unstable limit cycle is created by means of H$_1$. An unstable 2D torus is created by the Neimark–Sacker bifurcation TR$_1$ in region ⑤. In region ⑥, the unstable 2D torus of region ⑤ undergoes a heteroclinic bifurcation, resulting in a stable 3D torus. Increasing the value of $d_{11}$ will make the 3D torus collapse and the 2D torus stabilize in region ⑦. Subsequently, the stable 2D torus collapses on the Neimark–Sacker bifurcation TR$_2$ and two stable limit cycles coexist (region ⑧). Within region ①, one of the stable limit cycles vanishes at the Hopf curve H$_2$ and the equilibrium $e_0$ at the origin turns stable. Crossing the Hopf curve H$_1$, the scheme returns to the initial place in the region ②.

The phase diagrams corresponding to the three situations of region ⑤−⑦ are presented in Fig. 4(Ia)–(IIIa), (Ib)–(IIIb) show the waveform diagrams of the three distinct torus corresponding to Fig. 4(Ia)–(IIIa), respectively. The location of the projection of the unstable 2D torus on the plane $y_1$–$y_2$ is $(d_{11}, k_{11}) = (2.25970, 0.49995)$, the position of the stable 3D torus is $(d_{11}, k_{11}) = (2.25990, 0.49995)$ and the site of stable 2D torus is $(d_{11}, k_{11}) = (2.26010, 0.49995)$.

Table 3 Labels and colors of bifurcation curves used in the figures

4 “Nonlocal” dynamical analysis near the resonant Hopf–Hopf bifurcation

In this section, several near-resonant Hopf–Hopf bifurcations are performed by means of numerical continuation methods. Bifurcation diagrams in the parameter plane ($d_{11}$, $k_{11}$) are shown for five distinct values of $k_{22}$, namely $k_{22} = 3.322$, 1.78, 1.332, 1.084 and 1.01, corresponding to the Hopf–Hopf bifurcation near 1:1, 2:3, 1:2, 1:3 and 1:4 resonance, respectively. The labels and colors of several bifurcation curves used in the figures are presented in Table 3.

The first Lyapunov coefficient (${\textit{FLC}}$) and the second Lyapunov coefficient (${\textit{SLC}}$) are applied to judge the type of Hopf bifurcation. The index c(0) denotes normal form coefficients of cyclic fold bifurcation, cyclic cusp bifurcation and cyclic Neimark–Sacker bifurcation. Furthermore, when Chenciner bifurcation is non-degenerate [1], the coefficient of the resonant cubic term ${\textit{Re}}(e)$ is nonzero, two positive fixed points with opposite stability exist in the vicinity of the origin. If ${\textit{Re}}(e) < 0$, the outer one of the two fixed points is stable. If ${\textit{Re}}(e) > 0$, the inner one is stable.

4.1 Parameter values close to the 1:1 resonant Hopf–Hopf bifurcation condition

The focus in this section is to explore the dynamics near the 1:1 resonant Hopf–Hopf bifurcation when $k_{22} = 3.322$. The Hopf–Hopf singularity point HH$_{1:1}$ is located at $d^*_{11} = 2.260007$ and $k^*_{11} = 2.622000$. The frequencies of the Hopf bifurcation curves H$_{1,2}$ can be detected in Matcont, where $\omega _1 = 1.77824, \omega _2 = 1.79497$ and thus the frequency ratio $\omega _1:\omega _2\approx 0.9907$, which is quite close to 1:1 resonant condition. Two generalized Hopf bifurcation points GH$_{1,2}$ (see Fig. 5a) such that the index ${\textit{FLC}}$ vanishes emerge on the Hopf curves H$_{1,2}$, respectively, as shown below:

$$\begin{aligned}&\hbox {GH}_1,\;d_{11}=2.197291,\;{k}_{11}=2.613999,\\&\quad \hbox {Period}_1=3.033659,\;\hbox {SLC}=-0.5111842,\\&\hbox {GH}_2,\;{d}_{11}=2.262327,\;{k}_{11}=2.622129,\\&\quad \hbox {Period}_2=3.196912,\;\hbox {SLC}=29575.65. \end{aligned}$$

As presented in Fig. 5b, the point GH$_1$ where the cyclic fold curve LPC appears is a generalized Hopf bifurcation point such that the index ${\textit{FLC}}$ is zero, the curve LPC runs very close to the Hopf curve H$_1$ and is connected to GH$_2$, in particular, GH$_2$ can be detected in the vicinity of HH$_ {1:1}$. The cyclic cusp point C emerging on LPC is near to GH$_1$, which is located at $d_{11} = 2.197297$ and $k_{11} = 2.614000$.

Fig. 5

a Bifurcation diagram for $k_{22} = 3.322$ near the 1:1 resonant Hopf–Hopf bifurcation. b Expanded view close to the singularity point HH$_{1:1}$ for $(d^*_{11}, k^*_{11}) = (2.260007, 2.622000)$

Fig. 6

a–c Bifurcation structures for $d_{11} = 2.12$, 2.197291 (GH$_1$), 2.20, respectively. The black solid curves denote stable equilibria and stable limit cycles, the black dotted curves indicate unstable equilibria and unstable limit cycles, the yellow and red curves signify cyclic neutral saddles and cyclic limit points, respectively. (Color figure online)

Table 4 Labels and colors of bifurcation curves used in the figures

In this case, both the Hopf curves H$_{1,2}$ intersect at HH$_{1:1}$ and do not form a closed loop. In addition, a neutral saddle curve NS born at HH$_{1:1}$ forms a closed curve and returns to the initial place. In addition, the global bifurcation scenario near the 1:1 resonant Hopf–Hopf bifurcation is not involved in cyclic Neimark–Sacker bifurcation.

In Fig. 5b, taking GH$_1$ as a dividing point, the supercritical Hopf bifurcation happens on the left of GH$_1$ and the subcritical Hopf bifurcation happens on the right side. Corresponding to distinct $d_{11}$, the coexistence of equilibria and limit cycles detected between two Hopf bifurcation points H$_{1,2}$ is shown in Fig. 6a–c, and their bifurcation values are listed in Table 4. The limit cycles born at the supercritical Hopf bifurcation point (${\textit{FLC}}<0$) are stable. The limit cycles born at the subcritical Hopf bifurcation point (${\textit{FLC}}>0$) are unstable. The negative normal form coefficient c(0) indicates that the limit cycles born at the cyclic limit point are stable. The positive index c(0) indicates that the limit cycles born at the cyclic limit point are unstable. In particular, if the cyclic limit point LPC coincides with GH$_1$, the index c(0) is equal to 0.

Fig. 7

a Cyclic bifurcation structure for $d_{11} = 2.1$ and $k_{22} = 3.322$ on 2D plane. The black solid curves indicate stable limit cycles, the yellow curves signify cyclic neutral saddles. b Cyclic bifurcation structure in 3D space corresponds to the labels in a. (Color figure online)

In Fig. 7, the cyclic bifurcation behaviors undergo a cyclical process, which is portrayed between two Hopf bifurcation points H$_{1,2}$. When $d_{11} = 2.1$, the cyclic bifurcation structure in 2D plane is displayed in Fig. 7a, and a stereoscopic bifurcation structure in 3D space is exhibited in Fig. 7b. Due to the index ${\textit{FLC}} = -0.03513515$, a family of stable limit cycles are arisen from H$_1$ at $k_{11} = 2.594947$. As $k_{11}$ increases, the limit cycles finally reach H$_2$ after undergoing two cyclic neutral saddles NS$^\pm$. The negative index ${\textit{FLC}} = -0.1331188$ indicates the stability of the limit cycles born at H$_2$ remains unchanged.

In addition, the cyclical process between two Hopf bifurcation points H$_{1,2}$ is shown as: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^-$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^+$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^+$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^-$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$. (Here, SC denotes stable limit cycles portrayed by black solid curves). The loop indicates that the stable limit cycles generated by the wheelset coexist within the region of H$_{1}$ and H$_{2}$.

4.2 Parameter values close to the 2:3 resonant Hopf–Hopf bifurcation condition

In order to analyze the Hopf–Hopf bifurcation close to 2:3 resonance, as presented in Fig. 8a, $k_{22}$ is fixed at 1.78. The singularity point HH$_{2:3}$ is located at $d^*_{11} = 2.259995$ and $k^*_{11} = 1.079998$. In the present case, the frequencies $\omega _1 = 1.0080$, $\omega _2= 1.5112$, i.e., $\omega _1:\omega _2\approx 0.6670$ is relatively close to the 2:3 resonant condition.

Fig. 8

a Bifurcation diagram for $k_{22} = 1.78$ near the 2:3 resonant Hopf–Hopf bifurcation. b Magnified view close to the singularity point HH$_{2:3}$ for ($d^*_{11}$, $k^*_{11}$) = (2.259995, 1.079998). c Bifurcation diagram associated with the Neimark–Sacker bifurcation curve TR$_1$. d Bifurcation diagram related to the Neimark–Sacker bifurcation curve TR$_2$

The dynamic scene near the 2:3 resonant Hopf–Hopf singularity point can qualitatively describe the complexity of this case. The detection of two Neimark–Sacker branches TR$_{1,2}$ and two cyclic fold curves LPC$_{1,2}$ are shown in the magnified view of Fig. 8b. Two distinct Neimark–Sacker bifurcation structures TR$_{1,2}$ associated with the Hopf curves H$_{1,2}$ can be clearly determined. One of the outstanding features is that the branches TR$_{1,2}$ are connected by a neutral saddle curve NS to form a closed curve starting and ending at HH$_{2:3}$.

The two points where the curves LPC$_{1,2}$ emerge are generalized Hopf bifurcation points GH$_{1,2}$ such that the index FLC vanishes, which are involved in the connection of the cyclic fold curves. Specifically, the coordinates and properties of the points GH$_{1,2}$ (see Fig. 8b) are as follows:

$$\begin{aligned}&\hbox {GH}_1,\;{d}_{11}=2.128304,\;{k}_{11}=1.033156,\\&\quad \hbox {Period}_1=0.976125,\;\hbox {SLC}=0.09138855,\\&\hbox {GH}_2,\;{d}_{11}=2.719480,\;{k}_{11}=1.003051,\\&\quad \hbox {Period}_2=2.158481,\;\hbox {SLC}=0.05694257. \end{aligned}$$

In addition, both the curves LPC$_{1,2}$ encounter each other where a cyclic cusp point C: ($d_{11}$, $k_{11}$) = (2.017879, 0.9955397) with $c(0) = 11762.70$ appears, as indicated in Fig. 8c. Moreover, a 1:1 resonance point R$^a_1$ near to C is detected on the curve LPC$_1$, this cycle has a double Floquet multipliers with $\mu _{1,2} = 1$ at this singularity point.

The bifurcation diagram related to the branch TR$_1$ is presented in Fig. 8c, a couple of Fold-Neimark–Sacker points, denoted as LPNS$^a_{1,2}$, located near the ends of TR$_1$. Moreover, there is a 1:3 resonance point (two Floquet multipliers at $e^{\pm i(2\pi /3)}$) and a 1:4 resonance point (two Floquet multipliers at $e^{\pm i(\pi /2)}$) on the branch TR$_1$, denoted as R$^a_3$ and R$^a_4$, respectively. Finally, the branch TR$_1$ ends at R$^a_1$ and connects the curve NS. As mentioned for R$^a_1$, which is on both the curves TR$_1$ and LPC$_1$, and divides this curve into TR$_1$ and NS.

In Fig. 8d, a Fold-Neimark–Sacker point LPNS$^b_1$ is detected in the vicinity of HH$_{2:3}$, which is similar to LPNS$^a_1$ on the branch TR$_1$. A Chenciner bifurcation point CH$^b$: ($d_{11}$, $k_{11}$) = (2.480187, 1.021899) with ${\textit{Re}}(e) =-86.50386$ is situated on TR$_2$ related to the limit cycle emanated from the Hopf curve H$_2$, thus the outer fixed point is stable and the inner one is unstable. Moreover, a 1:4 resonance point R$^b_4$ is observed here. Ultimately, the branch TR$_2$ ends at a 1:1 resonance point R$^b_1$ near to another point LPNS$^b_2$.

In general, the Neimark–Sacker branch TR$_1$ born at the singularity point HH$_{2:3}$ connects the neutral saddle curve NS after reaching the 1:1 resonance point R$^a_1$. Then NS arrives at R$^b_1$ after two turns, which is connected to the Neimark–Sacker branch TR$_2$, and finally forms a closed curve.

Fig. 9

a Cyclic bifurcation structure for $d_{11} = 2.1$ and $k_{22} = 1.78$ on 2D plane. The black solid curves stand for stable limit cycles and the black dashed curves stand for unstable ones. The red, yellow and green curves stand for cyclic limit points, cyclic neutral saddles and cyclic Neimark–Sacker bifurcation points, respectively. The labels and types corresponding to the following situations have the same implications. b Cyclic bifurcation structure in 3D space with respect to the labels in a. (Color figure online)

In Fig. 9, the same parameter $d_{11}$ is fixed at 2.1 to continue $k_{11}$ and to observe the cyclic bifurcation behaviors. Due to the negative index ${\textit{FLC}} = -0.004220202$, thus the limit cycles born at H$_1$ are stable. As $k_{11}$ increases, the stability of limit cycles remains unchanged when undergoing a cyclic limit point LPC$_1$ with normal form coefficient $c(0) = -0.003745364$. Subsequently, due to the positive index $c(0) = 0.0001374898$, a series of limit cycles become unstable when a double complex Floquet multipliers are outside the unit circle, which indicates that an unstable torus is created via a cyclic Neimark–Sacker bifurcation point TR$_1$. The limit cycles restore stability until the point LPC$_2$ with $c(0) = -0.1138517$ emerges and then a cyclic neutral saddle NS is detected. Ultimately, the limit cycles return to the point H$_2$ with ${\textit{FLC}} = -0.05211610$ and start a recurrence.

Between two Hopf bifurcation points H$_{1,2}$, the loop in the process of numerical simulation can be shown as: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$ LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$. (Here, SC denotes stable limit cycles portrayed by black solid curves, and UC denotes unstable limit cycles portrayed by black dotted curves). Within the region of LPC$_1$ and TR$_1$, the stable limit cycles arisen from the wheelset coexist. Within the region of TR$_1$ and LPC$_2$, the stable limit cycles arisen at LPC$_2$ coexist with unstable limit cycles born at TR$_1$, which indicates the presence of an unstable torus.

4.3 Parameter values close to the 1:2 resonant Hopf–Hopf bifurcation condition

A global unfolding of the Hopf–Hopf bifurcation near 1:2 resonance is depicted in Fig. 10a, the singularity point HH$_{1:2}$ at $d^*_{11} = 2.260000$ and $k^*_{11} = 0.632000$ appears when $k_{22} = 1.332$. The ratio of both frequencies $\omega _1 =0.694406$ and $\omega _2 = 1.38631$ is approximately 0.5009, which satisfies the resonant condition close to 1:2. This kind of connection of a neutral saddle curve NS and two Neimark–Sacker branches TR$_{1,2}$ is similar to the case near 2:3 resonance. Two generalized Hopf bifurcation points GH$_{1,2}$ (see Fig. 10b) emerge on two Hopf bifurcation curves H$_{1,2}$, respectively, noted as

$$\begin{aligned}&\hbox {GH}_1,\;{d}_{11}=2.133968,\;{k}_{11}=0.582715,\\&\quad \hbox {Period}_1=0.448234,\;\hbox {SLC}=0.1660530,\\&\hbox {GH}_2,\;{d}_{11}=2.857789,\;{k}_{11}=0.511944,\\&\quad \hbox {Period}_2=1.785885,\;\hbox {SLC}=0.04155471. \end{aligned}$$

A similar scenario observed is that the curves LPC$_{1,2}$ born at GH$_{1,2}$ intersect at a cusp point, this point is detected at C: ($d_{11}$, $k_{11}$) = (1.970543, 0.5222585) with $c(0) = 11888.44$. For the 1:1 resonance point R$^a_1$ near to C, as depicted in Fig. 10c, is encountered on both the curves LPC$_1$ and TR$_1$.

Fig. 10

a Bifurcation diagram for $k_{22} = 1.332$ near the 1:2 resonant Hopf–Hopf bifurcation. b Expanded view close to the singularity point HH$_{1:2}$ for ($d^*_{11}$, $k^*_{11}$) = (2.260000, 0.632000). c Bifurcation diagram associated with the Neimark–Sacker bifurcation curve TR$_1$. d Bifurcation diagram related to the Neimark–Sacker bifurcation curve TR$_2$

The bifurcation diagram of the semi-structure related to the branch TR$_1$ is exhibited in Fig. 10c. Compared with the Hopf–Hopf bifurcation near 2:3 resonance, more strong resonances such as two 1:3 and two 1:4 resonance points are detected, denoted as R$^a_3$ and R$^a_4$, respectively. In addition, the same scenario as both the branches TR$_1$ is the presence of the points LPNS$^a_{1,2}$, TR$_1$ intersects with LPC$_1$ at a 1:1 resonance point R$^a_1$ and ends with this point.

The dynamics of the semi-structure associated with the branch TR$_2$ is illustrated in Fig. 10d . The backward numerical continuation produces one Fold-Neimark–Sacker point LPNS$^b_1$ close to HH$_{1:2}$, and the other LPNS$^b_2$ near to R$^b_1$ is created by the forward numerical continuation. Among them, a 1:4 resonance point R$^b_4$ is observed near the curve NS, a Chenciner bifurcation point CH$^b$: ($d_{11}$, $k_{11}$) = (2.552513, 0.5444179) with ${\textit{Re}}(e) = -137.8334$ emerges on the branch TR$_2$. Compared with the case near 2:3 resonance, the similar scenario of two Neimark–Sacker branches TR$_2$ are that both generate a point CH$^b$ and a couple of points LPNS$^b_{1,2}$, and end in a 1:1 resonance point R$^b_1$. However, the discrepancy is the presence of a 1:3 resonance point R$^b_3$.

Fig. 11

a Cyclic bifurcation structure for $d_{11} = 2.1$ and $k_{22} = 1.332$ on 2D plane. b Cyclic bifurcation structure in 3D space with respect to the labels in a

Analogously, the parameter $d_{11}$ is fixed at 2.1 to observe the cyclic bifurcation behaviors when $k_{11}$ changes in Fig. 11. The structure similar to the Hopf–Hopf bifurcation near 2:3 resonance occurs in the process of numerical continuation, just like the above analysis. The inner Hopf bifurcation point H$_1$ with ${\textit{FLC}} = -0.005551508$ and the outer one H$_2$ with ${\textit{FLC}} = -0.05254251$ indicate that the limit cycles born at H$_{1,2}$ are both stable. Two cyclic limit points are detected at LPC$_1$ with $c(0) = -0.001739350$ and LPC$_2$ with $c(0) = -0.1104969$. A series of unstable limit cycles exist till a Neimark–Sacker bifurcation point labeled by TR$_1$ is encountered at $k_{11} = 0.5591471$, at which a positive index c(0) reveals that an unstable torus is created. The presence of a cyclic neutral saddle NS is located between H$_2$ and LPC$_2$.

An analogous loop between two Hopf bifurcation points H$_{1,2}$ can be exhibited as: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$ H$_1$. The structure further explains that the cyclic bifurcation behaviors emanated from the wheelset are very close to the 2:3 resonant case.

4.4 Parameter values close to the 1:3 resonant Hopf–Hopf bifurcation condition

Let us investigate the unfolding of the Hopf–Hopf bifurcation near 1:3 resonance depicted in Fig. 12a, the parameter $k_{22}$ is settled at 1.084. The singularity point HH$_{1:3}$ is situated at $d^*_{11} = 2.259999$ and $k^*_{11} = 0.384000$. The frequencies $\omega _1 = 0.436733$ and $\omega _2= 1.31047$, i.e., $\omega _1:\omega _2\approx 0.3333$ is fairly close to the condition of 1:3 resonance. Two generalized Hopf bifurcation points GH$_{1,2}$ (see Fig. 12b) are shown below:

$$\begin{aligned}&\hbox {GH}_1,\;{d}_{11}=2.138557,\;{k}_{11}=0.334344,\\&\quad \hbox {Period}_1=0.159838,\;\hbox {SLC}=-1.451423,\\&\hbox {GH}_2,\;{d}_{11}=2.941620,\;{k}_{11}=0.235757,\\&\quad \hbox {Period}_2=1.575520,\;\hbox {SLC}=0.03593939. \end{aligned}$$

In this case, two cyclic fold curves arisen from GH$_{1,2}$ no longer encounter at a cusp point. The curve LPC$^1_{1}$ born at GH$_1$ runs very close to the Hopf bifurcation curve H$_1$, a 1:1 resonance point R$^1_1$ is observed on this curve, and a cusp point C$^1$: ($d_{11}$, $k_{11}$) = (2.25999, 0.383996) with $c(0)=638.4611$ appears in the vicinity of HH$_{1:3}$, then C$^1$ joins the curve LPC$^1_2$. The curve LPC$^2_1$ born at GH$_2$ intersects the neutral saddle curve NS at a 1:1 resonance point R$^a_1$, then forms a cusp point C$^2_1$ with the curve LPC$^2_2$, also LPC$^2_2$ forms a cusp point C$^2_2$ with the curve LPC$^2_3$. Among them, these cusp points are detected at C$^2_1$: ($d_{11}$, $k_{11}$) = (1.944105, 0.2595407) with $c(0)= 195.0080$, and C$^2_2$: ($d_{11}$, $k_{11}$) = (2.007971, 0.2819056) with $c(0)=0.02310147$.

Fig. 12

a Bifurcation diagram for $k_{22} = 1.084$ near the 1:3 resonant Hopf–Hopf bifurcation. b Expanded view close to the singularity point HH$_{1:3}$ for ($d^*_{11}$, $k^*_{11}$) = (2.259999, 0.384000). c Bifurcation diagram associated with the Neimark–Sacker bifurcation curve TR$_1$. d Bifurcation diagram related to the Neimark–Sacker bifurcation curve TR$_2$

The structure related to the left branch TR$_1$ is shown in Fig. 12c, compared with the previous two cases near 2:3 and 1:2 resonance, the discrepancy about this branch is that there is a Fold-Neimark–Sacker point LPNS$^a_1$ near to HH$_{1:3}$ and it no longer ends with a 1:1 resonance point. Furthermore, more complicated resonance phenomena consisting of more strong resonance points occur. There are a pair of 1:1, two pairs of 1:3 and two pairs of 1:4 resonance points emerging on TR$_1$, denoted as R$^a_1$, R$^a_3$ and R$^a_4$, respectively. In addition, between two resonance points R$^a_1$ and R$^a_4$, a Chenciner bifurcation point is detected at CH: ($d_{11}$, $k_{11}$) = (2.240148, 0.3674266) with ${\textit{Re}}(e) = 2.357679$, which indicates the inner fixed point is stable and the outer one is unstable.

The structure associated with the right branch TR$_2$ is depicted in Fig. 12d, a Chenciner bifurcation point is detected at CH: ($d_{11}$, $k_{11}$) = (2.600987, 0.2768758) with ${\textit{Re}}(e) = -207.8293$. The scenario similar to before is that a couple of Fold-Neimark–Sacker points LPNS$^b_{1,2}$ emerge and this branch ends at a 1:1 resonance point R$^b_1$. In particular, TR$_2$ produces three 1:3 resonance points R$^b_3$, two of which are near to HH$_{1:3}$. A 1:4 resonance point R$^b_4$ is observed below the curve NS and above the curve LPC$^2_1$.

Fig. 13

a Cyclic bifurcation structure for $d_{11} = 2.1$ and $k_{22} = 1.084$ on 2D plane. b Cyclic bifurcation structure in 3D space with respect to the labels in a

In Fig. 13, the cyclic bifurcation behaviors are observed by keeping $d_{11} = 2.1$ unchanged and changing $k_{11}$. The negative index ${\textit{FLC}} = -0.007029457$ indicates that a series of stable limit cycles are emanated from the Hopf bifurcation point H$_1$. When undergoing the cyclic limit point LPC$^1_2$, the negative index $c(0) = -3.436286$ indicates that the stable limit cycles still exist. As $k_{11}$ decreases, the stability of limit cycles vanishes when the cyclic Neimark–Sacker point TR$_1$ with $c(0) = 0.0002820793$ emerges, which indicates an unstable torus is created. Then the limit cycles restore stability until LPC$^2_1$ with $c(0) = -0.1014374$ arises. Finally, the limit cycles return to the point H$_2$ after passing a cyclic neutral saddle NS.

The loop between two Hopf bifurcation points H$_{1,2}$ can be shown as: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$. Within the region of LPC$^1_2$ and TR$_1$, the stable limit cycles arisen from the wheelset coexist. Within the region of TR$_1$ and LPC$^2_1$, the stable limit cycles arisen at LPC$^2_1$ coexist with unstable limit cycles born at TR$_1$, which indicates that the wheelset gives birth to an unstable torus via TR$_1$.

4.5 Parameter values close to the 1:4 resonant Hopf–Hopf bifurcation condition

When considering the Hopf–Hopf bifurcation near 1:4 resonance, the parameter $k_{22}$ is set at $k_{22} = 1.01$, the singularity point HH$_{1:4}$ is located at $d^*_{11} = 2.260000$ and $k^*_{11}=0.310000$. The frequencies $\omega _1 = 0.3228$ and $\omega _2 = 1.2868$, i.e., $\omega _1:\omega _2\approx 0.2508$ is quite close to the 1:4 resonant condition. Two generalized Hopf bifurcation points GH$_{1,2}$ (see Fig. 13a) are as follows:

$$\begin{aligned}&\hbox {GH}_1,\;{d}_{11}=2.140128,\;{k}_{11}=0.260366,\\&\quad \hbox {Period}_1=0.074224,\;\hbox {SLC}=-0.01398757,\\&\hbox {GH}_2,\;{d}_{11}=2.967883,\;{k}_{11}=0.152679,\\&\quad \hbox {Period}_2=1.512267,\;\hbox {SLC}=0.03449155. \end{aligned}$$

In Fig. 14a, the condition close to the singularity point HH$_{1:4}$ leads to an extremely complicated global dynamics scenario. It is noteworthy that two neutral saddle curves NS$_{1,2}$ and three Neimark–Sacker branches TR$_{1,2,3}$ are detected, one NS$_1$ connects TR$_1$ and TR$_3$ and the other NS$_2$ connects TR$_2$ and TR$_3$, finally return to HH$_{1:4}$ after four turns. The cyclic fold curves LPC$^1_{1,2}$ and LPC$^2_{1,2,3}$ have an analogous structure in two cases compared with the Hopf–Hopf bifurcation near 1:3 resonance.

Fig. 14

a Bifurcation diagram for $k_{22}= 1.01$ near the 1:4 resonant Hopf–Hopf bifurcation. b Expanded view close to the singularity point HH$_{1:4}$ for ($d^*_{11}$, $k^*_{11}$) = (2.260000, 0.310000). c Bifurcation diagram associated with the Neimark–Sacker bifurcation curve TR$_1$. d Bifurcation diagram related to the Neimark–Sacker bifurcation curve TR$_2$. e Bifurcation diagram with respect to the Neimark–Sacker bifurcation curve TR$_3$. f Schematic diagram in the vicinity of the curves LPC$^2_{1,2,3}$

The bifurcation structure of Fig. 14c is involved in the cyclic fold curves born at GH$_1$. The curve LPC$^1_1$ forms a cusp point C$^1_1$ with the curve LPC$^1_2$, the cusp point is detected at C$^1_1$: ($d_{11}$, $k_{11}$) = (2.253659, 0.3048403) with $c(0)= 0.1469519$. In particular, a 1:1 resonance point R$^a_1$ is encountered on both the curves LPC$^1_1$ and TR$_1$.

Starting from GH$_2$, the curve LPC$^2_1$ forms a cusp point C$^2_1$ with the second curve LPC$^2_2$, then LPC$^2_2$ ends in a cusp point C$^2_2$ along with the third curve LPC$^2_3$, which form a closed curve resembling a triangle shape, as depicted in the magnified view of Fig. 14f. These cusp points are detected at C$^2_1$: ($d_{11}$, $k_{11}$) = (1.934561, 0.1807090) with $c(0)= 0.09944319$, and C$^2_2$: ($d_{11}$, $k_{11}$) = (1.945775, 0.1843113) with $c(0)= 0.09944319$.

The substantial difference between the cases near 1:3 and 1:4 resonance lies in the cyclic fold curves LPC$^3_{1,2}$ in Fig. 14d, which contain a couple of cusp points, these cusp points are detected at C$^3_{1}$: ($d_{11}$, $k_{11}$) = (2.237032, 0.3015403) with $c(0)=-56.60203$, and C$^3_{2}$: ($d_{11}$, $k_{11}$) = (2.560117, 0.4154234) with $c(0) = 0.6525401$. Moreover, in addition to a couple of 1:1 resonance points R$^3_1$ on LPC$^3_2$, the upper part of the branch TR$_3$ intersects LPC$^3_1$ at LPNS$^3_1$, and the lower part of the branch TR$_3$ intersects LPC$^3_2$ at LPNS$^3_2$ (see Fig. 14c).

On the branch TR$_1$ (Fig. 14c), two 1:3 resonance points R$^a_3$ and two 1:4 resonance points R$^a_4$ are observed here. The Chenciner bifurcation point near LPC$^1_1$ is detected at CH$^a$: ($d_{11}$, $k_{11}$) = (2.248896, 0.3035769) with ${\textit{Re}}(e)=131.4880$. A couple of Fold-Neimark–Sacker points LPNS$^a_{1,2}$ emerge at the ends of this branch. Moreover, a 1:1 resonance point R$^a_1$ is encountered on both the curves TR$_1$ and LPC$^1_1$.

On the branch TR$_2$ (Fig. 14d), there also exist a couple of Fold-Neimark–Sacker points LPNS$^b_{1,2}$, one of which LPNS$^b_1$ is near to HH$_{1:4}$, and the other LPNS$^b_2$ is close to R$^b_1$ . Four strong resonances such as a 1:1, two 1:3 and a 1:4 resonance points appear, which are denoted as R$^b_1$, R$^b_3$ and R$^b_4$, respectively. In addition, this branch ends with R$^b_1$.

On the branch TR$_3$ (Fig. 14e), the difference from TR$_{1,2}$ is that it forms a closed loop. The most notable is that a couple of Chenciner bifurcation points CH$^c_{1,2}$ emerge here, one CH$^c_{1}$ is close to LPC$^2_1$, and the other CH$^c_{2}$ is between R$^c_1$ and R$^c_4$. In the left half of CH$^c_1$, a 1:1 resonance point R$^c_1$ divides this curve into TR$_3$ and NS$_1$. In the left half of CH$^c_2$, there exist three 1:1 resonance points R$^c_1$ and a Fold-Neimark–Sacker point LPNS$^c$, among them, LPNS$^c$ divides this curve into TR$_3$ and NS$_2$ (see Fig. 14f). Moreover, there are two 1:3 and two 1:4 resonance points, denoted as R$^c_3$ and R$^c_4$, respectively. In the right half of CH$^c_2$, the branch produces a couple of 1:3 resonance points R$^c_3$ and a 1:4 resonance point R$^c_4$. Furthermore, the left part of CH$^c_{1,2}$ with positive index c(0) are the subcritical Neimark–Sacker bifurcations, which shows the presence of unstable torus, whereas the part between CH$^c_{1,2}$ with negative index c(0) is the supercritical Neimark–Sacker bifurcation, which gives birth to stable torus.

Fig. 15

a Cyclic bifurcation structure for $d_{11} = 2.1$ and $k_{22} = 1.01$ on 2D plane. b Cyclic bifurcation structure in 3D space with respect to the labels in a

In Fig. 15, more complex cyclic bifurcation behaviors occur when the same $d_{11}$ is fixed. The negative index ${\textit{FLC}}= -0.007540120$ indicates that the Hopf bifurcation point H$_1$ develops a family of stable limit cycles, then a cyclic neutral saddle NS$_1$ arises at $k_{11} = 0.2607852$. A cyclic limit point LPC$^1_2$ is detected as $k_{11}$ increases, the stability of the limit cycles remains unchanged due to the index $c(0) = -14.07494$. Two cyclic Neimark–Sacker bifurcation points are detected at TR$^{+}_3$: $k_{11} = 0.3426828$ with $c(0) = 0.285738$, and TR$^{-}_3$: $k_{11} = 0.2287775$ with $c(0) = 0.0002770011$, which indicate that the limit cycles born at TR$^{\pm }_3$ are both unstable, thus two unstable torus can be observed. So far the limit cycles have become distorted with complex resonance. The stability of the limit cycles restores via LPC$^2_1$ with $c(0) =-0.09781862$, then a cyclic neutral saddle NS$_2$ emerges at $k_{11} = 0.2219031$. Finally, the limit cycles begin a recurrence after reaching the point H$_2$ with ${\textit{FLC}} = -0.05429647$.

A more complex loop between two Hopf bifurcation points H$_{1,2}$ can be shown as: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$^{+}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{-}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{-}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{+}_3$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$. Within the region of LPC$^1_2$ and TR$^+_3$, the stable limit cycles arisen from the wheelset coexist. Within the region of TR$^+_3$ and TR$^-_3$, the stable limit cycles arisen at H$_{1}$ and LPC$^2_1$ coexist with the unstable limit cycles born at TR$^+_3$, which indicates the presence of an unstable torus via TR$^+_3$. Within the region of TR$^-_3$ and LPC$^2_1$, the stable limit cycles arisen at LPC$^2_1$ coexist with the unstable limit cycles born at TR$^-_3$, which indicates the presence of another unstable torus via TR$^-_3$.

5 Conclusions

Due to the interaction of lateral and yaw motion of the simplified railway wheelset, the dynamics of the non-resonant and near-resonant Hopf–Hopf bifurcations are taken into account in this paper, which involves local and global dynamical scenarios, respectively. The parameter $k_{22}$ plays a crucial role in the transitions of distinct Hopf–Hopf bifurcations, and the result shows that the ratio of the oscillation frequencies $\omega _1$/$\omega _2$ at the Hopf–Hopf singularity point will reduce with the decrease in $k_{22}$ within a certain range.

At first, the local dynamics with respect to the truncated normal form of the non-resonant Hopf–Hopf bifurcation on this wheelset model has been presented, which belongs to the “difficult” case VI. Two Neimark–Sacker branches TR$_{1,2}$ without emerging strong resonance indicate that the running wheelset will not produce the maximum oscillation amplitude induced by the resonance point. The wheelset gives birth to an unstable 2D torus when undergoing TR$_1$, and a stable 2D torus is created at TR$_2$. In addition, the unstable 2D torus will lead to a stable 3D torus after suffering a heteroclinic bifurcation.

Secondly, the global dynamics of five near-resonant Hopf–Hopf bifurcations have been discussed. These results show that near-resonant Hopf–Hopf bifurcation scenario becomes more complicated as $k_{22}$ decreases. In particular, an extremely complex global bifurcation phenomenon occurs when $k_{22}$ is reduced to satisfy the case close to 1:4 resonance, which is the most remarkable condition that affects wheelset hunting motions and resonances, as follows:

• (1) Case I: near the 1:1 resonant Hopf–Hopf bifurcation. The intersection of two Hopf curves H$_{1,2}$ does not produce a closed loop, a neutral saddle curve NS between H$_{1,2}$ forms a closed curve starting and ending at the singularity point HH$_{1:1}$. Two generalized Hopf bifurcation points GH$_{1,2}$ are connected by the cyclic fold curve LPC, and the cyclic cusp point C emerging on LPC is near to GH$_1$.

• (2) Case II: near the 2:3 resonant Hopf–Hopf bifurcation. The curves LPC$_{1,2}$ born at GH$_{1,2}$ intersect at a cusp point C. Two Neimark–Sacker branches TR$_{1,2}$ born at HH$_{2:3}$ are connected by a neutral saddle curve NS, which give birth to a closed curve after two turns. A Chenciner bifurcation point CH$^b$ emerges on TR$_2$, and several strong resonance points are detected on TR$_{1,2}$.

• (3) Case III: near the 1:2 resonant Hopf–Hopf bifurcation. This case undergoes the similar bifurcation as near the 2:3 resonant condition, for example, the curves LPC$_{1,2}$ in both cases intersect at a cusp point C, and a Chenciner bifurcation point CH$^b$ is detected on TR$_2$. The discrepancy is that the number of the strong resonance points on TR$_{1,2}$ grows.

• (4) Case IV: near the 1:3 resonant Hopf–Hopf bifurcation. Compared with the Hopf–Hopf bifurcation near 2:3 and 1:2 resonance, the similar scenario is that a neutral saddle curve NS joins two Neimark–Sacker branches TR$_{1,2}$ and forms a closed curve after two turns, the discrepancy is that the number and structure of cyclic fold curves have changed. The cyclic fold curves born at GH$_{1,2}$ no longer encounter at a cusp point, the curve LPC$^1_1$ born at GH$_1$ forms C$^1$ and then joins LPC$^1_2$. The curve LPC$^2_1$ born at GH$_2$ forms C$^2_1$ with LPC$^2_2$, then the curve LPC$^2_2$ ends at C$^2_2$ along with LPC$^2_3$. In particular, a couple of points CH$^{a,b}$ emerge on TR$_{1,2}$, respectively. More strong resonance points can be detected on TR$_{1,2}$.

• (5) Case V: near the 1:4 resonant Hopf–Hopf bifurcation. Compared with the previous conditions near resonance, it is the most complicated one that contains quite rich dynamics scenario. One neutral saddle curve NS$_1$ joins TR$_{2,3}$ and the other NS$_2$ joins TR$_{1,3}$, which form a closed curve after four turns. The curves LPC$^1_{1,2}$ and LPC$^2_{1,2,3}$ born at GH$_{1,2}$ are analogous in structure and quantity to the 1:3 resonant case. A particular structure is that the presence of LPC$^3_{1,2}$ and TR$_3$. A couple of Chenciner bifurcation points CH$^c_{1,2}$ divide TR$_3$ into three parts, the branch TR$_3$ between CH$^c_{1,2}$ with negative index c(0) shows the existence of stable torus, and the positive index c(0) of other parts of this branch indicates the presence of unstable torus. In addition, the significant increase in the number of the strong resonance points on TR$_{1,2,3}$ means that more complex resonance phenomena occur.

At last, under the near-resonant conditions, the parameter $d_{11}$ is fixed at 2.1 to observe the cyclic bifurcation structures when $k_{11}$ changes. These results show the coexistence of multiple limit cycles arisen from the wheelset. The loop of equilibria and limit cycles detected between two Hopf bifurcation points H$_{1,2}$ indicates that the wheelset will develop a cyclical motion in lateral and yaw direction, as follows:

• For case I: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^-$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^+$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^+$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$^-$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$, which indicates that the stable limit cycles emanated from the wheelset at H$_{1,2}$ coexist.

• For case II: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$, which indicates that the coexistence of stable limit cycles arisen from the wheelset within the region of LPC$_1$ and TR$_1$. Within the region of TR$_1$ and LPC$_2$, the stable limit cycles born at LPC$_2$ coexist with an unstable torus via TR$_1$.

• For case III: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_2$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$, which indicates that the cyclic bifurcation structure is similar to case II.

• For case IV: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$, which indicates that the stable limit cycles emanated from the wheelset coexist within the region of LPC$^1_2$ and TR$_1$. Within the region of TR$_1$ and LPC$^2_1$, the stable limit cycles born at LPC$^2_1$ coexist with an unstable torus via TR$_1$.

• For case V: H$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$TR$^{+}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{-}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^2_1$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{-}_3$ ${\mathop {\longrightarrow }\limits ^{\text {UC}}}$TR$^{+}_3$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$LPC$^1_2$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$NS$_1$ ${\mathop {\longrightarrow }\limits ^{\text {SC}}}$H$_1$, which indicates that the coexistence of stable limit cycles arisen from the wheelset within the region of LPC$^1_2$ and TR$^+_3$. Within the region of TR$^+_3$ and TR$^-_3$, the stable limit cycles born at H$_{1}$ and LPC$^2_1$ coexist with an unstable torus via TR$^+_3$. Within the region of TR$^-_3$ and LPC$^2_1$, the stable limit cycles born at LPC$^2_1$ coexist with another unstable torus via TR$^-_3$.

These obtained results indicate that the change in frequency ratio induced by the intersection of the lateral and yaw motion of the unbalanced wheelset will greatly affect the hunting motions and resonances of railway vehicles. Therefore, appropriately increasing the value of $k_{22}$ is helpful to maintain the vehicle stability. It is noted that what we present in this paper is only the global dynamics scenarios of the non-resonant and the near-resonance Hopf–Hopf bifurcations in a simplified wheelset model, while it will be an extremely complex task when it comes to discuss a bogie frame or even a carbody. These issues are for future research to investigate.