1 Introduction

Bifurcation control, chaos control and sliding mode control have been extensively examined in control theory over the past decades [1,2,3,4,5,6], among which bifurcation control has played a significant role in control theory. It is well stated that bifurcation properties of a system can be modified through various feedback control methods, the common approach is the use of linear or nonlinear state-feedback control [7,8,9]. The objective of bifurcation control may include to delay the arises of an inherent bifurcation, to change the parameter value at bifurcation point, to stabilize the bifurcation solution, to modify the bifurcation type, to alter the amplitude and frequency of some limit cycles produced by bifurcation, etc [1]. Compared with the bifurcation control, anti-control of bifurcation means that a certain type of bifurcation is generated or enhanced at a pre-specified location with expected properties by proper control when it is beneficial and useful. The goal of anti-control is aimed to introduce new bifurcations to the nominal branch of the system output [10]. In our work, we intend to discuss anti-control of Hopf bifurcation in the Shimizu–Morioka system. Hopf bifurcation is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues cross imaginary axis, small-amplitude limit cycle branches from the fixed point. Hopf bifurcation is a universal phenomenon and extensively exists in systems among biological, physical, engineering, mechanical and computer networks [11,12,13,14,15,16,17,18] and so on. The classical Shimizu–Morioka system is

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = y, \\ \dot{y} = x-by-xz,\\ \dot{z} = -az+x^{2}, \end{array}\right. \end{aligned}$$
(1)

where \((x,y,z)\in R^{3}\) are the states variables, a and b are the real parameters. The Shimizu–Morioka system is a simpler model instead of the Lorenz system, it was proposed by [19], this model shows a similar bifurcation as in the Lorenz model and exists a stable symmetric limit cycle under some parameter values, the symmetric cycle becomes unstable and bifurcates to two asymmetric limit cycles when the parameter varies, in addition, the Shimizu–Morioka system is more easy to handle and get the analytic form of limit cycles compared to the Lorenz system. For Shimizu–Morioka system, most of the researches mainly focus on the bifurcation analysis [20,21,22] and various of synchronization issues [23,24,25]. To the best of our knowledge, until now anti-control of Hopf bifurcation for Shimizu–Morioka system using an explicit criterion has not been found. Anti-control of bifurcation is motivated by observation in some applications such as mixing, low-energy navigation control, monitoring and fault diagnosis [10, 26]. Anti-control of Hopf bifurcation for Shimizu–Morioka system can be regarded as a method to design limit cycle or nonlinear oscillation into it. This new bifurcation solution may be served as a new and more appropriate operating condition or region which can not be obtained through conventional control means. Especially, it can be served as a warning signal of impending disaster or suspension in an electric system by generating a supercritical Hopf bifurcation near the bifurcation point. Besides, anti-control of bifurcation not only can be available for bifurcation itself but also provide an effective way for anti-control of chaos [10, 27]. In addition, the traditional conditions for the existence of Hopf bifurcation are stated in terms of the properties of eigenvalues. Even though numerical computation of eigenvalues is feasible in general. It is ideal to have a criterion stated in terms of the coefficients of the characteristic equation for theoretical analysis especially when it is difficult to find characteristic roots for high-order equation, this explicit criterion is put forward in [28], which is closely related to the Routh-Hurwitz criterion.

Anti-control of bifurcation makes with the aid of washout filter in general [26, 27, 29], the main benefit of using washout filters is that all the equilibrium points of the open-loop system are preserved; moreover, washout filters facilitate automatic track the targeted operating point [30]. By incorporating the feedback control and washout filters into the Shimizu–Morioka system, we obtain the closed-loop control system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=y+u_{1}, \\ \dot{y}=x-by-xz+u_{2},\\ \dot{z}=-az+x^{2},\\ \dot{w_{1}}=A_{1}x+A_{2}y+A_{3}z-d_{1}w_{1},\\ \dot{w_{2}}=A_{4}x+A_{5}y+A_{6}z-d_{2}w_{2}, \end{array}\right. \end{aligned}$$
(2)

in the expanded system we choose \(\mu =a\) as the bifurcation parameter, the nonlinear feedback controller \(u_{1}\) and \(u_{2}\) are designed as follows

$$\begin{aligned} \left\{ \begin{array}{lll} u_{1}=k_{11}s_{1}+k_{21}s_{1}^{2}+k_{31}s_{1}^{3},\\ u_{2}=k_{12}s_{2}+k_{22}s_{2}^{2}+k_{32}s_{2}^{3}, \end{array}\right. \end{aligned}$$
(3)

where \(s_{1}=A_{1}x+A_{2}y+A_{3}z-d_{1}w_{1}\) and \(s_{2}=A_{4}x+A_{5}y+A_{6}z-d_{2}w_{2}\). When \(s_{i}=0(i=1,2)\), the controller \(u_{i}=0,(i=1,2)\). This preserves the equilibrium structure of the original system (1) during a control process. The control gains \(k_{11}\) and \(k_{12}\) control the Hopf bifurcation parameter location, whereas the gains \(k_{21}\), \(k_{22}\), \(k_{31}\) and \(k_{32}\) have influenced on the stability of the Hopf bifurcation solutions and the amplitude and frequency of the created limit circle.

2 Anti-control of Hopf bifurcation in Shimizu–Morioka system

In this section, we first discuss the existence of Hopf bifurcation for system (2).

2.1 The linear control gains for the existence of Hopf bifurcation

The system (2) can be rewritten as

$$\begin{aligned} \dot{X}=\tilde{F}(X,\mu ,K_{1},K_{2},K_{3}), \end{aligned}$$
(4)

where

$$\begin{aligned}&X=(x,y,z,w_{1},w_{2})^{T},\\&\tilde{F}=\left( \begin{array}{lll} y+k_{11}s_{1}+k_{21}s_{1}^{2}+k_{31}s_{1}^{3}\\ x-by-xz+k_{12}s_{2}+k_{22}s_{2}^{2}+k_{32}s_{2}^{3}\\ -az+x^{2}\\ A_{1}x+A_{2}y+A_{3}z-d_{1}w_{1}\\ A_{4}x+A_{5}y+A_{6}z-d_{2}w_{2}\\ \end{array}\right) ,\\&K_{1}=\left[ \begin{matrix} k_{11} &{} 0 \\ 0 &{} k_{12} \\ \end{matrix}\right] ,\quad K_{2}=\left[ \begin{matrix} k_{21} &{} 0 \\ 0 &{} k_{22} \\ \end{matrix}\right] ,\quad \\&\quad K_{3}=\left[ \begin{matrix} k_{31} &{} 0 \\ 0 &{} k_{32}\\ \end{matrix}\right] . \end{aligned}$$

There are three equilibria in system (1), which are (0, 0, 0), \((\sqrt{a},0,1)\) and \((-\sqrt{a},0,1)\), respectively. In the following discussion, we only consider the local Hopf bifurcation nearby the equilibrium \((\sqrt{a},0,1)\), the analysis of other two equilibria is similar to \((\sqrt{a},0,1)\), so we omit it.

The Jacobian matrix of system (4) at equilibrium \(X^{*}=\big (\sqrt{a},0,1,(A_{1}\sqrt{a}+A_{3})/d_{1},(A_{4}\sqrt{a}+A_{6})/d_{2}\big )\) has the form

$$\begin{aligned} \begin{array}{l} J_{X}\tilde{F}=\left[ \begin{matrix} k_{11}A_{1} &{} k_{11}A_{2}+1 &{} k_{11}A_{3} &{} -k_{11}d_{1} &{} 0\\ k_{12}A_{4} &{} k_{12}A_{5}-b &{} k_{12}A_{6}-\sqrt{a} &{} 0 &{} -k_{12}d_{2}\\ 2\sqrt{a} &{} 0 &{} -a &{} 0 &{} 0\\ A_{1} &{} A_{2} &{} A_{3} &{} -d_{1} &{} 0\\ A_{4} &{} A_{5} &{} A_{6} &{} 0 &{} -d_{2}\\ \end{matrix}\right] , \end{array}\nonumber \\ \end{aligned}$$
(5)

the characteristic equation of the Jacobian matrix \(J_{X}\tilde{F}\) is written as

$$\begin{aligned} a_{5}\lambda ^{5}+a_{4}\lambda ^{4}+a_{3}\lambda ^{3}+a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}=0, \end{aligned}$$
(6)

where

$$\begin{aligned} a_{5}= & {} 1, a_{4}= a+b+d_{1}+d_{2}-k_{11}A_{1}-k_{12}A_{5},\\ a_{3}= & {} ab+ad_{1}+ad_{2}+bd_{1}+bd_{2}+d_{1}d_{2}\\&+\,k_{11}k_{12}A_{1}A_{5}-\,ak_{11}A_{1}-bk_{11}A_{1}-d_{2}k_{11}A_{1}\\&-\,2\sqrt{a}k_{11}A_{3}-\,k_{11}k_{12}A_{2}A_{4}-ak_{12}A_{5}-k_{12}A_{4}\\&-\,d_{1}k_{12}A_{5},\\ a_{2}= & {} 2a+ab(d_{1}+d_{2})+d_{1}d_{2}(a+b)+2ak_{11}A_{2} \\&+\,ak_{11}k_{12}A_{1}A_{5}+2\sqrt{a}k_{11}k_{12}A_{3}A_{5} -abk_{11}A_{1}\\&-\,ad_{2}k_{11}A_{1}-bd_{2}k_{11}A_{1} -2\sqrt{a}bk_{11}A_{3}-ak_{12}A_{4}\\&-\,2\sqrt{a}d_{2}k_{11}A_{3}-d_{1}k_{12}A_{4} -ad_{1}k_{12}A_{5}\\&-\,2\sqrt{a}k_{12}A_{6}-\,ak_{11}k_{12}A_{2}A_{4}-2\sqrt{a}k_{11}k_{12}A_{2}A_{6},\\ a_{1}= & {} 2a(d_{1}+d_{2})+abd_{1}d_{2}+2ad_{2}k_{11}A_{2}-abd_{2}k_{11}A_{1}\\&-\,2\sqrt{a}bd_{2}k_{11}A_{3} -\,ad_{1}k_{12}A_{4}-2\sqrt{a}d_{1}k_{12}A_{6},\\ a_{0}= & {} 2ad_{1}d_{2}. \end{aligned}$$

In order to create Hopf bifurcation of system (4), the eigenvalues of characteristic Eq. (6) should be satisfied with the conditions that there exists a pair of purely imaginary roots, the real parts of other eigenvalues are negative and guarantee the transversality when the bifurcation parameter passes through the critical value. However, it is not easy to obtain the root’s analytical expression for (6), so we employ an explicit criterion of Hopf bifurcation without using eigenvalues [28], the explicit criterion of Hopf bifurcation is formulated through the coefficients of characteristic equation.

Lemma 1

[28] There exists a Hopf bifurcation for system (4) if the following two conditions hold.

$$\begin{aligned}&(C1)D_{0}(\mu _{0})>0,D_{1}(\mu _{0})>0,\ldots ,D_{n-1}(\mu _{0})=0;\nonumber \\&(C2)dD_{n-1}(\mu _{0})/d\mu \ne 0. \end{aligned}$$
(7)

It is obvious that \(D_{n}(\mu _{0})=0\) since \(D_{n}(\mu )=a_{n}(\mu )D_{n-1}(\mu )\) and \(a_{n}(\mu )=1\).

For the characteristic Eq. (6), the two conditions in (7) can be expressed as follows:

$$\begin{aligned}&(C1):\nonumber \\&D_{0}(\mu _{0})=a_{0}(\mu _{0})>0,\nonumber \\&D_{1}(\mu _{0})=a_{1}(\mu _{0})>0,\nonumber \\&D_{2}(\mu _{0})=\det \left[ \begin{array}{ll} a_{1} &{} a_{0}\\ a_{3} &{} a_{2} \end{array}\right] \nonumber \\&\quad =a_{1}(\mu _{0})a_{2}(\mu _{0})-a_{0}(\mu _{0})a_{3}(\mu _{0})>0, \nonumber \\&D_{3}(\mu _{0})=\det \left[ \begin{array}{lll} a_{1} &{} a_{0} &{} 0\\ a_{3} &{} a_{2} &{} a_{1} \\ a_{5} &{} a_{4} &{} a_{3} \end{array}\right] \nonumber \\&\quad =a_{1}a_{2}a_{3}+a_{0}a_{1}a_{5}-a_{0}a_{3}^2 -a_{1}^2a_{4}>0,\ \mu =\mu _{0},\nonumber \\&D_{4}(\mu _{0})=\det \left[ \begin{array}{llll} a_{1} &{} a_{0} &{} 0 &{}0\\ a_{3} &{} a_{2} &{} a_{1} &{}a_{0}\\ a_{5} &{} a_{4} &{} a_{3} &{}a_{2}\\ 0 &{} 0 &{} a_{5} &{} a_{4}\\ \end{array}\right] \nonumber \\&\quad =2a_{0}a_{1}a_{4}a_{5}+a_{0}a_{2}a_{3}a_{5}+a_{1}a_{2}a_{3}a_{4}-a_{0}^2a_{5}^2\nonumber \\&\quad -\, a_{0}a_{4}a_{3}^2-a_{1}^2a_{4}^2-a_{2}^2a_{1}a_{5}=0,\ \mu =\mu _{0},\nonumber \\&(C2):\nonumber \\&dD_{4}(\mu _{0})/d\mu \!=\!(-2a_{0}a_{5}^2-a_{4}a_{3}^2+2a_{1}a_{4}a_{5}\nonumber \\&\quad +\, a_{2}a_{3}a_{5})a_{0}^{'}+ (-2a_{1}a_{4}^2+2a_{0}a_{4}a_{5}+a_{2}a_{3}a_{4}\nonumber \\&\quad -\, a_{2}^2a_{5})a_{1}^{'} +\,(-2a_{1}a_{2}a_{5}+a_{1}a_{3}a_{4}+a_{0}a_{3}a_{5})a_{2}^{'}\nonumber \\&\quad +\,(a_{1}a_{2}a_{4}+a_{0}a_{2}a_{5}-2a_{0}a_{3}a_{4})a_{3}^{'}\nonumber \\&\quad +\,(-2a_{1}^2a_{4}+2a_{0}a_{1}a_{5}+a_{1}a_{2}a_{3}-a_{0}a_{3}^2)a_{4}^{'}\nonumber \\&\quad \ne 0,\quad \mu =\mu _{0}, \end{aligned}$$
(8)

where \(a_{i}^{'}(i=0,\ldots ,4)\) denote the derivative of \(a_{i}(\mu ,K_{1})\) with respect to \(\mu \) at \(\mu =\mu _{0}\). From formula (8), the condition \(D_{4}(\mu _{0})=0\) ensures that a pair of conjugate eigenvalues of characteristic Eq. (6) are located on the imaginary axis when \(\mu =\mu _{0}\), the condition \(D_{i}(\mu _{0})>0,(i=0,\ldots ,3)\) ensures that the other eigenvalues have negative parts when \(\mu =\mu _{0}\), and the condition \(dD_{4}(\mu _{0})/d\mu \ne 0\) guarantees that the pair of complex conjugate eigenvalues crosses imaginary axis at nonzero rate when the bifurcation parameter \(\mu \) varies.

2.2 The nonlinear control gains for the stability of Hopf bifurcation

Next, we provide the stability condition of Hopf limit circle in this subsection.

Assume that \(\lambda _{1}(\mu _{0})=i\omega _{0}\), \(\lambda _{2}=\bar{\lambda }_{1}(\mu _{0})=-i\omega _{0}\) with \(\omega _{0}=Im(\lambda _{1}(\mu _{0}))\) is a pair of purely imaginary conjugate eigenvalues of characteristic Eq. (6), and we let \(P=(\text {Re} v_{1},\text {-Im} v_{1},r_{3},r_{4},r_{5})\), where \(v_{1}\) is the eigenvector of \(\lambda _{1}(\mu _{0})\) and \(r_{3},r_{4},r_{5}\) are any set of real 5-dim vectors which span the union of the (generalized)eigenspaces for \(\lambda _{3},\lambda _{4},\lambda _{5}\). Perform the change of variables \(X=X^{*}+PY\), \(Y=(y_{1},\ldots ,y_{5})^T\), then we can convert the system (4) into the form

$$\begin{aligned} \dot{Y}=F(Y,\mu )=(F^1,F^2,F^3,F^4,F^5)^T, \end{aligned}$$
(9)

with zero equilibrium and its Jacobian matrix has the real canonical form

$$\begin{aligned} \begin{array}{ll} J_{Y}F(0,\mu _{0}))=\left[ \begin{array}{ccc} 0 &{} -\omega _{0} &{} 0\\ \omega _{0} &{} 0 &{} 0 \\ 0 &{} 0 &{} D \end{array}\right] . \end{array} \end{aligned}$$
(10)

According to bifurcation theory [11, 12], the stability condition of Hopf limit circle is

$$\begin{aligned} \begin{array}{ll} \beta (\mu _{0},K_{2},K_{3})=2\text {Re}[c_{1}(0)], \end{array} \end{aligned}$$
(11)

where

$$\begin{aligned}&c_{1}(0)=\dfrac{i}{2\omega _{0}}\bigg [g_{20}g_{11}-2|g_{11}|^2-\dfrac{1}{3}|g_{02}|^2\bigg ]+\dfrac{g_{21}}{2},\nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned}&g_{11}(\mu _{0},K_{2})=\dfrac{1}{4}\bigg [\dfrac{\partial ^2 F^1}{\partial y_{1}^2}+\dfrac{\partial ^2 F^1}{\partial y_{2}^2}\nonumber \\&\quad +i\bigg (\dfrac{\partial ^2 F^2}{\partial y_{1}^2}+\dfrac{\partial ^2 F^2}{\partial y_{2}^2}\bigg ) \bigg ],\nonumber \\&g_{02}(\mu _{0},K_{2})=\dfrac{1}{4}\bigg [\dfrac{\partial ^2 F^1}{\partial y_{1}^2}-\dfrac{\partial ^2 F^1}{\partial y_{2}^2}-2\dfrac{\partial ^2 F^2}{\partial y_{1}\partial y_{2}}\nonumber \\&\quad +i\bigg (\dfrac{\partial ^2 F^2}{\partial y_{1}^2}-\dfrac{\partial ^2 F^2}{\partial y_{2}^2}+2\dfrac{\partial ^2 F^1}{\partial y_{1}\partial y_{2}}\bigg ) \bigg ], \nonumber \\&g_{20}(\mu _{0},K_{2})=\dfrac{1}{4}\bigg [\dfrac{\partial ^2 F^1}{\partial y_{1}^2}-\dfrac{\partial ^2 F^1}{\partial y_{2}^2}+2\dfrac{\partial ^2 F^2}{\partial y_{1}\partial y_{2}}\nonumber \\&\quad +i\bigg (\dfrac{\partial ^2 F^2}{\partial y_{1}^2}-\dfrac{\partial ^2 F^2}{\partial y_{2}^2}-2\dfrac{\partial ^2 F^1}{\partial y_{1}\partial y_{2}}\bigg ) \bigg ],\nonumber \\&g_{21}(\mu _{0},K_{2},K_{3})=G_{21}\nonumber \\&\quad +\sum \limits _{k=1}^{3}\bigg (2G_{110}^kw_{11}^k+G_{101}^kw_{20}^k\bigg ), \end{aligned}$$
(13)

where

$$\begin{aligned}&G_{21}(\mu _{0},K_{3})=\dfrac{1}{8}\bigg [\, \dfrac{\partial ^3 F^1}{\partial y_{1}^3}+\dfrac{\partial ^3 F^1}{\partial y_{1}\partial y_{2}^2}+\dfrac{\partial ^3 F^2}{\partial y_{1}^2\partial y_{2}}\\&\quad +\dfrac{\partial ^3 F^2}{\partial y_{2}^3} +i\bigg (\dfrac{\partial ^3 F^2}{\partial y_{1}^3}+\dfrac{\partial ^3 F^2}{\partial y_{1}\partial y_{2}^2}\\&\quad -\dfrac{\partial ^3 F^1}{\partial y_{1}^2\partial y_{2}}-\dfrac{\partial ^3 F^1}{\partial y_{2}^3}\bigg )\,\bigg ],\\&G_{110}^{k-2}(\mu _{0},K_{2})=\dfrac{1}{2}\bigg [\dfrac{\partial ^2 F^1}{\partial y_{1}\partial y_{k}}+\dfrac{\partial ^2 F^2}{\partial y_{2}\partial y_{k}}\\&\quad +i\bigg (\dfrac{\partial ^2 F^2}{\partial y_{1}\partial y_{k}}-\dfrac{\partial ^2 F^1}{\partial y_{2}\partial y_{k}}\bigg ) \bigg ], k=3,4,5,\\&G_{101}^{k-2}(\mu _{0},K_{2})=\dfrac{1}{2}\bigg [\dfrac{\partial ^2 F^1}{\partial y_{1}\partial y_{k}}-\dfrac{\partial ^2 F^2}{\partial y_{2}\partial y_{k}}\\&\quad +i\bigg (\dfrac{\partial ^2 F^1}{\partial y_{2}\partial y_{k}}+\dfrac{\partial ^2 F^2}{\partial y_{1}\partial y_{k}}\bigg ) \bigg ], k=3,4,5. \end{aligned}$$

In Eq. (13), \(w_{11}^k\) and \(w_{20}^k\) are the components of the 3-dim vectors \(w_{11}=(w_{11}^1,w_{11}^2,w_{11}^3)^T\) and \(w_{20}=(w_{20}^1,w_{20}^2,w_{20}^3)^T\), respectively. The vectors \(w_{11}\) and \(w_{20}\) are the solutions of the following linear equations, respectively,

$$\begin{aligned} Dw_{11}=-h_{11}, \quad (D-2i\omega _{0}I)w_{20}=-h_{20}, \end{aligned}$$
(14)

where D is given in Eq. (10) and I denotes the unit matrix, \(h_{11}=(h_{11}^1,h_{11}^2,h_{11}^3)^T\) and \(h_{20}=(h_{20}^1,h_{20}^2,h_{20}^3)^T\) are 3-dim vectors with the components of the form

$$\begin{aligned}&h_{11}^{k-2}(\mu _{0},K_{2})=\dfrac{1}{4}\bigg (\dfrac{\partial ^2 F^k}{\partial y_{1}^2}+\dfrac{\partial ^2 F^k}{\partial y_{2}^2}\bigg ) , k=3,4,5,\\&h_{20}^{k-2}(\mu _{0},K_{2})=\dfrac{1}{4}\bigg (\dfrac{\partial ^2 F^k}{\partial y_{1}^2}-\dfrac{\partial ^2 F^k}{\partial y_{2}^2}-2i\dfrac{\partial ^2 F^k}{\partial y_{1}\partial y_{2}}\bigg ),\\&\quad k=3,4,5. \end{aligned}$$

The sign of \(\beta (\mu _{0},K_{2},K_{3})\) of the condition (11) indicates the stability of the bifurcation periodic solutions for system (4). The created Hopf bifurcation is stable if \(\beta (\mu _{0},K_{2},K_{3})<0\) and unstable if \(\beta (\mu _{0},K_{2},K_{3})>0\). By the formulas (9)–(14), it is evident that the stability condition (11) could be available for the coefficients of the corresponding expression of system (9). Consequently, we can choose suitable \(K_{2}\), \(K_{3}\) to adjust the sign of \(\beta (\mu _{0},K_{2},K_{3})\) and then change the stability of the desired bifurcation periodic solutions.

2.3 The nonlinear control gains for amplitude and frequency of Hopf bifurcation

Once the Hopf limit cycle of system (4) is generated in virtue of the control gains in Sects. 2.1 and 2.2, the amplitude and frequency of the created limit cycle could be adjusted by the designed controller (3).

Lemma 2

[26] The amplitude of the created limit cycle after Hopf bifurcation in system (4) is given by the form

$$\begin{aligned}&\varepsilon (K_{2},K_{3})\nonumber \\&\quad =\!\bigg [\! \!-\!\dfrac{D_{4}^{'}(\mu _{0})}{2Re[c_{1}(0)]\prod _{p<q}^{1,\ldots ,5} \big (\lambda _{p}(\mu _{0})+\lambda _{q}(\mu _{0})\big )}\mu _{1}\!\bigg ] ^{\dfrac{1}{2}},\nonumber \\ \end{aligned}$$
(15)

where \(\mu _{1}=(\mu -\mu _{0})\), \(D_{4}^{'}(\mu _{0})\) denotes the derivative of \(D_{4}\) with respect to \(\mu \) at \(\mu =\mu _{0}\), \(D_{4}\) is the same in (8). \(c_{1}(0)\) is the expression in (12). \(\lambda _{p}(\mu _{0})\) and \(\lambda _{q}(\mu _{0})\) are two eigenvalues of characteristic Eq. (6), but \((\lambda _{p}+\lambda _{q})\) does not include the term of \((\lambda _{1}+\lambda _{2})\).

Based on the center manifold theory and normal form reduction, the approximate amplitude of Hopf limit cycles in nonlinear systems near the bifurcation point \(\mu _{0}\) has the form

$$\begin{aligned} \begin{array}{ll} \varepsilon =\sqrt{\dfrac{\mu -\mu _{0}}{v_{2}}}, \end{array} \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{array}{ll} v_{2}=-\dfrac{Re[c_{1}(0)]}{\alpha ^{'}(0)},\quad \alpha ^{'}(0) =\dfrac{d(Re(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}. \end{array}\nonumber \\ \end{aligned}$$
(17)

By using the formula of Orlando \( D_{n-1}=(-1)^{n(n-1)/2}a_{n}^{n-1}\prod \limits _{i<j}^{1,\ldots ,5}\big (\lambda _{i}+\lambda _{j}\big )\)[31], the determinant \(D_{4}(\mu )\) can be expressed in terms of the highest coefficient \(a_{5}\) and the roots of characteristic Eq. (6)

$$\begin{aligned} \begin{array}{ll} D_{4}=a_{5}^{4}\prod \limits _{i<j}^{1,\ldots ,5}\big (\lambda _{i}+\lambda _{j}\big ). \end{array} \end{aligned}$$
(18)

The formula (18) can be rewritten as

$$\begin{aligned} \begin{array}{ll} D_{4}=a_{5}^{4}(\lambda _{1}+\lambda _{2})\prod \limits _{p<q}^{1,\ldots ,5}\big (\lambda _{p}+\lambda _{q}\big ), \end{array} \end{aligned}$$
(19)

where \(\big (\lambda _{p}+\lambda _{q}\big )\) does not include the term of \(\big (\lambda _{1}+\lambda _{2}\big )\). By calculating the derivative on both sides of Eq. (19) with respect to \(\mu \) at \(\mu =\mu _{0}\), we obtain

$$\begin{aligned} D_{4}^{'}(\mu _{0})= & {} 2a_{5}^{4}\dfrac{d(Re(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}\prod \limits _{p<q}^{1,\ldots ,5}\big (\lambda _{p}+\lambda _{q}\big )\nonumber \\= & {} 2a_{5}^{4}\alpha ^{'}(0)\prod \limits _{p<q}^{1,\ldots ,5}\big (\lambda _{p}+\lambda _{q}\big ). \end{aligned}$$
(20)

From the expression (20) and \(a_{5}=1\), we have

$$\begin{aligned} \alpha ^{'}(0)=\dfrac{D_{4}^{'}(\mu _{0})}{2\prod \limits _{p<q}^{1,\ldots ,5}\big (\lambda _{p}+\lambda _{q}\big )}. \end{aligned}$$
(21)

Substituting the formula (21) into (16) and (17), the formula (15) is obvious.

Lemma 3

[26] The frequency of the created limit cycle after Hopf bifurcation in system (4) is given by the form

$$\begin{aligned} f(K_{2},K_{3})\!=\!\dfrac{\omega _{0}}{2\pi \bigg (1\!-\!\dfrac{Im(c_{1}(0)) \!+\!v_{2}Im(\psi _{1})}{\omega _{0}}\varepsilon ^2\bigg )},\nonumber \\ \end{aligned}$$
(22)

where \(\omega _{0}=Im(\lambda _{1}(\mu _{0}))\), \(v_{2}=\dfrac{-2Re[c_{1}(0)]\prod _{p<q}^{1,\ldots ,5}\big (\lambda _{p}+\lambda _{q}\big )}{D_{4}^{'}(\mu _{0})}\), \(\psi _{1}=V_{L1}(X^{*},\mu _{0},K_{1})\dfrac{\partial \big (J_{X}\tilde{F}(X^{*},\mu _{0},K_{1})\big )}{\partial \mu }V_{R1}(X^{*},\mu _{0},K_{1})\), \(V_{L1}(X^{*},\mu _{0},K_{1})\) and \(V_{R1}(X^{*},\mu _{0},K_{1})\) are the left and right eigenvectors of the Jacobian matrix \(J_{X}\tilde{F}(X^{*},\mu _{0},K_{1})\), \(\varepsilon \) is the amplitude of the limit cycle in Lemma 2.

We know that the approximate period in close vicinity to the Hopf bifurcation point is

$$\begin{aligned} T=\dfrac{2\pi }{\omega _{0}}\big (1+\tau _{2}\varepsilon ^2\big ), \end{aligned}$$
(23)

where

$$\begin{aligned}&\tau _{2}=-\!\dfrac{Im(c_{1}(0))\!+\!\mu _{2}\omega ^{'}(0)}{\omega _{0}}, \quad \mu _{2}\!=\!-\!\dfrac{Re[c_{1}(0)]}{\alpha ^{'}(0)},\nonumber \\&\omega ^{'}(0)=\dfrac{d(Im(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}. \end{aligned}$$
(24)

In the following, we show that \(\omega ^{'}(0)\) in (24) can be expressed in the form

$$\begin{aligned} \omega ^{'}(0)=\dfrac{d(Im(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}=Im(\psi _{1}). \end{aligned}$$
(25)

According to the definitions for the left and right eigenvectors of the matrix, we have

$$\begin{aligned}&V_{L1}(X^{*},\mu ,K_{1})J_{X}\tilde{F}(X^{*},\mu ,K_{1})\nonumber \\&\quad =\lambda _{1}(\mu )V_{L1}(X^{*},\mu ,K_{1}),\nonumber \\&J_{X}\tilde{F}(X^{*},\mu ,K_{1}) V_{R1}(X^{*},\mu ,K_{1})\nonumber \\&\quad =\lambda _{1}(\mu )V_{R1}(X^{*},\mu ,K_{1}), \end{aligned}$$
(26)

where the left and right eigenvectors satisfy the normal condition

$$\begin{aligned} V_{L1}(X^{*},\mu ,K_{1})V_{R1}(X^{*},\mu ,K_{1})=1. \end{aligned}$$
(27)

From Eqs. (26) and (27), it can be shown that

$$\begin{aligned}&V_{L1}(X^{*},\mu ,K_{1}) J_{x}\tilde{F}(X^{*},\mu ,K_{1})\nonumber \\&\quad V_{R1}(X^{*},\mu ,K_{1})\!=\!\lambda _{1}(\mu ). \end{aligned}$$
(28)

By differentiating (28) with respect to \(\mu \) at \(\mu =\mu _{0}\) and using the following formula

$$\begin{aligned}&\dfrac{\partial V_{L1}(x^{*},\mu _{0},K_{1})}{\partial \mu } J_{x}\tilde{F}(x^{*},\mu _{0},K_{1})V_{R1}(x^{*},\mu _{0},K_{1}) \\&\qquad +V_{L1}(x^{*},\mu _{0},K_{1})J_{x}\tilde{F}(x^{*},\mu _{0},K_{1})\dfrac{\partial V_{R1}(x^{*},\mu _{0},K_{1})}{\partial \mu }\\&\quad =\lambda _{1}(\mu _{0})\bigg [\dfrac{\partial V_{L1}(x^{*},\mu _{0},K_{1})}{\partial \mu } V_{R1}(x^{*},\mu _{0},K_{1})\\&\qquad +V_{L1}(x^{*},\mu _{0},K_{1})\dfrac{\partial V_{R1}(x^{*},\mu _{0},K_{1})}{\partial \mu }\bigg ]\\&\quad =0, \end{aligned}$$

we have

$$\begin{aligned} \psi _{1}= & {} V_{L1}(x^{*},\mu _{0},K_{1})\dfrac{\partial \big (J_{x}\tilde{F}(x^{*},\mu _{0},K_{1})\big )}{\partial \mu }\nonumber \\&V_{R1}(x^{*},\mu _{0},K_{1})=\dfrac{d(Re(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}\nonumber \\&+i\dfrac{d(Im(\lambda _{1}(\mu )))}{d\mu }\bigg |_{\mu =\mu _{0}}. \end{aligned}$$
(29)

From the expression (29), we easily obtain the expression (25). Then, we substitute the expressions (25) and (21) into (23) and (24), and use the relation of frequency and period \(f=\dfrac{1}{T}\), the expression (22) is obtained.

As we stated earlier, the eigenvalues \(\lambda _{i}(\mu _{0})(i=1,\ldots ,5)\) and the expression \(D^{'}_{4}(\mu _{0})\) in the formula (15) and (22) are only related with the linear gain \(K_{1}\) due to the expressions (6) and (8). Moreover, it is clear that the control of amplitude of limit cycle without calculating the derivative of eigenvalue \(\lambda _{1}(\mu )\), which is more convenient than the original classic form. Although the generating of limit cycle is only related to the linear gain \(K_{1}\) according to Lemma 1. Nevertheless, the approximate expressions of amplitude and frequency of the limit cycle can be influenced by the nonlinear control gain matrixes \(K_{2}\) and \(K_{3}\) because of the term \(c_{1}(0)\) according to Lemma 2 and 3. Generally, we pay attention to the stable limit cycle of Hopf bifurcation when \(\beta (\mu _{0},K_{2},K_{3})<0\) to adjust the amplitude and frequency of limit cycle. In other words, once the bifurcation parameter \(\mu \) is determined, the amplitude and frequency of limit cycle could be controlled by the nonlinear gains \(K_{2}\) and \(K_{3}\).

Fig. 1
figure 1

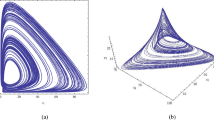
Bifurcation diagram of system (1) with respect to a and \(b=0.75\)

Full size image

3 Numerical analysis

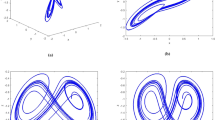
In this section, some numerical results of simulating system (4) are presented to verify the main conclusion of the second part. First, let \(b=0.75\), \(u_{1}=0\), \(u_{2}=0\), bifurcation parameter a varies at the interval [0, 1], the bifurcation diagram of system (1) without feedback control is given (see Fig. 1). From Fig. 1, we can see that the system undergoes the alternation of bifurcation and chaotic dynamical behaviors at first, and then it reaches a steady state. For instance, when \(a=0.18\), system (1) lies in the chaotic region, but at \(a=0.22\), system (1) falls back to stable state, If a is increased to 0.4, system (1) locates at chaotic region again, and when a increases further to 0.8, system (1) returns to the stable state, the corresponding phase diagrams (where we only provide y-z planes, the phase portraits for other planes are omitted) are given in Fig. 2a–d respectively.

Fig. 2
figure 2

Comparison of periodic and chaotic states for system (1) with respect to a. a a=0.18, b a=0.22, c a=0.4, d a=0.8

Full size image

In this paper, we aim to let the system produce Hopf limit cycle through washout filter feedback control. From Lemma 1, system (4) will produce Hopf limit cycle if the condition (7) is satisfied. We fix bifurcation parameter \(\mu =a=0.5\), system (1) without feedback control is under chaotic state (see Fig. 1). However, system (4) will produce Hopf limit cycle if we choose suitable parameters \(k_{11}\) and \(k_{12}\). By Fig. 3, the green area indicates that \(D_{0}>0,D_{1}>0,D_{2}>0,D_{3}>0,D_{4}>0\), the cyan area indicates that \(D_{0}>0,D_{1}>0,D_{2}>0,D_{3}>0,D_{4}<0\), when \(k_{11}\) and \(k_{12}\) locate in the two areas, the system will not generate Hopf limit cycle, because the condition (7) is not satisfied owing to \(D_{4}>0\) or \(D_{4}<0\). The two red lines show \(D_{4}(\mu _{0})=0\) when we choose certain \(k_{11}\) and \(k_{12}\), while the two black lines show \(dD_{4}(\mu _{0})/d\mu =0\) when we choose other \(k_{11}\) and \(k_{12}\), therefore, when \(k_{11}\) and \(k_{12}\) locate on the red line \(l_{1}\) except the intersection point \(P_{1}\) with the line \(dD_{4}(\mu _{0})/d\mu =0\) (\(P_{1}\) does not satisfy the transversality condition), system (4) will generate Hopf limit cycle.

Fig. 3
figure 3

The range of linear feedback control for generating Hopf limit cycle. \(A_{1}=1, A_{2}=-1, A_{3}=1, A_{4}=1, A_{5}=-1, A_{6}=1, d_{1}=2, d_{2}=2, a=0.5, b=0.85\)

Full size image

Next, we consider the stability of the limit cycle. Supposing that the nonlinear gain \(k_{21}\) (or \(k_{22}\)) in the matrix \( K_2 \) and the \(k_{31}\) (or \(k_{32}\)) in the matrix \(K_3\) are chosen as the control parameters. The stability condition derived by the center manifold theory and normal form reduction is as follows:

$$\begin{aligned} \beta (\mu _{0},k_{22}, k_{31})= & {} -0.00051476\!*\!k_{22}^2\!+\! 0.01153*k_{22}\nonumber \\&+\,0.076654*k_{31} \!+\! 0.048809, \end{aligned}$$
(30)

or

$$\begin{aligned} \beta (\mu _{0},k_{21}, k_{32})= & {} 0.038076*k_{21}^2+ 0.17928*k_{21} \nonumber \\&+\,0.0076547*k_{32} + 0.048809,\nonumber \\ \end{aligned}$$
(31)

by using the analytical expressions (30) and (31), and the stability region of limit cycle is shown in the Fig. 4 a, b respectively. The cyan area in Fig. 4a stands for the stable region of limit cycle where the inequality \(\beta (\mu _{0}, k_{22}, k_{31}) < 0\) holds and the cyan area in Fig. 4b stands for the stable region of limit cycle where the inequality \(\beta (\mu _{0}, k_{21}, k_{32}) < 0\) holds(for simplicity, we fix \(k_{21}=0, k_{32}=0\) in Fig. 4a, and \( k_{22}=0, k_{31}=0\) in Fig. 4b). As an example, we choose two points in stable region as the nonlinear control gains, one point is \((k_{22},k_{31},k_{21},k_{32})= (30,-20,0,0)\) which ensures \(\beta (\mu _{0}, k_{22}, k_{31}) < 0\) holds and the other is \((k_{22},k_{31},k_{21},k_{32})= (0,0,-2,5)\) which ensures \(\beta (\mu _{0}, k_{21}, k_{32}) < 0\) holds, thus if we choose the two points as the nonlinear feedback control which can ensure that the created limit cycles are stable (see Fig. 5a, b). Besides, we can also adjust the amplitude of limit cycle through nonlinear feedback control. In Fig. 6, we continue to fix linear feedback control \(k_{11}, k_{12}\) as same as Figs. 4 and 5, other three nonlinear feedback control fix as \(k_{22}=1, k_{21}=0, k_{32}=0\)(Fig. 6a) or \(k_{22}=0, k_{31}=0, k_{21}=-2\)(Fig. 6b), from Fig. 6a, b, we obtain that the amplitude of the limit cycle increases with the feedback control \(k_{31}\) or \(k_{32}\). It is obvious that \(k_{31}=-20,-2,-1,0.5,0\) (see Fig. 6a) all locate in the stable region in Fig. 4a and \(k_{32}=-20,0,15,18,19,20\) (see Fig. 6b) all locate in the stable region in Fig. 4b.

Fig. 4
figure 4

The range of nonlinear feedback control for generating stable Hopf limit cycle. \(a=4.5, b=8.85, A_{1}=1, A_{2}=-1, A_{3}=1, A_{4}= 1, A_{5}=-1, A_{6}=1, d_{1}=2.5, d_{2}=2.5, k_{11}=0.98420365, k_{12}=2; \mathbf a \,k_{21}=0, k_{32}=0; \mathbf b \,k_{22}=0, k_{31}=0\)

Full size image
Fig. 5
figure 5

Control parameter bifurcation diagram with respect to \(a=4.5, b=8.85, A_{1}=1, A_{2}=-1, A_{3}=1, A_{4}=1, A_{5}=-1, A_{6}=1, d_{1}=2.5, d_{2}=2.5, k_{11}=0.98420365, k_{12}=2; \mathbf a \,k_{22}=30, k_{31}=-20, k_{21}=0, k_{32}=0; \mathbf b \,k_{22}=0, k_{31}=0, k_{21}=-2, k_{32}=5\)

Full size image
Fig. 6
figure 6

The limit circles under different nonlinear gains. \(\mu =\mu _{0}-0.05\), \(a=4.5, b=8.85, A_{1}=1, A_{2}=-1, A_{3}=1, A_{4}=1, A_{5}=-1, A_{6}=1, d_{1}=2.5, d_{2}=2.5, k_{11}=0.98420365, k_{12}=2; \mathbf a \,k_{22}=1, k_{21}=0, k_{32}=0; \mathbf b \,k_{22}=0, k_{31}=0, k_{21}=-2\)

Full size image

From the numerical simulation, we can see that generating Hopf bifurcation only refers to the linear feedback control \(k_{11}\) and \(k_{12}\), if we fix other parameters of system (4), the linear control \(k_{11}\) and \(k_{12}\) can be determined to generate Hopf bifurcation (see Fig. 3). However, the stability of limit cycle as well as the amplitude will be changed by the nonlinear feedback control. We also can be easy to find the stable region for limit cycle about the nonlinear feedback control \(k_{21}, k_{22}, k_{31}, k_{32}\)(see Fig. 4). Similarly, the amplitude will be adjusted by the nonlinear feedback control, we fixed other three nonlinear control, varied one nonlinear feedback control, and it is seen that the amplitude becomes greater when the nonlinear feedback control increases (see Fig. 6).

4 Conclusion

In this paper, we have considered anti-control of Hopf bifurcation for Shimizu–Morioka system. The existence conditions of Hopf limit cycle needed to derive the roots of the characteristic equation for the work of Hopf bifurcation in the past, to verify whether there exists a pair of purely imaginary eigenvalues, and the transversality condition is satisfied. These two conditions are related to the eigenvalues and the derivative of one of conjugate eigenvalues. However, it is difficult to find characteristic roots for high-order equation. We have adopted the explicit criterion to describe the existence of Hopf bifurcation, that is, the explicit criterion is formulated through the coefficients of characteristic equation instead of calculating the eigenvalues directly. The two conditions are expressed by the form of Hurwitz determinant and the derivative of the coefficients of characteristic equation with respect to bifurcation parameter, and the coefficients of the characteristic equation are relatively easy to obtain. Thus, our approach has effectively avoided to compute the eigenvalues and eigenvalue’s derivative. Besides, the formulas of amplitude and frequency of limit cycle are also improved on account of the amplitude and frequency of limit cycle no longer need to calculate the derivative of the eigenvalue.