1 Introduction

Hopf bifurcation control and anti-control have become hotspots in nonlinear dynamics. The objective of Hopf bifurcation control is to delay the emergence of Hopf bifurcation by setting linear and nonlinear controllers, to expand the stable region of the system [1,2,3,4,5]. Anti-control of Hopf bifurcation is the inverse process of control. Setting the appropriate controller can make the Hopf bifurcation arise at the specified or expected position [6,7,8,9,10,11]. Cheng uses the Washout-filters method to achieve the anti-control of Hopf bifurcation for Chen's system by a delay feedback controller and analyzes the stability of the system [6]. By using explicit criteria, Yang carries out the anti-control of Hopf bifurcation for the three-dimensional Shimizu–Morioka system and analyzes the stability and bifurcation periodic solution of the system [7]. Chen sets up the appropriate controller for the system, which is to arise bifurcation at the expected position. Based on scour filter a dynamic anti-controller is proposed, in which the limit cycle of the system has oscillation behavior [8].

Liu studies the anti-control of the Hopf bifurcation for the four-dimensional Qi system with the linear and nonlinear controllers. By analyzing the characteristics of the Hopf bifurcation, the parameters of the linear and nonlinear controllers are determined [9]. Zhang analyzes the anti-control of the vibrating screen system by using a linear feedback controller. By adjusting the control parameters, the anti-control of Hopf–Hopf bifurcation can be realized, and the vibration mechanical efficiency can be improved [10]. Wen carries out the anti-control of Hopf bifurcation for centrifugal speed regulating system by using a feedback controller. The correctness of theoretical analysis is verified by simulation [11].

The Willamowski–Rössler system is one of the most common nonlinear reaction systems in chemistry. The system state variables represent the elements of chemical reactions. Each differential equation represents the rate of a chemical reaction. The system has obvious nonlinear characteristics. Bodale studies the chaos control of the Willamowski–Rössler system. Synchronous control is carried out by setting up a nonlinear controller for the system [12]. Aguda analyzes the synchronization characteristic and periodicity of the Willamowski–Rössler system and studies the oscillation characteristic of the system based on Shi'nikov theory [13]. Sun simulates the process of the Willamowski–Rössler system from period-doubling bifurcation to chaos state and then to period-doubling bifurcation again. The global exponential synchronization control of the system is realized by a controller [14]. Wu calculates the micromechanical system of the Willamowski–Rössler system and analyzes the dynamic characteristics of the noise of the system, as well as the interaction among the spatial degree of freedom, the size, and the internal fluctuation [15]. Chávez investigates the multi-step reaction mechanism of the Willamowski–Rössler system, which has oscillatory and chaotic dynamic characteristics. The condition of the appearance of bifurcation for the system is studied. The bifurcation which can lead to the arisen of simple or double chaotic characteristics—oscillatory attractor is verified [16]. Wang studies the chaos control of the Willamowski–Rössler system by using the continuous feedback control method and analyzes the influence of fluctuation on chaos control. The noise of the continuous feedback control method is instability [17]. Stucki analyzes the chaotic attractor and bifurcation of the Willamowski–Rössler system and studies the steady-state value and other nonlinear characteristics during oscillation [18]. At present, the researches mainly focus on the chaotic oscillation of the Willamowski–Rössler system and the analysis of chaos synchronization control of the system. The study of Hopf bifurcation is rare, especially the anti-control of Hopf bifurcation. By studying the anti-control of Hopf bifurcation for the Willamowski–Rössler system, the stable region of the system can be identified and expanded. Furthermore, stable chemical reaction rates can be obtained.

Based on the higher-dimensional Hopf bifurcation, the Hopf bifurcation characteristic of the Willamowski–Rössler system is analyzed in this paper. A state feedback control method is proposed to carry out the anti-control of Hopf bifurcation for the system. The Hopf bifurcation characteristics can arise at the specified position by changing the control parameters. The correctness of the theoretical analysis is verified by simulation.

The paper structure is arranged as follows: In Sect. 2, the differential equations of the Willamowski–Rössler system are introduced. In Sect. 3, the dynamical behavior of the system is investigated by Hopf bifurcation. In Sect. 4, a state feedback control method is proposed. In Sect. 5, with the state feedback control method, a hybrid controller is set up for the system to anti-control of Hopf bifurcation. Finally, Sect. 6 summarizes this paper.

2 Willamowski–Rössler system

The Willamowski–Rössler system is proposed in reference [12]. It has the form:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = ax_{{1}} - fx_{1}^{2} - bx_{1} x_{2} - dx_{1} x_{3} } \hfill \\ {\dot{x}_{2} = bx_{1} x_{2} - cx_{2} } \hfill \\ {\dot{x}_{3} = - dx_{1} x_{3} + ex_{3} - gx_{3}^{2} } \hfill \\ \end{array} } \right. $$
(1)

where \(x_{1} ,x_{2} ,x_{3}\) are state variables of the system, which represent the substances in a chemical reaction. \(a,b,c,d,e,f,g\) are positive real parameters, which represent the reaction speed. When the initial value is \(\left( {x_{1} ,x_{2} ,x_{3} } \right)^{T} = \left( {0.{21},0.01,0.12} \right)^{T}\) and the parameters are fixed as \( \left[ {a,b,c,d,ef,g} \right]^{T} = \left[ {30,1,10,1,16.5,0.25,0.5} \right]^{T}\), the system has a chaotic attractor, which is shown in Fig. 1.

Fig. 1
figure 1

When \(a = 30\), \(b = 1\), \(c = 10\), \(d = 1\), \(e = 16.5\), \(f = 0.25\), \(g = 0.5\), the chaotic attractor of the system (1)

Full size image

3 Hopf bifurcation

When \(d^{2} - fg \ne 0,b \ne 0,g \ne 0\),the system has six equilibrium points, given by:

\(X_{1} = (0,0,0)\),\(X_{2} = (\frac{a}{f},0,0)\),\(X_{3} = (0,0,\frac{e}{{\text{g}}})\),\(X_{4} = (\frac{c}{b},\frac{ab - cf}{{b^{2} }},0)\),\(X_{5} = (\frac{de - ag}{{d^{2} - fg}},0,\frac{ad - ef}{{d^{2} - fg}})\),

\(X_{6} = \left(\frac{c}{b},\frac{{cd^{2} - bde + abg - cfg}}{{b^{2} g}},\frac{be - cd}{{bg}}\right)\).

Each equilibrium point has its own characteristics, which are equilibrium points with complex dynamic characteristics. Therefore, by analyzing the dynamic characteristics of anyone non-zero equilibrium point, we can understand the dynamic characteristics of the system. Taking the non-zero equilibrium point \(X_{6}\) as the research object, the Hopf bifurcation characteristic of the system (1) is analyzed.

The Jacobi matrix of the system (1) at the equilibrium point \(X_{6}\) is:

$$ J\left( {X_{6} } \right) = \left[ {\begin{array}{*{20}c} { - \frac{fc}{{\text{b}}}} & { - c} & { - \frac{dc}{b}} \\ {\frac{{cd^{2} - bde + abg - cfg}}{bg}} & 0 & 0 \\ { - \frac{{bde - cd^{2} }}{bg}} & 0 & {\frac{cd - be}{b}} \\ \end{array} } \right] $$
(2)

The characteristic equation of the system (1) is:

$$ \lambda^{3} + p_{1} \lambda^{2} + p_{2} \lambda + p_{3} = 0 $$
(3)

where \(p_{1} = \frac{cd}{b} + \frac{cf}{b} + e\), \(p_{2} = ac - \frac{{c^{2} f}}{b} - \frac{{c^{2} df}}{{b^{2} }} + \frac{cef}{b} + \frac{{c^{2} d^{2} }}{bg} + \frac{{c^{2} d^{3} }}{{b^{2} g}} - \frac{cde}{g} - \frac{{cd^{2} e}}{bg}\),. \(p_{3} = ace - \frac{{ac^{2} d}}{b} + \frac{{c^{3} df}}{{b^{2} }} - \frac{{c^{2} ef}}{b} - \frac{{c^{3} d^{3} }}{{b^{2} g}} + \frac{{2c^{2} d^{2} e}}{bg} - \frac{{cde^{2} }}{g}\).

Based on the Routh–Hurwitz criterion, the conditions for the existence of Hopf bifurcation at the equilibrium point \(X_{6}\) are as follows:

$$ p_{1} > 0,p_{2} > 0,p_{1} p_{2} - p_{3} = 0 $$

Taking the real parameter \(e\) as the bifurcation parameter of the system (1), the critical value of Hopf bifurcation can be obtained as follows:

$$ e_{0} = \frac{{cQ_{1} + \sqrt {cfQ_{2} } }}{{2b\left( {d^{2} - fg} \right)}} $$

where

\(Q_{1} = 2d^{3} - d^{2} f + f^{2} g - df\left( {b + 2g} \right),\)

\(Q_{2} = \left( {d^{2} - fg} \right)\left[ {2bcf\left( {d - 2g} \right) + cf\left( {d^{2} - fg} \right)} \right.\left. { + 4ab^{2} g} \right] + b^{2} cd^{2} f.\)

When \(e = e_{0}\), the characteristic Eq. (2) of the system has a pair of pure imaginary roots \(\lambda_{1,2} = \pm i\omega_{0} = \pm i\sqrt {Q_{3} + Q_{4} e_{0} }\), and a negative real root \(\lambda_{3} = - (\frac{cd}{b} + \frac{cf}{b} + e_{0} )\).where \(Q_{3} = \frac{c}{{b^{2} g}}\left[ {ab^{2} g + c\left( {d^{2} - fg} \right)\left( {b + d} \right)} \right]\), \(Q_{4} = \frac{cf}{b} - \frac{cd}{g} - \frac{{cd^{2} }}{bg}\).

From the characteristic Eq. (3), we get

$$ \lambda^{\prime}(e) = - \frac{{\lambda^{2} + Q_{4} \lambda + Q_{5} - \frac{2cd}{g}e}}{{3\lambda^{2} + 2\left( {\frac{cd}{b} + \frac{cf}{b} + e} \right)\lambda + Q_{3} + Q_{4} e}} $$
(4)

where \(Q_{5} = ac - \frac{{c^{2} f}}{b} + \frac{{2c^{2} d^{2} }}{bg}\).

Substituting the value of pure imaginary root \(+ i\omega_{0}\) and \(e_{0}\) into the Eq. (4).

$$ \begin{aligned}{\text{Re}} \left( {\lambda^{\prime}(e)} \right) &= \frac{{2\left( {Q_{3} + Q_{4} } \right)}}{gT}\Bigg[ 2cde_{0} + gQ_{3} \\ &\quad + gQ_{4} (2e_{0} + \frac{cd + cf}{b}) - gQ_{5} \Bigg] \ne 0 \end{aligned}$$
(5)
$$ \begin{aligned}{\text{Im}} \left( {\lambda^{\prime}(e)} \right) & = - \frac{{2\sqrt {Q_{3} + e_{0} Q_{4} } }}{{{\text{g}}T}}\left[ {gQ_{4} \left( {Q_{3} + e_{0} Q_{4} } \right)} \right. \\ &\quad - \left. \left( {\frac{cd + cf}{b} + e_{0} } \right)\left( 2cde_{0} + gQ_{3} + e_{0} gQ_{4} \right.\right. \\ &\quad - \left.\left. - gQ_{5} \right) \right] \ne 0 \end{aligned}$$
(6)

where \(T = {4}\left( {Q_{3} + Q_{4} e_{0} } \right)\left[ {\left( {\frac{cd + cf}{b} + e_{0} } \right)^{2} + Q_{3} + Q_{4} e_{0} } \right]\).

The transversality is satisfied. According to the higher-dimensional Hopf bifurcation theory, when \(e = e_{0}\), the Hopf bifurcation of the system is appeared.

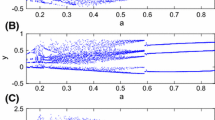
When \(a = 30\),\(b = 1\),\(c = 10\),\(d = 1\),\(f = 0.25\),\(g = 0.5\), the critical value of Hopf bifurcation is \(e_{0} = {14}{\text{.137}}\) and the Hopf bifurcation of the system is appeared. The bifurcation diagram of the system is shown in Fig. 2.

Fig. 2
figure 2

When \(a = 30\), \(b = 1\), \(c = 10\), \(d = 1\), \(f = 0.25\), \(g = 0.5\),the bifurcation diagram of the system (1)

Full size image

When \(e = 13.5\), the equilibrium point \(X_{6}\) is gradually stable, as shown in Fig. 3.

Fig. 3
figure 3

When \(a = 30\), \(b = 1\), \(c = 10\), \(d = 1\), \(f = 0.25\), \(g = 0.5\) and \(e = 13.5\), sequence diagram and phase diagram of the system (1)

Full size image

When \(e = 15\), the equilibrium point \(X_{6}\) is unstable and the system has a stable periodic solution, as shown in Fig. 4.

Fig. 4
figure 4

When \(a = 30\), \(b = 1\), \(c = 10\), \(d = 1\), \(f = 0.25\), \(g = 0.5\) and \(e = 15\), sequence diagram and phase diagram of the system (1)

Full size image

4 State feedback control method

According to the high-dimensional Hopf bifurcation theory, the n-dimensional dynamic system is defined as:

$$ \dot{x} = f\left( {x,\mu } \right) $$
(7)

where \(f:R^{n + 1} \to R^{n}\), \(x \in R^{n}\), \(\mu \in R\). \(x\) is the system state variable. \(\mu\) is the real parameter of the system. \(f\) is continuously differentiable for \(x\) and \(\mu\) in the domain.

Suppose the equilibrium point of the system (7) is \(X^{e} = \left( {X_{1}^{e} ,X_{2}^{e} , \cdots ,X_{i}^{e} , \cdots ,X_{n}^{e} } \right)\), \(i \ge 1\). The Jacobian matrix of the system at \(X^{e}\) is \(J\left( {X^{e} ,\mu } \right)\). If the conditions are satisfied [19]:

(1) Jacobian matrix \(J\left( {X^{e} ,\mu^{e} } \right)\) has a pair of pure imaginary root eigenvalues \(\lambda \left( {\mu^{e} } \right){ = } \pm i\omega\), other eigenvalues have negative real parts;

(2) When the eigenvalue \(\lambda \left( {\mu^{e} } \right)\) is nonzero, it crosses the imaginary axis.

$$ \left. {\frac{{{\text{d}}\left( {{\text{Re}} \lambda \left( \mu \right)} \right)}}{{{\text{d}}\mu }}} \right|_{{\mu = \mu^{e} }} \ne 0 $$

The Hopf bifurcation of the system appears at \(\mu^{e}\).

For the anti-control of Hopf bifurcation, the controller should be set up to the system. Defined

$$ \left\{ {\begin{array}{*{20}c} {u = u\left( {x,y} \right)} \\ {\dot{y} = h\left( {x,y} \right)} \\ \end{array} } \right. $$
(8)

where \(y \in R^{m}\)\(\left( {1 \le m \le n} \right)\) is the new state variable of the system. The controller \(u\left( {x,y} \right)\) and range \(h\left( {x,y} \right)\) are continuously differentiable for \(x\) and \(y\). The controller is a hybrid controller, which is composed of linear and nonlinear controllers. Namely

$$ \left\{ {\begin{array}{*{20}l} {u_{j} \left( {x_{j} ,y_{j} } \right) = k_{{1_{j} }} x_{j} + k_{{2j}} \left( {x_{j} - X_{i}^{e} } \right)^{3} - k_{{3j}} y_{j} } \hfill \\ {\dot{y} = u_{j} \left( {x_{j} ,y_{j} } \right)} \hfill \\ \end{array} } \right. $$
(9)

where \(X_{i}^{e}\) is the state variable at any equilibrium point of the system (7). The parameters of the controller are:\(k_{1j} = \left( {k_{11} ,k_{12} , \cdots ,k_{1m} } \right)\), \(k_{2j} = \left( {k_{21} ,k_{22} , \cdots ,k_{2m} } \right)\), \(k_{3j} = \left( {k_{31} ,k_{32} , \cdots ,k_{3m} } \right)\).

Then the controlled system is

$$ \left\{ {\begin{array}{*{20}l} {\dot{x} = f\left( {x,y} \right) + u\left( {x,y} \right)} \hfill \\ {\dot{y} = h\left( {x,y} \right)} \hfill \\ \end{array} } \right. $$
(10)

where \(u\left( {x,y} \right) = \left( {u_{1} \left( {x_{1} ,y_{1} } \right), \cdots u_{m} \left( {x_{m} ,y_{m} } \right),0, \cdots ,0} \right)_{n}^{T}\),\(h\left( {x,y} \right) = \left( {u_{1} \left( {x_{1} ,y_{1} } \right), \cdots u_{m} \left( {x_{m} ,y_{m} } \right)} \right)^{T} \).

According to Laplace transform, suppose \(z{}_{j} = k_{1j} x_{j} + k_{2j} \left( {x_{j} - X^{e} } \right)^{3}\) as a function of \(x_{j}\). It is substituted into the second Eq. (9). The results are as follows:

$$ u_{j} \left( s \right) = z_{j} \left( s \right) - k_{3j} y_{j} \left( s \right) $$
(11)
$$ z_{j} \left( s \right) = \left( {s + k_{3j} } \right)y_{j} \left( s \right) $$
(12)

Define

$$ G{}_{j}\left( s \right) = \frac{{u_{j} \left( s \right)}}{{z_{j} \left( s \right)}} = \frac{s}{{s + k_{3j} }} $$
(13)

Therefore, \(k_{3j}\) is a positive real number.

The controlled system is defined as:

$$ \dot{X} = F\left( {X,\mu } \right) $$
(14)

where \(\dot{X} = \left( {x,y} \right)^{T}\), \(F = \left( {f\left( {x,y} \right) + u\left( {x,y} \right),h\left( {x,y} \right)} \right)^{T}\).

Suppose \(J_{C} \left( {X,\mu } \right) = \frac{{\partial F\left( {X,\mu } \right)}}{\partial X}\) is the Jacobi matrix of the controlled system (14).

$$ J_{C} \left( {X,\mu } \right) = \left[ {\begin{array}{*{20}c} {J(x) + P_{1} (x)} & {P_{2} (x)} \\ {P_{3} (x)} & {P_{4} (x)} \\ \end{array} } \right] $$

where \(J(x)\) is the Jacobi matrix of the original system. Namely

\(J(x) = \frac{{\partial f\left( {x,\mu } \right)}}{\partial x}\), \(P_{1} (x) = \frac{{\partial u\left( {x,y} \right)}}{\partial x}\), \(P_{2} (x) = \frac{{\partial u\left( {x,y} \right)}}{\partial y}\), \(P_{3} (x) = \frac{{\partial h\left( {x,y} \right)}}{\partial x}\), \(P_{4} (x) = \frac{{\partial h\left( {x,y} \right)}}{\partial y}\).

We define as \(P_{1} (x) = \left[ {\begin{array}{*{20}c} M & {0_{(n - m) \times (n - m)} } \\ {0_{(n - m) \times (n - m)} } & {0_{(n - m) \times (n - m)} } \\ \end{array} } \right]\), \(P_{2} (x) = \left[ {\begin{array}{*{20}c} N \\ {0_{(n - m) \times (n - m)} } \\ \end{array} } \right]\), \(P_{3} (x) = \left[ {\begin{array}{*{20}c} M & {0_{(n - m) \times (n - m)} } \\ \end{array} } \right]\), \(P_{4} (x) = N\).where

$$ M = \left[ {\begin{array}{*{20}c} {k_{11} + 3k_{21} \left( {x_{1} - X_{1}^{e} } \right)^{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {k_{1m} + 3k_{2m} \left( {x_{m} - X_{m}^{e} } \right)^{2} } \\ \end{array} } \right],N = \left[ {\begin{array}{*{20}c} {k_{31} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {k{}_{3m}} \\ \end{array} } \right] $$

The characteristic equation of the Jacobi matrix \(J_{C} \left( {X,\mu } \right)\) of the controlled system (14) at the equilibrium point \(X^{e}\) is obtained as follows:

$$ Q\left( {\lambda ,\mu_{e} } \right) = q_{0} \left( {\mu_{e} } \right)\lambda^{n + m} + q_{1} \left( {\mu_{e} } \right)\lambda^{n + m - 1} + \cdots + q_{n + m} \left( {\mu_{e} } \right) $$
(15)

Suppose

$$ H_{n} = \left[ {\begin{array}{*{20}c} {q_{1} \left( {\mu _{e} } \right)} & {q_{0} \left( {\mu _{e} } \right)} & \cdots & 0 \\ {q_{3} \left( {\mu _{e} } \right)} & {q_{2} \left( {\mu _{e} } \right)} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {q_{{2(n + m) - 1}} \left( {\mu _{e} } \right)} & {q_{{2\left( {n + m} \right) - 2}} \left( {\mu _{e} } \right)} & \cdots & {q_{{n_{{ + m}} }} \left( {\mu _{e} } \right)} \\ \end{array} } \right] $$

When the following conditions are met:

$$ \left\{ {\begin{array}{*{20}l} {q_{n + m} \left( {\mu_{e} } \right) > 0} \hfill \\ {\Delta_{\omega } (\mu_{e} ) = \det \left[ {H_{i} \left( {\mu_{e} } \right)} \right] > 0,\omega = 1,2, \cdots ,n + m - 2} \hfill \\ {\left. {\frac{{d\left( {\Delta_{n + m - 1} \left( \mu \right)} \right)}}{d\mu }} \right|_{{\mu = \mu_{e} }} \ne 0} \hfill \\ \end{array} } \right. $$

The Hopf bifurcation of the controlled system (14) is occurred. According to

$$ \Delta_{n + m - 1} \left( {\mu_{e} } \right) = \det \left[ {H_{n + m - 1} \left( {\mu_{e} } \right)} \right] = 0 $$

the control parameters of the controlled system (14) are determined.

5 Anti-control of Hopf bifurcation

According to the state feedback control method, a controller \(u_{1} \left( {x_{1} ,y_{1} } \right)\) is set for the system (1). The controlled system is as follows:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = ax_{{1}} - fx_{1}^{2} - bx_{1} x_{2} - dx_{1} x_{3} } \hfill \\ {\dot{x}_{2} = bx_{1} x_{2} - cx_{2} { + }k_{{1{1}}} x_{{1}} + k_{{2{1}}} (x_{{1}} - X_{{{1}1}}^{e} )^{3} - k_{{3{1}}} y} \hfill \\ \begin{gathered} \dot{x}_{3} = - dx_{1} x_{3} + ex_{3} - gx_{3}^{2} \hfill \\ \dot{y} = k_{{1{1}}} x_{{1}} + k_{{2{1}}} (x_{1} - X_{{{1}1}}^{e} )^{3} - k_{{3{1}}} y \hfill \\ \end{gathered} \hfill \\ \end{array} } \right. $$
(16)

Equilibrium point \(X^{\prime}_{6} = \left( {X_{1} ,X_{2} ,X_{3} ,Y_{4} } \right)\) of the controlled system (16) is

$$ X_{6}{\prime} = \left( {\frac{c}{b},\frac{{cd^{2} - bde + abg - cfg}}{{b^{2} g}},\frac{be - cd}{{bg}},\frac{{b^{2} ck_{{1{1}}} + \left( {c - bX_{{{1}1}}^{e} } \right)^{3} k_{{2{1}}} }}{{b^{3} k_{{3{1}}} }}} \right) $$

According to the state feedback control method, each matrix is as follows:

$$ J\left( {X^{\prime}_{6} } \right) = \left[ {\begin{array}{*{20}l} { - \frac{fc}{{\text{b}}}} & { - c} & { - \frac{dc}{b}} \\ {\frac{{cd^{2} - bde + abg - cfg}}{bg}} & 0 & 0 \\ { - \frac{{bde - cd^{2} }}{bg}} & 0 & {\frac{cd - be}{b}} \\ \end{array} } \right],P_{1} (x) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ {k_{{1{1}}} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],P_{2} (x) = \left[ {\begin{array}{*{20}c} 0 \\ { - k_{{3{1}}} } \\ 0 \\ \end{array} } \right] $$

\(P_{3} (x) = \left[ {\begin{array}{*{20}c} M & 0 & 0 & 0 \\ \end{array} } \right]\),\(P_{4} (x) = N\).

The Jacobi matrix of the controlled system (16) at the equilibrium point \(X^{\prime}_{6}\) is:

$$ J_{c} \left( {X^{\prime}_{6} } \right) = \left[ {\begin{array}{*{20}l} { - \frac{fc}{{\text{b}}}} & { - c} & { - \frac{dc}{b}} & 0 \\ {\frac{{cd^{2} - bde + abg - cfg}}{bg} + k_{11} } & 0 & 0 & { - k_{{3{1}}} } \\ { - \frac{{bde - cd^{2} }}{bg}} & 0 & {\frac{cd - be}{b}} & 0 \\ {k_{11} } & 0 & 0 & { - k_{{3{1}}} } \\ \end{array} } \right] $$

The characteristic equation of the Jacobi matrix \(J_{c} \left( {X^{\prime}_{6} } \right)\) is written as

$$ Q\left( {\lambda ,\mu_{e} } \right) = q_{0} \left( {\mu_{e} } \right)\lambda^{4} + q_{1} \left( {\mu_{e} } \right)\lambda^{3} + q_{2} \left( {\mu_{e} } \right)\lambda^{2} + q{}_{3}\left( {\mu_{e} } \right)\lambda + q_{4} \left( {\mu_{e} } \right) $$
(17)

where \(q_{0} \left( {\mu_{e} } \right) = 1\),\(q_{1} \left( {\mu_{e} } \right) = k_{{3{1}}} { + }e + \frac{c}{b}\left( {f - d} \right)\),

$$ q_{2} \left( {\mu_{e} } \right) = \frac{1}{{b^{2} g}}\left( {bc^{2} d^{2} + c^{2} d^{3} - b^{2} cde - bcd^{2} e + } \right.ab^{2} cg - bc^{2} fg - c^{2} dfg + bcefg + b^{2} gck_{11} - bcgdk_{31} + b^{2} gek_{31} + \left. {bcfgk_{31} } \right) $$
$$ \begin{aligned} q_{3} \left( {\mu_{e} } \right) & = \frac{1}{{b^{2} g}}\left[ {ab^{2} gck_{31} - c\left( {c^{2} d^{3} - } \right.} \right.2bcd^{2} e \\&+ b^{2} de^{2} + abcdg - ab^{2} eg - c^{2} dfg \\& + bcgdk_{11} - b^{2} gek_{11} + b^{2} dek_{31} + bcgfk_{32} \\&+ cdgfk_{31} - begfk_{31} - bcd^{2} k_{31} - cd^{3} k_{31} + \left. {\left. {bd^{2} ek_{31} } \right)} \right], \\ \end{aligned} $$
$$ q_{4} \left( {\mu_{e} } \right) = \frac{{ck_{31} \left( {be - cd} \right)\left( {bde - cd^{2} - abg + cfg} \right)}}{{b^{2} g}}. $$

When \(a = 30,b = 1,c = 10,d = 1,f = 0.25,\) \(g = 0.5\), the relationship between the bifurcation parameter \(e\) and the control parameters \(k_{11} ,k_{31}\) is obtained.

$$ \begin{gathered} 350\left( {e - 23.75} \right)\left( {e - 14.1375} \right)\left( {e - 10} \right)\left( {e - } \right.\left. {0.505} \right) \hfill\\+ \left( {1.235 \times 10^{6} - 80187.5e - } \right.10859.4e^{2} + 656\left. {.25e^{3} } \right)k{}_{31} - 17.5 \hfill \\ \quad \times \left( {e + 29.401} \right)\left( {e^{2} - 36.115e + 368.792} \right)k_{31}^{2} \hfill\\- 17.5\left( {e - 10.034} \right)\left( {e + 10.82} \right)k_{31}^{3} + k_{11}^{2} \hfill\\ \left[ {250e + \left( {100e - 1000} \right)k_{31} - \left. {2500} \right]} \right. \hfill \\ \quad + \left[ { - 175\left( {e - 10} \right)} \right. \times \left( {e - } \right.\left. {15.66} \right)\left( {e + 3.876} \right) \hfill\\ + 10k_{31} \left( {e - 10.148} \right)\left( {e - } \right.\left. {29.25} \right)\left( {e - 5.6} \right) \hfill\\+ 10k_{31}^{2} \left( {e - 44.856} \right)\left. {\left( {e - 10.14} \right)} \right]k_{11} = 0 \hfill \\ \end{gathered} $$

By determining the value of the bifurcation parameter \(e\) which Hopf bifurcation occurs at the expected point, the values of the control parameters \(k_{11}\) and \(k_{31}\) can be determined. When the bifurcation parameter \(e < 14.137\), the Hopf bifurcation of the system appears ahead of time and the stable region decreases. When the bifurcation parameter \(e > 14.137\), the Hopf bifurcation of the system is delayed, which expands the stable region. The object of anti-control of the Hopf bifurcation for the Willamowski–Rössler system is realized. The relationship between the value range of the bifurcation parameter \(e\) and the control parameters \(k_{11}\) and \(k_{31}\) is shown in Fig. 5.

Fig. 5
figure 5

Range of bifurcation parameter \(e\)

Full size image

When the bifurcation parameter \(e = 20\) and the control parameter \(k_{31} = 0.5\), the other control parameter is \(k_{11} = 68.823\). The bifurcation diagram of the system is shown in Fig. 6.

Fig. 6
figure 6

When \(k_{11} = 68.823\),\(k_{31} = 0.5\), the bifurcation diagram of controlled system (16)

Full size image

When the bifurcation parameter \(e = 12.5\) and the control parameter \(k_{31} = 0.5\), the other control parameter is \(k_{{1{1}}} { = } - {5}{\text{.13}}\). The bifurcation diagram of the system is shown in Fig. 7.

Fig. 7
figure 7

When \(k_{11} = - 5.13\),\(k_{31} = 0.5\), the bifurcation diagram of controlled system (16)

Full size image

Although the control parameter \(k_{{2{1}}}\) can not change the bifurcation parameter \(e\), the amplitude of the limit cycle for the system can be altered by it, as shown in Fig. 8.

Fig. 8
figure 8

Amplitude of limit cycle of controlled system (16) is influenced by different \(k_{{2{1}}}\)

Full size image

From the above analysis, it shows that the control parameter \(k_{{2{1}}}\) has no effect on the value of the bifurcation parameter \(e\), but the control parameter \(k_{{2{1}}}\) has an effect on the amplitude of the bifurcation limit cycle. With increasing the value of \(k_{{2{1}}}\), the amplitude of the limit cycle gradually decreases, which the anti-control of the amplitude of the limit cycle can be realized.

6 Conclusion

In this paper, we have considered the anti-control of Hopf bifurcation for the Willamowski-Rössler system. According to the high dimensional Hopf bifurcation theory, the characteristics of Hopf bifurcation at the non-zero equilibrium point of the system are analyzed, and the critical value of Hopf bifurcation is studied. When \(a = 30,\)\(b = 1,c = 10,d = 1,f = 0.25\),\(g = 0.5\), the critical value of the Hopf bifurcation parameter \(e\) of the system is \(e_{0} = {14}{\text{.137}}\).Therefore, when \(e < e_{0}\), the system is gradually stable. When \(e > e_{0}\),the system is unstable.

A state feedback control method is proposed. Anti-control of Hopf bifurcation for the Willamowski- Rössler system is carried out by setting a hybrid controller, which is composed of linear and nonlinear controllers. The relationship between the control parameters and the bifurcation parameter is obtained. By specifying the position of Hopf bifurcation, the values of the control parameters are determined, and the purpose of anti-control is realized. Namely, the advance or delay of Hopf bifurcation is determined by the control parameters of the linear controllers, and the amplitude of the limit cycle is determined by the control parameter of the nonlinear controller. The correctness of the theoretical analysis is verified by numerical simulation.