1 Introduction

There are several successful industrial uses for nonlinear control systems. Researchers and designers in aviation control, robotics, process control, and biomedical engineering are investigating nonlinear control approaches [1,2,3,4]. Cai and Yuan [5] proposed a hybrid control strategy with state feedback and parameter control. The results dedicated that hybrid control could chang the critical value for Hopf bifurcation. Yang and Wei [6] also proposed a nonlinear control scheme, which allowed a much parameter regain and could be extended to degenerate Hopf bifurcation. A hybrid control strategy for controlling the Hopf bifurcation in a modified hyperchaotic Lü system was proposed by Tang [7]. They were able to delay the Hopf bifurcation by selecting an appropriate parameter control, thereby extending the system’s stability range.

As evidenced by the literature, more work on Hopf bifurcation control has been done [8,9,10,11,12,13,14,15]. Du et al. [16] studied Hopf bifurcation with center manifold theorem and normal form. A washout controller was designed to control bifurcation at the equilibrium \(E_{0}\) by adjusting the controller parameters. Kim and Chang [17] proposed a new chaotic system and examined its compound structures. This paper seeks to design a controller to further delay the bifurcation at the equilibrium point \(P_{0}\) and also to extend the stability range of the system [17].

2 Stability Analysis

Consider a governing system as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = a(y-x),\\ \dot{y} = xz +by, \\ \dot{z} = -x^{2}-cz,\\ \end{array}\right. } \end{aligned}$$
(1)

where x, y, z are state variables, a, b and c are system parameters.

System (1) has a chaotic attractor for \( a = 2, b = 1, c = 0.6 \) as shown in Fig. 1.

The system has three equilibrium points, i.e., \( P_{0}(0,0,0), P_{+}(\sqrt{bc}, \sqrt{bc}, -b) \), and \( P_{-}(-\sqrt{bc}, -\sqrt{bc}, -b)\) if \( bc>0 \). Obviously, the equilibrium point is stable when \(a, c>0\) and \(b<0\) and unstable when \( a<0\) or \(b>0\) or \(c<0\).

The Hopf bifurcation at the equilibrium point \(P_0\), on the other hand, cannot occur. Dias et al. [19, 20] looked into the existence of invariant set of topological circles to find a good set of parameters for the equilibrium \( P_{+} \).

3 Bifurcation method

This section describes how to compute the first and the second Lyapunov coefficients, as represented by \( l_{1} \) and \( l_{2} \), respectively.

Consider the following differential equation

$$\begin{aligned} \dot{x} = f(x,\xi ) \end{aligned}$$
(2)

where \(x\in R^{4}\) are the state variables, and \(\xi \in R^{n}\) are control parameters. It is also assumed that \( f\in C^{1}[R^{4}\times R^{n}]\). If system (2) has the equilibrium point \(x = x_{0}\) at \( \xi = \xi _{0}\), and \(x = x-x_{0}\), then

$$\begin{aligned} F(x) = f(x, \xi _{0}) \end{aligned}$$
(3)

F(x) is smooth and can be expressed in the Taylor series expansion as follows

$$\begin{aligned} F(x) = \frac{1}{2}B(x,x)+\frac{1}{6}C(x,x,x)+O(||x||^{4}), \end{aligned}$$
(4)

where \(A = f_{x}(0,\xi _{0})\), \(i = 1,2,3,4\).

$$\begin{aligned}&B_{i}(x,y) = \sum _{j,k=1}^{4}\frac{\partial ^{2}F_{i}(\xi )}{\partial \xi _{j} \partial \xi _{k}} \mid _{\xi = 0}, x_{j} y_{k}, \nonumber \\&C_{i}(x,y,z) = \sum _{j,k,l=1}^{4}\frac{\partial ^{3}F_{i}(\xi )}{\partial \xi _{j}\partial \xi _{k}\partial \xi _{l}} \mid _{\xi = 0}, x_{j}y_{k}y_{l}. \end{aligned}$$
(5)

Assume A has a pair of purely imaginary eigenvalues, denoting as \(\lambda _{2,3}=\pm i\omega _{0}, (\omega _{0}>0)\) at \((x_{0},\xi _{0})\), where these eigenvalues admit no other eigenvalues with \(Re\lambda = 0\), \(p,q\in \mathbb {C}^{n}\) are vectors satisfying

$$\begin{aligned} Aq = i\omega _{0}q, A^{T}p = -i\omega _{0}p, \langle p,q\rangle = \sum \limits _{i=1}^{n} \overline{p_{i}}p_{i} = 1. \end{aligned}$$
(6)

For any vector in the eigenspace \(y\in T^{c}\), one can describe it as \(y = \omega q +\overline{\omega q}\), where \(\omega = \langle p, y \rangle \in \mathbb {C}\). The center manifold associated with \(\lambda _{2,3} = \pm i\omega _{0}\) is parametrized by \(\omega \) and \(\overline{\omega }\), employing an immersion with the form \( x= H(\omega , \overline{\omega })\), where \( H:\mathbb {C}^{2} \longrightarrow R^{4}\) can be expanded as follows

$$\begin{aligned} H(\omega ,\overline{\omega })=\omega q +\overline{\omega q} + \sum _{2\le j+k\le 5}\frac{1}{j!k!}h_{jk} \omega ^{j} \omega ^{-k} + O(\mid \omega \mid ^{6}), \end{aligned}$$
(7)

where \( h_{jk} \in \mathbb {C}^{4}\) and \(h_{jk} = \overline{ h_{jk}}\). Substituting the derivative of \(H(\omega ,\overline{\omega })\) into (4) yields

$$\begin{aligned} H_{\omega } \omega ^{'} + H_{\overline{\omega }} \overline{\omega }^{'} = F(H(\omega ,\overline{\omega } )). \end{aligned}$$
(8)

The vector \(h_{jk}\) can be obtained according to (9). Thus, on the center manifold, we have

$$\begin{aligned} \omega ^{'} = i \omega _{0} \omega + \frac{1}{2}G_{32} \omega \mid \omega \mid ^{4} + O(\mid \omega \mid ^{6}), \end{aligned}$$
(9)

where \(G_{jk} \in \mathbb {C}^{2}\). The first Lyapunov coefficient

$$\begin{aligned} l_{1} = \frac{1}{2}Re G_{21}, \end{aligned}$$
(10)

where \(G_{21} = \langle p,H_{21} \rangle , H_{21} = C(q,q,\bar{q}) + B(\bar{q}, h_{20}) + 2B(q,h_{11}), h_{20} = (2i\omega _{0} I_{4})^{-1} B (q,q), h_{11} = -A^{-1} B(q,\bar{q}),\) and \( I_{4} \) are unit \(4\times 4\) matrices.

The second Lyapunov coefficient

$$\begin{aligned} l_{2} = \frac{1}{12}Re G_{32}, \end{aligned}$$
(11)

where

$$\begin{aligned} G_{32}&= \langle p,H_{32} \rangle ,\nonumber \\ H_{32}&= 6B(h_{11}, h_{21}) + B(\bar{h}_{20}, h_{30}) + 3B(\bar{h}_{21}, \bar{h}_{20})\nonumber \\&\quad + 3B(q,h_{22})+ 2B(\bar{q}, h_{31})+ 6C(q, h_{11},h_{11})\nonumber \\&\quad + 3C(q,\bar{h}_{20} ,h_{20})+ 3C(q,q,\bar{h}_{21})\nonumber \\&\quad + 6C(q,\bar{q},h_{21}) + 6C(\bar{q}, h_{20}, h_{11}) \nonumber \\&\quad + C(\bar{q}, \bar{q},h_{30})+ D(q,q,q,\bar{h}_{20}) \nonumber \\&\quad + 6D(q,q,\bar{q},h_{11}) + 3D(q,\bar{q},\bar{q},h_{20}) \nonumber \\&\quad + E(q,q,q, \bar{q}, \bar{q}) - 6G_{21}h_{21}. \end{aligned}$$
(12)

By solving the following \(n+1\)-dimensional equation

$$\begin{aligned} \begin{pmatrix} i\omega _{0}I_{4} &{} q \\ \bar{p} &{} 0 \end{pmatrix} \begin{pmatrix} h_{21} \\ s \end{pmatrix} = \begin{pmatrix} h_{21} \\ 0 \end{pmatrix} \end{aligned}$$
(13)

with the condition \(\langle p, h_{21} \rangle \),the vector \(h_{21}\) can be obtained.

$$\begin{aligned} h_{30}&= (3i\omega _{0} I_{4} - A)^{-1}[3B(q,h_{20} + C(q,q,q))],\nonumber \\ h_{31}&= (2i\omega _{0} I_{4} - A)^{-1}[3B(q,h_{21}) + B(\bar{q}, h_{30}) \nonumber \\&\quad + 3B(h_{20}, h_{11}) +3C(q,q,h_{11})\nonumber \\&\quad +3C(q,\bar{q},h_{20}) + D(q,q,q,\bar{q}) - 3G_{21} h_{20}],\nonumber \\ h_{22}&= -A^{-1}[D(q,q,q,\bar{q}) +4C(q,\bar{q},h_{11}) + 2B(q,\bar{h}_{21})\nonumber \\&\quad + 2B(\bar{q}, h_{21}) + B(\bar{h}, h_{20})]. \end{aligned}$$
(14)

4 Hopf bifurcation at \(P_{0}\)(0,0,0)

Now consider the stability of \(P_{0}(0,0,0)\) in the controlled system as illustrated below:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = a(y-x)\\ \dot{y} = xz + by+u \\ \dot{z} = -x^{2}-cz\\ \dot{v} = y-mv \\ \end{array}\right. }, \end{aligned}$$
(15)

where \( u = k_{1}(y-mv) +k_{2}(y-mv)^{2}\), \(k_{1}, k_{2}\) are the gains and m is the constant time coefficient which satisfies \(m>0\) and \( \mu (0)=0\).

The Jacobian matrix of the system (15) evaluated at \(P_{0}(0,0,0)\) is

$$\begin{aligned} P_{0} = \begin{pmatrix} -a &{}\quad a&{}\quad 0&{}\quad 0\\ 0&{}\quad b+k_{1}&{}\quad 0&{}\quad -mk_{1}\\ 0&{}\quad 0&{}\quad -c&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad -m\\ \end{pmatrix}. \end{aligned}$$
(16)

Characteristic polynomial evaluated at the equilibrium point \(P_{0}(0,0,0)\) is

$$\begin{aligned} P(\lambda )&= (\lambda +c)[\lambda ^{3} + (abm-k_{1})\lambda ^{2} \nonumber \\&\quad + (am-ak_{1} - abm) \lambda +a^{2}bm]. \end{aligned}$$
(17)

If \(c>0\), \(ab+m-k_{1}\), \(a^{2}bm<0\), and

$$\begin{aligned} b<b_{0} = \frac{m^{2}+k_{1}^{2}-2mk_{1} + am-ak_{1}}{a^{2}+2am-ak_{1}}, \end{aligned}$$
(18)

The equilibrium point \(P_{0}\) is stable. If \(b>b_{0}\), the equilibrium point \(P_{0}\) is unstable. Equation (18) will be used to study the Hopf bifurcation at \(P_{0}\) which occurs at system (15).

The multi-linear symmetric functions of the smooth function f can be written as

$$\begin{aligned} B(x,y)&= (0, -a(x_{1}y_{3} + x_{3}y_{1}),x_{1}y_{2} + x_{2}y_{1}, 0)^{T}\nonumber \\ C(x,y,z)&= (0,6k_{2}(x_{2},y_{2},z_{2}-m^{3} x_{4} y_{4} z_{4} m^{2} x_{2} y_{4} z_{4} \nonumber \\&\quad + m^{2} x_{4} y_{2} z_{4}+ m^{2} x_{4} y_{4} z_{2}\nonumber \\&\quad - mx_{2} y_{2} z_{4} -mx_{4} y_{2} z_{2}),0,0 )^{T}. \end{aligned}$$
(19)

The eigenvalues of matrix A are

$$\begin{aligned}&\lambda _{1,2} = \pm i\omega _{0} = \pm i\sqrt{am-ak_{1} - a^{2} b }, \nonumber \\&\quad \lambda _{3} = -c, \,\,\text {and}\,\, \lambda _{4} = -(ab+m-k_{1}). \end{aligned}$$
(20)

From (8), we have

$$\begin{aligned} q= & {} \begin{pmatrix} \frac{a(am+ \omega _{0}^{2}) + a\omega _{0}(a-m)i}{a^{2} + \omega _{0}^{2}}\\ m+\omega _{0}i\\ 0\\ 1 \end{pmatrix},\nonumber \\ p= & {} (\Bbbk _{1} +\Bbbk _{2}i, \Bbbk _{3} + \Bbbk _{4}i, 0, \Bbbk _{5}i)^{T}, \end{aligned}$$
(21)

where

$$\begin{aligned} \sigma _{1}= & {} (a^{2} +\omega _{0}^{2})(m^{2} -\omega _{0}^{2} +mk_{1}) \nonumber \\&- (2k_{1} m +\omega _{0}^{2})\nonumber \\&\times (am + \omega _{0}^{2}) -\omega _{0}^{2}(m-k_{1})(a-m),\nonumber \\ \sigma _{2}= & {} 2m\omega _{0}^{2}(a^{2} + \omega _{0}^{2}) - \omega _{0}(m-k_{1}) (am+\omega _{0}^{2}) \nonumber \\&- \omega _{0}(a-m)(2k_{1}m+\omega _{0}^{2}),\nonumber \\ \Bbbk _{1}= & {} \frac{(a^{2} +\omega _{0}^{2}) [\sigma _{2}\omega _{0} (m-k_{1}) -\sigma _{1} (2k_{1}m - \omega _{0}^{2})]}{a(\sigma _{1}^{2} + \sigma _{2}^{2})},\nonumber \\ \Bbbk _{2}= & {} \frac{(a^{2} +\omega _{0}^{2}) [-\sigma _{2}(2k_{1}m-\omega _{0}^{2}) - \sigma _{1} \omega _{0} (m-k_{1})]}{a(\sigma _{1}^{2} + \sigma _{2}^{2})},\nonumber \\ \Bbbk _{3}= & {} \frac{(a^{2} +\omega _{0}^{2}) (\sigma _{1}m + \sigma _{2}\omega _{0})}{a(\sigma _{1}^{2} + \sigma _{2}^{2})},\nonumber \\ \Bbbk _{4}= & {} \frac{(a^{2} +\omega _{0}^{2}) (\sigma _{1} \omega _{0} - \sigma _{2}m)}{a(\sigma _{1}^{2} + \sigma _{2}^{2})},\nonumber \\ \Bbbk _{5}= & {} \frac{mk_{1} (a^{2} +\omega _{0}^{2}) (\sigma _{1} + \sigma _{2})}{a(\sigma _{1}^{2} + \sigma _{2}^{2})},\nonumber \\ B(q,q)= & {} \begin{pmatrix} 0\\ \frac{2a[(a\omega _{0}^{2} -am^{2} 2m\omega _{0}^{2}) + (m^{2}\omega _{0} + 2am\omega _{0} - \omega _{0}^{2})i]}{a^{2} + \omega _{0}^{2}}\\ 0\\ 0 \end{pmatrix},\nonumber \\ B(q,\bar{q})= & {} \begin{pmatrix} 0\\ \frac{2a(m^{2} + \omega _{0}^{2})}{a^{2} + \omega _{0}^{2}}\\ 0\\ 0\\ \end{pmatrix},\nonumber \\ h_{11}= & {} \begin{pmatrix} \frac{-2a(m^{2} + \omega _{0}^{2})}{b(a^{2} + \omega _{0}^{2})}\\ \frac{-2a(m^{2} + \omega _{0}^{2})}{b(a^{2} + \omega _{0}^{2})}\\ 0\\ \frac{-2a(m^{2} + \omega _{0}^{2})}{bm(a^{2} + \omega _{0}^{2})} \end{pmatrix},\nonumber \\ h_{20}= & {} (2i\omega _{0} I_{3} - A)^{-1}B(q,q) = (\hbar _{1},\hbar _{2},0,\hbar _{3})^{T},\nonumber \\ \sigma _{3}= & {} (ci - 2\omega _{0}) (2am\omega _{0} - 8\omega _{0}^{2}-2ak_{1}\omega _{0} \nonumber \\&- 4k_{1}\omega _{0}^{2}i -2a^{2}b\omega _{0}\nonumber \\&+4m\omega _{0}^{2}i+4am\omega _{0}^{2}i + a^{2}bmi),\nonumber \\ \sigma _{4}= & {} a(-2a\omega _{0} + mi)(8\omega _{0}^{3} - 4k_{1}\omega _{0}^{2}i \nonumber \\&+2ak_{1}\omega _{0} - 2am\omega _{0} \nonumber \\&\quad + 2a^{2}b\omega _{0} + 4m\omega _{0}^{2}i+4am\omega _{0}^{2}i + a2bmi),\nonumber \\ \sigma _{5}= & {} a^{2}b^{2}m^{2} + 4a^{2}b^{2}\omega _{0}^{2} + 8a^{2}bk_{1}\omega _{0}^{2} - 8a^{2}bk_{1} m\omega _{0}^{2} \nonumber \\&+ 8a^{2}bm^{2}\omega _{0}^{2} + 32a^{2}b\omega _{0}^{2}\nonumber \\&+4a^{2}k_{1}^{2}\omega _{0}^{2} - 8a^{2}k_{1}m\omega _{0}^{2}+4a^{2}m^{2}\omega _{0}^{2} + 16a^{2}\omega _{0}^{2}\nonumber \\&+ 16k_{1}^{2}\omega _{0}^{4} - 32k_{1}m\omega _{0}^{4} +16m^{2}\omega _{0}^{4} +64\omega _{0}^{6},\nonumber \\ \hbar _{1}= & {} (2a\sigma _{4} [(a\omega _{0}^{2} -am^{2} -2m\omega _{0}^{2}) \nonumber \\&\times +(m_{2}\omega _{0} +2am\omega _{0} -\omega _{0}^{3})i]) (\sigma _{5}(a^{2} \omega _{0}^{2}))^{-1},\nonumber \\ \hbar _{2}= & {} (2(a+\omega _{0}(c+2\omega _{0}i)(m+2\omega _{0}i) \nonumber \\&\times [(a\omega _{0}^{2} -am^{2} -2m\omega _{0}^{2})\nonumber \\&+(m_{2}\omega _{0} +2am\omega _{0} -\omega _{0}^{3})i]) \times (\sigma _{3}(a^{2} \omega _{0}^{2}))^{-1},\nonumber \\ \hbar _{3}= & {} (2(c+2\omega _{0}i)(c+2\omega _{0}i) \nonumber \\&\times [(a\omega _{0}^{2} -am^{2} -2m\omega _{0}^{2}) +(m_{2}\omega _{0} \nonumber \\&+2am\omega _{0} -\omega _{0}^{3})i])\nonumber \\&\times (\sigma _{3}(a^{2} \omega _{0}^{2}))^{-1}. \end{aligned}$$
(22)

One also has

$$\begin{aligned} B(q,h_{11})= & {} (0,0,((-2a(m^{2}+\omega _{0}^{2}) \nonumber \\&\times [a\omega _{0}^{2} + m2a^{2} + m\omega _{0}^{2} \nonumber \\&+\omega _{0}(2a^{2} + \omega _{0}^{2} - am)i]) \nonumber \\&\times (b(a^{2} +\omega _{0}^{2})^{2})^{-1}),0)^{T},\nonumber \\ B(\bar{q},h_{20})= & {} (0,0,((a\hbar _{2}[(am+\omega _{0}^{2}) - \omega _{0}(a-m)i]\nonumber \\&+ \hbar _{1}(a_{2}+\omega _{0}^{2})(m-\omega _{0}i))\nonumber \\&\times (a^{2} + \omega _{0}^{2})^{-1}, 0)^{T},\nonumber \\ C(q,q,\bar{q})= & {} (0,\hbar _{4} + \hbar _{5}i,0,0)^{T},\nonumber \\ H_{21}= & {} (0,\hbar _{4 + \hbar _{5}i, \hbar _{6} + \hbar _{7}i,0})^{T},\nonumber \\ G_{21}= & {} (\hbar _{4} \Bbbk _{3} - \hbar _{5} \Bbbk _{3} + \hbar _{4} \Bbbk _{4})i, \end{aligned}$$
(23)

where

$$\begin{aligned} \hbar _{4}&= 6mk_{2}[(m+1)(\omega _{0}^{2} + 3m^{2}) - (3m^{2} + 2\omega _{0}^{2})],\nonumber \\ \hbar _{5}&= 6k_{2}\omega _{0}^{3},\nonumber \\ \hbar _{6}&= ab(am+\omega _{0}^{2}) + \hbar _{1}bm(a^{2} + \omega _{0}^{2}) \nonumber \\&\quad - 4a(m^{2} + \omega _{0}^{2}) [a(a^{2}m + \omega _{0}^{2}) + m(a^{2} + \omega _{0}^{2})],\nonumber \\ \hbar _{7}&= -ab\omega _{0}(a-m) - \hbar _{1}b\omega _{0}(a^{2} + \omega _{0}^{2}) - 4a\omega _{0}(m^{2} + \omega _{0}^{2})\nonumber \\&\quad \times [a(am + \omega _{0}^{2}) + m(a^{2} + \omega _{0}^{2})]. \end{aligned}$$
(24)

It is now only necessary to confirm the Hopf bifurcation’s transversal condition. Consider differential equations (1) with the parameter b as a dependent variable. At the crucial parameter \(b=b_{0}\), the real part of the complex eigenvalues confirms

$$\begin{aligned} \xi ^{'}(b_{0}) = Re \Bigg \langle p,\frac{dA}{db}\mid _{b=b_{0},q} \Bigg \rangle \end{aligned}$$
(25)

The Hopf point’s transversal condition holds as \(\xi ^{'}(b_{0}) \ne 0\).

Theorem 1

For the differential equation (15), the first Lyapunov coefficient for the point \(P_{0}\) is as follows:

$$\begin{aligned} l_{1} = \frac{1}{2}(\hbar _{4}\Bbbk _{3} - \hbar _{5}\Bbbk _{4}) \end{aligned}$$
(26)

If \(l_{1}\) is greater than zero and the Hopf point transversal condition holds,then a transversal Hopf point at \(P_{0}\) exists in equation (15).

Letting \(m=0.5\), the controller is

$$\begin{aligned} u = k_{1}(y-mv) +k_{2}(y-mv)^{2}. \end{aligned}$$
(27)

If \(0<k_{1}<1\), a transversal Hopf point at \(P_{0}\) exists in equation (15) when \( a=2, c=4\). Furthermore, if \(k_{1}>0\), there exist a stable periodic orbit close to \(P_{0}\). The dynamical evolution as b increases is as follows:

  1. 1.

    When \(0.2< b <1.1\), the system is stable,

  2. 2.

    When \(1.1< b <1.4\), the system is chaotic with one periodic window in the chaotic band.

Now, if we fix \(a=2, b=1,\) and vary c, the dynamic route of the system is summarized as follows:

  1. 1.

    If \(3.5<c<20\), the system becomes stable,

  2. 2.

    If \(20<b<40\), Chaos exists foe this system with some periodic windows in the chaotic band,

  3. 3.

    If \(40<c<80\), a long period-doubling bifurcation window exists.

According to the analysis performed here, the Hopf bifurcation at \(P_{0}\) cannot occur when \(b\in [1.1,1.4]\). We devise a control law with which the system (15) exhibits a Hopf bifurcation when \(b=0.8215\), illustrated in Figs. 2, 3, 4.

Let \(a=2, c=0.6, k_{1}=0.3\) and \(k_{2} = 0.1\); then, the Hopf bifurcation value can be calculated as \(b_{0} = 0.8215\). As shown in Figs. 2 and 3, the equilibrium is stable when \(b=0.6132<b_{0}\) and unstable when \(b=0.9321>b_{0}\). A transversal Hopf point at \(P_{0}\) occurs when \(b_{0} = 0.8215\) as shown in Fig. 4. By computation, one can obtain \(l_{1} = -2.59570\). As a result, the stable periodic solution that bifurcates from \(P_{0}\) is supercritical.

Fig. 1
figure 1

Trajectory of the chaotic attractor in various projections

Full size image
Fig. 2
figure 2

Time history and phase trajectory of system (15) with \(a=2, b=0.6, c=4, m=0.5, k_{1}=0.3, k_{2}=0.1\)

Full size image
Fig. 3
figure 3

Time history and trajectory of system (15) with \(a=2, b=0.9132, c=4, m=0.5, k_{1}=0.3, k_{2}=0.1\)

Full size image
Fig. 4
figure 4

Time history and trajectory of system (15) with \(a=2, b=0.8215, c=4, m=0.5, k_{1}=0.3, k_{2}=0.1\)

Full size image

5 Hopf bifurcation at \(P_{+}\)

We investigate the stability of \(P_{+}\) in system (15) in this section . The Jacobian matrix at \(P_{+}\) is

$$\begin{aligned} P_{+} = \begin{pmatrix} -a &{}a&{}0&{}0\\ -b&{}b+k_{1}&{}\sqrt{bc}&{}-mk_{1}\\ -2\sqrt{bc}&{}0&{}-c&{}0\\ 0&{}1&{}0&{}-m\\ \end{pmatrix}. \end{aligned}$$
(28)

Characteristic polynomial of the matrix \(P_{+}\) is

$$\begin{aligned} p(\lambda ) = \lambda ^{4} +Q\lambda ^{3} +R\lambda ^{2} + S\lambda + T, \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{array}{lll} Q = a+m+c-k_{1},\\ \\ R = abc + mc-ck_{1} + am +ac -ak_{1},\\ \\ S = a^{2}bc - ack_{1} + mac + mabc +abc,\\ \\ T = 2a^{2}bcm. \end{array} \end{aligned}$$
(30)

If \(Q>0, R>0, S>0, T>0\) and

$$\begin{aligned} S(S-QR) + Q^{2}T = 0, \end{aligned}$$
(31)

system (15) has transversal Hopf points at \(P_{+}\).

Dias et al.[11], found out that the equilibrium point \(P_{+}\) is stable.

The controller in this section is designed as

$$\begin{aligned} u = k_{1}(y-0.5v) +k_{2}(y-0.5v)^{2}, \end{aligned}$$
(32)

to set off Hopf bifurcation at \(P_{+}\).

If system (15) experiences Hopf bifurcation at the equilibrium \(P_{+}\), then condition (34) is satisfied. The multi-linear symmetric functions corresponding to f are

$$\begin{aligned} B(x,y)= & {} (0,-x_{1}y_{3} - x_{3}y_{1}, x_{1}y_{2}+x_{2}y_{1},0)^{T},\nonumber \\ C(x,y,z)= & {} (0, 6k_{2}(x_{2}y_{2}z_{2} - m^{3}x_{4}y_{4}z_{4} \nonumber \\&+ m^{2}x_{2}y_{4}z_{4} + m^{2}x_{4}y_{2}z_{4}+ m^{2}x_{4}y_{4}z_{2}\nonumber \\&- mx_{2}y_{2}z_{4} - mx_{4}y_{2}z_{4}),0,0)^{T}. \end{aligned}$$
(33)

The eigenvalues of A are

$$\begin{aligned} \lambda _{1,2} = \pm 1.2346i, \lambda _{3}=-0.4201, \lambda _{4} = -1.2156 \end{aligned}$$
(34)
Fig. 5
figure 5

Time history and trajectory of system (1) with \(a=2, b=1, c=4\)

Full size image
Fig. 6
figure 6

Time history and trajectory of system (15) with \(a=2, b=1, c=4, m=0.5, k_{1}=0.3, k_{2}=0.1\)

Full size image
Fig. 7
figure 7

Bifurcation diagram of x in terms of parameter c (b) Lyapunov exponents spectrum

Full size image
Fig. 8
figure 8

Bifurcation diagram of x in terms of parameter b (b) Lyapunov exponents spectrum

Full size image

From (7), we have

$$\begin{aligned} q= & {} \begin{pmatrix} 0.5106-0.1734i\\ 0.3035+0.5671i\\ 0.9015+1.0013i 1 \end{pmatrix},\nonumber \\ p= & {} \begin{pmatrix} 0.0145-0.3015i\\ 0.18075+0.2301i\\ 0.167+0.3642i\\ 0.2601+0.0115i \end{pmatrix},\nonumber \\ B(q,q)= & {} \begin{pmatrix} 0\\ 8.7215+2.4112i\\ -0.2657-0.1502i \\ 0 \end{pmatrix},\nonumber \\ B(q,\bar{q})= & {} \begin{pmatrix} 0\\ 2.6356\\ -0.6265 \\ 0 \end{pmatrix},\nonumber \\ h_{11}= & {} \begin{pmatrix} 0.4556\\ 0.5667\\ 3.0854 \\ 2.8456 \end{pmatrix},\nonumber \\ h_{20}= & {} \begin{pmatrix} -0.0225+0.3675i\\ -0.8720+0.3056i\\ 0.1034+0.5983i \\ -0.0859+0.7146i \end{pmatrix},\nonumber \\ B(q,h_{11})= & {} \begin{pmatrix} 0\\ -0.3147+0.7594i\\ -0.3421+0.6921i \\ 0 \end{pmatrix},\nonumber \\ B(\bar{q},h_{20})= & {} \begin{pmatrix} 0\\ -0.1673+0.3117i\\ -0.6115+0.5954i \\ 0 \end{pmatrix},\nonumber \\ C(q,q,\bar{q})= & {} \begin{pmatrix} 0\\ 3.2i\\ 0 \\ 0 \end{pmatrix},\nonumber \\ H_{21}= & {} \begin{pmatrix} 0\\ 3.2+2.1157i\\ -0.7649+1.3954\\ 0 \end{pmatrix},\nonumber \\ G_{21}= & {} -3.9815+0.8516i. \end{aligned}$$
(35)

Considering equation (15) depended on the parameter c, at \(c=c_{0}\) verifies

$$\begin{aligned} \xi ^{'}(c_{0}) = Re \Bigg \langle p,\frac{dA}{db}\mid _{c=c_{0},q} \Bigg \rangle = 0.2875>0 \end{aligned}$$
(36)

Thus, the transversal condition holds.

Theorem 2

Considering equation (15), the first Lyapunov coefficient related to \(P_{+}\) is

$$\begin{aligned} l_{1} = -2.5957k_{2} - 0.259 \end{aligned}$$
(37)

If \(k_{2} \ne -0.259\),then, \(l_{1} \ne 0\) which proves that (15) has transversal Hopf points at \(P_{+}\) for \(a=2,b=1\) and \(c=0.6\). The \(k_{2}\) determines the sign of the first Lyapunov coefficient. The first Lyapunov coefficient vanishes when \(k_{2} = -0.259\).

Given that

$$\begin{aligned} a&=2, b=1, c=0.6134, m = 0.5121, k_{1} \nonumber \\&= 0.3423, k_{2} = -0.259 \end{aligned}$$
(38)

Consider system (15) for \((a,b,c,k_{1},k_{2})\), after tedious calculations, we have

$$\begin{aligned} C(q,q,\bar{q})= & {} \begin{pmatrix} 0\\ -0.2583+2.0014i\\ 0\\ 0 \end{pmatrix},\nonumber \\ H_{21}= & {} \begin{pmatrix} 0\\ -0.9645+2.8745i\\ -0.9476+3.0015i\\ 0 \end{pmatrix},\nonumber \\ G_{21}= & {} 2.1159i,\nonumber \\ h_{30}= & {} \begin{pmatrix} 1.0012+0.3753i\\ -0.7854+1.8975i\\ -0.1320+0.4596i\\ -0.4713+0.2005i \end{pmatrix},\nonumber \\ h_{31}= & {} \begin{pmatrix} -3.7732+0.2593i\\ -0.96754-0.8513i\\ -2.0031+0.7642i\\ -0.7639-0.0167i \end{pmatrix},\nonumber \\ h_{21}= & {} \begin{pmatrix} -5.0034+0.5934i\\ -5.2632-6.0158i\\ -6.7456+1.6632i\\ -2.9763+1.9654i \end{pmatrix},\nonumber \\ h_{22}= & {} \begin{pmatrix} -3.0016+4.7421i\\ -1.8534+6.0139i\\ -7.3375-25.6614i\\ 6.2754-11.0220i \end{pmatrix},\nonumber \\ G_{32}= & {} -2.52391-8.4632i,\nonumber \\ l_{2}= & {} \frac{1}{12}ReG_{32} = -0.2103258333. \end{aligned}$$
(39)
Fig. 9
figure 9

Time history and trajectory of system (15) with \(a=2, b=1, c=6.1324, m=0.5, k_{1}=0.3, k_{2}=0.1\)

Full size image

Theorem 3

Consider \((a,b,c,m,k_{1},k_{2}) \in \Phi \) for equation (15), the second Lyapunov coefficient related to \(P_{+}\) is

$$\begin{aligned} l_{2} = -0.2103258333. \end{aligned}$$
(40)

As \(l_{2}\ne 0\), system (15) has a transversal Hopf point of codimension 2 at \(P_{+}\).

Letting \( m=0.5, k_{1} = 0.3, k_{2} = 0.1\), the controller is designed as

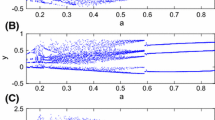
$$\begin{aligned} u = 0.3(y-0.5v) + 0.1(y-0.5v)^{2} \end{aligned}$$
(41)

In an uncontrolled system, \(P_{+}\) is locally stable. While comparing the controlled system (15) to the uncontrolled system (1), we can see that a transversal Hopf point exists in system (15) at \(P_{+}\) under the parameter region, shown in Figs. 5 and 6. We obtained distinct dynamical phenomena for system (1) and (15) if we fix parameters \(a=2\) and \(b=1\) and vary c in the interval [3, 4]. The bifurcation diagram in relation to parameter a and c, is shown in Figs. 7 and 8, respectively.

As we increase c, system (1) goes through the following dynamical paths:

There is a period-two orbit window when \(c\in [0,2.9] \). When \(c\in (0,3.9]\), the system becomes chaotic. When \(c=4\), a Hopf bifurcation for the uncontrolled system occurs at the equilibrium \(P +\). In Figure 9, we design a controller to make that system (15) undergoes a Hopf bifurcation when \(c=6.1324\). The analysis performed here shows that Hopf bifurcation is delayed. By calculation, \(l_{1} = -2.59570\) cab be obtained. As a result, the periodic solution that bifurcates from \(P_{+}\) is supercritical as well as stable.

6 Conclusions

The control of Hopf bifurcation for a new system is investigated in this paper. Through the use of appropriate controls, the controller is built with the desired location and properties. Numerical simulations demonstrate that supercritical Hopf bifurcation exists. The controller ensures that \(P_{0}\) undergoes a controllable Hopf bifurcation. Adjusting the controller parameters, the Hopf bifurcation at the equilibrium point \(P_{+}\) is delayed.