The Melnikov method for detecting chaotic dynamics in a planar hybrid piecewise-smooth system with a switching manifold

Abstract

In this paper, we extend the classical Melnikov method for smooth systems to a class of planar hybrid piecewise-smooth system subjected to a time-periodic perturbation. In this class, we suppose there exists a switching manifold with a more general form such that the plane is divided into two zones, and the dynamics in each zone is governed by a smooth system. Furthermore, we assume that the unperturbed system is a general planar piecewise-smooth system with non-zero trace and possesses a piecewise-smooth homoclinic orbit transversally crossing the switching manifold. We also define a reset map to describe the instantaneous impact rule on the switching manifold when a trajectory arrives at the switching manifold. Through a series of geometrical analysis and perturbation techniques, we obtain a Melnikov-type function to measure the separation of the unstable manifold and stable manifold under the effect of the time-periodic perturbations and the reset map. Finally, we use the presented Melnikov function to study global bifurcations and chaotic dynamics for a concrete planar piecewise-linear oscillator.

1 Introduction

Along with the development of nonlinear science, non-smooth dynamical systems are becoming more and more active in the world. Mechanical engineering [1, 2], power electronics [3], walking machines [4], control science [5] and other fields of natural science and social science often employ non-smooth functions to describe dynamical models. Therefore, developing mathematical methods and studying the dynamics for non-smooth dynamical systems is very important. At present, global bifurcations and chaotic dynamics for non-smooth dynamical systems are interesting but complicated topics.

It is well known that homoclinic bifurcations for smooth dynamical systems are a usual route for the occurrence of chaotic dynamics. The classical Melnikov method provides analytical tools for determining the persistence of homoclinic/heteroclinic connections for planar regular systems subjected to periodic perturbations [6,7,8,9]. More specifically, the existence of a simple zero of the corresponding Melnikov function implies the existence of a transversal homoclinic point of the periodic map of the perturbed non-autonomous smooth systems. Chaotic dynamics for these systems can be furthermore explained mathematically by the corresponding invariant Smale horseshoe set for the periodic map [7]. This is perhaps the most known route to chaos for non-autonomous smooth systems; however, there exists a special case with a different route given by Pascoletti and Zanolin [10].

How to understand the mechanism of global bifurcations and chaotic dynamics for discontinuous systems is a valuable and active topic. The basic idea is to extend the classical Melnikov method to discontinuous systems. Many scholars have made a lot of efforts and obtained some representative results about the Melnikov method of non-smooth systems in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] and chaotic dynamics in [26,27,28]. For example, Du and Zhang [11] have developed the Melnikov method for homoclinic bifurcation in nonlinear impact oscillators. Gao and Du [12] studied homoclinic bifurcation for an impact inverted pendulum under a quasiperiodically excitation. For the case of a homoclinic orbit which crosses transversally a switching manifold but without jumping on it, some scholars in [13,14,15,16,17,18,19,20] have successfully put forward the Melnikov method to study the persistence of the homoclinic orbit. Kunze [13], Shi [14] and Kukučka [15] have presented a Melnikov function but with difference items induced by the discontinuity of vector fields on a switching manifold for a two-dimensional periodic perturbed system. The switching manifold considered in [13, 14] is a special straight line and the Melnikov theory derived has good geometrical intuition; however, the difference items in the Melnikov function looks hard to calculate in [13,14,15].

Battelli and Fečkan have made great contribution to homoclinic bifurcations and chaotic dynamics for non-smooth systems. For example, Battelli and Fečkan in [16, 17] have discussed a class of high-dimensional non-smooth systems in which a piecewise-smooth homoclinic orbit transversally crossing a switching manifold is subjected to small non-autonomous perturbations. Battelli and Fečkan [18] also presented the Melnikov method for sliding homoclinic cases on a switching manifold for high-dimensional systems. Considering the perturbations with periodic, and the almost periodic cases (and even the case of weaker recurrence properties), they prove the existence of a transversal homoclinic point which immediately gives persistence of the homoclinic trajectory and which also furthermore proves the occurrence of chaos. The proofs are carried on in [16,17,18] and then they are surveyed in [19]. Since the systems considered is high-dimensional case, Battelli and Feckan have to deal with the adjoint variational system and with its unique bounded solution. However, when the two-dimensional case is deduced from the general one, the geometrical intuition is less transparent. In order to pursuit geometrical intuition and solve the problem of the difference items hard to calculate in [13,14,15] in the Melnikov function for non-smooth system, Li et al. [20] have considered a planar piecewise Hamiltonian system with a homoclinic orbit transversally crossing a switching manifold, then studied the persistence of this homoclinic orbit subjected to a periodic perturbation. They have tried to employ geometrical idea based on the classical Melnikov method in [7] and found the relationship of a trajectory between two sides of a switching manifold; then, they have presented a Melnikov function in complete integral forms. Although the result can already be found in [16, 19] for two-dimensional cases, the proof is different and simpler with great advantage of engineering application.

For the case of trajectories jumping on switching manifolds, Granados et al. [21] also extended the Melnikov methods for heteroclinic and subharmonic orbits in a piecewise-smooth system with a concrete impact rule on a discontinuous separation line; furthermore, they employed the Melnikov method to study a mechanical system of slender rocking block. Carmona et al. [22] studied the Melnikov theory of periodic orbits for a class of planar autonomous hybrid systems. Based on the idea presented in [21, 22], Li et al. [23] presented the Melnikov method for a class of planar piecewise-smooth systems with an impacting rule described by a reset map on a switching manifold. Furthermore, Li et al. [24] considered a piecewise Hamiltonian system with a heteroclinic orbit transversally crossing two switching manifolds and presented the Melnikov method with a simpler derivation and proof to study the persistence of this heteroclinic orbit under the effect of a periodic perturbation and reset maps.

In this paper, based on the work presented by Li et al. [20, 23], we want to study global bifurcations and chaotic dynamics for a planar hybrid discontinuous system. We suppose that there exists a switching manifold with a more general form such that the plane is divided into two zones, and the dynamics in each zone is governed by a smooth system. Furthermore, we assume that the unperturbed system is a general planar piecewise-smooth system with possibly non-zero trace, and possesses a piecewise-smooth homoclinic orbit transversally crossing the switching manifold. We also define a small reset map to describe the instantaneous impact rule when a trajectory arrives at the switching manifold. Through a series of geometrical analysis and perturbation techniques, we obtain a Melnikov-type function to measure the separation of the unstable manifold and stable manifold under the effect of the time-periodic perturbations and the reset map. Finally, we use the presented Melnikov function to study global bifurcations and chaotic dynamics for a concrete planar piecewise-linear oscillator.

In this paper, we will mainly focus on the analysis of the reset map and derivation of the Melnikov function by using a simpler procedure and geometrical idea. When the reset map is not considered, the Proposition 2 of this paper is indeed covered by Theorem 2.13 in [16], and then surveyed in [19]. However, the proof in this paper is different and simpler with good geometrical intuition. Another point needing some illustration is that we prove the existence of a transversal homoclinic point and conclude that implies the existence of chaotic dynamics but without giving a rigorous proof. It is indeed not rigorous because there is a case where the critical point might be on the switching manifold showing that the existence of a transversal homoclinic point may not imply the insurgence of a chaotic pattern in [25]. However, without the presence of the reset map, Battelli and Fečkan in [17] have presented a full fledged proof of the existence of chaos when a transversal homoclinic point is present for high-dimensional case. Hence, a similar fashion as in [17] can be carried out to conclude the existence of chaotic dynamics when the reset map considered here is small.

Here, we will also give some explanations of different points between our work with the one presented by Li et al. [20, 23]. Firstly, the unperturbed system considered here is a general piecewise-smooth system with a possibly non-zero trace, while the unperturbed system studied by Li et al. [20, 23] is a piecewise-defined Hamiltonian system. Secondly, a switching manifold with a general form and impacting rules are considered in this paper, while a particular separation line is defined as the switching manifold in Li et al. [23] and the orbits do not jump on the switching manifold in Li et al. [20]. Thirdly, more complicated perturbation techniques and geometric methods for discontinuous systems are extended here to derive the non-smooth Melnikov function. Furthermore, several lemmas and propositions are given to facilitate the calculation of the Melnikov function and help to understand different points between smooth and non-smooth systems.

This paper is organized as follows. In Sect. 2, the statement of the problem is described, the non-smooth Melnikov function for the planar hybrid piecewise-smooth systems is obtained. In Sect. 3, global bifurcations and chaotic dynamics for a concrete planar hybrid piecewise-linear oscillator are studied by the obtained Melnikov function. Numerical simulations are also shown to verify the theoretical analysis. Finally, the conclusions are given.

2 Statement of the problem

2.1 System description

We first define a scalar function $h{:}{\mathbb {R}}^{2}\rightarrow {\mathbb {R}},\,h\in {C}^{r}({\mathbb {R}}^{2},{\mathbb {R}}),\, r\ge 1$ such that the state-space ${\mathbb {R}}^{2}$ is split into two open, disjoint subsets $V_{-}$ and $V_{+}$ by a switching manifold $\Sigma$. The subsets $V_{-}$ and $V_{+}$ and the switching manifold $\Sigma$ can be formulated as

$$\begin{aligned} V_{-}= & {} \left\{ (x,y)\in {\mathbb {R}}^{2}\,\,|\,\,h(x,y)<0\right\} ,\nonumber \\ \Sigma= & {} \left\{ (x,y)\in {\mathbb {R}}^{2}\,\,|\,\,h(x,y)=0\right\} ,\nonumber \\ V_{+}= & {} \left\{ (x,y)\in {\mathbb {R}}^{2}\,\,|\,\,h(x,y)>0\right\} . \end{aligned}$$

(1)

The normal of the switching manifold $\Sigma$ is denoted by

$$\begin{aligned} \mathbf {n}=\mathbf {n}(x,y)=\mathbf {grad}(h(x,y)),\,\,\,\,\,(x,y)\in \Sigma , \end{aligned}$$

(2)

which is a row vector, and we also assume that the scalar function h is chosen such that $\mathbf {n}(x,y)\ne 0$ for $(x,y)\in \Sigma$.

We consider a general planar piecewise-smooth system as follows:

$$\begin{aligned} \left( {\begin{array}{ll}{\dot{x}}\\ {\dot{y}}\end{array}}\right) =\left\{ \begin{array}{ll}f_{-}(x,y)+\epsilon g_{-}(x,y,\,t),&{}(x,y)\in {V_{-}},\\ f_{+}(x,y)+\epsilon g_{+}(x,y,\,t), &{} (x,y)\in {V_{+}},\end{array}\right. \end{aligned}$$

(3)

where $(x,y)\in {\mathbb {R}}^{2}$ and $\epsilon \,(0<\epsilon \ll 1)$ is a small parameter. We suppose that the function $f_{\pm }:{\mathbb {R}}^{2}\rightarrow {\mathbb {R}}$ are $C^{r}$ with $r\ge 2$ for any $(x,y)\in {\mathbb {R}}^{2}$, and $g_{\pm }:{\mathbb {R}}^{2} \times {\mathbb {R}}\rightarrow {\mathbb {R}}^{2}$ are $C^{r}$ with $r\ge 2$ and ${\hat{T}}-$periodic in t.

In order to describe impacting rules of trajectories on the switching manifold $\Sigma$, let us consider a reset map for system (3) given as follows:

$$\begin{aligned}&{\tilde{\rho }}_{\epsilon }:\Sigma \rightarrow \Sigma \nonumber \\&(x, y)\mapsto {\tilde{\rho }}_{\epsilon }(x,y)=({\tilde{\rho }}_{1,\epsilon }(x,y),{\tilde{\rho }}_{2,\epsilon }(x,y)) \end{aligned}$$

(4)

satisfying ${\tilde{\rho }}_{0}(x,y)=(x,y)$ and $h({\tilde{\rho }}_{\epsilon }(x,y))=0$ for any $(x,y)\in \Sigma$, where $0<\epsilon \ll 1,\,$ ${\tilde{\rho }}_{i,\epsilon }\in {C}^{r}({\mathbb {R}}^{2})\,\,(i=1,2)$ with $r\ge 1$. We denote by ${{\tilde{\rho }}}_{\epsilon }^{-1}(x,y)=(\tilde{\eta }_{1,\epsilon }(x,y),\tilde{\eta }_{2,\epsilon }(x,y))$ the inverse mapping of ${\tilde{\rho }}_{\epsilon }(x,y)$ for any $(x,y)\in {\mathbb {R}}^{2}$, and $0<\epsilon \ll 1$.

In the aforementioned assumptions and definitions, the switching manifold $\Sigma$ divides the plane into two zones whose dynamics in each zone is governed by a smooth system. We hope that the reset map ${\tilde{\rho }}_{\epsilon }$ will be adopted instantaneously when a trajectory arrive at some point (x, y) on the switching manifold $\Sigma$ at $t=t^{*}$. That is to say, the point $(x,y)\in \Sigma$ in this trajectory will jump to the point ${\tilde{\rho }}_{\epsilon }(x,y)\in \Sigma$ instantaneously and then this trajectory will enter into another zone. Before the assumptions are presented, based on our expectation of geometrical structure, we first simply describe a solution of the system (3) and (4), we let $q^{-}(t; t_{0}, x_{0},y_{0},\epsilon )$ be the flow of system (3) restricted to $V_{-}$, and $t_{1}>t_{0}$ is the smallest value of t satisfying the condition

$$\begin{aligned} h(q^{-}(t_{1}; t_{0}, x_{0}, y_{0},\epsilon ))=0. \end{aligned}$$

(5)

Similarly, $q^{+}(t; t_{0}, x_{1}, y_{1},\epsilon )$ is the flow of system (3) restricted to $V_{+}$, and $t_{2}>t_{0}$ is the smallest value of t satisfying the condition

$$\begin{aligned} h(q^{+}(t_{2}; t_{0}, x_{1}, y_{1},\epsilon ))=0. \end{aligned}$$

(6)

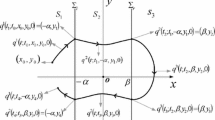
According to the position of $(x_{0},\,y_{0})$ in $V_{+}$ or $V_{-}$, we apply either $q^{-}(t;t_{0},x_{0},y_{0},\epsilon )$ or $(q^{+}(t; t_{0}, x_{1}, y_{1},\epsilon ))$ until the trajectory of system (3) reaches $\Sigma$, then we apply (4). In order to let readers easily understand what is a solution for a discontinuous system stated above, here we present a trajectory of system (3) and (4) with initial condition $(x_{0},y_{0},t_{0})$ in Figs. 1 and 2 for $\epsilon =0$ and $\epsilon >0$, respectively.

Fig. 1

A solution of system (3) and (4) for $\epsilon =0$

Fig. 2

A solution of system (3) and (4) for $\epsilon >0$

In order to extend the Melnikov method to a general non-smooth planar hybrid system and guarantee the aforementioned structure, we make the assumptions about geometrical structure of the unperturbed system of system (3) and(4) as follows:

(H1) For $\epsilon =0$, system (3) has a fixed point $p_{0}\in V_{-}$ and a continuous, piecewise-smooth solution $\gamma (t)\in {\mathbb {R}}^{2}$ which is homoclinic to $p_{0}$. The analytical expression for the homoclinic orbit is assumed as follows:

$$\begin{aligned} \gamma (t)=\left\{ \begin{array}{ll}\gamma _{-}^{1}(t),&{} \mathrm{for}\,\,t\le t^{u}\\ \gamma _{+}(t), &{} \mathrm{for}\,\,t^{u}\le t\le t^{s}\\ \gamma _{-}^{2}(t), &{} \mathrm{for}\,\,t\ge t^{s} \end{array}\right. \end{aligned}$$

(7)

where $t^{u}<0<t^{s}$, $\gamma _{-}^{1,\,2}(t)\in V_{-}$ for $t<t^{u}$ and $t> t^{s}$, $\gamma _{+}(t)\in V_{+}$ for $t^{u}<t<t^{s}$, $\gamma _{-}^{1}(t^{u})=\gamma _{+}(t^{u})\in \Sigma$ and $\gamma _{-}^{2}(t^{s})=\gamma _{+}(t^{s})\in \Sigma$.

(H2) $[\mathbf {n}\cdot f_{-}(\gamma _{-}^{1}(t^{u}))]\cdot [\mathbf {n}\cdot f_{+}(\gamma _{-}^{1}(t^{u}))]>0$,  $[\mathbf {n}\cdot f_{-}(\gamma _{-}^{2}(t^{s}))]\cdot [\mathbf {n}\cdot f_{+}(\gamma _{-}^{2}(t^{s}))]>0$.

Without loss of generality, we assume the homoclinic orbits for the unperturbed system of (3) and (4) is clockwise oriented and topologically equivalent to the one shown in Fig. 3.

Fig. 3

The homoclinic orbit of the unperturbed system of (3) and (4)

We give some definitions and lemmas utilized in the following analysis. Firstly, let $\mathbf {a}=(x_{1},y_{1})^\mathrm{T}$, $\mathbf {b}=(x_{2},y_{2})^\mathrm{T}$ and $\mathbf {n}=(n_{1},n_{2})$, then the wedge product and the inner product of two vectors is defined as $\mathbf {a}\wedge \mathbf {b}=x_{1}y_{2}-x_{2}y_{1}$, $\mathbf {n}\cdot \mathbf {a}=n_{1}a_{1}+n_{2}a_{2}$, respectively. Next, we give some lemmas.

Lemma 1

Let $\mathbf {a}=(x_{1},x_{2})^\mathrm{T}$, $\mathbf {b}=(y_{1},y_{2})^\mathrm{T}$, A is a $2\times 2$ matrix, then we have the formula as follows:

$$\begin{aligned} (A\mathbf {b})\wedge {\mathbf {a}}+\mathbf {b}\wedge (A{\mathbf {a}})=\mathbf {trace}A(\mathbf {b}\wedge \mathbf {a}), \end{aligned}$$

(8)

where $\mathbf {trace}A$ is the trace of the matrix A.

Proof

Let

$$\begin{aligned} A=\left( {\begin{array}{l}\,\,\,{a}_{11}\,\,\,{a}_{12}\\ \,\,{a}_{21}\,\,\,\,{a}_{22}\end{array}}\right) , \end{aligned}$$

then

$$\begin{aligned}&(A{\mathbf {b}})\wedge {\mathbf {a}}+\mathbf {b}\wedge (A{\mathbf {a}})\\&\quad = \left| \begin{array}{cc} {a}_{11}{y}_{1}+{a}_{12}{y}_{2} &{}\quad {x}_{1}\\ {a}_{21}{y}_{1}+{a}_{22}{y}_{2} &{}\quad {x}_{2} \end{array}\right| + \left| \begin{array}{cc} {y}_{1} &{}\quad {a}_{11}{x}_{1}+{a}_{12}{x}_{2}\\ {y}_{2} &{}\quad {a}_{21}{x}_{1}+{a}_{22}{x}_{2} \end{array}\right| \\&\quad = {a}_{11}{y}_{1}{x}_{2}-{x}_{1}{a}_{22}{y}_{2}+{y}_{1}{a}_{22}{x}_{2}-{y}_{2}{a}_{11}{x}_{1}\\&\quad = {a}_{11}({y}_{1}{x}_{2}-{y}_{2}{x}_{1}+{a}_{22}({x}_{2}{y}_{1}-{x}_{1}{y}_{2})\\&\quad = {a}_{11} \left| \begin{array}{cc} {y}_{1}&{} {x}_{1}\\ {y}_{2} &{} {x}_{2} \end{array}\right| +{a}_{22} \left| \begin{array}{cc} {y}_{1} &{} {x}_{1}\\ {y}_{2} &{} {x}_{2} \end{array}\right| \\&\quad =({a}_{11}+{a}_{22})(\mathbf {b}\wedge \mathbf {a}) =\mathbf {trace}A(\mathbf {b}\wedge \mathbf {a}). \end{aligned}$$

$\square$

Lemma 2

Let $\mathbf {a}=(a_{1},\,\,a_{2})^\mathrm{T}$, $\mathbf {b}=(b_{1},\,\,b_{2})^\mathrm{T}$, $\mathbf {c}=(c_{1},\,\,c_{2})^\mathrm{T}$, and $\mathbf {n}=(n_{1},n_{2})$, A is a $2\times 2$ matrix, $A^{*}$ is denoted as the adjoint of the matrix A, then we have the formula as follows:

$$\begin{aligned} \mathbf {b}\wedge \left\{ {\left[ A+\frac{(\mathbf {b}-A\mathbf {a})\mathbf {n}}{\mathbf {n}\cdot \mathbf {a}}\right] \mathbf {c}}\right\} = {\frac{(\mathbf {n}A^{*})\cdot \mathbf {b}}{\mathbf {n}\cdot \mathbf {a}}}\mathbf {a}\wedge \mathbf {c}. \end{aligned}$$

(9)

Proof

The formula (9) can be verified by some complicated matrix calculations. The Lemma 2 is an important fact and will be useful for deriving the third equality of (37), which is a main technique in this paper to simplify the non-smooth Melnikov function. $\square$

Lemma 3

If the equation $\dot{w}(t)=A(t)w(t)+h(t)$ satisfies the conditions for the existence and uniqueness of solutions, then the solution of this equation with the initial condition $w(t_{0})=w_{0}$ can be given by $\displaystyle w(t)=\bigg [w_{0}+\int _{t_{0}}^{t}h(s)\exp \left( \int _{s}^{t} A(u)\mathrm{d}u\right) \mathrm{d}s\bigg ]$.

Proof

The Lemma 3 can be easily verified by the method of variation of constant. The Lemma 3 is also an important fact and will be useful for solving the nonhomogeneous differential equations with variable coefficients.

In order to study the global dynamics of system (3) and (4), we rewrite the equivalent suspended system of (3) and (4) to (10) and (11):

$$\begin{aligned}&\left( {\begin{array}{ll}{\dot{x}}\\ {\dot{y}}\end{array}}\right) =\left\{ \begin{array}{ll}f_{-}(x,y)+\epsilon g_{-}(x,y,\theta ), &{}\quad (x, y)\in {V_{-}},\\ f_{+}(x,y)+\epsilon g_{+}(x,y,\theta ),&{}\quad (x, y)\in {V_{+}},\end{array}\right. \nonumber \\&\dot{\theta }=1,\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned}&(x, y)\mapsto {\tilde{\rho }}_{\epsilon }(x,y)=({\tilde{\rho }}_{1,\epsilon }(x,y),{\tilde{\rho }}_{2,\epsilon }(x,y)),\quad (x, y)\in \Sigma ,\nonumber \\ \end{aligned}$$

(11)

where $\theta =t(\mathbf {mod}\,{\hat{T}})\in {S^{1}}$.

In three-dimensional phase space ${\mathbb {R}}^{2}\times S^{1}$, by extending the Lemma 4.5.1 and Lemma 4.5.2 in [7] we get the following proposition:$\square$

Proposition 1

For $\epsilon =0$, under the assumptions (H1)–(H2), the suspended system (10) and (11) has a hyperbolic periodic orbit $\psi _{0}=\{(p_{0},\theta ): p_{0}\in V_{-}, \theta \in S^{1}\}$. Moreover, $\psi _{0}$ has piecewise $C^{r}$ two-dimensional stable and unstable manifolds denoted by $W^{s}(\psi _{0})$ and $W^{u}(\psi _{0})$, respectively, which intersect in a two-dimensional homoclinic manifold

$$\begin{aligned} \Gamma \equiv \left\{ (\gamma (t),\,\theta )\in {\mathbb {R}}^{2}\times S^{1}\right\} . \end{aligned}$$

For $\epsilon >0$ sufficiently small, the suspended system (10) and (11) has a hyperbolic periodic orbit $\psi _{\epsilon }=\{(p_{\epsilon },\theta ): p_{\epsilon }\in V_{-}, \theta \in S^{1}\}$ with $p_{\epsilon }=p_{0}+O(\epsilon )\in {\mathbb {R}}^{2}$. Moreover, $\psi _{\epsilon }$ has piecewise $C^{r}$ two-dimensional stable manifold $W^{s}(\psi _{\epsilon })$ and unstable manifold $W^{u}(\psi _{\epsilon })$, which are $\epsilon -$ close to $W^{s}(\psi _{0})$ and $W^{u}(\psi _{0})$, respectively.

In order to discuss $W^{s}(\psi _{\epsilon })$ and $W^{u}(\psi _{\epsilon })$ for perturbed system (10) and (11), based on the idea presented by Kunze in [13], we fix $\theta _{0}\in S^{1}\cong [0,{\hat{T}}]$ and denote by L, a line segment in the plane $\Sigma _{\theta _{0}}={\mathbb {R}}^{2}\times \{\theta _{0}\}$ that is perpendicular to the homoclinic orbit at $\gamma _{+}(0)$, and therefore points in the direction of the normal vector of $f_{+}(\gamma _{+}(0))$. Furthermore, denote by $p_{\epsilon ,\,\theta _{0}}$ the intersection of $\psi _{\epsilon ,\,\theta _{0}}$ with $\Sigma _{\theta _{0}}$, and let $q^{u,s}(t,\theta _{0},\epsilon )$ be the unique trajectory of system (10) and (11) that lie in the unstable $W^{u}(p_{\epsilon ,\,\theta _{0}})$ and stable $W^{s}(p_{\epsilon ,\,\theta _{0}})$ of $p_{\epsilon ,\,\theta _{0}}$, cross L at shortest distance to $\gamma _{+}(0)$ (see Fig. 4).

Fig. 4

The stable and unstable manifolds of $p_{\epsilon }(\theta _{0})$

Let $\theta _{0}+T^{u,s}(\theta _{0},\epsilon )$ be the time when the perturbed orbit $q^{u,s}(t;\theta _{0},\epsilon )$ will cross the switching manifold, denoted by $\tau ^{u}_{\epsilon }$ and $\tau ^{s}_{\epsilon }$. Obviously,

$$\begin{aligned} \tau ^{u}_{\epsilon }{:}= & {} \theta _{0}+T^{u}(\theta _{0},\epsilon )=\theta _{0}+t^{u}+O(\epsilon ),\nonumber \\ \tau ^{s}_{\epsilon }{:}= & {} \theta _{0}+T^{s}(\theta _{0},\epsilon )=\theta _{0}+t^{s}+O(\epsilon ). \end{aligned}$$

(12)

Based on the ahead of assumptions and notations, we give some Lemmas.

Lemma 4

For each $\theta _{0}\in [0, \hat{T}]$ and sufficiently small $\epsilon >0$, there exist $\delta _{i}(\epsilon )>0, \,(i=1,\,2,\,3,\,4)$ such that $\theta _{0}+t^{u}-\delta _{1}(\epsilon )<\tau _{\epsilon }^{u}<\theta _{0}+t^{u}+\delta _{2}(\epsilon )$ and $\theta _{0}+t^{s}-\delta _{3}(\epsilon )<\tau _{\epsilon }^{s}<\theta _{0}+t^{s}+\delta _{4}(\epsilon )$, and the perturbed orbit $q^{u}(t;\theta _{0},\epsilon )$ and $q^{s}(t;\theta _{0},\epsilon )$ can respectively be expressed as

$$\begin{aligned} q^{u}(t;\theta _{0},\epsilon ) =\left\{ \begin{array}{ll}q^{u,-}(t;\theta _{0},\epsilon )=\hat{\gamma }^{1}(t-\theta _{0})+ \epsilon q_{1}^{u,-}(t,\theta _{0})+O(\epsilon ^{2}),&{} \quad \mathrm{if}\,t\in (-\infty , \tau ^{u}_{\epsilon }),\\ q^{u,+}(t;\theta _{0},\epsilon )=\hat{\gamma }^{2}(t-\theta _{0})+\epsilon q_{1}^{u,+}(t,\theta _{0})+ O(\epsilon ^{2}),&{}\quad \mathrm{if}\,t\in (\tau ^{u}_{\epsilon },\theta _{0}) \end{array}\right. \end{aligned}$$

(13)

with $\tilde{\rho }_{\epsilon }(q^{u,-}(\tau ^{u}_{\epsilon };\theta _{0},\epsilon ))=q^{u,+}(\tau ^{u}_{\epsilon };\theta _{0},\epsilon ))$, and

$$\begin{aligned} q^{s}(t;\theta _{0},\epsilon )=\left\{ \begin{array}{ll}q^{s,+}(t;\theta _{0},\epsilon )=\hat{\gamma }^{2}(t-\theta _{0})+ \epsilon q_{1}^{s,+}(t,\theta _{0})+O(\epsilon ^{2}),&{} \quad \mathrm{if}\,t\in (\theta _{0}, \tau ^{s}_{\epsilon }),\\ q^{s,-}(t;\theta _{0},\epsilon )=\hat{\gamma }^{3}(t-\theta _{0})+\epsilon q_{1}^{s,-}(t,\theta _{0})+ O(\epsilon ^{2}),&{} \quad \mathrm{if}\,t\in (\tau ^{s}_{\epsilon },+\infty )\end{array}\right. \end{aligned}$$

(14)

with $\tilde{\rho }_{\epsilon }(q^{s,+}(\tau ^{s}_{\epsilon };\theta _{0},\epsilon ))=q^{s,-}(\tau ^{s}_{\epsilon };\theta _{0},\epsilon ))$, where

$$\begin{aligned}&\hat{\gamma }^{1}(t-\theta _{0})\nonumber \\&\quad =\left\{ \begin{array}{ll}\gamma ^{1}_{-}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (-\infty , \theta _{0}+t^{u}),\\ \gamma ^{1,\,E}_{-}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (\theta _{0}+t^{u},\theta _{0}+t^{u}+\delta _{2}(\epsilon )) \end{array}\right. \end{aligned}$$

is the solution of equation $({\dot{x}},{\dot{y}})^\mathrm{T}=f_{-}(x,y)+\epsilon g_{-}(x,y,\,t)$ defined in ${\mathbb {R}}^{2}$, namely, $\gamma ^{1,\,E}_{-}(t-\theta _{0})$ is the extension of the solution $\gamma ^{1}_{-}(t-\theta _{0})$ in the $V_{+}$ beyond the switching manifold $\Sigma$, and

$$\begin{aligned}&\hat{\gamma }^{2}(t-\theta _{0})\\&\quad =\left\{ \begin{array}{ll} \gamma ^{1,\,E}_{+}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (\theta _{0}\!+\!t^{u}\!-\!\delta _{1}(\epsilon ), \theta _{0}\!+\!t^{u}),\\ \gamma _{+}(t-\theta _{0}),&{} \mathrm{if}\, \,\,\,t\in (\theta _{0}+t^{u},\theta _{0}+t^{s}),\\ \gamma ^{2,\,E}_{+}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (\theta _{0}+t^{s},\theta _{0}+t^{s}+\delta _{4}(\epsilon )) \end{array}\right. \\ \end{aligned}$$

is the solution of equation $({\dot{x}},{\dot{y}})^\mathrm{T}=f_{+}(x,y)+\epsilon g_{+}(x,y,\,t)$ defined in ${\mathbb {R}}^{2}$, namely $\gamma ^{1,\,E}_{+}(t-\theta _{0})$ and $\gamma ^{2,\,E}_{+}(t-\theta _{0})$ are the extensions of the solution $\gamma _{+}(t-\theta _{0})$ in the $V_{-}$ beyond the switching manifold $\Sigma$, and

$$\begin{aligned}&\hat{\gamma }^{3}(t-\theta _{0})\\&\quad =\left\{ \begin{array}{ll}\gamma ^{2,\,E}_{-}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (\theta _{0}+t^{s}-\delta _{3}(\epsilon ),\,\theta _{0}+t^{s}),\\ \gamma ^{2}_{-}(t-\theta _{0}),&{} \mathrm{if}\, \,\,t\in (\theta _{0}+t^{s},+\infty ) \end{array}\right. \\ \end{aligned}$$

is the solution of equation $({\dot{x}},{\dot{y}})^\mathrm{T}=f_{-}(x,y)+\epsilon g_{-}(x,y,\,t)$ defined in ${\mathbb {R}}^{2}$, namely, $\gamma ^{2,\,E}_{-}(t-\theta _{0})$ is the extension of the solution $\gamma ^{2}_{-}(t-\theta _{0})$ in the $V_{+}$ beyond the switching manifold $\Sigma$. Furthermore, $q_{1}^{u,\pm }(t,\theta _{0})$ and $q_{1}^{s,\pm }(t,\theta _{0})$ are the solutions of the following linearized equation

$$\begin{aligned} \dot{w}= & {} Df_{\pm }(\hat{\gamma }^{i}(t-\theta _{0}))w+g_{\pm }(\hat{\gamma }^{i}(t-\theta _{0}),\,t),\,\,\nonumber \\&i=1,2,3, \end{aligned}$$

(15)

$\textit{where} \ w=(w_{1}, w_{2})^\mathrm{T}\in {\mathbb {R}}^{2}$.

Proof

The proof consists of a straightforward modification of the proof for Lemma 4.5.2 of [7] for smooth systems. In order to overcome the difficulties induced by the discontinuity of vector fields on the switching $\Sigma$, we only need to extend the solution $\gamma (t-\theta _{0})$ to be $\hat{\gamma }^{i}(t-\theta _{0})$ beyond the switching manifold and we can show that the following argument does not depend on the extension. Now, we define a separation between the unstable manifold $W^{u}(p_{\epsilon ,\,\theta _{0}})$ and stable manifold $W^{s}(p_{\epsilon ,\,\theta _{0}})$ on the section $\Sigma _{\theta _{0}}$ along the direction of the normal vector of $f_{+}(\gamma _{+}(0))$ as

$$\begin{aligned} d(\theta _{0})=\frac{ f_{+}(\gamma _{+}(0))\wedge (q^{u}(\theta _{0};\theta _{0},\epsilon )-q^{s}(\theta _{0};\theta _{0},\epsilon ))}{\Vert f_{+}(\gamma _{+}(0))\Vert }. \end{aligned}$$

(16)

By carrying on the Taylor expansion of the displacement function defined in (16) to the first order in the perturbation parameter $\epsilon$ near $\epsilon =0$ and obtain that

$$\begin{aligned} d(\theta _{0})= & {} \epsilon \frac{ f_{+}(\gamma _{+}(0))\wedge (q_{1}^{u,+}(\theta _{0},\theta _{0})-q_{1}^{s,+}(\theta _{0},\theta _{0}))}{\Vert f_{+}(\gamma _{+}(0))\Vert }\nonumber \\&+O(\epsilon ^{2}). \end{aligned}$$

(17)

Let

$$\begin{aligned} \Delta ^{u(s),\pm }(t,\theta _{0})=f_{\pm }(\gamma (t-\theta _{0}))\wedge q_{1}^{u(s),\pm }(t,\theta _{0}), \end{aligned}$$

(18)

according to the (17) and (18), it is easy to get

$$\begin{aligned} d(\theta _{0})=\epsilon \frac{\Delta ^{u,+}(\theta _{0},\theta _{0})-\Delta ^{s,+}(\theta _{0},\theta _{0})}{\Vert f_{+}(\gamma _{+}(0))\Vert }+O(\epsilon ^{2}). \end{aligned}$$

(19)

We denote by

$$\begin{aligned} d(\theta _{0})=\epsilon \frac{M(\theta _{0})}{\Vert f_{+}(\gamma _{+}(0))\Vert }+O(\epsilon ^{2}) \end{aligned}$$

(20)

where

$$\begin{aligned} M(\theta _{0})= & {} \Delta ^{u,\,+}(\theta _{0},\,\theta _{0})-\Delta ^{s,\,+}(\theta _{0},\,\theta _{0})\nonumber \\= & {} \left[ \Delta ^{u,\,+}(\theta _{0},\,\theta _{0})-\Delta ^{u,\,+}(\theta _{0}+t^{u},\,\theta _{0})\right] \nonumber \\&+\left[ \Delta ^{s,\,+}(\theta _{0}+t^{s},\,\theta _{0})-\Delta ^{s,\,+}(\theta _{0},\,\theta _{0})\right] \nonumber \\&+\Delta ^{u,\,+}(\theta _{0}+t^{u},\,\theta _{0})\nonumber \\&-\Delta ^{s,\,+}(\theta _{0}+t^{s},\,\theta _{0}). \end{aligned}$$

(21)

$\square$

In the next main work, we want to derive $M(\theta _{0})$ in a simple form. First, we calculate the derivative of ${\Delta }^{u(s),\pm }(t,\theta _{0})$ with respect to t and obtain that

$$\begin{aligned} \dot{\Delta }^{u(s),\pm }(t,\theta _{0})= & {} \mathbf {trace}Df_{\pm }(\gamma (t-\theta _{0})) \Delta ^{u(s),\pm }(t,\theta _{0})\nonumber \\&+f_{\pm }(\gamma (t-\theta _{0}))\nonumber \\&\wedge g_{\pm }(\gamma (t-\theta _{0}),t). \end{aligned}$$

(22)

We notice that $\Delta ^{u,-}(-\infty ,\theta _{0})= \Delta ^{s,-}(+\infty ,\theta _{0})=0$ due to $f_{-}(P_{0})=0$ and $q_{1}^{u(s),-}(t,\theta _{0})$ are bounded. Employing the Lemma 3 and integrating (22) from $-\infty$ to $\theta _{0}+t^{u}$ and employing the change of variables $t\rightarrow t+\theta _{0}$, we have

$$\begin{aligned}&\Delta ^{u,-}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =\displaystyle \int _{-\infty }^{\,t^{u}}f_{-}(\gamma ^{1}_{-}(t))\wedge g_{-}(\gamma ^{1}_{-}(t),t+\theta _{0})\nonumber \\&\qquad \times \exp \left( \displaystyle \int _{t}^{\,t^{u}}\mathrm{trace}Df_{-}(\gamma ^{1}_{-}(s))\mathrm{d}s\right) \mathrm{d}t, \end{aligned}$$

(23)

Similar calculations give

(24)

(25)

(26)

It is not easy to calculate straightly $\Delta ^{{u},+}(\theta _{0}+t^{u},\theta _{0})$ and $\Delta ^{{s},+}(\theta _{0}+t^{s},\theta _{0})$ by the equation (18), since we do not know the exact $q_{1}^{u,s}$ in the asymptotic expansion of the solutions of the perturbed system (10) and (15). In this paper, we can apply some skillful methods to obtain the relationship between $\Delta ^{u(s),\,+}(\theta _{0}+t^{u(s)},\,\theta _{0})$ and $\Delta ^{u(s),\,-}(\theta _{0}+t^{u(s)},\theta _{0})$. First, we need to obtain the relationship between $q_{1}^{u(s),+}(t,\theta _{0})$ and $q_{1}^{u(s),-}(t,\theta _{0})$. So we give some lemmas.

Lemma 5

$$\begin{aligned} q_{1}^{u,\,+}(\theta _{0}+t^{u},\theta _{0})= & {} \bigg (\frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&+\mathbb {M} q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0}), \end{aligned}$$

(27)

$$\begin{aligned} q_{1}^{s,+}(\theta _{0}+t^{s},\theta _{0})= & {} \bigg (\frac{\partial \tilde{\rho }_{\epsilon }^{-1}((\gamma (t^{s}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&+\mathbb {M'} q_{1}^{s,-}(\theta _{0}+t^{s},\theta _{0}), \end{aligned}$$

(28)

where the matrix $\mathbb {M}$ and $\mathbb {M'}$ are respectively given by

$$\begin{aligned} \mathbb {M}= & {} D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\nonumber \\&+\frac{[\dot{\gamma }_{+}(t^{u})-D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }^{1}_{-}(t^{u})]\mathbf {n}(\gamma (t^{u}))}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}, \nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} \mathbb {M'}= & {} D\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{s}))|_{\epsilon =0}\nonumber \\&+\frac{[\dot{\gamma }_{+}(t^{s})-D\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{s}))|_{\epsilon =0}\dot{\gamma }^{2}_{-}(t^{s})]\mathbf {n}(\gamma (t^{s}))}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{2}_{-}(t^{s})},\nonumber \\ \end{aligned}$$

(30)

Moreover,

$$\begin{aligned}&\Delta ^{u,+}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =\dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\quad +\displaystyle \frac{\mathbf {n}(\gamma (t^{u})) D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}\Delta ^{u,-}\nonumber \\&\quad \times \, (\theta _{0}+t^{u},\theta _{0}), \end{aligned}$$

(31)

$$\begin{aligned}&\Delta ^{s,+}(\theta _{0}+t^{s},\theta _{0})\nonumber \\&\quad =\dot{\gamma }_{+}(t^{s})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }^{-1}((\gamma (t^{s}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\quad +\displaystyle \frac{\mathbf {n}(\gamma (t^{s})) D^{*}\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{s}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{s})}{\mathbf {n}(\gamma (t^{s}))\cdot \dot{\gamma }^{2}_{-}(t^{s})}\Delta ^{s,-}\nonumber \\&\quad \times \, (\theta _{0}+t^{s},\theta _{0}), \end{aligned}$$

(32)

where

$$\begin{aligned}&D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\\&\quad =\left( {\begin{array}{l}\,\displaystyle \frac{\partial \tilde{\rho }_{1,\,\epsilon }(\gamma (t^{u}))}{\partial x}\,\,\,\,\displaystyle \frac{\partial \tilde{\rho }_{1,\,\epsilon }(\gamma (t^{u}))}{\partial y}\\ \,\displaystyle \frac{\partial \tilde{\rho }_{2,\,\epsilon }(\gamma (t^{u}))}{\partial x}\,\,\,\,\displaystyle \frac{\partial \tilde{\rho }_{2,\,\epsilon }(\gamma (t^{u}))}{\partial y}\end{array}}\right) _{|_{\epsilon =0}},\\&D\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{s}))_{|_{\epsilon =0}}\nonumber \\&\quad =\left( {\begin{array}{l}\,\displaystyle \frac{\partial \tilde{\eta }_{1,\,\epsilon }(\gamma (t^{s}))}{\partial x}\,\,\,\,\displaystyle \frac{\partial \tilde{\eta }_{1,\,\epsilon }(\gamma (t^{s}))}{\partial y}\\ \,\displaystyle \frac{\partial \tilde{\eta }_{2,\,\epsilon }(\gamma (t^{s}))}{\partial x}\,\,\,\,\displaystyle \frac{\partial \tilde{\eta }_{2,\,\epsilon }(\gamma (t^{s}))}{\partial y}\end{array}}\right) _{|_{\epsilon =0}} \end{aligned}$$

are $2\times 2$ matrix, and $D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}$ and $D^{*}\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{s}))|_{\epsilon =0}$ respectively denote the adjoint of $D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}$ and $D\tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{s}))|_{\epsilon =0}$.

Proof

For $t\in (\tau ^{u}_{\epsilon },\theta _{0})$ we have

$$\begin{aligned} q^{u,+}(t;\theta _{0},\epsilon )= & {} \bigg (\tilde{\rho }_{\epsilon }(q^{u,-}(\tau ^{u}_{\epsilon };\theta _{0},\epsilon ),\epsilon )\bigg )^\mathrm{T}\nonumber \\&+\int ^{t}_{\tau ^{u}_{\epsilon }}(f_{+}(q^{u,+}(t;\theta _{0},\epsilon ))\nonumber \\&+\,\epsilon g_{+}(q^{u,+}(t;\theta _{0},\epsilon ),\,t))\mathrm{d}t. \end{aligned}$$

(33)

Differentiating (33) with respect to $\epsilon$ and substituting $\theta _{0}+t^{u}$ into t and 0 into $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&\displaystyle {q_{1}^{u,+}(\theta _{0}+t^{u},\theta _{0})}\\&\quad =\bigg (\displaystyle {\frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }}|_{\epsilon =0}\bigg )^\mathrm{T}\\&\qquad +D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0})\\&\qquad +\displaystyle {[D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0} \dot{\gamma }^{1}_{-}(t^{u})-\dot{\gamma }_{+}(t^{u})] \frac{\mathrm{d}\tau ^{u}_{\epsilon }}{\mathrm{d}\epsilon }|_{\epsilon =0}}. \end{aligned} \end{aligned}$$

(34)

Since $q^{u,-}(\tau ^{u}_{\epsilon };\theta _{0},\epsilon )\in \Sigma$, we have

$$\begin{aligned} h(q^{u,-}(\tau ^{u}_{\epsilon };\theta _{0},\epsilon ))=0. \end{aligned}$$

(35)

Differentiating (35) with respect to $\epsilon$ and letting $\epsilon =0$, we obtain

$$\begin{aligned} \frac{\mathrm{d}\tau ^{u}_{\epsilon }}{\mathrm{d}\epsilon }|_{\epsilon =0}=-\frac{\mathbf {n}(\gamma (t^{u}))\cdot q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}. \end{aligned}$$

(36)

Substituting (36) into (34), we can obtain the expressions (27) and (28). Substituting (27) and (29) into (18), we can obtain the expression (31) as follows:

$$\begin{aligned}&\Delta ^{u,+}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =f_{+}(\gamma (t^{u}))\wedge q_{1}^{u,+}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =\dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\qquad + \,\dot{\gamma }_{+}(t^{u})\wedge \mathbb {M}q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =\dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\qquad + \dot{\gamma }_{+}(t^{u})\wedge \bigg (D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\nonumber \\&\qquad + \,\frac{\left[ \dot{\gamma }_{+}(t^{u})-D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }^{1}_{-}(t^{u})\right] \mathbf {n}(\gamma (t^{u}))}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}\bigg )\nonumber \\&\qquad \times \, q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad =\dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\qquad + \,\displaystyle {\frac{\mathbf {n}(\gamma (t^{u})) D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}} \dot{\gamma }^{1}_{-}(t^{u}))\nonumber \\&\qquad \wedge q_{1}^{u,-} (\theta _{0}+t^{u},\theta _{0})\nonumber \\&\quad = \dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&\qquad + \displaystyle {\frac{\mathbf {n}(\gamma (t^{u})) D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}} \nonumber \\&\qquad \Delta ^{u,-} (\theta _{0}+t^{u},\theta _{0}), \end{aligned}$$

(37)

where the fourth equality is obtained directly by the Lemma 2 if we let the column vectors $\mathbf {a}=\dot{\gamma }^{1}_{-}(t^{u})$, $\mathbf {b}=\dot{\gamma }_{+}(t^{u})$, $\mathbf {c}=q_{1}^{u,-}(\theta _{0}+t^{u},\theta _{0})$, and the matrix $A=D\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}$.

The proof about the conclusions (28) and (32) is similar with the aforementioned method; hence, we omit it. Now substituting (23) and (26) into (21) and employing the equations (31) and (32), we can obtain the first-order non-smooth Melnikov-type function as follows:

$$\begin{aligned} M(\theta _{0})= & {} \dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\nonumber \\&-\dot{\gamma }_{+}(t^{s})\wedge \bigg (\frac{\partial \tilde{\rho }_{\epsilon }^{-1}((\gamma (t^{s}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T} \nonumber \\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{u})) D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}}\nonumber \\&\times \,\displaystyle \int _{-\infty }^{\,t^{u}}f_{-}(\gamma ^{1}_{-}(t))\wedge g_{-}(\gamma ^{1}_{-}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( \displaystyle \int _{t}^{\,t^{u}}\mathrm{trace}Df_{-}(\gamma ^{1}_{-}(s))\mathrm{d}s\right) \mathrm{d}t \nonumber \\&+\displaystyle \int _{\,t^{u}}^{\,t^{s}}f_{+}(\gamma _{+}(t))\wedge g_{+}(\gamma _{+}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( -\displaystyle \int _{0}^{\,t}\mathrm{trace}Df_{+}(\gamma _{+}(\mu ))\mathrm{d}\mu \right) \mathrm{d}t\nonumber \\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{s})) D^{*}\tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{s}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{s})}{\mathbf {n}(\gamma (t^{s}))\cdot \dot{\gamma }^{2}_{-}(t^{s})}}\nonumber \\&\times \,\displaystyle \int _{t^{s}}^{+\infty } f_{-}(\gamma ^{2}_{-}(t))\wedge g_{-}(\gamma ^{2}_{-}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( \displaystyle \int _{t}^{\,t^{s}}\mathrm{trace}Df_{-}(\gamma ^{2}_{-}(s))\mathrm{d}s\right) \mathrm{d}t.\nonumber \\ \end{aligned}$$

(38)

$\square$

Now, we present the main theorem in this section to study the global bifurcations and chaotic dynamics for the non-smooth system (3) and (4).

Theorem 1

Let $\epsilon$ be sufficiently small, and all assumptions $\mathrm{(H1)}$–$\mathrm{(H2)}$ are fulfilled, if there exists a number $\theta _{0}\in S^{1}\cong [0,\hat{T}]$ such that

$$\begin{aligned} M(\theta _{0})=0,\,\,DM(\theta _{0})\ne 0, \end{aligned}$$

then for $\epsilon$ be sufficiently small, $W^{s}(\psi _{\epsilon })$ and $W^{u}(\psi _{\epsilon })$ intersect transversely near $\theta _{0}$.

We also give a special result of the first-order non-smooth Melnikov-type function (38).

Proposition 2

Suppose the assumptions (H1)–(H2) hold and the system (3) and (4) satisfies $\tilde{\rho }_{\epsilon }(x,y)=(\rho _{1,\epsilon }(x,y),\rho _{2,\epsilon }(x,y))=(x,y)$, then the non-smooth Melnikov-type function defined in (38) becomes

$$\begin{aligned} M(\theta _{0})= & {} \displaystyle {\frac{\mathbf {n}(\gamma (t^{u}))\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}}\nonumber \\&\times \,\displaystyle \int _{-\infty }^{\,t^{u}}f_{-}(\gamma ^{1}_{-}(t))\wedge g_{-}(\gamma ^{1}_{-}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( \displaystyle \int _{t}^{\,t^{u}}\mathrm{trace}Df_{-}(\gamma ^{1}_{-}(s))\mathrm{d}s\right) \mathrm{d}t\nonumber \\&+\displaystyle \int _{\,t^{u}}^{\,t^{s}}f_{+}(\gamma _{+}(t))\wedge g_{+}(\gamma _{+}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( -\displaystyle \int _{0}^{\,t}\mathrm{trace}Df_{+}(\gamma _{+}(\mu ))\mathrm{d}\mu \right) \mathrm{d}t\nonumber \\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{s}))\dot{\gamma }_{+}(t^{s})}{\mathbf {n}(\gamma (t^{s}))\cdot \dot{\gamma }^{2}_{-}(t^{s})}}\nonumber \\&\times \,\displaystyle \int _{t^{s}}^{+\infty } f_{-}(\gamma ^{2}_{-}(t))\wedge g_{-}(\gamma ^{2}_{-}(t),t+\theta _{0})\nonumber \\&\times \,\exp \left( \displaystyle \int _{t}^{\,t^{s}}\mathrm{trace}Df_{-}(\gamma ^{2}_{-}(s))\mathrm{d}s\right) \mathrm{d}t.\nonumber \\ \end{aligned}$$

(39)

Proof

Since $\tilde{\rho }_{\epsilon }(x,y)=(\rho _{1,\epsilon }(x,y),\rho _{2,\epsilon }(x,y))=(x,y)$, we have

$$\begin{aligned} \displaystyle {\frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }}= & {} \displaystyle {\frac{\partial \tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{s}))}{\partial \epsilon }}=(0,0),\\ D\tilde{\rho }_{\epsilon }(x,y)= & {} D\tilde{\rho }^{-1}_{\epsilon }(x,y)=D^{*}\tilde{\rho }_{\epsilon }(x,y)\\= & {} D^{*}\tilde{\rho }^{-1}_{\epsilon }(x,y)=\left( {\begin{array}{l}\,1\,\,\,\,0\\ \,0\,\,\,\,1\end{array}}\right) . \end{aligned}$$

Hence, we can complete the proof through simple calculations. $\square$

Proposition 3

Suppose the assumptions (H1)–(H2) hold and the system (3) and (4) satisfies $\mathbf {trace}Df(x,y)=0$, then the non-smooth Melnikov-type function defined in (38) can be simplified to the following form

$$\begin{aligned} \begin{aligned} M(\theta _{0})=\,&\dot{\gamma }_{+}(t^{u})\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\\&-\dot{\gamma }_{+}(t^{s})\wedge \bigg (\frac{\partial \tilde{\rho }_{\epsilon }^{-1}((\gamma (t^{s}))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T} \\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{u})) D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}}\\&\times \,\displaystyle \int _{-\infty }^{\,t^{u}}f_{-}(\gamma ^{1}_{-}(t))\wedge g_{-}(\gamma ^{1}_{-}(t),t+\theta _{0})\mathrm{d}t \\&+\displaystyle \int _{\,t^{u}}^{\,t^{s}}f_{+}(\gamma _{+}(t))\wedge g_{+}(\gamma _{+}(t),t+\theta _{0})\mathrm{d}t\\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{s})) D^{*}\tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{s}))|_{\epsilon =0}\dot{\gamma }_{+}(t^{s})}{\mathbf {n}(\gamma (t^{s}))\cdot \dot{\gamma }^{2}_{-}(t^{s})}}\\&\times \,\displaystyle \int _{t^{s}}^{+\infty } f_{-}(\gamma ^{2}_{-}(t))\wedge g_{-}(\gamma ^{2}_{-}(t),t+\theta _{0})\mathrm{d}t. \end{aligned} \end{aligned}$$

(40)

Proposition 4

Suppose the assumptions (H1)–(H2) hold, and the system (3) and (4) satisfies $\mathbf {trace}Df(x,y)=0$ and $\tilde{\rho }_{\epsilon }(x,y)=(\rho _{1,\epsilon }(x,y),\rho _{2,\epsilon }(x,y))=(x,y)$, then the non-smooth Melnikov-type function defined in (38) can be further simplified to the following form

$$\begin{aligned} \begin{aligned} M(\theta _{0})=\,&\displaystyle {\frac{\mathbf {n}(\gamma (t^{u}))\dot{\gamma }_{+}(t^{u})}{\mathbf {n}(\gamma (t^{u}))\cdot \dot{\gamma }^{1}_{-}(t^{u})}}\\&\displaystyle \int _{-\infty }^{\,t^{u}}f_{-}(\gamma ^{1}_{-}(t))\wedge g_{-}(\gamma ^{1}_{-}(t),t+\theta _{0})\mathrm{d}t \\&+\displaystyle \int _{\,t^{u}}^{\,t^{s}}f_{+}(\gamma _{+}(t))\wedge g_{+}(\gamma _{+}(t),t+\theta _{0})\mathrm{d}t\\&+\displaystyle {\frac{\mathbf {n}(\gamma (t^{s}))\dot{\gamma }_{+}(t^{s})}{\mathbf {n}(\gamma (t^{s}))\cdot \dot{\gamma }^{2}_{-}(t^{s})}}\\&\displaystyle \int _{t^{s}}^{+\infty } f_{-}(\gamma ^{2}_{-}(t))\wedge g_{-}(\gamma ^{2}_{-}(t),t+\theta _{0})\mathrm{d}t. \end{aligned} \end{aligned}$$

(41)

Next we apply the obtained results to study the bifurcations and chaotic dynamics of a concrete piecewise-smooth linear system under a periodic and a viscous damping.

3 Application

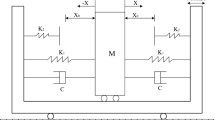
The equation considered in this example can be written as

$$\begin{aligned} \left\{ \begin{array}{ll}{\dot{x}}=y,\\ {\dot{y}}=x+\epsilon (-\mu y+f_{0}\cos \Omega t). \end{array}\right. \quad&|x|<1,\,\, \nonumber \\ \left\{ \begin{array}{ll}{\dot{x}}=y,\\ {\dot{y}}=-x+\epsilon (-\mu y+f_{0}\cos \Omega t ). \end{array}\right. \quad&|x|>1, \end{aligned}$$

(42)

where $\epsilon \,(0 < \epsilon \ll 1)$ is a small parameter, $\mu$ is the damping and $f_{0}$ is the excitation.

The reset map is given as follows:

$$\begin{aligned} \tilde{\rho }_{\epsilon }(\pm 1,y)= \left\{ \begin{array}{l}\displaystyle \left( \pm 1,\frac{y}{1+\epsilon \rho _{0} y}\right) ,\,\,\,\,\,y>0;\\ \displaystyle \left( \pm 1,\frac{y}{1-\epsilon \rho _{0}y}\right) ,\,\,\,\,\,y<0. \end{array}\right. \end{aligned}$$

(43)

where $\rho _{0}$ is a positive parameter. The inverse mapping of $\tilde{\rho }_{\epsilon }(x,y)$ can be expressed as:

$$\begin{aligned} \tilde{\rho }_{\epsilon }^{-1}(\pm 1,y)= \left\{ \begin{array}{l}\displaystyle \left( \pm 1,\frac{y}{1-\epsilon \rho _{0} y}\right) ,\,\,\,\,\,y>0;\\ \displaystyle \left( \pm 1,\frac{y}{1+\epsilon \rho _{0}y}\right) ,\,\,\,\,\,y<0. \end{array}\right. \end{aligned}$$

(44)

The unperturbed system of (42) and (43), which is a piecewise-defined Hamiltonian system and obtained by letting $\epsilon =0$, can be written in the following form:

$$\begin{aligned} {\dot{x}}= & {} \displaystyle \frac{\partial {H}}{\partial {y}},\nonumber \\ {\dot{y}}= & {} -\displaystyle \frac{\partial {H}}{\partial {x}}, \end{aligned}$$

(45)

where the piecewise-defined Hamiltonian function is

$$\begin{aligned} H(x,\,y)=\left\{ \begin{array}{ll} H_{-}(x,\,y)= \frac{1}{2}y^{2}-\frac{1}{2}x^{2}+1,&{}\quad |x|<1,\\ H_{+}(x,\,y)=\frac{1}{2}y^{2}+\frac{1}{2}x^{2},&{}\quad |x|>1.\end{array}\right. \end{aligned}$$

(46)

The equilibria of the unperturbed system (42) and (43) can be easily given by $(0,\,0).$ For $-1<x<1$, the eigenvalues of the Jacobian matrix at the equilibria of the unperturbed system of (42) can be obtained to show that $(0,\,0)$ is a saddle point. Furthermore, there exists a pair of homoclinic orbits connecting $(0,\,0)$ to itself. The phase structure of the unperturbed system (42) and (44) is shown in Fig. 5. The right homoclinic orbit can be divided by the vertical line $x=1$ into an elliptical segment, marked as $\gamma _{+}(t)$, and two line segments, marked as $\gamma _{-}^{1}(t)$ and $\gamma _{-}^{2}(t)$ which meet at the point $(0,\,0)$ as $t\rightarrow -\infty$ and $t\rightarrow +\infty$, respectively. The analytical expression of the homoclinic orbit is given by

Fig. 5

The homoclinic orbit of the system (42) and (44)

$$\begin{aligned} \gamma (t)=\left\{ \begin{array}{ll}\gamma _{-}^{1}(t)=(\exp (t+T),\,\exp (t+T))^\mathrm{T},&{} for\,\,t\le -T\\ \gamma _{+}(t)=(\sqrt{2}\cos t,\,-\sqrt{2}\sin t)^\mathrm{T},&{} for\,\,-T\le t\le T\\ \gamma _{-}^{2}(t)=(\exp (-(t-T)),\,-\exp (-(t-T)))^\mathrm{T},&{} for\,\,t\ge T \end{array}\right. \end{aligned}$$

(47)

where

$$\begin{aligned} T=\frac{\pi }{4}. \end{aligned}$$

(48)

Applying the reset mapping (43) and (44), we have the conclusion:

$$\begin{aligned} \gamma (t^{u})= & {} \gamma (-T)=\gamma _{-}^{1}(-T)=\gamma _{+}(-T)=(1,\,1)^\mathrm{T},\nonumber \\ \gamma (t^{s})= & {} \gamma (T)=\gamma _{-}^{2}(T)=\gamma _{+}(T)=(1,\,-1)^\mathrm{T}, \end{aligned}$$

(49)

and

$$\begin{aligned} \begin{array}{l} \displaystyle {\frac{\partial \tilde{\rho }_{\epsilon }(\gamma (t^{u}))}{\partial \epsilon }|_{\epsilon =0}}=(0, -\rho _{0}),\\ \displaystyle {\frac{\partial \tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{s}))}{\partial \epsilon }|_{\epsilon =0}}=(0, -\rho _{0}),\\ D\tilde{\rho }_{\epsilon }(\gamma (t^{u(s)})|_{\epsilon =0}=D\tilde{\rho }_{\epsilon }^{-1}(\gamma (t^{u(s)})|_{\epsilon =0}=\left( {\begin{array}{l}\,0\,\,\,\,0\\ \,0\,\,\,\,1\end{array}}\right) \\ D^{*}\tilde{\rho }_{\epsilon }(\gamma (t^{u(s)})|_{\epsilon =0}=D^{*}\tilde{\rho }^{-1}_{\epsilon }(\gamma (t^{u(s)})|_{\epsilon =0}=\left( {\begin{array}{l}\,1\,\,\,\,0\\ \,0\,\,\,\,0\end{array}}\right) \end{array}\nonumber \\ \end{aligned}$$

(50)

Considering the expressions and the non-smooth Melnikov function with $g(x,y)=(0,\,-\mu y+f_{0}\cos \Omega t)$ and $\mathbf {n}(h(x,y))=\mathbf {grad}(h(x,y))=(1,\,0)$, we obtain the corresponding Melnikov function for this example as follows:

$$\begin{aligned} \begin{aligned} M(\theta _{0})=\,&\dot{\gamma }_{+}(-T)\wedge \bigg (\displaystyle \frac{\partial \tilde{\rho }_{\epsilon }(\gamma (-T))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\\&-\dot{\gamma }_{+}(T)\wedge \bigg (\frac{\partial \tilde{\rho }_{\epsilon }^{-1}((\gamma (T))}{\partial \epsilon }|_{\epsilon =0}\bigg )^\mathrm{T}\\&+\int _{-\infty }^{-T}f_{-}(\gamma _{-}^{1}(t))\wedge g_{-}(\gamma _{-}^{1}(t),t+\theta _{0})\mathrm{d}t\\&+\int _{-T}^\mathrm{T}f_{+}(\gamma _{+}(t))\wedge g(\gamma (t),t+\theta _{0})\mathrm{d}t\\&+\int _{T}^{+\infty }f_{-}(\gamma _{-}^{2}(t))\wedge g_{-}(\gamma _{-}^{2}(t),t+\theta _{0})\mathrm{d}t. \end{aligned} \end{aligned}$$

(51)

Fig. 6

The chaotic thresholds for system (42) and (44) obtained by the Melnikov analysis: a for $\rho _0=0.2$, b for $\mu =0.01$

Furthermore, we obtain

$$\begin{aligned} \begin{aligned} M(\theta _{0})=&-2\rho _{0}-2\mu T\\&+f_0(B_1(T)+B_2(T))\sin (\Omega \theta _{0}), \end{aligned} \end{aligned}$$

(52)

where

$$\begin{aligned} B_1(T)= & {} \frac{2(\sin (\Omega T)+\Omega \cos (\Omega T))}{\Omega ^{2}+1},\\ B_2(T)= & {} \frac{-2(\sin (\Omega T)+\Omega \cos (\Omega T))}{\Omega ^{2}-1},\\ T= & {} \frac{\pi }{4}, \end{aligned}$$

In the Melnikov function obtained above, the corresponding parameter T has been given in (48). It can be seen that

$$\begin{aligned} M(\theta _{0})=0, \end{aligned}$$

(53)

has a simple zero for $\theta _{0}$ if and only if the following inequality holds:

$$\begin{aligned} 2\rho _{0}+2\mu T<f_{0}|(B_1(T)+B_2(T))| \end{aligned}$$

(54)

Next, in the following numerical simulations, we are going to verify the criterion obtained in the above section. When the impacting coefficient $\rho _0$ of the reset map $\tilde{\rho }_{\epsilon }$ is given as $\rho _0=0.2$, the thresholds of parameters for the existence of a transverse homoclinic orbit of the system (42) and (43) obtained by the Melnikov function are shown in Fig. 6a with different parameters $\mu$. When the value of the damping $\mu$ is chosen as $\mu =0.01$, the thresholds of parameters for the existence of a transverse homoclinic cycle of the system (42) and (43) obtained by the Melnikov function are shown in Fig. 6b with different impacting parameters $\rho _0$. Above the detected boundaries in Fig. 6a, b, complicated dynamics near the unperturbed homoclinic cycle will be generated.

When the value of the excitation parameter is restricted as $f_0=0.2$, the detected thresholds of parameters for system (42) and (44) obtained by the Melnikov function are shown in Fig. 7a with different parameters $\mu$. When we restrict the value of the damping $\mu =0.2$, the detected thresholds of parameters for system (42) and (44) obtained by the Melnikov function are shown in Fig. 7b for different excitation parameters $f_0$. Below the detected boundaries in Fig. 7a, b, complicated dynamics near the unperturbed homoclinic cycle will be generated.

Fig. 7

The chaotic thresholds for system (42) and (44) obtained by the Melnikov analysis: a for $f_0=0.2$, b for $\mu =0.2$

We have employed the Melnikov function to obtain the thresholds of parameters for the existence of a transversal homoclinic orbit of system (42) and (44). All parameters chosen in the following numerical analysis guarantee the criterion for the existence of a transverse homoclinic orbit.

For one case, we do not consider the influence of the reset map (43) and (44) by letting $\rho _{0}=0$. Firstly, we restrict the value of the parameter $\epsilon$ and the frequency $\Omega$ of the external excitation to $\epsilon =0.9$ and $\Omega =1.05$. Chaotic motions are found and shown in Fig. 8a, b. The parameters are, respectively, chosen as $\mu =0.75$, $f_{0}=1.3$ in Fig. 8a and $\mu =1.08$, $f_{0}=1.25$ in Fig. 8b.

Fig. 8

The phase portraits of the chaotic motions for system (42) and (43): a for $\mu =0.75, f_{0}=1.3$, b for $\mu =1.08, f_{0}=1.3$

Secondly, we restrict the damping $\mu$ and the perturbation parameter $\epsilon$, chaotic motions are found and shown in Fig. 9a, b. The value of amplitude $f_{0}$ and the frequency $\Omega$ of the external excitation are, respectively, chosen as $f_{0}=1.25$, $\Omega =0.92$ in Fig. 9a and $f_{0}=1.05$, $\Omega =0.85$ in Fig. 9b.

Fig. 9

The phase portraits of the chaotic motions for system (42) and (43): a for $f_{0}=1.25$ and $\Omega =0.92,$ b for $f_{0}=1.05$ and $\Omega =0.85$.

For another case, we consider the influence of the reset map (43) and (44) by letting $\rho _{0}=0.05$ and $\rho _{0}=0.35$, respectively. Chaotic motions are found and shown in Fig. 10a, b. The parameters are chosen as $\mu =0.8 ,f_{0}=1.2$ and $\Omega =1.05$.

Fig. 10

The phase portraits of the chaotic motions for system (42) and (43): a for $\rho _{0}=0.05$, b for $\rho _{0}=0.35$

4 Conclusions

In this paper, we turn our attention from the famous Melnikov method for smooth systems to a general planar hybrid piecewise-smooth system under a time-periodic perturbation. We consider a general system such that its unperturbed part has a piecewise-smooth homoclinic orbit transversally crossing a switching manifold. The switching manifold we considered is a hypersurface which divides the plane into two zones, and the dynamics in each zone is governed by a smooth system. A reset map will be worked and describes the instantaneous impacting rule when a trajectory arrives at the switching manifold. Then, we employ some perturbation techniques to derive a Melnikov-type function to measure the separation of the unstable manifold and stable manifold under perturbation, which extends the classical Melnikov function for smooth systems. Finally, we apply the obtained results to study the chaotic dynamics of a concrete piecewise smooth system. Numerical simulations are also presented to show that the analytical non-smooth Melnikov method is an effective tool to study the global bifurcations and chaotic dynamics for non-smooth systems.