The analytical method of studying subharmonic periodic orbits for planar piecewise-smooth systems with two switching manifolds

Abstract

Piecewise linear approach is one of important methods to study nonlinear dynamics of oscillators with complex nonlinear restoring forces, so piecewise-smooth systems with multiple switching manifolds sometimes are ideal mathematical models to analyze the nonlinear dynamics of nonlinear oscillators. In this paper, inspired by the work presented by Cao et al. (Philos Trans R Soc A 366(1865):635–652, 2008) and Granados et al. (SIAM J Appl Dyn Syst 11(3):801–830, 2012), we want to formulate an analytical method for studying subharmonic periodic orbits for piecewise-smooth systems with two switching manifolds. We will define what are subharmonic orbits for this class of piecewise-smooth systems and develop a Melnikov-type analytical method to detect the existence of subharmonic orbits. In order to obtain this objective, we assume that the plane is divided into three zones by the two switching manifolds which may not be symmetric, and the dynamics in each zone is decided by a smooth system. Furthermore, we suppose that the unperturbed system is a piecewise-defined Hamiltonian system and possesses a pair of piecewise-smooth homoclinic orbits crossing the two switching manifolds transversally exactly twice and connecting origin to itself. The region outside the pair of homoclinic orbits is fully covered by periodic orbits crossing respectively the two switching manifolds transversally exactly twice. Finally, we want to study the persistence of those continuum of periodic orbits outside the pair of homoclinic orbits when a small time-periodic perturbation is considered. By choosing an appropriate Poincaré section, constructing a Poincaré map and applying perturbation techniques, we obtain the Melnikov function of subharmonic orbits for the class of planar piecewise-smooth systems and employ it to study the existence of subharmonic periodic motions for a piecewise-linear oscillator. Numerical simulations are also shown the effectiveness of the analytical method to detect the parameters and initial conditions for the existence of subharmonic orbits in piecewise-smooth oscillators.

1 Introduction

In recent years, more and more scholars are interested in non-smooth dynamical systems, because such systems are frequently used to model non-smooth phenomena in many fields, such as simplest walking machines [1], relay feedback systems in control theory [2], mechanical engineering with dry frictions [3, 4], switching circuits for electrical engineers [5] and so on. In another aspect, piecewise linear approach is also one of important methods to study nonlinear dynamics of oscillators with complex nonlinear restoring forces. For example, a smooth and discontinuous (SD) oscillator was first proposed by Thompson and Hunt [6] from an archetypal system, extended and defined by Cao et al. [7]. The model is shown in Fig. 1. The dimensionless form of the SD oscillator is given by

$$\begin{aligned} \ddot{x}+2\mu \dot{x}+x\,\bigg (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^{2}}}\bigg ) =f_{0}\cos \omega t, \end{aligned}$$

(1)

where $\alpha \ge 0$ defines the geometry of the SD oscillator, $\mu$ is a linear damping coefficient, $f_{0}$ is the forcing amplitude and $\omega$ is the forcing frequency. The irrational restoring force is given by

$$\begin{aligned} F(x)=-x\,\bigg (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^{2}}}\bigg ). \end{aligned}$$

(2)

which is shown in Fig. 2 for different parameter $\alpha$ and its piecewise linear approach.

Fig. 1

SD oscillator model

Fig. 2

The irrational restoring force

It is very difficult to study the dynamics of the SD oscillator directly by analytical method. So Cao et al. [8] have shown that piecewise linear approach is indeed a good method to model oscillators with complex restoring forces. Granados et al. [9] have formulated a general theory of Melnikov method and subharmonic orbits in piecewise-smooth systems with a switching manifold in order to study the dynamics with linearization of a slender rocking block. Hence the piecewise-smooth systems with multiple switching manifolds sometimes are ideal mathematical models to analyze the nonlinear dynamics of nonlinear oscillators with complex restoring forces. Inspired by the work presented by Cao et al. [8] and Granados et al. [9], in this paper we want to formulate an analytical method for studying subharmonic periodic orbits for piecewise-smooth systems with two switching manifolds.

Now a lot of efforts studying the homoclinic bifurcations and chaotic dynamics for non-smooth dynamical systems have been made in [10,11,12,13,14,15,16,17,18,19,20,21] to extend the classical Melnikov method presented in [22,23,24] to non-smooth dynamical systems. Whether the Melnikov method for subharmonic orbits in smooth time-periodic dynamical systems presented in [24] can also be extended to non-smooth dynamical systems. How to define what are subharmonic orbits for non-smooth time-periodic dynamical systems. Some authors have tried to answer these problems by some concrete non-smooth oscillators or theoretical analysis. For examples, Granados et al. [9] has developed the Melnikov method for subharmonic orbits in a planar piecewise-smooth time-periodic perturbation system with a concrete impact rule on a switching manifold. Li et al. [25] presented the Melnikov method for a three-zonal planar autonomous hybrid piecewise-smooth system and studied the existence of periodic orbits. Shen and Du [26] studied subharmonic periodic orbits with double impact for a inverted pendulum, Shen et al. [27] studied subharmonic and grazing bifurcations for a simple bilinear oscillator. They have also presented the definition of subharmonic orbits for non-smooth time-periodic systems with only one switching manifold through constructing appropriate Poincaré map. However, to the best of our knowledge, there are not any results about the Melnikov method of subharmonic orbits for time-periodic dynamical systems with more than one switching manifold.

In this paper, we want to extend the Melnikov method of subharmonic orbits presented in [9] to a non-smooth time-periodic perturbation systems with two switching manifold $x=-\,\alpha$ and $x=\beta$, which may not be symmetric and will lead to not only complicated calculations but also rich subharmonic orbits. We will define what are subharmonic orbits for this class of non-smooth dynamical systems and develop a Melnikov-type analytical method to detect the existence of subharmonic orbits. We firstly assume that the switching manifolds are two straight lines $x=-\,\alpha$ and $x=\beta$ which divide the plane into three zones, and the dynamics in each zone is decided by a smooth system. Secondly, we suppose that the unperturbed system is a piecewise-defined Hamiltonian system and has a special geometrical structure which consists of a pair of piecewise smooth homoclinic orbits crossing the two switching manifolds transversally exactly twice and connecting origin to itself. The region outside the pair of homoclinic orbits is fully covered by periodic orbits crossing respectively the two switching manifolds transversally exactly twice. Next, considering a small time-periodic perturbation, we construct a Poincaré map to study the persistence of the periodic orbits outside the pair of homoclinic orbits and present the definition of subharmonic orbits and the Melnikov function of subharmonic orbits for the class of planar no-smooth dynamical systems. Finally, we employ the Melnikov method to study the existence of subharmonic orbits for a concrete example. Numerical simulations are also shown to verify the effectiveness of the extended Melnikov method for detecting the existence of subharmonic orbits for a piecewise-smooth oscillators.

This paper is organized as follows. In Sect. 2, the statement of the mathematical problem is described, the Melnikov function of subharmonic orbits for a planar piecewise-smooth systems with two switching manifolds is obtained. In Sect. 3, we applied the analytical method to study the existence of subharmonic orbits for a concrete planar piecewise-smooth oscillator. Finally, we give a summary in Sect. 4.

2 Statement of the mathematical problem

2.1 System description

We divide the plane into three sets,

$$\begin{aligned} M_{1}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\,x<-\,\alpha \},\nonumber \\ M_{2}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\,-\,\alpha<x<\beta \},\nonumber \\ M_{3}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\,x>\beta \}, \end{aligned}$$

(3)

separated by two switching manifolds $\Sigma _{1}$ and $\Sigma _{2}$, where

$$\begin{aligned} \Sigma _{1}= & {} \Sigma _{1}^{+}\cup \Sigma _{1}^{-}\cup (-\,\alpha ,0),\nonumber \\ \Sigma _{2}= & {} \Sigma _{2}^{+}\cup \Sigma _{2}^{-}\cup (\beta ,0), \end{aligned}$$

(4)

and

$$\begin{aligned} \Sigma _{1}^{+}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\,x=-\,\alpha ,\quad y>0\},\nonumber \\ \Sigma _{1}^{-}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\, x=-\,\alpha ,\quad y<0\},\nonumber \\ \Sigma _{2}^{+}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\,x=\beta ,\quad y>0\},\nonumber \\ \Sigma _{2}^{-}= & {} \{(x,y)\in \mathbb {R}^{2}\,\,|\,\, x=\beta ,\quad y<0\}, \end{aligned}$$

(5)

where $\alpha$ and $\beta$ are two positive constants.

Then we consider a planar piecewise-smooth system

$$\begin{aligned} \left( {\begin{array}{l} \dot{x}\\ \dot{y}\\ \end{array}} \right)= & {} f(x,y)+\epsilon g(x,y,t)\nonumber \\= & {} \textit{JDH}(x,y)\nonumber \\&+ \left\{ \begin{array}{ll} \epsilon g_{1}(x,y,t),&{}\qquad (x, y)\in {M_{1}},\\ \epsilon g_{2}(x,y,t),&{}\qquad (x, y)\in {M_{2}},\\ \epsilon g_{3}(x,y,t),&{}\qquad (x, y)\in {M_{3}},\\ \end{array} \right. \end{aligned}$$

(6)

where

$$\begin{aligned} H(x,y):=\left\{ \begin{array}{ll} H_{1}(x,y):=\frac{y^{2}}{2}+V_{1}(x),&{}\qquad (x, y)\in {M_{1}},\\ H_{2}(x,y):=\frac{y^{2}}{2}+V_{2}(x),&{}\qquad (x, y)\in {M_{2}},\\ H_{3}(x,y):=\frac{y^{2}}{2}+V_{3}(x),&{}\qquad (x, y)\in {M_{3}},\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(7)

and we assume $g_{i}:\mathbb {R}^{2}\times \mathbb {R}\rightarrow \mathbb {R}^{2}$ are $C^{\infty }$ and $\hat{T}-$periodic in t for $i=1,\,2,\,3$, $(x, y)\in \mathbb {R}^{2}$ and $\epsilon \, (0<\epsilon \ll 1)$ is a small parameter. The functions $V_{i},\,i=1,\,2,\,3$ are $C^{\infty }(\mathbb {R})$ satisfying $V_{1}(-\,\alpha )=V_{2}(-\,\alpha )$ and $V_{2}(\beta )=V_{3}(\beta )$. We note that $D\equiv (\frac{\partial }{\partial x}, \frac{\partial }{\partial y})$ denotes the gradient operator and the matrix J is the usual symplectic matrix

$$\begin{aligned} \left( { \begin{array}{ll} 0&{} \quad 1\\ -1&{} \quad 0 \end{array}}\right) \end{aligned}$$

2.2 Geometrical structure

In the above aforementioned description, the plane is divided into three zones by the switching manifolds which are two straight lines $x=-\,\alpha$ and $x=\beta$, and the dynamics in each zone is controlled by a smooth system. From the definition of the Hamiltonian function H, it is easy to know that $\dot{x}=y+O(\epsilon )$, so every trajectory of system (6) is clockwise oriented in the phase plane for small perturbation parameter $\epsilon$. In order to develop the Melnikov method of subharmonic orbits, it is necessary to present the geometrical structure of the unperturbed system of (6) obtained by letting $\epsilon =0$ as follows:

(H1) There exists a saddle point $(0,\,0)$ by requiring $V'_{2}(0)=0$ and $V''_{2}(0)<0$ and a pair of piecewise smooth homoclinic orbits crossing the switching manifolds $\Sigma _{1}$ and $\Sigma _{2}$ transversally exactly twice, connecting $(0,\,0)$ to itself and belonging to the energy level

$$\begin{aligned}&\left\{ (x,y)\in \mathbb {R}^{2}|H_{1}(x,y)=H_{2}(x,y)\right. \nonumber \\&\quad \left. =H_{3}(x,y)=H_{2}(0,\,0)=c_{1}>0\right\} . \end{aligned}$$

(8)

(H2) The region outside the pair of homoclinic orbits is fully covered by periodic orbits crossing respectively the switching manifolds $\Sigma _{1}$ and $\Sigma _{2}$ transversally exactly twice given by

$$\begin{aligned} \Lambda _{c}= & {} \left\{ (x,y)\in \mathbb {R}^{2}|H_{1}(x,y)\right. \nonumber \\= & {} \left. H_{2}(x,y)=H_{3}(x,y)=c>c_{1}\right\} . \end{aligned}$$

(9)

(H3) The period of $\Lambda _{c}$ is a regular function of c with strictly negative derivative for $c>c_{1}$.

The phase portrait of the unperturbed system of (6) is topological equivalent to the one shown in Fig. 3, which is different from the one given by Granados et al. [9]. We must note that the region covered by $\Lambda _{c}$ is an unbounded region. Our main goal is to study the persistence of those periodic orbits in $\Lambda _{c}$ under time-periodic perturbations. These answers are given completely by the classical Melnikov method [24] for subharmonic orbits of smooth dynamical systems. We will check whether this classical tool can be extended to study the subharmonic orbits for the aforementioned piecewise-smooth systems with two switching manifolds.

Fig. 3

The phase portrait of the system (6) for $\epsilon =0$

We also give some notations which will be used in the following analysis. $\Pi _{x}:\mathbb {R}^{2}\rightarrow \mathbb {R}$ is a projection defined by $\Pi _{x}(x,y)=x$. Similarly, we define $\Pi _{y}(x,y)=y$. The wedge product of two vectors $a=(x_{1},y_{1})$ and $b=(x_{2},y_{2})$ is given by $a\wedge b=x_{1}y_{2}-x_{2}y_{1}$

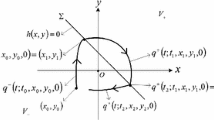
For the class of piecewise-smooth systems (6), it is important to make a precise statement of what is the solution of system (6). The key technique is to concatenate the smooth solutions on both sides of switching manifolds. So we let $\phi _{1}(t; t_{0}, x_{0}, y_{0},\epsilon )$ be the flow of system (6) restricted to $M_{1}$ with initial condition $(x_{0}, y_{0})\in M_{1}$ for $t=t_{0}$, and $t_{1}>t_{0}$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{1}(t_{1}; t_{0}, x_{0}, y_{0},\epsilon ))=-\,\alpha .$ Similarly, let $\phi _{2}^{+}(t; t_{0}, x_{1}, y_{1},\epsilon )$ for $y_{1}>0$ and $\phi _{2}^{-}(t; t_{0}, x_{1}, y_{1},\epsilon )$ for $y_{1}<0$ be the flow associated with system (6) restricted to $M_{2}$ , and $t_{2}>t_{0}$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{2}^{+}(t_{2}; t_{0}, x_{1}, y_{1},\epsilon ))=\beta$ for $y_{1}>0$ and $\Pi _{x}(\phi _{2}^{-}(t_{2}; t_{0}, x_{1}, y_{1},\epsilon ))=-\,\alpha$ for $y_{1}<0$. Similarly, $\phi _{3}(t; t_{0}, x_{2}, y_{2},\epsilon )$ be the flow associated with system (6) restricted to $M_{3}$. Hence, one can extend the definition of a solution, $\phi (t; t_{0}, x_{0}, y_{0},\epsilon )$, of system (6) for all $t\ge t_{0}$ by properly concatenating $\phi _{1}$, $\phi _{2}^{\pm }$ or $\phi _{3}$ whenever the flows cross $\Sigma _{1}\cup \Sigma _{2}$ transversally. A solution for system (6) is shown in Fig. 4.

Fig. 4

The phase portrait of the system (6) for $\epsilon >0$

2.3 Poincaré section and Poincaré map

Now we consider the extended phase space $\mathbb {R}^{2}\times \mathbb {R}$ adding time as a system variable and equation $\dot{t}=1$ to Eq. (6). In this paper, we only concern the periodic orbits respectively crossing the switching manifold $\Sigma _{1}$ and $\Sigma _{2}$ exactly twice in the motions of each circle, we define in this extended phase-space the Poincaré section

$$\begin{aligned} \tilde{\Sigma }_{1}^{+}= & {} \left\{ (-\,\alpha ,y,t)\in \mathbb {R}^{2}\times \mathbb {R}\,\,|\sqrt{2V_{2}(0)-2V_{1}(-\,\alpha )}<y\right\} .\nonumber \\ \end{aligned}$$

(10)

Other sections are also defined as follows:

$$\begin{aligned} \tilde{\Sigma }_{2}^{+}= & {} \left\{ (\beta ,y,t)\in \mathbb {R}^{2}\times \mathbb {R}\,\,|\sqrt{2V_{2}(0)-2V_{3}(\beta )}<y\right\} ,\nonumber \\ \tilde{\Sigma }_{1}^{-}= & {} \left\{ (-\,\alpha ,y,t)\in \mathbb {R}^{2}\times \mathbb {R}\,\,|\,\,y<-\,\sqrt{2V_{2}(0)-2V_{1}(-\,\alpha )}\right\} ,\nonumber \\ \tilde{\Sigma }_{2}^{-}= & {} \left\{ (\beta ,y,t)\in \mathbb {R}^{2}\times \mathbb {R}\,\,|\,\,y<-\,\sqrt{2V_{2}(0)-2V_{3}(\beta )}\right\} . \end{aligned}$$

(11)

We define the map

$$\begin{aligned} P_{\epsilon }^{c^{+}}:U_{1}^{+}\subset \tilde{\Sigma }_{1}^{+}\rightarrow \tilde{\Sigma }_{2}^{+}, \end{aligned}$$

such that

$$\begin{aligned}&P_{\epsilon }^{c^{+}}(-\,\alpha ,y_{0},t_{0})\nonumber \\&\quad =\left( \beta ,\Pi _{y}(\phi _{2}^{+}(t_{1}^{\epsilon };t_{0},-\,\alpha ,y_{0},\epsilon )),t_{1}^{\epsilon }\right) \nonumber \\&\quad =\left( \beta ,y_{1}^{\epsilon },t_{1}^{\epsilon }\right) , \end{aligned}$$

(12)

where $t_{1}^{\epsilon }>t_{0}$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{2}^{+}(t_{1}^{\epsilon };t_{0},-\,\alpha ,y_{0},\epsilon ))=\beta$.

Similarly, we consider

$$\begin{aligned} P_{\epsilon }^{r}:U_{2}^{+}\subset \tilde{\Sigma }_{2}^{+}\rightarrow \tilde{\Sigma }_{2}^{-}, \end{aligned}$$

for $(\beta ,y_{1}^{\epsilon },t_{1}^{\epsilon })\in U_{1}^{+}\subset \tilde{\Sigma }_{2}^{+}$ such that

$$\begin{aligned}&P_{\epsilon }^{r}\left( \beta ,y_{1}^{\epsilon },t_{1}^{\epsilon }\right) \nonumber \\&\quad =\left( \beta ,\Pi _{y}\left( \phi _{3}\left( t_{2}^{\epsilon };t_{1}^{\epsilon },\beta ,y_{1}^{\epsilon },\epsilon \right) \right) ,t_{2}^{\epsilon }\right) \nonumber \\&\quad =\left( \beta ,y_{2}^{\epsilon },t_{2}^{\epsilon }\right) , \end{aligned}$$

(13)

where $t_{2}^{\epsilon }>t_{1}^{\epsilon }$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{3}(t_{2}^{\epsilon };t_{1}^{\epsilon },\beta ,y_{1}^{\epsilon },\epsilon ))=\beta .$

Furthermore, we consider

$$\begin{aligned} P_{\epsilon }^{c^{-}}:U_{2}^{-}\subset \tilde{\Sigma }_{2}^{-}\rightarrow \tilde{\Sigma }_{1}^{-}, \end{aligned}$$

for $(\beta ,y_{2}^{\epsilon },t_{2}^{\epsilon })\in U_{2}^{-}\subset \tilde{\Sigma }_{2}^{-}$ defined by

$$\begin{aligned}&P_{\epsilon }^{c^{-}}\left( \beta ,y_{2}^{\epsilon },t_{2}^{\epsilon }\right) \nonumber \\&\quad =\left( -\,\alpha ,\Pi _{y}\left( \phi _{2}^{-}\left( t_{3}^{\epsilon };t_{2}^{\epsilon },\beta ,y_{2}^{\epsilon },\epsilon \right) \right) ,t_{3}^{\epsilon }\right) \nonumber \\&\quad =\left( -\,\alpha ,y_{3}^{\epsilon },t_{3}^{\varepsilon }\right) , \end{aligned}$$

(14)

where $t_{3}^{\epsilon }>t_{2}^{\epsilon }$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{2}^{-}(t_{3}^{\epsilon };t_{2}^{\epsilon },\beta ,y_{2}^{\epsilon },\epsilon ))=-\,\alpha .$

Finally, we consider

$$\begin{aligned} P_{\epsilon }^{l}:U_{1}^{-}\subset \tilde{\Sigma }_{1}^{-}\rightarrow \tilde{\Sigma }_{1}^{+}, \end{aligned}$$

for $(-\,\alpha ,y_{3}^{\epsilon },t_{3}^{\varepsilon })\in U_{1}^{-}\subset \tilde{\Sigma }_{1}^{-}$ such that

$$\begin{aligned}&P_{\epsilon }^{l}\left( -\,\alpha ,y_{3}^{\epsilon },t_{3}^{\epsilon }\right) \nonumber \\&\quad =\left( -\,\alpha ,\Pi _{y}\left( \phi _{1}\left( t_{4}^{\epsilon };t_{3}^{\epsilon },-\,\alpha ,y_{3}^{\epsilon },\epsilon \right) \right) ,t_{4}^{\epsilon }\right) \nonumber \\&\quad =\left( -\,\alpha ,y_{4}^{\epsilon },t_{4}^{\varepsilon }\right) , \end{aligned}$$

(15)

where $t_{4}^{\epsilon }>t_{3}^{\epsilon }$ is the smallest value of t satisfying the condition $\Pi _{x}(\phi _{1}(t_{4}^{\epsilon };t_{3}^{\epsilon },-\,\alpha ,y_{2}^{\epsilon },\epsilon ))=-\,\alpha .$

Now we can define the Poincaré map is shown in Fig. 5 as the composition

$$\begin{aligned}&P_{\epsilon }:U_{1}^{+}\subset \tilde{\Sigma }_{1}^{+}\rightarrow \tilde{\Sigma }_{1}^{+}\nonumber \\&\quad (-\,\alpha ,y_{0},t_{0})\mapsto P_{\epsilon }^{l}\circ P_{\epsilon }^{c^{-}}\circ P_{\epsilon }^{r}\circ P_{\epsilon }^{c^{+}} \end{aligned}$$

(16)

Fig. 5

The Poincaré map of the system (6) for $\epsilon >0$

We assume $T^{c^{+}}_{\epsilon }=t_{1}^{\epsilon }-t_{0}$, $T^{r}_{\epsilon }=t_{2}^{\epsilon }-t_{1}^{\epsilon }$, $T^{c^{-}}_{\epsilon }=t_{3}^{\epsilon }-t_{2}^{\epsilon }$, $T^{l}_{\epsilon }=t_{4}^{\epsilon }-t_{3}^{\epsilon }$ and $P_{0}$ is the Poincaré map for $\epsilon =0$, then without proving, we obtain

$$\begin{aligned} T^{c^{+}}_{\epsilon }= & {} T^{c^{+}}_{0}+O(\epsilon ), \quad T^{r}_{\epsilon }=T^{r}_{0}+O(\epsilon ), \nonumber \\ T^{c^{-}}_{\epsilon }= & {} T^{c^{-}}_{0}+O(\epsilon ),\quad T^{l}_{\epsilon }=T^{l}_{0}+O(\epsilon ), \end{aligned}$$

(17)

and

$$\begin{aligned}&P_{0}(-\,\alpha ,y_{0},t_{0})\nonumber \\&\quad =(-\,\alpha ,y_{0},t_{0}+T^{c^{+}}_{0}+T^{r}_{0}+T^{c^{-}}_{0}+T^{l}_{0}). \end{aligned}$$

(18)

Based on notations and geometrical structures for the unperturbed system aforementioned, any periodic orbit with initial condition $(-\,\alpha ,y_{0},t_{0})\in \tilde{\Sigma }_{1}^{+}$ has period

$$\begin{aligned} T(y_{0})=T^{c^{+}}_{0}+T^{r}_{0}+T^{c^{-}}_{0}+T^{l}_{0}. \end{aligned}$$

(19)

Now we will employ the maps presented above to define the intersection sequences of solutions on switching manifolds with initial conditions $(-\,\alpha ,y_{0},t_{0})\in \tilde{\Sigma }_{1}^{+}$ as

$$\begin{aligned} (x^{\epsilon },\,y^{\epsilon },\,t^{\epsilon }) = \left\{ \begin{array}{ll} \left( \beta ,y_{4i+1}^{\epsilon },t_{4i+1}^{\epsilon }\right) =p_{\epsilon }^{c^{+}}\left( -\,\alpha ,y_{4i}^{\epsilon },t_{4i}^{\epsilon }\right) ,&{}\quad \left( -\,\alpha ,y_{4i}^{\epsilon },t_{4i}^{\epsilon }\right) \in \tilde{\Sigma }_{1}^{+},\\ \left( \beta ,y_{4i+2}^{\epsilon },t_{4i+2}^{\epsilon }\right) =p_{\epsilon }^{r}\left( \beta ,y_{4i+1}^{\epsilon },t_{4i+1}^{\epsilon }\right) ,&{}\quad \left( \beta ,y_{4i+1}^{\epsilon },t_{4i+1}^{\epsilon }\right) \in \tilde{\Sigma }_{2}^{+},\\ \left( -\,\alpha ,y_{4i+3}^{\epsilon },t_{4i+3}^{\epsilon }\right) =p_{\epsilon }^{c^{-}}\left( \beta ,y_{4i+2}^{\epsilon },t_{4i+2}^{\epsilon }\right) ,&{}\quad \left( \beta ,y_{4i+2}^{\epsilon },t_{4i+2}^{\epsilon }\right) \in \tilde{\Sigma }_{2}^{-},\\ \left( -\,\alpha ,y_{4i+4}^{\epsilon },t_{4i+4}^{\epsilon }\right) =p_{\epsilon }^{l}\left( -\,\alpha ,y_{4i+3}^{\epsilon },t_{4i+3}^{\epsilon }\right) ,&{}\quad \left( -\,\alpha ,y_{4i+3}^{\epsilon },t_{4i+3}^{\epsilon }\right) \in \tilde{\Sigma }_{1}^{-},\\ \end{array} \right. \end{aligned}$$

(20)

where $i=0, 1, 2 \ldots ,$ such that $(-\,\alpha ,y_{0}^{\epsilon },t_{0}^{\epsilon })=(-\,\alpha ,y_{0},t_{0})$. We here note that $p_{\epsilon }^{c^{+}}$, $p_{\epsilon }^{r}$, $p_{\epsilon }^{c^{-}}$, and $p_{\epsilon }^{l}$, are defined in equations (12)–(15).

Hence, a solution of the non-autonomous system (6) with initial condition $(-\,\alpha , y_{0}, t_{0})\in \tilde{\Sigma }^{+}_{1}$ can be concatenated and defined as

$$\begin{aligned}&\phi (t;t_{0},-\,\alpha ,y_{0},\epsilon )\nonumber \\&\quad =\left\{ \begin{array}{ll} \phi ^{+}_{2}\left( t;t^{\epsilon }_{4i},-\,\alpha ,y^{\epsilon }_{4i},\epsilon \right) ,&{} \quad if \,\, t^{\epsilon }_{4i}<t<t^{\epsilon }_{4i+1}, \\ \phi _{3}\left( t;t^{\epsilon }_{4i+1},\beta ,y^{\epsilon }_{4i+1},\epsilon \right) ,&{} \quad if\,\, t^{\epsilon }_{4i+1}<t<t^{\epsilon }_{4i+2}, \\ \phi ^{-}_{2}\left( t;t^{\epsilon }_{4i+2},\beta ,y^{\epsilon }_{4i+2},\epsilon \right) ,&{} \quad if\,\, t^{\epsilon }_{4i+2}<t<t^{\epsilon }_{4i++3}, \\ \phi _{1}\left( t;t^{\epsilon }_{4i+3},-\,\alpha ,y^{\epsilon }_{4i+3},\epsilon \right) ,&{} \quad if \,\,t^{\epsilon }_{4i+3}<t<t^{\epsilon }_{4i+4},\\ \end{array}\right. \nonumber \\&\quad i \ge 0. \end{aligned}$$

(21)

2.4 Definition and existence of subharmonic orbits

We will employ the Poincaré map defined in (16) and the intersection sequences of solutions on switching manifolds presented in (20) to define what is subharmonic periodic orbits. The idea is from Granados et al. [9].

Definition 1

For any $\epsilon \,(0<\epsilon \ll 1)$ and the Poincaré map defined in (16), if there exist a point $(-\,\alpha ,\,y_{0},\,t_{0})\in U_{1}^{+}\subset \tilde{\Sigma }_{1}^{+}$, a positive integer n and a smallest positive integer m such that the following equation is satisfied

$$\begin{aligned} P_{\epsilon }^{m}(-\,\alpha ,y_{0},t_{0})= & {} (-\,\alpha ,y_{0},t_{0}+n\hat{T}), \end{aligned}$$

(22)

then, $\phi (t;t_{0},-\,\alpha ,y_{0},\epsilon )$ will be a periodic orbit of period $n\hat{T}$, which crosses the switching manifolds $\Sigma _{1}$ and $\Sigma _{2}$ exactly 2m times. This periodic orbit is called a subharmonic periodic orbit of type (n, m).

Next, we will study the existence of (n, m)-type subharmonic orbits. Firstly, we give an integral notation for convenient writing in following analysis as follows:

$$\begin{aligned}&\int _{t_{0}}^{t_{4m}^{\epsilon }}f(\phi _(t; t_{0}, -\,\alpha , y_{0},\epsilon ))\nonumber \\&\qquad \wedge \, g(\phi (t; t_{0}, -\,\alpha , y_{0},\epsilon ),t)dt\nonumber \\&\quad =\sum _{i=0}^{m-1}\int _{t_{4i}^{\epsilon }}^{t_{4i+1}^{\epsilon }}{} \textit{JDH}_{2}\left( \phi _{2}^{+}\left( t; t_{4i}^{\epsilon }, -\,\alpha , y_{4i}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{2}\left( \phi _{2}^{+}\left( t; t_{4i}^{\epsilon }, -\,\alpha , y_{4i}^{\epsilon },\epsilon \right) ,t\right) dt\nonumber \\&\qquad +\sum _{i=0}^{m-1}\int _{t_{4i+1}^{\epsilon }}^{t_{4i+2}^{\epsilon }}{} \textit{JDH}_{3}\left( \phi _{3}\left( t; t_{4i+1}^{\epsilon }, \beta , y_{4i+1}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \,g_{3}\left( \phi _{3}\left( t; t_{4i+1}^{\epsilon }, \beta , y_{4i+1}^{\epsilon },\epsilon \right) ,t\right) dt\nonumber \\&\qquad +\sum _{i=0}^{m-1}\int _{t_{4i+2}^{\epsilon }}^{t_{4i+3}^{\epsilon }}{} \textit{JDH}_{2}\left( \phi _{2}^{-}\left( t; t_{4i+2}^{\epsilon }, \beta , y_{4i+2}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{2}\left( \phi _{2}^{-}\left( t; t_{4i+2}^{\epsilon }, \beta , y_{4i+2}^{\epsilon },\epsilon \right) ,t\right) dt\nonumber \\&\qquad +\sum _{i=0}^{m-1}\int _{t_{4i+3}^{\epsilon }}^{t_{4i+4}^{\epsilon }}{} \textit{JDH}_{1}\left( \phi _{1}\left( t; t_{4i+3}^{\epsilon }, -\,\alpha , y_{4i+3}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{1}\left( \phi _{1}\left( t; t_{4i+3}^{\epsilon }, -\,\alpha , y_{4i+3}^{\epsilon },\epsilon \right) ,t\right) dt. \end{aligned}$$

(23)

In order to obtain the main result of this paper about the existence of subharmonic periodic orbits, we next present a lemma.

Lemma 1

Let $m\ge 1$ and $(-\,\alpha ,y_{0},t_{0})\in \tilde{\Sigma }_{1}^{+}$, and let $(\beta ,y_{4i+1}^{\epsilon },t_{4i+1}^{\epsilon })$, $(\beta ,y_{4i+2}^{\epsilon },t_{4i+2}^{\epsilon })$, $(-\,\alpha ,y_{4i+3}^{\epsilon },t_{4i+3}^{\epsilon })$ and $(-\,\alpha ,y_{4i+4}^{\epsilon },t_{4i+4}^{\epsilon })$, $i=0,\ldots , m-1$, be its associated sequences defined in (20). We can use the Hamiltonian function $H_{2}$ to measure the distance between the points $(-\,\alpha , y_{0})$ and $(-\,\alpha , y_{4m}^{\epsilon })$. Then,

$$\begin{aligned}&H_{2}\left( -\,\alpha ,y_{4m}^{\epsilon }\right) -H_{2}(-\,\alpha ,y_{0})\nonumber \\&\quad =\epsilon \int _{t_{0}}^{t_{4m}^{\epsilon }}f(\phi (t; t_{0}, -\,\alpha , y_{0},\epsilon ))\nonumber \\&\qquad \wedge \,g(\phi (t; t_{0}, -\,\alpha , y_{0},\epsilon ),t)dt\nonumber \\&\quad =\epsilon \int _{t_{0}}^{t_{0}+mT(y_{0})}f(\phi (t; t_{0}, -\,\alpha , y_{0},0))\nonumber \\&\qquad \, \wedge \,g(\phi (t; t_{0}, -\,\alpha , y_{0},0),t)dt+o(\epsilon ), \end{aligned}$$

(24)

where $\phi (t; t_{0}, -\,\alpha , y_{0},0)$ is denoted as a periodic orbit in the region outside the pair of homoclinic orbits.

Proof

Since

$$\begin{aligned}&H_{2}\left( -\,\alpha ,y_{4m}^{\epsilon }\right) -H_{2}(-\,\alpha ,y_{0})\nonumber \\&\quad =\sum _{i=0}^{m-1}\left[ H_{2}\left( -\,\alpha , y_{4i+4}^{\epsilon }\right) -H_{2}\left( -\,\alpha , y_{4i+3}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{2}\left( -\,\alpha , y_{4i+3}^{\epsilon }\right) -H_{2}\left( \beta , y_{4i+2}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{2}\left( \beta , y_{4i+2}^{\epsilon }\right) -H_{2}\left( \beta , y_{4i+1}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{2}\left( \beta , y_{4i+1}^{\epsilon }\right) -H_{2}\left( -\,\alpha , y_{4i}^{\epsilon }\right) \right] \nonumber \\&\quad =\sum _{i=0}^{m-1}\left[ H_{1}\left( -\,\alpha , y_{4i+4}^{\epsilon }\right) -H_{1}\left( -\,\alpha , y_{4i+3}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{2}\left( -\,\alpha , y_{4i+3}^{\epsilon }\right) -H_{2}\left( \beta , y_{4i+2}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{3}\left( \beta , y_{4i+2}^{\epsilon }\right) -H_{3}\left( \beta , y_{4i+1}^{\epsilon }\right) \right] \nonumber \\&\qquad +\sum _{i=0}^{m-1}\left[ H_{2}\left( \beta , y_{4i+1}^{\epsilon }\right) -H_{2}\left( -\,\alpha , y_{4i}^{\epsilon }\right) \right] , \end{aligned}$$

(25)

and noticing the following fact

$$\begin{aligned}&\frac{d}{dt}H_{1}(\phi _{1}(t;t^{*},-\,\alpha ,y^{*},\epsilon ))\\&\quad =\epsilon JD_{x}H_{1}(\phi _{1}(t;t^{*},-\,\alpha ,y^{*},\epsilon ))\\&\qquad \wedge \, g_{1}(\phi _{1}(t;t^{*},-\,\alpha ,y^{*},\epsilon ),t),\\&\frac{d}{dt}H_{2}\left( \phi _{2}^{\pm }\left( t;t^{*},-\,\alpha ,y^{*},\epsilon \right) \right) \\&\quad =\epsilon JD_{x}H_{2}(\phi _{2}^{\pm }(t;t^{*},-\,\alpha ,y^{*},\epsilon ))\\&\qquad \wedge \, g_{2}\left( \phi _{2}^{\pm }\left( t;t^{*},-\,\alpha ,y^{*},\epsilon \right) ,t\right) , \end{aligned}$$

and

$$\begin{aligned}&\frac{d}{dt}H_{3}(\phi _{3}(t;t^{*},\beta ,y^{*},\epsilon ))\\&\quad =\epsilon JD_{x}H_{3}(\phi _{3}(t;t^{*},\beta ,y^{*},\epsilon ))\\&\qquad \wedge \,g_{3}(\phi _{3}(t;t^{*},\beta ,y^{*},\epsilon ),t) \end{aligned}$$

for any $(-\,\alpha , y^{*}, t^{*})\in \tilde{\Sigma }_{1}^{-}$ and $t>t^{*}$ such that $\phi _{1}(t, t^{*}, -\,\alpha , y^{*}, \epsilon )\in M_{1}$; for any $(-\,\alpha , y^{*}, t^{*})\in \tilde{\Sigma }_{1}^{+}$ and $t>t^{*}$ such that $\phi _{2}^{+}(t, t^{*}, -\,\alpha , y^{*}, \epsilon )\in M_{2}$; for any $(\beta , y^{*}, t^{*})\in \tilde{\Sigma }_{2}^{+}$ and $t>t^{*}$ such that $\phi _{3}(t, t^{*}, \beta , y^{*}, \epsilon )\in M_{3}$; and for any $(\beta , y^{*}, t^{*})\in \tilde{\Sigma }_{2}^{-}$ and $t> t^{*}$ such that $\phi _{2}^{-}(t, t^{*}, \beta , y^{*}, \epsilon )\in M_{2}$, then for $0\le i\le m-1$, we obtain

$$\begin{aligned}&H_{2}\left( \beta , y_{4i+1}^{\epsilon }\right) -H_{2}\left( -\,\alpha , y_{4i}^{\epsilon }\right) \nonumber \\&\quad =\epsilon \int _{t_{4i}^{\epsilon }}^{t_{4i+1}^{\epsilon }}JD_{x}H_{2}\left( \phi _{2}^{+}\left( t; t_{4i}^{\epsilon },-\,\alpha , y_{4i}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{2}\left( \phi _{2}^{+}\left( t; t_{4i}^{\epsilon },-\,\alpha , y_{4i}^{\epsilon },\epsilon \right) ,t\right) dt, \end{aligned}$$

(26)

$$\begin{aligned}&H_{3}\left( \beta , y_{4i+2}^{\epsilon }\right) -H_{3}\left( \beta , y_{4i+1}^{\epsilon }\right) \nonumber \\&\quad =\epsilon \int _{t_{4i+1}^{\epsilon }}^{t_{4i+2}^{\epsilon }}(JD_{x}H_{2}\left( \phi _{3}\left( t; t_{4i+1}^{\epsilon },\beta , y_{4i+1}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{3}\left( \phi _{3}\left( t; t_{4i+1}^{\epsilon },\beta , y_{4i+1}^{\epsilon },\epsilon \right) ,t\right) dt, \end{aligned}$$

(27)

$$\begin{aligned}&H_{2}\left( -\,\alpha , y_{4i+3}^{\epsilon }\right) -H_{2}\left( \beta , y_{4i+2}^{\epsilon }\right) \nonumber \\&\quad =\epsilon \int _{t_{4i+2}^{\epsilon }}^{t_{4i+3}^{\epsilon }}JD_{x}H_{2}\left( \phi _{2}^{-}\left( t; t_{4i+2}^{\epsilon },\beta , y_{4i+2}^{\epsilon },\epsilon \right) \right) \nonumber \\&\qquad \wedge \, g_{2}\left( \phi _{2}^{-}\left( t; t_{4i+2}^{\epsilon },\beta , y_{4i+2}^{\epsilon },\epsilon \right) ,t\right) dt, \end{aligned}$$

(28)

$$\begin{aligned}&H_{1}(-\,\alpha , y_{4i+4}^{\epsilon })-H_{1}(-\,\alpha , y_{4i+3}^{\epsilon })\nonumber \\&\quad =\epsilon \int _{t_{4i+3}^{\epsilon }}^{t_{4i+4}^{\epsilon }}JD_{x}H_{1}(\phi _{1}(t; t_{4i+3}^{\epsilon },-\,\alpha , y_{4i+3}^{\epsilon },\epsilon ))\nonumber \\&\qquad \wedge \, g_{1}(\phi _{1}(t; t_{4i+3}^{\epsilon },-\,\alpha , y_{4i+3}^{\epsilon },\epsilon ),t)dt. \end{aligned}$$

(29)

Hence, substituting (26)–(29) into (25) and carrying on the expansion in the perturbation parameter $\epsilon$, we can respectively obtain the first and second equality of (24) and we have completed the proof of Lemma 1. $\square$

Now we can define the Melnikov-type function for possible subharmonic periodic orbits as follows:

(30)

The main theorem for the existence of subharmonic orbits is based on the idea in Granados et al. [9] and presented as follows:

Theorem 1

A system defined in (6) with two switching manifolds $x=-\,\alpha$ and $x=\beta$ satisfies assumptions $(\mathrm{H}1)--(\mathrm{H}3)$, and $T(y_{0})$ defined in (19) is the period of for an periodic orbit in the region outside the pair of homoclinic orbits. Assume that the point $(-\,\alpha , \bar{y}_{0}, \bar{t}_{0})\in \tilde{\Sigma }^{+}$ satisfies

• (B1) $T(\bar{y}_{0})=\displaystyle \frac{n\hat{T}}{m}$, with $n, m\in Z$ relatively prime.

• (B2) $\bar{t}_{0}\in [0,\hat{T}]$ is a simple zero of the $M(t_{0}, \bar{y}_{0})$ with the form

$$\begin{aligned} M(t_{0},\bar{y}_{0})= & {} \int _{0}^{mT(\bar{y}_{0})}f(\phi (t; 0, -\,\alpha , \bar{y}_{0},0))\nonumber \\&\quad \wedge \, g(\phi (t; 0, -\,\alpha , \bar{y}_{0}, 0), t+t_{0})dt, \end{aligned}$$

(31)

where $\phi (t; 0, -\,\alpha , \bar{y}_{0}, 0)$ is denoted as a periodic orbit with period $T(\bar{y}_{0})=n/m\hat{T}$ in the region outside the pair of homoclinic orbits for the unperturbed system.

Then, there exists $\epsilon _{0}$ such that for every $0<\epsilon <\epsilon _{0}$, one can find $y^{*}_{0}$ and $t^{*}_{0}$ such that $\phi (t; t^{*}_{0}, -\,\alpha , y^{*}_{0}, \epsilon )$ is an subharmonic periodic orbit with type (n, m), where $y^{*}_{0}=\bar{y}_{0}+O(\epsilon )$ and $t^{*}_{0}=t_{0}+O(\epsilon )$.

Proof

Based on the definition of the subharmonic periodic orbit with type (n, m) with the help of Poincaré map, we can rewrite (22) as follows:

$$\begin{aligned}&\left( { \begin{array}{l} H_{2}\bigg (-\,\alpha ,\Pi _{y}(P_{\epsilon }^{m}(-\,\alpha ,y_{0}, t_{0}))\bigg )\\ \Pi _{t}(P_{\epsilon }^{m}(-\,\alpha ,y_{0}, t_{0})) \end{array}} \right) - \left( { \begin{array}{l} H_{2}(-\,\alpha ,y_{0})\\ t_{0}+n\hat{T} \end{array}} \right) \nonumber \\&\quad =\left( { \begin{array}{l} 0\\ 0\\ \end{array}} \right) . \end{aligned}$$

(32)

Expanding this equation in powers of $\epsilon$ and employing the Eqs. (24) and (30), we obtain

$$\begin{aligned}&G_{n,\,m}(y_{0}, t_{0}, \epsilon ) :=\left( { \begin{array}{l} M(t_{0}, y_{0})+O(\epsilon )\\ mT(y_{0})-n\hat{T}+O(\epsilon )\\ \end{array}} \right) \nonumber \\&\quad =\left( { \begin{array}{l} 0\\ 0\\ \end{array}} \right) , \end{aligned}$$

(33)

where the order in $\epsilon$ of the first component has been reduced. $\square$

By the conditions (B1) and (B2) in the Theorem 1 and the assumption (H3), there exist $\bar{t}_{0}$ and $\bar{y}_{0}$ such that $G_{n,\,m}(\bar{y}_{0}, \bar{t}_{0}, 0)=(0, 0)^{T}$ and $\det \bigg (D_{y_{0}, t_{0}}(G_{n,\,m}(\bar{y}_{0}, \bar{t}_{0}, 0))\bigg )\ne 0$, where $D_{y_{0}, t_{0}}\bigg (G_{n,\,m}(\bar{y}_{0}, \bar{t}_{0}, 0)\bigg )$ is the Jacobian with respect to the variable $y_{0}$ and $t_{0}$ shown as follows:

$$\begin{aligned}&D_{y_{0}, t_{0}}\bigg (G_{n,\,m}(\bar{y}_{0}, \bar{t}_{0}, 0)\bigg )= \left( {\begin{array}{l} \,\displaystyle \frac{\partial M(\bar{t}_{0}, \bar{y}_{0})}{\partial y_{0}}\,\,\displaystyle \frac{\partial M(\bar{t}_{0}, \bar{y}_{0})}{\partial t_{0}}\\ \,\,\,mT_{c}^{'}(\bar{y}_{0})\,\,\,\,\,\,\,\,\,\,\,\,\,0\\ \end{array}} \right) . \end{aligned}$$

Next, applying the implicit function theorem to (33) at $(y_{0}, t_{0}, \epsilon )=(\bar{y}_{0}, \bar{t}_{0}, 0)$, there exists $\epsilon _{0}$ such that for every $0<\epsilon <\epsilon _{0}$, one can find unique $y_{0}^{*}$ and $t_{0}^{*}$ solutions of the Eq. (33) such that $y_{0}^{*}=\bar{y}_{0}+O(\epsilon )$ and $t_{0}^{*}=\bar{t}_{0}+O(\epsilon )$. Hence, $\phi (t; t_{0}^{*},-\,\alpha , y_{0}^{*})$ is an (n, m)—periodic orbit with period $n\hat{T}$ and respectively impacts 2m times with the switching manifold $\Sigma _{1}$ and $\Sigma _{2}$ in every period.

This Theorem 1 is very important because it provides an estimation about the initial condition for the existence of subharmonic orbits in this class of non-smooth dynamical system. Next, we will summarize the procedures to show how to apply this Theorem 1 to study the existence of subharmonic orbits. Firstly, we should check whether the geometrical structure of the unperturbed system satisfies the assumptions (H1)–(H3), and if it does, we need to obtain the analytical expressions $\phi (t, 0, -\,\alpha , y_{0}, 0)$ with period $T(y_{0})$ for the piecewise-defined periodic orbits in the region outside the pair of homoclinic orbits. Secondly, we calculate the Melnikov function (30) and choose $n, m\in Z$ relatively prime such that the conditions (B1) and (B2) in the theorem are satisfied. Then we can obtain $(\bar{t}_{0},\,\bar{y}_{0})$ which are likely to be multiple choices. Next, we can obtain the initial conditions $(t_{0}^{*}, -\,\alpha , y_{0}^{*})$ such that $y_{0}^{*}=\bar{y}_{0}+O(\epsilon )$ and $t_{0}^{*}=\bar{t}_{0}+O(\epsilon )$. Finally, we carry on numerical simulations for the system (6) with the initial condition $(t_{0}^{*}, -\,\alpha , y_{0}^{*})$ to verify the existence of subharmonic orbits with type $(n,\,m)$.

There are other important points which should be noted clearly here. Noticing the geometrical structure of the unperturbed system of (6), the period $T(y_{0})$ will tend to infinity when the periodic orbits approach the pair of homoclinic orbits or $y_{0}$ tends to $\sqrt{2V_{2}(0)-2V_{1}(-\,\alpha )}$. So in this case, the perturbation technique should be made some minor revision and is not illustrated clearly in this paper. Another point is noticed that the Melnikov function for homoclinic orbits has been presented by Li et al. [19]. However, the relation between homoclinic and subharmonic Melnikov methods has not been found for planar non-smooth dynamical systems and it is an open problem so far.

3 A piecewise-smooth oscillator

In this section, we apply the obtained results in Sect. 2 to study the existence of subharmonic orbits for a concrete planar piecewise-smooth oscillator. The equation considered in this example can be written as

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}=y,\\ \dot{y}=-x-2 \mu y+f_{0}\cos \omega t.\\ \end{array} \right. \qquad |x|>\alpha , \end{aligned}$$

(34)

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}=y,\\ \dot{y}=x-2 \mu y+f_{0}\cos \omega t.\\ \end{array} \right. \qquad |x|<\alpha , \end{aligned}$$

(35)

where $\mu$ is the damping and $f_{0}$ is the excitation, $\alpha$ is a constant with $0<\alpha <1$.

The unperturbed system of (34), (35), which is a piecewise Hamiltonian system and obtained by letting $\mu =f_{0}=0$, can be written in the following form:

$$\begin{aligned} \dot{x}= & {} \displaystyle \frac{\partial {H}}{\partial {y}},\nonumber \\ \dot{y}= & {} -\displaystyle \frac{\partial {H}}{\partial {x}}, \end{aligned}$$

(36)

where the piecewise Hamiltonian function is

$$\begin{aligned}&H(x,\,y)\nonumber \\&\quad =\left\{ \begin{array}{ll} H_{1}(x,\,y)= \displaystyle \frac{1}{2}y^{2}+\frac{x^{2}}{2}-\frac{\alpha ^{2}}{2},&{}\qquad x<-\,\alpha ,\\ H_{2}(x,\,y)=\displaystyle \frac{1}{2}y^{2}-\frac{x^{2}}{2}+\frac{\alpha ^{2}}{2},\,&{}\qquad |x\,|<\alpha ,\\ H_{3}(x,\,y)=\displaystyle \frac{1}{2}y^{2}+\frac{x^{2}}{2}-\frac{\alpha ^{2}}{2},\,&{}\qquad x>\alpha .\\ \end{array} \right. \end{aligned}$$

(37)

We can check that the assumptions (H1)–(H3) described in Sect. 2 for system (36) are satisfied, and the phase portrait of the unperturbed system with two symmetric switching manifolds $\Sigma =\{(x,y)|x=\pm \alpha , y\in \mathbb {R}\}$ is equivalent to the one shown in Fig. 3. The analytical expression for the period orbit with initial condition $(t_{0},\,-\,\alpha , y_{0})$ for $y_{0}>\alpha$ is given by

$$\begin{aligned}&\phi (t;t_{0},-\,\alpha ,y_{0},0)\nonumber \\&\quad =\left\{ \begin{array}{l} \phi ^{+}_{2}(t;t_{0},-\,\alpha ,y_{0},0)=\bigg (a_{1}e^{t}+a_{2}e^{-t},\,a_{1}e^{t}-a_{2}e^{-t}\bigg ),\\ if~~ t_{0}<t<t_{0}+T_{c}^{+}, \\ \phi _{3}(t;t_{0}+T_{c}^{+},\alpha ,y_{0},0)\\ \quad =\bigg (\alpha \cos (t-T_{c}^{+})+y_{0}\sin (t-T_{c}^{+}),\,-\,\alpha \sin (t-T_{c}^{+})+y_{0}\cos (t-T_{c}^{+})\bigg ), \\ if~~ t_{0}+T_{c}^{+}<t<t_{0}+T_{c}^{+}+T_{r}, \\ \phi ^{-}_{2}(t;t_{0}+T_{c}^{+}+T_{r} ,\alpha ,-y_{0},0)\\ \quad =\bigg (-a_{1}e^{t-T_{c}^{+}-T_{r}}-a_{2}e^{-t+T_{c}^{+}+T_{r}},\,-a_{1}e^{t-T_{c}^{+}-T_{r}}+a_{2}e^{-t+T_{c}^{+}+T_{r}}\bigg )\\ if~~ t_{0}+T_{c}^{+}+T_{r}<,t<t_{0}+2T_{c}^{+}+T_{r}, \\ \phi _{1}(t;t_{0}+2T_{c}^{+}+T_{r},-\,\alpha ,-y_{0},0)\\ \quad =\bigg (-\,\alpha \cos (t-2T_{c}^{+}-T_{r})-y_{0}\sin (t-2T_{c}^{+}-T_{r}),\,\\ \alpha \sin (t-2T_{c}^{+}-T_{r})-y_{0}\cos (t-2T_{c}^{+}-T_{r})\bigg ),\\ if~~ t_{0}+2T_{c}^{+}+T_{r}<t<T(y_{0}), \end{array} \right. \end{aligned}$$

(38)

where

$$\begin{aligned} a_{1}= & {} \displaystyle \frac{y_{0}-\,\alpha }{2},\quad a_{2}=-\frac{y_{0}+\alpha }{2},\quad T_{c}^{+}=\ln \displaystyle \frac{\alpha +y_{0}}{y_{0}-\,\alpha },\nonumber \\ \sin T_{r}= & {} \displaystyle \frac{2\alpha y_{0}}{\alpha ^{2}+y_{0}^{2}}, \quad \cos T_{r}=\displaystyle \frac{\alpha ^2-y_{0}^2}{\alpha ^{2}+y_{0}^{2}}, \nonumber \\ T_{r}= & {} \pi -\arcsin \displaystyle \frac{\alpha ^2-y_{0}^2}{\alpha ^{2}+y_{0}^{2}},\nonumber \\ T(y_{0})= & {} 2(T_{c}^{+}+T_{r}),\,T'(y_{0})<0. \end{aligned}$$

(39)

In order to study the existence of subharmonic orbits with type $(n,\,m)$, we first let

$$\begin{aligned} T(y_{0})=\displaystyle \frac{n\hat{T}}{m}=\frac{2n\pi }{m\omega }, \end{aligned}$$

(40)

and employ the Melnikov function defined in (30) to obtain the corresponding Melnikov function for the planar piecewise-smooth system (34) and (35) as follows:

$$\begin{aligned}&M(t_{0},\,y_{0})\nonumber \\&\quad =\sum _{j=0}^{m-1}\int _{0}^{T_{c}^{+}}-2\mu \left[ \Pi _{y}\left( \phi ^{+}_{2}\left( t;0,-\,\alpha ,y_{0},0\right) \right) \right] ^{2} \nonumber \\&\qquad +f_{0}\left[ \Pi _{y}\left( \phi ^{+}_{2}\left( t;0,-\,\alpha ,y_{0},0\right) \right) \right] \cos \left( \omega \left( t+t_{0}+j\frac{n\hat{T}}{m}\right) \right) dt\nonumber \\&\qquad +\sum _{j=0}^{m-1}\int _{T_{c}^{+}}^{T_{c}^{+}+T_{r}}-2\mu \left[ \Pi _{y}\left( \phi _{3}\left( t;T_{c}^{+},\alpha ,y_{0},0\right) \right) \right] ^{2} \nonumber \\&\qquad +f_{0}\left[ \Pi _{y}\left( \phi _{3}\left( t;T_{c}^{+},\alpha ,y_{0},0\right) \right) \right] \cos \left( \omega \left( t+t_{0}+j\frac{n\hat{T}}{m}\right) \right) dt\nonumber \\&\qquad +\sum _{j=0}^{m-1}\int _{T_{c}^{+}+T_{r}}^{2T_{c}^{+}+T_{r}} -2\mu \left[ \Pi _{y}(\phi ^{-}_{2}(t;T_{c}^{+}+T_{r},\alpha , -y_{0},0))\right] ^{2} \nonumber \\&\qquad +f_{0}\left[ \Pi _{y}\left( \phi ^{-}_{2}\left( t;T_{c}^{+}+T_{r} ,\alpha ,-y_{0},0\right) \right) \right] \cos \left( \omega \left( t+t_{0}+j \frac{n\hat{T}}{m}\right) \right) dt\nonumber \\&\qquad +\sum _{j=0}^{m-1}\int _{2T_{c}^{+}+T_{r}}^{T}-2\mu \left[ \Pi _{y} \left( \phi _{1}(t;2T_{c}^{+}+T_{r},-\,\alpha ,-y_{0},0)\right) \right] ^{2} \nonumber \\&\qquad +f_{0}\left[ \Pi _{y}\left( \phi _{1}\left( t;2T_{c}^{+}+T_{r},-\,\alpha ,-y_{0},0\right) \right) \right] \cos \left( \omega \left( t+t_{0}+j\frac{n\hat{T}}{m}\right) \right) dt.\nonumber \\ \end{aligned}$$

(41)

and, after some calculations shown in the Appendix in detail, we have

$$\begin{aligned} M(t_{0},\,y_{0})= & {} -\,2m\mu \bigg ([y_{0}^{2}-\,\alpha ^{2}]T_{c}^{+}+[\alpha ^{2}+y_{0}^{2}]T_{r}\bigg )\nonumber \\&\quad +\sum _{j=0}^{m-1}\frac{4f_{0}}{1+\omega ^{2}}\sin \bigg (\omega t_{0}+j\displaystyle \frac{2n\pi }{m}+\frac{\omega T_{c}^{+}}{2}\nonumber \\&\quad +\displaystyle \frac{n\pi }{2m}\bigg ) \bigg (\alpha \cos \frac{\omega T_{c}^{+}}{2}+y_{0}\omega \sin \frac{\omega T_{c}^{+}}{2}\bigg )\sin \bigg (\displaystyle \frac{n\pi }{2m}\bigg )\nonumber \\&\quad +\sum _{j=0}^{m-1} \frac{2\alpha f_{0}}{1+\omega }\cos \bigg (\omega t_{0}+j\displaystyle \frac{2n\pi }{m}+\frac{n\pi }{m}\nonumber \\&\quad +\frac{\omega T_{c}^{+}}{2}+\frac{T_{r}}{2}\bigg )\sin \frac{(1+\omega )T_{r}}{2} \sin \displaystyle \frac{n\pi }{2m}\nonumber \\&\quad -\sum _{j=0}^{m-1} \frac{2\alpha f_{0}}{1-\omega }\cos \bigg (\omega t_{0}+j\displaystyle \frac{2n\pi }{m}+\frac{n\pi }{m}\nonumber \\&\quad +\frac{\omega T_{c}^{+}}{2}-\frac{T_{r}}{2}\bigg )\sin \frac{(1-\omega )T_{r}}{2} \sin \displaystyle \frac{n\pi }{2m}\nonumber \\&\quad +\sum _{j=0}^{m-1} \frac{2y_{0} f_{0}}{1+\omega }\sin \bigg (\omega t_{0}+j\displaystyle \frac{2n\pi }{m}+\frac{n\pi }{m}\nonumber \\&\quad +\frac{\omega T_{c}^{+}}{2}+\frac{T_{r}}{2}\bigg )\sin \frac{(1+\omega )T_{r}}{2} \sin \displaystyle \frac{n\pi }{2m}\nonumber \\&\quad +\sum _{j=0}^{m-1} \frac{2y_{0} f_{0}}{1-\omega }\sin \bigg (\omega t_{0}+j\displaystyle \frac{2n\pi }{m}+\frac{n\pi }{m}\nonumber \\&\quad +\frac{\omega T_{c}^{+}}{2}-\frac{T_{r}}{2}\bigg )\sin \frac{(1-\omega )T_{r}}{2} \sin \displaystyle \frac{n\pi }{2m}. \end{aligned}$$

(42)

In order to study the existence of subharmonic orbits with (n, m)-type , we only consider the case of $\dfrac{n}{m}=4k+1$ for $k\ge 0$, then the Melnikov function can be further simplified as

$$\begin{aligned} M(t_{0},y_{0})= & {} -\,2m\mu \bigg ([y_{0}^{2}-\,\alpha ^{2}]T_{c}^{+}+[\alpha ^{2}+y_{0}^{2}]T_{r}\bigg )\nonumber \\&+\frac{4mf_s{0}}{1+\omega ^{2}}\cos \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}\bigg ) \bigg (\alpha \cos \frac{\omega T_{c}^{+}}{2}\nonumber \\&+y_{0}\omega \sin \frac{\omega T_{c}^{+}}{2}\bigg )\nonumber \\&-\frac{2m\alpha f_{0}}{1+\omega }\cos \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}+\frac{T_{r}}{2}\bigg )\sin \frac{(1+\omega )T_{r}}{2}\nonumber \\&+\frac{2m\alpha f_{0}}{1-\omega }\cos \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}-\frac{T_{r}}{2}\bigg )\sin \frac{(1-\omega )T_{r}}{2}\nonumber \\&-\frac{2my_{0} f_{0}}{1+\omega }\sin \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}+\frac{T_{r}}{2}\bigg )\sin \frac{(1+\omega )T_{r}}{2}\nonumber \\&-\frac{2my_{0} f_{0}}{1-\omega }\sin \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}-\frac{T_{r}}{2}\bigg )\sin \frac{(1-\omega )T_{r}}{2}\nonumber \\= & {} -2m\mu A(\alpha ,\,\omega ,\,y_{0})\nonumber \\&+2mf_{0}\bigg [B(\alpha ,\,\omega ,\,y_{0})\sin \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}\bigg )\nonumber \\&+C(\alpha ,\,\omega ,\,y_{0})\cos \bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}\bigg )\bigg ]\nonumber \\= & {} -2m\mu A(\alpha ,\,\omega ,\,y_{0})\nonumber \\&+2mf_{0}\sqrt{B(\alpha ,\,\omega ,\,y_{0})^2+C(\alpha ,\,\omega ,\,y_{0})^{2}}\sin \nonumber \\&\bigg (\omega t_{0}+\frac{\omega T_{c}^{+}}{2}+\Phi \bigg ), \end{aligned}$$

(43)

where

$$\begin{aligned}&A(\alpha ,\,\omega ,\,y_{0})\nonumber \\&\quad =\left[ y_{0}^{2}-\,\alpha ^{2}\right] T_{c}^{+}+\left[ \alpha ^{2}+y_{0}^{2}\right] T_{r},\nonumber \\&B(\alpha ,\,\omega ,\,y_{0})\nonumber \\&\quad =\bigg (\alpha \sin \displaystyle \frac{T_{r}}{2}-y_{0}\cos \displaystyle \frac{T_{r}}{2}\bigg ) \nonumber \\&\quad \left( \displaystyle \frac{\sin \displaystyle \frac{(1+\omega )T_{r}}{2}}{1+\omega }+\displaystyle \frac{\sin \displaystyle \frac{(1-\omega )T_{r}}{2}}{1-\omega }\right) ,\nonumber \\&C(\alpha ,\,\omega ,\,y_{0})\nonumber \\&\quad =\frac{2}{1+\omega ^{2}}\bigg (\alpha \cos \frac{\omega T_{c}^{+}}{2}+y_{0}\omega \sin \frac{\omega T_{c}^{+}}{2}\bigg )\nonumber \\&\quad +\bigg (\alpha \cos \displaystyle \frac{T_{r}}{2}+y_{0}\sin \displaystyle \frac{T_{r}}{2}\bigg )\nonumber \\&\quad \left( \displaystyle \frac{\sin \displaystyle \frac{(1-\omega )T_{r}}{2}}{1-\omega }-\displaystyle \frac{\sin \displaystyle \frac{(1+\omega )T_{r}}{2}}{1+\omega }\right) ,\nonumber \\&\cos \Phi =\frac{B(\alpha ,\,\omega ,\,y_{0})}{\sqrt{B(\alpha ,\,\omega ,\,y_{0})^2+C(\alpha ,\,\omega ,\,y_{0})^{2}}},\, \nonumber \\&\sin \Phi =\frac{C(\alpha ,\,\omega ,\,y_{0})}{\sqrt{B(\alpha ,\,\omega ,\,y_{0})^2+C(\alpha ,\,\omega ,\,y_{0})^{2}}}. \end{aligned}$$

(44)

Fig. 6

The relation between $y_{0}$ and the forcing frequencies for $\alpha =0.6$

In the following analysis, we need to find $(\bar{t}_{0},\,\bar{y}_{0})$ such that

$$\begin{aligned} M(\bar{t}_{0},\,\bar{y}_{0})=0, \quad \dfrac{\partial M(\bar{t}_{0},\,\bar{y}_{0})}{\partial t_{0}}\ne 0, \end{aligned}$$

(45)

which implies

$$\begin{aligned} \frac{\mu }{f_{0}}<\frac{\sqrt{B(\alpha ,\,\omega ,\,\bar{y}_{0})^2+C(\alpha ,\,\omega ,\,\bar{y}_{0})^{2}}}{A(\alpha ,\,\omega ,\,\bar{y}_{0})} \end{aligned}$$

(46)

and we obtain

$$\begin{aligned} \bar{t}_{0}^{\,\,1}= & {} \frac{1}{\omega }\arcsin \displaystyle \frac{\mu A(\alpha ,\,\omega ,\,\bar{y}_{0})}{f_{0}\sqrt{B(\alpha ,\,\omega ,\,\bar{y}_{0})^2+C(\alpha ,\,\omega ,\,\bar{y}_{0})^{2}}}\nonumber \\&-\displaystyle \frac{\omega T_{c}^{+}}{2}-\Phi ,\quad \bar{t}_{0}^{\,\,2}=\pi -\bar{t}_{0}^{\,\,1}. \end{aligned}$$

(47)

Solving the Eq. (40), we obtain

$$\begin{aligned} \ln \displaystyle \frac{\alpha +y_{0}}{y_{0}-\,\alpha }+\arccos \displaystyle \frac{\alpha ^{2}-y_{0}^{2}}{\alpha ^{2}+y^{2}}=\frac{n\pi }{m\omega }. \end{aligned}$$

(48)

For fixed $\alpha =0.6$, the relation between $y_{0}$ and the forcing frequencies $\omega$ with $n/m=1$ and $n/m=3$, respectively is shown in Fig. 6. So when we only consider the case of $n/m=1$ and $\alpha =0.6$, we can get different $\bar{y}_{0}$ for different frequencies $\omega$, then, for given $f_{0}$ and $\mu$, we can obtain $\bar{t}_{0}^{\,1}$ and $\bar{t}_{0}^{\,2}$ by employing the formula (47). All the relation is shown in Table 1.

Table 1 $n/m=1$

Based on the Theorem 1, for $\epsilon >0$ is small enough, the system (34) and (35) possesses subharmonic (n, m)-periodic orbits with $n/m=1$ for the initial conditions which are $\epsilon$—close to $(\bar{t}_{1},-\,\alpha , \bar{y}_{0})$ and $(\bar{t}_{2},-\,\alpha , \bar{y}_{0})$. The existence of (n, m)-periodic orbits with $n/m=3$ can be analyzed in a similar technique and omitted here.

Fig. 7

The periodic orbit: $\mu =0.06, f_{0}=0.29, w=0.5506, y^{*}_{0}=0.6202, t^{*}_{0}=6.1784$

Fig. 8

The periodic orbit: $\mu =0.1, f_{0}=0.35, w=0.6008, y^{*}_{0}=0.6436, t^{*}_{0}=0.7643$

Next, we want to carry out numerical simulations to verify the existence of many kinds of subharmonic orbits. We first fix $\alpha =0.6$, choose the value of the parameters listed in the Table 1 and obtain the periodic orbits from Figs. 7, 8, 9, 10, and  11. However, we must emphasize that the periodic orbit in Fig. 7 is not the one analyzed in Sect. 2. Detailed analysis for these kinds of periodic orbits in Fig. 7 need to construct more Poincaré maps from $\tilde{\Sigma }_{1}^{+}\rightarrow \tilde{\Sigma }_{1}^{-}$ and $\tilde{\Sigma }_{2}^{-}\rightarrow \tilde{\Sigma }_{2}^{+}$ when the orbit will stay in the zone $M_{2}$.

Fig. 9

The periodic orbit: $\mu =0.1, f_{0}=0.4, w=0.7514, y^{*}_{0}=0.7512, t^{*}_{0}=4.6686$

Fig. 10

The periodic orbit: $\mu =0.4, f_{0}=0.8, w=0.8512, y^{*}_{0}=0.8410, t^{*}_{0}=5.3485$

Fig. 11

The periodic orbit: $\mu =0.05, f_{0}=0.65, w=0.6510, y^{*}_{0}=0.6526, t^{*}_{0}=4$

4 Conclusions

In this paper, based on the work by Cao et al. [8] and Granados et al. [9], we extend the Melnikov method of subharmonic orbits for a class of periodic perturbed planar piecewise-smooth systems with two switching manifolds. This system can be seen as a piecewise linear approach to nonlinear oscillators with complex nonlinear restoring force. The main technique depends on the geometrical structure of the unperturbed system and perturbation analysis by building an appropriate Poincaré map. The main objective is to find out analytical or numerical formulas of the parameters and initial conditions to ensure the existence of subharmonic orbits for this class of piecewise-smooth systems. A concrete piecewise-smooth oscillator is also chosen to show the effectiveness of the theoretical analysis. How to study stabilities of subharmonic orbits and how to find out the relation between homoclinic and subharmonic Melnikov methods are open problem so far.