Homoclinic bifurcation in a quasiperiodically excited impact inverted pendulum

Abstract

Homoclinic bifurcation for a nonlinear inverted pendulum impacting between two rigid walls under external quasiperiodic excitation is analyzed. The results for the homoclinic bifurcation of quasiperiodically excited smooth systems obtained by Ide and Wiggins are extended to the non-smooth ones. We present a method of Melnikov type to derive sufficient conditions under which the perturbed stable and unstable manifolds intersect transversally. Such a transversal Intersection implies the appearance of Smale horseshoe-type chaotic dynamics that is similar to that in the periodically forced smooth systems. As an application, by using a combination of analytical and numerical methods, a quasiperiodically excited impact oscillator of Duffing type with two frequencies is studied in detail.

1 Introduction

Many problems from mechanics, electrical engineering, and control theory are modelled by piecewise smooth (PWS) dynamical systems. As a result, the study of bifurcation phenomena in those systems has become very popular in recent years. Like for smooth systems, it is very important to investigate the appearance of chaos for PWS systems. A typical route to chaos for PWS systems is through discontinuity-induced bifurcations, such as grazing, sliding, chattering, and border collision. There are many works on this subject. See, for example, the monographs [1–6] and the survey articles [7–12], and the references therein.

For many smooth systems, a common route to chaos is via homoclinic bifurcation. The Melnikov method is a powerful tool to deal with this kind of problems [4, 13–19]. It is then natural to ask whether the Melnikov method established for smooth systems used to analyze subharmonic and homoclinic bifurcations can be extended to PWS systems. Many efforts have been made on this problem. To mention only a few of them, see [1, 6, 20–25]. All of those works assume that the unperturbed homoclinic or periodic orbit intersects the discontinuity surface transversally. In recent years, more attentions have been paid to the more interesting and difficult cases of bifurcations of sliding and grazing homoclinic orbits. In [4, 26–29], Battelli, Fečkan, Awrejcewicz et al. extended the Melnikov method to bifurcation of sliding homoclinic orbits of general $n$-dimensional PWS systems, and for the first time, they show rigorously the existence of Smale horseshoe-type chaos in these systems. Grazing homoclinic bifurcation for a nonlinear inverted pendulum impacting between two rigid walls under external periodic excitation was also studied in [30].

Since many systems are externally excited by more than one frequency, systems under the action of quasiperiodic or almost periodic force are often encountered in real-world applications. Quasiperiodically forced smooth systems have been well studied in the past decades [17, 31–35]. Particularly, in [17, 31, 32], Ide and Wiggins applied the Melnikov method to analyze homoclinic bifurcations of quasiperiodically forced smooth systems. However, although there has been big progress made in the study of homoclinic bifurcations in periodically forced PWS systems, little work has been done for quasiperiodically forced PWS systems. It is worth noting that in [36], Avramov and Awrejcewicz studied almost periodically forced frictional oscillations. They used the method of multiple scales to derive the modulation equations and constructed Melnikov function to study chaotic solutions of the system. In [4, 20, 21, 27–29], Battelli and Fečkan investigated homoclinic bifurcations and chaos of quasiperiodically or almost periodically forced PWS systems.

A class of the most studied PWS systems is impact systems where a vibrator collides with one or more rigid walls or another moving object. Being typical PWS systems, impact oscillators are found in many mechanical systems, such as print hammers, rigid blocks, and walking machines. There are many interesting examples and applications of impact oscillators given in [2, 5, 6].

Motivated by the works of Ide and Wiggins [17, 31, 32], Battelli and Fečkan [4, 20, 21, 27–29], in this paper, we consider for the first time homoclinic bifurcation of the following quasiperiodically forced nonlinear impact system:

$$\begin{aligned} \left\{ \begin{array}{ll} \ddot{x}+ g(x)=\varepsilon f(x, \dot{x}, t), &{} \quad \hbox {as } |x|<1, \\ \dot{x}\mapsto -(1-\varepsilon \rho )\dot{x}, &{} \quad \hbox {as } |x|=1, \end{array}\right. \end{aligned}$$

(1)

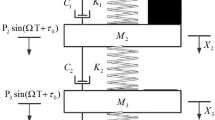
where $|\varepsilon |\le \varepsilon _0\ll 1$ for some $\varepsilon _0>0$ and the difference $1-\varepsilon \rho \in (0,1]$ is the coefficient of restitution representing energy loss during impact. System (1) can be used to model an inverted pendulum impacting on rigid walls as depicted in Fig. 1. Let $I=[-1, 1], \mu >0$ be a constant and $J_\mu =(-1-\mu , 1+\mu )\subset I$. Assume that functions $f$ and $g$ satisfy the following hypotheses:

• (H1) $g: J_\mu \rightarrow \mathbb {R}$ is $C^{2}$, where $g(0)=0$, $g^{\prime }(0)<0, g(x)\ne 0$ for $x\in I-\{0\}$.

• (H2) $f: J_\mu \times \mathbb {R}\times \mathbb {R} \rightarrow \mathbb {R}$ is $C^{2}$ and quasiperiodic in $t$ with fundamental frequencies $\omega _1, \ldots , \omega _m$, where $m\ge 2$ is an integer. Hence, $f(x, y, t)$ can be written as $f(x, y, \theta _1, \ldots , \theta _m)$ with $\theta _k=\omega _k t$ for $1\le k \le m$. Thus, for each fixed $(x, y)\in J_\mu \times \mathbb {R}, f(x, y, \theta _1, \ldots , \theta _m)$ is $2\pi$-periodic in each of the $\theta _k$ coordinates for $1\le k\le m$.

Let $\dot{x}=y$. For $\varepsilon =0$, the unperturbed system describes a free impact oscillator and is equivalent to

$$\begin{aligned}&\dot{x}=y,\quad \dot{y}=-g(x),\quad |x|<1, \end{aligned}$$

(2)

$$\begin{aligned}&y\mapsto -y, \quad |x|=1. \end{aligned}$$

(3)

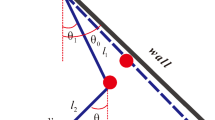
By Hypothesis (H1), system (2) has a unique equilibrium at the origin $O(0, 0)$ for $x\in I$, which is a saddle. Considering the identification given by the impact rule (3), the phase portrait of system (2–3) is qualitatively the same as shown in Fig. 2. Note that the unperturbed system (2–3) has a saddle at the origin $O$ and two homoclinic loops $\varGamma _{+}= OAA ^{\prime }O$ and $\varGamma _-= OBB ^{\prime }O$. Here, $A^{\prime }, B^{\prime }$ are the reflection points of $A, B$, respectively. Clearly, $\varGamma _{+}$ (respectively, $\varGamma _{-}$) intersects $x=+1$ (respectively, $x=-1$) transversally.

Fig. 1

Inverted pendulum

Fig. 2

Orbits of unperturbed system

The impact inverted pendulum (1) was proposed by Chow et al. in [37, 38]. It has been used in the modelling of many mechanical devices, such as rings, rigid standing structures, and a mooring buoy. Hence, periodically excited impact inverted pendulum has been extensively studied for various choices of $f$ and $g$ [23, 30, 37–47]. In particular, in [23, 45, 46], the Melnikov methods for homoclinic and subharmonic bifurcations established for smooth systems were extended to be applicable to the nonlinear impact inverted pendulum. Grazing homoclinic bifurcation was also studied in [30]. However, to the best of our knowledge, there is still no result on the study of homoclinic bifurcation of quasiperiodically excited impact inverted pendulum in the literature. The purpose of this paper was to make some efforts on this problem.

More precisely, we discuss the perturbation of the homoclinic orbit $\varGamma _{+}$. The discussion for $\varGamma _{-}$ is similar and is omitted for brevity. Let $S^1$ be the circle of period $2\pi$, $T^m:=S^1\times \cdots \times S^1$ be the $m$-torus. Since system (1) is quasiperiodically excited, we consider the orbits of (1) and (2–3) in the region $|x|<1$ in the space $\{ (x, y) \ | \ |x|<1, y\in \mathbb {R} \}\times T^m$. Then, system (2–3) has a normally hyperbolic $m$-torus $T_{0}:=\{ (x, y)\in \mathbb {R}^2, (\theta _1, \ldots , \theta _m)\in T^m \ | \ (x, y)=(0, 0) \}$ whose right branch of $(m+1)$-dimensional stable manifold $W_0^s$ and unstable manifold $W_0^u$ coincide along the homoclinic manifold $\varGamma _{+}\times T^m$. Then, for sufficiently small $|\varepsilon |$, the normally hyperbolic $m$-torus $T_{0}$ persists, which has a stable manifold $W_{\varepsilon }^s$ and an unstable manifold $W_{\varepsilon }^u$. We are interested in the question: under what conditions the perturbed stable manifold $W_{\varepsilon }^s$ and unstable manifold $W_{\varepsilon }^u$ intersect transversally? By the generalization of the Smale–Birkhoff Homoclinic Theorem to the case of orbits homoclinic to normally hyperbolic invariant tori (Theorem 3.4.1 in [17, p. 322]), such a transversal intersection implies the appearance of chaotic dynamics that is similar to the Smale horseshoe chaos in periodically forced system.

We extend the results for homoclinic bifurcation of quasiperiodically excited smooth systems obtained by Ide and Wiggins [17, 31, 32] to the general nonlinear quasiperiodically excited impact inverted pendulum (1). We present a method of Melnikov type to derive sufficient conditions under which the perturbed stable manifold $W_{\varepsilon }^s$ and unstable manifold $W_{\varepsilon }^u$ intersect transversally. Compare to the works [17, 31, 32], the main difficulty in our work is that, for system (1), in order to estimate the gap between $W_{\varepsilon }^s$ and $W_{\varepsilon }^u$, we must estimate the time and velocity at which the orbit of (1) reaches the walls $|x|=1$. This is overcome by using the perturbation method. As an application, by using a combination of analytical and numerical methods, a quasiperiodically excited impact inverted pendulum of Duffing type with two frequencies is studied in detail.

This paper is organized as follows. We introduce the Poincaré section and the Poincaré map for system (1) and present a method of Melnikov type to derive sufficient conditions under which $W_{\varepsilon }^s$ and $W_{\varepsilon }^u$ intersect transversally in Sect. 2. In Sect. 3, we apply this method to discuss the bifurcations of homoclinic loops for a quasiperiodically excited impact oscillator of Duffing type with two frequencies. Numerical simulations of this system are given in Sect. 4. Finally, discussion and some concluding remarks are given in Sect. 5.

2 Melnikov method

By (H2), for each fixed $(x, y)\in J_\mu \times \mathbb {R}, f(x, y, \theta _1, \theta _2, \ldots , \theta _m)$ can be viewed as a function on the $m$-torus $T^m$. Thus, system (1) is equivalent to the following suspended system

$$\begin{aligned}&\left. \begin{array}{l} \dot{x}=y \\ \dot{y}=-g(x)+\varepsilon f(x, y, \theta _1, \ldots , \theta _m) \\ \dot{\theta }_1=\omega _1 \\ \qquad \vdots \\ \dot{\theta }_m=\omega _m \end{array}\right\} \quad \hbox {as } |x|<1, \end{aligned}$$

(4)

$$\begin{aligned}&y\mapsto -(1-\varepsilon \rho )y \quad \hbox {as } |x|=1, \end{aligned}$$

(5)

where $(\theta _1, \ldots , \theta _m)\in T^m$. The solution of (4) with the initial conditions $x=x_0, y=y_0$, $\theta _1=\theta _{10}, \ldots , \theta _m=\theta _{m0}$ is denoted by $x=x(t; x_0, y_0, \theta _{10}, \ldots , \theta _{m0}), y=y(t; x_0, y_0, \theta _{10}, \ldots , \theta _{m0})$. For $\varepsilon =0$, the unperturbed system is given by

$$\begin{aligned}&\left. \begin{array}{l} \dot{x}=y \\ \dot{y}=-g(x) \\ \dot{\theta }_1=\omega _1 \\ \qquad \vdots \\ \dot{\theta }_m=\omega _m \end{array}\right\} \quad \hbox {as } |x|<1, \end{aligned}$$

(6)

$$\begin{aligned}&y\mapsto -y \quad \hbox {as } |x|=1. \end{aligned}$$

(7)

By (H1–H2), system (6–7) has a normally hyperbolic $m$-torus $T_{0}:=\{ (x, y)\in \mathbb {R}^2, (\theta _1, \ldots , \theta _m)\in T^m \ | \ (x, y)=(0, 0) \}$ whose right branch of $(m+1)$-dimensional stable and unstable manifolds $W_0^s$ and $W_0^u$ coincides along the homoclinic manifold $\varGamma _{+}\times T^m$. By Proposition 4.1.5 in [17, p. 354], for sufficiently small $\varepsilon$, the perturbed system (4–5) has a normally hyperbolic $m$-torus $T_{\varepsilon }$, which has $(m+1)$-dimensional $C^2$ stable and unstable manifolds $W_{\varepsilon }^s$ and $W_{\varepsilon }^u$.

Because of the nature of the vector field (4–5), in order to study the perturbation of the right homoclinic orbit $\varGamma _{+}$, the Poincaré section is taken to be the following set

$$\begin{aligned} {\varSigma }&= \{(x,y, \theta _1, \ldots , \theta _m)\in I\times {\mathbb R} \times S^1\times \cdots \times S^1 \ | \ \\&\quad x=1, y>0\}= {\mathbb R}^{+}\times T^m. \end{aligned}$$

Let

$$\begin{aligned} {\varSigma }_-&= \{(x,y, \theta _1, \ldots , \theta _m)\in I\times {\mathbb R} \times S^1\times \cdots \times S^1 \ | \ \\&\quad x=1, y<0\}= {\mathbb R}^{-}\times T^m. \end{aligned}$$

Elements in both ${\varSigma }$ and ${\varSigma }_-$ are denoted by $(y, \theta _1, \ldots , \theta _m)$. The Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$ is defined as follows. Consider a point $(y_0, \varTheta _{0})\in {\varSigma }$, where $\varTheta _{0}:=(\theta _{10}, \ldots , \theta _{m0})$. It is immediately mapped to $(-(1-\varepsilon \rho )y_0, \varTheta _{0})\in {\varSigma }_-$ by the impact law (5). Then, under the flow of system (4), it returns to ${\varSigma }$ after a free flight of duration $\tau (y_0, \varTheta _{0})$. Then,

$$\begin{aligned} \fancyscript{P}(y_0, \varTheta _{0})&= (y(\tau (y_0, \varTheta _{0}); 1, -(1-\varepsilon \rho )y_0, \varTheta _{0}),\\&\quad (\omega _1\tau (y_0, \varTheta _{0})+\theta _{10})(\mathrm{mod}\,\, T_1), \\&\quad \ldots ,(\omega _m\tau (y_0, \varTheta _{0})+\theta _{m0})(\mathrm{mod}\,\, T_m)), \end{aligned}$$

where $T_i=2\pi /\omega _i$ for $i=1, \ldots , m$.

For any $(\theta _{10}, \ldots , \theta _{m0})\in T^{m}$ and sufficiently small $\varepsilon$, a branch of the unstable (respectively, stable) manifold $W^u_\varepsilon$ (respectively, $W^s_\varepsilon$) intersects ${\varSigma }$ (resp. ${\varSigma }_{-}$) in a $m$-dimensional manifold, denoted by $\varDelta ^u_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ (respectively, $\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$). The point $(\theta _{10}, \ldots , \theta _{m0})\in T^{m}$ can be viewed as parameters along the unperturbed homoclinic manifold $\varGamma _{+}\times T^m$. Moreover, the impact rule (5) defines a $1$–$1$ map ${\fancyscript{I}}: {\varSigma }\rightarrow {\varSigma }_{-}$ such that

$$\begin{aligned} (y, \theta _1, \ldots , \theta _m)\mapsto (-(1-\varepsilon \rho )y, \theta _1, \ldots , \theta _m). \end{aligned}$$

Hence, the manifold $\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ is the image of the map ${\fancyscript{I}}$ of the manifold $-(1-\varepsilon \rho )^{-1}\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ on ${\varSigma }$. The separation between $W^s_\varepsilon$ and $W^u_\varepsilon$ in ${\varSigma }$ is given by

$$\begin{aligned} {\varDelta }_\varepsilon (\theta _{10}, \ldots , \theta _{m0})&= {\varDelta }^u_\varepsilon (\theta _{10}, \ldots , \theta _{m0})\nonumber \\&\quad +\frac{1}{1-\varepsilon \rho }\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0}), \end{aligned}$$

(8)

where $(\theta _{10}, \ldots , \theta _{m0})\in T^m$. If $\varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ has no zeros, then $W^s_\varepsilon$ and $W^u_\varepsilon$ do not intersect, while if $\varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ has simple zeros, then $W^s_\varepsilon$ and $W^u_\varepsilon$ intersect transversally. If $\varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ has quadratic zeros, then $W^s_\varepsilon$ and $W^u_\varepsilon$ intersect with quadratic tangencies. By the generalization of the Smale–Birkhoff Homoclinic Theorem to the case of orbits homoclinic to normally hyperbolic invariant tori (Theorem 3.4.1 in [17, p. 322]), if $W^s_\varepsilon$ intersects $W^u_\varepsilon$ transversally, then the Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$ possesses transversal homoclinic torus, implying the appearance of chaotic dynamics that is similar to the Smale horseshoe chaos in periodically forced system.

Usually, it is impossible to find a closed form of the separation $\varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})$. It has to be approximated by perturbation methods. Since $W^s_\varepsilon$ and $W^u_\varepsilon$ are $C^{2}$ in $\varepsilon$ under Hypotheses (H1) and (H2), $\varDelta ^u_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$, $\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ and $\varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ are all $C^{2}$ in $\varepsilon$ from the way they are defined. Suppose that $\varDelta ^u_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ and $\varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})$ have the following Taylor expansions near $\varepsilon =0$:

$$\begin{aligned} \varDelta ^u_\varepsilon (\theta _{10}, \ldots , \theta _{m0})&= M^u_0(\theta _{10}, \ldots , \theta _{m0})\nonumber \\&\quad +\,M^u_1(\theta _{10}, \ldots , \theta _{m0})\varepsilon + O(\varepsilon ^{2}),\end{aligned}$$

(9)

$$\begin{aligned} \varDelta ^s_\varepsilon (\theta _{10}, \ldots , \theta _{m0})&= M^s_0(\theta _{10}, \ldots , \theta _{m0})\nonumber \\&\quad +\,M^s_1(\theta _{10}, \ldots , \theta _{m0})\varepsilon + O(\varepsilon ^{2}).\nonumber \\ \end{aligned}$$

(10)

Clearly $M^u_0(\theta _{10}, \ldots , \theta _{m0})\equiv -M^s_0(\theta _{10}, \ldots , \theta _{m0})\equiv \sqrt{-2G(1)}$, where

$$\begin{aligned} G(x):=\int _0^{x} g(s) \mathrm{d}s, \quad x\in J. \end{aligned}$$

Hence, from (8)–(10), we obtain

$$\begin{aligned} \varDelta _\varepsilon (\theta _{10}, \ldots , \theta _{m0})= M_1(\theta _{10}, \ldots , \theta _{m0})\varepsilon + O(\varepsilon ^{2}),\nonumber \\ \end{aligned}$$

(11)

where $M_1(\theta _{10}, \ldots , \theta _{m0})$ is called the first-order Melnikov function and is given by

$$\begin{aligned} M_1(\theta _{10}, \ldots , \theta _{m0}) \!&= \! -\rho \sqrt{-2G(1)} \!+\! M^u_1(\theta _{10}, \ldots , \theta _{m0})\nonumber \\&\quad +\,M^s_1(\theta _{10}, \ldots , \theta _{m0}). \end{aligned}$$

(12)

Similar to Theorem 2.2 of [32], we obtain the following result:

Theorem 1

Let $\nabla M_1$ be the gradient of $M_1(\theta _{10}, \ldots , \theta _{m0})$. If $M_1(\theta _{10}, \ldots , \theta _{m0})$ has a simple zero $(\bar{\theta }_{10}, \ldots , \bar{\theta }_{m0})$, namely $M_1(\bar{\theta }_{10}, \ldots , \bar{\theta }_{m0})=0$ and $\nabla M_1(\bar{\theta }_{10}, \ldots , \bar{\theta }_{m0})\ne 0$, then for sufficiently small $\varepsilon >0$, the perturbed manifolds $W^s_\varepsilon$ and $W^u_\varepsilon$ intersect transversally in ${\varSigma }$ near $(\bar{\theta }_{10}, \ldots , \bar{\theta }_{m0})$. Furthermore, if $\nabla M_1(\theta _{10}, \ldots , \theta _{m0})\ne 0$ for all $(\theta _{10}, \ldots , \theta _{m0})\in T^m$, then this zero of $M_1(\theta _{10}, \ldots , \theta _{m0})$ can be continued to a $m$-dimensional transverse homoclinic torus.

Now, we describe how to compute the first-order Melnikov function $M_1(\theta _{10}, \ldots , \theta _{m0})$. Select $P_0^{u}$: $(x_0^u(0),y_0^u(0))$ and $P_0^{s}$: $(x_0^s(0),y_0^s(0))$ on the unperturbed (i.e., $\varepsilon =0$) unstable manifold $W_0^{u}$ and stable manifold $W_0^{s}$ of the saddle $O$ of (4), respectively, such that $0<x_0^u(0)<\mu$, $0<x_0^s(0)<\mu$. Let $\gamma _0^u: (x_0^u(t),y_0^u(t))$ and $\gamma _0^s: (x_0^s(t),y_0^s(t))$ denote the orbits of (4) for $\varepsilon =0$ passing through $P_0^{u}$ and $P_0^{s}$ at $t=0$, respectively, which of course lie in $W_0^{u}$ and $W_0^{s}$, respectively. Let $\tau ^{u}_0$ and $\tau ^{s}_0$ be the time at which the orbits $\gamma _0^u$, $\gamma _0^s$ reach the wall $x=1$, respectively, i.e., $x^s_0(\tau ^s_0)=x^u_0(\tau ^u_0)=1$. Clearly, when $1<x_0^u(0)<\mu$ and $1<x_0^s(0)<\mu$, we have $\tau ^u_0<0$ and $\tau ^s_0>0$; when $0<x_0^u(0)\le 1$ and $0<x_0^s(0)\le 1$, we have $\tau ^u_0\ge 0$ and $\tau ^s_0\le 0$. Then, similar to the derivation given in [23], we obtain

Theorem 2

Let $x_0^u, y_0^u, x_0^s, y_0^s$ and $\tau ^{u}_0, \tau ^{s}_0$ be given above. Then, the first-order Melnikov function $M_1(\theta _{10}, \ldots , \theta _{m0})$ is calculated by

$$\begin{aligned}&M_1(\theta _{10}, \ldots , \theta _{m0})= -\rho \sqrt{-2G(1)}+\frac{1}{\sqrt{-2G(1)}}\\&\left\{ \int \nolimits _{-\infty }^{\tau ^{u}_0} F^{u}(\tau , \varTheta _{0}) \mathrm{d}\tau +\int \nolimits _{\tau ^{s}_0}^{+\infty } F^{s}(\tau , \varTheta _{0}) \mathrm{d}\tau \right\} , \end{aligned}$$

where

$$\begin{aligned} F^{u}(\tau , \varTheta _{0})&= f\left( x_0^{u}(\tau ), y_0^{u}(\tau ), \omega _1(\tau -\tau ^u_0)+\theta _{10},\right. \\&\quad \left. \ldots , \omega _m (\tau -\tau ^u_0) +\theta _{m0})\right) y^{u}_0(\tau ), \\ F^{s}(\tau , \varTheta _{0})&= f\left( x_0^{s}(\tau ), y_0^{s}(\tau ), \omega _1(\tau -\tau ^s_0) +\theta _{10}, \right. \\&\quad \left. \ldots , \omega _m (\tau -\tau ^s_0) + \theta _{m0})\right) y^{s}_0(\tau ). \end{aligned}$$

The proof for Theorem 2 is similar to the proof for Theorem 3.1 in [23] and thus is omitted here for brevity.

3 Impact duffing system

It is well known that Duffing’s equation has been found in many mechanical problems [15, p. 82]. Thus, naturally we consider the following quasiperiodically forced impact Duffing system with two fundamental frequencies:

$$\begin{aligned}&\left\{ \begin{array}{ll} \ddot{x}+\varepsilon \delta \dot{x}-x+x^3=\varepsilon \sum \nolimits _{k=1}^{2} \gamma _k \cos \omega _k t,\quad &{} |x|<1, \\ \dot{x}\mapsto -(1-\varepsilon \rho )\dot{x},\quad &{} |x|=1, \end{array}\right. \nonumber \\ \end{aligned}$$

(13)

where $\varepsilon \ge 0, \delta \ge 0, \gamma _1, \gamma _2>0$, $\omega _1, \omega _2>0$ and $\rho \ge 0$. Let $y=\dot{x}$, system (13) is equivalent to the following system

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}=y \\ \dot{y}=x-x^3+\varepsilon \left( -\delta y+\sum \nolimits _{k=1}^{2} \gamma _k \cos \omega _k t\right) , \end{array}\right. \quad \text{ as } \,|x|<1, \end{aligned}$$

(14)

$$\begin{aligned}&y\mapsto -(1-\varepsilon \rho )y, \quad \text{ as } \, |x|=1. \end{aligned}$$

(15)

When $\varepsilon =0$, the phase portrait of the unperturbed system of (14–15) is topologically equivalent to that shown in Fig. 2. Take

$$\begin{aligned}&\left( x^{u}_0(t),y^{u}_0(t)\right) \!=\! \left( \sqrt{2}\mathrm{sech}\,t, -\sqrt{2}\mathrm{sech}\,t\tanh t \right) , \quad t\in (-\infty , 0],\\&\left( x^{s}_0(t),y^{s}_0(t)\right) \!=\! \left( \sqrt{2}\mathrm{sech}\,t, -\sqrt{2}\mathrm{sech}\,t\tanh t \right) , \quad t\in [0, +\infty ). \end{aligned}$$

Let $\kappa =\ln (\sqrt{2}+1)$. Then, $\tau ^u_0=-\kappa$, $\tau ^s_0=\kappa$. By Theorem 2, we have

$$\begin{aligned} M_1(\theta _{10}, \theta _{20})&= -\frac{\rho }{\sqrt{2}}-\frac{2\delta }{3}\left( 2\sqrt{2}-1\right) \nonumber \\&\quad +\,4\gamma _1 I(\omega _1)\sin \theta _{10}\nonumber \\&\quad +\,4\gamma _2I(\omega _2) \sin \theta _{20}, \end{aligned}$$

(16)

where $\theta _{10}, \theta _{20}\in [0, 2\pi ]$ and

$$\begin{aligned} I(\omega ) =\omega \int \nolimits ^{+\infty }_0\mathrm {sech\ }(t+\kappa )\cos (\omega {}t)\mathrm {d}t. \end{aligned}$$

From (16), it is clear that if

$$\begin{aligned} \frac{\rho }{\sqrt{2}}+\frac{2\delta }{3}\left( 2\sqrt{2}-1\right) <4\gamma _1 I(\omega _1)+4\gamma _2 I(\omega _2), \end{aligned}$$

then the first-order Melnikov function $M_1(\theta _{10}, \theta _{20})$ has a simple zero. Thus, in the six-dimensional parameter space $(\rho , \delta , \gamma _1, \gamma _2, \omega _1, \omega _2)$, the bifurcation set is given by the five-dimensional surface

$$\begin{aligned} \frac{\rho }{\sqrt{2}}\!+\!\frac{2\delta }{3}\left( 2\sqrt{2}-1\right) =4\gamma _1 I(\omega _1)+4\gamma _2 I(\omega _2). \end{aligned}$$

(17)

Since the left side of (17) is a linear combination of $\rho$ and $\delta$ with constant coefficients, without the loss of generality, let $\alpha :=\frac{\rho }{\sqrt{2}}+\frac{2\delta }{3}(2\sqrt{2}-1), I_1:=I(\omega _1)$ and $I_2:=I(\omega _2)$ in the rest of the paper. Then, (17) can be rewritten in the following form

$$\begin{aligned} -\frac{1}{4}\alpha +\gamma _1 I_1+\gamma _2 I_2=0. \end{aligned}$$

(18)

As shown in Fig. 3, the function $I(\omega )$ has a unique maximum $\omega _m\approx 0.930895866$ with $I_m:=I(\omega _m)\approx 0.376828848$. Furthermore, $I(\omega )$ is strictly increasing for $\omega \in (0, \omega _m)$ and strictly decreasing for $\omega \in (\omega _m, +\infty )$. If $\alpha >4(\gamma _1+\gamma _2)I_m$, then $M_1(\theta _{10}, \theta _{20})<0$, implying that for sufficiently small $\varepsilon >0$, $W_{\varepsilon }^s$ and $W_{\varepsilon }^u$ do not intersect. If $\alpha =4(\gamma _1+\gamma _2)I_m$, then $M_1(\theta _{10}, \theta _{20})$ has a unique zero $\theta _{10}=\theta _{20}=\frac{\pi }{2}$ if and only if $\omega _1=\omega _2=\omega _m$. Furthermore, if $\omega _1=\omega _2=\omega _m$, then $\nabla M_1(\frac{\pi }{2}, \frac{\pi }{2})=0$.

Fig. 3

Graph of $I(\omega )$ for $\omega >0$. $\omega _m$ is the unique maximum of $I(\omega )$

In the rest of the paper, we focus our attention on the case $\alpha < 4(\gamma _1+\gamma _2)I_m$. Clearly, for a given value of $(\alpha , \gamma _1, \gamma _2)$, points in the $I_1 - I_2$ plane above the line segment given by (18) inside the rectangle $\fancyscript{D}:=\{ (I_1, I_2)\in \mathbb {R}^2 \ |\ 0\le I_1, I_2\le I_m \}$ correspond to transverse homoclinic tori. Let $\omega ^+(I)$ (respectively, $\omega ^-(I)$) be the inverse function of $I(\omega )$ for $\omega \in (0, \omega _m)$ (respectively, $\omega \in (\omega _m, +\infty )$). In the following, we use the same method in [32] to represent the bifurcation sets for the case $\alpha < 4(\gamma _1+\gamma _2)I_m$ in the $\omega _1-\omega _2$ plane. Our discussion can be divided into nine cases as follows, where for each case in the diagram of the corresponding bifurcation set, the shaded area corresponds to transverse homoclinic tori. Parameters chosen from this area correspond to the chaotic behavior of system (13), thus the area is called chaotic zone.

• (1) If $4I_{m}\max \{\gamma _1,\gamma _2\}<\alpha < 4(\gamma _1+\gamma _2)I_m$, then the line (18) intersects $\partial \fancyscript{D}$ at $(I_{h1}, I_m)$ and $(I_m, I_{v1})$ with $0<I_{h1}, I_{v1}<I_m$, where $\partial \fancyscript{D}$ is the boundary of $\fancyscript{D}$ and

  $$\begin{aligned} I_{h1}\!=\!\frac{1}{\gamma _1}\left( \frac{1}{4}\alpha \!-\!\gamma _2 I_m\right) , \quad I_{v1}\!=\!\frac{1}{\gamma _2}\left( \frac{1}{4}\alpha \!-\!\gamma _1 I_m\right) . \end{aligned}$$

  The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4a. The corresponding chaotic zone is denoted by $\fancyscript{C}_1$.

  Fig. 4

  

  Bifurcation sets in $\omega _1-\omega _2$ plane, the shaded area corresponds to transverse homoclinic tori. a $4I_{m}\max \{\gamma _1,\gamma _2\}<\alpha < 4(\gamma _1+\gamma _2)I_m$. b $\gamma _1 > \gamma _2$ and $\alpha =4\gamma _1 I_{m}$. c $\gamma _1 > \gamma _2$ and $\alpha =4\gamma _1 I_{m}$. d $\gamma _1=\gamma _2$ and $\alpha =4\gamma _1 I_{m}$. e $\gamma _1 > \gamma _2$ and $4\gamma _2 I_{m} <\alpha <4\gamma _1 I_{m}$. f $\gamma _1 < \gamma _2$ and $4\gamma _1 I_{m}<\alpha <4\gamma _2 I_{m}$. g $\gamma _1 > \gamma _2$ and $\alpha =4\gamma _2 I_{m}$. h $\gamma _1 < \gamma _2$ and $\alpha =4\gamma _1 I_{m}$. i $0<\alpha <4I_{m}\min \{\gamma _1,\gamma _2\}$.

• (2) If $\gamma _1 > \gamma _2$ and $\alpha =4I_{m}\max \{\gamma _1,\gamma _2\}=4\gamma _1 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(I_m, 0)$ and $(I_{h2}, I_m)$ with $0<I_{h2}=I_m(\gamma _1-\gamma _2)/\gamma _1<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4b. The corresponding chaotic zone is denoted by $\fancyscript{C}_2$.

• (3) If $\gamma _1 < \gamma _2$ and $\alpha =4I_{m}\max \{\gamma _1,\gamma _2\}=4 \gamma _2 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(0, I_m)$ and $(I_m, I_{v3})$ with $0<I_{v3}=I_m(\gamma _2-\gamma _1)/\gamma _2<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4c. The corresponding chaotic zone is denoted by $\fancyscript{C}_3$.

• (4) If $\gamma _1=\gamma _2$ and $\alpha =4I_{m}\max \{\gamma _1,\gamma _2\} =4 \gamma _2 I_{m}=4 \gamma _1 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(0, I_m)$ and $(I_m, 0)$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4d. The corresponding chaotic zone is denoted by $\fancyscript{C}_4$.

• (5) If $\gamma _1 > \gamma _2$ and $4\gamma _2 I_{m}<\alpha <4\gamma _1 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(I_{h5A}, 0)$ and $(I_{h5B}, I_m)$ with $0<I_{h5A}=\frac{\alpha }{4\gamma _1}$, $I_{h5B}=I_{h1}<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4e. The corresponding chaotic zone is denoted by $\fancyscript{C}_5$.

• (6) If $\gamma _1 < \gamma _2$ and $4 \gamma _1 I_{m}<\alpha <4 \gamma _2 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(0, I_{v6A})$ and $(I_m, I_{v6B})$ with $0<I_{v6A}=\frac{\alpha }{4\gamma _2}, I_{v6B}=I_{v1}<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4f. The corresponding chaotic zone is denoted by $\fancyscript{C}_6$.

• (7) If $\gamma _1 > \gamma _2$ and $\alpha =4I_{m}\min \{\gamma _1,\gamma _2\}=4 \gamma _2 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(0, I_m)$ and $(I_{h7}, 0)$ with $0<I_{h7}=\frac{\gamma _2}{\gamma _1}I_m<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4g. The corresponding chaotic zone is denoted by $\fancyscript{C}_7$.

• (8) If $\gamma _1 < \gamma _2$ and $\alpha =4I_{m}\min \{\gamma _1,\gamma _2\}=4 \gamma _1 I_{m}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(I_m, 0)$ and $(0, I_{v8})$ with $0<I_{v8}=\frac{\gamma _1}{\gamma _2}I_m<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4h. The corresponding chaotic zone is denoted by $\fancyscript{C}_8$.

• (9) If $0<\alpha <4I_{m}\min \{\gamma _1,\gamma _2\}$, then the line (18) intersects $\partial \fancyscript{D}$ at $(I_{h9}, 0)$ and $(0, I_{v9})$ with $0<I_{h9}=\frac{\alpha }{4\gamma _1}, I_{v9}=\frac{\alpha }{4\gamma _2}<I_m$. The corresponding bifurcation set in the $\omega _1-\omega _2$ plane is given in Fig. 4i. The corresponding chaotic zone is denoted by $\fancyscript{C}_9$.

4 Numerical simulations

In this section, we present numerical simulations for the impact Duffing system (13) to show the theoretical results from the Melnikov method in Sect. 3. It is easy to see that for the nine bifurcation sets described in Sect. 3, by switching the roles of $\gamma _1$ and $\gamma _2$, cases (3), (6), and (8) are the same as cases (2), (5), and (7), respectively. Thus, we omit cases (3), (6), and (8) in the numerical simulations for brevity. The computations are implemented in MATLAB.

When performing numerical simulations for system (13), it is important and difficult to detect the impacting time and velocity accurately. We adopt an event-driven method described in [2, 48] for this purpose. We implement this method by using the built-in event detection routines along with the built-in ODE solvers of MATLAB. In this way, we are able to detect the impacting events as accurate as the accuracy of MATLAB allows as suggested by Piiroinen and Kuznetsov in [48].

We first describe how to plot the intersections of the perturbed unstable manifold $W_{\varepsilon }^{u}$ and stable manifold $W_{\varepsilon }^{s}$ in a fixed slice of the Poincaré section ${\varSigma }$ given by

$$\begin{aligned} {\varSigma }_{\theta _{1m}, \theta _{1M}}^{\theta _{20*}}\!=\!\{ (y, \theta _1, \theta _2)\!\in \! {\varSigma } \ | \ \theta _1\!\in \! [\theta _{1m}, \theta _{1M}], \theta _2\!=\!\theta _{20*}\}, \end{aligned}$$

where $\theta _{1m}, \theta _{1M}$, and $\theta _{20*}$ are constants, $\theta _{1M}-\theta _{1m}\ge T_1$. For this purpose, we modified the method for the computation of stable and unstable manifolds of hyperbolic trajectories in two-dimensional aperiodically time-dependent systems proposed by Mancho et al. [49] so it is applicable to system (13). The algorithm is described as follows.

The first step is to find the distinguished hyperbolic trajectory $\xi _{DHT}(t,\varepsilon ):=(x_{DHT}(t,\varepsilon ), y_{DHT}(t,\varepsilon ))$ of system (13) (see [49] for the definition), which is the unique quasiperiodic orbit of (13) such that $\xi _{ DHT }(t,\varepsilon )\rightarrow (0, 0)$ uniformly for $t\in (-\infty , +\infty )$ as $\varepsilon \rightarrow 0$. Thus we have

$$\begin{aligned} \xi _{ DHT }(t,\varepsilon )&= \varepsilon \sum \limits _{k=1}^{2}\frac{\gamma _k}{1+\omega _k^2} (-\cos \omega _k t, \omega _k\sin \omega _k t) +\varepsilon ^2\\&\quad \sum \limits _{k=1}^{2}\frac{\delta \gamma _k\omega _k}{(1+\omega _k^2)^2} (\sin \omega _k t, \omega _k\cos \omega _k t)+O(\varepsilon ^3). \end{aligned}$$

The second step is to approximate the local stable and unstable manifolds. As described in [49], they are given by the straight line segment between $\xi _{ DHT }(t,\varepsilon )$ and

$$\begin{aligned} \xi _{W}^{u, s}(t,\varepsilon )=\xi _{ DHT }(t,\varepsilon )+\frac{1}{\sqrt{2}}\lambda \left( e^{u, s}(t)+O(\varepsilon ^2)\right) , \end{aligned}$$

where $e^{u}(t)=(1, 1), e^{s}(t)=(-1, 1), \lambda$ is a parameter that can be adjusted if necessary during the computation. In the third step, the interval $[\theta _{1m}, \theta _{1M}]$ is partitioned equally into $N$ parts by $\theta _{1m}=\theta _1^0< \theta _1^2<\cdots <\theta _1^N=\theta _{1M}$, where $N$ is a sufficiently large positive integer. Then, for each $\theta _1^j (0\le j \le N)$, we apply the method described in [49] to compute $W_{\varepsilon }^{u}$ and $W_{\varepsilon }^{s}$ in the time slice

$$\begin{aligned} \varPi _{\theta _1^j}:=\left\{ (x, y, t)\in \mathbb {R}^3 \ | \ t={\theta _1^j}\right\} \end{aligned}$$

until $x=1$, and we obtain a point $(1, y_{\theta _1^j}, \theta _1^j)\in \varPi _{\theta _1^j}$. Consequently, for $W_{\varepsilon }^{u}$, we obtain a point $(y_{\theta _1^j}, \theta _1^j, \theta _{20*}) \in {\varSigma }_{\theta _{1m}, \theta _{1M}}^{\theta _{20*}}$; for $W_{\varepsilon }^{s}$, applying the impact law (15), we obtain a point $(-(1-\varepsilon \rho )^{-1}y_{\theta _1^j}, \theta _1^j, \theta _{20*}) \in {\varSigma }_{\theta _{1m}, \theta _{1M}}^{\theta _{20*}}$. By this method, we in fact approximated the curves $\varDelta _{\varepsilon }^{u}(\theta _1, \theta _{20*})$ and $\varDelta _{\varepsilon }^{s}(\theta _1, \theta _{20*})$ defined in Sect. 2. Clearly, if $\varDelta _{\varepsilon }^{u}(\theta _1, \theta _{20*})$ and $\varDelta _{\varepsilon }^{s}(\theta _1, \theta _{20*})$ intersect transversally, then the two surfaces $\varDelta _{\varepsilon }^{u}(\theta _1, \theta _{2})$ and $\varDelta _{\varepsilon }^{s}(\theta _1, \theta _{2})$ also intersect transversally, implying that $W_{\varepsilon }^u$ and $W_{\varepsilon }^s$ intersect transversally.

For the sake of brevity, we only show one instance of the computation. Take $\gamma _1=1.1, \gamma _2=1.0$, $\omega _1=\frac{\pi }{3}, \omega _2=0.7, \varepsilon =0.04$, $\delta =1.6, \rho =0, [\theta _{1m}, \theta _{1M}]=[-\frac{7}{6}\pi , \frac{3}{2}\pi ], \theta _{20*}=0.5\pi$. It is easy to check that the parameters are in the chaotic zone $\fancyscript{C}_1$, and the result is shown in Fig. 5. As can be seen that the two curves $\varDelta _{\varepsilon }^{u}(\theta _1, \theta _{20*})$ and $\varDelta _{\varepsilon }^{s}(\theta _1, \theta _{20*})$ intersect transversally at $\theta _1\approx 0.5389$ and $\theta _1\approx 2.6233$, implying that $W_{\varepsilon }^u$ and $W_{\varepsilon }^s$ intersect transversally. Hence, the result confirms the theoretical prediction given in Sect. 3.

Fig. 5

The intersections of $W_{\varepsilon }^{u}$ and $W_{\varepsilon }^{s}$ in ${\varSigma }_{\theta _{1m}, \theta _{1M}}^{\theta _{20*}}$, where $\gamma _1=1.1, \gamma _2=1.0$, $\omega _1=\frac{\pi }{3}, \omega _2=0.7, \varepsilon =0.04$, $\delta =1.6, \rho =0, [\theta _{1m}, \theta _{1M}]=[-\frac{7}{6}\pi , \frac{3}{2}\pi ]$ and $\theta _{20*}=0.5\pi$

As pointed out in [33] and [35], since the Poincaré map for system (13) is a three-dimensional map, the fractal nature of the strange attractor of the map, if it exits, is not evident. We adopt the double Poincaré section technique proposed by Moon and Holmes in [33] to overcome this difficulty as follows. Take a thin section

$$\begin{aligned} {\varSigma }^{\theta _{20},\varDelta \theta _2} = \{(y, \theta _1, \theta _2)\in {\varSigma } \ | \ \theta _2\in [\theta _{20},\theta _{20}+\varDelta \theta _2]\}, \end{aligned}$$

where $\varDelta \theta _2$ is small. Then, the double Poincaré map $\fancyscript{P}^{\theta _{20},\varDelta \theta _2}: {\varSigma }^{\theta _{20},\varDelta \theta _2}\rightarrow {\varSigma }^{\theta _{20},\varDelta \theta _2}$ is well defined. Furthermore, we compute the spectrum of Lyapunov exponents for each case by the method for impact systems presented in [50, 51] to verify the chaotic motions for the chosen parameters. It is elementary to prove that one of the three Lyapunov exponents is zero. Thus, we only need to compute the other two Lyapunov exponents. To approximate the Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$, the fourth-fifth-order Runge–Kutta–Fehlberg method is chosen to solve system (13) for $|x|<1$.

Since the left side of (17) is a linear combination of $\rho$ and $\delta$ with constant coefficients, without the loss of generality, we fix $\rho =0$ in this section. We also fix $\varepsilon =0.04, \delta =1.6$ and $\omega _1=\frac{\pi }{3}$. Hence, $\alpha =\frac{\rho }{\sqrt{2}}+\frac{2\delta }{3}(2\sqrt{2}-1)\approx 1.950322266$. Let $\gamma _m=\frac{\alpha }{4 I_m}\approx 1.293904566$. Parameters $\gamma _1, \gamma _2$, and $\omega _2$ are chosen from the chaotic zone for each case, so that system (13) exhibits chaotic behavior. In each case, we choose the values of $\bar{\theta }_{10}, \bar{\theta }_{20}$ and simulate an orbit of (13) starting from $(x_0+10^{-10}, y_0+10^{-10}, \bar{\theta }_{10}, \bar{\theta }_{20})$, where $y_0=0$, $x_0$ is the solution of the equation

$$\begin{aligned} x_0-x_0^3-\varepsilon \left( \gamma _1\cos \bar{\theta }_{10}+\gamma _2\cos \bar{\theta }_{20}\right) =0. \end{aligned}$$

(19)

Equation (19) is solved by the Newton–Raphson method with initial guess $x_0^0=0$. The Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$ is iterated for 180,000 times with the first 2,000 iterations omitted for transients to decay. In each case, we plot (a) the convergent sequences in the iteration process of the spectrum of Lyapunov exponents; (b) the three-dimensional Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$; (c) a projection of the double Poincaré map $\fancyscript{P}^{\theta _{20},\varDelta \theta _2}: {\varSigma }^{\theta _{20},\varDelta \theta _2}\rightarrow {\varSigma }^{\theta _{20},\varDelta \theta _2}$ on to the $(\theta _1, y)$ plane; (d) a projection of the Poincaré map $\fancyscript{P}: {\varSigma }\mapsto {\varSigma }$ on to the $(\theta _1, \theta _2)$ plane and (e) on to the $(\theta _1, y)$ plane and (f) on to the $(\theta _2, y)$ plane.

In Table 1, the parameters chosen from the six chaotic zones $\fancyscript{C}_k$ ($k=1, 2, 4, 5, 7, 9$) for numerical simulations and the largest Lyapunov exponent $\lambda _{\max }$ are listed, where $\bar{\theta }_{10}$ and $\bar{\theta }_{20}$ are used to solve (19) to obtain initial conditions, ${\theta }_{20}$ and $\varDelta \theta _{2}$ are used to define the double Poincaré map $\fancyscript{P}^{\theta _{20},\varDelta \theta _2}: {\varSigma }^{\theta _{20},\varDelta \theta _2}\rightarrow {\varSigma }^{\theta _{20},\varDelta \theta _2}$. The results are shown in Figs. 6, 7, 8, 9, 10, and 11. From Table 1 and the figures, it is easy to see that for the chosen parameters for each chaotic zone, the largest Lyapunov exponent is positive and the double Poincaré map has an attractor of fractal-like structure, suggesting that the system is chaotic. Therefore, the numerical experiments confirm our theoretical predictions.

Fig. 6

Parameters are chosen from $\fancyscript{C}_1$ with $\gamma _1=1.1, \gamma _2=1, \omega _2=0.7$ and $\bar{\theta }_{10}=\bar{\theta }_{20}=0.5\pi$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Fig. 7

Parameters are chosen from $\fancyscript{C}_2$ with $\gamma _1=\gamma _m, \gamma _2=1, \omega _2=0.5, \bar{\theta }_{10}=0.5\pi$ and $\bar{\theta }_{20}=1.6$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Fig. 8

Parameters are chosen from $\fancyscript{C}_4$ with $\gamma _1=\gamma _2=\gamma _m, \omega _2=0.5$, $\bar{\theta }_{10}=\frac{\pi }{7}$ and $\bar{\theta }_{20}=1$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Fig. 9

Parameters are chosen from $\fancyscript{C}_5$ with $\gamma _1=1.5, \gamma _2=1, \omega _2=0.4$ and $\bar{\theta }_{10}=\bar{\theta }_{20}=0.5\pi$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Fig. 10

Parameters are chosen from $\fancyscript{C}_7$ with $\gamma _1=1.5, \gamma _2=\gamma _m, \omega _2=0.3$, $\bar{\theta }_{10}=0.4\pi$ and $\bar{\theta }_{20}=1.55$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Fig. 11

Parameters are chosen from $\fancyscript{C}_9$ with $\gamma _1=1.6, \gamma _2=1.5, \omega _2=0.3$, $\bar{\theta }_{10}=\frac{\pi }{3}$ and $\bar{\theta }_{20}=1.5$. a Convergent sequences of the Lyapunov exponents, b the Poincaré map, c a projection of the double Poincaré map on to the $(\theta _1,y)$ plane, d a projection of the Poincaré map on to the $(\theta _1,\theta _2)$ plane and e on to the $(\theta _1,y)$ plane and f on to the $(\theta _2,y)$ plane.

Table 1 Parameters for numerical simulation and the largest Lyapunov exponent $\lambda _{\max }$, where $\gamma _m\approx 1.293904566$. The other parameters are fixed as $\rho =0$, $\varepsilon =0.04, \delta =1.6$ and $\omega _1=\frac{\pi }{3}$

5 Discussion and remarks

In this paper, we discussed for the first time the homoclinic bifurcation of a quasiperiodically excited nonlinear impact inverted pendulum. By using a method of Melnikov type, we extended the results of Ide and Wiggins [17, 31, 32] for homoclinic bifurcation of quasiperiodically excited smooth systems to the non-smooth ones. We are able to give a criterion for the appearance of Smale horseshoe-type chaotic dynamics of the system.

As an important application, by using a combination of analytical and numerical methods, we studied a quasiperiodically excited impact oscillator of Duffing type with two frequencies in detail. We give a complete description of the bifurcation sets and the chaotic zones in the parameter space. Numerical simulations have been performed for parameters chosen from the chaotic zones. The numerical results confirm the theoretical predictions.

It is worth mentioning that in addition to the work of Ide and Wiggins in [32], Parthasarathy also studied homoclinic bifurcation sets of quasiperiodically excited Duffing oscillator with two frequencies in [52]. Compared to their works, the main difference here is that the example considered in Sects. 3 and 4 is an impact system, which is non-smooth, while the systems studied in [32, 52] are smooth. Hence, the expressions for the corresponding Melnikov functions are quite different. As can be seen from (16) that the Melnikov function $M_1(\theta _{10}, \theta _{20})$ computed in this paper involves in an additional parameter $\rho$ due to the impact law given in (15), the integral $I(\omega )$ cannot be found analytically. Consequently, the resulting bifurcation sets for system (13) are different from those presented in [32, 52]. Furthermore, the new feature of our work includes a comprehensive numerical simulations to validate the theoretical results, which is not a trivial task for non-smooth systems.