Nonlinear coupling of transverse modes of a fixed–fixed microbeam under direct and parametric excitation

Abstract

Tuning of linear frequency and nonlinear frequency response of microelectromechanical systems is important in order to obtain high operating bandwidth. Linear frequency tuning can be achieved through various mechanisms such as heating and softening due to DC voltage. Nonlinear frequency response is influenced by nonlinear stiffness, quality factor and forcing. In this paper, we present the influence of nonlinear coupling in tuning the nonlinear frequency response of two transverse modes of a fixed–fixed microbeam under the influence of direct and parametric forces near and below the coupling regions. To do the analysis, we use nonlinear equation governing the motion along in-plane and out-of-plane directions. For a given DC and AC forcing, we obtain static and dynamic equations using the Galerkin’s method based on first-mode approximation under the two different resonant conditions. First, we consider one-to-one internal resonance condition in which the linear frequencies of two transverse modes show coupling. Second, we consider the case in which the linear frequencies of two transverse modes are uncoupled. To obtain the nonlinear frequency response under both the conditions, we solve the dynamic equation with the method of multiple scale (MMS). After validating the results obtained using MMS with the numerical simulation of modal equation, we discuss the influence of linear and nonlinear coupling on the frequency response of the in-plane and out-of-plane motion of fixed–fixed beam. We also analyzed the influence of quality factor on the frequency response of the beams near the coupling region. We found that the nonlinear response shows single curve near the coupling region with wider width for low value of quality factor, and it shows two different curves when the quality factor is high. Consequently, we can effectively tune the quality factor and forcing to obtain different types of coupled response of two modes of a fixed–fixed microbeam.

1 Introduction

Microelectromechanical systems (MEMS) have been the subject of intense research in the design of sensitive sensors and actuators. The performance of MEMS-based sensors and actuators is mainly dependent on their resonance frequencies. Hence, it is important to study the linear and nonlinear frequency tuning of such devices. While the linear frequency tuning can be achieved through various mechanisms such as hardening due to residual stresses, softening due to heating and DC voltage, and their combined effect, the nonlinear frequency response can be tuned due to nonlinear stiffness, quality factor and forcing [1–5]. In this paper, we discuss about the tuning of nonlinear frequency response of a fixed–fixed microbeam under the direct and parametric excitation by controlling the linear and nonlinear stiffness through the coupling of two transverse modes and their quality factors at different excitation force.

Many researchers have analyzed the linear and nonlinear frequency response of in-plane or out-of-plane motion of a fixed–fixed or cantilever beam using one degree of freedom model. Younis and Nayfey [6], and Nayfeh et al. [7] studied the linear and nonlinear response of out-of-plane motion of a fixed–fixed beam subjected to direct forcing. Dumitru et al. [8] analyzed the nonlinear behavior of out-of-plane motion of a cantilever beam subjected to the fringing and direct forces. Linzon et al. [9] studied the parametric response of a cantilever beam in out-of-plane direction under the influence of fringing forces from two symmetrically placed side electrodes. Gutschmidt and Gottlieb [10, 11] studied the in-plane motion of an array of fixed–fixed beams under the parametric excitation. Lifshitz et al. [12] analyzed the parametric response of an array of fixed–fixed beams along in-plane direction and compared the results with experiments conducted by Buks and Roukes [13]. Kambali and Pandey [14] studied nonlinear response of out-of-plane motion of a fixed–fixed beam under the combined effect of direct and fringing forces. While the direct force leads to the nonlinear Duffing response, the fringing force induces parametric response. The combined effect of direct and fringing force results in the nonlinear Duffing response with enhanced amplitude as well as frequency width. To analyze the influence of the coupling of two or more modes, Nayfeh et al. [15] analyzed the nonlinear response of longitudinal and transverse motion of a taut string subjected to end excitation. Daqaq et al. [16] studied the linear and nonlinear coupled behavior of torsional micromirror when its torsional and transverse modes show 2:1 internal resonance condition. Isacsson et al. [17] presented numerical and analytical study of the linear and nonlinear coupled behavior of longitudinal and transverse motion of an array of carbon nanotube with fixed-free condition under parametric excitation. Samanta et al. [18] studied nonlinear coupling between various transverse modes of a Mo$\mathrm {S}_{2}$ nanomechanical beam under 1:1, 1:2 and 1:3 internal resonance conditions. Recently, Ramini et al. [19] presented experimental studies of primary and parametric resonances of a MEMS arch resonator. Wie et al. [20] investigated the weak and strong coupling in a periodically driven Duffing resonator elastically coupled to a van der Pol oscillator under 1:1 internal resonance condition. Matheny et al. [21] studied intra- and intermodal nonlinear coupling of a doubly clamped piezoelectric beam. Westra et al. [22] presented theoretical and experimental studies of nonlinear intermodal coupling between the flexural vibration modes of a single clamped–clamped beam. Conley et al. [23] analyzed the nonlinear dynamics of fixed–fixed nanowire and found the transition from a planer motion to whirling motion on increasing excitation amplitude. Mahboob et al. [24] analyzed the nonlinear coupling of nanomechanical resonators by the coupled Vander Pol–Duffing equations. In this paper, we model and analyze the nonlinear coupling of two transverse modes of a fixed–fixed beam under the condition of 1:1 internal resonance.

To do nonlinear coupled analysis of in-plane and out-of-plane modes near and away from the coupling region, we consider the dimensions and properties of a fixed–fixed beam separated by two side electrodes and a bottom electrode as described by Kambali et al. [2]. The electrostatic force along the out-of-plane direction is based on direct forcing between the bottom electrode and the beam, and the parametric forcing between the beam and side electrodes. The force along in-plane direction is pure parametric forcing between the beam and the symmetrically placed side electrodes. Under the electrostatic forcing, we apply Galerkin’s method to governing equations along two directions and obtain the reduced-order form of corresponding static and dynamics equations. To obtain the condition of coupling, we take appropriate value of DC voltage such that the linear frequencies of in-plane mode, $\omega _{1}$, and out-of-plane mode, $\omega _{1}$, show coupling. To obtain the nonlinear coupled response, we solve the modal dynamic equation using the method of multiple scales under the condition of $\omega _{1}\approx \omega _{2}$. After validating the multiple-scale solution with numerical results obtained by solving modal dynamic equations, we analyze the influence of quality factor on nonlinear frequency response near the coupling region.

Fig. 1

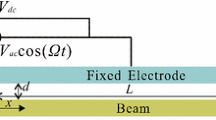
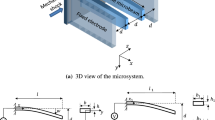
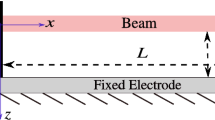
a A fixed–fixed beam of width B, thickness H separated from the side electrodes, $E_{1}$ and $E_{2}$, by $g_{0}$, $g_{1}$ and the ground electrode $E_{g}$ by distance d is subjected to direct force, $Q_{z}$, and fringing field force, $Q_{y}$; b top view of a fixed–fixed beam of length L separated from the side electrodes, $E_{1}$ and $E_{2}$, by $g_{0}$, $g_{1}$, respectively

2 Governing equations

To present the partial differential equations governing the in-plane and out-of-plane motions of a fixed–fixed microbeam, we consider a beam of length L, width B and thickness H, which is separated from the two side electrodes $E_{1}$ and $E_{2}$ by gaps of $g_{0}$ and $g_{1}$, respectively, and the bottom electrode $E_{g}$ by a gap of d as shown in Fig. 1a, b. Taking the deflection of the beam along in-plane and out-of-plane as y(x, t) and z(x, t), respectively, as shown in Fig. 1a, the governing equation of motion along in-plane and out-of-plane directions considering damping, residual tension and mid-plane stretching [1] can be written as:

$$\begin{aligned}&EI_{\bar{z}}\bar{y}^{\prime \prime \prime \prime }+\rho A \ddot{\bar{y}}+C_{1}\dot{\bar{y}}\nonumber \\&\qquad -\,\Bigg [N_{0}+\frac{EA}{2L}\int _{0}^{L}\Big (\bar{z}^{\prime 2}+\bar{y}^{\prime 2}\Big )\mathrm{d}\bar{x} \Bigg ] \bar{y}_{n}^{\prime \prime }\nonumber \\&\quad =Q_{\bar{y}}(\bar{y},\bar{z},\bar{t})\qquad \end{aligned}$$

(2.1)

$$\begin{aligned}&EI_{\bar{y}}\bar{z}^{\prime \prime \prime \prime }+\rho A \ddot{\bar{z}}+C_{3}\dot{\bar{z}}\nonumber \\&\qquad -\,\Bigg [N_{0}+\frac{EA}{2L}\int _{0}^{L}\Big (\bar{z}^{\prime 2}+\bar{y}^{\prime 2}\Big )\mathrm{d}\bar{x} \Bigg ] \bar{ z}_{n}^{\prime \prime }\nonumber \\&\quad = Q_{\bar{z}}(\bar{y},\bar{z},\bar{t}) \qquad \end{aligned}$$

(2.2)

where the subscripts prime and dot represent differentiation with respect to x and t, respectively, $N_{0}$ is the initial tension induced in the beam by fabrication processes and heating [2], E is the Young’s modulus of the beam, EI is the bending rigidity, $I_{z}=HB^{3}/12$, $I_{y}=BH^{3}/12$ are area moment of inertia about z and y-axes, and $\rho$ is the material density. The boundary conditions for the fixed–fixed beam are taken as

$$\begin{aligned} \bar{y}(0,t)= & {} \bar{y}(L,t)=0,\quad \bar{z}(0,t)=\bar{z}(L,t)=0, \nonumber \\ \bar{y}^{\prime }(0,t)= & {} \bar{y}^{\prime }(L,t)=0 \nonumber \\ \bar{z}^{\prime }(0,t)= & {} \bar{z}^{\prime }(L,t)=0. \end{aligned}$$

(2.3)

The forcing $Q_{y}$ and $Q_{z}$ are the effective electrostatic forces per unit length along y and z directions for the beam under the direct and fringing field effect as shown in Fig. 1a. The expressions for the forcing are given by [2]

$$\begin{aligned} Q_{\bar{y}}(\bar{y},\bar{z},\bar{t})= & {} \frac{1}{2}{k_{1}\epsilon _{0}H}\nonumber \\&\times \,\Bigg [\frac{\left( V_{10}+v(t)\right) ^2}{\left( g_{0}-\bar{y}\right) ^2} -\frac{\left( V_{12}+v(t)\right) ^2}{\left( g_{1}+\bar{y}\right) ^2}\Bigg ]\qquad \end{aligned}$$

(2.4)

$$\begin{aligned} Q_{\bar{z}}(\bar{y},\bar{z},\bar{t})= & {} \frac{1}{2}\frac{{V_{1g}}^{2}\epsilon _{{0}}}{{{B}^{2}\left( d-\bar{z}\right) ^{2}}}\,\nonumber \\&\times \,\big [ 4.32\,{B}^{3}+0.0182\,B \big ( d-\bar{z} \big )^{2}\nonumber \\&-\,k_{2}0.00068\, \left( d-\bar{z}\right) ^{3}\big ] \nonumber \\&-\,\frac{1}{2}\frac{\epsilon _{0}H}{g_{0}{B^2}}\big (k_{3}0.156\bar{z}+0.0049B\big )\nonumber \\&\times \,\big [\left( V_{10}+v(t)\right) ^2+\left( V_{12}+v(t)\right) ^2\big ]\nonumber \\ \end{aligned}$$

(2.5)

where $\epsilon _{0}=8.85\times 10^{-12}$ F/m is the vacuum permittivity. Here, $k_{1}$ contributes for the net effect of fringing and direct fields in y direction, $k_{2}$ and $k_{3}$ represent the strength of the fringing field effects from the bottom electrode and two side electrodes in the z direction deflection. Further details regarding the extraction of electrostatic force parameters can be found in [25]. $V_{ij}= V_{i}-V_{j}$ is the voltage difference between the beam and electrodes and $v(t)=V_\mathrm{ac}\cos (\varOmega t)$.

2.1 Non-dimensionalization

To obtain the non-dimensional form of the governing equations, we define the ratio of the beam and side electrode gaps as $r_{0}=({g_{0}}/{g_{0}})$, $r_{1}=({g_{1}}/{g_{0}})$ and use the variables $x={\bar{x}}/{L}$, $y={\bar{y}}/{g_{0}}$, $z={\bar{z}}/{d}$, $t={\bar{t}}/{T}$, where $T=\sqrt{\rho A L^{4}/EI_{z}}$. Finally, the non-dimensional nonlinear dynamic equations along the in-plane and out-of-plane directions for fixed–fixed beam under direct and parametric excitation can be written as:

$$\begin{aligned}&y^{\prime \prime \prime \prime }+{\ddot{y}}+c_{1}{\dot{y}}\nonumber \\&\quad -\,[N+\alpha _{1}\varGamma (y,y)+\alpha _{2}\varGamma (z,z)]y^{\prime \prime } \nonumber \\&\qquad = \beta _{s}\bigg [\frac{(V_{10}+v(t))^2}{(1-y)^2}-\frac{(V_{12}+v(t))^2}{(r_{1}+y)^2}\bigg ]\nonumber \\ \end{aligned}$$

(2.6)

$$\begin{aligned}&z^{\prime \prime \prime \prime }+\alpha _{3}{\ddot{z}}+c_{3}{\dot{z}}-\alpha _{3}[N+\alpha _{1}\varGamma (y,y)+\alpha _{2}\varGamma (z,z)] z^{\prime \prime }\nonumber \\&\quad = \left( \beta _{g}+\beta _{2g}(1-z)^2-\beta _{3g}(1-z)^3\right) \nonumber \\&\quad \quad \times \frac{(V_{1g}+v(t))^2}{(1-z)^2}-(\alpha _{g}+\alpha _{2g}z)\nonumber \\&\quad \quad \times \left[ (V_{10}+v(t))^2+(V_{12}+v(t))^2\right] . \end{aligned}$$

(2.7)

The corresponding non-dimensional form of the boundary conditions can be written as

$$\begin{aligned} y(0,t)= & {} y(1,t)=0,\quad z(0,t)=z(1,t)=0,\nonumber \\ y^{\prime }(0,t)= & {} y^{\prime }(1,t)=0,\nonumber \\ z^{\prime }(0,t)= & {} z^{\prime }(1,t)=0 . \end{aligned}$$

(2.8)

The various non-dimensionalized parameters as mentioned in above equations are defined as

$$\begin{aligned}&\varGamma (p(x,t),q(x,t))=\int _{0}^{1}\frac{\partial p}{\partial x}\frac{\partial q}{\partial x}{\mathrm {d}x},\nonumber \\&N=\frac{N_{0}L^2}{EI_{z}},\quad \alpha _{1}=\frac{6g_{0}^{2}}{B^{2}},\nonumber \\&\alpha _{2}=\frac{6d^{2}}{B^{2}},\quad \alpha _{3}=\left( \frac{I_{z}}{I_{y}}\right) ,\nonumber \\&\beta _{s}=\frac{6k_{1}\sigma _{1}}{B^3g_{0}^3},\quad \beta _{g}=\frac{25.92\sigma _{1}}{H^3d^3},\nonumber \\&\beta _{2g}=\frac{0.1092\sigma _{1}}{B^2H^3d}, \nonumber \\&\beta _{3g}=\frac{k_{2}4.08\times 10^{-3}\sigma _{1}}{H^3B^3}, \nonumber \\&\sigma _{1}=\frac{\epsilon _{0}L^4}{E},\quad \alpha _{g}= \frac{0.0294\sigma _{1}}{g_{0}B^2H^2d}, \nonumber \\&\alpha _{2g}=\frac{k_{3}9.36\times 10^{-1}\sigma _{1}}{g_{0}B^3H^2},\nonumber \\&c_{1}={\frac{C_{{1}}{L}^{4}}{E{ Iz}\,T}},\quad c_{3}={\frac{C_{{3}}{L}^{4}}{E{ Iy}\,T\alpha _{{3}}}}. \end{aligned}$$

(2.9)

Since the beam deflection is based on its static component due to DC voltage and dynamic component due to AC voltage, the deflection along y and z directions can be written as [1]

$$\begin{aligned} y(x,t)=u_{s}(x)\,{+}\,u(x,t),\quad z(x,t)=w_{s}(x)\,{+}\,w(x,t).\nonumber \\ \end{aligned}$$

(2.10)

where $u_{s}(x)$ and $w_{s}(x)$ are static deflections. By substituting Eq. (2.10) in Eqs. (2.6) and (2.7), and subsequently setting the time derivatives and dynamic forcing terms equal to zero, we get the static equations as:

$$\begin{aligned}&u^{\prime \prime \prime \prime }_{s}-\left[ N+\alpha _{1}\varGamma (u_{s},u_{s})+\alpha _{2}\varGamma (w_{s},w_{s}) \right] u^{\prime \prime }_{s}\nonumber \\&\quad =\beta _{s} \bigg [\frac{(V_{10})^2}{(1-u_{s})^2} -\frac{(V_{12})^2}{(r_{1}+u_{s})^2}\bigg ]\qquad \end{aligned}$$

(2.11)

$$\begin{aligned}&w^{\prime \prime \prime \prime }_{s}-\alpha _{3}\left[ N+\alpha _{1}\varGamma (u_{s},u_{s})+\alpha _{2}\varGamma (w_{s},w_{s}) \right] w^{\prime \prime }_{s}\nonumber \\&\quad = \left( \beta _{g}+\beta _{2g}(1-w_{s})^2-\beta _{3g}(1-w_{s})^3\right) \nonumber \\&\qquad \times \,\frac{(V_{1g})^2}{(1-w_{s})^2} -\alpha _{g}\left[ (V_{10})^2+(V_{12})^2\right] \nonumber \\&\qquad -\,\alpha _{2g}\left[ (V_{10})^2w_{s}+(V_{12})^2w_{s}\right] . \end{aligned}$$

(2.12)

Similarly, substituting Eq. (2.10) in Eqs. (2.6) and (2.7), expanding the forcing terms about $u_{n}=0$ and $w_{n}=0$ up to the first order and subtracting the contribution of the nonlinear static terms given by Eqs. (2.11) and (2.12), we get the nonlinear dynamic equations for beam as:

$$\begin{aligned}&u^{\prime \prime \prime \prime }+u_{tt}+c_{1}u_{t}-[\alpha _{1}\varGamma (u,u)+2\alpha _{1}\varGamma (u_{s},u)\nonumber \\&\quad +\,\alpha _{2}\varGamma (w,w)+2\alpha _{2}\varGamma (w_{s},w)]u^{\prime \prime }_{s}\nonumber \\&\quad -\, [N+\alpha _{1}\varGamma (u_{s},u_{s}) +\alpha _{1}\varGamma (u,u)\nonumber \\&\quad +\,2\alpha _{1}\varGamma (u_{s},u)+\,\alpha _{2}\varGamma (w_{s},w_{s}) +\alpha _{2}\varGamma (w,w)\nonumber \\&\quad +\,2\alpha _{2}\varGamma (w_{s},w)] u^{\prime \prime }= 2\beta _{s} \Big [ \frac{(V_{10})^2 u}{(1-u_{s})^3}\nonumber \\&\quad +\,\frac{(V_{12})^2u}{({r_{1}}+u_{s})^3}\Big ]+\beta _{s} \frac{2V_{10}v(t)+{v(t)}^{2} }{(1-u_{s})^2} \nonumber \\&\quad \times \, \Big [1+\frac{2u}{(1-u_{s})}\Big ]-\beta _{s} \frac{2V_{12}v(t)+{v(t)}^{2} }{({r_{1}}+u_{s})^2} \nonumber \\&\quad \times \, \Big [1-\frac{2u}{({r_{1}}+u_{s})}\Big ] \end{aligned}$$

(2.13)

$$\begin{aligned}&w^{\prime \prime \prime \prime }+\alpha _{3}w_{tt}+c_{3}w_{t}-\alpha _{3}[\alpha _{1}\varGamma (u,u)+2\alpha _{1}\varGamma (u_{s},u)\nonumber \\&\quad +\,\alpha _{2}\varGamma (w,w)+2\alpha _{2}\varGamma (w_{s},w) ]w^{\prime \prime }_{s}\nonumber \\&\quad -\,\alpha _{3}[N +\alpha _{1}\varGamma (u_{s},u_{s}) +\alpha _{1}\varGamma (u,u)\nonumber \\&\quad +2\alpha _{1}\varGamma (u_{s},u)+\,\alpha _{2}\varGamma (w_{s},w_{s}) +\alpha _{2}\varGamma (w,w)\nonumber \\&\quad +\,2\alpha _{2}\varGamma (w_{s},w) ]w^{\prime \prime }=\left( 2\beta _{g}+\beta _{3g}(1-w_{s})^3\right) w \nonumber \\&\quad \times \, \frac{(V_{1g})^2}{(1-w_{s})^3}+\beta _{g} \frac{2V_{1g}v(t)+{v(t)}^{2} }{(1-w_{s})^2}\nonumber \\&\quad \times \,\Big [1+\frac{2w}{(1-w_{s})}\Big ]-\beta _{2g} \left( 2V_{1g}v(t)+{v(t)}^{2}\right) \nonumber \\&\quad -\,\beta _{3g} \left( 2V_{1g}v(t)+{v(t)}^{2}\right) (1-w_{s} -w)\nonumber \\&\quad -\,\alpha _{2g}w\left[ (V_{10})^2 +(V_{12})^2\right] - \left( 2V_{10}v(t)+{v(t)}^{2}\right) \nonumber \\&\quad \times \, (\alpha _{g}-\alpha _{2g}w_{s}-\alpha _{2g}w)\nonumber \\&\quad -\, \left( 2V_{12}v(t)+{v(t)}^{2}\right) (\alpha _{g}-\alpha _{2g}w_{s}-\alpha _{2g}w)\nonumber \\ \end{aligned}$$

(2.14)

2.2 Reduced-order model

To obtain the static and dynamic equations to perform coupled analysis under 1:1 internal resonance condition near the coupling region which is much below the pull-in voltage [3], we use Galerkin method based on first-mode approximation of the in-plane and out-of-plane displacements with negligible error [26]. Assuming the static and dynamic displacements subjected to the first transverse mode $\phi (x)$, the displacement along in-plane and out-of-plane directions can be written as [2, 3]:

$$\begin{aligned}&u_{s}(x)= q_{1}(y,z)\phi (x), \quad w_{s}(x)=q_{2}(y,z)\phi (x), \end{aligned}$$

(2.15)

$$\begin{aligned}&u(x,t)=P_{1}(t)\phi (x), \quad w(x,t)=P_{2}(t)\phi (x), \end{aligned}$$

(2.16)

where $q_{1}$ and $q_{2}$ are static deflections, and $P_{1}(t)$ and $P_{2}(t)$ are non-dimensional modal variables. $\phi (x)$ is undamped exact mode shape [2] which is taken as $\phi (x)=\cosh (\zeta x)-\cos (\zeta x)-\nu (\sinh (\zeta x)-\sin (\zeta x))$, where for the first mode $\zeta =4.73$, and $\nu =0.9825$ such that $\int _0^1(\phi _1(x))^2\mathrm{d}x=1$. After premultiplying the denominator terms on either side of the Eqs. (2.11), (2.12), substituting the assumed solution given by Eq. (2.15) and applying Galerkin’s method, we obtain the nonlinear static equations in both the directions which are given in “Appendix 1.”

Similarly, by premultiplying the denominator terms on either side of Eqs. (2.13) and (2.14), substituting the assumed static and dynamic solutions given by Eqs. (2.15) and (2.16), and applying Galerkin’s method, we obtain the nonlinear modal dynamic equations in both the directions as:

$$\begin{aligned}&P_{{1tt}}(t)+\lambda _{1}^2P_{1}(t)+t_{1}P_{1}(t)^3+t_{2}P_{1}(t)^2\nonumber \\&\quad +\,\big [t_{3}P_{2}(t)^2+t_{4}P_{2}(t)+t_{5}(2V_{10}v(t)+v(t)^2)\nonumber \\&\quad +\,t_{6}(2V_{12}v(t)+v(t)^2)\big ]P_{1}(t)\nonumber \\&\quad +\,t_{11}P_{1t}(t)+t_{7}P_{2}(t)^2+t_{8}P_{2}(t) \nonumber \\&\quad +\,t_{9}(2V_{10}v(t)+v(t)^2)\nonumber \\&\quad +\,t_{10}(2V_{12}v(t)+v(t)^2)=0 \end{aligned}$$

(2.17)

$$\begin{aligned}&P_{{2tt}}(t)+\lambda _{2}^2P_{2}(t)+s_{1}P_{2}(t)^3+s_{2}P_{2}(t)^2 \nonumber \\&\quad +\,\big [s_{3}P_{2}(t)^2+s_{4}P_{2}(t)+s_{5}(2V_{1g}v(t)\nonumber \\&\quad +\,v(t)^2)+s_{6}(2V_{10}v(t)+2V_{12}v(t)+2v(t)^2)\big ]P_{1}(t)\nonumber \\&\quad +\,s_{11}P_{2t}(t)+s_{7}P_{1}(t)^2+s_{8}P_{1}(t)\nonumber \\&\quad +\,s_{9}(2V_{1g}v(t)+v(t)^2)+s_{10}(2V_{10}v(t)\nonumber \\&\quad +\,2V_{12}v(t)+2v(t)^2)=0\qquad \end{aligned}$$

(2.18)

where all coefficients of each term in above Eqs. (2.17) and (2.18) are given in “Appendix 1.” Neglecting the damping term, nonlinear terms and the dynamic forcing terms from above Eqs. (2.17) and (2.18), we get linear modal dynamic equations as:

$$\begin{aligned}&P_{{1tt}}(t)+\lambda _{1}^2P_{1}(t)+t_{8}P_{2}(t)=0 \end{aligned}$$

(2.19)

$$\begin{aligned}&P_{{2tt}}(t)+\lambda _{2}^2P_{2}(t)+s_{8}P_{1}(t)=0. \end{aligned}$$

(2.20)

To obtain the linear frequency from the above equation, we assume the solution of Eqs. (2.19) and (2.20) as

$$\begin{aligned} P_{1}(t)=\beta e^{i\omega t},\quad P_{2}(t)=\gamma e^{i\omega t}. \end{aligned}$$

Substituting the assumed solutions in the modal Eqs. (2.19) and (2.20), we get

$$\begin{aligned}&(\lambda _{1}^2-\omega ^2)\beta + t_{8}\gamma =0 \\&(\lambda _{2}^2-\omega ^2)\gamma + s_{8}\beta =0 \end{aligned}$$

For non-trivial solution, the determinant of these system of equations should be zero. After solving the resulting equation, we get two values of $\omega$ corresponding to two directions as

$$\begin{aligned} \omega _{1,2}=\sqrt{\frac{1}{2}\bigg [\bigg (\lambda _{1}^2+\lambda _{2}^2\bigg )\pm \sqrt{\bigg (\lambda _{1}^2-\lambda _{2}^2\bigg )^2+4t_{8}s_{8}}\bigg ]}\nonumber \\ \end{aligned}$$

(2.21)

where $\lambda _{1}$, $\lambda _{2}$, $t_{8}$ and $s_{8}$ are given in “Appendix 1.”

3 Method of multiple scale

In this section, we apply the method of multiple scales (MMS) in solving Eqs. (2.17) and (2.18) assuming the modal displacements as functions multiple time scales, $T_{0}=t$, $T_{1}=\epsilon t$ and $T_{2}=\epsilon ^2t$ as

$$\begin{aligned} P_{1}(t)= & {} \epsilon x_{11}(T_{0},T_{1},T_{2})+\epsilon ^2 x_{12}(T_{0},T_{1},T_{2})\nonumber \\&+\,\epsilon ^3 x_{13}(T_{0},T_{1},T_{2})+ O(\epsilon ^4)\nonumber \\ P_{2}(t)= & {} \epsilon x_{21}(T_{0},T_{1},T_{2})+\epsilon ^2 x_{22}(T_{0},T_{1},T_{2})\nonumber \\&+\,\epsilon ^3 x_{23}(T_{0},T_{1},T_{2})+ O(\epsilon ^4), \end{aligned}$$

(3.1)

where $\epsilon$ is a dimensionless small positive number. Subsequently, the derivative terms with respect to t can be defined in terms of new time scales as:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}= & {} \frac{\partial }{\partial T_{0}}\frac{dT_{0}}{\mathrm{d}t}+\frac{\partial }{\partial T_{1}}\frac{dT_{1}}{\mathrm{d}t}+\frac{\partial }{\partial T_{2}}\frac{dT_{2}}{\mathrm{d}t} \nonumber \\= & {} \left( D_{0}+\epsilon D_{1}+\epsilon ^2 D_{2}\right) \nonumber \\ \frac{\mathrm{d}^2}{\mathrm{d}t^2}= & {} \bigg (\frac{\mathrm{d}}{\mathrm{d}t}\bigg )^2=\left( D_{0}+\epsilon D_{1}+\epsilon ^2 D_{2}\right) ^2\nonumber \\= & {} \left( D_{0}^2+2\epsilon D_{0}D_{1}+\epsilon ^2 D_{1}^2+2\epsilon ^2 D_{0}D_{2}\right) \nonumber \\&+\, H.O.T \end{aligned}$$

(3.2)

Rescaling the damping and forcing terms with different powers of $\epsilon$ as

$$\begin{aligned} t_{11}=\epsilon t_{11} ,\quad s_{11}=\epsilon s_{11},\quad v(t)=\epsilon ^2 V_\mathrm{ac} \cos (\varOmega t),\nonumber \\ \end{aligned}$$

(3.3)

substituting the assumed solution from Eqs. (3.1) to (3.3) in Eqs. (2.17) and (2.18), and by comparing different powers of $\epsilon$ up to third order, we get the following three sets of equations as

$$\begin{aligned}&O(\epsilon ^1)\nonumber \\&\quad \rightarrow D_{0}^2x_{11}+\lambda _{1}^2x_{11}+t_{8}x_{21}=0\nonumber \\&\qquad \quad D_{0}^2x_{21}+\lambda _{2}^2x_{21}+s_{8}x_{11}=0 \end{aligned}$$

(3.4)

$$\begin{aligned}&O(\epsilon ^2)\nonumber \\&\quad \rightarrow D_{0}^2x_{12}+\lambda _{1}^2x_{12}+t_{8}x_{22}=-2D_{0}D_{1}x_{11}\nonumber \\&\qquad \quad -t_{11}D_{0}x_{11}-t_{2}x_{11}^2-t_{4}x_{11}x_{21}\nonumber \\&\qquad \quad -t_{7}x_{21}^2-t_{9}\eta _{11}\cos (\omega _\mathrm{ac}t)-t_{10}\eta _{12}\cos (\omega _\mathrm{ac}t)\nonumber \\&\qquad \quad D_{0}^2x_{22}+\lambda _{2}^2x_{22}+s_{8}x_{12}=-2D_{0}D_{1}x_{21}\nonumber \\&\qquad \quad -s_{11}D_{0}x_{21}-s_{2}x_{21}^2-s_{4}x_{11}x_{21}\nonumber \\&\qquad \quad -s_{7}x_{11}^2-s_{9}\eta _{21}\cos (\omega _\mathrm{ac}t)\nonumber \\&\qquad \quad -s_{10}(\eta _{11}+\eta _{12})\cos (\omega _\mathrm{ac}t) \end{aligned}$$

(3.5)

$$\begin{aligned}&O(\epsilon ^3)\nonumber \\&\quad \rightarrow D_{0}^2x_{13}+\lambda _{1}^2x_{13}+t_{8}x_{23}=-t_{11}(D_{0}x_{12} +D_{1}x_{11})\nonumber \\&\qquad \quad -(2D_{0}D_{1}x_{12} +D_{1}^2x_{11}+2D_{0}D_{2}x_{11})\nonumber \\&\quad \quad -t_{1}x_{11}^3-2t_{2}x_{11}x_{12}-t_{3}x_{11}x_{21}^2\nonumber \\&\qquad \quad -t_{4}(x_{11} x_{22} +x_{12} x_{21})\nonumber \\&\qquad \quad -t_{5}\eta _{11}\cos (\omega _\mathrm{ac}t)x_{11}-t_{6}\eta _{12}\cos (\omega _\mathrm{ac}t)x_{11}\nonumber \\&\qquad \quad -2t_{7}x_{21}x_{22} \nonumber \\&\qquad \quad D_{0}^2x_{23}+\lambda _{2}^2x_{23}+s_{8}x_{13}=-s_{11}(D_{0}x_{22}+D_{1}x_{21})\nonumber \\&\qquad \quad -(2D_{0}D_{1}x_{22}+D_{1}^2x_{21}+2D_{0}D_{2}x_{21})\nonumber \\&\qquad \quad -s_{1}x_{21}^3-2s_{2}x_{21}x_{22}-s_{3}x_{21}x_{11}^2\nonumber \\&\qquad \quad -s_{4}(x_{11} x_{22} +x_{12} x_{21})\nonumber \\&\qquad \quad -s_{5}\eta _{21}\cos (\omega _\mathrm{ac}t)x_{21}\nonumber \\&\qquad \quad -s_{6}(\eta _{11}+\eta _{12})\cos (\omega _\mathrm{ac}t)x_{21}\nonumber \\&\qquad \quad -2s_{7}x_{11}x_{12} \end{aligned}$$

(3.6)

where $\eta _{11}=2V_{10}V_\mathrm{ac}$, $\eta _{12}=2V_{12}V_\mathrm{ac}$ and $\eta _{21}=2V_{1g}V_\mathrm{ac}$.

3.1 Solution of 1st-order equation

Solutions $x_{11}$ and $x_{21}$ for the two homogeneous second- order coupled equations given by Eq. (3.4) can be written as

$$\begin{aligned} x_{11}= & {} A_{1}(T_{1},T_{2})e^{i\omega _{1}T_{0}} +A_{2}(T_{1},T_{2})e^{i\omega _{2}T_{0}}\nonumber \\&+\,\bar{A_{1}}(T_{1},T_{2})e^{-i\omega _{1}T_{0}}+\bar{A_{2}}(T_{1},T_{2})e^{-i\omega _{2}T_{0}} \nonumber \\ x_{21}= & {} k_{1}A_{1}(T_{1},T_{2})e^{i\omega _{1}T_{0}}+k_{2}A_{2}(T_{1},T_{2})e^{i\omega _{2}T_{0}}\nonumber \\&+\,k_{1}\bar{A_{1}}(T_{1},T_{2})e^{-i\omega _{1}T_{0}} +k_{2}\bar{A_{2}}(T_{1},T_{2})e^{-i\omega _{2}T_{0}}\nonumber \\ \end{aligned}$$

(3.7)

where $\omega _{1}$ and $\omega _{2}$ are the coupled natural frequencies of the system in two orthogonal directions obtained from linear analysis. Substituting the assumed form of the solution from Eq. (3.7) into Eq. (3.4), we get

$$\begin{aligned}&\left[ \left( \lambda _{1}^2-\omega _{1}^2\right) +t_{8}k_{1}\right] A_{1}e^{i\omega _{1}T_{0}}\nonumber \\&\quad +\,\left[ \left( \lambda _{1}^2-\omega _{2}^2\right) +t_{8}k_{2}\right] A_{2}e^{i\omega _{2}T_{0}}=0\nonumber \\&\left[ \left( \lambda _{2}^2-\omega _{1}^2\right) k_{1}+s_{8}\right] A_{1}e^{i\omega _{1}T_{0}}\nonumber \\&\quad +\,\left[ \left( \lambda _{2}^2-\omega _{2}^2\right) k_{2}+s_{8}\right] A_{2}e^{i\omega _{2}T_{0}}=0. \end{aligned}$$

(3.8)

Equating the coefficients of different terms on both sides of Eq. (3.8), we get

$$\begin{aligned}&\left( \lambda _{1}^2-\omega _{1}^2\right) +t_{8}k_{1}=0, \nonumber \\&\left( \lambda _{1}^2-\omega _{2}^2\right) +t_{8}k_{2}=0, \end{aligned}$$

(3.9)

$$\begin{aligned}&\left( \lambda _{2}^2-\omega _{1}^2\right) k_{1}+s_{8}=0, \nonumber \\&\left( \lambda _{2}^2-\omega _{2}^2\right) k_{2}+s_{8}=0. \end{aligned}$$

(3.10)

On solving Eqs. (3.9) and (3.10) for $k_{1}$ and $k_{2}$, we get the solvability condition as

$$\begin{aligned} k_{n}= \bigg (\frac{\omega _{n}^2-\lambda _{1}^2}{t_{8}}\bigg ) =\bigg ( \frac{s_{8}}{\omega _{n}^2-\lambda _{2}^2}\bigg ), \end{aligned}$$

(3.11)

where $n=1$ and 2.

3.2 Solution of 2nd-order equation

To obtain the solution of Eq. (3.5), we substitute Eq. (3.7) into it and eliminate the secular terms. Taking the detuning parameters $\sigma _{1}$ and $\sigma _{2}$ as

$$\begin{aligned} \varOmega =\omega _{1}+\epsilon \sigma _{1},~~~ \omega _{2}=\omega _{1}+\epsilon \sigma _{2}. \end{aligned}$$

(3.12)

and substituting $x_{11}$ and $x_{21}$ from Eq. (3.7) into Eq. (3.5), we get

$$\begin{aligned}&D_{0}^2x_{12}+\lambda _{1}^2x_{12}+t_{8}x_{22}\nonumber \\&\quad =-2i\big (\omega _{1}D_{1}A_{1}e^{i\omega _{1}T_{0}}+\omega _{2}D_{1}A_{2}e^{i\omega _{2}T_{0}}\big )\nonumber \\&\qquad -\,it_{11}\big (A_{1}\omega _{1}e^{i\omega _{1}T_{0}}+A_{2}\omega _{2}e^{i\omega _{2}T_{0}}\big )\nonumber \\&\qquad -\,t_{2}\big (A_{1}^2e^{2i\omega _{1}T_{0}}+A_{1}\bar{A_{1}}\nonumber \\&\qquad +\,A_{2}^2e^{2i\omega _{2}T_{0}}+A_{2}\bar{A_{2}}+2A_{1}\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&\qquad +\,2A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}\big )-t_{4}\big (A_{1}^2k_{1}e^{2i\omega _{1}T_{0}}\nonumber \\&\qquad +\,A_{1}\bar{A_{1}}k_{1}+\,A_{2}^2k_{2}e^{2i\omega _{2}T_{0}}+A_{2}\bar{A_{2}}k_{2}\nonumber \\&\qquad +\,A_{1}\bar{A_{2}}\big (k_{1}+k_{2}\big )e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&\qquad +\,A_{1}A_{2}\big (k_{1}+k_{2}\big )e^{i(\omega _{1}+\omega _{2})T_{0}}\big )\nonumber \\&\qquad -\,t_{7}\big (k_{1}^2A_{1}^2e^{2i\omega _{1}T_{0}}+k_{1}^2A_{1}\bar{A_{1}}\nonumber \\&\qquad +\,k_{2}^2A_{2}^2e^{2i\omega _{2}T_{0}}+k_{2}^2A_{2}\bar{A_{2}}+2k_{1}k_{2}A_{1}\nonumber \\&\qquad \times \,\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}+2k_{1}k_{2}A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}\big )\nonumber \\&\qquad +\,\frac{t_{9}}{2}\eta _{11}e^{i\omega _\mathrm{ac}T_{0}}-\frac{t_{10}}{2}\eta _{12}e^{i\omega _\mathrm{ac}T_{0}}+cc \end{aligned}$$

(3.13)

$$\begin{aligned}&D_{0}^2x_{22}+\lambda _{2}^2x_{22}+s_{8}x_{12}\nonumber \\&\quad =-2i\big (\omega _{1}k_{1}D_{1}A_{1}e^{i\omega _{1}T_{0}}+k_{2}\omega _{2}D_{1}A_{2}e^{i\omega _{2}T_{0}}\big )\nonumber \\&\qquad -\,is_{11}\big (k_{1}A_{1}\omega _{1}e^{i\omega _{1}T_{0}}+k_{2}A_{2}\omega _{2}e^{i\omega _{2}T_{0}}\big )\nonumber \\&\qquad -\,s_{2}\big (k_{1}^2A_{1}^2e^{2i\omega _{1}T_{0}}+k_{1}^2A_{1}\bar{A_{1}}+k_{2}^2A_{2}^2e^{2i\omega _{2}T_{0}}\nonumber \\&\qquad +\,k_{2}^2A_{2}\bar{A_{2}}\nonumber \\&\qquad +\,2k_{1}k_{2}A_{1}\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&\qquad +\,2k_{1}k_{2}A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}\big )-s_{4}\big (A_{1}^2k_{1}e^{2i\omega _{1}T_{0}}\nonumber \\&\qquad +\,A_{1}\bar{A_{1}}k_{1}+\,A_{2}^2k_{2}e^{2i\omega _{2}T_{0}}+A_{2}\bar{A_{2}}k_{2}\nonumber \\&\qquad +\,A_{1}\bar{A_{2}}\big (k_{1}+k_{2}\big )e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&\qquad +\,A_{1}A_{2}\big (k_{1}+k_{2}\big )e^{i(\omega _{1}+\omega _{2})T_{0}}\big )\nonumber \\&\qquad -\,s_{7}\big (A_{1}^2e^{2i\omega _{1}T_{0}}+A_{1}\bar{A_{1}}+A_{2}^2e^{2i\omega _{2}T_{0}}\nonumber \\&\qquad +\,A_{2}\bar{A_{2}}+2A_{1}\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&\qquad +\,2A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}\big )+\frac{s_{9}}{2}\eta _{21}e^{i\omega _\mathrm{ac}T_{0}}\nonumber \\&\qquad -\,\frac{s_{10}}{2}\big (\eta _{11}+\eta _{12}\big )e^{i\omega _\mathrm{ac}T_{0}}+cc. \end{aligned}$$

(3.14)

Assuming the solution of homogeneous form of Eq. (3.5) as

$$\begin{aligned} x_{12}= & {} P_{11}e^{i\omega _{1}T_{0}}+P_{12}e^{i\omega _{2}T_{0}}+cc,\nonumber \\ x_{22}= & {} P_{21}e^{i\omega _{1}T_{0}}+P_{22}e^{i\omega _{2}T_{0}}+cc \end{aligned}$$

(3.15)

and substituting it in Eqs. (3.13) and (3.14), and eliminating the secular terms, we get

$$\begin{aligned}&\big (\lambda _{1}^2-\omega _{1}^2\big )P_{11}e^{i\omega _{1}T_{0}}+\big (\lambda _{1}^2-\omega _{2}^2\big )P_{12}e^{i\omega _{2}T_{0}}\nonumber \\&\quad +\,t_{8}\big (P_{21}e^{i\omega _{1}T_{0}}+P_{22}e^{i\omega _{2}T_{0}}\big )=R_{11}e^{i\omega _{1}T_{0}}\nonumber \\&\quad +\,R_{12}e^{i\omega _{2}T_{0}} \end{aligned}$$

(3.16)

$$\begin{aligned}&\big (\lambda _{2}^2-\omega _{1}^2\big )P_{21}e^{i\omega _{1}T_{0}}+\big (\lambda _{2}^2-\omega _{2}^2\big )P_{22}e^{i\omega _{2}T_{0}}\nonumber \\&\quad +\,s_{8}\big (P_{11}e^{i\omega _{1}T_{0}}+P_{12}e^{i\omega _{2}T_{0}}\big )=R_{21}e^{i\omega _{1}T_{0}}\nonumber \\&\quad +\,R_{22}e^{i\omega _{2}T_{0}}. \end{aligned}$$

(3.17)

The above equations can also be written in the matrix form as

$$\begin{aligned} \left[ \begin{array}{cc} \left( \lambda _{1}^2-\omega _{n}^2\right) &{}\quad t_{8}\\ s_{8}&{}\quad \left( \lambda _{2}^2-\omega _{n}^2\right) \end{array} \right] \left[ \begin{array}{c} {P}_{1n} \\ {P}_{2n} \end{array} \right] =\left[ \begin{array}{c} {R}_{1n} \\ {R}_{2n} \end{array} \right] \end{aligned}$$

where $n=1$ and 2, $R_{1n}$ and $R_{2n}$ are the coefficients of $e^{i\omega _{1}T_{0}}$ and $e^{i\omega _{2}T_{0}}$ appearing in Eqs. (3.13) and (3.14) as

$$\begin{aligned} R_{11}= & {} -2i\omega _{1}D_{1}A_{1}-2i\omega _{2}D_{1}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,it_{11}A_{1}\omega _{1}-it_{11}A_{2}\omega _{2}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,\bigg (\frac{t_{9}\eta _{11}+t_{10}\eta _{12}}{2}\bigg )e^{i\sigma _{1}T_{1}}\nonumber \\ R_{12}= & {} -2i\omega _{1}D_{1}A_{1}e^{-i\sigma _{2}T_{1}}-2i\omega _{2}D_{1}A_{2}\nonumber \\&-\,it_{11}A_{1}\omega _{1}e^{-i\sigma _{2}T_{1}}-it_{11}A_{2}\omega _{2}\nonumber \\&-\,\bigg (\frac{t_{9}\eta _{11}+t_{10}\eta _{12}}{2}\bigg )e^{i(\sigma _{1}-\sigma _{2})T_{1}}\nonumber \\ R_{21}= & {} -2i\omega _{1}k_{1}D_{1}A_{1}-2ik_{2}\omega _{2}D_{1}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,is_{11}k_{1}A_{1}\omega _{1}-is_{11}k_{2}A_{2}\omega _{2}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,\bigg (\frac{s_{9}\eta _{21}+s_{10}(\eta _{11}+\eta _{12})}{2}\bigg )e^{i\sigma _{1}T_{1}}\nonumber \\ R_{22}= & {} -2i\omega _{1}k_{1}D_{1}A_{1}e^{-i\sigma _{2}T_{1}}-2i\omega _{2}k_{2}D_{1}A_{2}\nonumber \\&-\,is_{11}k_{1}A_{1}\omega _{1}e^{-i\sigma _{2}T_{1}}-is_{11}k_{2}A_{2}\omega _{2}\nonumber \\&-\,\bigg (\frac{s_{9}\eta _{21}+s_{10}(\eta _{11}+\eta _{12})}{2}\bigg )e^{i(\sigma _{1}-\sigma _{2})T_{1}}.\nonumber \\ \end{aligned}$$

(3.18)

Solving Eqs. (3.16) and (3.17), and using Eq. (3.11), we get the solvability conditions in terms of $R_{1n}$ and $R_{2n}$ as

$$\begin{aligned} R_{1n}= & {} \frac{t_{8}}{(\lambda _{2}^2-\omega _{n}^2)}R_{2n}\nonumber \\= & {} -\bigg (\frac{t_{8}}{s_{8}}\bigg ) k_{n} R_{2n} = -\bar{k_{n}} R_{2n}, \end{aligned}$$

(3.19)

where $\bar{k_{n}}=(\frac{t_{8}}{s_{8}}) k_{n}$. For $n=1$ and $\bar{k_{1}}=(\frac{t_{8}}{s_{8}}) k_{1}$, the solvability condition $R_{11}+\bar{k_{1}} R_{21}=0$ reduces to

$$\begin{aligned}&-2i\omega _{1}(1+k_{1}\bar{k_{1}})D_{1}A_{1} -2i\omega _{2}(1+k_{2}\bar{k_{1}})D_{1}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&\quad =i\omega _{1}A_{1}(t_{11}+s_{11}k_{1}\bar{k_{1}})\nonumber \\&\qquad +\,i\omega _{2}A_{2}(t_{11}+s_{11}k_{2}\bar{k_{1}})e^{i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bigg (\frac{t_{9}\eta _{11}+t_{10}\eta _{12}+\bar{k_{1}}s_{9}\eta _{21}+\bar{k_{1}}s_{10}(\eta _{11}+\eta _{12})}{2}\bigg )\nonumber \\&\qquad \times \, e^{i\sigma _{1}T_{1}}. \end{aligned}$$

(3.20)

Similarly, for $n=$2 and $\bar{k_{2}}=(\frac{t_{8}}{s_{8}}) k_{2}$, the solvability condition $R_{12}+\bar{k_{2}} R_{22}=0$ can be written as

$$\begin{aligned}&-2i\omega _{1}(1+k_{1}\bar{k_{2}})D_{1}A_{1}e^{-i\sigma _{2}T_{1}}-2i\omega _{2}(1+k_{2}\bar{k_{2}})D_{1}A_{2}\nonumber \\&\quad =i\omega _{2}A_{2} \times (t_{11}+s_{11}k_{2}\bar{k_{2}})+i\omega _{1}A_{1}(t_{11}\nonumber \\&\qquad +\,s_{11}k_{1}\bar{k_{2}})e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bigg (\frac{t_{9}\eta _{11}+t_{10}\eta _{12}+\bar{k_{2}}s_{9}\eta _{21}{+}\bar{k_{2}}s_{10}(\eta _{11}{+}\eta _{12})}{2}\bigg )\nonumber \\&\qquad \times \, e^{i(\sigma _{1}-\sigma _{2})T_{1}}. \end{aligned}$$

(3.21)

Solving Eqs. (3.20) and (3.21), simultaneously, we find the expressions for $D_{1}A_{1}$ and $D_{1}A_{2}$ as:

$$\begin{aligned} D_{1}A_{1}= & {} \frac{B_{1}A_{1}+B_{2}A_{2}e^{i\sigma _{2}T_{1}}+iB_{3}e^{i\sigma _{1}T_{1}}}{B_{4}}\nonumber \\ D_{1}A_{2}= & {} \frac{B_{5}A_{2}+B_{6}A_{1}e^{-i\sigma _{2}T_{1}}+iB_{7}e^{i(\sigma _{1}-\sigma _{2})T_{1}}}{B_{8}}\nonumber \\ \end{aligned}$$

(3.22)

where $B_{1},B_{2},\ldots ,B_{8}$ are defined in “Appendix 2.” Now, substituting $D_{1}A_{1}$ and $D_{1}A_{2}$ from Eq. (3.22) into the second-order Eqs. (3.13) and (3.14), we obtain the complete solution for second-order equations as

$$\begin{aligned} x_{12}= & {} A_{3}(T_{1},T_{2})e^{i\omega _{1}T_{0}}+A_{4}(T_{1},T_{2})e^{i\omega _{2}T_{0}}\nonumber \\&+\,c_{11}A_{1}^2e^{2i\omega _{1}T_{0}}+c_{12}A_{1}\bar{A_{1}}+c_{13}A_{2}^2e^{2i\omega _{2}T_{0}}\nonumber \\&+\,c_{14}A_{2}\bar{A_{2}}+c_{15}A_{1}\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&+\,c_{16}A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}+cc\nonumber \\ x_{22}= & {} k_{1}A_{3}(T_{1},T_{2})e^{i\omega _{1}T_{0}}+k_{2}A_{4}(T_{1},T_{2})e^{i\omega _{2}T_{0}}\nonumber \\&+\,c_{21}A_{1}^2e^{2i\omega _{1}T_{0}}+c_{22}A_{1}\bar{A_{1}}+c_{23}A_{2}^2e^{2i\omega _{2}T_{0}}\nonumber \\&+\,c_{24}A_{2}\bar{A_{2}}+c_{25}A_{1}\bar{A_{2}}e^{i(\omega _{1}-\omega _{2})T_{0}}\nonumber \\&+\,c_{26}A_{1}A_{2}e^{i(\omega _{1}+\omega _{2})T_{0}}+cc \end{aligned}$$

(3.23)

On substituting Eq. (3.23) in Eqs. (3.13) and (3.14), and comparing the coefficients of same terms on both side of the resulting equations, we obtain the following equations in terms of coefficients $c_{ij}$.

Coefficients of $A^{2}_{1}e^{2i\omega _{1} T_{0}}$:

$$\begin{aligned} -4c_{11}\omega ^{2}_{1}+c_{11}\lambda ^{2}_{1}+t_{8}c_{21}=-t_{2}-t_{4}k_{1}-t_{7}k^{2}_{1}\nonumber \\ -4c_{21}\omega ^{2}_{1}+c_{21}\lambda ^{2}_{2}+s_{8}c_{11}=-s_{7}-s_{4}k_{1}-s_{2}k^{2}_{1} \nonumber \\ \end{aligned}$$

(3.24)

Coefficients of $A_{1}\bar{A_{1}}$:

$$\begin{aligned}&\lambda ^{2}_{1}c_{12}+t_{8}c_{22}=-2t_{2}-2t_{4}k_{1}-2t_{7}k^{2}_{1}\nonumber \\&\lambda ^{2}_{2}c_{22}+s_{8}c_{12}=-2s_{7}-2s_{4}k_{1}-2s_{2}k^{2}_{1} \end{aligned}$$

(3.25)

Coefficients of $A^{2}_{2}e^{2i\omega _{2} T_{0}}$:

$$\begin{aligned} -4c_{13}\omega ^{2}_{2}+c_{13}\lambda ^{2}_{1}+t_{8}c_{23}=-t_{2}-t_{4}k_{2}-t_{7}k^{2}_{2}\nonumber \\ -4c_{23}\omega ^{2}_{2}+c_{23}\lambda ^{2}_{2}+s_{8}c_{13}=-s_{7}-s_{4}k_{2}-s_{2}k^{2}_{2} \nonumber \\ \end{aligned}$$

(3.26)

Coefficients of $A_{2}\bar{A_{2}}$:

$$\begin{aligned}&\lambda ^{2}_{1}c_{14}+t_{8}c_{24}=-2t_{2}-2t_{4}k_{2}-2t_{7}k^{2}_{2}\nonumber \\&\lambda ^{2}_{2}c_{24}+s_{8}c_{14}=-2s_{7}-2s_{4}k_{2}-2s_{2}k^{2}_{2} \end{aligned}$$

(3.27)

Coefficients of $A_{1}\bar{A}_{2}e^{i(\omega _{1}-\omega _{2}) T_{0}}$:

$$\begin{aligned}&-c_{15}(\omega _{1}-\omega _{2})^{2}+\lambda ^{2}_{1}c_{15}+t_{8}c_{25}\nonumber \\&\quad =-2t_{2}-t_{4}(k_{1}+k_{2})-2t_{7}k_{1}k_{2}\nonumber \\&-\,c_{25}(\omega _{1}-\omega _{2})^{2}+\lambda ^{2}_{2}c_{25}+s_{8}c_{15}\nonumber \\&\quad =-2s_{7}-s_{4}(k_{1}+k_{2})-2s_{2}k_{1}k_{2} \end{aligned}$$

(3.28)

Coefficients of $A_{1}{A}_{2}e^{i(\omega _{1}+\omega _{2}) T_{0}}$:

$$\begin{aligned}&-c_{16}(\omega _{1}+\omega _{2})^{2}+\lambda ^{2}_{1}c_{16}+t_{8}c_{26}\nonumber \\&\quad =-2t_{2}-t_{4}(k_{1}+k_{2})-2t_{7}k_{1}k_{2}\nonumber \\&-\,c_{26}(\omega _{1}+\omega _{2})^{2}+\lambda ^{2}_{2}c_{26}+s_{8}c_{16}\nonumber \\&\quad =-2s_{7}-s_{4}(k_{1}+k_{2})-2s_{2}k_{1}k_{2} \end{aligned}$$

(3.29)

Solving above equations simultaneously, the coefficients $c_{ij}$ are obtained which are given in “Appendix 2.”

3.3 Solution of 3rd-order equation

Substituting Eqs. (3.7) and (3.23) into Eq. (3.6), using $\varOmega =\omega _{1}+\epsilon \sigma _{1}$, $\omega _{2}=\omega _{1}+\epsilon \sigma _{2}$ and separating the secular terms similar to previous section, we obtain the following equations:

$$\begin{aligned} R_{11}= & {} -2i\omega _{1}(D_{1}A_{3}+D_{2}A_{1})-D^{2}_{1}A_{1}-t_{11}D_{1}A_{1}\nonumber \\&-\,\big [2i\omega _{2}(D_{1}A_{4}+D_{2}A_{2})+D^{2}_{1}A_{2}\nonumber \\&+\,t_{11}D_{1}A_{2}\big ] e^{i\sigma _{2}T_{1}}-it_{11}\omega _{1}A_{3}\nonumber \\&-\,it_{11}\omega _{2}A_{4}e^{i\sigma _{2}T_{1}}-g_{11}A^{2}_{1}\bar{A}_{2}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,g_{12}A^{2}_{2}\bar{A}_{2}e^{i\sigma _{2}T_{1}}-g_{13}A_{2}A_{1}\bar{A}_{1}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,g_{14}A^{2}_{2}\bar{A}_{1}e^{2i\sigma _{2}T_{1}}-g_{15}A^{2}_{1}\bar{A}_{1}\nonumber \\&-\,g_{16}A_{1}A_{2}\bar{A}_{2} \end{aligned}$$

(3.30)

$$\begin{aligned} R_{12}= & {} -2i\omega _{2}(D_{1}A_{4}+D_{2}A_{2})-D^{2}_{2}A_{2}-t_{11}D_{1}A_{2}\nonumber \\&-\,\big [2i\omega _{1}(D_{1}A_{3}+D_{2}A_{1})+D^{2}_{1}A_{1}\nonumber \\&-t_{11}D_{1}A_{1}\big ] e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,it_{11}\omega _{2}A_{4}-it_{11}\omega _{1}A_{3}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,f_{11}A^{2}_{2}\bar{A}_{1}e^{i\sigma _{2}T_{1}}-f_{12}A^{2}_{1}\bar{A}_{1}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,f_{13}A_{1}A_{2}\bar{A}_{2}e^{-i\sigma _{2}T_{1}}-f_{14}A^{2}_{1}\bar{A}_{2}e^{-2i\sigma _{2}T_{1}}\nonumber \\&-\,f_{15}A^{2}_{2}\bar{A}_{2}-f_{16}A_{2}A_{1}\bar{A}_{1} \end{aligned}$$

(3.31)

$$\begin{aligned} R_{21}= & {} -2i\omega _{1}k_{1}(D_{1}A_{3}+D_{2}A_{1})\nonumber \\&-\,k_{1}D^{2}_{1}A_{1}-s_{11}k_{1}D_{1}A_{1}\nonumber \\&-\,\big [2ik_{2}\omega _{2}(D_{1}A_{4}+D_{2}A_{2})\nonumber \\&+\,k_{2}D^{2}_{1}A_{2} +k_{2}s_{11}D_{1}A_{2}\big ]e^{i\sigma _{2}T_{1}}\nonumber \\&-\,is_{11}k_{1}\omega _{1}A_{3}-is_{11}k_{2}\omega _{2}A_{4}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,g_{21}A^{2}_{1}\bar{A}_{1}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,\left( g_{22}A^{2}_{2}\bar{A}_{2}+g_{23}A_{2}A_{1}\bar{A}_{1}\right) e^{i\sigma _{2}T_{1}}\nonumber \\&-\,g_{24}A^{2}_{2}\bar{A}_{1}e^{2i\sigma _{2}T_{1}}\nonumber \\&-\,g_{25}A^{2}_{1}\bar{A}_{1}-g_{26}A_{1}A_{2}\bar{A}_{2} \end{aligned}$$

(3.32)

$$\begin{aligned} R_{22}= & {} -2ik_{2}\omega _{2}(D_{1}A_{4}+D_{2}A_{2})-k_{2}D^{2}_{1}A_{2}\nonumber \\&-s_{11}k_{2}D_{1}A_{2}\nonumber \\&-\,\big [2ik_{1}\omega _{1}(D_{1}A_{3}+D_{2}A_{1})+k_{1}D^{2}_{1}A_{1}\nonumber \\&+s_{11}k_{1}D_{1}A_{1}\big ]e^{-i\sigma _{2}T_{1}}\nonumber \\&-ik_{2}s_{11}\omega _{2}A_{4}-ik_{1}s_{11}\omega _{1}A_{3}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,f_{21}A^{2}_{2}\bar{A}_{1}e^{i\sigma _{2}T_{1}}-\,f_{22}A^{2}_{1}\bar{A}_{1}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,f_{23}A_{1}A_{2}\bar{A}_{2}e^{-i\sigma _{2}T_{1}}-\,f_{24}A^{2}_{1}\bar{A}_{2}e^{-2i\sigma _{2}T_{1}}\nonumber \\&-\,f_{25}A^{2}_{2}\bar{A}_{2}-f_{26}A_{2}A_{1}\bar{A}_{1} \end{aligned}$$

(3.33)

where ${g}_{n1},\ldots ,{g}_{n6}$ and ${f}_{n1},\ldots ,{f}_{n6}$ for ${n}=1$ and 2 are given in “Appendix 2.” Substituting the above equations in solvability condition given by Eq. (3.19), we get the following two conditions

$$\begin{aligned}&-2i\omega _{1}B_{11}(D_{1}A_{3}+D_{2}A_{1})-B_{11}D_{1}^2A_{1}-B_{13}D_{1}A_{1}\nonumber \\&\qquad -\,\big [2i\omega _{2}B_{12}(D_{1}A_{4}+D_{2}A_{2})\nonumber \\&\qquad +\,B_{12}D_{1}^2A_{2}+B_{14}D_{1}A_{2}\big ]e^{i\sigma _{2}T_{1}}\nonumber \\&\quad =i\omega _{1}B_{13}A_{3}+i\omega _{2}B_{14}A_{4}e^{i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{g_{1}}\bar{A_{2}}A_{1}^2e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{g_{2}}\bar{A_{2}}A_{2}^2e^{i\sigma _{2}T_{1}}+\bar{g_{3}}A_{1}A_{2}\bar{A_{1}}e^{i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{g_{4}}A_{2}^2\bar{A_{1}}e^{2i\sigma _{2}T_{1}}+\bar{g_{5}}A_{1}^2\bar{A_{1}}\nonumber \\&\qquad +\,\bar{g_{6}}A_{1}\bar{A_{2}}A_{2} \end{aligned}$$

(3.34)

$$\begin{aligned}&-2i\omega _{2}G_{12}(D_{1}A_{4}+D_{2}A_{2})-G_{12}D_{1}^2A_{2}-G_{13}D_{1}A_{2}\nonumber \\&\qquad -\,\big [2i\omega _{1}G_{11}(D_{1}A_{3}+D_{2}A_{1})+G_{11}D_{1}^2A_{1}\nonumber \\&\qquad +\,G_{14}D_{1}A_{1}\big ]e^{-i\sigma _{2}T_{1}}\nonumber \\&\quad =i\omega _{2}G_{13}A_{4}+i\omega _{1}G_{14}A_{3}e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{1}}\bar{A_{1}}A_{2}^2e^{i\sigma _{2}T_{1}}+\bar{f_{2}}\bar{A_{1}}A_{1}^2e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{3}}A_{1}A_{2}\bar{A_{2}}e^{-i\sigma _{2}T_{1}}+\bar{f_{4}}A_{1}^2\bar{A_{2}}e^{-2i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{5}}A_{2}^2\bar{A_{2}}+\bar{f_{6}}A_{1}\bar{A_{1}}A_{2}, \end{aligned}$$

(3.35)

where $\bar{g_{n}} = g_{1n}+\bar{k_{1}}g_{2n}$, $\bar{f_{n}} = f_{1n}+\bar{k_{2}}f_{2n}$, and the coefficients $B_{11}$, $B_{12}$, $B_{13}$, $B_{14}$, $G_{11}$, $G_{12}$, $G_{13}$, $G_{14}$, $f_{1n}$ and $g_{1n}$ for ${n}=1,\ldots ,6$ are mentioned in “Appendix 2.”

Now, by following the procedure as mentioned in [16, 27], we find $A_{3}$ and $A_{4}$ so as to eliminate $D_{1}^2A_{1}$ and $D_{1}^2A_{2}$ from Eqs. (3.34) and (3.35). Such conditions lead to the following equations:

$$\begin{aligned}&D_{1}[2i\omega _{1}A_{3}+D_{1}A_{1}]=0 \nonumber \\&\quad \Rightarrow [2i\omega _{1}A_{3}+D_{1}A_{1}]=h_{11}(T_{2}),\nonumber \\&D_{1}[2i\omega _{2}A_{4}+D_{1}A_{2}]=0 \nonumber \\&\quad \Rightarrow [2i\omega _{2}A_{4}+D_{1}A_{2}]=h_{12}(T_{2}); \end{aligned}$$

(3.36)

However, it is evident from Eq. (3.22) that $D_{1}A_{1}$ and $D_{1}A_{2}$ are implicit functions of slow time scale $T_{2}$. Thus, we take $h_{11}(T_{2})=h_{12}(T_{2})=$0. Now, using Eqs. (3.22) and (3.36), the expressions for $A_{3}$ and $A_{4}$ can be written as:

$$\begin{aligned} A_{3}= & {} \frac{iB_{1}}{2\omega _{1}B_{4}}A_{1}+\frac{iB_{2}}{2\omega _{1}B_{4}}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&-\,\frac{B_{3}}{2\omega _{1}B_{4}}e^{i\sigma _{1}T_{1}}\nonumber \\ A_{4}= & {} \frac{iB_{5}}{2\omega _{2}B_{8}}A_{2}+\frac{iB_{6}}{2\omega _{2}B_{8}}A_{1}e^{-i\sigma _{2}T_{1}}\nonumber \\&-\,\frac{B_{7}}{2\omega _{2}B_{8}}e^{i(\sigma _{1}-\sigma _{2})T_{1}}. \end{aligned}$$

(3.37)

Using Eq. (3.37) in Eqs. (3.34) and (3.35), we can find the values for $D_{2}A_{1}$ and $D_{2}A_{2}$ by solving the following equations:

$$\begin{aligned}&-2i\omega _{1}B_{11}D_{2}A_{1}-2i\omega _{2}B_{12}D_{2}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&\quad = B_{13}D_{1}A_{1}+B_{14}D_{1}A_{2}e^{i\sigma _{2}T_{1}}+i\omega _{1}B_{13}A_{3}\nonumber \\&\qquad +\,i\omega _{2}B_{14}A_{4}e^{i\sigma _{2}T_{1}}+\bar{g_{1}}\bar{A_{2}}A_{1}^2e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{g_{2}}\bar{A_{2}}A_{2}^2e^{i\sigma _{2}T_{1}}+\bar{g_{3}}A_{1}A_{2}\bar{A_{1}}e^{i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{g_{4}}A_{2}^2\bar{A_{1}}e^{2i\sigma _{2}T_{1}}+\bar{g_{5}}A_{1}^2\bar{A_{1}}+\bar{g_{6}}A_{1}\bar{A_{2}}A_{2}\nonumber \\ \end{aligned}$$

(3.38)

$$\begin{aligned}&-2i\omega _{1}G_{11}D_{2}A_{1}e^{-i\sigma _{2}T_{1}}-2i\omega _{2}G_{12}D_{2}A_{2}\nonumber \\&\quad = G_{13}D_{1}A_{2}+G_{14}D_{1}A_{1}e^{-i\sigma _{2}T_{1}}+i\omega _{2}G_{13}A_{4}\nonumber \\&\qquad +\,i\omega _{1}G_{14}A_{3}e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{1}}\bar{A_{1}}A_{2}^2e^{i\sigma _{2}T_{1}}+\bar{f_{2}}\bar{A_{1}}A_{1}^2e^{-i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{3}}A_{1}A_{2}\bar{A_{2}}e^{-i\sigma _{2}T_{1}}+\bar{f_{4}}A_{1}^2\bar{A_{2}}e^{-2i\sigma _{2}T_{1}}\nonumber \\&\qquad +\,\bar{f_{5}}A_{2}^2\bar{A_{2}}+\bar{f_{6}}A_{1}\bar{A_{1}}A_{2}. \end{aligned}$$

(3.39)

The expressions for $D_{2}A_{1}$ and $D_{2}A_{2}$ can be obtained as

$$\begin{aligned} D_{2}A_{1}= & {} \frac{i}{2\omega _{1}(B_{11}G_{12}-B_{12}G_{11})}\nonumber \\&\times \,\bigg [(B_{14}G_{12}-B_{12}G_{13})D_{1}A_{2}e^{i\sigma _{2}T_{1}}\nonumber \\&+\,(B_{13}G_{12}-\,B_{12}G_{14})D_{1}A_{1}+i\omega _{1}(B_{13}G_{12}\nonumber \\&-\,B_{12}G_{14})A_{3}+i\omega _{2}(B_{14}G_{12}\nonumber \\&-\,B_{12}G_{13})A_{4}e^{i\sigma _{2}T_{1}}+\,G_{12}\bar{G}-B_{12}\bar{F}e^{i\sigma _{2}T_{1}}\bigg ], \nonumber \\ D_{2}A_{2}= & {} \frac{i}{2\omega _{2}(B_{12}G_{11}-B_{11}G_{12})}\nonumber \\&\times \,\bigg [(B_{14}G_{11}-B_{11}G_{13})D_{1}A_{2}+(B_{13}G_{11}\nonumber \\&-\,B_{11}G_{14})D_{1}A_{1}e^{-i\sigma _{2}T_{1}}+i\omega _{2}(B_{14}G_{11}\nonumber \\&-\,B_{11}G_{13})A_{4}+i\omega _{1}(B_{13}G_{11}\nonumber \\&-\,B_{11}G_{14})A_{3}e^{-i\sigma _{2}T_{1}}\nonumber \\&+\,G_{11}\bar{G}e^{-i\sigma _{2}T_{1}}-B_{11}\bar{F}\bigg ] \end{aligned}$$

(3.40)

where $\bar{F}$ and $\bar{G}$ are given in the “Appendix 2.” To get the final solution, we apply the method of reconstitution [16, 27] and write modulation in the following form

$$\begin{aligned} \frac{\mathrm{d}A_{1}}{\mathrm{d}t}= & {} \epsilon D_{1}A_{1}+\epsilon ^2 D_{2}A_{1}+\cdots \nonumber \\ \frac{\mathrm{d}A_{2}}{\mathrm{d}t}= & {} \epsilon D_{1}A_{2}+\epsilon ^2 D_{2}A_{2}+\cdots . \end{aligned}$$

(3.41)

Substituting the values of $D_{1}A_{1}$ and $D_{1}A_{2}$ from Eq. (3.22), $D_{2}A_{1}$ and $D_{2}A_{2}$ from Eq. (3.40), and $A_{3}$ and $A_{4}$ from Eq. (3.37) into Eq. (3.41), and setting $\epsilon = 1$ such that $T_{0} = T_{1} = T_{2} = t$, we get the reconstituted modulation equations as

$$\begin{aligned} \dot{A_{1}}= & {} \bigg [1+i\frac{(B_{13}G_{12}-G_{14}B_{12})}{4\omega _{1}(B_{11}G_{12}-G_{11}B_{12})}\bigg ]\nonumber \\&\times \,\bigg [\frac{B_{1}}{B_{4}}A_{1}+\frac{B_{2}}{B_{4}}A_{2}e^{i\sigma _{2}t}+i\frac{B_{3}}{B_{4}}e^{i\sigma _{1}t}\bigg ]\nonumber \\&+\, i\bigg [\frac{(B_{14}G_{12}-G_{13}B_{12})}{4\omega _{1}(B_{11}G_{12}-G_{11}B_{12})} \bigg ]\nonumber \\&\times \, e^{i\sigma _{2}t}\bigg [\frac{B_{5}}{B_{8}}A_{2}+\frac{B_{6}}{B_{8}}A_{1}e^{-i\sigma _{2}t}+i\frac{B_{7}}{B_{8}}e^{i(\sigma _{1}-\sigma _{2})t}\bigg ] \nonumber \\&+\, i\bigg [\frac{(G_{12}\bar{G}-B_{12}\bar{F}e^{i\sigma _{2}t})}{2\omega _{1}(B_{11}G_{12}-G_{11}B_{12})}\bigg ], \end{aligned}$$

(3.42)

$$\begin{aligned} \dot{A_{2}}= & {} i\bigg [\frac{(B_{13}G_{11}-G_{14}B_{11})}{4\omega _{2}(B_{12}G_{11}-G_{12}B_{11})}\bigg ]e^{-i\sigma _{2}t}\nonumber \\&\times \, \bigg [\frac{B_{1}}{B_{4}}A_{1}+\frac{B_{2}}{B_{4}}A_{2}e^{i\sigma _{2}t}+i\frac{B_{3}}{B_{4}}e^{i\sigma _{1}t}\bigg ]\nonumber \\&+\, \bigg [1+i\frac{(B_{14}G_{11}-G_{13}B_{11})}{4\omega _{2}(B_{12}G_{11}-G_{12}B_{11})}\bigg ]\nonumber \\&\times \, \bigg [\frac{B_{5}}{B_{8}}A_{2}+\frac{B_{6}}{B_{8}}A_{1}e^{-i\sigma _{2}t}+i\frac{B_{7}}{B_{8}}e^{i(\sigma _{1}-\sigma _{2})t}\bigg ] \nonumber \\&+\, i\bigg [\frac{(G_{11}\bar{G}e^{-i\sigma _{2}t}-B_{11}\bar{F})}{2\omega _{2}(B_{12}G_{11}-G_{12}B_{11})}\bigg ]. \end{aligned}$$

(3.43)

To express the modulation equations in polar form, we rewrite $A_{1}$ and $A_{2}$ as:

$$\begin{aligned} A_{n}=\frac{1}{2}a_{n}e^{i\beta _{n}}, \quad n=1,2. \end{aligned}$$

(3.44)

Here, $a_{n}$ and $\beta _{n}$ are real functions of time t; hence, $\dot{A_{1}}$ and $\dot{A_{2}}$ can be written as

$$\begin{aligned}&A_{1}=\frac{1}{2}a_{1}e^{i\beta _{1}} \Rightarrow \dot{A_{1}}=\frac{1}{2}\left( \dot{a_{1}}e^{i\beta _{1}}+ia_{1}\dot{\beta _{1}}e^{i\beta _{1}}\right) \nonumber \\&A_{2}=\frac{1}{2}a_{2}e^{i\beta _{2}} \Rightarrow \dot{A_{2}}=\frac{1}{2}\left( \dot{a_{2}}e^{i\beta _{2}}+ia_{2}\dot{\beta _{2}}e^{i\beta _{2}}\right) .\nonumber \\ \end{aligned}$$

(3.45)

Substituting Eq. (3.45) into Eqs. (3.42) and (3.43), we get

$$\begin{aligned}&\frac{1}{2}\left( \dot{a_{1}}e^{i\beta _{1}}+ia_{1}\dot{\beta _{1}}e^{i\beta _{1}}\right) =\big (1+ih_{11}\big )\nonumber \\&\quad \times \,\big [h_{22}a_{1}e^{i\beta _{1}}+h_{33}a_{2}e^{i(\beta _{2} +\sigma _{2}t)}+ih_{44}e^{i\sigma _{1}t}\big ]\nonumber \\&\quad +\,ih_{55}e^{i\sigma _{2}t}\big [h_{66}a_{2}e^{i\beta _{2}} +h_{77}a_{1}e^{i(\beta _{1}-\sigma _{2}t)}\nonumber \\&\quad +ih_{88}e^{i(\sigma _{1}-\sigma _{2})t}\big ]+\,ih_{99}\bigg [\bar{g_{1}}a_{1}^2a_{2} e^{i(2\beta _{1} -\beta _{2}-\sigma _{2}t)}\nonumber \\&\quad +\,\bar{g_{2}}a_{2}^3e^{i(\beta _{2}+\sigma _{2}t)}+\bar{g_{3}}a_{1}^2a_{2}e^{i(\beta _{2}+\sigma _{2}t)}\nonumber \\&\quad +\,\bar{g_{4}}a_{1}a_{2}^2e^{i(2\beta _{2}-\beta _{1}+2\sigma _{2}t)}{+}\bar{g_{5}}a_{1}^3e^{i\beta _{1}}{+}\bar{g_{6}}a_{1}a_{2}^2e^{i\beta _{1}}\bigg ]\nonumber \\&\quad -\,ih_{1010}\bigg [\bar{f_{1}}a_{1}a_{2}^2e^{i(2\sigma _{2}t-\beta _{1}+2\beta _{2})}+\bar{f_{2}}a_{1}^3e^{i\beta _{1}} \nonumber \\&\quad +\bar{f_{3}}a_{1}a_{2}^2e^{i\beta _{1}}+\,\bar{f_{4}}a_{1}^2a_{2}e^{i(2\beta _{1}-\beta _{2}-\sigma _{2}t)}\nonumber \\&\quad +\bar{f_{5}}a_{2}^3e^{i(\beta _{2}+\sigma _{2}t)}+\bar{f_{6}}a_{1}^2a_{2}e^{i(\beta _{2}+\sigma _{2}t)}\bigg ] \end{aligned}$$

(3.46)

$$\begin{aligned}&\frac{1}{2}\left( \dot{a_{2}}e^{i\beta _{2}}+ia_{2}\dot{\beta _{2}}e^{i\beta _{2}}\right) =\big (1+il_{11}\big )\nonumber \\&\quad \times \, \big [l_{22}a_{2}e^{i\beta _{2}}+l_{33}a_{1}e^{i(\beta _{1} -\sigma _{2}t)}+il_{44}e^{i(\sigma _{1}-\sigma _{2})t}\big ]\nonumber \\&\quad +\,il_{55}e^{-i\sigma _{2}t}\big [l_{66}a_{1}e^{i\beta _{1}} {+}l_{77}a_{2}e^{i(\beta _{2}{+}\sigma _{2}t)}{+}il_{88}e^{i\sigma _{1}t}\big ]\nonumber \\&\quad +\,il_{99}\bigg [\bar{g_{1}}a_{1}^2a_{2}e^{i(2\beta _{1} -\beta _{2}-2\sigma _{2}t)}+\bar{g_{2}}a_{2}^3e^{i\beta _{2}}\nonumber \\&\quad +\,\bar{g_{3}}a_{1}^2a_{2}e^{i\beta _{2}}+\,\bar{g_{4}}a_{1}a_{2}^2e^{i(2\beta _{2}-\beta _{1}+\sigma _{2}t)} \nonumber \\&\quad +\,\bar{g_{5}}a_{1}^3e^{i(\beta _{1}-\sigma _{2}t)}+\,\bar{g_{6}}a_{1}a_{2}^2e^{i(\beta _{1}-\sigma _{2}t)}\bigg ]\nonumber \\&\quad -\,il_{1010}\bigg [\bar{f_{1}}a_{1}a_{2}^2e^{i(\sigma _{2}t-\beta _{1}+2\beta _{2})}\nonumber \\&\quad +\,\bar{f_{2}}a_{1}^3e^{i(\beta _{1}-\sigma _{2}t)} +\bar{f_{3}}a_{1}a_{2}^2e^{i(\beta _{1}-\sigma _{2}t)}\nonumber \\&\quad +\,\bar{f_{4}}a_{1}^2a_{2}e^{i(2\beta _{1}-\beta _{2}-2\sigma _{2}t)}+\bar{f_{5}}a_{2}^3e^{i\beta _{2}}\nonumber \\&\quad +\,\bar{f_{6}}a_{1}^2a_{2}e^{i\beta _{2}}\bigg ]\qquad \end{aligned}$$

(3.47)

where $h_{11},~h_{22},\ldots ,h_{1010}$ and $l_{11},~l_{22},\ldots ,l_{1010}$ are given in “Appendix 2.” Finally, we convert the above non-autonomous equations into autonomous forms by defining two new variables and their corresponding time derivative terms as

$$\begin{aligned} \theta _{1}=(\sigma _{1}t-\beta _{1}),~~\theta _{2}=(\sigma _{1}-\sigma _{2})t-\beta _{2},\nonumber \\ \dot{\theta _{1}}=(\sigma _{1}-\dot{\beta _{1}}), ~~~~\dot{\theta _{2}}=(\sigma _{1}-\sigma _{2})-\dot{\beta _{2}} \end{aligned}$$

(3.48)

Substituting Eq. (3.48) into Eqs. (3.46) and (3.47), and separating the real and imaginary parts, we get the following form of modulation equations

$$\begin{aligned} \dot{a_{1}}= & {} h_{2}a_{1}+h_{3}a_{2}\cos (\theta _{1}-\theta _{2})\nonumber \\&-\,h_{4}\sin (\theta _{1})+h_{1}[-h_{3}a_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&-\,h_{4}\cos (\theta _{1})] + h_{5}[-h_{6}a_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&-h_{8}\cos (\theta _{1})]\nonumber \\&+\,h_{9}\left[ \bar{g_{1}}a^{2}_{1}a_{2}\sin (\theta _{1}-\theta _{2})-\bar{g_{2}}a^{3}_{2}\sin (\theta _{1}\right. \nonumber \\&-\theta _{2})-\,\bar{g_{3}}a^{2}_{1}a_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&\left. -\bar{g_{4}}a^{2}_{2}a_{1}\sin {2(\theta _{1} -\theta _{2})}\right] \nonumber \\&-\,h_{10}\left[ -\bar{f_{1}}a^{2}_{2}a_{1}\sin {2(\theta _{1}-\theta _{2})}\right. \nonumber \\&+\,\bar{f_{4}}a^{2}_{1}a_{2}\sin (\theta _{1}-\theta _{2}) -\bar{f_{5}}a^{3}_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&\left. - \bar{f_{6}}a^{2}_{1}a_{2}\sin {(\theta _{1} -\theta _{2})}\right] \end{aligned}$$

(3.49)

$$\begin{aligned} \dot{a_{1}}\dot{\theta _{1}}= & {} a_{1}\sigma _{1}-h_{3}a_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&-\,h_{4}\cos (\theta _{1})-h_{1}[h_{2}a_{1}+h_{3}a_{2}\cos (\theta _{1}\nonumber \\&-\theta _{2})-\,h_{4}\sin (\theta _{1})]-h_{5}[h_{6}a_{2}\cos (\theta _{1}-\theta _{2})\nonumber \\&+\,h_{7}a_{1}-h_{8}\sin (\theta _{1})]\nonumber \\&-\,h_{9}\left[ \bar{g_{1}}a^{2}_{1}a_{2}\cos (\theta _{1}-\theta _{2})+\bar{g_{2}}a^{3}_{2}\cos (\theta _{1}\right. \nonumber \\&-\theta _{2})+\,\bar{g_{3}}a^{2}_{1}a_{2}\cos (\theta _{1}-\theta _{2})+\bar{g_{4}}a^{2}_{2}a_{1}\nonumber \\&\left. \times \cos {2(\theta _{1} -\theta _{2})}+\bar{g}_{5}{a}^{3}_{1}+\bar{g}_{6}a_{1}{a}^{2}_{2}\right] \nonumber \\&+\,h_{10}\left[ \bar{f_{1}}a^{2}_{2}a_{1}\cos {2(\theta _{1}-\theta _{2})}+\bar{f}_{2}{a}^{3}_{1}\right. \nonumber \\&+\, \bar{f}_{3}a_{1}{a}^{2}_{2}+\bar{f_{4}}a^{2}_{1}a_{2}\cos (\theta _{1}-\theta _{2})\nonumber \\&\left. +\bar{f_{5}}a^{3}_{2}\cos (\theta _{1}-\theta _{2}) + \bar{f_{6}}a^{2}_{1}a_{2}\cos {(\theta _{1} -\theta _{2})}\right] \nonumber \\ \end{aligned}$$

(3.50)

$$\begin{aligned} \dot{a_{2}}= & {} l_{2}a_{2}+l_{3}a_{1}\cos (\theta _{1}-\theta _{2})-l_{4}\sin (\theta _{2})\nonumber \\&+\,l_{1}[l_{3}a_{1}\sin (\theta _{1}-\theta _{2})-l_{4}\cos (\theta _{2})]\nonumber \\&+\, l_{5}[l_{6}a_{1}\sin (\theta _{1}-\theta _{2})-l_{8}\cos (\theta _{2})]\nonumber \\&+\,l_{9}\left[ \bar{g_{1}}a^{2}_{1}a_{2}\sin {2(\theta _{1}-\theta _{2})}-\bar{g_{4}}a^{2}_{2}a_{1}\right. \nonumber \\&\times \,\sin (\theta _{1}-\theta _{2}) +\bar{g_{5}}a^{3}_{1}a_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&\left. +\bar{g_{6}}a^{2}_{2}a_{1}\sin {(\theta _{1} -\theta _{2})}\right] -l_{10}\left[ -\bar{f_{1}}a^{2}_{2}a_{1}\right. \nonumber \\&\times \, \sin {(\theta _{1}-\theta _{2})}+\bar{f_{2}}a^{3}_{1}\sin (\theta _{1}-\theta _{2})\nonumber \\&+\,\bar{f_{3}}a_{1}a^{2}_{2}\sin (\theta _{1}-\theta _{2})\nonumber \\&\left. + \bar{f_{4}}a^{2}_{1}a_{2}\sin {2(\theta _{1} -\theta _{2})}\right] \end{aligned}$$

(3.51)

$$\begin{aligned} \dot{a_{2}}\dot{\theta _{2}}= & {} a_{2}(\sigma _{1}-\sigma _{2})+l_{3}a_{1}\sin (\theta _{1}-\theta _{2})\nonumber \\&-\,l_{4}\cos (\theta _{2})-l_{1}[l_{2}a_{2}+l_{3}a_{1}\cos (\theta _{1}-\theta _{2})\nonumber \\&-\,l_{4}\sin (\theta _{2})]\nonumber \\&-\,l_{5}[l_{6}a_{1}\cos (\theta _{1}-\theta _{2})+l_{7}a_{2}-l_{8}\sin (\theta _{2})]\nonumber \\&-\,l_{9}\left[ \bar{g_{1}}a^{2}_{1}a_{2}\cos {2(\theta _{1}-\theta _{2})}\right. \nonumber \\&+\, \bar{g}_{2}{a}^{3}_{2}+\bar{g}_{3}a_{2}{a}^{2}_{1}+\bar{g_{4}}a^{2}_{2}a_{1}\cos (\theta _{1}-\theta _{2})\nonumber \\&\left. +\bar{g_{5}}a^{3}_{1}\cos (\theta _{1}-\theta _{2}) + \bar{g_{6}}a^{2}_{2}a_{1}\cos (\theta _{1}-\theta _{2})\right] \nonumber \\&+\,l_{10}\left[ \bar{f_{1}}a^{2}_{2}a_{1}\cos {(\theta _{1}-\theta _{2})}\right. \nonumber \\&+\bar{f_{2}}a^{3}_{1}\cos (\theta _{1}-\theta _{2})+\, \bar{f_{3}}a_{1}a^{2}_{2}\cos (\theta _{1}-\theta _{2}) \nonumber \\&+\,\bar{f_{4}}a^{2}_{1}a_{2}\cos {2(\theta _{1} -\theta _{2})} \nonumber \\&\left. +\bar{f}_{5}{a}^{3}_{2}+\bar{f}_{6}a_{2}{a}^{2}_{1}\right] \end{aligned}$$

(3.52)

where $h_{1},~h_{2},\ldots ,~h_{10}$ and $l_{1},~l_{2},\ldots ,l_{10}$ are given in “Appendix 2.”

To obtain the equilibrium solution, we set time derivative terms to zero in Eqs. (3.49)–(3.52) and solve the resulting equations. Finally, the response of the beam up to second term can be written using Eqs. (3.1), (3.7), (3.23) and (3.44), and $\epsilon = 1$ as:

$$\begin{aligned} P_{1}(t)= & {} x_{11}+x_{12}\nonumber \\= & {} \bigg (1+i\frac{\varLambda _{11}}{2}\bigg )a_{1} \cos (\omega _{1}t+\beta _{1})\nonumber \\&+\,\bigg (1+i\frac{\varLambda _{12}}{2}\bigg )a_{2} \cos (\omega _{2}t+\beta _{2})\nonumber \\&+\,\varLambda _{13} \cos [(\omega _{1}+\sigma _{1})t]\nonumber \\&+\frac{1}{2}c_{11} a_{1}^2 \cos 2(\omega _{1}t+\beta _{1})\nonumber \\&+\,\frac{1}{2}c_{12} a_{1}^2+\frac{1}{2}c_{13} a_{2}^2 \cos 2(\omega _{2}t+\beta _{2})\nonumber \\&+\,\frac{1}{2}c_{14} a_{2}^2+\frac{1}{2}c_{15} a_{1}a_{2} \nonumber \\&\times \, \cos 2[(\omega _{1}-\omega _{2})t+\beta _{1}-\beta _{2}]\nonumber \\&+\,\frac{1}{2}c_{16} a_{1}a_{2} \cos 2[(\omega _{1}+\omega _{2})t+\beta _{1}+\beta _{2}] \end{aligned}$$

(3.53)

$$\begin{aligned} P_{2}(t)= & {} x_{21}+x_{22}=k_{1} \bigg (1+i\frac{\varLambda _{11}}{2}\bigg )\nonumber \\&\times \,a_{1} \cos (\omega _{1}t+\beta _{1})+k_{2}\bigg (1+i\frac{\varLambda _{12}}{2}\bigg )\nonumber \\&\times \,a_{2} \cos (\omega _{2}t+\beta _{2})\nonumber \\&+\,\varLambda _{14} \cos [(\omega _{1}+\sigma _{1})t]+\frac{1}{2}c_{21} a_{1}^2 \nonumber \\&\times \, \cos 2(\omega _{1}t+\beta _{1})+\frac{1}{2}c_{22} a_{1}^2+\frac{1}{2}c_{23} a_{2}^2 \nonumber \\&\times \, \cos 2(\omega _{2}t+\beta _{2})+\frac{1}{2}c_{24} a_{2}^2\nonumber \\&+\,\frac{1}{2}c_{25} a_{1}a_{2} \cos 2[(\omega _{1}-\omega _{2})t\nonumber \\&+\,\beta _{1}-\beta _{2}] +\frac{1}{2}c_{26} a_{1}a_{2} \nonumber \\&\times \, \cos 2[(\omega _{1}+\omega _{2})t+\beta _{1}+\beta _{2}] \end{aligned}$$

(3.54)

where the terms $\varLambda _{11},~\varLambda _{12},~\varLambda _{13}$ and $\varLambda _{14}$ are defined as:

$$\begin{aligned} \varLambda _{11}= & {} \bigg [\frac{B_{1}}{\omega _{1}B_{4}}+\frac{B_{6}}{\omega _{2}B_{8}}\bigg ], \nonumber \\ \varLambda _{12}= & {} \bigg [\frac{B_{2}}{\omega _{1}B_{4}}+\frac{B_{5}}{\omega _{2}B_{8}}\bigg ],\nonumber \\ \varLambda _{13}= & {} \bigg [\frac{B_{3}}{\omega _{1}B_{4}}+\frac{B_{7}}{\omega _{2}B_{8}}\bigg ], \nonumber \\ \varLambda _{14}= & {} \bigg [k_{1}\frac{B_{3}}{\omega _{1}B_{4}}+k_{2}\frac{B_{7}}{\omega _{2}B_{8}}\bigg ]. \end{aligned}$$

(3.55)

4 Results and discussion

In this section, we first study the linear frequency variation of in-plane and out-of-plane modes of a microbeam to locate the coupling region. Subsequently, we validate the modulation equations developed by the method of multiple scales with numerical solution obtained by solving the modal dynamic equations. Finally, we use the method of multiple scale to study coupled nonlinear response near and away from the coupling region. Additionally, we also analyze the influence of quality factor on the nonlinear frequency response near the coupled region. To do the study, we consider the dimensions, material properties and electrostatic force coefficients in a fixed–fixed microbeam as mentioned in [2] and are given in Table 1.

Table 1 Dimensions, material properties and the electrostatic force coefficients in a fixed–fixed microbeam [2]

Fig. 2

a Variation of static deflection $q_{1}$ verses DC voltage for in-plane mode. b Variation of static deflection $q_{2}$ verses DC voltage for out-of-plane mode. c Variation of in-plane and out-of-plane frequencies with DC voltage for equal interbeam gaps ($g_{0}=g_{0}=4.5\, \upmu \hbox {m}$) and unequal interbeam gaps ($g_{0}=4.5 \,\upmu \hbox {m}$, $g_{1}=7~\upmu \hbox {m}$) and their comparison with experimental results [2]. It also shows 1:1 internal resonance at $V_\mathrm{dc}=81$ V

4.1 Linear frequency analysis

To analyze the variation of linear frequency of two transverse modes of a fixed–fixed microbeam, we numerically solve the nonlinear static equations (given in “Appendix 1”) and linear modal dynamic equations given by Eqs. (2.19) and (2.20) as described in [2]. Subsequently, we obtain linear frequencies corresponding to both the modes from Eq. (2.21). Figure 2a, b shows the variation of static deflection verses DC voltage for in-plane and out-plane modes with a pull-in voltage of about $V_\mathrm{dc}=199$ V. Figure 2c shows the variation of in-plane and out-of-plane linear frequencies verses DC voltage and their comparison with experiments from [2]. As the DC voltage is varied from 0 to 90 V, the in-plane frequency decreases due to electrostatic softening effect and the out-of-plane frequency increases due to stretching of the beam in the in-plane direction. Consequently, the two frequencies come near to each other, and they, eventually, show 1:1 internal resonance at DC voltage of 81 V. We define this point as coupling point or region. It also shows the variation in-plane and out-of-plane frequencies with DC voltage for equal interbeam gaps ($g_{0}=g_{0}=4.5 \,\upmu \hbox {m}$) with no coupling. In the following section, we apply the method of multiple scales to find nonlinear frequency response near the coupling region. We also compare the nonlinear response of different modes when the operating linear frequencies are below the coupling range.

Fig. 3

a Uncoupled frequency verses $\frac{\varOmega }{\omega _{1}}$ showing parametric response for in-plane mode. b Uncoupled nonlinear frequency verses $\frac{\varOmega }{\omega _{2}}$ showing duffing response for out-of-plane mode. Here, LP denotes limit point

4.2 Nonlinear response of uncoupled in-plane and out-of-plane modes

At very low DC voltage, the linear frequencies of in-plane and out-of-plane modes do not show any coupling region. To find the nonlinear response of uncoupled modes much below the coupling region, we neglect the coupling terms from Eqs. (2.17) and (2.18) and solve the governing equations of each modes, separately. To solve the nonlinear dynamic equation, we consider only the dynamic component as the static deflection is negligible at low DC voltage. Subsequently, the method of multiple scales can be used to obtain the modulation equations for each modes, separately. While the nonlinear response of in-plane mode turns out to be purely parametric, the nonlinear response of out-of-plane mode shows Duffing-like response under the influence of direct and parametric forces [14]. Figure 3 shows uncoupled nonlinear frequency verses $\frac{\varOmega }{\omega _{1}}$ showing parametric response for in-plane mode in Fig. 3a when $V_\mathrm{ac}=0.07$ V, $V_\mathrm{dc}=0.05$ V and $Q_{1}=5\times 10^5$. Figure 3b shows uncoupled nonlinear response verses $\frac{\varOmega }{\omega _{2}}$ for the out-of-plane mode when $V_\mathrm{ac}=5$ V, $V_\mathrm{dc}=2$ V and $Q_{1}=5\times 10^5$. The values of AC and DC voltages are selected to show bi-stability region in the nonlinear response. Now, we present coupled nonlinear frequency response of two modes near the coupling region using the methods of multiple scales presented in the theoretical section.

Fig. 4

a Comparison of numerical results with solutions based on MMS for in-plane mode at coupling point. b Comparison of numerical results with solutions based on MMS for out-of-plane mode at coupling point. Here, we take $V_\mathrm{dc}=81$ V, $V_\mathrm{ac}=0.05$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, $\sigma _{2}=-0.0858$, respectively

Fig. 5

Long time histories at coupling point for $V_\mathrm{dc}=81$ V, $V_\mathrm{ac}=0.05$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, when $\sigma _{1}=0.1$ and $\sigma _{2}=-0.0858$

Fig. 6

a Comparison of numerical results with solutions based on MMS for in-plane mode at coupling point. b Comparison of numerical results with solutions based on MMS for out-of-plane mode at coupling point. Here, we take $V_\mathrm{dc}=81$ V, $V_\mathrm{ac}=0.0009$ V, $Q_{1}=5\times 10^5$, $Q_{2}=2\times 10^8$, $\sigma _{2}=-0.0858$, respectively

4.3 Validation of MMS solution near coupling region

To validate the solutions obtained by solving the modulation Eqs. (3.49), (3.50), (3.51) and (3.52) from the method of multiple scales (MMS) near the coupling region, we solve the original modal dynamic Eqs. (2.17) and (2.18) using the Runge–Kutta method. To compare the results, we convert $a_{1}$ and $a_{2}$ appearing in the modulation equations to equivalent expression of $P_{1}(t)$ and $P_{2}(t)$ as given by Eqs. (3.53) and (3.54). Thus, $P_{1}(t)$ and $P_{2}(t)$ obtained from MMS are compared with the solutions obtained from the original equations. Figure 4a, b shows comparisons between numerical results and the solutions based on MMS for in-plane and out-of-plane modes near the coupling point for the parameter values $V_\mathrm{dc}=81$ V, $V_\mathrm{ac}=0.05$ V, $Q_{1}=5\times 10^4, Q_{2}=2\times 10^6$ and $\sigma _{2}=-0.0858$. Figure 5a, b shows the long time histories of the response for in-plane and out-of-plane modes when $\sigma _{1}=0.1$ and $\sigma _{2}=-0.0.0858$. The time histories show that the steady- state response of in-plane and out-of-plane modes consists of single frequency.

Fig. 7

Long time histories at coupling point for $V_\mathrm{dc}=81$ V, $V_\mathrm{ac}=0.0009$ V, $Q_{1}=5\times 10^5$, $Q_{2}=2\times 10^8$, when $\sigma _{1}=-0.1$ and $\sigma _{2}=-0.0858$

Fig. 8

Frequency response for different AC voltages below coupling point corresponding to a in-plane mode and b out-of-plane mode. Here, $V_\mathrm{dc}=70$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, $\sigma _{2}=-1.069$. LP denotes limit point

Fig. 9

Frequency response for different AC voltages at coupling point corresponding to a in-plane mode and b out-of-plane mode. Here, $V_\mathrm{dc}=81$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, $\sigma _{2}=-0.0858$. LP denotes limit point and H denotes Hopf bifurcation point

Similarly, the comparisons between the numerical results and the solutions based on MMS for in-plane and out-of-plane modes at coupling point ($V_\mathrm{dc}=81$ V and $V_\mathrm{ac}=0.0009$ V) at different quality factors $Q_{1}=5\times 10^5$ and $Q_{2}=2\times 10^8$ are shown in Fig. 6a, b. In this case, both in-plane and out-of-plane frequency response show two peaks. The long time histories as shown in Fig. 7a, b for $\sigma _{1}=-0.1$ and $\sigma _{2}=-0.0858$ also show that the steady-state response of both in-plane and out-of-plane modes consists of two frequencies corresponding to two peaks appearing in the response. Thus, it shows clearly the influence of one mode on another.

Fig. 10

Frequency response for different AC voltages at coupling point corresponding to a in-plane mode and b out-of-plane mode. Here, $V_\mathrm{dc}=81$ V, $Q_{1}=5\times 10^5$, $Q_{2}=2\times 10^8$, $\sigma _{2}=-0.0858$. LP denotes limit point

Fig. 11

Frequency response below coupling point corresponding to a in-plane mode and b out-of-plane mode. Here, $V_\mathrm{dc}=79$ V, $V_\mathrm{ac}=0.001$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, $\sigma _{2}=-0.25571538$. LP denotes limit point

4.4 Nonlinear response near and below the coupling region

In this section, to show the influence of coupling on nonlinear response near and below the coupling region, we analyze the variation of $a_{1}$ and $a_{2}$ corresponding to in-plane and out-of-plane modes. For the linear frequency relation below the coupling region at $V_\mathrm{dc}=70$ V and near the coupling region at $V_\mathrm{dc}=81$ V, we take $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$. Figure 8a, b shows the frequency response for different AC voltages below coupling point along in-plane and out-of-plane directions. With the increase in $V_\mathrm{ac}$ from 0.04 to 0.06, the response amplitude increases in both the cases. However, only single peak is observed in both the cases due to relatively low quality factor. The frequency response for in-plane motion is found to be linear, whereas out-of-plane motion shows nonlinear response. By operating the beam near the coupling region at $V_\mathrm{dc}=81$ V, the nonlinear coupled response of two modes shows combined effect of parametric and Duffing-like response when the quality factors remain same as $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$ which are shown in Fig. 9a, b. The coupling between parametric and duffing response at coupling point is due to simultaneous parametric and direct excitation of microbeam by two symmetrically placed side electrodes and a bottom electrode [14]. It is also observed that as AC voltage $V_\mathrm{ac}$ is increased from 0.05 to 0.14 V, the response amplitude and the bandwidth gradually increase with increasing hardening effect. To see the influence of quality factor on the nonlinear coupled response near the coupling region, we take another set of quality factors $Q_{1}=5\times 10^5$ and $Q_{2}=2\times 10^8$ as shown in Fig. 10a, b. It is observed that coupled response shows two peaks, thus clearly indicating the influence of one mode on another. With further increase in AC voltage, $V_\mathrm{ac}$, from 0.0005 to 0.002 V, the response amplitude of two modes increases gradually along both directions and frequency response of one of the two modes becomes nonlinear showing hardening effect when $V_\mathrm{ac}$ is more than 0.0009 V. Figure 11a, b shows the frequency response of the in-plane and out-of-plane directions below the coupling point at DC voltage $V_\mathrm{dc}=79$ V when $V_\mathrm{ac}=0.001$ V, $Q_{1}=5\times 10^4$ and $Q_{2}=2\times 10^6$. Similarly, the frequency response along the in-plane and out-of-plane directions above the coupling point at a DC voltage of $V_\mathrm{dc}=83$ V for $V_\mathrm{ac}=0.006$ V and same values of quality factors is shown in Fig. 12a, b. The results in both the cases show that the coupled effect reduces drastically as we go up or below the coupled region.

Fig. 12

Frequency response above coupling point corresponding to a in-plane mode and b out-of-plane mode. Here, $V_\mathrm{dc}=83$ V, $V_\mathrm{ac}=0.06$ V, $Q_{1}=5\times 10^4$, $Q_{2}=2\times 10^6$, $\sigma _{2}=0.18365234$. LP denotes limit point

Finally, we state the tuning of nonlinear frequency response of two modes near and below the coupling region by the application of DC voltage and quality factors. The study presented in this paper can also be extended to understand the coupling of different modes of beams in MEMS arrays.

5 Conclusion

In this paper, we have developed a theoretical model for in-plane and out-of-plane motions of a fixed–fixed microbeam separated from two symmetrically placed side electrodes and a bottom electrode. Using the electrostatic force model based on the direct and fringing forces, we obtain the partial differential equations governing the nonlinear motion of in-plane and out-of-plane motions. To do linear and nonlinear analysis, we obtain the reduced-order form of the equations using the Galerkin’s method. To analyze the variation of two modes at different DC voltage, we plot linear frequencies versus DC voltage. We found that the two modes show coupling at around DC voltage of 81 V. Thus, we obtain 1:1 internal resonance condition near the coupling region. To find the nonlinear response near and below the coupling region, we apply the method of multiple scales (MMS). After validating the solution from MMS with numerical solution near the coupling region, we analyze the influence of ac voltage and quality factor on the nonlinear response at and near the coupling point. We found that the nonlinear response below the coupling point shows uncoupled response of each modes and the response near the coupling region shows different types of coupled response at different quality factors.

Appendices

Appendix 1

Nonlinear static equations

$$\begin{aligned}&758.48\,{q_{{1}}}^{7}\alpha _{{1}}+ \left( 1022.84\,r_{{1}} \alpha _{{1}}- 1022.84\,\alpha _{{1}} \right) {q_{{1}}}^{6}\\&\quad +\, \big ( 347.07\,\alpha _{{1}}+ 347.07\,{r_{{1}}}^{2} \alpha _{{1}}+ 758.48\alpha _{{2}}{q_{{2}}}^{2}\\&\quad +\, 61.66\,N+\, 1934.02- 1388.29\,r_{{1}}\alpha _{{1}} \big ) {q_{{1}}}^{5}\\&\quad +\, \big ( 2654.13\,r_{{1}}- 470.92 {r_{{1}}}^{2}\alpha _{{1}}\\&\quad -\, 2654.13- 1022.84\alpha _{{2}}{q_{{2}}}^{2}+ 83.15\,r_{ {1}}N\\&\quad +\, 1022.84\, r_{{1}}\alpha _{{2}}{q_{{2}}}^{2}+ 470.92\,r_{ {1}}\alpha _{{1}} \\&\quad -\, 83.15\,N \big ) {q_{{1}}}^{4}+ \big ( 347.07{r_{{1}}}^{2}\alpha _{{2}}{q_{{2}}}^{2} + 927.00\\&\quad +\, 28.21\,N- 3708.01\,r_{{1}}+ 927.00\,{r_{{1}}}^{2} \\&\quad +\, 151.34\,{r_{{1}}}^{2}\alpha _{{1}}- 112.85\,r_{{1}}N- 1388.29r_{{1}}\alpha _{{2}}{q_{{2}}}^{2}\\&\quad +\, 347.07\,\alpha _{{ 2}}{q_{{2}}}^{2}+ 28.21\,{r_{{1}}}^{2}N \big ) \\&\quad \times \,{q_{{1}}}^{3} + \big ( 38.28\,r_{{1}}N- 1.33\,\beta _{{s}}{V_{{10}}}^{2} \\&\quad +\, 1330.88\,r_{{1}}- 470.92\,{r_{{1}}}^{2}\alpha _{{2}}{q_{{2}} }^{2}+ 470.92\,r_{{1}}\alpha _{{2}}{q_{{2}}}^{2} \\&\quad -\, 1330.88\,{r_ {{1}}}^{2}- 38.28\,{r_{{1}}}^{2}N+ 1.33\,\beta _{{s}}{V_{{ 12}}}^{2} \big ) \\&\quad \times \,{q_{{1}}}^{2}+ \big ( 12.30\,{r_{{1}}}^{2}N- 2.00\,\beta _{{s}}{V_{{12}}}^{2} \\&\quad -\, 2.00\,\beta _{{s}}{V_{{ 10}}}^{2}r_{{1}}+ 500.56\,{r_{{1}}}^{2}+ 151.34\,{r_{{1}}}^{ 2}\alpha _{{2}}{q_{{2}}}^{2} \big ) \\&\quad \times q_{{1}}+ 0.83\,\beta _{{s}} {V_{{12}}}^{2} - 0.83\,\beta _{{s}}{V_{{10}}}^{2}{r_{{1}}}^{2}=0 \end{aligned}$$

$$\begin{aligned}&347.07\,{q_{{2}}}^{5}\alpha _{{3}}\alpha _{{2}}- 470.92\,{q_{{2}}}^{4} \alpha _{{3}}\alpha _{{2}}\\&\quad +\, \big ( 151.34\,\alpha _{{3}}\alpha _{{2}}- 1.85\,{V_{{g}}}^{2}\beta _{{3\,g}}\\&\quad +\, 927.0+ 347.07 \alpha _{{3}}\alpha _ {{1}}{q_{{1}}}^{2}+ 1.85\,{V_{{10}}}^{2}\alpha _{{2\,g}}\\&\quad +\, 1.85\,{V_{{12 }}}^{2}\alpha _{{2\,g}}+ 28.21\,\alpha _{{3}}N \big ) {q_{{2}}}^{3}+ \big (-\!2.66 {V_{{12}}}^{2}\alpha _{{2\,g}}\\&\quad -\, 38.28\,\alpha _{{3}}N- 2.66\,{V_{{10}}}^{2}\alpha _{{2\,g}}- 1330.88\\&\quad +\, 1.33\,{V_{{10}}}^{2} \alpha _{{g}}+ 1.33\,{V_{{12}}}^{2}\alpha _{{g}} + 3.99{V_{{g}}}^{2} \beta _{{3\,g}}\\&\quad -\, 1.33\,{V_{{g}}}^{2}\beta _{{2\,g}}- 470.92\,\alpha _{{3} }\alpha _{{1}}{q_{{1}}}^{2} \big ) {q_{{2}}}^{2}\\&\quad +\, \big ( - 2.0\,{V_{{ 12}}}^{2}\alpha _{{g}}+ 500.56 + 151.34\alpha _{{3}}\alpha _{{1}}{q_{{1} }}^{2}\\&\quad -\, 3.0\,{V_{{g}}}^{2}\beta _{{3\,g}}+ 2.0\,{V_{{g}}}^{2}\beta _{{2 \,g}}+ 12.30\alpha _{{3}}N\\&\quad +\, 1.0\,{V_{{12}}}^{2}\alpha _{{2\,g}} + 1.0\, {V_{{10}}}^{2}\alpha _{{2\,g}}- 2.0\,{V_{{10}}}^{2}\alpha _{{g}} \big )\\&\quad \times \, q_{{2}}- 0.831\,{V_{{g}}}^{2}\beta _{{g}}- 0.831\,{V_{{g}}}^{2 }\beta _{{2\,g}} \\&\quad +\, 0.831\,{V_{{g}}}^{2}\beta _{{3\,g}}+ 0.831\,{V_{{10}}} ^{2}\alpha _{{g}}\\&\quad +\, 0.831\,{V_{{12}}}^{2}\alpha _{{g}}=0 \end{aligned}$$

In-plane equation coefficients

$$\begin{aligned} m_{1i}= & {} 5.56\,{{ q_{1}}}^{2}{r_{{1}}}^{3}- 11.59\,{{ q_{1}}}^{4} {r_{{1}}}^{2}- 17.11\,{{ q_{1}}}^{5}r_{{1}}\\&+\, 3.98\,{r_{{1 }}}^{2}{ q_{1}}- 2.65\,{{ q_{1}}}^{3}{r_{{1}}}^{3} + 23.86 \,{r_{{1}}}^{2}{{ q_{1}}}^{3}\\&-\, 3.98\,{ q_{1}}\,{r_{{1}}}^{3}+ 34.77\,{{ q_{1}}}^{4}r_{{1}}- 16.67\,{{ q_{1}}}^{2}{r_{{1 }}}^{2}\\&-\, 23.86\,{{ q_{1}}}^{3}r_{{1}} + 5.55\,r_{{1}}{{ q_{1}}}^{2}+ {r_{{1}}}^{3}+ 2.65\,{{ q_{1}}}^{3}\\&-\, 8.49\,{{ q_{1}}}^{6}- 11.59\,{{ q_{1}}}^{4}+ 17.11 \,{{ q_{1}}}^{5} \end{aligned}$$

$$\begin{aligned} k_{1i}= & {} 511.42\,{{ q_{1}}}^{3}{r_{{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2}+ 2119.14\,{r_{{1}}}^{2}{{ q_{1}}}^{3}\alpha _{{1}} \\&-\, 1534.26{{ q_{1}}} ^{5}{r_{{1}}}^{3}\alpha _{{1}}- 11.11\beta _{{s}}{V_{{12}}}^{2}{{ q_{1}}}^{2} \\&+\, 151.34\,{r_{{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2}+ 276.20\,{{ q_{1}}}^{5}N \\&-\, 6826.314\,{{ q_{1}}}^{6}{r_{{1}}}^{2}\alpha _{{1}} + 13808.31\,{{ q_{1}}}^{5}{r_{{1}}}^{2}\alpha _{{1}} \\&- \,41.57\,{{ q_{1}}}^ {3}{r_{{1}}}^{3}N-2\,\beta _{{s}}{V_{{12}}}^{2} \\&-\, 11.11\,\beta _{{s}}{V_{ {10}}}^{2}r_{{1}}{{ q_{1}}}^{2}\\&+\, 554.90\,{{ q_{1}}}^{4}r_{{1}}N 41.57 \,{{ q_{1}}}^{3}N \\&+\, 374.15\,{r_{{1}}}^{2}{{ q_{1}}}^{3}N+500.56\,{r_{{ 1}}}^{3} \\&-\, 5802.07\,{{ q_{1}}}^{4}+ 8563.10\,{{ q_{1}}}^{5} 253.92\,{{ q_{1}}}^{2}{r_{{1}}}^{2}N \\&+\, 1327.064733\,{{ q_{1}}}^{3} - 4252.39{{ q_{1}}}^{6}\\&+ 2781.01{{ q_{1}}}^{2} {r_{{1}}}^{3} \\&+\, 57.42{r_{{1}}}^{ 2}{ q_{1}}\,N+ 511.42\,{{ q_{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2} \\&-\, 5802.07\,{{ q_{1}}}^{4}{r_{{1}}}^{2}- 8563.10\,{{ q_{1}}}^{5}r_{{1}} \\&+\, 1996.33{r_{{1}}}^{2}{ q_{1}} -1327.06\,{{ q_{1}}}^{3}{r_{{1}}}^{3}\\&+\, 11943.58\,{r_{{1}}}^{2}{{ q_{1}}}^{3} - 1996.33\,{ q_{1}}\,{r_{{1}}}^{ 3}\\&+\, 17406.21\,{{ q_{1}}}^{4}r_{{1}} 8343.02\,{{ q_{1}}}^{2}{r_{{1}}}^ {2} \\&-\, 11943.58\,{{ q_{1}}}^{3}r_{{1}}+ 2781.01\,r_{{1}}{{ q_{1}}}^{2} \\&+\, 3397.83\,{{ q_{1}}}^{5}\alpha _{{2}}{{ q_{2}}}^{2} - 3123.66\,{{ q_{1}} }^{2}{r_{{1}}}^{2}\alpha _{{2}}{{ q_{2}}}^{2} \\&+\, 6826.31\,{{ q_{1}}}^{4}r _{{1}}\alpha _{{2}}{{ q_{2}}}^{2}- 184.97\,{{ q_{1}}}^{4}N \\&-\, 138.32\,{{ q_{1}}}^{6}N 12.31\,{r_{{1}}}^{3}N - 6826.31\,{{ q_{1}}}^{6}\alpha _{{ 1}}\\&+\, 10193.49\,{{ q_{1}}}^{7}\alpha _{{1}} - 5104.69\,{{ q_{1}}}^{8} \alpha _{{1}}\\&+\, 1534.26{{ q_{1}}}^{5}\alpha _{{1}}+ 454.01{{ q_{1}}}^ {2}{r_{{1}}}^{3}\alpha _{{1}} \\&-\,13808.31{{ q_{1}}}^{5}r_{{1}}\alpha _{{ 1}} -10193.49{{ q_{1}}}^{7}r_{{1}}\alpha _{{1}}\\&+\,3123.66{{ q_{1}}}^ {4}{r_{{1}}}^{3}\alpha _{{1}} + 7.98\,\beta _{{s}}{V_{{12}}}^{2}{ q_{1}}\\&+\, 84.64\,{{ q_{1}}}^{2}{r_{{1}}}^{3}N + 3123.66{{ q_{1}}}^{4}r_{{1}} \alpha _{{1}} \\&-\, 276.21\,{{ q_{1}}}^{5}r_{{1}}N -2119.14\,{{ q_{1}}}^{3}{ r_{{1}}}^{3}\alpha _{{1}} \\&+\, 5.30\,\beta _{{s}}{V_{{12}}}^{2}{{ q_{1}}}^{3 }+ 20478.94\,{{ q_{1}}}^{6}r_{{1}}\alpha _{{1}} \\&-\, 5.30\,\beta _{{s}}{V_{{ 10}}}^{2}{{ q_{1}}}^{3}- 374.15\,{{ q_{1}}}^{3}r_{{1}}N \\&-\,57.42\,{ q_{1}}\,{r_{{1}}}^{3}N-2\,\beta _{{s}}{V_{{10}}}^{2}{r_{{1}}}^{3} \\&-\, 9370.99 \,{{ q_{1}}}^{4}{r_{{1}}}^{2} \alpha _{{1}}- 2275.44\,{{ q_{1}}}^{4} \alpha _{{2}}{{ q_{2}}}^{2} \\&-\, 1701.56\,{{ q_{1}}}^{6}\alpha _{{2}}{{ q_{2}}}^{2} + 84.64\,r_{{1}}{{ q_{1}}}^{2}N \\&+\, 706.38\,{r_{{1}}}^{2}{ q_{1}} \,\alpha _{{2}}{{ q_{2}}}^{2} - 7.97\,\beta _{{s}}{V_{{10}}}^{2}{r_{{1}}} ^{2}{ q_{1}}\\&- \,706.38\,{ q_{1}}\,{r_{{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2 } - 4602.77\,{{ q_{1}}}^{3} r_{{1}}\alpha _{{2}}{{ q_{2}}}^{2}\\&+\,1041.22\, {{ q_{1}}}^{2}{r_{{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2} + 4602.77\,{r_{{1 }}}^{2}{{ q_{1}}}^{3}\alpha _{{2}}{{ q_{2}}}^{2} \\&-\, 3397.83\,{{ q_{1}}}^{ 5}r_{{1}}\alpha _{{2}}{{ q_{2}}}^{2} 184.97\,{{ q_{1}}}^{4}{r_{{1}}}^{ 2}N \\&-\, 2275.44\,{{ q_{1}}}^{4}{r_{{1}}}^{2}\alpha _{{2}}{{ q_{2}}}^{2} + 1041.22\,r_{{1}}{{ q_{1}}}^{2}\alpha _{{2}}{{ q_{2}}}^{2} \end{aligned}$$

$$\begin{aligned} n_{1i}= & {} 1041.22\,{{ q_{1}}}^{2}{r_{{1}}}^{3}\alpha _{{1}} + 511.42\,{{ q_{1}}}^ {3}\alpha _{{1}}\\&- 706.38\,{ q_{1}}\,{r_{{1}}}^{3}\alpha _{{1}}s+ 151.33\, {r_{{1}}}^{3}\alpha _{{1}}\\&-\, 3123.66\,{r_{{1}}}^{2}{{ q_{1}}}^{2}\alpha _ {{1}}+706.38\,{r_{{1}}}^{2}{ q_{1}}\,\alpha _{{1}}\\&+\, 6826.31\,{{ q_{1}} }^{4}r_{{1}}\alpha _{{1}}- 2275.44\,{{ q_{1}}}^{4}\alpha _{{1}} \\&-\, 511.42 \,{{ q_{1}}}^{3}{r_{{1}}}^{3}\alpha _{{1}}- 2275.44\,{{ q_{1}}}^{4}{r_{ {1}}}^{2}\alpha _{{1}}\\&-\,1701.56\,{{ q_{1}}}^{6}\alpha _{{1}}+ 1041.22\,r _{{1}}{{ q_{1}}}^{2}\alpha _{{1}} \\&+\, 74602.77{r_{{1}}}^{2}{{ q_{1}}}^{3} \alpha _{{1}}- 3397.83{{ q_{1}}}^{5}r_{{1}}\alpha _{{1}}\\&+\, 3397.83{{ q_{1}}}^{5}\alpha _{{1}} - 4602.77{{ q_{1}}}^{3}r_{{1}}\alpha _{{1}} \\ n_{2i}= & {} - 6826.31{{ q_{1}}}^{5}{r_{{1}}}^{2}\alpha _{{1}}- 5104.69{{ q_{1}} }^{7}\alpha _{{1}}\\&-\,13808.31{{ q_{1}}}^{4}r_{{1}}\alpha _{{1}}- 9370.99{r_{{1}}}^{2}{{ q_{1}}}^{3}\alpha _{{1}} \\&+\, 1534.26\,{{ q_{1}}} ^{4}\alpha _{{1}}+ 10193.49\,{{ q_{1}}}^{6}\alpha _{{1}}\\&+\, 13808.31\,{{ q_{1}}}^{4}{r_{{1}}}^{2}\alpha _{{1}}+ 454.01\,{ q_{1}}\,{r_{{1}}}^{3} \alpha _{{1}} \\&- \, 1534.26\,{{ q_{1}}}^{4}{r_{{1}}}^{3}\alpha _{{1}}+ 3123.66\,{{ q_{1}}}^{3}{r_{{1}}}^{3}\alpha _{{1}}\\&-\, 6826.31\,{{ q_{1}}} ^{5}\alpha _{{1}}- 2119.14\,{{ q_{1}}}^{2}{r_{{1}}}^{3}\alpha _{{1}}\\&+\, 3123.66\,{{ q_{1}}}^{3}r_{{1}}\alpha _{{1}}+ 20478.94\,{{ q_{1}}}^{5}r _{{1}}\alpha _{{1}} \\&-\,10193.49\,{{ q_{1}}}^{6}r_{{1}}\alpha _{{1}} + 2119.14\,{r_{{1}}}^{2}{{ q_{1}}}^{2}\alpha _{{1}}\\ n_{3i}= & {} - 4602.77\,{{ q_{1}}}^{3}r_{{1}}\alpha _{{2}}- 2275.44\,{{ q_{1}}}^{4}{ r_{{1}}}^{2}\alpha _{{2}}\\&-\, 3123.66\,{{ q_{1}}}^{2}{r_{{1}}}^{2}\alpha _{ {2}}+ 4602.77\,{r_{{1}}}^{2} {{ q_{1}}}^{3}\alpha _{{2}} \\&-\,3397.83{{ q_{1}}}^{5}r_{{1}}\alpha _{{2}}- 1701.56{{ q_{1}}}^{6}\alpha _{{2}}\\&+\, 706.38{r_{{1}}}^{2}{ q_{1}}\alpha _{{2}}+ 511.42{{ q_{1}}}^{3} \alpha _{{2}}+ 151.34\,{r_{{1}}}^{3}\alpha _{{2}}\\&+\,6826.31{{ q_{1}}}^{ 4}r_{{1}}\alpha _{{2}}+ 1041.22{{ q_{1}}}^{2}{r_{{1}}}^{3}\alpha _{{2} }\\&+\, 1041.22r_{{1}}{{ q_{1}}}^{2} \alpha _{{2}}- 511.42{{ q_{1}}}^{3}{ r_{{1}}}^{3}\alpha _{{2}}\\&- 706.38{ q_{1}}{r_{{1}}}^{3}\alpha _{{2}}{-} 2275.44{{ q_{1}}}^{4}\alpha _{{2}}{+} 3397.83{{ q_{1}}}^{5}\alpha _{{ 2}}\\ n_{4i}= & {} - 4550.87{{ q_{1}}}^{4}\alpha _{{2}}{ q_{2}}- 1022.84{{ q_{1}}}^{3} {r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}\\&-\, 4550.87{{ q_{1}}}^{4}{r_{{1}}}^{2 }\alpha _{{2}}{ q_{2}}\\&+\,13652.63 {{ q_{1}}}^{4}r_{{1}}\alpha _{{2}}{ q_{2}}+9205.54\,{{ q_{1}}}^{3}{r_{{1}}}^{2}\alpha _{{2}}{ q_{2}}\\&-\, 6795.66\,{{ q_{1}}}^{5}r_{{1}}\alpha _{{2}}{ q_{2}}- 9205.54\,{{ q_{1} }}^{3}r_{{1}}\alpha _{{2}}{ q_{2}}\\&+\, 1412.76\,{r_{{1}}}^{2}{ q_{1}}\, \alpha _{{2}}{ q_{2}}-1412.76\\&\times \,{ q_{1}}\,{r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}- 6247.33\,{r_{{1}}}^{2}{{ q_{1}}}^{2}\alpha _{{2}}{ q_{2}}\\&+\, 2082.44\,r_{{1}}{{ q_{1}}}^{2}\alpha _{{2}}{ q_{2}}+2082.44\,{{ q_{1} }}^{2}{r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}\\&+\,1022.84\,{{ q_{1}}}^{3}\alpha _{{2}}{ q_{2}}+ 302.67 {r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}\\&+\, 6795.66\,{{ q_{1}}}^{5}\alpha _{{2}}{ q_{2}}- 3403.13\,{{ q_{1}}}^{6}\alpha _{{2}}{ q_{2}}\\ n_{5i}= & {} - 2.0\,\beta _{{s}}{r_{{1}}}^{3}- 7.98\,\beta _{{s}}{r_{{1}}}^{2}{ q_{1} }\\&-\, 11.11\,\beta _{{s}}r_{{1}}{{ q_{1}}}^{2}- 5.30\,\beta _{{s}}{{ q_{1}} }^{3}\\ n_{6i}= & {} 3.70\,\beta _{{s}}{{ q_{1}}}^{3}- 1.66\,\beta _{{s}}+ 6.0\,\beta _{{s}}{ q_{1}}- 7.98\,\beta _{{s}}{{ q_{1}}}^{2} \end{aligned}$$

$$\begin{aligned} n_{7i}= & {} 1041.22{{ q_{1}}}^{3}r_{{1}}\alpha _{{2}}- 706.38{{ q_{1}}}^{2}{r_ {{1}}}^{3}\alpha _{{2}}\\&-\, 2275.44{{ q_{1}}}^{5}{r_{{1}}}^{2}\alpha _{{2 }}+ 151.33\,{ q_{1}}{r_{{1}}}^{3}\alpha _{{2}}\\&-\, 3397.83\,{{ q_{1}}}^{ 6}r_{{1}}\alpha _{{2}}-\,4602.77\,{{ q_{1}}}^{4}r_{{1}}\alpha _{{2}}\\&+\,3397.83\,{{ q_{1}}}^{6}\alpha _{{2}}+\, 511.42\,{{ q_{1}}}^{4}\alpha _{{2 }}\\&+\, 1041.22\,{{ q_{1}}}^{3}{r_{{1}}}^{3}\alpha _{{2}}-\, 1701.56\,{{ q_{1}}}^{7}\alpha _{{2}}\\&-\,3123.66\,{r_{{1}}}^{2}{{ q_{1}}}^{3}\alpha _{{2}} + 4602.77\,{{ q_{1}}}^{4}{r_{{1}}}^{2} \alpha _{{2}}\\&-\,511.42{{ q_{1}}} ^{4}{r_{{1}}}^{3}\alpha _{{2}}-\, 2275.44{{ q_{1}}}^{5}\alpha _{{2}}\\&+\, 6826.31{{ q_{1}}}^{5}r_{{1}}\alpha _{{2}}+\, 706.38{{ q_{1}}}^{2}{r_ {{1}}}^{2}\alpha _{{2}}\\ n_{8i}= & {} - 6795.66{{ q_{1}}}^{6}r_{{1}}\alpha _{{2}}{ q_{2}}- 9205.54{{ q_{1}}}^{4}r_{{1}}\alpha _{{2}}{ q_{2}}\\&-\, 1412.76{{ q_{1}}}^{2}{r_{{1}}}^ {3}\alpha _{{2}}{ q_{2}}-\, 6247.33{{ q_{1}}}^{3} {r_{{1}}}^{2}\alpha _{{ 2}}{ q_{2}}\\&-\,4550.87{{ q_{1}}}^{5}{r_{{1}}}^{2}\alpha _{{2}}{ q_{2}}+ 2082.44{{ q_{1}}}^{3}{r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}\\&+\, 1412.76{r _{{1}}}^{2}{{ q_{1}}}^{2}\alpha _{{2}}{ q_{2}} + 302.67\,{ q_{1}}\,{r_{{ 1}}}^{3}\alpha _{{2}}{ q_{2}}\\&+\,1022.84\,{{ q_{1}}}^{4}\alpha _{{2}}{ q_{2}}- 1022.84\,{{ q_{1}}}^{4}{r_{{1}}}^{3}\alpha _{{2}}{ q_{2}}\\&+\, 6795.66 \,{{ q_{1}}}^{6} \alpha _{{2}}{ q_{2}}-\,4550.87\,{{ q_{1}}}^{5}\alpha _{{ 2}}{ q_{2}}\\&+\,2082.44\,{{ q_{1}}}^{3}r_{{1}}\alpha _{{2}}{ q_{2}}+\, 13652.63\,{{ q_{1}}}^{5}r_{{1}}\alpha _{{2}}{ q_{2}}\\&- \, 3403.13\,{{ q_{1}}}^{7}\alpha _{{2}}{ q_{2}}+\, 9205.54\,{{ q_{1}}}^{4}{r_{{1}}}^{2} \alpha _{{2}}{ q_{2}} \end{aligned}$$

$$\begin{aligned} n_{9i}= & {} - 3.98\,\beta _{{s}}r_{{1}}{{ q_{1}}}^{2}+ 2.65\,\beta _{{s}}{{ q_{1}}}^ {4}\\&+\, 3.98\,\beta _{{s}}{r_{{1}}}^{2}{{ q_{1}}}^{2}+ 5.55\,\beta _{{s}}r_ {{1}}{{ q_{1}}}^{3}\\&+\,\beta _{{s}}{r_{{1}}}^{3}{ q_{1}} - 1.85\,\beta _{{s} }{{ q_{1}}}^{3}-0.83\,\beta _{{s}}{r_{{1}}}^{3}\\&-\, 3.0\,\beta _{{s}}{r_{{ 1}}}^{2}{ q_{1}}\\ n_{10i}= & {} - 3.0\,\beta _{{s}}{{ q_{1}}}^{2}- 2.49\,\beta _{{s}}r_{{1}}{ q_{1}}\\&-\, 1.33\,\beta _{{s}}r_{{1}}{{ q_{1}}}^{3}+\beta _{{s}}r_{{1}}- 1.85\, \beta _{{s}}{{ q_{1}}}^{4}\\&+\, 3.98\,\beta _{{s}}{{ q_{1}}}^{3} + 0.83\, \beta _{{s}}{ q_{1}}\\&+\,3.0\,\beta _{{s}}r_{{1}}{{ q_{1}}}^{2}\\ n_{11i}= & {} - 8.49\,{{ q_{1}}}^{6}c_{{1}}- 11.59\,{{ q_{1}}}^{4}{r_{{1}}}^{2}c_{{1 }}\\&+\, 3.98\,{r_{{1}}}^{2}{ q_{1}}\,c_{{1}}+ 5.55\,{{ q_{1}}}^{2}{r_{{1}} }^{3}c_{{1}}\\&+\, 5.55\,r_{{1}}{{ q_{1}}}^{2}c_{{1}} - 3.98\,{ q_{1}}\,{r_{ {1}}}^{3}c_{{1}}-23.86\,{{ q_{1}}}^{3}r_{{1}}c_{{1}}\\&+\, 17.11\,{{ q_{1} }}^{5}c_{{1}}+ 23.86\,{{ q_{1}}}^{3}{r_{{1}}}^{2}c_{{1}}+ 2.65\,{{ q_{1}}}^{3}c_{{1}} \\&-\, 16.67\,{r_{{1}}}^{2}{{ q_{1}}}^{2}c_{{1}}- 11.59\,{{ q_{1}}}^{4}c_{{1}}\\&-\,17.11\,{{ q_{1}}}^{5}r_{{1}}c_{{1}}- 2.65\,{{ q_{1}}}^{3}{r_{{1}}}^{3}c_{{1}}\\&+\,{r_{{1}}}^{3}c_{{1}} + 34.77\,{{ q_{1}}}^{ 4}r_{{1}}c_{{1}} \end{aligned}$$

$$\begin{aligned} \lambda _{1}= & {} \sqrt{\frac{k_{1i}}{m_{1i}}},\quad t_{1}=\frac{n_{1i}}{m_{1i}},\quad t_{2}=\frac{n_{2i}}{m_{1i}}, \\ t_{3}= & {} \frac{n_{3i}}{m_{1i}},\quad t_{4}=\frac{n_{4i}}{m_{1i}},\quad t_{5}=\frac{n_{5i}}{m_{1i}}, \\ t_{6}= & {} \frac{n_{6i}}{m_{1i}},\quad t_{7}=\frac{n_{7i}}{m_{1i}},\quad t_{8}=\frac{n_{8i}}{m_{1i}},\quad t_{9}=\frac{n_{9i}}{m_{1i}}, \\ t_{10}= & {} \frac{n_{10i}}{m_{1i}},\quad t_{11}=\frac{n_{11i}}{m_{1i}} \end{aligned}$$

Out-of-plane equation coefficients

$$\begin{aligned} m_{o}= & {} - 2.65\,{{ q_{2}}}^{3}\alpha _{{3}}+\alpha _{{3}}+ 5.56\,\alpha _{{3}}{{ q_{2}}}^{2}-\, 3.98\,{ q_{2}}\,\alpha _{{3}}\\ k_{o}= & {} - 1996.33\,{ q_{2}}- 1327.06\,{{ q_{2}}}^{3}+ 2781.01\,{{ q_{2}}}^{2}\\&-\, 1534.26\,{{ q_{2}}}^{5}\alpha _{{3}}\alpha _{{2}}-\, 2.65\,\alpha _{{2\,g} }{{ q_{2}}}^{3} {V_{{12}}}^{2}\\&-\,41.57\,{{ q_{2}}}^{3}\alpha _{{3}}N+\,3.98\,{V_{{1g}}}^{2}\beta _{{3\,g}}{ q_{2}}\\&+\, 5.56\,\alpha _{{2\,g}}{{q_{2}}}^{2}{V_{{12}}}^{2}+\, 5.56\,\alpha _{{2\,g}}{{ q_{2}}}^{2} {V_{{10 }}}^{2}\\&-\, 3.98\,\alpha _{{2\,g}}{ q_{2}}\,{V_{{10}}}^{2}+\,84.64\,\alpha _ {{3}}{{ q_{2}}}^{2}N\\&+\, 3123.66\,{{ q_{2}}}^{4}\alpha _{{3}}\alpha _{{2}}+\, 151.34\,\alpha _{{3}} \alpha _{{1}}{{ q_{1}}}^{2}\\&-\, 5.56\,{V_{{1g}}}^{2} \beta _{{3\,g}}{{ q_{2}}}^{2}-\, 57.42\,{ q_{2}}\,\alpha _{{3}}N\\&-\,3.98\, \alpha _{{2\,g}}{ q_{2}}\,{V_{{12}}}^{2}-\, 2119.14 {{ q_{2}}}^{3}\alpha _{{3}}\alpha _{{2}}\\&+\, 454.01\,\alpha _{{3}}{{ q_{2}}}^{2}\alpha _{{2}}+ 500.56 \\&-\, 1.0\,{V_{{1g}}}^{2}\beta _{{3\,g}}-511.42\,{{ q_{2}}}^{3} \alpha _{{3}}\alpha _{{1}}{{ q_{1}}}^{2} \\&+\, 1041.22\,\alpha _{{3}}{{ q_{2}} }^{2}\alpha _{{1}}{{ q_{1}}}^{2}- 706.38\,{ q_{2}}\,\alpha _{{3}}\alpha _ {{1}}{{ q_{1}}}^{2}\\&+\, 1.0\,\alpha _{{2\,g}}{V_{{12}}}^{2}-\,2.65\,\alpha _ {{2\,g}}{{ q_{2}}}^{3} {V_{{10}}}^{2}\\&+\, 2.65\,{V_{{1g}}}^{2}\beta _{{3\,g} }{{ q_{2}}}^{3}+\, 1.0\,\alpha _{{2\,g}}{V_{{10}}}^{2}\\&- \,2.0\,{V_{{1g}}}^{2 }\beta _{{g}}+ 12.30\,\alpha _{{3}}N\\ n_{1o}= & {} - 706.38\,\alpha _{{3}}{ q_{2}}\,\alpha _{{2}}+ 1041.22\,\alpha _{{3}}{{ q_{2}}}^{2}\alpha _{{2}}\\&+\, 151.34\,\alpha _{{3}}\alpha _{{2}}- 511.42\,{{ q_{2}}}^{3}\alpha _{{3}}\alpha _{{2}}\\ n_{2o}= & {} - 1534.26\,{{ q_{2}}}^{4}\alpha _{{3}}\alpha _{{2}}- 2119.14\,\alpha _{{3 }}{{ q_{2}}}^{2}\alpha _{{2}}\\&+\, 3123.66\,{{ q_{2}}}^{3}\alpha _{{3}} \alpha _{{2}} + 454.01\,\alpha _{{3}}{ q_{2}}\,\alpha _{{2}}\\ n_{3o}= & {} 151.34\,\alpha _{{3}}\alpha _{{1}}- 511.42\,{{ q_{2}}}^{3}\alpha _{{3}} \alpha _{{1}}\\&-\, 706.38\,{ q_{2}}\,\alpha _{{3}}\alpha _{{1}}+ 1041.22\, \alpha _{{3}}{{ q_{2}}}^{2}\alpha _{{1}}\\ n_{4o}= & {} - 1412.76\,\alpha _{{3}}{ q_{2}}\,\alpha _{{1}}{ q_{1}}- 1022.84\,{{ q_{2}}}^{3}\alpha _{{3}}\alpha _{{1}}{ q_{1}}\\&+\, 302.67\,\alpha _{{3}}\alpha _{ {1}}{ q_{1}} + 2082.44\,{{ q_{2}}}^{2}\alpha _{{3}}\alpha _{{1}}{ q_{1}}\\ n_{5o}= & {} - 2.0\,\beta _{{g}}- 1.0\,\beta _{{3\,g}}+ 3.98\,\beta _{{3\,g}}{ q_{2}}\\&+\, 2.65\,\beta _{{3\,g}}{{ q_{2}}}^{3}- 5.56\,\beta _{{3\,g}}{{ q_{2}}}^{2 }\\ n_{6o}= & {} 5.56\,\alpha _{{2\,g}}{{ q_{2}}}^{2}- 2.55\,\alpha _{{2\,g}}{{ q_{2}}}^ {3}\\&-\, 3.98\,\alpha _{{2\,g}}{ q_{2}}+ 1.0\,\alpha _{{2\,g}} \end{aligned}$$

$$\begin{aligned} n_{7o}= & {} 151.34\,{ q_{2}}\,\alpha _{{3}}\alpha _{{1}}- 706.38\,\alpha _{{3}}{{ q_{2}}}^{2}\alpha _{{1}}\\&+\, 1041.22\,{{ q_{2}}}^{3}\alpha _{{3}}\alpha _{{ 1}}- 511.42\,{{ q_{2}}}^{4}\alpha _{{3}}\alpha _{{1}}\\ n_{8o}= & {} - 1412.76\,{{ q_{2}}}^{2}\alpha _{{3}}\alpha _{{1}}{ q_{1}}+ 302.67\, \alpha _{{3}}{ q_{2}}\,\alpha _{{1}}{ q_{1}}\\&+\, 2082.44\,{{ q_{2}}}^{3} \alpha _{{3}}\alpha _{{1}}{ q_{1}} - 1022.84\,{{ q_{2}}}^{4}\alpha _{{3}} \alpha _{{1}}{ q_{1}}\\ n_{9o}= & {} 2.65\,\beta _{{3\,g}}{{ q_{2}}}^{4}- 7.41\,\beta _{{3\,g}}{{ q_{2}}}^{3 }\\&+\, 7.98\,\beta _{{3\,g}}{{ q_{2}}}^{2}- 4.0\,\beta _{{3\,g}}{ q_{2}} + 0.83\,\beta _{{3\,g}}\\&-\, 0.83\,\beta _{{g}}+ 1.0\,\beta _{{g}}{ q_{2}}\\ n_{10o}= & {} - 1.85\,\alpha _{{g}}{{ q_{2}}}^{3}+ 1.0\,\alpha _{{2\,g}}{ q_{2}}- 2.55 \,\alpha _{{2\,g}}{{ q_{2}}}^{4}\\&-\, 3.0\,\alpha _{{g}}{ q_{2}}+ 0.83\, \alpha _{{g}}\\&+\, 5.56 \alpha _{{2\,g}}{{ q_{2}}}^{3}-3.98\,\alpha _{{2\,g }}{{ q_{2}}}^{2}\\&+\, 3.98\,\alpha _{{g}}{{ q_{2}}}^{2}\\ n_{11o}= & {} - 3.98\,{ q2}\,c_{{3}}- 2.65\,{{ q2}}^{3}c_{{3}}+ 1.0\,c_{{2}}\\&+\, 5.56\,{{ q2}}^{2}c_{{3}} \end{aligned}$$

$$\begin{aligned} \lambda _{2}= & {} \sqrt{\frac{k_{o}}{m_{o}}},\quad s_{1}=\frac{n_{1o}}{m_{o}},\quad s_{2}=\frac{n_{2o}}{m_{o}}, \\ s_{3}= & {} \frac{n_{3o}}{m_{o}},\quad s_{4}=\frac{n_{4o}}{m_{o}},\quad s_{5}=\frac{n_{5o}}{m_{o}}, \\ s_{6}= & {} \frac{n_{6o}}{m_{o}},\quad s_{7}=\frac{n_{7o}}{m_{o}},\quad s_{8}=\frac{n_{8o}}{m_{o}}, \\ s_{9}= & {} \frac{n_{9o}}{m_{o}},\quad s_{10}=\frac{n_{10o}}{m_{o}},\quad s_{11}=\frac{n_{11o}}{m_{o}} \end{aligned}$$

Appendix 2

$$\begin{aligned} B_{1}= & {} \left( 2\,k_{{2}}t_{{11}}-2\,k_{{1}}s_{{11}} \right) \omega _{{1}},\\ B_{2}= & {} \left( 2\,k_{{2}}t_{{11}}-2\,k_{{2}}s_{{11}} \right) \omega _{{2}}, \\ B_{3}= & {} s_{{9}}\eta _{{21}}+s_{{10}} ( \eta _{{11}} +\eta _{{12}} ) -k_ {{2}} \left( t_{{9}}\eta _{{11}}+t_{{10}}\eta _{{12}} \right) \\ B_{4}= & {} 4\,\omega _{{1}} \left( k_{{1}}-k_{{2}} \right) \quad B_{5}=\left( 2\,k_{{2}}s_{{11}}-2\,k_{{1}}t_{{11}} \right) \omega _{{2}} , \\ B_{6}= & {} \left( 2\,k_{{1}}s_{{11}}-2\,k_{{1}}t_{{11}} \right) \omega _{{1}}, \\ B_{7}= & {} k_{{1}} \left( t_{{9}}\eta _{{11}}+t_{{10}}\eta _{{12}} \right) -s_{{9}} \eta _{{21}}-s_{{10}} \left( \eta _{{11}}+\eta _{{12}} \right) ,\\ B_{8}= & {} 4\,\omega _{{2}} \left( k_{{1}}-k_{{2}} \right) . \end{aligned}$$

$$\begin{aligned} c_{11}= & {} -{\frac{-{\lambda _{{2}}}^{2}t_{{2}}+t_{{8}}s_{{2}}{k_{{1}}}^{2}+t_{{8 }}s_{{4}}k_{{1}}+t_{{8}}s_{{7}}+4\,{\omega _{{1}}}^{2}t_{{2}}+4\,{ \omega _{{1}}}^{2}t_{{4}}k_{{1}}+4\,{\omega _{{1}}}^{2}t_{{7}}{k_{{1}}}^ {2}-{\lambda _{{2}}}^{2}t_{{7}}{k_{{1}}}^{2}-{\lambda _{{2}}}^{2}t_{{4}} k_{{1}}}{t_{{8}}s_{{8}}-16\,{\omega _{{1}}}^{4}+4\,{\omega _{{1}}}^{2}{ \lambda _{{1}}}^{2}+4\,{\lambda _{{2}}}^{2}{\omega _{{1}}}^{2}-{\lambda _{ {2}}}^{2}{\lambda _{{1}}}^{2}}} \\ c_{12}= & {} -2\,{\frac{-{\lambda _{{2}}}^{2}t_{{2}}+t_{{8}}s_{{2}}{k_{{1}}}^{2}+t_ {{8}}s_{{4}}k_{{1}}+t_{{8}}s_{{7}}-{\lambda _{{2}}}^{2}t_{{4}}k_{{1}}-{ \lambda _{{2}}}^{2}t_{{7}}{k_{{1}}}^{2}}{t_{{8}}s_{{8}}-{\lambda _{{2}}} ^{2}{\lambda _{{1}}}^{2}}} \\ c_{13}= & {} -{\frac{-{\lambda _{{2}}}^{2}t_{{2}}+t_{{8}}s_{{2}}{k_{{2}}}^{2}+t_{{8 }}s_{{4}}k_{{2}}+t_{{8}}s_{{7}}+4\,{\omega _{{2}}}^{2}t_{{2}}+4\,{ \omega _{{2}}}^{2}t_{{4}}k_{{2}}+4\,{\omega _{{2}}}^{2}t_{{7}}{k_{{2}}}^ {2}-{\lambda _{{2}}}^{2}t_{{7}}{k_{{2}}}^{2}-{\lambda _{{2}}}^{2}t_{{4}} k_{{2}}}{t_{{8}}s_{{8}}-16\,{\omega _{{2}}}^{4}+4\,{\omega _{{2}}}^{2}{ \lambda _{{1}}}^{2}+4\,{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-{\lambda _{ {2}}}^{2}{\lambda _{{1}}}^{2}}} \\ c_{14}= & {} -2\,{\frac{-{\lambda _{{2}}}^{2}t_{{2}}+t_{{8}}s_{{2}}{k_{{2}}}^{2}+t_ {{8}}s_{{4}}k_{{2}}+t_{{8}}s_{{7}}-{\lambda _{{2}}}^{2}t_{{4}}k_{{2}}-{ \lambda _{{2}}}^{2}t_{{7}}{k_{{2}}}^{2}}{t_{{8}}s_{{8}}-{\lambda _{{2}}} ^{2}{\lambda _{{1}}}^{2}}}, \\ c_{15}= & {} \frac{c_{15N}}{c_{15D}}, \\ c_{16}= & {} \frac{c_{16N}}{c_{16D}} \end{aligned}$$

$$\begin{aligned} c_{15N}= & {} - 2\,t_{{8}}s_{{2}}k_{{1}}k_{{2}}+2\,{\omega _{{1}}}^{2}t_{{7}}k _{{1}}k_{{2}}\\&+\,{\omega _{{2}}}^{2}t_{{4}}k_{{2}}-2\,\omega _{{1}}\omega _{ {2}}t_{{4}}k_{{1}}-2\,\omega _{{1}}\omega _{{2}}t_{{4}}k_{{2}}\\&+\,2\,{ \omega _{{2}}}^{2} t_{{7}}k_{{1}}k_{{2}}+\,2\,{\omega _{{1}}}^{2}t_{{2}}\\&-\,2 \,{\lambda _{{2}}}^{2}t_{{7}}k_{{1}}k_{{2}}\\&-\,4\,\omega _{{1}}\omega _{{2}} t_{{7}}k_{{1}}k_{{2}}-{\lambda _{{2}}}^{2}t_{{4}}k_{{2}}\\&+\,t_{{8}}s_{{4}} k_{{1}} - {\lambda _{{2}}}^{2}t_{{4}}k_{{1}}\\&+\,t_{{8}}s_{{4}}k_{{2}}+2\,t_{ {8}}s_{{7}}+{\omega _{{1}}}^{2}t_{{4}}k_{{1}}\\&-\,4\,\omega _{{1}}\omega _{{2 }}t_{{2}}+{\omega _{{2}}}^{2}t_{{4}}k_{{1}} \\&+\, {\omega _{{1}}}^{2}t_{{4}}k_ {{2}}-2\,{\lambda _{{2}}}^{2}t_{{2}}\\&+\,2\,{\omega _{{2}}}^{2}t_{{2}}\\ c_{15D}= & {} - 2\,\omega _{{1}}\omega _{{2}}{\lambda _{{1}}}^{2}-2\,{\lambda _{{2}}}^{2} \omega _{{1}}\omega _{{2}}\\&+\,4\,{\omega _{{1}}}^{3}\omega _{{2}}+t_{{8}}s_{{ 8}}-{\omega _{{2}}}^{4}\\&-\,{\omega _{{1}}}^{4}-6\,{\omega _{{1}}}^{2}{\omega _{{2}}}^{2} \\&+\, {\omega _{{1}}}^{2}{\lambda _{{1}}}^{2}+4\,\omega _{{1}}{ \omega _{{2}}}^{3}\\&+\,{\omega _{{2}}}^{2}{\lambda _{{1}}}^{2}+{\lambda _{{2}} }^{2}{\omega _{{1}}}^{2}\\&+\,{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-{\lambda _{{2}}}^{2}{\lambda _{{1}}}^{2}\\ c_{16N}= & {} -2\,t_{{8}}s_{{2}}k_{{1}}k_{{2}}+2\,{\omega _{{1}}}^{2}t_{{7}}k _{{1}}k_{{2}}\\&+\,2\,\omega _{{1}}\omega _{{2}}t_{{4}}k_{{1}}+2\,\omega _{{1} }\omega _{{2}}t_{{4}}k_{{2}}\\&+\,2\,{\omega _{{2}}}^{2}t_{{7}}k_{{1}}k_{{2}}-\, 2\,{\lambda _{{2}}}^{2}t_{{7}}k_{{1}}k_{{2}} \\&-\,{\lambda _{{2}}}^{2}t_{{4} }k_{{1}}+t_{{8}}s_{{4}}k_{{2}} +\,4\,\omega _{{1}}\omega _{{2}}t_{{7}}k_{{1 }}k_{{2}}\\&+\,t_{{8}}s_{{4}}k_{{1}}+{\omega _{{2}}}^{2}t_{{4}}k_{{2}}+2\,t_ {{8}}s_{{7}}\\&-\,{\lambda _{{2}}}^{2}t_{{4}}k_{{2}}+{\omega _{{1}}}^{2}t_{{4 }}k_{{1}}+2\,{\omega _{{2}}}^{2}t_{{2}} \\&+\,{\omega _{{2}}}^{2}t_{{4}}k_{{1} } - 2\,{\lambda _{{2}}}^{2}t_{{2}}\\&+\,2\,{\omega _{{1}}}^{2}t_{{2}}+4\,\omega _{{1}}\omega _{{2}}t_{{2}}+{\omega _{{1}}}^{2}t_{{4}}k_{{2}} \end{aligned}$$

$$\begin{aligned} c_{16D}= & {} 2\,\omega _ {{1}}\omega _{{2}}{\lambda _{{1}}}^{2}+2\,{\lambda _{{2}}}^{2}\omega _{{1} }\omega _{{2}}\\&-\,{\omega _{{1}}}^{4}-{\omega _{{2}}}^{4}+t_{{8}}s_{{8}}-4\, {\omega _{{1}}}^{3}\omega _{{2}}\\&-\,6\,{\omega _{{1}}}^{2}{\omega _{{2}}}^{2} +{\omega _{{1}}}^{2}{\lambda _{{1}}}^{2}-4\,\omega _{{1}}{\omega _{{2}}}^{ 3}\\&+\,{\omega _{{2}}}^{2}{\lambda _{{1}}}^{2}+{\lambda _{{2}}}^{2}{\omega _{{ 1}}}^{2}\\&+\,{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-{\lambda _{{2}}}^{2}{ \lambda _{{1}}}^{2} \end{aligned}$$

$$\begin{aligned} c_{21}= & {} {\frac{{\lambda _{{1}}}^{2}s_{{7}}-t_{{2}}s_{{8}}-4\,{\omega _{{1}}}^{2 }s_{{7}}-4\,{\omega _{{1}}}^{2}s_{{4}}k_{{1}}+{\lambda _{{1}}}^{2}s_{{4} }k_{{1}}-t_{{4}}k_{{1}}s_{{8}}-4\,{\omega _{{1}}}^{2}s_{{2}}{k_{{1}}}^{ 2}+{\lambda _{{1}}}^{2}s_{{2}}{k_{{1}}}^{2}-t_{{7}}{k_{{1}}}^{2}s_{{8}} }{t_{{8}}s_{{8}}-16\,{\omega _{{1}}}^{4}+4\,{\omega _{{1}}}^{2}{\lambda _ {{1}}}^{2}+4\,{\lambda _{{2}}}^{2}{\omega _{{1}}}^{2}-{\lambda _{{2}}}^{2 }{\lambda _{{1}}}^{2}}} \\ c_{22}= & {} 2\,{\frac{{\lambda _{{1}}}^{2}s_{{2}}{k_{{1}}}^{2}+{\lambda _{{1}}}^{2} s_{{4}}k_{{1}}+{\lambda _{{1}}}^{2}s_{{7}}-t_{{2}}s_{{8}}-t_{{4}}k_{{1} }s_{{8}}-t_{{7}}{k_{{1}}}^{2}s_{{8}}}{t_{{8}}s_{{8}}-{\lambda _{{2}}}^{ 2}{\lambda _{{1}}}^{2}}} \\ c_{23}= & {} {\frac{-4\,{\omega _{{2}}}^{2}s_{{7}}+{\lambda _{{1}}}^{2}s_{{7}}-t_{{2 }}s_{{8}}-4\,{\omega _{{2}}}^{2}s_{{4}}k_{{2}}+{\lambda _{{1}}}^{2}s_{{4 }}k_{{2}}-t_{{4}}k_{{2}}s_{{8}}-4\,{\omega _{{2}}}^{2}s_{{2}}{k_{{2}}}^ {2}+{\lambda _{{1}}}^{2}s_{{2}}{k_{{2}}}^{2}-t_{{7}}{k_{{2}}}^{2}s_{{8} }}{t_{{8}}s_{{8}}-16\,{\omega _{{2}}}^{4}+4\,{\omega _{{2}}}^{2}{\lambda _{{1}}}^{2}+4\,{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-{\lambda _{{2}}}^{ 2}{\lambda _{{1}}}^{2}}} \\ c_{24}= & {} 2\,{\frac{{\lambda _{{1}}}^{2}s_{{2}}{k_{{2}}}^{2}+{\lambda _{{1}}}^{2} s_{{4}}k_{{2}}+{\lambda _{{1}}}^{2}s_{{7}}-t_{{2}}s_{{8}}-t_{{4}}k_{{2} }s_{{8}}-t_{{7}}{k_{{2}}}^{2}s_{{8}}}{t_{{8}}s_{{8}}-{\lambda _{{2}}}^{ 2}{\lambda _{{1}}}^{2}}},\\ c_{25}= & {} \frac{c_{25N}}{c_{25D}}, \\ c_{26}= & {} \frac{c_{26N}}{c_{26D}} \end{aligned}$$

$$\begin{aligned} c_{25N}= & {} - 2\,{\omega _{{1}}}^{2}s_{{2}}k_{{1}}k_{{2}}+2\,\omega _{{1}} \omega _{{2}}s_{{4}}k_{{2}}+2\,\omega _{{1}}\omega _{{2}}s_{{4}}k_{{1}}\\&-\,2 \,{\omega _{{2}}}^{2}s_{{2}}k_{{1}}k_{{2}}+2\,{\lambda _{{1}}}^{2}s_{{2} }k_{{1}}k_{{2}}- 2\,t_{{7}}k_{{1}}k_{{2}}s_{{8}}\\&-\,2\,{\omega _{{2}}}^{2}s _{{7}}+2\,{\lambda _{{1}}}^{2}s_{{7}}-2\,t_{{2}}s_{{8}}-2\,{\omega _{{1} }}^{2}s_{{7}}\\&-{\omega _{{1}}}^{2}s_{{4}}k_{{2}}-\,{\omega _{{1}}}^{2}s_{{4 }}k_{{1}}+4\,\omega _{{1}}\omega _{{2}}s_{{7}}\\&-\,{\omega _{{2}}}^{2}s_{{4}} k_{{2}}-{\omega _{{2}}}^{2}s_{{4}}k_{{1}}+{\lambda _{{1}}}^{2}s_{{4}}k_{ {2}}+{\lambda _{{1}}}^{2}s_{{4}}k_{{1}}\\&-\,t_{{4}}k_{{1}}s_{{8}}-t_{{4}}k_ {{2}}s_{{8}}+4\,\omega _{{1}}\omega _{{2}}s_{{2}}k_{{1}}k_{{2}}\\ c_{25D}= & {} - 2\,\omega _{{1}}\omega _{{2}}{\lambda _{{1}}}^{2}-2\,{\lambda _{{2}}}^{2} \omega _{{1}}\omega _{{2}}\\&+\,4\,{\omega _{{1}}}^{3}\omega _{{2}}+t_{{8}}s_{{ 8}}-{\omega _{{2}}}^{4}-{\omega _{{1}}}^{4}\\&-\,6\,{\omega _{{1}}}^{2}{\omega _{{2}}}^{2}+{\omega _{{1}}}^{2}{\lambda _{{1}}}^{2}+4\,\omega _{{1}}{ \omega _{{2}}}^{3}\\&+\,{\omega _{{2}}}^{2}{\lambda _{{1}}}^{2}+{\lambda _{{2}} }^{2}{\omega _{{1}}}^{2}\\&+\,{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-{\lambda _{{2}}}^{2}{\lambda _{{1}}}^{2} \\ c_{26N}= & {} - 2\,{\omega _{{1}}}^{2}s_{{2}}k_{{1}}k_{{2}}-2\,\omega _{{1}} \omega _{{2}}s_{{4}}k_{{2}}-2\,\omega _{{1}}\omega _{{2}}s_{{4}}k_{{1}}\\&-\,2 \,{\omega _{{2}}}^{2}s_{{2}}k_{{1}}k_{{2}}+2\,{\lambda _{{1}}}^{2}s_{{2} }k_{{1}}k_{{2}} \\&-\, 2\,t_{{7}}k_{{1}}k_{{2}}s_{{8}}-2\,{\omega _{{2}}}^{2}s _{{7}}+2\,{\lambda _{{1}}}^{2}s_{{7}}\\&-\,2\,t_{{2}}s_{{8}}-2\,{\omega _{{1} }}^{2}s_{{7}}-{\omega _{{1}}}^{2}s_{{4}}k_{{2}}-{\omega _{{1}}}^{2}s_{{4 }}k_{{1}} \\&-\, 4\,\omega _{{1}}\omega _{{2}}s_{{7}}-{\omega _{{2}}}^{2}s_{{4}} k_{{2}}\\&-\,{\omega _{{2}}}^{2}s_{{4}}k_{{1}}+{\lambda _{{1}}}^{2}s_{{4}}k_{ {2}}\\&+\,{\lambda _{{1}}}^{2}s_{{4}}k_{{1}}-t_{{4}}k_{{1}}s_{{8}}-t_{{4}}k_ {{2}}s_{{8}} \\&-\, 4\,\omega _{{1}}\omega _{{2}}s_{{2}}k_{{1}}k_{{2}}\\ c_{26D}= & {} 2\,\omega _{{1}}\omega _{{2}}{\lambda _{{1}}}^{2}+2\,{\lambda _{{2}}}^{2} \omega _{{1}}\omega _{{2}}-\,{\omega _{{1}}}^{4}\\&-\,{\omega _{{2}}}^{4}+t_{{8}} s_{{8}}-4\,{\omega _{{1}}}^{3}\omega _{{2}}-\,6\,{\omega _{{1}}}^{2}{\omega _{{2}}}^{2}\\&+\, {\omega _{{1}}}^{2}{\lambda _{{1}}}^{2} -4\,\omega _{{1}}{ \omega _{{2}}}^{3}+\,{\omega _{{2}}}^{2}{\lambda _{{1}}}^{2}\\&+\,{\lambda _{{2}} }^{2}{\omega _{{1}}}^{2}+{\lambda _{{2}}}^{2}{\omega _{{2}}}^{2}-\,{\lambda _{{2}}}^{2}{\lambda _{{1}}}^{2} \end{aligned}$$

$$\begin{aligned} g_{11}= & {} 2\,t_{{2}}c_{{15}}+2\,t_{{2}}c_{{11}}+t_{{3}}{k_{{1}}}^{2}+t_{{4}}c_{{ 21}}\\&+\,t_{{4}}c_{{25}}+t_{{4}}k_{{1}}c_{{15}}+2\,t_{{3}}k_{{1}}k_{{2}}+t _{{4}}k_{{2}}c_{{11}}\\&+\,2\,t_{{7}}k_{{1}}c_{{25}}+2\,t_{{7}}k_{{2}}c_{{ 21}}+3\,t_{{1}}\\ g_{12}= & {} t_{{4}}k_{{2}}c_{{13}}+3\,t_{{1}}+2\,t_{{2}}c_{{13}}+3\,t_{{3}}{k_{{2} }}^{2}\\&+\,2\,t_{{2}}c_{{14}}+t_{{4}}k_{{2}}c_{{14}}+2\,t_{{7}}k_{{2}}c_{{ 24}}\\&+\,2\,t_{{7}}k_{{2}}c_{{23}}+t_{{4}}c_{{24}}+t_{{4}}c_{{23}}\\ g_{13}= & {} 2\,t_{{7}}k_{{2}}c_{{22}}+t_{{4}}c_{{22}}+t_{{4}}c_{{26}}+t_{{4}}k_{{2 }}c_{{12}}\\&+\,2\,t_{{2}}c_{{16}}+t_{{4}}k_{{1}}c_{{16}}+2\,t_{{2}}c_{{12} }\\&+\,4\,t_{{3}}k_{{1}}k_{{2}}+2\,t_{{3}}{k_{{1}}}^{2}+6\,t_{{1}}+2\,t_{{7 }}k_{{1}}c_{{26}}\\ g_{14}= & {} 2\,t_{{2}}c_{{13}}+t_{{3}}{k_{{2}}}^{2}+t_{{4}}c_{{23}}+2\,t_{{3}}k_{{ 1}}k_{{2}}\\&+\,t_{{4}}k_{{1}}c_{{13}}+2\,t_{{7}}k_{{1}}c_{{23}}+3\,t_{{1}}\\ g_{15}= & {} 2\,t_{{7}}k_{{1}}c_{{22}}+2\,t_{{7}}k_{{1}}c_{{21}}+t_{{4}}k_{{1}}c_{{ 12}}\\&+\,2\,t_{{2}}c_{{12}}+t_{{4}}c_{{22}}+t_{{4}}k_{{1}}c_{{11}}+3\,t_{{ 3}}{k_{{1}}}^{2}\\&+\,t_{{4}}c_{{21}}+3\,t_{{1}}+2\,t_{{2}}c_{{11}}\\ g_{16}= & {} t_{{4}}k_{{1}}c_{{14}}+2\,t_{{7}}k_{{1}}c_{{24}}+t_{{4}}k_{{2}}c_{{15} }\\&+\,t_{{4}}k_{{2}}c_{{16}}+2\,t_{{7}}k_{{2}}c_{{25}}\\&+\,4\,t_{{3}}k_{{1}}k_ {{2}}+2\,t_{{7}}k_{{2}}c_{{26}}+2\,t_{{3}}{k_{{2}}}^{2}\\&+\,t_{{4}}c_{{25} }+t_{{4}}c_{{26}}+2\,t_{{2}}c_{{14}}+2\,t_{{2}}c_{{16}}\\&+\,t_{{4}}c_{{24} }+2\,t_{{2}}c_{{15}}+6\,t_{{1}}\\ f_{11}= & {} 2\,t_{{2}}c_{{13}}+t_{{3}}{k_{{2}}}^{2}+t_{{4}}c_{{23}}+2\,t_{{3}}k_{{ 1}}k_{{2}}\\&+\,t_{{4}}k_{{1}}c_{{13}}+2\,t_{{7}}k_{{1}}c_{{23}}+3\,t_{{1}}\\ f_{12}= & {} 2\,t_{{7}}k_{{1}}c_{{22}}+2\,t_{{7}}k_{{1}}c_{{21}}+t_{{4}}k_{{1}}c_{{ 12}}\\&+\,2\,t_{{2}}c_{{12}}+t_{{4}}c_{{22}}+t_{{4}}k_{{1}}c_{{11}}+3\,t_{{ 3}}{k_{{1}}}^{2}\\&+\,t_{{4}}c_{{21}}+3\,t_{{1}}+2\,t_{{2}}c_{{11}}\\ f_{13}= & {} t_{{4}}k_{{1}}c_{{14}}+2\,t_{{7}}k_{{1}}c_{{24}}+t_{{4}}k_{{2}}c_{{15} }\\&+\,t_{{4}}k_{{2}}c_{{16}}+2\,t_{{7}}k_{{2}}c_{{25}}+4\,t_{{3}}k_{{1}}k_ {{2}}\\&+\,2\,t_{{7}}k_{{2}}c_{{26}}+2\,t_{{3}}{k_{{2}}}^{2}+t_{{4}}c_{{25} }\\&+\,t_{{4}}c_{{26}}+2\,t_{{2}}c_{{14}}+2\,t_{{2}}c_{{16}}+t_{{4}}c_{{24} }\\&+\,2\,t_{{2}}c_{{15}}+6\,t_{{1}} \end{aligned}$$

$$\begin{aligned} f_{14}= & {} 2\,t_{{2}}c_{{15}}+2\,t_{{2}}c_{{11}}+t_{{3}}{k_{{1}}}^{2}+t_{{4}}c_{{ 21}}\\&+\,t_{{4}}c_{{25}}+t_{{4}}k_{{1}}c_{{15}}+2\,t_{{3}}k_{{1}}k_{{2}}+t _{{4}}k_{{2}}c_{{11}}\\&+\, 2\,t_{{7}}k_{{1}}c_{{25}}+2\,t_{{7}}k_{{2}}c_{{ 21}}+3\,t_{{1}} \\ f_{15}= & {} t_{{4}}k_{{2}}c_{{13}}+3\,t_{{1}}+2\,t_{{2}}c_{{13}}+3\,t_{{3}}{k_{{2} }}^{2}\\&+\,2\,t_{{2}}c_{{14}}+t_{{4}}k_{{2}}c_{{14}}+2\,t_{{7}}k_{{2}}c_{{ 24}}+2\,t_{{7}}k_{{2}}c_{{23}} \\&+\, t_{{4}}c_{{24}}+t_{{4}}c_{{23}} \\ f_{16}= & {} 2\,t_{{7}}k_{{2}}c_{{22}}+t_{{4}}c_{{22}}+t_{{4}}c_{{26}}+t_{{4}}k_{{2 }}c_{{12}}\\&+\,2\,t_{{2}}c_{{16}}+t_{{4}}k_{{1}}c_{{16}}+2\,t_{{2}}c_{{12} }+4\,t_{{3}}k_{{1}}k_{{2}}\\&+\, 2\,t_{{3}}{k_{{1}}}^{2}+6\,t_{{1}}+2\,t_{{7 }}k_{{1}}c_{{26}} \end{aligned}$$

$$\begin{aligned} g_{21}= & {} s_{{4}}c_{{21}}+s_{{3}}k_{{2}}+2\,s_{{3}}k_{{1}}+s_{{4}}c_{{25}}+2\,s_ {{7}}c_{{15}}\\&+\,3\,s_{{1}}{k_{{1}}}^{2}k_{{2}}+s_{{4}}c_{{15}}k_{{1}}+2 \,s_{{2}}k_{{1}}c_{{25}}2\,s_{{2}}k_{{2}}c_{{21}}\\&+\,2\,s_{{7}}c_{{11}}+ s_{{4}}c_{{11}}k_{{2}}\\ g_{22}= & {} 2\,s_{{2}}k_{{2}}c_{{24}}+3\,s_{{3}}k_{{2}}+2\,s_{{7}}c_{{14}}+s_{{4}} c_{{24}}\\&+\,s_{{4}}c_{{23}}+s_{{4}}c_{{13}}k_{{2}}+2\,s_{{2}}k_{{2}}c_{{ 23}}\\&+\,s_{{4}} c_{{14}}k_{{2}}+2\,s_{{7}}c_{{13}}+3\,s_{{1}}{k_{{2}}}^{3}\\ g_{23}= & {} s_{{4}}c_{{12}}k_{{2}}+2\,s_{{3}}k_{{2}}+2\,s_{{7}}c_{{12}}+6\,s_{{1}} {k_{{1}}}^{2}k_{{2}}\\&+\,2\,s_{{7}}c_{{16}}+s_{{4}}c_{{22}}+4\,s_{{3}}k_{{ 1}}+2\,s_{{2}} k_{{1}}c_{{26}}\\&+\,s_{{4}}c_{{26}}+2\,s_{{2}}k_{{2}}c_{{22} }+s_{{4}}c_{{16}}k_{{1}}\\ g_{24}= & {} 2\,s_{{2}}k_{{1}}c_{{23}}+3\,s_{{1}}{k_{{2}}}^{2}k_{{1}}+s_{{4}}c_{{13 }}k_{{1}}\\&+\,s_{{4}}c_{{23}}+2\,s_{{7}}c_{{13}}+s_{{3}}k_{{1}}+2\,s_{{3}} k_{{2}}\\ g_{25}= & {} 2\,s_{{7}}c_{{12}}+2\,s_{{2}}k_{{1}}c_{{22}}+3\,s_{{3}}k_{{1}}+s_{{4}} c_{{12}}k_{{1}}\\&+\,s_{{4}}c_{{11}}k_{{1}}+2\,s_{{2}}k_{{1}}c_{{21}}+s_{{4 }}c_{{22}}s_{{4}}c_{{21}}\\&+\,2\,s_{{7}}c_{{11}}+3\,s_{{1}}{k_{{1}}}^{3}\\ g_{26}= & {} s_{{4}}c_{{14}}k_{{1}}+6\,s_{{1}}{k_{{2}}}^{2}k_{{1}}+2\,s_{{2}}k_{{1} }c_{{24}}\\&+\,s_{{4}}c_{{15}}k_{{2}}+s_{{4}}c_{{16}}k_{{2}}+2\,s_{{2}}k_{{ 2}}c_{{25}}2\,s_{{2}}k_{{2}}c_{{26}}\\&+\,2\,s_{{7}}c_{{14}}+2\,s_{{7}}c_{ {15}}+4\,s_{{3}}k_{{2}}+2\,s_{{3}}k_{{1}}\\&+\,2\,s_{{7}}c_{{16}}+s_{{4}}c_ {{24}}s_{{4}}c_{{26}}+s_{{4}}c_{{25}}\\ f_{21}= & {} 2\,s_{{2}}k_{{1}}c_{{23}}+3\,s_{{1}}{k_{{2}}}^{2}k_{{1}}+s_{{4}}c_{{13 }}k_{{1}}\\&+\,s_{{4}}c_{{23}}+2\,s_{{7}}c_{{13}}+s_{{3}}k_{{1}}+2\,s_{{3}} k_{{2}}\\ f_{22}= & {} 2\,s_{{7}}c_{{12}}+2\,s_{{2}}k_{{1}}c_{{22}}+3\,s_{{3}}k_{{1}}+s_{{4}} c_{{12}}k_{{1}}\\&+\,s_{{4}}c_{{11}}k_{{1}}+2\,s_{{2}}k_{{1}}c_{{21}}+s_{{4 }}c_{{22}}s_{{4}}c_{{21}}\\&+\,2\,s_{{7}}c_{{11}}+3\,s_{{1}}{k_{{1}}}^{3}\\ f_{23}= & {} s_{{4}}c_{{14}}k_{{1}}+6\,s_{{1}}{k_{{2}}}^{2}k_{{1}}+2\,s_{{2}}k_{{1} }c_{{24}}\\&+\,s_{{4}}c_{{15}}k_{{2}}+s_{{4}}c_{{16}}k_{{2}}+2\,s_{{2}}k_{{ 2}}c_{{25}}2\,s_{{2}}k_{{2}}c_{{26}}\\&+\,2\,s_{{7}}c_{{14}}+2\,s_{{7}}c_{ {15}}\\&+\,4\,s_{{3}}k_{{2}}+2\,s_{{3}}k_{{1}}+2\,s_{{7}}c_{{16}}+s_{{4}}c_ {{24}}s_{{4}}c_{{26}}+s_{{4}}c_{{25}}\\ f_{24}= & {} s_{{4}}c_{{21}}+s_{{3}}k_{{2}}+2\,s_{{3}}k_{{1}}+s_{{4}}c_{{25}}+2\,s_ {{7}}c_{{15}}\\&+\,3\,s_{{1}}{k_{{1}}}^{2}k_{{2}}+s_{{4}}c_{{15}}k_{{1}}2 \,s_{{2}}k_{{1}}c_{{25}}\\&+\,2\,s_{{2}}k_{{2}}c_{{21}}+2\,s_{{7}}c_{{11}}\\&+\, s_{{4}}c_{{11}}k_{{2}}\\ f_{25}= & {} 2\,s_{{2}}k_{{2}}c_{{24}}+3\,s_{{3}}k_{{2}}+2\,s_{{7}}c_{{14}}+s_{{4}} c_{{24}}\\&+\,s_{{4}}c_{{23}}+s_{{4}}c_{{13}}k_{{2}}+2\,s_{{2}}k_{{2}}c_{{ 23}}s_{{4}}c_{{14}}k_{{2}}+2\,s_{{7}}c_{{13}}\\&+\,3\,s_{{1}}{k_{{2}}}^{3}\\ f_{26}= & {} s_{{4}}c_{{12}}k_{{2}}+2\,s_{{3}}k_{{2}}+2\,s_{{7}}c_{{12}}+6\,s_{{1}} {k_{{1}}}^{2}k_{{2}}\\&+\,2\,s_{{7}}c_{{16}}+s_{{4}}c_{{22}}+4\,s_{{3}}k_{{ 1}}2\,s_{{2}}k_{{1}}c_{{26}}\\&+\,s_{{4}}c_{{26}}2\,s_{{2}}k_{{2}}c_{{22} }+s_{{4}}c_{{16}}k_{{1}} \end{aligned}$$

$$\begin{aligned} B_{11}= & {} 1+k_{{1}}\bar{k_{{1}}}, \quad B_{12}=1+k_{{2}}\bar{k_{{1}}},\\ B_{13}= & {} t_{{11}}+s_{{11}}k_{{1}}\bar{k_{{1}}},\\ B_{14}= & {} t_{{11}}+s_{{11}}k_{{2}}\bar{k_{{1}}}, \quad G_{11} = 1+k_{{1}}\bar{k_{{2}}}, \\ G_{12}= & {} 1+k_{{2}}\bar{k_{{2}}}, \\ G_{13}= & {} t_{{11}}+s_{{11}}k_{{2}}\bar{k_{{2}}}, G_{14}=t_{{11}}+s_{{11}}k_{{1}}\bar{k_{{2}}}\\ g_{1}= & {} g_{{11}}+\bar{k_{{1}}}g_{{21}}, \quad g_{2}=g_{{12}}+\bar{k_{{1}}}g_{{22}}, \\ g_{3}= & {} g_{{13}}+\bar{k_{{1}}}g_{{23}}, \\ g_{4}= & {} g_{{14}}+\bar{k_{{1}}}g_{{24}}, \quad g_{5}=g_{{15}}+\bar{k_{{1}}}g_{{25}}, \\ g_{6}= & {} g_{{16}}+\bar{k_{{1}}}g_{{26}}, \\ f_{1}= & {} f_{{11}}+\bar{k_{{2}}}f_{{21}}, \quad f_{2}=f_{{12}}+\bar{k_{{2}}}f_{{22}}, \\ f_{3}= & {} f_{{13}}+\bar{k_{{2}}}f_{{23}},\\ f_{4}= & {} f_{{14}}+\bar{k_{{2}}}f_{{24}}, \quad f_{5}=f_{{15}}+\bar{k_{{2}}}f_{{25}}, \\ f_{6}= & {} f_{{16}}+\bar{k_{{2}}}f_{{26}} \end{aligned}$$

$$\begin{aligned} \bar{G}= & {} \bar{g_{1}}\bar{A_{2}}A_{1}^2e^{-i\sigma _{2}T_{1}}+\bar{g_{2}}\bar{A_{2}}A_{2}^2e^{i\sigma _{2}T_{1}}\nonumber \\&+\bar{g_{3}}A_{1}A_{2}\bar{A_{1}}e^{i\sigma _{2}T_{1}}\\&+\,\bar{g_{4}}A_{2}^2\bar{A_{1}}e^{2i\sigma _{2}T_{1}} + \bar{g_{5}}A_{1}^2\bar{A_{1}}+\bar{g_{6}}A_{1}\bar{A_{2}}A_{2}; \\ \bar{F}= & {} \bar{f_{1}}\bar{A_{1}}A_{2}^2e^{i\sigma _{2}T_{1}}+\bar{f_{2}}\bar{A_{1}}A_{1}^2e^{-i\sigma _{2}T_{1}}\\&+\,\bar{f_{3}}A_{1}A_{2}\bar{A_{2}}e^{-i\sigma _{2}T_{1}}+\bar{f_{4}}A_{1}^2\bar{A_{2}}e^{-2i\sigma _{2}T_{1}} \\&+\, \bar{f_{5}}A_{2}^2\bar{A_{2}}+\bar{f_{6}}A_{1}\bar{A_{1}}A_{2}; \end{aligned}$$

$$\begin{aligned}&h_{11}=1/4\,{\frac{B_{{13}}G_{{12}}-B_{{12}}G_{{14}}}{\omega _{{1}} \left( B_ {{11}}G_{{12}}-B_{{12}}G_{{11}} \right) }}, \\&h_{22}=1/2\,{\frac{B_{{1}}}{B_{{4}}}}, \quad h_{33}=1/2\,{\frac{B_{{2}}}{B_{{4}}}},\\&h_{44}={\frac{B_{{3}}}{B_{{4}}}}, \\&h_{55}=1/4\,{\frac{B_{{14}}G_{{12}}-B_{{12}}G_{{13}}}{\omega _{{1}} \left( B_{{11}}G_{{12}}-B_{{12}}G_{{11}} \right) }}, \\&h_{66}=1/2\,{\frac{B_{{5}}}{B_{{8}}}}, \quad h_{77}=1/2\,{\frac{B_{{6}}}{B_{{8}}}}, \\&h_{88}={\frac{B_{{7}}}{B_{{8}}}}, \\&h_{99}=1/16\,{\frac{G_{{12}}}{\omega _{{1}} \left( B_{{11}}G_{{12}}-B_{{12}}G_{{11}} \right) }}, \\&h_{1010}=1/16\,{\frac{B_{{12}}}{\omega _{{1}} \left( B_{{11}}G_{{12}}-B_{{12}}G _{{11}} \right) }} \\&h_{1}=h_{11},\quad h_{2}=2h_{22},\quad h_{3}=2h_{33}, \, h_{4}=2h_{44}, \\&h_{5}=2h_{55},\quad h_{6}=h_{66},\\&h_{7}=h_{77}, \quad h_{8}=h_{88},\quad h_{9}=2h_{99},\quad h_{10}=2h_{1010} \end{aligned}$$

$$\begin{aligned} l_{11}= & {} 1/4\,{\frac{B_{{14}}G_{{11}}-B_{{11}}G_{{13}}}{\omega _{{2}} \left( B_ {{12}}G_{{11}}-B_{{11}}G_{{12}} \right) }},\quad l_{22}=1/2\,{\frac{B_{{5}}}{B_{{8}}}},\\ l_{33}= & {} 1/2\,{\frac{B_{{6}}}{B_{{8}}}},\quad l_{44}={\frac{B_{{7}}}{B_{{8}}}}\\ l_{55}= & {} 1/4\,{\frac{B_{{13}}G_{{11}}-B_{{11}}G_{{14}}}{\omega _{{2}} \left( B_{{12}}G_{{11}}-B_{{11}}G_{{12}} \right) }}, \\ l_{66}= & {} 1/2\,{\frac{B_{{1}}}{B_{{4}}}},\quad l_{77}=1/2\,{\frac{B_{{2}}}{B_{{4}}}}, \\ l_{88}= & {} {\frac{B_{{3}}}{B_{{4}}}}, \\ l_{99}= & {} 1/16\,{\frac{G_{{11}}}{\omega _{{2}} \left( B_{{12}}G_{{11}}-B_{{11}}G _{{12}} \right) }}, \\ l_{1010}= & {} 1/16\,{\frac{B_{{11}}}{\omega _{{2}} \left( B_{{12}}G_{{11}}-B_{{11}}G _{{12}} \right) }} \\ l_{1}= & {} l_{11},\quad l_{2}=2l_{22},\,l_{3}=2l_{33}, \\ l_{4}= & {} 2l_{44},\quad l_{5}=2l_{55},\,l_{6}=l_{66},\\ l_{7}= & {} l_{77},\quad l_{8}=l_{88},\\ l_{9}= & {} 2l_{99},\quad l_{10}=2l_{1010} \end{aligned}$$