Nonlinear coupled vibration of electrostatically actuated clamped–clamped microbeams under higher-order modes excitation

Abstract

Nonlinear modal interactions have recently become the focus of intense research in micro-resonators for their use to improve oscillator performance and probe the frontiers of fundamental physics. Understanding and controlling nonlinear coupling between vibrational modes is critical for the development of advanced micromechanical devices. This article aims to theoretically investigate the influence of antisymmetry mode on nonlinear dynamic characteristics of electrically actuated microbeam via considering nonlinear modal interactions. Under higher-order modes excitation, two nonlinear coupled flexural modes to describe microbeam-based resonators are obtained by using Hamilton’s principle and Galerkin method. Then, the Method of Multiple Scales is applied to determine the response and stability of the system for small amplitude vibration. Through Hopf bifurcation analysis, the bifurcation sets for antisymmetry mode vibration are theoretically derived, and the mechanism of energy transfer between antisymmetry mode and symmetry mode is detailed studied. The pseudo-trajectory processing method is introduced to investigate the influence of external drive on amplitude and bifurcation behavior. Results show that nonlinear modal interactions can transit vibration energy from one mode to nearby mode. In what follows, an effective way is proposed to suppress midpoint displacement of the microbeam and to reduce the possibility of large deflection. The quantitative relationship between vibrational modes is also obtained. The displacement of one mode can be predicted by detecting another mode, which shows great potential of developing parameter design in MEMS. Finally, numerical simulations are provided to illustrate the effectiveness of the theoretical results.

1 Introduction

Doubly clamped microbeams have been widely applied in many micro-electro-mechanical systems (MEMS) devices, such as energy harvester [1], microbeam resonator [2,3,4], gyroscope [5], sensor [6, 7] and so on. As the existence of structure nonlinearity and nonlinear electrostatic force, they can exhibit rich nonlinear dynamic behaviors [8,9,10]. These behaviors have attracted a lot of attention and have been studied by many MEMS communities. The great majority of the models in previous papers are based on the fundamental frequency vibration. With the wide application of MEMS, nonlinear modal interactions have recently become the focus of intense research in micro- and nano-scale resonators for their use to improve oscillator performance and probe the frontiers of fundamental physics [11]. For example, the mode coupling can adjust the pull-in voltage and resonant frequency of the doubly clamped beam [4]. Besides, the complex bifurcation behaviors and the energy transfer between vibrational modes can be caused by the mode coupling [12].

Early studies mainly focus on the static and dynamic behavior of microbeam, which considered the fundamental frequency vibration. Many researchers studied pull-in instability which is always a key issue in the design of MEMS [13]. For instance, Han et al. [14] investigated the static and dynamic characteristics of a doubly clamped microbeam-based resonator driven by two electrodes and studied its dynamic pull-in. Younis et al. [15] presented an analytical approach and accurately predicted the pull-in voltage of microbeam-based MEMS. Krylov [16] proposed a largest Lyapunov exponent criterion and well evaluated the dynamic pull-in instability of a doubly clamped microbeam. Nonlinear model analysis was introduced to investigate the dynamics of a doubly clamped microswitch in the presence of geometric nonlinearity and nonlinear energy coupling [17]. Besides, considering primary resonance and high order vibration, Younis et al. [18,19,20,21,22,23,24] traversed nonlinear dynamic behaviors of electrically actuated MEMS beams and arches. Galerkin method, Differential Quadrature method and Shooting method were introduced to investigate numerically static pull-in and dynamic pull-in phenomena. However, most of the above examples are mostly concerning the single degree of freedom models that approximate an underlying continuous system, which is impossible to study coupled vibrations.

Recently, coupled vibrations have become the focus of intense research in micro- and nano-scale resonators for their use to reveal the mechanism of the complex dynamic behaviors. Studies of coupling between individual resonators or arrays of them have introduced a host of nonlinear phenomena into the purview of microscale research [25,26,27,28]. In some cases two driving forces were applied to a single resonator [29, 30]. Recent experimental work has moved in this direction by exploring coupling between different eigenmodes of a single clamped–clamped beam [31,32,33]. Accounting for the effect of other modes enables precise determination of intra- and inter-modal coupling coefficients. Kirkendall and Kwon [11] reported multistable energy transfer between internally resonant modes of an electroelastic crystal plate and used a mixed analytical–numerical approach to provide new insight into these complex interactions. The results revealed a rich bifurcation structure marked by nested regions of multistability. Antonio et al. [34] provided a way to stabilize the oscillation frequency of nonlinear self-sustaining micromechanical resonators by coupling two different vibrational modes through an internal resonance, which was a new strategy for engineering low-frequency noise oscillators capitalizing on the intrinsic nonlinear phenomena of micromechanical resonators. Vyas et al. [35] introduced a unique T-beam microresonator designed to operate on the principle of nonlinear modal interactions due to 1:2 internal resonance. The T-beam resonator showed a high sensitivity to mass perturbations and hold great potential as a radio frequency filter–mixer and mass sensor. Labadze et al. [36] investigated the behaviors of two nonlinearly coupled flexural modes of a doubly clamped suspended beam and found that the behaviors of the non-driven mode were reminiscent of that of a parametrically driven linear oscillator. Younis and Nayfeh [37] considered modal interactions among the microbeam modes involving the first mode and investigated possibility of activating a three-to-one internal resonance between the first and second modes. The analysis showed that these two modes are nonlinearly uncoupled, and hence this internal resonance cannot be activated. Parametric mode mixing can transfer the mechanical oscillation from one mode to the other and enable rapid switching of mechanical oscillation between modes. Yamaguchi et al. [38] proposed a novel concept for controlling high-Q micromechanical resonators. Besides, a model for the microscopic mechanism of parametric mixing between different modes in a single doubly clamped beam resonator was presented [39]. The results showed that the modulation can also mix modes with different parities by introducing the beam-shape and mass-load asymmetry. Ramini et al. [12] demonstrated well-controlled and repeatable experiments to study nonlinear mode coupling among micro- and nanobeam resonators and proposed three different kinds of nonlinear interactions among the first and third bending modes of vibrations of slightly curved beams. Samanta et al. [40] reported on all electrical actuation and detection of few-layer MoS2 resonator and detected three distinct internal resonances. Hajjaj et al. [41] experimentally demonstrated an exploitation of the nonlinear softening, hardening, and veering phenomena, where the frequencies of two vibration modes got close to each other, to realize a bandpass filter of sharp roll off from the passband to the stopband. There is a growing body of literature on the study of coupled vibrations to reveal the mechanism of the complex dynamic behaviors and improve oscillator performance [42].

It can be concluded from the above analysis that complex dynamic behaviors and oscillator performance are both important in the design of MEMS and should be taken into account [11, 43]. Meanwhile, coupled vibration behaviors caused by internal resonance are gradually considered in the design of the MEMS. A doubly clamped microbeam actuated by one electrode has been widely applied in many MEMS devices. For the appropriate geometry size, when the system is driven with higher-order modes excitation, coupled vibration behaviors will appear. It can exhibit rich dynamic behaviors and multiple-mode-coupling vibration wherein the perturbation theory and numerical simulation are not enough to describe accurately the mechanism of the complex dynamic behaviors of the MEMS and Hopf bifurcation analysis is introduced for its ability to predict the threshold and the mechanism of energy transfer of the coupled system. However, to the best of our knowledge, there are fewer quantitative results about a general analysis of coupled vibration system by using Hopf bifurcation theory. Besides, antisymmetric mode has important influence on the vibration behaviors of the system [36]. The research on energy transfer mechanism between antisymmetric mode and symmetric mode is incomplete. Through Hopf bifurcation analysis and pseudo-trajectory processing method, the influence of system parameters on transition mechanism of nonlinear jumping phenomena and complex nonlinear dynamic behaviors can be predicted, which motivates our present work. In this study we exploit nonlinear coupling between modes of an individual resonator driven by one electrode to quantitatively make a complete description of the transition mechanism of nonlinear jumping phenomena and the law of energy transfer between vibrational modes.

The structure of this paper is as follows. In Sect. 2, the Hamilton’s principle and Galerkin discretization is applied to obtain two degrees of freedom equation. Then static analysis is carried out under a DC voltage. In Sect. 3, the method of multiple scales (MMS) is applied to produce an approximate solution. In Sect. 4, we analyze the stability and bifurcation near the origin and the threshold of coupled vibration is theoretically derived by the application of Hopf bifurcation theory. In Sect. 5, the influences of electrostatic force and frequency on the coupled vibration system are introduced. In Sect. 6, case studies of a microbeam are done to investigate the effect of some physical parameters on the coupled vibration of the system. Finally, summary and conclusions are presented in the last section.

2 Problem formulation

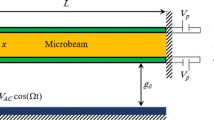
As shown in Fig. 1, a clamped–clamped microbeam-based resonator is considered. The actuation of the microbeam is realized by means of a bias voltage and an AC voltage component. By using Hamilton’s principle, the equation of motion that governs the transverse deflection $\hat{{w}}(\hat{{x}},\hat{{t}})$ is written as [37]

$$\begin{aligned}&\rho A\ddot{\hat{{w}}}+EI\hat{{w}}^{\mathrm{iv}}+c\dot{\hat{{w}}}\nonumber \\&\quad =\left( \frac{EA}{2L}\int _0^L {\hat{{w}^{\prime }}^{2}} \hbox {d}x\right) \hat{{w}^{\prime \prime }}+\frac{\varepsilon _0 b[V_\mathrm{dc} +V_\mathrm{ac} \cos (\hat{{\Omega }}\hat{{t}})]^{2}}{2(d-\hat{{w}})^{2}}\nonumber \\ \end{aligned}$$

(1)

with the following boundary conditions

$$\begin{aligned} \hat{{w}}(0,\hat{{t}})=\hat{{{w}^{\prime }}}(0,\hat{{t}}) =\hat{{w}}(L,\hat{{t}})=\hat{{{w}^{\prime }}}(L,\hat{{t}})=0 \end{aligned}$$

(2)

where $\dot{\hat{{w}}}=\frac{\partial \hat{{w}}}{\partial t}$ and $\hat{{w}^{\prime }}=\frac{\partial \hat{{w}}}{\partial x}$.

Fig. 1

Schematic of an electrically actuated microbeam

Fig. 2

a The transverse deflection obtained by using the software COMSOL when $V_\mathrm{dc} =40$ V; b center deflection under different voltages obtained by using the Galerkin method (line) and FEM (point)

The first term on the right hand of Eq. (1) represents mid-plane stretching effects. Here, $\hat{{x}}$ is the position along the plate length, A and I are the area and moment of inertia of the cross section, L is the length of beam, E is Young’s modulus, $\hat{{t}}$ is time, $\rho$ is the material density, b is the microbeam width, d is the gap width, and $\varepsilon _0$ is the dielectric constant of the gap medium. The last term in Eq. (1) represents the parallel-plate electric actuation which is composed of DC and AC components.

For convenience, the following non-dimensional variables are introduced

$$\begin{aligned} w=\frac{\hat{{w}}}{d}, \quad x=\frac{\hat{{x}}}{L}, \quad t=\hat{{t}}\sqrt{\frac{EI}{\rho AL^{4}}} \end{aligned}$$

(3)

Substituting the non-dimensional variables into Eqs. (1), (2) yields the following non-dimensional equation of motion of the microresonator

$$\begin{aligned}&\ddot{w}+w^{\mathrm{iv}}+c_n \dot{w}-\left( \alpha _1 \int _0^1 {{w}^{\prime 2}} \hbox {d}x\right) {w}^{\prime \prime }\nonumber \\&\quad =\alpha _2 \frac{V_\mathrm{dc}^2}{(1-w)^{2}}+\alpha _2 \frac{2V_\mathrm{dc} V_\mathrm{ac} \cos \Omega t+(V_\mathrm{ac} \cos \Omega t)^{2}}{(1-w)^{2}}\nonumber \\ \end{aligned}$$

(4)

with boundary conditions

$$\begin{aligned} w(0,t)={w}^{\prime }(0,t)=w(1,t)={w}^{\prime }(1,t)=0 \end{aligned}$$

(5)

The parameters appearing in Eq. (4) are

$$\begin{aligned} \alpha _1 =6\times \left( \frac{d}{h}\right) ^{2}, \quad \alpha _2 =\frac{6\varepsilon _0 L^{4}}{Ed^{3}h^{3}} \end{aligned}$$

(6)

where h represents thickness of microbeam, $\alpha _{1}$ represents ratio coefficient of the gap width to the mircobeam thickness, $\alpha _{2}$ represents electrostatic force coefficient.

The microbeam deflection under an electric force is composed of a static component due to the DC voltage, denoted by $w_\mathrm{dc} (x)$, and a dynamic component due to the AC voltage, denoted by $w_\mathrm{ac} (x)$; that is

$$\begin{aligned} w=w_\mathrm{dc} +w_\mathrm{ac} \end{aligned}$$

(7)

To calculate the static deflection of the microbeam, we set the time derivatives and the AC forcing term in Eq. (4) equal to zero and obtain

$$\begin{aligned} w_\mathrm{dc}^\mathrm{iv} -\left( \alpha _{1} \int _{0}^{1} {{w^{\prime }}_\mathrm{dc}^{2}\hbox {d}x}\right) {w^{\prime \prime }}_\mathrm{dc} =\alpha _{2} \frac{V_\mathrm{dc}^{2}}{(1-w_\mathrm{dc})^{2}} \end{aligned}$$

(8)

Here, Galerkin method is introduced to calculate Eq. (8). Figure 2 shows the relationship between midpoint deflections of a microbeam and the DC voltages obtained with Galerkin method and Finite element method (FEM). Herein, in order to study the behavior of internal resonance between antisymmetry mode and symmetry mode, the geometric and the material parameters for the microbeam are taken as $E=169$ GPa, $\rho =2300$ kg/m$^3$, $L=150~\upmu$m, $h=1~\upmu$m, $d=1.5~\upmu$m and $b=10~\upmu$m [44]. Results are presented for values of $V_\mathrm{dc}$ ranging from 0 V to pull-in voltage, where the solid line denotes the Galerkin results and the points denote the finite element results. They agree with each other. Here, the finite element method results are obtained from the software COMSOL by using the multi-field solver [45], as shown in Fig. 2a.

We generate the problem governing the dynamic behavior of the microbeam around the deflected shape by substituting Eq. (7) into Eq. (4) and using Eq. (8) to eliminate the terms representing the equilibrium position. To third-order in $w_\mathrm{ac}$, the result is

$$\begin{aligned}&\ddot{w}_\mathrm{ac} +c_n \dot{w}_\mathrm{ac}+\left[ w_\mathrm{ac}^{\mathrm{iv}} -\alpha _1 {w}_\mathrm{ac}^{\prime \prime } \int _0^1 {{w}_\mathrm{dc}^{\prime 2} \hbox {d}x} -2\alpha _{1} {w}_\mathrm{dc}^{\prime \prime }\right. \nonumber \\&\quad \left. \int _{0}^{1} {{w}_\mathrm{ac}^{\prime } {w}_\mathrm{dc}^{\prime } \hbox {d}x} -2\alpha _{2} \frac{V_\mathrm{dc}^{2} w_\mathrm{ac}}{(1-w_\mathrm{dc})^{3}}\right] \nonumber \\&\qquad -\,\alpha _1 {w}_\mathrm{dc}^{\prime \prime } \int _0^1 {{w}_\mathrm{ac}^{\prime 2} \hbox {d}x} -\alpha _1 {w}_\mathrm{ac}^{\prime \prime } \nonumber \\&\int _0^1 {2{w}_\mathrm{ac}^{\prime } {w}_\mathrm{dc}^{\prime } \hbox {d}x} -3\alpha _2 \frac{V_\mathrm{dc}^2 w_\mathrm{ac}^2}{(1-w_\mathrm{dc})^{4}} \nonumber \\&\qquad -\,\alpha _1 {w}_\mathrm{ac}^{\prime \prime } \int _0^1 {{w}_\mathrm{ac}^{\prime 2} \hbox {d}x} -4\alpha _2 \frac{V_\mathrm{dc}^2 w_\mathrm{ac}^3}{(1-w_\mathrm{dc})^{5}} \nonumber \\&\quad =2\alpha _2 \frac{V_\mathrm{dc} V_\mathrm{ac} \cos \Omega t}{(1-w_\mathrm{dc})^{2}} \end{aligned}$$

(9)

Due to $V_\mathrm{dc} \gg V_\mathrm{ac}$ [14, 15], $(V_\mathrm{dc} +V_\mathrm{ac} \cos \Omega t)^{2}\approx V_\mathrm{dc}^2 +2V_\mathrm{dc} V_\mathrm{ac} \cos \Omega t$ is obtained.

We express the solution of Eq. (9) as $w_\mathrm{ac} (x,t)=\sum \nolimits _{i=1}^\infty {u_i (t)\phi _i (x)}$, where $\phi _i$ is the i-th linear undamped mode shape of the straight microbeam. Here, the linear undamped eigenvalue problem is obtained

$$\begin{aligned} \phi _{i}^{iv} =\left( \alpha _1 \int _0^1 {{w}_{\mathrm{dc}^{2}}^{\prime } \hbox {d}x}\right) \phi _{i}^{\prime \prime }+\beta _{i}^{2} \phi _{i} \end{aligned}$$

(10)

Substituting Eq. (10) into the resulting Eq. (9), multiplying by $\phi _i$, and integrating the outcome from $x=0$ to 1, yield [46]

$$\begin{aligned}&\ddot{u}_n +c_n \dot{u}_n +\beta _n^2 u_n -\sum _{i=1}^M \left[ 2\alpha _1 \int _0^1 {{w}^{\prime \prime }_\mathrm{dc} \phi _n \hbox {d}x} \int _0^1 {{\phi }^{\prime }_i{w}^{\prime }_\mathrm{dc} \hbox {d}x} \right. \nonumber \\&\qquad \left. +\,2\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _i \phi _n }{(1-w_\mathrm{dc})^{3}}\hbox {d}x} \right] u_i \nonumber \\&\qquad -\,\sum _{i,j=1}^M \left[ \alpha _1 \int _0^1 {{w}^{\prime \prime }_\mathrm{dc} \phi _n \hbox {d}x} \int _0^1 {{\phi }^{\prime }_i {\phi }^{\prime }_j \hbox {d}x} \right. \nonumber \\&\qquad +\,\alpha _1 \int _0^1 {{\phi }^{\prime \prime }_i \phi _n \hbox {d}x} \int _0^1 {2{\phi }^{\prime }_j {w}^{\prime }_\mathrm{dc} \hbox {d}x} \nonumber \\&\qquad \left. +\,3\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _i \phi _j \phi _n \hbox {d}x}{(1-w_\mathrm{dc})^{4}}} \right] u_i u_j \nonumber \\&\qquad -\,\sum _{i,j,k=1}^M \left[ \alpha _1 \int _0^1 {{\phi }^{\prime }_i {\phi }^{\prime }_j \hbox {d}x} \int _0^1 {{\phi }^{\prime \prime }_k \phi _n \hbox {d}x} \right. \nonumber \\&\qquad \left. +\,4\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _i \phi _j \phi _k \phi _n \hbox {d}x}{(1-w_\mathrm{dc})^{5}}} \right] u_i u_j u_k\nonumber \\&\quad =f_n \cos \Omega t \end{aligned}$$

(11)

Here

$$\begin{aligned} f_n =2\alpha _2 V_\mathrm{dc} V_\mathrm{ac} \int _0^1 {\frac{\phi _n \hbox {d}x}{(1-w_\mathrm{dc})^{2}}} \end{aligned}$$

Through Eq. (11), we know that the linear term of equation is decoupled and we can obtain the resonant frequency.

$$\begin{aligned} \omega _n =\sqrt{\beta _n^2 -2\alpha _1 \int _0^1 {{w}^{\prime \prime }_\mathrm{dc} \phi _n \hbox {d}x} \int _0^1 {{\phi }^{\prime }_n {w}^{\prime }_\mathrm{dc} \hbox {d}x} -2\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _n^2}{(1-w_\mathrm{dc})^{3}}\hbox {d}x}} \end{aligned}$$

(12)

where $\omega _n$ is the resonant frequency of the n-th order mode.

Here, the first four natural frequencies of the system are obtained by Eq. (12), as shown in Fig. 3. Meanwhile, the results obtained by FEM are given. They are agreement with each other. It is found that the third-order frequency is approximately equal to two times of the second-order frequency. In this paper, we consider nonlinear modal interactions with the higher-order modes excitation. It follows from Fig. 3 that $\omega _2 \approx {\omega _3}/2$ for some range of $V_\mathrm{dc}$, and hence we study the possibility of activating a 1:2 internal resonance between the second and third modes when the third mode is excited with a higher-order excitation.

Fig. 3

Variation of the first four natural frequencies of a microbeam with various values of DC voltages (the solid lines denote the theoretical results and the points denote the finite element results)

In order to quantify the coupling between the flexural modes of the microbeam, the equations are derived for the general situation with modes coupled. Here, we take $w_\mathrm{ac} (x,t)\approx \sum \nolimits _{i=2}^3 {u_i (t)\phi _i (x)}$ and obtain that

$$\begin{aligned}&\ddot{u}_2 +c_n \dot{u}_2 +\omega _2^2 u_2 +a_{2r} u_2 u_3 +a_{2s} u_2^3\nonumber \\&\quad +\,a_{2t} u_2 u_3^2 =0\nonumber \\&\ddot{u}_3 +c_n \dot{u}_3 +\omega _3^2 u_3 +a_{3r} u_2^2 +a_{3s} u_3^2 \nonumber \\&\quad +\,a_{3t} u_3^3 +a_{3p} u_2^2 u_3 =f_3 \cos \Omega t \end{aligned}$$

(13)

where the dots indicate the time derivative and the parameters are given in “Appendix”.

For the second-order vibration, forced excitation term vanishes and parametric excitation term exists as shown in Eq. (13), which is caused by the antisymmetry of the second-order mode. When the driving frequency is close to two times of the natural frequency of the second-order mode, the coupling vibration may occur.

3 Perturbation analysis

In this section, the method of multiple scales is directly used to investigate the response of the MEMS resonator with small amplitude vibration around equilibrium position. To indicate the significance of each term in the equation of motion, $\varepsilon$ is introduced as a small non-dimensional bookkeeping parameter. Considering the electrostatic force term $f_3 =O(\varepsilon ^{3})$, scaling the dissipative terms, we obtain

$$\begin{aligned}&\ddot{u}_2 +\varepsilon ^{2}c_n \dot{u}_2 +\omega _2^2 u_2 +a_{2r} u_2 u_3 +a_{2s} u_2^3 \nonumber \\&\quad +\,a_{2t} u_2 u_3^2 =0\nonumber \\&\ddot{u}_3 +\varepsilon ^{2}c_n \dot{u}_3 +\omega _3^2 u_3 +a_{3r} u_2^2 +a_{3s} u_3^2 \nonumber \\&\quad +\,a_{3t} u_3^3 +a_{3p} u_2^2 u_3 =\varepsilon ^{3}f_3 \cos \Omega t \end{aligned}$$

(14)

To describe the nearness of the resonance, detuning parameters $\delta$ and $\Delta$ are introduced and defined by

$$\begin{aligned} \omega _3 =2\omega _2 -\varepsilon ^{2}\Delta ,\quad \Omega =\omega _3 -\varepsilon ^{2}\delta \end{aligned}$$

(15)

We seek the approximate solution of Eq. (14) in the form

$$\begin{aligned}&u_2 =\varepsilon u_{21} (T_0,T_1,T_2)+\varepsilon ^{2}u_{22} (T_0,T_1,T_2)\nonumber \\&\quad +\,\varepsilon ^{3}u_{23} (T_0,T_1,T_2)\nonumber \\&u_3 =\varepsilon u_{31} (T_0,T_1,T_2)+\varepsilon ^{2}u_{32} (T_0,T_1,T_2)\nonumber \\&\quad +\,\varepsilon ^{3}u_{33} (T_0,T_1,T_2) \end{aligned}$$

(16)

where $T_n =\varepsilon ^{n}t$

Substituting Eqs. (15) and (16) into Eq. (14) and equating coefficients of like powers of $\varepsilon$ yield

$$\begin{aligned}&O({\varepsilon ^{1}}):D_0^2 u_{21} +\omega _2^2 u_{21} =0 \nonumber \\&D_0^2 u_{31} +\omega _3^2 u_{31} =0 \end{aligned}$$

(17)

$$\begin{aligned}&O({\varepsilon ^{2}}):D_0^2 u_{22} +\omega _2^2 u_{22} =-2D_0 D_1 u_{21} -a_{2r} u_{21} u_{31} \nonumber \\&D_0^2 u_{32} +\omega _3^2 u_{32} =-2D_0 D_1 u_{31} -a_{3r} u_{21}^2 -a_{3s} u_{31}^2\nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}&O({\varepsilon ^{3}}):D_0^2 u_{23} +\omega _2^2 u_{23} =-2D_0 D_2 u_{21} -D_1^2 u_{21} \nonumber \\&\quad -\,2D_0 D_1 u_{22} -c_n D_0 u_{21} -a_{2r} u_{21} u_{32} \nonumber \\&\quad -\,a_{2r} u_{22} u_{31} -a_{2s} u_{21}^3 -a_{2t} u_{21} u_{31}^2 \nonumber \\&D_0^2 u_{33} +\omega _3^2 u_{33} =-2D_0 D_2 u_{31} -D_1^2 u_{31} -2D_0 D_1 u_{32} \nonumber \\&\quad -\,c_n D_0 u_{31} -2a_{3r} u_{21} u_{22} -2a_{3s} u_{32} u_{31} \nonumber \\&\quad -\,a_{3t} u_{31}^3 -a_{3p} u_{31} u_{21}^2 +f_3 \cos (\omega _3 T_0 -\delta T_2) \end{aligned}$$

(19)

The general solution of Eq. (17) can be written as

$$\begin{aligned}&u_{21} (T_0,T_1,T_2)=A_{21} (T_1,T_2)e^{i\omega _2 T_0}\nonumber \\&\quad +\,\bar{{A}}_{21} (T_1,T_2)e^{-i\omega _2 T_0}\nonumber \\&u_{31} (T_0,T_1,T_2)=A_{31} (T_1,T_2)e^{i\omega _3 T_0}\nonumber \\&\quad +\,\bar{{A}}_{31} (T_1,T_2)e^{-i\omega _3 T_0} \end{aligned}$$

(20)

Here, it is convenient to express $A_{21}$ and $A_{31}$ in the polar form

$$\begin{aligned} A_{21} =\frac{1}{2}a_2 e^{i\theta _2}, \quad A_{31} =\frac{1}{2}a_3 e^{i\theta _3} \end{aligned}$$

where $a_2$ and $a_3$ indicate the amplitudes of the second-order vibration mode and the third-order vibration mode, respectively.

Substituting Eq. (20) into Eqs. (18)–(19) yields the secular terms

$$\begin{aligned}&\dot{a}_2 =\frac{a_{2r} a_2 a_3}{4\omega _2}\sin \varphi -\frac{c_n a_2}{2} \nonumber \\&\dot{\varphi }=\delta +\Delta +\frac{a_{2r} a_3}{2\omega _2}\cos \varphi +\kappa _1 a_2^2 +\kappa _2 a_3^2 \nonumber \\&\dot{a}_3 =-\frac{a_{3r} a_2^2}{4\omega _3}\sin \varphi -\frac{c_n a_3}{2}-\frac{f_3}{2\omega _3}\sin \beta \nonumber \\&\dot{\beta }=\delta +\frac{a_{3r} a_2^2}{4\omega _3 a_3}\cos \varphi +\kappa _3 a_3^2 \nonumber \\&\qquad \,\, +\,\kappa _4 a_2^2 -\frac{f_3}{2\omega _3 a_3 }\cos \beta \end{aligned}$$

(21)

Here

$$\begin{aligned}&\varphi =2\theta _2 +\Delta t-\theta _3, \quad \beta =\delta t+\theta _3\nonumber \\&\kappa _1 =\frac{3a_{2s}}{4\omega _2}-\frac{a_{2r} a_{3r} }{2\omega _3^2 \omega _2} \nonumber \\&\kappa _2 =\frac{a_{2t}}{2\omega _2}-\frac{a_{2r} a_{3s} }{2\omega _3^2 \omega _2}+\frac{a_{2r}^2}{32\omega _2^3 -24\omega _2^2 \Delta }\nonumber \\&\kappa _3 =\frac{3a_{3t}}{8\omega _3}-\frac{5a_{3s}^2 }{12\omega _3^3} \nonumber \\&\kappa _4 =\frac{a_{3p}}{4\omega _3}-\frac{a_{3s} a_{3r} }{2\omega _3^3}+\frac{a_{2r} a_{3r}}{32\omega _2^2 \omega _3 -24\omega _2 \omega _3 \Delta } \end{aligned}$$

To determine the stability of the periodic solution, we evaluate the Jacobian matrix of Eq. (21) at $(a_{20},\varphi _0,a_{30},\beta _0)$ as

$$\begin{aligned} J=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\frac{a_{2r} a_{30}}{4\omega _2}\sin \varphi _0 -\frac{c_n}{2}}&{} {\frac{a_{2r} a_{20} a_{30}}{4\omega _2}\cos \varphi _0}&{} {\frac{a_{2r} a_{20}}{4\omega _2}\sin \varphi _0}&{} 0 \\ {2\kappa _1 a_{20}}&{} {-\frac{a_{2r} a_{30}}{2\omega _2}\sin \varphi _0 }&{} {\frac{a_{2r}}{2\omega _2}\cos \varphi _0 +2\kappa _2 a_{30}}&{} 0 \\ {-\frac{a_{3r} a_{20}}{2\omega _3}\sin \varphi _0}&{} {-\frac{a_{3r} a_{20}^2}{4\omega _3}\cos \varphi _0}&{} {-\frac{c_n}{2}}&{} {-\frac{f_3 }{2\omega _3}\cos \beta _0} \\ {\frac{a_{3r} a_{20}}{2\omega _3 a_{30}}\cos \varphi _0 +2\kappa _4 a_{20}}&{} {-\frac{a_{3r} a_{20}^2}{4\omega _3 a_{30}}\sin \varphi _0}&{} {2\kappa _3 a_{30}}&{} {\frac{f_3}{2\omega _3 a_{30}}\sin \beta _0} \\ \end{array} \right] \end{aligned}$$

(22)

When all the matrix eigenvalues is negative, the system is stable; otherwise, the system is unstable.

Finally, the frequency response equation can be derived as

$$\begin{aligned}&c_n^2 +\left[ \left( \delta +\Delta \right) +\kappa _2 a_3^2 \right] ^{2}-\frac{a_{2r}^2 a_3^2}{4\omega _2^2}\nonumber \\&\quad +\,2\kappa _1 \left[ \left( \delta +\Delta \right) +\kappa _2 a_3^2 \right] a_2^2 +\kappa _1^2 a_2^4 =0 \end{aligned}$$

(23)

$$\begin{aligned}&(\delta +\kappa _3 a_3^2 +\kappa _4 a_2^2)^{2}a_3^2 +\frac{c_n^2 }{4}a_3^2 +\left( \frac{a_{3r} a_2^2}{4\omega _3 }\right) ^{2}\nonumber \\&\quad +\frac{c_n^2}{8}a_2^2 -\frac{1}{4}(\delta +\Delta +\kappa _1 a_2^2 +\kappa _2 a_3^2)\nonumber \\&\quad \left( \delta +\kappa _3 a_3^2 +\kappa _4 a_2^2 \right) a_2^2 =\frac{f_3^2}{4\omega _3^2} \end{aligned}$$

(24)

In this paper, pseudo-trajectory processing method is introduced to solve Eqs. (23), (24), and the stability of the solutions is calculated by Eq. (22).

4 Hopf bifurcation analysis

As is known to all, when the electrostatic excitation is too small or the driving frequency is far away from two times of the natural frequency, there is no second-order vibration. In order to obtain the physical conditions of the second-order vibration induced by the modal coupling, Hopf bifurcation analysis is introduced. For determining the critical states of this system, it turns out to be advantageous to introduce the new unknown variables. We obtain an alternate form of the equation by transforming from polar coordinates $a_2$ and $\varphi$ to rectangular coordinates u and v, where

$$\begin{aligned} u=a_2 \cos \frac{\varphi }{2},\quad v=a_2 \sin \frac{\varphi }{2} \end{aligned}$$

(25)

Substituting Eq. (25) into Eq. (21), results in the form:

$$\begin{aligned} \dot{u}= & {} -\frac{c_n}{2}u+\left( \frac{a_{2r} a_3}{4\omega _2 }-\frac{\delta +\Delta +\kappa _2 a_3^2}{2}\right) v\nonumber \\&-\frac{\kappa _1 }{2}v(u^{2}+v^{2}) \nonumber \\ \dot{v}= & {} -\frac{c_n}{2}v+\left( \frac{a_{2r} a_3}{4\omega _2 }+\frac{\delta +\Delta +\kappa _2 a_3^2}{2}\right) u\nonumber \\&+\frac{\kappa _1 }{2}u(u^{2}+v^{2}) \end{aligned}$$

(26)

From the Eq. (26), the Jacobian matrix is obtained:

$$\begin{aligned} J=\left| {{\begin{array}{c@{\quad }c} {-\frac{c_n}{2}}&{} {\frac{a_{2r} a_3}{4\omega _2}-\frac{\delta +\Delta +\kappa _2 a_3^2}{2}} \\ {\frac{a_{2r} a_3}{4\omega _2}+\frac{\delta +\Delta +\kappa _2 a_3^2}{2}}&{} {-\frac{c_n}{2}} \\ \end{array}}} \right| \end{aligned}$$

(27)

The trace and determinant of the Jacobian matrix evaluated at an equilibrium point contain the local stability information. From Eq. (27), it is found that there is no second-order vibration when $a_3$ is small. For presence of the second-order amplitude, a critical point generically occurs when $\hbox {Det}(J)=0$.

Here, the threshold of third-order amplitude is obtained

$$\begin{aligned} a_3^2 =\frac{\frac{a_{2r}^2}{4\omega _2^2}-2\kappa _2 (\delta +\Delta )-\sqrt{\left[ \frac{a_{2r}^2}{4\omega _2^2}-2\kappa _2 \left( \delta +\Delta \right) \right] ^{2}-4\kappa _2^2 \left[ \left( \delta +\Delta \right) ^{2}+c_n^2 \right] }}{2\kappa _2^2} \end{aligned}$$

(28)

When third-order amplitude is more than the above threshold, the second-order vibration may occur. From Eq. (28), the physical condition of the second-order vibration is obtained.

$$\begin{aligned} \frac{a_{2r}^2}{4\omega _2^2}>2\kappa _2 (\delta +\Delta )+2\kappa _2 \sqrt{\left[ \left( \delta +\Delta \right) ^{2}+c_n^2 \right] } \end{aligned}$$

(29)

In this paper, Eq. (29) is defined as the basic physical condition of modal coupling vibration. With the increase in third-order amplitude, the energy transfers from the third-order mode to the second-order mode. Then, in order to further study, the complex dynamic behaviors when the second-order vibration occurs. The stability analysis of the nontrivial solution is introduced. As is known to all, the supercritical Hopf bifurcation can lead to stable branches near the critical points. On the contrary, subcritical Hopf bifurcation can lead to unstable branches. Here, we study Hopf bifurcation of critical points to determine the stability of periodic vibration. And Hopf bifurcation equation is obtained by Eq. (27)

$$\begin{aligned}&c_n^2 +\left[ \left( \delta +\Delta \right) +\kappa _2 a_3^2\right] ^{2}-\frac{a_{2r}^2 a_3^2}{4\omega _2^2}\nonumber \\&\quad +\,2\kappa _1 \left[ \left( \delta +\Delta \right) +\kappa _2 a_3^2\right] a_2^2 =0 \end{aligned}$$

(30)

Substituting Eq. (28) into Eq. (30) yields the discriminant

$$\begin{aligned} M=\kappa _1 \left[ a_{2r}^2 (\delta +\Delta )+4\omega _2^2 \kappa _2 c_n^2\right] \end{aligned}$$

(31)

The case $M<0$ results in the subcritical Hopf bifurcation. With the increase in third-order amplitude, the jump phenomenon appears in the second-order mode. Likewise, the case $M>0$ results in the supercritical Hopf bifurcation. With the increase in third-order amplitude, there appears the small vibration in the second-order mode. Meanwhile, it is found that when $M=0$, the threshold of third-order amplitude is minimum. In other word, the relatively small electrostatic force may motivate the second-order vibration.

Fig. 4

Variation of the bifurcation behavior versus $\delta$ and $V_\mathrm{dc}$ [solid line the critical value of Eq. (29), dashed line the critical value of Eq. (31)]

Figure 4 shows variation of the bifurcation behavior versus $\delta$ and $V_\mathrm{dc}$. The increase in the DC voltage enhances the modal coupling coefficient and makes nonlinear modal interactions occur easy. It is interesting to note that low-frequency perturbation parameter is more advantageous to realize the coupled vibration than the high frequency perturbation parameter.

5 Dynamic analysis

To further research on nonlinear dynamics behavior under different Hopf bifurcation parameter range, the influences of electrostatic force and frequency on the system are introduced. In this section, we study the complex dynamics behaviors of the coupled vibration and some interesting phenomena are obtained.

Fig. 5

Variation of the amplitude versus electrostatic force $f_3$ corresponding to point C in Fig. 4 (solid line theoretical solution, point numerical solution)

Fig. 6

Comparison of the force–amplitude curves obtained by pseudo-trajectory processing method (line) and long-time integration method (point) corresponding to A–B in Fig. 4 (solid line stable, dashed line unstable)

5.1 Electrostatic force

The third-order amplitude can be approximately equal to ${f_3}/{\sqrt{(\Omega ^{2}-\omega _3^2)^{2}+(c_n \Omega )^{2}}}$ under the small amplitude vibration. With the increase in $f_3$, the third-order amplitude increases. When the third-order amplitude exceeds the threshold, the second-order amplitude appears. For low values of the coupling constant $a_{2r}$, the amplitude of the third-order mode is not big enough to bring the second-order mode into the parametric resonance region, i.e., the effective coupling constant is below the parametric resonance threshold. Thus, in this case, the second mode has zero amplitude, while the third mode responds to the driving frequency in a simple harmonic manner, see Fig. 5. At the resonance and for sufficiently strong coupling $a_{2r}$, the system is driven over the threshold for Eq. (28), so that the second mode has a finite amplitude. The value of the threshold increases if one moves further away from the resonance. Figure 6 shows the coupled vibration behaviors. Here, pseudo-trajectory processing method is introduced to solve Eqs. (23), (24) and the theoretical results are obtained. When $V_\mathrm{dc} =40$ V and $\delta =-0.8$, subcritical Hopf bifurcation occurs. With the increase in $f_3$, the jump phenomenon appears in the second-order mode and the amplitude of the second mode is much larger than that of the third mode as shown in Fig. 6a, b. Similarly, When $V_\mathrm{dc} =40$ V and $\delta =-0.45$, supercritical Hopf bifurcation occurs as shown in Fig. 6c, d. Besides, under the fixed parameters, five cycles vibration may exist in the nonlinear coupling vibration system, which makes the dynamic behavior more complicated. In order to validate the above analysis, long-time integration (LTI) of Eq. (13) is used to obtain some numerical solutions (discrete points), compared with the analytical solution derived from the method of multiple scales.

Fig. 7

a Amplitude–frequency response curve of the third-order vibration mode without considering the coupled vibration; b amplitude–frequency response curve of the system with considering the coupled vibration (line the results obtained by pseudo-trajectory processing method, point the results obtained by long-time integration method)

Fig. 8

a Amplitude–frequency response curve of the third-order vibration mode without considering the coupled vibration; b amplitude–frequency response curve of the system with considering the coupled vibration (line the results obtained by pseudo-trajectory processing method, point the results obtained by long-time integration method)

5.2 Frequency

To further study the influence of frequency on the coupled mode vibration, a series of frequency response curves are obtained. When driving both modes nonlinear, interesting features are observed. Figure 7a shows amplitude frequency curve without considering the coupled vibration. Meanwhile, critical curve of coupled vibration is obtained by Eq. (28). As the amplitude exceeds the critical value, vibrational energy transfers from the third-order mode to the second order mode, and the third-order vibration is suppressed. Here, P1, P2, P3 and P4 indicate the turning points of the coupling vibration. From Fig. 7a, it is found that: (1) when the frequency is less than P1, there is no coupling vibration; (2) when the frequency is between P1 and P2, the coupling vibration occurs and there is only one periodic solution in the system; (3) when the frequency is between P2 and P3, the coupling vibration may occur and there are two stable and an unstable periodic solutions in the system. Then, the second-order amplitude and third-order amplitude are plotted versus the driving frequency as shown in Fig. 7b. The two modes interact with each other as the nonlinear line shape of one mode is reflected in the response of the other mode. Also a frequency response with two peaks, which is clearly different from a Duffing line shape, is observed. These two amplitudes correspond to two values of the tension and the electrostatic force, which leads to two resonance frequencies of the second mode and two peaks in its frequency response. This indicates that the model captures the coupling mechanism in detail.

Fig. 9

The force–amplitude curves obtained by pseudo-trajectory processing method at the case of $V_\mathrm{dc} =40$ V and $\Omega =13545$ K rad/s (solid line stable, dashed line unstable)

Fig. 10

The vibration profile curves are obtained using LTI under different simulation cases corresponding to A–D in Fig. 9

Similarly, Fig. 8 shows the frequency response curve when $V_\mathrm{dc} =43$ V and $f_3 =0.4$. Here, there are only two turning points of the coupling vibration, which means that the frequency response curve of the second-order mode is continuous. From Fig. 8b, it is found that: (1) a frequency response with two peaks is observed; (2) Monostable dynamic behavior exists between two resonant frequencies, which can eliminate dynamic bifurcation and improve system stability; (3) the amplitude of the second mode is much larger than that of the third mode near the resonant frequencies; (4) considering coupled vibration, the original third-order amplitude becomes unstable when the third-order amplitude exceeds the threshold.

Away from the resonant frequency, the third mode shows a Duffing-like. However, when driving the third mode on resonance, the third mode displays a complex dynamic response, which can be understood as follows: when the second mode enters its resonance, its amplitude increases and the increased tension and electrostatic force tune the resonance frequency of the third mode. The amplitude of the third mode then drops, reducing the tension and electrostatic force and changing the resonance frequency of the second mode. This feedback mechanism reduces the nonlinear stiffness of the third mode and makes the third mode linear, thereby increasing the linear dynamic range.

Fig. 11

Swept harmonic responses for midpoint displacement when $V_\mathrm{dc} =43$ V and $V_\mathrm{ac} =0.24$ V: a without considering the coupled vibration; b with considering the coupled vibration

The second-order mode is antisymmetric. Here, our analysis shows that there is a way to produce antisymmetric vibration mode by using symmetric electrostatic force. As shown in Figs. 6b and 8b, when the third-order amplitude exceeds the critical value, the system is mainly carried out by the second-order mode. This is a very interesting phenomenon. Besides, the quantitative relationship between the second-order amplitude and the third-order amplitude is obtained. We can predict the vibration behavior of one mode by detecting the displacement of another mode [36], which may be useful to improve sensor. For example, we can predict the vibration behavior of the second-order mode by detecting the midpoint displacement of the microbeam.

6 Dynamics simulation

In this section, case studies of a microbeam are done to investigate the effect of some physical parameters on the coupled vibration of the system. An effective way is proposed to suppress large amplitude vibration of the third-order mode and to reduce the possibility of large deflection. The maximum static deflection appears at the midpoint of the microbeam. As we know, the second-order mode cannot cause the vibration of the midpoint. However, the maximum displacement of the third-order mode appears at the midpoint. When the coupled vibration occurs, vibrational energy transfers from the third-order mode to the second-order mode. Based on the analysis in former section, the coupled vibration behaviors can be predicted at the case of $V_\mathrm{dc} =40$ V and $\hat{{\Omega }}=13545$ K rad/s, as shown in Fig. 9. To observe the coupled vibration behavior of microbeam, the vibration profile curves along the beam length are obtained by using LTI of Eq. (9) under different simulation cases, as is shown in Fig. 10. When the third modal amplitude is below the critical value, only the third modal amplitude appears, as shown in Fig. 10a. As the third mode amplitude exceeds the critical value, the vibrational energy transfers from the third-order mode to the second-order mode. In Fig. 10b, the second-order amplitude is much greater than that of the third order. In Fig. 10c, d, the obvious coupled vibration behaviors appear.

From Fig. 10, the red line represents the contour of the maximum displacement without considering the coupled vibration. Through Fig. 10b–d, it is found that when the coupled vibration occurs, the midpoint displacement is below the red line and the vibration of midpoint is suppressed, which is advantageous to reduce the possibility of large deflection. Then, to study the midpoint dynamics behavior under the variable frequency, swept harmonic response for midpoint displacement is obtained, as shown in Fig. 11. The base excitation is assumed as a swept cosine function in the form $f_3 \cos \Omega (t)t$, where $\Omega (t)$ is the time-dependent frequency and increases linearly with time. It can be found that when considering the coupled vibration, the midpoint displacement is greatly suppressed. Besides, multi-jump frequency phenomena occur, which means the complex energy exchange between the second-order mode and the third-order mode.

7 Conclusion

This paper presents mechanism of energy transfer between second order and third-order modes caused by the geometric nonlinearity and electrostatic nonlinearity and reveals the complex nonlinear dynamics behaviors. Nonlinear modal interactions play an important role in micro-resonators for their use to improve oscillator performance and probe the frontiers of fundamental physics. Hopf bifurcation analysis is carried out to investigate the physical conditions of the energy transfer. Through analysis, bifurcation sets of the second-order mode are obtained and the threshold of the third-order amplitude is theoretically derived.

In conclusion, an effective way is proposed to suppress large amplitude vibration of the midpoint and to reduce the possibility of large deflection. When the third-order amplitude is more than the threshold, the second-order vibration occurs and the vibrational energy transfers from the third-order mode to the second-order mode. Meanwhile, an effective way is proposed to drive the antisymmetric mode by using electrostatic force, which may be useful to improve sensor. The framework presented here overcomes many problems of accurately predicting complex dynamics in MEMS. It should be emphasized that all the theoretical results in this paper are compared with numerical results, which guarantees the accuracy of our whole investigations.

Appendix

$$\begin{aligned} a_{2r}= & {} -\left[ \alpha _1 \int _0^1 {{\phi }_2^{\prime \prime } \phi _2 \hbox {d}x} \int _0^1 {2{\phi }_3^{\prime } {w}_\mathrm{dc}^{\prime } \hbox {d}x} \right. \nonumber \\&\left. +\,6\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _3 \phi _2^2 \hbox {d}x}{(1-w_\mathrm{dc})^{4}}} \right] \end{aligned}$$

(32)

$$\begin{aligned} a_{2s}= & {} -\left[ \alpha _1 \int _0^1 {{\phi }_2^{\prime 2} \hbox {d}x} \int _0^1 {{\phi }_2^{\prime \prime } \phi _2 \hbox {d}x}\right. \nonumber \\&\left. +\,4\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _2^4 \hbox {d}x}{(1-w_\mathrm{dc})^{5}}} \right] \end{aligned}$$

(33)

$$\begin{aligned} a_{2t}= & {} -\left[ \alpha _1 \int _0^1 {{\phi }_3^{\prime 2} \hbox {d}x} \int _0^1 {{\phi }_2^{\prime \prime } \phi _2 \hbox {d}x}\right. \nonumber \\&\left. +\,12\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _2^2 \phi _3^2 \hbox {d}x}{(1-w_\mathrm{dc})^{5}}} \right] \end{aligned}$$

(34)

$$\begin{aligned} a_{3r}= & {} -\left[ \alpha _1 \int _0^1 {{w}_\mathrm{dc}^{\prime \prime } \phi _3 \hbox {d}x} \int _0^1 {{\phi }_2^{\prime } {\phi }_2^{\prime } \hbox {d}x}\right. \nonumber \\&\left. +\,3\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _2 \phi _2 \phi _3 \hbox {d}x}{(1-w_\mathrm{dc})^{4}}} \right] \end{aligned}$$

(35)

$$\begin{aligned} a_{3s}= & {} -\left[ \alpha _1 \int _0^1 {{w}_\mathrm{dc}^{\prime \prime } \phi _3 \hbox {d}x} \int _0^1 {{\phi }_3^{\prime } {\phi }_3^{\prime } \hbox {d}x} \right. \nonumber \\&+\,\alpha _1 \int _0^1 {{\phi }_3^{\prime \prime } \phi _3 \hbox {d}x} \int _0^1 {2{\phi }_3^{\prime } {w}_\mathrm{dc}^{\prime } \hbox {d}x}\nonumber \\&\left. +\,3\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _3 \phi _3 \phi _3 \hbox {d}x}{(1-w_\mathrm{dc})^{4}}} \right] \end{aligned}$$

(36)

$$\begin{aligned} a_{3t}= & {} -\left[ \alpha _1 \int _0^1 {{\phi }_3^{\prime } {\phi }_3^{\prime } \hbox {d}x} \int _0^1 {{\phi }_3^{\prime \prime } \phi _3 \hbox {d}x} \right. \nonumber \\&\left. +\,4\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _3 \phi _3 \phi _3 \phi _3 \hbox {d}x}{(1-w_\mathrm{dc})^{5}}} \right] \end{aligned}$$

(37)

$$\begin{aligned} a_{3p}= & {} -\left[ \alpha _1 \int _0^1 {{\phi }_2^{\prime } {\phi }_2^{\prime } \hbox {d}x} \int _0^1 {{\phi }_3^{\prime \prime } \phi _3 \hbox {d}x} \right. \nonumber \\&\left. +\,12\alpha _2 V_\mathrm{dc}^2 \int _0^1 {\frac{\phi _2 \phi _2 \phi _3 \phi _3 \hbox {d}x}{(1-w_\mathrm{dc})^{5}}} \right] \end{aligned}$$

(38)