Nonlinear dynamic response of nanotube-reinforced composite plates resting on elastic foundations in thermal environments

Abstract

This paper presents an investigation on the nonlinear dynamic response of carbon nanotube-reinforced composite (CNTRC) plates resting on elastic foundations in thermal environments. Two configurations, i.e., single-layer CNTRC plate and three-layer plate that is composed of a homogeneous core layer and two CNTRC surface sheets, are considered. The single-walled carbon nanotube (SWCNT) reinforcement is either uniformly distributed (UD) or functionally graded (FG) in the thickness direction. The material properties of FG-CNTRC plates are assumed to be graded in the thickness direction, and are estimated through a micromechanical model. The motion equations are based on a higher-order shear deformation theory with a von Kármán-type of kinematic nonlinearity. The thermal effects are also included and the material properties of CNTRCs are assumed to be temperature-dependent. The equations of motion that includes plate-foundation interaction are solved by a two-step perturbation technique. Two cases of the in-plane boundary conditions are considered. Initial stresses caused by thermal loads or in-plane edge loads are introduced. The effects of material property gradient, the volume fraction distribution, the foundation stiffness, the temperature change, the initial stress, and the core-to-face sheet thickness ratio on the dynamic response of CNTRC plates are discussed in detail through a parametric study.

1 Introduction

Recently, a new class of promising materials known as carbon nanotubes (CNTs) has drawn considerable attention. CNTs are considered as a potential candidate for the reinforcement of polymer composites. It has been reported that the aligned nanotube-reinforced composites were fabricated [1, 2]. Sun et al. [3] reported that carbon nanotubes (CNTs) have extraordinary mechanical properties over carbon fibers. The considerable advantages offered by carbon nanotube-reinforced composites (CNTRCs) have prompted an increased use of laminated structures with CNTRC layers. The major difference between the carbon fiber-reinforced composites and the carbon nanotube-reinforced composites lies in that the latter contain a low percentage of CTNs (2∼5 % by weight) [4–7]. This is due to the fact that their mechanical properties will deteriorate if the volume fraction increases beyond certain limit [8]. Therefore, in the modeling of CNTRC the concept of functionally graded materials might be incorporated to effectively make use of the CNTs. Shen [9] firstly studied the nonlinear bending behavior of CNTRC plates and found that the load-bending moment curves of the plates can be considerably improved through the use of a functionally graded distribution of CNTs in the matrix. Applying the concept of functionally graded materials to the nanocomposites, Shen and his coauthors [10–16] investigated the postbuckling and nonlinear vibration of functionally graded CNTRC plates and shells under a low nanotube volume fraction. They found that the linear functionally graded CNT reinforcements can increase the buckling load as well as postbuckling strength of the plate/shell structures under mechanical load, whereas this effect is less pronounced for the thermal buckling of the same plate/shell structure. They also concluded that the functionally graded CNT reinforcements have a significant effect on the nonlinear vibration characteristics of CNTRC plates and shells. Moreover, Zhu et al. [17] presented linear bending and free vibration of functionally graded CNTRC plates with various boundary conditions by using finite element method (FEM). Mehrabadi et al. [18] presented linear buckling of functionally graded CNTRC plates subjected to uniaxial and biaxial compression. Aragh and Hedayati [19] studied linear free vibration of functionally graded CNTRC cylindrical panels based on the Eshelby–Mori–Tanaka approach. On the other hand, Ke et al. [20] investigated the nonlinear free vibration of functionally graded CNTRC Timoshenko beams. They found that both linear and nonlinear frequencies of functionally graded CNTRC beams with symmetrical distribution of CNTs are higher than those of beams with uniform or unsymmetrical distribution of CNTs. Yas and Heshmati [21] presented a dynamic analysis of functionally graded nanocomposite beams under the action of moving load.

A functionally graded CNT reinforced aluminum matrix composite was recently fabricated by a powder metallurgy route to support the concept of functionally graded materials to the nanocomposites [22]. The sandwich construction has become even more attractive to the introduction of CNTRC for the face sheets [23, 24]. In the present work, we focus our attention on the nonlinear dynamic response of CNTRC composite plates resting on an elastic foundation of Pasternak-type. Two configurations, i.e., single-layer CNTRC plate and three-layer plate that is composed of a homogeneous core layer and two CNTRC surface sheets, are considered. Two kinds of CNTRC layers, namely, uniformly distributed (UD) and functionally graded (FG) reinforcements, are considered. The material properties of FG-CNTRC layers are assumed to be graded in the thickness direction, and are estimated through a micromechanical model in which the CNT efficiency parameter is estimated by matching the elastic modulus of CNTRCs observed from the molecular dynamics (MD) simulation results with the numerical results obtained from the extended rule of mixture. The motion equations are based on Reddy’s higher-order shear deformation theory [25] and general von Kármán-type equations [26]. The plate-foundation interaction and thermal effects are also included. The material properties of both CNTRC layer and homogeneous core layer are assumed to be temperature-dependent. Initial stresses caused by thermal loads or in-plane edge loads are introduced. All four edges of the plate are assumed to be simply supported and two cases of in-plane boundary conditions are considered. The numerical illustrations show the nonlinear dynamic response of single-layer CNTRC plates and sandwich plates with CNTRC face sheets resting on an elastic foundation under different sets of environmental conditions.

2 Material properties of functionally graded CNTRCs

We assume that an CNTRC layer is made of a mixture of single-walled carbon nanotubes (SWCNTs) and the matrix which is assumed to be isotropic. The SWCNT reinforcement is either uniformly distributed (UD) or functionally graded (FG) in the thickness direction. At the nanoscale, the structure of the carbon nanotube strongly influences the overall properties of the composite. Several micromechanical models have been developed to predict the effective material properties of CNTRCs, e.g., the Mori–Tanaka model [27, 28] and the Voigt model as the rule of the mixture [29, 30]. The Mori–Tanaka model is applicable to micro-particles and the rule of mixture is simple and convenient to apply for predicting the overall material properties and responses of the CNTRC structures. At nanoscale, both Mori–Tanaka and Voigt models need to be extended to the case involving the small scale effect. It has been shown that the Voigt and Mori–Tanaka models have the same accuracy in predicting the buckling and vibration characteristics of functionally graded ceramic-metal beams [31], plates [32], and shells [33]. According to the extended rule of mixture, the effective Young’s modulus and shear modulus of CNTRCs can be expressed as [9]

(1a)

(1b)

(1c)

where $E_{11}^{\mathrm{CN}}, E_{22}^{\mathrm{CN}}$, and $G_{12}^{\mathrm{CN}}$ are the Young’s and shear moduli of the CNT, E ^m and G ^m are the corresponding properties for the matrix, and the η _j (j=1,2,3) are the CNT efficiency parameters, respectively. In addition, V _CN and V _m are the volume fractions of the CNT and the matrix, which satisfy the relationship of V _CN+V _m =1.

As has been shown [27, 34], the load transfer between the nanotube and polymeric phases is less than perfect (e.g., the surface effects, strain gradients effects, intermolecular coupled stress effects, etc.). Hence, we introduce the CNT efficiency parameter η _j (j=1,2,3) into Eqs. (1a)–(1c) to consider the small scale effect and other effects on the material properties of CNTRCs. The values of η _j will be determined later by matching the elastic moduli of CNTRCs predicted by the MD simulations with the prediction of the extended rule of mixture in Eqs. (1a)–(1c).

The material properties of functionally graded ceramic-metal materials vary continuously from one surface to the other and, therefore, the volume fractions of the constituents may follow a simple power law [31–33, 35]. In contrast, for functionally graded fiber-reinforced composites, to avoid abrupt change of the material properties, only linear distribution can readily be achieved in practice. Three types of FG-CNTRC layers are configured. For Type V, the outer surface (Z=t ₀) of the layer is CNT-rich, referred to as FG-V. For Type Λ, the distribution of CNT reinforcements is inversed and the inner surface (Z=t ₁) of the layer is CNT-rich, referred to as FG-Λ. For Type X, a mid-plane symmetric graded distribution of CNT reinforcements is achieved and both outer and inner surfaces are CNT-rich, referred to as FG-X. Consequently, we assume the volume fraction V _CN for the top layer of the sandwich plate follows as

$$ V_{\mathrm{CN}} = 2\biggl( \frac{t_{1} - Z}{t_{1} - t_{0}} \biggr)V_{\mathrm{CN}}^{*} $$

(2a)

and for the bottom layer follows as

$$ V_{\mathrm{CN}} = 2 \biggl( \frac{Z - t_{2}}{t_{3} - t_{2}} \biggr)V_{\mathrm{CN}}^{*} $$

(2b)

in which Z=t ₀=−h/2,Z=t ₃=h/2 and

$$ V_{\mathrm{CN}}^{*} = \frac{w_{\mathrm{CN}}}{w_{\mathrm{CN}} + (\rho^{\mathrm{CN}}/\rho^{m}) - (\rho^{\mathrm{CN}}/\rho^{m})w_{\mathrm{CN}}} $$

(2c)

where w _CN is the mass fraction of nanotube, and ρ ^CN and ρ ^m are the densities of carbon nanotube and matrix, respectively, and the mass density of the CNTRC is defined by ρ=V _CN ρ ^CN+V _m ρ ^m. In such a way, the two cases of uniformly distributed (UD), i.e., $V_{\mathrm{CN}} = V_{\mathrm{CN}}^{*}$, and functionally graded (FG) CNTRCs will have the same value of mass fraction of nanotube.

The thermal expansion coefficients in the longitudinal and transverse directions can be expressed by

(3a)

(3b)

where $\alpha_{11}^{\mathrm{CN}}, \alpha_{22}^{\mathrm{CN}}$, and α ^m are thermal expansion coefficients, and $\nu_{12}^{\mathrm{CN}}$ and ν ^m are Poisson’s ratios, respectively, of carbon nanotube and matrix. Note that α ₁₁ and α ₂₂ are also graded in the thickness direction. Furthermore, we assume that the material properties of the CNTs and the matrix are temperature dependant. Thus, the effective material properties of FG-CNTRCs, such as Young’s modulus, shear modulus, and thermal expansion coefficients, are functions of temperature and position. Accordingly, the effective Poisson’s ratio depends weakly on temperature change and position and is expressed as

$$ \nu_{12} = V_{\mathrm{CN}}^{*} \nu_{12}^{\mathrm{CN}} + V_{m}\nu^{m} $$

(4)

3 Nonlinear forced vibration of CNTRC sandwich plates

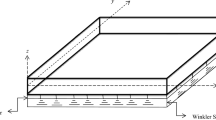
Sandwich structures represent a special form of a layered structure that consists of two thin stiff and strong face sheets separated and a relatively thick, lightweight, and soft core material [36]. Recently, the sandwich plate with relatively stiff core has drawn considerable attention [37]. The length, width, and total thickness of the sandwich plate are a,b, and h. The thickness of each CNTRC face sheet is h _F , while the thickness of the homogeneous core layer is h _H , as shown in Fig. 1. The plate is exposed to elevated temperature and is subjected to a transverse dynamic load Q(X,Y,t) combined with initial in-plane edge loads if any. As usual, the coordinate system has its origin at the corner of the plate on the mid-plane. Let $\bar{U}, \bar{V}$, and $\bar{W}$ be the plate displacements parallel to a right-hand set of axes (X,Y,Z), where X is longitudinal and Z is perpendicular to the plate. $\bar{\varPsi}_{x}$ and $\bar{\varPsi}_{y}$ are the mid-plane rotations of the normals about the Y and X axes, respectively. The plate rests on an elastic foundation. As is customary [38, 39], the foundation is assumed to be a compliant foundation, which means that no part of the plate lifts off the foundation in the large deflection region. The load-displacement relationship of the foundation is assumed to be $p = \bar{K}_{1}\bar{W} - \bar{K}_{2}\nabla^{2}\bar{W}$, where p is the force per unit area, $\bar{K}_{1}$ is the Winkler foundation stiffness and $\bar{K}_{2}$ is the shearing layer stiffness of the foundation, and ∇² is the Laplace operator in X and Y.

Fig. 1

Configuration of a CNTRC laminated plate resting on an elastic foundation

Reddy [25] developed a simple higher order shear deformation plate theory. This theory assumes that the transverse shear strains are parabolically distributed across the plate thickness. The advantages of this theory over the first order shear deformation theory are that the number of independent unknowns ($\bar{U}, \bar{V}, \bar{W}, \bar{\varPsi}_{x}$, and $\bar{\varPsi}_{y}$) is the same as in the first order shear deformation theory, but no shear correction factors are required. Based on Reddy’s higher order shear deformation plate theory, Shen [26] derived a set of general von Kármán-type equations which can be expressed in terms of a transverse displacement $\bar{W}$, two rotations $\bar{\varPsi}_{x}$ and $\bar{\varPsi}_{y}$, and stress function $\bar{F}$ defined by $\bar{N}_{x} = \bar{F},_{YY}$, $\bar{N}_{y} = \bar{F},_{XX}$, and $\bar{N}_{xy} = - \bar{F},_{XY}$. Hence, the motion equations of a sandwich plate, which includes the plate-foundation interaction and thermal effects, can be expressed by

(5)

(6)

(7)

(8)

in which

(9a)

(9b)

and the other linear operators $\tilde{L}_{ij}( )$ are defined as in [12], and I _j are defined in Eqs. (18a), (18b) below. Note that the geometric nonlinearity in the von Kármán sense is given in terms of $\tilde{L}( )$ in Eqs. (5) and (6). If the sandwich-type structure is mid-plane symmetric, the stretching/bending coupling is zero-valued, i.e., B _ij =E _ij =0. Hence, $\tilde{L}_{14}()=\tilde{L}_{15}()=\tilde{L}_{22}()= \tilde{L}_{23}()=\tilde{L}_{24}()=\tilde{L}_{34}()=\tilde{L}_{35}()= \tilde{L}_{44}()=\tilde{L}_{45}()=0$.

In the above equations, the superposed dots indicate differentiation with respect to time t. $\bar{N}^{T}, \bar{M}^{T}$, and $\bar{P}^{T}$ are the thermal forces, moments and higher order moments caused by elevated temperature, and are defined by

(10a)

(10b)

where ΔT=T−T ₀ is the temperature rise from the reference temperature T ₀ at which there are no thermal strains, and

$$ \left [ \begin{array}{l} A_{x} \\ A_{y} \\ A_{xy} \\ \end{array} \right ] = - \left [ \begin{array}{l@{\quad }l@{\quad }l} \bar{Q}_{11} & \bar{Q}_{12} & \bar{Q}_{16} \\ \bar{Q}_{12} & \bar{Q}_{22} & \bar{Q}_{26} \\ \bar{Q}_{16} & \bar{Q}_{26} & \bar{Q}_{66} \\\end{array} \right ] \left [ \begin{array}{l@{\quad }l} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\\end{array} \right ] \left [ \begin{array}{l} \alpha_{11} \\ \alpha_{22} \\ \end{array} \right ] $$

(11)

in which α ₁₁ and α ₂₂ are the thermal expansion coefficients measured in the longitudinal and transverse directions, respectively, and $\bar{Q}_{ij}$ are the transformed elastic constants, details of which can be found in [25, 26]. Note that for an FG-CNTRC layer, $\bar{Q}_{ij} = Q_{ij}$ in which

(12)

where E ₁₁,E ₂₂,G ₁₂,ν ₁₂, and ν ₂₁ are the effective Young’s and shear moduli and Poisson’s ratios of the FG-CNTRC layer, respectively. They are derived from the corresponding properties of the CNTs and the matrix by the use of a micromechanical model as described in Sect. 2.

We assume that all the edges of the plate are simply supported. Depending upon the in-plane behavior at the edges, two cases will be considered.

Case 1::

The edges are simply supported and freely movable in both the X and Y directions, and the uniaxial or biaxial edge loads are acting in the X and Y directions, respectively.

Case 2::

Four edges are simply supported with no in-plane displacements.

The boundary conditions of above two cases can be expressed as

(13a)

(13b)

(13c)

(13d)

(13e)

(13f)

(13g)

(13h)

where σ _x and σ _y are average compressive stresses in the X and Y directions, $\bar{M}_{x}$ and $\bar{M}_{y}$ are the bending moments and $\bar{P}_{x}$ and $\bar{P}_{y}$ are the higher order moments as defined in [25].

The conditions expressing the immovability conditions (13d) and (13h) are fulfilled on the average senses as [9]

(14a)

(14b)

in which

(15a)

(15b)

In the above equations, the reduced stiffness matrices $[A_{ij}^{ *} ], [B_{ij}^{ *} ], [D_{ij}^{ *} ], [E_{ij}^{*}], [F_{ij}^{*}]$, and $[H_{ij}^{*}]$ are functions of T and Z, determined through relationships [26]

(16)

where A _ij ,B _ij , etc., are the plate stiffnesses, defined by

(17a)

(17b)

and the inertias I _i (i=1,2,3,4,5,7) are defined by

(18a)

and

(18b)

4 Solution procedure

Before carrying out the solution process, it is convenient to first define the following dimensionless quantities for such plates, in which the alternative forms k ₁ and k ₂ are not needed until the numerical examples are considered

(19)

in which ρ ₀ and E ₀ are the reference values of ρ ^m and E ^m at the room temperature (T ₀=300 K), and $A_{x}^{T}, A_{y}^{T}, D_{x}^{T},D_{y}^{T},F_{x}^{T}$, and $F_{x}^{T}$ are defined by

(20)

where A _x and A _y are given in detail in Eq. (11).

The nonlinear Eqs. (5)–(8) may then be written in dimensionless form as

(21)

(22)

(23)

(24)

where

(25a)

(25b)

and other nondimensional linear operators L _ij () are defined as in [12].

The boundary conditions of Eqs. (13a)–(13h) become

(26a)

(26b)

(26c)

(26d)

(26e)

(26f)

We assume that the solutions of Eqs. (21)–(24) can be expressed as

(27)

where W ^∗(x,y) is an initial deflection due to initial thermal bending moment, and $\tilde{W}(x,y,\tau)$ is an additional deflection. $\varPsi_{x}^{*}(x,y), \varPsi_{y}^{*}(x,y)$ and F ^∗(x,y) are the mid-plane rotations and stress function corresponding to W ^∗(x,y). $\tilde{\varPsi}_{x}(x,y,\tau),\tilde{\varPsi}_{y}(x,y,\tau)$ and $\tilde{F}(x,y,\tau)$ are defined analogously to $\varPsi_{x}^{*}(x,y)$, $\varPsi_{y}^{*}(x,y)$ and F ^∗(x,y), but is for $\tilde{W}(x,y,\tau)$. If the sandwich-type structure is mid-plane symmetric, no initial thermal bending occurs under uniform temperature field, and in such a case $W^{*}(x,y)=\varPsi_{x}^{*}(x,y)=\varPsi_{y}^{*}(x,y)= F^{*}(x,y)= 0$.

Substituting Eq. (27) into Eqs. (21)–(24), we obtain two sets of equations and can be solved in sequence. The first set of equations yields the particular solution of thermal bending which can be obtained in the similar form as in [40]. The second set of equations gives the homogeneous solution of vibration characteristics on the initial deflected plate that can be expressed by

(28)

(29)

(30)

(31)

(32)

In Eq. (32), ($A_{11}^{(1)}\varepsilon$) is taken as the second perturbation parameter relating to the dimensionless amplitude W _m . From Eq. (28), taking (x,y)=(π/2m,π/2n) yields

$$ A_{11}^{(1)}\varepsilon = \tilde{W}_{m} - \varTheta_{1}\tilde{W}_{m}^{3} + \cdots $$

(33)

Substituting Eq. (33) into Eq. (32), and applying Galerkin procedure, one has

(34)

in which coefficients g ₄₀ to g ₄₃ are all functions of Z and T, and

$$ \bar{\lambda}_{q}(\tau) = \frac{4}{\pi^{2}}\int _{0}^{\pi} \int_{0}^{\pi} \lambda_{q}(x,y,\tau) \sin mx\sin ny\,dx\,dy $$

(35)

All symbols used in Eqs. (28)–(34) are described in detail in Appendix. If zero-valued initial conditions prevail, i.e., $\tilde{W}_{m}(0) = \dot{\tilde{W}}_{m}(0) = 0$, Eq. (34) may then be solved by using the Runge–Kutta iteration scheme. Substituting these solved solutions back into Eqs. (28)–(31), we obtain both displacements and stress function of the plate.

5 Numerical results and discussion

Numerical results are presented in this section for single-layer CNTRC plates and sandwich plates with CNTRC face sheets resting on elastic foundations in thermal environments. We first need to determine the effective material properties of CNTRCs. Poly (methyl methacrylate), referred to as PMMA, is selected for the matrix, and the material properties of which are assumed to be $\rho^{m}=1150~\mathrm{kg/m}^{3}$, ν ^m=0.34, α ^m=45(1+0.0005ΔT)×10⁻⁶/K and E ^m=(3.52−0.0034T) GPa, in which T=T ₀+ΔT and T ₀=300 K (room temperature). In such a way, α ^m=45.0×10⁻⁶/K and E ^m=2.5 GPa at T=300 K. The (10,10) SWCNTs are selected as reinforcements. Han and Elliott [6] chose $E_{11}^{\mathrm{CN}}=600~\mbox{GPa}$, $E_{22}^{\mathrm{CN}}=10~\mbox{GPa}$, $G_{12}^{\mathrm{CN}}=17.2~\mbox{GPa}$ and $\nu_{12}^{\mathrm{CN}}=0.19$ for (10,10) SWCNTs. Such a low value of Young’s modulus is due to the fact that the effective thickness of CNTs is assumed to be 0.34 nm or more. However, a recent report [41] suggested that the effective thickness of SWCNTs should be smaller than 0.142 nm. Therefore, the material properties and effective thickness of SWCNTs need to be properly chosen either by experiments or molecular dynamics (MD) simulations. Typical results are listed in Table 1 [10]. These results confirm that the material properties of CNTs are size-dependent and temperature-dependent. It is noted that the effective wall thickness obtained for (10,10)-tube is 0.067 nm, which satisfies the Vodenitcharova–Zhang criterion [41], and the wide used value of 0.34 nm for tube wall thickness is thoroughly inappropriate for SWCNTs.

Table 1 Temperature-dependent material properties for (10,10) SWCNT (tube length=9.26 nm, tube mean radius=0.68 nm, tube thickness=0.067 nm, $\nu_{12}^{\mathrm{CN}}=0.175$)

The key issue for successful application of the extended rule of mixture to CNTRCs is to determine the CNT efficiency parameter η _j (j=1,2,3) properly. For short fiber composites η ₁ is usually taken to be 0.2 [42]. However, there are no experiments conducted to determine the value of η _j for CNTRCs. In the present study, we estimated the estimation of CNT efficiency parameters η ₁,η ₂, and η ₃ by matching the Young’s moduli E ₁₁ and E ₂₂ and shear modulus G ₁₂ of CNTRCs predicted from the extended rule of mixture to those from the MD simulations given by Han and Elliott [6] and Griebel and Hamaekers [4], as previously reported in [10]. For example, η ₁=0.137,η ₂=1.022 and η ₃=0.715 for the case of $V_{\mathrm{CN}}^{*}=0.12$, and η ₁=0.142,η ₂=1.626 and η ₃=1.138 for the case of $V_{\mathrm{CN}}^{*}=0.17$, and η ₁=0.141,η ₂=1.585 and η ₃=1.109 for the case of $V_{\mathrm{CN}}^{*}=0.28$. These values are used in all the following examples, in which we assume that G ₁₃=G ₁₂ and G ₂₃=1.2G ₁₂ [5].

5.1 Comparison studies

To ensure the accuracy and effectiveness of the present method, three test examples were re-solved for forced vibrations of single-layer isotropic plates and sandwich plates with isotropic or composite face sheets.

Firstly, the curves of central deflection and moment as functions of time for a simply supported isotropic square plate (a/h=10, ν=0.25) subjected to a suddenly applied uniform load resting on a Pasternak foundation are plotted and compared in Fig. 2 with the method of fundamental solution (MFS) results of Wen [43]. In Fig. 2, the dimensionless time is defined by (t/a)[E/2(1+ν)ρ]^1/2, and the dimensionless foundation stiffnesses are defined by $K_{W} = \bar{K}_{1}a^{4}/D$ and $K_{S} = \bar{K}_{2}a^{2}/D$.

Fig. 2

Comparisons of dynamic response of an isotropic plate resting on a Pasternak foundation subjected to a suddenly applied uniform load: (a) Center deflection; (b) Center bending moment

Secondly, the central deflection versus time curves for a sandwich square plate with isotropic face sheets subjected to a suddenly applied uniform load are plotted and compared in Fig. 3 with the FEM results of Ramachandra and Meyer-Piening [44] using their material properties, i.e., E=71.238 GPa, ν=0.33 for the aluminum face sheet, and E _c =60 MPa, G _c =21 MPa, ν _c =0.20 for the PVC foam core. The mass density of the plate is taken to be $\rho = 308.27~\mathrm{kg/m}^{3}$. The sandwich plate is made up of 0.5 mm thick aluminum face sheets and 13 mm thick PVC foam core, and a=b=500 mm. The suddenly applied uniform load has q ₀=40 Pa.

Fig. 3

Comparisons of dynamic response for a sandwich plate with isotropic face sheets subjected to a suddenly applied uniform load

Finally, the curves of central deflection for a square sandwich plate with composite face sheets subjected to a suddenly applied transverse sinusoidal load are plotted and compared in Fig. 4 with the FEM results of Nayak et al. [45]. The sandwich plate has a PVC foam core layer and two face sheets made of 5 plies of graphite-epoxy composites, referred to as (0/90/0/90/0/core/0/90/0/90/0). The computing data adopted are: a=b=1 m, h=0.01 m and face thickness h _F =0.00025 m; E ₁₁=128.0 GPa, E ₂₂=11.0 GPa, ν ₁₂=0.25,G ₁₂=G ₁₃=4.48 GPa, G ₂₃=1.53 GPa, $\rho = 1500~\mathrm{kg/m}^{3}$ for the face sheets, and E _c =0.10363 GPa, ν _c =0.32,G _core=0.050 GPa, $\rho_{c}= 130~\mathrm{kg/m}^{3}$ for the core layer. The transverse sinusoidal load is assumed to be q ₀sin(πX/a)sin(πY/b) where q ₀=1 Pa.

Fig. 4

Comparisons of dynamic response for a (0/90/0/90/0/core/0/90/0/90/0) sandwich plate subjected to a suddenly applied transverse sinusoidal load

These three comparisons show that the present results agree well with existing results. Note that in these examples, the material properties are assumed to be independent of temperature.

5.2 Dynamic response of single-layer CNTRC plates

Parametric studies are first carried out to examine the nonlinear dynamic response of single-layer CNTRC plates with or without elastic foundations in thermal environments. Three types of FG-CNTRC plates, i.e., FG-V, FG-Λ and FG-X, are considered. An UD-CNTRC plate with the same thickness is also considered as a comparator. The plate geometric parameter are taken to be a/b=1, b/h=10, h=2 mm. The deflected mode is taken to be (m,n)=(1,1). The time step for Runge–Kutta iteration method is Δτ=0.2 μs. The dynamic load is assumed to be a suddenly applied uniform load with q ₀=2 MPa. The boundary condition is assumed to be immovable (case 2) except for Figs. 9 and 14.

Table 2 presents the nonlinear to linear frequency ratios ω _NL/ω _L for single layer CNTRC square plates resting on elastic foundations at T=300 and 500 K. The dimensionless frequency is defined by $\tilde{\varOmega} = \varOmega(a^{2}/h)\sqrt{\rho_{0} / E_{0}}$. The CNT volume fraction is taken to be $V_{\mathrm{CN}}^{*}=0.17$. As expected, the fundamental frequencies are increased with increase in foundation stiffness. It can be seen that the fundamental frequencies are reduced, but the nonlinear to linear frequency ratios are increased with increase in temperature. The results show that the fundamental frequencies of FG-X CNTRC plate are higher, but the nonlinear to linear frequency ratios of the same plate are lower than those of plates with uniform or unsymmetrical distribution of CNTs.

Table 2 Nonlinear to linear frequency ratios ω _NL/ω _L for CNTRC square plates resting on elastic foundations in thermal environments (a/b=1.0, b/h=10, h=2 mm, $V_{\mathrm{CN}}^{*}=0.17$)

Figure 5 presents the dynamic response of three types of single layer FG-CNTRC plates and compares with that of the UD-CNTRC plate. The CNT volume fraction is taken to be $V_{\mathrm{CN}}^{*}=0.28$. It can be seen that the FG-CNTRC plate of type X has lowest deflection and largest bending moment, while the FG-CNTRC plate of type V has largest deflection and lowest bending moment among the four. Hence, in the following examples only UD-CNTRC plate and FG-CNTRC plate of Type X are considered.

Fig. 5

Effects of CNT reinforcements on the dynamic response of a single-layer CNTRC plate: (a) Central deflection; (b) Central bending moment

Figure 6 shows the effect of CNT volume fraction $V_{\mathrm{CN}}^{*}$ (=0.12,0.17 and 0.28) on the dynamic response of a single layer FG-CNTRC plate. It can be seen that the central deflections are decreased with increase in CNT volume fraction. In contrast, the bending moments are weakly increased when the CNT volume fraction rises.

Fig. 6

Effect of CNT volume fraction on the dynamic response of a single-layer CNTRC plate: (a) Central deflection; (b) Central bending moment

Figure 7 shows the effect of temperature changes (T=300, 500, and 700 K) on the dynamic response of a single layer FG-CNTRC plate ($V_{\mathrm{CN}}^{*}=0.12$). It can be seen that the curve of central deflection versus time becomes higher, but the curve of bending moment versus time becomes lower when the temperature rises.

Fig. 7

Effect of temperature changes on the dynamic response of a single-layer CNTRC plate in thermal environments: (a) Central deflection; (b) Central bending moment

Figure 8 shows the effect of foundation stiffness on the dynamic response of a single layer FG-CNTRC plate ($V_{\mathrm{CN}}^{*}=0.12$) resting on elastic foundations. Two foundation models are considered. The stiffnesses are (k ₁,k ₂)=(100,10) for the Pasternak elastic foundation, (k ₁,k ₂)=(100,0) for the Winkler elastic foundation and (k ₁,k ₂)=(0,0) for the plate without any elastic foundation. As expected, both central deflections and bending moments are reduced when the foundation becomes stiffer.

Fig. 8

Effect of foundation stiffness on the dynamic response of a single-layer CNTRC plate resting on elastic foundations: (a) Central deflection; (b) Central bending moment

Figure 9 presents the dynamic response of a single layer FG-CNTRC plate with $V_{\mathrm{CN}}^{*}=0.17$ under initial uniaxial in-plane loads. In this example, the in-plane boundary condition is assumed to be movable (case 1). The initial uniaxial edge loads are taken to be P/P _cr=−0.5,0.0, and 0.5, in which P _cr is the critical buckling load for the UD-CNTRC plate under uniaxial compression in the X direction. It can be seen that the initial in-plane compressive load increases both deflection and bending moment of the plate. On the other hand, the initial in-plane tension load softens both deflection and bending moment curves.

Fig. 9

Effect of initial uniaxial in-plane loads P/P _cr on the dynamic response of a single-layer CNTRC plate: (a) Central deflection; (b) Central bending moment

5.3 Dynamic response of sandwich plates with CNTRC face sheets

For all cases below, the plate geometric parameter a/b=1, b/h=10, the thickness of each CNTRC face sheet is identical and the plate is mid-plane symmetric, and the thickness of each CNTRC face sheet h _F =1 mm whereas the thickness of the homogeneous substrate is taken to be h _H =4,6, and 8 mm, so that the core-to-face sheet thickness ratio h _H /h _F =4, 6, and 8, respectively. Titanium alloy, referred to as Ti-6Al-4V is selected for the homogeneous core layer, and the material properties of which are assumed to be nonlinear function of temperature [46], i.e., α _H =7.5788×(1+6.638×10⁻⁴ T−3.147×10⁻⁶ T ²)×10⁻⁶ K and E _H =122.56×(1−4.586×10⁻⁴ T) GPa. Poisson’s ratio is assumed to be a constant, and $\nu_{H}= 0.29.\ \rho_{H}=4429~\mathrm{kg/m}^{3}$.

Table 3 presents the nonlinear to linear frequency ratios ω _NL/ω _L for UD and FG sandwich plates with CNTRC face sheets resting on elastic foundations at T=300 and 500 K. The CNT volume fraction is taken to be $V_{\mathrm{CN}}^{*}=0.17$. The core-to-face sheet thickness ratios are taken to be h _H /h _F =8,6 and 4. It can be seen that the fundamental frequencies are increased, but the nonlinear to linear frequency ratios are decreased with increase in h _H /h _F . The results show that the fundamental frequencies of the sandwich plate with FG-CNTRC face sheets are higher, but the nonlinear to linear frequency ratios of the same plate are lower than those of the plates with UD-CNTRC face sheets.

Table 3 Nonlinear to linear frequency ratios ω _NL/ω _L for sandwich plates with CNTRC face sheets resting on elastic foundations (a/b=1.0, b/h=10, $V_{\mathrm{CN}}^{*}=0.17$)

Figure 10 shows the effect of the core-to-face sheet thickness ratio h _H /h _F (=8,6, and 4) on the dynamic response of sandwich plates with FG-CNTRC face sheets subjected to a suddenly applied uniform load at T=300 K. The CNT volume fraction of CNTRC face sheets is taken to be $V_{\mathrm{CN}}^{*}=0.17$. It can be seen that the sandwich plate with FG-CNTRC face sheets has higher deflection along with higher bending moment when it has higher core-to-face sheet thickness ratio.

Fig. 10

Effect of core-to-face sheet thickness ratio on the dynamic response of sandwich plate with FG-CNTRC face sheets: (a) Central deflection; (b) Central bending moment

Figures 11, 12, 13, 14 are dynamic responses of the sandwich plates with FG-CNTRC face sheets analogous to the dynamic results of Figs. 6, 7, 8, 9, which are for the single-layer CNTRC plates. To compare Figs. 11 and 6, it can be seen that now the effect of CNT volume fraction on the curves of bending moment versus time for the sandwich plate is more pronounced than that for the single layer CNTRC plate. Also, to compare Figs. 12 and 7, it can be seen that now both deflections and bending moments of sandwich plate keep increasing when the temperature rises. Otherwise, they lead to broadly the same conclusions as do Figs. 8 and 9.

Fig. 11

Effect of CNT volume fraction on the dynamic response of a sandwich plate with FG-CNTRC face sheets: (a) Central deflection; (b) Central bending moment

Fig. 12

Effect of temperature changes on the dynamic response of a sandwich plate with FG-CNTRC face sheets in thermal environments: (a) Central deflection; (b) Central bending moment

Fig. 13

Effect of foundation stiffness on the dynamic response of a sandwich plate with FG-CNTRC face sheets resting on elastic foundations: (a) Central deflection; (b) Central bending moment

Fig. 14

Effect of initial uniaxial in-plane loads P/P _cr on the dynamic response of a sandwich plate with FG-CNTRC face sheets: (a) Central deflection; (b) Central bending moment

6 Conclusions

Nonlinear dynamic responses of single-layer CNTRC plates and sandwich plates with CNTRC face sheets resting on a Pasternak elastic foundation in thermal environments have been presented. Two cases of in-plane boundary conditions are considered. Initial stresses caused by thermal loads or in-plane edge loads are examined. The parametric studies have been carried out after three comparisons which demonstrated the accuracy and effectiveness of the present method. The results obtained illustrate that the linear functionally graded CNT reinforcement has a quantitative effect on the nonlinear dynamic responses of CNTRC plates. The numerical results show that the CNT volume fraction, the foundation stiffness and initial stress have a significant effect on the dynamic response of both single-layer CNTRC plate and sandwich plate with CNTRC face sheets. The temperature changes have a significant effect on the deflections of the plate, whereas this effect is less pronounced on the bending moments of the same plate. They also show that the core-to-face sheet thickness ratio has a significant effect on the dynamic response of sandwich plates with CNTRC face sheets.

Appendix

In Eqs. (28)–(31)

(36)

In Eqs. (33) and (34)

(37)

for initially thermal stressed plates (immovable edge condition)

(38)

and for initially compressed stressed plates (movable edge condition)

(39)

in which P _cr is the critical buckling load for the UD plate (or sandwich plate) under uniaxial compression in the X direction, and η is the load proportion ratio, defined by σ _y =ησ _x . In the above equations (with others are defined as in [12]).

(40)