Introduction

Since being first identified in 1991 by Iijima [6], carbon nanotubes (CNTs) have been in high demand in a variety of industries, including mechanical, biomechanics, chemical, aeronautical, electronics, and automobiles [1,2,3,4,5]. CNTs' outstanding chemical and mechanical properties have contributed to the sudden increase in demand. Since graphene sheet is the starting material for CNT production, their mechanical characteristics are comparable [7, 8]. When a single graphene sheet or more than one graphene sheet is rolled together into a concentric cylinder, the CNTs are referred to as single walled carbon nano tubes (SWCNTs) [9, 10] and multi walled carbon nano tubes (MWCNTs) [11].

The mechanical behavior of composite plates, particularly those reinforced with carbon nanotubes (CNTs), has been a subject of extensive research due to the exceptional mechanical properties of CNTs. Previous studies have demonstrated the significant improvements in stiffness, strength, and thermal properties that CNT reinforcement can bring to composite materials. The incorporation of CNTs into polymer matrices has been shown to enhance the overall performance of composite plates, making them suitable for advanced engineering applications [1,2,3,4,5]. Since their discovery by Iijima [6] in 1991, carbon nanotubes (CNTs) have been extensively studied for their exceptional mechanical properties, which are akin to those of graphene, the precursor material for CNT production [7, 8]. CNTs are categorized based on their structure: single-walled carbon nanotubes (SWCNTs) [9, 10], formed by rolling a single graphene sheet into a cylinder, and multi-walled carbon nanotubes (MWCNTs) [11], created by rolling multiple graphene sheets into concentric cylinders. The analysis of composite plates on elastic foundations has garnered significant attention due to the critical role of the interaction between the plate and the foundation in determining structural behavior under various loading conditions. Pasternak's elastic foundation model, which incorporates both shear layer and Winkler modulus parameters, provides a more accurate representation of this interaction compared to the simpler Winkler model (Pasternak, 1954). Recent review articles have synthesized current developments in CNT research, addressing factors such as development, numerical implementation, structural advancement, and applications [12,13,14,15]. Ajayan et al. [16] introduced the initial structural application of CNTs as reinforcement with polymers, leading to their acceptance in elastic structures [17,18,19]. Wattanasakulpong and Ungbhakorn [20] employed several shear deformable theories to provide an analytical solution for the bending analysis of CNTRC beams with Winkler-Pasternak elastic foundations. Their research demonstrated that a functionally graded (FG)-X reinforcement distribution of CNTs effectively counteracts bending responses. Yas and Samadi [21] used Timoshenko beam theory to investigate the free vibration of CNTRC beams, finding that FG-X distribution yields the highest natural frequency. Shen and Xiang [22] used high order shear deformation theory (HSDT) to examine the non-linear bending behavior of CNTRC beams on Winkler elastic foundations. They investigated various CNT distribution patterns, finding that FG-A CNTs generate the highest transverse deflection. They also studied the non-linear bending behavior of CNTRC shells on Pasternak elastic foundations, revealing the impact of volume fraction and foundation parameters on non-linear bending behavior [23]. Additionally, they explored the effect of temperature rise on the natural frequency of CNTRC shells, showing that increased temperature leads to a decrease in natural frequency [24]. Zhang et al. [25] applied element-free IMLS-Ritz methods for non-linear buckling analysis of CNTRC plates on Winkler foundations and conducted non-linear bending analysis for similar systems [26]. Wattanasakulpong and Chaikittiratana [27] used third-order shear deformation theory (TSDT) and sinusoidal shear deformation theory (SSDT) to analyze static and dynamic responses of CNTRC plates with Pasternak elastic foundations, highlighting the effectiveness of FG-X reinforcement in balancing bending responses. Lei et al. [28] employed first-order shear deformation theory (FSDT) to analyze the buckling of CNTRC plates with Pasternak elastic foundations, concluding that volume fraction and foundation parameters significantly influence critical buckling loads. Their vibration analysis further confirmed the impact of these parameters on natural frequency [29]. Zhang and Liew [30] investigated the non-linear bending behavior of CNTRC skew plates on elastic foundations using FSDT, demonstrating the influence of skew angle and foundation parameters. Further studies explored various aspects of CNTRC structures on elastic foundations. Keleshteri et al. [31] analyzed vibration behavior of angular CNTRC plates with piezoelectric layers. Kutlu and Omurtag [32] examined bending behavior of elliptical CNTRC plates, and Duc et al. [33] investigated buckling of angular conical shells on elastic foundations. Ansari et al. [34] utilized the variational differential quadrature method to study free vibration of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) structures. Tham et al. [35] introduced a refined shell theory for analyzing free vibration behavior of multi-layered FG-CNTRC shallow shell panels. Thi et al. [36] applied the cell-based smoothed discrete shear gap method for static and free vibration analysis of CNTRC plates. Zghal et al. [37] explored free vibration in functionally graded composite shell structures reinforced by CNTs. Forooghi et al. [38] investigated stability and vibration properties of FG-SWCNTRC plates using higher-order shear deformation theory and a Visco-Hetenyi medium. Thai et al. [39] developed a size-dependent meshfree model for FG CNTRC nanoplates, integrating higher-order shear deformation plate theory with nonlocal Eringen elasticity theory. They also proposed a NURBS formulation based on refined plate theory for comprehensive analysis of multilayer FG GPLRC plates [40]. Daikh et al. [41] examined thickness stretching effects on multilayer FG CNTRC nanoplates, enhancing understanding of their free vibration, stability, and bending characteristics. Sharma et al. [42] studied buckling and free vibration traits of FG CNT-reinforced plates using an inverse hyperbolic shear deformation theory. Uymaz and Uymaz [43] explored three-dimensional thermal vibration analysis of FG-CNT reinforced composite plates under varying temperature distributions. Li et al. [44] investigated the nonlinear thermally induced vibration in sandwich beams with auxetic honeycomb cores under varied boundary conditions. Using first-order shear deformation theory and considering geometric nonlinearity and temperature effects, it employs finite element analysis and Newton–Raphson–Newmark method. Findings highlight how altering honeycomb geometry and thermal conditions can mitigate vibration, aiding in beam design. Zhang et al. [45] studied the graphene platelet (GPL)-reinforced nanocomposite lattice sandwich plates under supersonic airflow, integrating temperature- and moisture-dependent properties. It assesses GPL distribution and reinforcement in truss cores, employing Halpin–Tsai model for elasticity, and rule of mixture for properties. Flutter analysis via Lagrange method considers aerodynamic loads, emphasizing impacts of temperature, moisture, and GPL parameters on aero-thermo-elastic behavior. Wang et al. [46] employed a nonlinear energy sink (NES) to mitigate nonlinear aeroelastic responses in graphene platelet reinforced composite (GPLRC) lattice sandwich plates under supersonic airflow. It integrates Halpin–Tsai model for material properties, Kirchhoff and shear deformation theories for structural modeling, and Newmark method for analysis, showing effective suppression of flutter behavior with NES intervention. Yang et al. [47] examined the nonlinear free vibration and bifurcation in a carbon fiber-reinforced plastic (CFRP) truncated laminated conical shell using first-order shear deformation theory. It formulates governing equations via Hamilton's principle and Galerkin method, analyzing temperature and shell geometry effects on vibration behavior through parametric investigation. Yang et al. [48] investigated the static bending and buckling behavior of a simply supported truncated sandwich conical shell with a variable thickness core. The core's porous structure varies along its length, influencing system stiffness. Utilizing Hamilton's principle, First-Order Shear Deformation Theory (FSDT), and the Galerkin method, matrix equations are derived to analyze deflections and critical buckling loads under thermal conditions. Static properties and modes of the system are thoroughly examined, considering five different porosity distribution schemes for the foam core. Wang et al. [49] carried out the modelling and analysis for the free vibration of a truncated sandwich conical shell with a variable stiffness system, using a porous aluminum foam core and carbon fiber face sheets under simply supported conditions. It considers various porosity distributions and thermal effects, deriving nonlinear dynamic equations with first-order shear deformation theory and Hamilton’s principle. The study comprehensively examines natural frequencies, mode shapes, and their dependencies on key parameters. Yang et al. [50] investigated the static and dynamic stability of a laminated CFRP cylindrical shell under a non-normal boundary condition. It applies Hamilton's principle and von-Karman relationships with first-order shell theory, deriving equations via the Galerkin method. Stability is analyzed using eigenvalue analysis and the Bolotin method, exploring key influences on stability. Yang et al. [51] investigated the nonlinear dynamic responses and bifurcations of a truncated sandwich conical shell with varying thickness and porous core under 1:1 internal resonance. Using FSDT, von-Karman theory, Hamilton’s principle, and Galerkin method, it explores dynamic formulations, resonance effects, and influences of damping, detuning, temperature, and excitations. Chai et al. [52] carried out the free vibration of variable thickness graphene-reinforced porous cylindrical curved plates under simply supported boundaries. It employs the Halpin–Tsai model, mixing rule, FSDT, and Hamilton's principle to derive nonlinear dynamic equations and determine natural frequencies. Factors influencing frequencies and modal shapes are comprehensively analyzed. Grover et al. [53] proposed a shear deformation theory based on a secant function (SDTSF) for predicting static and dynamic characteristics of laminated composite plates. This theory does not require a shear correction factor as it satisfies the traction-free boundary conditions at the plate's top and bottom surfaces. The investigations confirmed SDTSF's effectiveness in predicting both static and dynamic behavior of laminated composite plates.

It is identified from the literature investigation that a lack of an analytical model for the bending, buckling and free vibration responses of the CNTRC plate resting on the Pasternak's elastic foundation with shear layer and Winkler springs in the framework of non-polynomial shear deformation theory based on secant function. In the current study, An analytical model for the bending, buckling, and free vibration responses of the CNTRC plate resting on the Pasternak's elastic foundation has been provided in order to fill in the informed gap in the literature. The bending, buckling, and free vibration behaviours of the CNTRC plate are examined under a variety of parametric conditions, including different CNTs volume fractions, CNTs distribution patterns, side thickness ratios, and spring constant factors. The bending, free vibration, and buckling of plates are carefully investigated and addressed in this study.

In conclusion, this research advances the understanding of CNTRC plate mechanics on Pasternak's foundations by elucidating the intricate interplay between material composition and foundation characteristics. The findings underscore the potential for tailored designs that optimize structural performance through judicious selection of foundation stiffness and carbon nanotube distribution. Such insights are critical for the development of robust CNTRC-based engineering structures that exhibit enhanced mechanical properties and stability, thereby opening new avenues for their application in demanding technological fields.

Geometrical Models and Properties

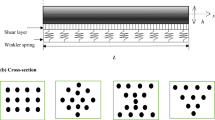
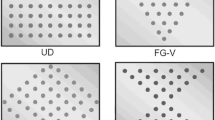
Figure 1 represents the CNTRC plate resting on the Pasternak elastic foundation with the Winkler spring and shear layer. The selected CNTRC plate includes the following dimensions: (a), (b), and (h) as length, width, and height respectively. Here, multiple dispersions of CNTs patterns that have been uniaxially aligned across the thickness of the CNTRC plate are taken into consideration for the study. For UD, FG-X, and FG-O reinforced CNTRC plates, the CNTs distribution patterns are symmetrical; for FG-V reinforced CNTRC plates, they are asymmetrical. Figure 2 displays the cross sections of the CNTRC plate with various CNTs dispersion patterns.

Fig. 1
figure 1

CNTRC plate resting on the Pasternak’s elastic foundation

Full size image
Fig. 2
figure 2

Cross section of CNTRC plate with different distribution pattern of CNTs a UD b FG-V c FG-X d FG-O

Full size image

Due to the different categories CNTs dispersion patterns throughout the plate's thickness, the mechanical properties of CNTRC plates change along with thickness. Table 1 lists the mathematical relationships that describe the different types of reinforcing distribution throughout the thickness of the composite plates. Table 2 lists the mechanical properties of the different elements of the CNTRC plate, specifically SWCNTs as reinforcement fibre and PmPV (methyl methacrylate-co-polyvinyl acetate) as the polymer matrix. The volume fraction of the CNTs influences the effectiveness of CNTRC plate. In Table 3, the efficiency parameter, ηi, for various CNTs volume fractions are listed.

Table 1 Distribution relationship of CNTRC plates
Full size table
Table 2 Material properties used for CNTRC plates
Full size table
Table 3 CNTs efficiency parameter for PmPV (M2)/CNT
Full size table

Rule of mixture (ROM) has been employed for analysing the mechanical properties of CNTRC plate and it is described as follows:

$$E_{11} = (\eta_1 )V_{CNT} E_{11}^{CNT} + V_m E^m$$
(1a)
$$\frac{(\eta_2 )}{{E_{22} }} = \frac{{V_{CNT} }}{{E_{22}^{CNT} }} + \frac{V_m }{{E^m }}$$
(1b)
$$\frac{(\eta_3 )}{{G_{12} }} = \frac{{V_{CNT} }}{{G_{22}^{CNT} }} + \frac{V_m }{{G^m }}$$
(1c)
$$v_{12} = V_{CNT}^* v_{12}^{CNT} + V_m v^m$$
(1d)
$$\rho = V_{CNT} \rho^{CNT} + V_m \rho^m$$
(1e)

where, E11, \({E}_{11}^{CNT}\), Em, E22 and \({E}_{22}^{CNT}\) are the Young’s moduli. G12, \({G}_{12}^{CNT}\) and Gm are the shear modulus. υ12, \({\upsilon }_{12}^{CNT}\) and υm are the Poisson’s ratios. \({V}_{CNT}^{*}\) and Vm are the volume fraction of CNTs and isotropic matrix. ηi (i = 1–3) is the coefficients of the CNTs efficiency parameters.

$$V_{CNT}^* + V_m = 1$$
(2)

where, \({V}_{CNT}^{*}\) is expressed as,

$$V_{CNT}^* = \frac{{w_{CNT} }}{{w_{CNT} + (\rho^{CNT} /\rho^m ) - (\rho^{CNT} /\rho^m )w_{CNT} }}$$
(3)

where wCNT is the mass fraction of the CNTs.

Mathematical Formulations

Displacement Field

The displacement field for non-polynomial shear deformation theory based on secant function [44] is chosen in order to forecast both the static and dynamic behaviour of the CNTRC plate supported by the Pasternak’s elastic foundation. The non-polynomial trigonometric function is selected here in such a way that it generates a non-linear distribution of transverse shear stresses. The transverse shear stress boundary conditions are implemented so that the transverse shear stresses at the boundary vanish, and this allows us to assess a constant parameter. Thus, the shear correction factor is no longer necessary because the considered non-polynomial displacement field fulfils the traction-free boundary conditions at the top and bottom of the plate.

$$\left[ {\begin{array}{*{20}c} {u(x,y,z,t)} \\ {v(x,y,z,t)} \\ {w(x,y,z,t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u_0 (x,y,t)} \\ {v_0 (x,y,t)} \\ {w_0 (x,y,t)} \\ \end{array} } \right] - z\left[ {\begin{array}{*{20}c} {\frac{\partial w_0 (x,y,t)}{{\partial x}}} \\ {\frac{\partial w_0 (x,y,t)}{{\partial y}}} \\ 0 \\ \end{array} } \right] + f(z)\left[ {\begin{array}{*{20}c} {\theta_x (x,y,t)} \\ {\theta_y (x,y,t)} \\ 0 \\ \end{array} } \right]$$
(4)

where \(u_0\), \(v_0\), \(w_0\), and \(\theta_x\),\(\theta_y\) are the displacement and shear deformations at the mid plane, respectively. f(z) = g(z) + Ωz in which g(z) = z(sec(rz/h)) and Ω = −sec(r/2) [1 + (r/2) tan(r/2)]. The value of the transvers shear stress parameter i.e. r = 0.1.

The strain in conjunction with the displacement field is expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\partial u_0 }{{\partial x}}} \\ {\frac{\partial v_0 }{{\partial y}}} \\ {\left( {\frac{\partial u_0 }{{\partial y}} + \frac{\partial v_0 }{{\partial x}}} \right)} \\ \end{array} } \right] - z\left[ {\begin{array}{*{20}c} {\frac{\partial^2 w_0 }{{\partial x^2 }}} \\ {\frac{\partial^2 w_0 }{{\partial y^2 }}} \\ {\frac{2\partial^2 w_0 }{{\partial x\partial y}}} \\ \end{array} } \right] + [g(z) + \Omega z]\left[ {\begin{array}{*{20}c} {\frac{\partial \theta_x }{{\partial x}}} \\ {\frac{\partial \theta_y }{{\partial y}}} \\ {\left( {\frac{\partial \theta_x }{{\partial y}} + \frac{\partial \theta_y }{{\partial x}}} \right)} \\ \end{array} } \right]$$
(5a)
$$\left[ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right] = f^{\prime}(z)\left[ {\begin{array}{*{20}c} {\theta_x } \\ {\theta_y } \\ \end{array} } \right]$$
(5b)

The stress in conjunction with the strain is expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\sigma_{_{xx} } } \\ {\sigma_{_{yy} } } \\ {\tau_{xy} } \\ {\tau_{_{yz} } } \\ {\tau_{_{xz} } } \\ \end{array} } \right]_n = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {Q_{16} } & 0 & 0 \\ {Q_{21} } & {Q_{22} } & {Q_{26} } & 0 & 0 \\ {Q_{16} } & {Q_{26} } & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & {Q_{45} } \\ 0 & 0 & 0 & {Q_{45} } & {Q_{55} } \\ \end{array} } \right]_n \left[ {\begin{array}{*{20}c} {\varepsilon_{_{xx} } } \\ {\varepsilon_{_{yy} } } \\ {\gamma_{_{xy} } } \\ {\gamma_{_{yz} } } \\ {\gamma_{_{xz} } } \\ \end{array} } \right]_n$$
(6)

where, [Q]n is known as the reduced stiffness matrix and it is used to relate the stress and strain vectors of the nth layer. The elements of reduced stiffness matrix are the functions of material properties E11, E22, G12, G23, G13, and ν12 which are function of thickness co-ordinate and depend upon the distribution of CNTs across the thickness. These elements are defined as

$$\begin{gathered} Q_{11} (z) = \frac{{E_{11} (z)}}{{1 - \nu_{12} (z)\nu_{21} (z)}}, \, Q_{22} (z) = \frac{{E_{22} (z)}}{{1 - \nu_{12} (z)\nu_{21} (z)}}, \, Q_{12} (z) = \frac{{\nu_{21} (z)E_{11} (z)}}{{1 - \nu_{12} (z)\nu_{21} (z)}}, \, Q_{66} (z) = G_{12} (z) \hfill \\ \, Q_{44} (z) = G_{23} (z), \, Q_{55} (z) = G_{13} (z) \hfill \\ \end{gathered}$$

Equation of Motion

The equation of motion of the CNTRC plate with Pasternak’s elastic basis is derived using Hamilton's principle.

$$\int_{ - h/2}^{h/2} {(\delta L)dt = 0}$$
(7)

where δL = δT − (δUs + δVf + δV); δT, δUs, δVf, and δV are the change in kinetic energy, change in strain energy, change in potential energy of elastic foundation and change in potential energy due to external applied load, respectively.

The change in the kinetic energy of the system is expressed as follows:

$$\delta T = \int_{\Omega_0 } {\left\{ {\int_{ - \frac{h}{2}}^\frac{h}{2} {\rho [\dot{u}\delta \dot{u} + \dot{v}\delta \dot{v} + \dot{w}\delta \dot{w}]} dz} \right\}} dxdy$$
(8)

The change in the strain energy of the system is expressed as follows:

$$\delta U = \int_{\Omega_0 } {\left\{ {\int_{ - \frac{h}{2}}^\frac{h}{2} {[\sigma_{xx} \delta \in_{xx} + \sigma_{yy} \delta \in_{yy} + \tau_{xy} \delta \gamma_{xy} + \tau_{yz} \delta \gamma_{yz} + \tau_{zx} \delta \gamma_{zx} ]} dz} \right\}} dxdy$$
(9)

where, \(\delta \in\) is the small variation in the strain at any point in the nth lamina defined in the material coordinate’s axes system.

The change in the potential energy of the system due to external applied load is expressed as follows:

$$\delta V = \int_{\Omega_0 } {q\delta w_0 } dxdy$$
(10)

The change in the potential energy of the system due to Pasternak elastic foundation is expressed as follows:

$$\delta V_f = \int_{\Omega_0 } {k_w w_0 \delta w_0 } dxdy + \int_{\Omega_0 } {k_s (\frac{\partial w_0 }{{\partial x}}\frac{\partial \delta w_0 }{{\partial x}} + \frac{\partial w_0 }{{\partial y}}\frac{\partial \delta w_0 }{{\partial y}})} dxdy$$
(11)

where Kw and Ks are the Winkler and shear layer spring constants, respectively

$$K_w = \frac{\beta_w D_0 }{{a^4 }}$$
$$K_s = \frac{\beta_s D_0 }{{a^2 }}$$
$$D_0 = \frac{E^p h^3 }{{12[1 - (\nu^p )^2 ]}}$$

here, βw and βs are the Winkler and shear layer spring constant factor, respectively.

The CNTRC plate with Pasternak elastic foundation is subjected to the transverse load q, which is the bending load and the in-plane compressive load of ΨxNcr and ΨyNcr which is the buckling load in x and y direction, respectively. The total potential energy of the system due to external applied load is expressed as follows:

$$\delta V_T = - \int_{\Omega_0 } {q\delta w_0 } dxdy + \int_{\Omega_0 } {(\psi_x N_{cr} \frac{\partial w_0 }{{\partial x}}\frac{\partial \delta w_0 }{{\partial x}} + \psi_y N_{cr} \frac{\partial w_0 }{{\partial y}}\frac{\partial \delta w_0 }{{\partial y}})} dxdy$$
(12)

The mid-plane displacement and rotation coefficients are separated, and the variation of the system's energies from Eqs. (8) to (12) is substituted in Eq. (7), Partial differential equation terms of the primary variables are separated for different displacement modes derived at the mid plane are shown in Appendix A. This process results in the development of the governing differential equation for the CNTRC plate with Pasternak’s elastic foundation, which is as follows:

$$\delta u_0 :\frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_0 {\mathop {u_0 }\limits^{..}} - I_1 \frac{{\partial {\mathop {w_0 }\limits^{..}} }}{\partial x} + I_3 {\mathop {\theta_x }\limits^{..}}$$
(13a)
$$\delta v_0 :\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = I_0 {\mathop {v_0 }\limits^{..}} - I_1 \frac{{\partial {\mathop {w_0 }\limits^{..}} }}{\partial y} + I_3 {\mathop {\theta_y }\limits^{..}}$$
(13b)
$$\begin{gathered} \delta w_0 :\frac{{\partial^2 M_{xx} }}{\partial x^2 } + 2\frac{{\partial^2 M_{xy} }}{\partial x\partial y} + \frac{{\partial^2 M_{yy} }}{\partial y^2 } + q - k_w w_0 + k_s \frac{\partial^2 w_0 }{{\partial x^2 }} + k_s \frac{\partial^2 w_0 }{{\partial y^2 }} + \overline{N}_{xx} \frac{\partial^2 w_0 }{{\partial x^2 }} + 2\overline{N}_{xy} \frac{\partial^2 w_0 }{{\partial x\partial y}} + \overline{N}_{yy} \frac{\partial^2 w_0 }{{\partial y^2 }} = \hfill \\ I_1 \left( {\frac{{\partial \ddot{u}_0 }}{\partial x} + \frac{{\partial \ddot{v}_0 }}{\partial y}} \right) - I_2 \left( {\frac{{\partial^2 \ddot{w}_0 }}{\partial x^2 } + \frac{{\partial^2 \ddot{w}_0 }}{\partial y^2 }} \right) + I_4 \left( {\frac{{\partial {\mathop {\theta_x }\limits^{..}} }}{\partial x} + \frac{{\partial \ddot{\theta }_y }}{\partial y}} \right) + I_0 \ddot{w}_0 \hfill \\ \end{gathered}$$
(13c)
$$\delta \theta_x :\Omega \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial P_{xx} }}{\partial x} + \Omega \frac{{\partial M_{xy} }}{\partial y} + \frac{{\partial P_{xy} }}{\partial y} - \Omega Q_1 - K_1 = I_3 {\mathop {u_0 }\limits^{..}} - I_4 \frac{{\partial {\mathop {w_0 }\limits^{..}} }}{\partial y} + I_5 {\mathop {\theta_x }\limits^{..}}$$
(13d)
$$\delta \theta_y :\Omega \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial P_{xy} }}{\partial x} + \Omega \frac{{\partial M_{yy} }}{\partial y} + \frac{{\partial P_{yy} }}{\partial y} - \Omega Q_2 - K_2 = I_3 {\mathop {v_0 }\limits^{..}} - I_4 \frac{{\partial {\mathop {w_0 }\limits^{..}} }}{\partial y} + I_5 {\mathop {\theta_y }\limits^{..}}$$
(13e)

The moment resultants associated with the governing differential equation of the CNTRC plate with Pasternak elastic foundation Eq. (13) is as follows:

$$\left[ {\begin{array}{*{20}c} {N_{xx} } & {M_{xx} } & {P_{xx} } \\ {N_{yy} } & {M_{yy} } & {P_{yy} } \\ {N_{xy} } & {M_{xy} } & {P_{xy} } \\ \end{array} } \right] = \int_{h_k }^{h_{k + 1} } {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right\}} [1 \, z \, g(z)] \, dz$$
(14)
$$\left[ {\begin{array}{*{20}c} {Q_2 } & {K_2 } \\ {Q_1 } & {K_1 } \\ \end{array} } \right] = \int_{h_k }^{h_{k + 1} } {\left\{ {\begin{array}{*{20}c} {\tau_{yz} } \\ {\tau_{xz} } \\ \end{array} } \right\}} [1 \, g^{\prime}(z)] \, dz$$
(15)
$$[I_0 \, I_1 \, I_2 \, I_3 \, I_4 \, I_5 ] = \int_{h_k }^{h_{k + 1} } {\rho^{(k)} } [1 \, z \, z^2 \, f(z) \, z.f(z) \, (f(z))^2 ] \, dz$$
(16)
$$[A_{ij} \, B_{ij} \, D_{ij} \, E_{ij} \, F_{ij} \, H_{ij} ] = \int_{h_k }^{h_{k + 1} } {\left[ {{\overline{Q}}_{ij}^{(k)} } \right]} \, [1 \, z \, z^2 \, g(z) \, z.g(z) \, (g(z))^2 ] \, dz$$
(17)

for i, j = 1, 2, and 3.

$$[K_{ij} \, L_{ij} ] = \int_{h_k }^{h_{k + 1} } {\left[ {{\overline{Q}}_{ij}^{(k)} } \right]_{2 \times 2} } \, [g^{\prime}(z) \, (g^{\prime}(z))^2 ] \, dz$$
(18)

for i, j = 4 and 5.

Analytical Solution Methodology

Using Navier's method, the governing differential equation of the CNTRC plate with the Pasternak elastic foundation Eq. (13) is solved. The CNTRC plate is simply supported from all four sides using the following boundary requirements.

$$\begin{gathered} {\text{at }}y\, = \,0,y\, = \,b\left( {{\text{parallel to }}x\;{\text{axis}}} \right) \hfill \\ u_0 = 0, \, w_0 = 0, \, \theta_x = 0, \, N_{yy} = 0, \, M_{yy} = 0, \, P_{yy} = 0. \hfill \\ {\text{at }}x\, = \,0,x\, = \,l\left( {{\text{parallel to }}y\;{\text{axis}}} \right) \hfill \\ v_0 = 0, \, w_0 = 0, \, \theta_y = 0, \, N_{xx} = 0, \, M_{xx} = 0, \, P_{xx} = 0. \hfill \\ \end{gathered}$$
(19)

The displacement variables are assumed in such a way that it satisfies the above mentioned boundary condition requirements.

$$u_0 = \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {u_{0_{mn} } e^{i\omega t} cos(\alpha x)sin(\beta y)} }$$
(20a)
$$v_0 = \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {v_{0_{mn} } e^{i\omega t} \sin (\alpha x)\cos (\beta y)} }$$
(20b)
$$w_0 = \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {w_{0_{mn} } e^{i\omega t} \sin (\alpha x)\sin (\beta y)} }$$
(20c)
$$\theta_x = \, \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {\theta_{x_{mn} } e^{i\omega t} \cos (\alpha x)\sin (\beta y)} }$$
(20d)
$$\theta_y = \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {\theta_{y_{mn} } e^{i\omega t} \sin (\alpha x)\cos (\beta y)} }$$
(20e)

where, \(u_{0_{mn} }\), \(v_{0_{mn} }\), \(w_{0_{mn} }\), \(\theta_{x_{mn} }\) and \(\theta_{y_{mn} }\) are the arbitrary parameter, ω is the natural frequency α = mπ/a, and β = mπ/b.

The transverse load q is defined as follow:

$$q_0 = \sum_{m = 1}^\infty {\sum_{n = 1}^\infty {q\sin (\alpha x)\cos (\beta y)} }$$
(21)

The simultaneous equation for static and dynamic analysis is obtained by substituting the assumed displacement variables from Eq. (20) into the governing differential equations of CNTRC plate resting on Pasternak's elastic foundation Eq. (13) that governs the CNTRC plate. This equation is as follows:

$$\left\{ {\left[ K \right]_{5 \times 5} - \omega^2 \left[ M \right]_{5 \times 5} } \right\}\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_0 } \\ {v_0 } \\ \end{array} } \\ {w_0 } \\ {\theta_x } \\ {\theta_y } \\ \end{array} } \right\}_{5 \times 1} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ q \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right\}_{5 \times 1}$$
(22)

where, [K] and [M] are the stiffness and mass matrix respectively, and the coefficients of mass matrix is discussed in Appendix B.

The in-plane compressive lode and natural frequency are removed from Eq. (22) for the static analysis of the CNTRC plate with Pasternak’s elastic foundation, and Eq. (22) is then transformed into the simultaneous equation for the static analysis of the CNTRC plate with Pasternak elastic foundation. The determent of the coefficient of the load vector is equal to zero to produce the set of homogeneous equations for the buckling and free vibration analysis of the CNTRC plate with Pasternak’s elastic basis. As an Eigen-value problem, the derived homogeneous equations are resolved.

Simultaneous Equations for Static and Dynamic Analysis

The simultaneous equation for static analysis of the CNTRC plate with Pasternak elastic foundation is mentioned as follows:

$$\left[ K \right]_{5 \times 5} \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_0 } \\ {v_0 } \\ \end{array} } \\ {w_0 } \\ {\theta_x } \\ {\theta_y } \\ \end{array} } \right\}_{5 \times 1} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ q \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right\}_{5 \times 1}$$
(23)

The simultaneous equation for the buckling analysis of the CNTRC plate with Pasternak elastic foundation is mentioned as follows:

$$\left\{ {\left[ K \right]_{5 \times 5} - N_{cr} \left[ G \right]_{5 \times 5} } \right\}\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_0 } \\ {v_0 } \\ \end{array} } \\ {w_0 } \\ {\theta_x } \\ {\theta_y } \\ \end{array} } \right\}_{5 \times 1} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right\}_{5 \times 1}$$
(24)

where, Ncr and [G] are the buckling load, and geometric stiffness matrix, respectively.

The governing equation for the vibration analysis of the CNTRC plate with Pasternak elastic foundation is mentioned as follows:

$$\left\{ {\left[ K \right]_{5 \times 5} - \omega^2 \left[ M \right]_{5 \times 5} } \right\}\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_0 } \\ {v_0 } \\ \end{array} } \\ {w_0 } \\ {\theta_x } \\ {\theta_y } \\ \end{array} } \right\}_{5 \times 1} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right\}_{5 \times 1}$$
(25)

Results and Discussions

The findings of the banding, buckling and free vibration analysis of the CNTRC plate with the Pasternak’s elastic foundation are carried out in detail in this part. The following non-dimensional parameter is used to provide the findings in dimensionless form.

$$\overline{w} = \frac{10^3 D_0 w}{{a^4 q_0 }}\left( {\frac{a}{2},\frac{b}{2},\frac{h}{2}} \right)$$
(26)
$$\overline{\sigma }_{xx} = \sigma_{xx} \frac{h^2 }{{a^2 q_0 }}\left( {\frac{a}{2},\frac{b}{2},\frac{h}{2}} \right)$$
(27)
$$\overline{\tau }_{xz} = \tau_{xz} \frac{h^2 }{{a^2 q_0 }}\left( {\frac{a}{2},0,0} \right)$$
(28)
$$\overline{\tau }_{xy} = \tau_{xy} \frac{h^2 }{{a^2 q_0 }}\left( {a,b,\frac{h}{2}} \right)$$
(29)
$$\overline{\omega } = \omega \frac{a^2 }{h}\sqrt {{\frac{\rho^m }{{E^m }}}} \,$$
(30)
$$D_0 = \frac{E^p h^3 }{{12[1 - (\nu^p )^2 ]}};\,\quad \overline{N}_{cr} = N_{cr} \frac{a^2 }{{\pi^2 D_0 }}$$
(31)

Static Analysis

This section goes into extensive detail on the static analysis of the CNTRC plate resting on Pasternak’s elastic base.

Table 4 investigates the non-dimensional transverse displacement for the variations in CNTs distributions, considering different thickness ratios, CNT volume fractions, and spring constant factors. The FG-V, FG-O, and FG-X distributions, along with the UD distribution, are specifically analyzed in the context of CNTRC plates with and without a Pasternak’s elastic foundation. These plates are composed of CNT fibers within a poly (methyl methacrylate)-polyvinylidene fluoride (PmPV) matrix. The analysis focuses on a square CNTRC plate with simple supported boundary conditions under sinusoidal loading. The findings are presented using a non-dimensional parameter as defined by Eq. (26). The non-dimensional transverse displacement data from this study are compared with those reported by Wattanasakulpong and Chaikittiratana [27]. For a side-to-thickness ratio of 10, the results align closely with those of Wattanasakulpong and Chaikittiratana [27]. It is apparent that among the reinforcement distributions examined UD, FG-O, FG-V, and FG-X, the FG-X distribution exhibits superior performance in minimizing non-dimensional transverse displacement, effectively countering bending responses in both the presence and absence of a Pasternak’s elastic foundation. This superior performance can be attributed to the optimal gradation of CNTs in the FG-X distribution, which enhances the stiffness and load-bearing capacity of the plate more effectively than the other distributions. The table also demonstrates that as the system stiffness increases, due to higher Winkler and shear layer spring constant factors, the non-dimensional transverse displacement of CNTRC plates with Pasternak’s elastic foundations decreases. Additionally, increasing the volume fraction of CNTs enhances the stiffness of the CNTRC plate for various CNTs distribution patterns. The higher CNT volume fraction increases the composite's overall rigidity, leading to a reduction in transverse displacement.

Table 4 Dimensionless deflection \(\overline{w }\left(\frac{a}{2};\frac{b}{2};\frac{h}{2}\right)\) of CNTRC plate with and without elastic foundation
Full size table

The non-dimensional transverse deflection of the CNTRC plate on a Pasternak elastic foundation is influenced by variations in the side-to-thickness ratio, as illustrated in Fig. 3. The study delves into non-dimensional transverse displacement variations across diverse CNT distributions, considering different thickness ratios and CNT volume fractions as 0.14 along with this the Winkler spring constant factors and shear layer spring constant factors set at 100 and 50, respectively. It scrutinizes FG-V, FG-O, FG-X, and UD distributions within the CNTRC plate. The analysis involves a square CNTRC plate with simple supported boundary conditions under sinusoidal loading, with findings expressed through a non-dimensional parameter specified in Eq. (26). Analysis indicates that among the UD, FG-V, and FG-O reinforcement distributions, the FG-X reinforcement distribution in the composite plate with a Pasternak’s elastic foundation results in the minimal transverse deflection. This superior performance of the FG-X distribution can be physically explained by the optimal gradation of CNTs, which enhances the stiffness and load-bearing capacity of the plate more effectively than other distributions. The FG-X distribution provides a more uniform distribution of stress and strain across the plate, thereby reducing localized bending and deformation. Additionally, the non-dimensional transverse displacement decreases with increasing system stiffness due to higher Winkler and shear layer spring constant factors. This behavior is due to the increased resistance provided by the stiffer foundation, which mitigates the bending and deflection of the plate under transverse loading. The stiffer foundation effectively supports the plate, distributing the load more evenly and reducing overall displacement.

Fig. 3
figure 3

The effect of side to thickness ratio on non-dimensional transverse deflection \(\overline{w }\) on CNTRC plate resting on the Pasternak’s elastic foundation

Full size image

The non-dimensional transverse deflection of the CNTRC plate on a Pasternak elastic foundation varies with the variations in the Winkler spring constant factors and shear layer spring constant factors, as depicted in Fig. 4. This study investigates the non-dimensional transverse displacement across different CNT distributions, considering thickness ratios as 10 and a CNT volume fraction of 0.17. The analysis examines FG-V, FG-O, FG-X, and UD distributions within the CNTRC plate. A square CNTRC plate with simply supported boundary conditions under sinusoidal loading is analyzed, with results presented using a non-dimensional parameter specified in Eq. (26). The figure shows that the non-dimensional transverse deflection of a CNTRC plate with a Pasternak’s elastic foundation reduces when the Winkler spring constant factors and shear layer spring constant factors are increased, due to increase in the stiffness of the system. The higher CNT volume fraction increases the composite's overall rigidity, leading to a reduction in transverse displacement. This enhancement in stiffness is due to the superior mechanical properties of CNTs, which improve the load-carrying capacity and structural integrity of the composite plate.

Fig. 4
figure 4

The effect of different spring constant factors on non-dimensional transverse deflection \(\overline{w }\) on CNTRC plate resting on the Pasternak’s elastic foundation

Full size image

Figure 5 illustrates the effect of non-dimensional axial stress variation across the thickness of a CNTRC plate resting on a Pasternak’s elastic foundation. This examines non-dimensional axial stress variations among different CNT distributions, considering span thickness ratios as 10 and CNTs volume fractions as 0.11 along with this Winkler and shear layer spring constants of 100 and 50, respectively. It analyzes FG-V, FG-O, FG-X, and UD distributions within CNTRC plates. The study focuses on a square CNTRC plate with simple supported boundary conditions under sinusoidal loading, presenting results via a non-dimensional parameter defined in Eq. (27). The figure reveals that the axial stress profile is symmetrical for symmetric CNT distribution patterns, such as UD, FG-X, and FG-O, across the mid-plane of the plate. In contrast, it is asymmetrical for the FG-V distribution pattern. The distribution patterns of CNTs across the thickness significantly influence the axial stress variation. Specifically, the FG-V distribution shows the highest axial stress at the top of the plate, approaching zero at the bottom. Similarly, the FG-O distribution results in an axial stress profile that approaches zero at both the top and bottom of the plate due to minimal CNT concentration in these regions. At the midpoint of the CNTRC plate, the axial stress profile is zero for the UD, FG-X, and FG-O distributions but non-zero for the FG-V distribution. This behavior is due to the symmetrical CNT distribution in the UD, FG-X, and FG-O patterns, and the asymmetrical distribution in the FG-V pattern. These findings highlight the importance of CNT distribution patterns in influencing the stress response of CNTRC plates. The choice of distribution pattern can significantly affect the stress profile, which in turn impacts the overall structural performance and reliability of the composite plate.

Fig. 5
figure 5

The variation of non-dimensional axial stress \({\bar{\sigma }}_{xx }\) across the thickness of CNTRC plate resting on the Pasternak’s elastic foundation for different distribution of CNTs

Full size image

Figure 6 depicts the variation of non-dimensional axial stress across the thickness of a CNTRC plate with FG-X CNT distribution, supported by a Pasternak’s elastic foundation. The analysis is performed on a square CNTRC plate with simple supported boundary conditions under sinusoidal loading. Findings are reported using a non-dimensional parameter described in Eq. (27). The variation of non-dimensional axial stress across the thickness of a CNTRC plate under different Winkler and shear layer spring constant factors demonstrates that as the values of the Winkler and shear layer spring constant factors increase, the non-dimensional axial stress decreases. These findings highlight the significant role of foundation stiffness and CNT distribution patterns in influencing the stress response of CNTRC plates. By selecting appropriate foundation parameters and CNT distributions, the structural performance and durability of CNTRC plates can be significantly improved.

Fig. 6
figure 6

The variation of non-dimensional axial stress \({\bar{\sigma }}_{xx }\) across the thickness of CNTRC plate resting on the Pasternak’s elastic foundation for FG-X CNTs distribution with different spring constant factors

Full size image

Figure 7 presents the fluctuation of non-dimensional transverse shear stress across the thickness of the CNTRC plate resting on a Pasternak elastic foundation. The analysis considers a side-to-thickness ratio of 10 and various CNT dispersion patterns, with a CNT volume fraction of 0.14, and Winkler and shear layer spring constant values of 100 and 50, respectively. The analysis involves a square CNTRC plate with simple supported boundary conditions and sinusoidal loading. Findings are expressed using a non-dimensional parameter specified in Eq. (28). The figure reveals that the transverse shear stress profile is symmetrical for symmetric CNT distribution patterns, such as UD, FG-X, and FG-O, across the mid-plane of the plate, while it is asymmetrical for the FG-V distribution. The distribution of CNTs significantly affects the transverse shear stress variation across the thickness. The FG-O distribution exhibits the highest non-dimensional transverse shear stress, whereas the FG-X distribution shows the lowest. These findings highlight the importance of selecting appropriate CNT distribution patterns to optimize the shear stress response of CNTRC plates. The choice of distribution pattern can significantly influence the transverse shear stress profile, impacting the overall structural performance and reliability of the composite plate.

Fig. 7
figure 7

The effect of variation of non-dimensional transverse shear stress \({\overline{\tau }}_{xz }\) across the thickness of CNTRC plate resting on the Pasternak’s elastic foundation for different distribution of CNTs

Full size image

Buckling Analysis

This section goes into comprehensive detail on the buckling analysis of the CNTRC plate with Pasternak’s elastic foundation under uniaxial and biaxial compressive stresses.

Table 5 presents the dimensionless critical buckling load of a CNTRC plate, both with and without a Pasternak’s elastic foundation, under a uniaxial compressive load (Ψx = −1, Ψy = 0). This research focuses on the variations in non-dimensional critical buckling load under a uniaxial compressive load (Ψx = −1, Ψy = 0) across different distributions of carbon nanotubes (CNTs), examining diverse thickness ratios and CNT volume fractions. The study scrutinizes FG-V, FG-O, and FG-X distributions, in addition to the UD distribution, within CNTRC plates. The analysis is conducted on a square CNTRC plate with simple supported boundary conditions subjected to sinusoidal loading. Results are reported using a non-dimensional parameter outlined in Eq. (31). The dimensionless critical buckling loads obtained are compared with those reported by Wattanasakulpong and Chaikittiratana [27], showing good agreement for a side-to-thickness ratio of 10. The table indicates that the FG-X CNT reinforcement distribution provides the highest dimensionless critical buckling load under a uniaxial compressive load (Ψx = −1, Ψy = 0), followed by the UD and FG-O distributions, for both the CNTRC plate with and without the Pasternak’s elastic foundation. The influence of the Winkler and shear layer spring constant factors is evident from the data due to which the lateral stiffness of the system increases due to higher Winkler and shear layer spring constant factors, the dimensionless critical buckling load under a uniaxial compressive load (Ψx = −1, Ψy = 0) also increases for the CNTRC plate with a Pasternak’s elastic foundation. Similarly, increasing the volume fraction of CNTs enhances the stiffness and, consequently, the dimensionless critical buckling load. These findings highlight the importance of selecting appropriate CNT distribution patterns and foundation stiffness parameters to optimize the buckling resistance of CNTRC plates. The choice of distribution pattern and foundation parameters can significantly influence the critical buckling load, impacting the overall structural performance and reliability of the composite plate.

Table 5 Dimensionless critical buckling load \({\overline{N} }_{cr}\) under uniaxial compressive load (Ψx = −1, Ψy = 0) for CNTRC plate with and without elastic foundation
Full size table

Table 6 shows the dimensionless critical buckling load under a biaxial compressive load (Ψx = −1, Ψy = −1). This analysis explores non-dimensional critical buckling load under a biaxial compressive load variation among various distributions of carbon nanotubes (CNTs), considering different thickness ratios and CNT volume fractions. FG-V, FG-O, and FG-X distributions, as well as UD distribution, are examined within the framework of CNTRC plates. The study focuses on a square CNTRC plate with simple supported boundary conditions under sinusoidal loading, presenting results through a non-dimensional parameter described in Eq. (31). Again, the results are compared with those of Wattanasakulpong and Chaikittiratana [27], and the agreement is satisfactory. A comparison of Tables 5 and 6 reveals that the dimensionless critical buckling loads under biaxial compressive loading are lower than those under uniaxial compressive loading for the same CNT volume fractions, distribution patterns, and spring constant factors. These findings underscore the importance of selecting appropriate CNT distribution patterns and foundation stiffness parameters to optimize the buckling resistance of CNTRC plates under various loading conditions. The choice of distribution pattern and foundation parameters can significantly influence the critical buckling load, impacting the overall structural performance and reliability of the composite plate.

Table 6 Dimensionless critical buckling load \({\overline{N} }_{cr}\) under bi axial compressive load (Ψx = −1, Ψy = −1) for CNTRC plate with and without elastic foundation
Full size table

Figure 8 illustrates the effect of varying the Winkler and shear layer spring constant factors on the non-dimensional critical buckling load of a CNTRC plate with a Pasternak’s elastic foundation with UD reinforcement distribution. The analysis involves a square CNTRC plate with simple supported boundary conditions and sinusoidal loading. Findings are expressed using a non-dimensional parameter specified in Eq. (31). The analysis includes different Winkler and shear layer spring constant factors and CNT volume fractions. The figure shows that for a given CNT volume fraction, the non-dimensional critical buckling load increases with the values of the Winkler and shear layer spring constant factors. In composite structures like CNTRC plates, the foundation stiffness plays a crucial role in resisting buckling under compressive loads. Higher values of the Winkler and shear layer spring constants result in a stiffer support system beneath the plate. This increased stiffness effectively distributes and absorbs the compressive forces applied to the plate, thereby increasing its buckling resistance. Essentially, the stiffer foundation reduces the magnitude of deformations that could lead to instability, thereby raising the critical buckling load. Similarly, for a given set of spring constant factors, the non-dimensional critical buckling load increases with the CNT volume fraction. This phenomenon occurs because higher CNT volume fractions enhance the overall stiffness and strength of the CNTRC plate. The increased stiffness provided by a higher volume fraction of CNTs allows the plate to withstand higher compressive loads before buckling occurs, thereby increasing the critical buckling load.

Fig. 8
figure 8

Effect of different spring constant factors on non-dimensional critical buckling load under uni-axial loading \({\overline{N} }_{cr}\) (Ψx = −1, Ψy = 0) condition for different volume fraction of CNTs on CNTRC plate resting on the Pasternak’s elastic foundation

Full size image

Figure 9 depicts the first six buckling mode shapes of a simply supported CNTRC plate on a Pasternak’s elastic foundation, focusing on the FG-X distribution of CNTs. The analysis is conducted on a square CNTRC plate with simple supported boundary conditions subjected to sinusoidal loading. Results are reported using a non-dimensional parameter outlined in Eq. (31). The mode shapes are constructed for a CNT volume fraction of 0.17 and a side-to-thickness ratio of 10, with shear layer spring constant factors of 50 and 100, respectively, for the Winkler spring constant factors. This phenomenon arises because the FG-X distribution effectively reinforces the plate, distributing compressive forces more evenly and resisting buckling across its surface.

Fig. 9
figure 9

First six mode shapes of simply supported CNTRC plate resting on the Pasternak’s elastic foundation for buckling loads \({\overline{N} }_{cr}\)

Full size image

Free Vibration Analysis

This section goes into extensive detail on the free vibration analysis of the CNTRC plate with Pasternak’s elastic foundation.

Table 7 presents the dimensionless natural frequency of the CNTRC plate with and without a Pasternak’s elastic foundation. This study explores the dimensionless natural frequency of CNTRC plates across various CNT volume fractions, CNT distribution patterns, and spring constant factors. The FG-V, FG-O, and FG-X distributions, along with the UD distribution, are specifically analyzed in the context of CNTRC plate with and without a Pasternak’s elastic foundation. The analysis focuses on a square CNTRC plate with simple supported boundary conditions. The findings are presented using a non-dimensional parameter as defined by Eq. (30). The results obtained align closely with those reported by Wattanasakulpong and Chaikittiratana [27]. For a side-to-thickness ratio of 10, the dimensionless natural frequency is computed for CNTRC plates both with and without the Pasternak elastic foundation. The table reveals that the FG-X reinforcement distribution of CNTs yields the highest natural frequency, followed by the UD, FG-V, and FG-O distributions. This trend can be explained by the superior mechanical properties imparted by the FG-X distribution, which optimally reinforces the plate against deformation and enhances its stiffness. As a result, the plate exhibits higher natural frequencies due to increased rigidity and reduced mass per unit area, leading to faster vibration cycles. The data indicate that the dimensionless natural frequency increases with higher Winkler spring constant factors and shear layer spring constant factors for the CNTRC plate with a Pasternak elastic foundation. Additionally, increasing the CNT volume fraction enhances the dimensionless natural frequency across different CNT distribution patterns. Additionally, increasing the CNT volume fraction enhances the dimensionless natural frequency across different distribution patterns. Higher volume fractions improve the overall stiffness and strength of the CNTRC plate, resulting in higher natural frequencies due to enhanced structural integrity and reduced deformation under vibrational modes.

Table 7 Dimensionless natural frequency \(\overline{\omega }\) for CNTRC plate with and without elastic foundation
Full size table

Figure 10 illustrates the first six mode shapes of the natural frequency for a simply supported CNTRC plate on a Pasternak elastic foundation. The mode shapes are depicted for an FG-O CNT distribution with a CNT volume fraction of 0.14 and a side-to-thickness ratio of 10. The shear layer spring constant factors and Winkler spring constant factors are set at 50 and 100, respectively. The mode shapes represent distinct vibrational patterns exhibited by the CNTRC plate under natural frequency conditions. Each mode shape corresponds to a specific vibration mode and frequency, characterized by the spatial distribution of displacements across the plate.

Fig. 10
figure 10

First six mode shapes of simply supported CNTRC plate resting on the Pasternak’s elastic foundation for free vibration \(\overline{\omega }\)

Full size image

Conclusions

The secant function-based non polynomial shear deformation theory (SDTSF) is employed to analyze the bending, buckling, and free vibration behaviors of a CNTRC plate resting on a Pasternak’s elastic foundation. This foundation model includes Winkler spring and shear layer components, which are fundamental to Pasternak's elastic theory. The equation of motion for the CNTRC plate with a Pasternak elastic foundation is derived using Hamilton's principle and solved using Navier's solution method. The static analysis reveals that the FG-X reinforcement distribution of CNTs in the composite plate with the Pasternak’s elastic foundation effectively minimizes transverse deflection, whereas the FG-O distribution results in the maximum transverse deflection. By adjusting the CNTs volume fraction, Winkler spring constant factors, and shear layer spring constant factors, the stiffness of the CNTRC plate can be optimized for various CNT distribution patterns. Axial stress and transverse shear stress profiles are found to be symmetrical for UD, FG-X, and FG-O CNT distribution patterns across the mid-plane of the plate, but asymmetrical for the FG-V pattern. Among the different distribution patterns, the FG-O distribution exhibits the highest non-dimensional transverse shear stress, while the FG-X distribution shows the lowest. Buckling analysis indicates that the FG-X reinforcement distribution of CNTs in the composite plate with the Pasternak elastic foundation achieves the highest dimensionless critical buckling load, followed by the UD and FG-O distributions. The FG-X distribution also results in the highest natural frequency, followed by UD, FG-V, and FG-O distributions. Increasing the volume fraction of CNTs, Winkler spring constant factors, and shear layer spring constant factors enhances the buckling and free vibration responses of CNTRC plates with Pasternak elastic foundations. However, the current study has some limitations that future work should address. The present analysis is restricted to simply supported boundary conditions, and extending it to other boundary conditions could provide a more comprehensive understanding of CNTRC plate behavior. Additionally, while this study considers static, buckling, and free vibration behavior, the effects of dynamic loading and thermal environments remain unexplored and warrant further investigation. Future studies could also incorporate more complex loading scenarios and explore the long-term durability and performance of CNTRC plates in real-world applications.