1 Introduction

As is well known, fiber-reinforced composite (FRC) materials have been widely used in aerospace industry due to its outstanding properties. However, cracks in a structural element cause local stiffness reduction [1] and change the global static and dynamic characteristics [2]. Hence, it is of prime importance to understand the vibration characteristics of cracked structures in structural health monitoring and nondestructive damage evaluation because the predicted vibration data can be used to detect, locate and quantify the extent of the cracks or damages in a structure. The problem of vibrational behavior of cracked composite plates has been extensively discussed in the last years [3–9]. However, a few of them [7–9] focus on the damage of matrix cracking which may be initiated as the first damage mode when the plate is subjected to tension or bending load [10, 11]. A test and prediction of natural frequencies of matrix-cracked square laminated plate were presented by Moon et al. [7]. In their analysis, the matrix crack was assumed to be located at 90-plies of the plate, and the reduction in laminate stiffness was derived based on a shear-lag model. Umesh and Ganguli [8] studied the vibration control of a cantilevered smart laminated plate with matrix cracks. The reduced stiffness for the plate with matrix cracks was obtained by using the self-consistent method. They found that the matrix cracks could reduce the natural frequency and the deflection for free and forced vibration, respectively. Adali and Makins [9] investigated the vibration characteristics of unsymmetric cross-ply laminated plate with matrix cracks. In their studies, the crack was modeled by a self-consistent method. They found that the effect of matrix crack located at the 90-ply was more significant on the linear frequencies than the same matrix crack located at the 0-ply. It is worth noting that in all the above studies, the classical laminate thin plate theory was adopted. The effect of transverse shear deformation is neglected in the classical thin plate theory based on the Kirchhoff hypothesis. Due to low transverse shear modulus relative to the in-plane Young’s modulus, transverse shear deformations play a much important role in the kinematics of composite laminates. Neglecting the transverse shear effects and rotary inertia yields incorrect results even for the thin composite laminated plates when the ratio of the two in-plane Young’s moduli of a lamina is more than 25 [12]. To account for the effect of transverse shear deformation in plates, several higher-order shear deformation plate theories have been developed, and the major difference of these higher-order shear deformation plate theories lies in that they use different shape functions in the displacement field. Reddy [13] developed a simple higher-order shear deformation plate theory. This theory not only allows parabolic variation of transverse shear strains but also satisfies the condition of the vanishing of transverse shear stresses at the top and bottom surface of the plate. Unlike the first-order shear deformation theory, no shear correction factors are required in this higher-order shear deformation theory, though there are the same numbers of independent unknowns in both the theories.

In the previous works, numerous models focus on the cases of cross-ply laminated plates with cracks only at 90-plies [14] and usually focus on the cases of cross-ply laminated plates with symmetric layup. For a cross-ply laminated plate, the matrix cracks may occur in both 0- and 90-plies. This is called doubly periodic matrix cracking [15, 16]. A number of models have been proposed to predict the stiffness reduction for this matrix cracking, for example self-consistent approach [17–19], variational principles [20–22] and equivalent constraint model [23–25]. As a simple and analytical way, the self-consistent method is applicable to the laminated plates with any kinds of cross-ply layup under different kinds of loading conditions.

Carbon nanotubes (CNTs) have shown the potential to become the important constituent of a new generation of composite materials, by virtue of their superior mechanical, thermal and electrical properties [26]. One of the potential applications of CNTRCs is in microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS) where CNTRCs can be used as key structural components [27]. Compared with the conventional carbon fiber-reinforced laminates, carbon nanotube-reinforced composites (CNTRCs) have the potential of significantly better strength and stiffness. The reinforcement effect of CNTs can be maximized if the CNTs are aligned in a given direction. This can be achieved as reported in recent publications [28, 29]. Several studies have been reported on the linear and nonlinear vibration of functionally graded CNTRC plates [30–34]. They found that a small percentage of nanotube reinforcement leads to significant improvements in plate vibration characteristics. The nonlinear vibration behaviors of a matrix-cracked hybrid laminated beam which contains CNTRC layers and resting on elastic foundations in thermal environments were recently studied by Fan and Wang [35]. In their analysis, a refined shear-lag model was adopted. Their results showed that the crack density plays an important role in the linear vibration of the hybrid laminated beam, but the effect of crack density is less pronounced on the nonlinear-to-linear frequency ratios of the same beam.

In the present work, the nonlinear free and forced vibrations of matrix-cracked hybrid laminated plates containing CNTRC layers resting on elastic foundations in thermal environments are investigated. The novelty of present work is to introduce the matrix cracking in both FRC and CNTRC layers. Unlike in [35], a self-consistent model instead of a refined shear-lag model is used to describe the stiffness reduction in plate due to the matrix cracks. Motion equations are derived based on Reddy’s higher-order shear deformation plate theory and solved by means of a two-step perturbation approach. The plate–foundation interaction and thermal effects are both taken into account, and the material properties of both FRC layers and CNTRC layers are assumed to be temperature dependent. The numerical illustrations show the effects of matrix cracks on the nonlinear dynamic responses of hybrid laminated plates under different conditions.

2 Self-consistent method for modeling

On the macroscale, the cracked unidirectional composite laminates can be regarded as an orthotropic homogeneous solid as shown in Fig. 1. The elastic properties of the matrix are identical with those of the fibrous composite and can be easily evaluated. When cracks are introduced, the macroscopic or overall elastic moduli of the solid may change. To make the concept of overall moduli meaningful, it is necessary to consider overall uniform loading. Thus, we introduce uniform overall average stresses \(\bar{\varvec{\sigma }}\) and strains \(\bar{\varvec{\varepsilon }}\), with components arranged in column vectors and related by constitutive equations

$$\begin{aligned} \bar{\varvec{\varepsilon }}=\varvec{S}\bar{{\varvec{\sigma }}} \end{aligned}$$
(1)

where \(\varvec{S}\) is the overall compliance matrix of the cracked composite.

Fig. 1
figure 1

Geometry of a cross-ply laminate and the distribution of matrix cracks

Full size image

Since we are concerned only with a 2-phase model (in which the intact composite is the matrix), here we use the subscript 0 to denote the properties of the intact composite. Following [36], the self-consistent estimates for the overall stiffness and compliance matrices can be expressed by

$$\begin{aligned} \varvec{S}=\varvec{S}_0 +\bar{{\rho }}_{crk} {\varvec{\Lambda }} \end{aligned}$$
(2)

where

$$\begin{aligned} \bar{{\rho }}_{crk} =\frac{1}{4}\pi \rho _{crk} \end{aligned}$$
(3)

in which the detailed expression of the crack density parameter \(\rho _{crk}\) is defined as [18]

$$\begin{aligned} \rho _{crk} =4\eta l^{2} \end{aligned}$$
(4)

where \(\eta \) is the number of cracks per unite area and l is the half length of two adjacent cracks. Note that the surface layer containing cracks may be regarded as half of a layer of the thickness. This means the crack density of a surface layer is twice as much as that of interior layer with the same angle-ply. The coordinate system presented is different from that used in [36], in which the fiber is aligned in the Z-direction, whereas in the present work the fiber is aligned in the X-direction, as shown in Fig. 1. Accordingly, the matrix \(\varvec{\Lambda }\) has three nonzero components, which are expressed in terms of compliances \(S_{ij}\) of effective medium as

$$\begin{aligned} {\Lambda }_{22}= & {} \frac{S_{11} S_{22} -S_{12}^2 }{S_{11} }(\sqrt{\alpha _1}+\sqrt{\alpha _2 }) \end{aligned}$$
(5)
$$\begin{aligned} {\Lambda }_{44}= & {} \frac{\sqrt{(S_{11} S_{22} -S_{12}^2 )(S_{11} S_{33} -S_{13}^2 )}}{S_{11}} \nonumber \\&\left( \sqrt{\alpha _1 }+\sqrt{\alpha _2} \right) \end{aligned}$$
(6)
$$\begin{aligned} {\Lambda }_{66}= & {} \sqrt{S_{55} S_{66} } \end{aligned}$$
(7)

where \(\alpha _{1}\) and \(\alpha _{2}\) are roots of

$$\begin{aligned}&\left( S_{11} S_{22} -S_{12}^2\right) \alpha ^{2}\!-\!\left[ S_{11} S_{44} +2(S_{11} S_{23} -S_{12} S_{13} )\right] \alpha \nonumber \\&\quad +S_{11} S_{33} -S_{13}^2 =0 \end{aligned}$$
(8)

These results imply that only three compliance coefficients \(S_{22}\), \(S_{44}\) and \(S_{66}\) are affected by the cracks. \(S_{66}\) can be obtained from Eqs. (2) and (7), while Eq. (8) can be solved by Newton–Raphson method as reported in [18]. In Eqs. (5)–(8), the compliance matrix \(\bar{\varvec{S}}\) can be expressed as

$$\begin{aligned} \left[ {{\begin{array}{c} {\bar{{S}}_{11} } \\ {\bar{{S}}_{12} } \\ {\bar{{S}}_{22} } \\ {\bar{{S}}_{16} } \\ {\bar{{S}}_{26} } \\ {\bar{{S}}_{66} } \\ \end{array} }} \right] \!= & {} \!\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {c^{4}}&{} {2s^{2}c^{2}}&{} {s^{4}}&{} {s^{2}c^{2}} \\ {s^{2}c^{2}}&{} {1-2s^{2}c^{2}}&{} {s^{2}c^{2}}&{} {-s^{2}c^{2}} \\ {s^{4}}&{} {2s^{2}c^{2}}&{} {c^{4}}&{} {s^{2}c^{2}} \\ {2sc^{3}}&{} {2sc(s^{2}-c^{2})}&{} {-2s^{3}c}&{} {sc(s^{2}-c^{2})} \\ {2s^{3}c}&{} {2sc(c^{2}-s^{2})}&{} {-2sc^{3}}&{} {sc(c^{2}-s^{2})} \\ {4s^{2}c^{2}}&{} {-8s^{2}c^{2}}&{} {4s^{2}c^{2}}&{} {1-4s^{2}c^{2}} \\ \end{array}}} \right] \nonumber \\&\times \left[ {{\begin{array}{c} {S_{11} } \\ {S_{12} } \\ {S_{22} } \\ {S_{66} } \\ \end{array} }} \right] \end{aligned}$$
(9)

where

$$\begin{aligned} c=\cos \theta , s=\sin \theta \end{aligned}$$
(10)

where \(\theta \) is the lamination angle with respect to the direction of X-axis. The relationships between stiffness coefficients \(\bar{{Q}}_{ij} \)and compliance coefficients \(\bar{{S}}_{ij} \)are

$$\begin{aligned} \bar{{Q}}_{11}= & {} \frac{\bar{{S}}_{22} }{\bar{{S}}_{11} \bar{{S}}_{22} -\bar{{S}}_{12}^2 }, \bar{{Q}}_{12} =-\frac{\bar{{S}}_{12} }{\bar{{S}}_{11} \bar{{S}}_{22} -\bar{{S}}_{12}^2 }, \bar{{Q}}_{22} \nonumber \\= & {} \frac{\bar{{S}}_{11} }{\bar{{S}}_{11} \bar{{S}}_{22} -\bar{{S}}_{12}^2} \nonumber \\ \bar{{Q}}_{44}= & {} \frac{1}{\bar{{S}}_{44} }, \bar{{Q}}_{55} =\frac{1}{\bar{{S}}_{55} }, \bar{{Q}}_{66} =\frac{1}{\bar{{S}}_{66}} \end{aligned}$$
(11)

Since we consider cross-ply laminated plate here, only 0-plies and 90-plies are needed to be taken into account.

2.1 Material properties of FRC 90-plies

It is assumed that the 90-plies are made of FRCs and the material properties of a FRC layer can be expressed as follows [37]

$$\begin{aligned}&E_{11} = V_f E_{11}^f +V_m E^{m}, \nonumber \\&\frac{1}{E_{22} } = \frac{V_f }{E_{22}^f }+\frac{V_m }{E^{m}} \nonumber \\&\quad -V_f V_m \frac{{V_f^2 E^{m}}/{E_{22}^f }+{V_m^2 E_{22}^f }/{E^{m}}-2v^{f}v^{m}}{V_f E_{22}^f +V_m E^{m}}, \nonumber \\&\frac{1}{G_{ij} } = \frac{V_f }{G_{ij}^f }+\frac{V_m }{G^{m}}\qquad \quad \quad (\textit{ij}=12,13\hbox { and }23) \nonumber \\&\rho = V_f \rho ^{f}+V_m \rho ^{m}, \nonumber \\&\nu _{12} = V_f \nu ^{f}+V_m \nu ^{m}, \end{aligned}$$
(12)

where \(E_{11}^f ,\, E_{22}^f,\, G_{12}^f \), \(G_{13}^f,\, G_{23}^f\) and \(\nu ^{f}\) are the Young’s moduli, shear moduli and Poisson’s ratio, respectively, of the fiber, while \(E^{m}\), \(G^{m}\) and \(\nu ^{m}\) are corresponding properties for the matrix. \(\rho ^{f}\), \(\rho ^{m}\)and \(\rho \) are the mass densities of the fiber, matrix and the ply. \(V_{f}\) and \(V_{m}\) are the fiber and matrix volume fractions and are related by \(V_{f}+V_{m} = 1\).

2.2 Material properties of CNTRC 0-plies

The 0-plies are assumed to be made of CNTRCs. Based on extended rule of mixture, the effective properties of CNTRC plies can be defined by [38]

$$\begin{aligned}&E_{11} = \eta _1 V_{CN} E_{11}^{CN} +V_m E^{m}, \nonumber \\&\frac{\eta _2 }{E_{22}} = \frac{V_{CN} }{E_{22}^{CN} }+\frac{V_m }{E^{m}}, \nonumber \\&\frac{\eta _3 }{G_{12}} = \frac{V_{CN} }{G_{12}^{CN} }+\frac{V_m }{G^{m}}, \nonumber \\&\rho = V_{CN} \rho ^{CN} +V_m \rho ^{m}, \nonumber \\&\nu _{12} = V_{CN}^*\nu _{12}^{CN} +V_m \nu ^{m}, \end{aligned}$$
(13)

in which \(E_{11}^{CN} \), \(E_{22}^{CN} \), \(G_{12}^{CN} \), \(\nu _{12}^{CN} \) and \(\rho ^{CN}\) are the Young’s and shear moduli, Poisson’s ratio and mass density of the single-walled carbon nanotubes (SWCNTs), respectively. \(\eta _j (j=1,2,3)\) are the CNT efficiency parameters, and \(V_{CN}\) is the volume fraction of the CNT, which satisfies the relationship of \(V_{CN}+V_{m} = 1\). Two types of FG-CNTRCs, i.e., FG-V, and FG-\({\Lambda } \), as defined in [39] are considered. The corresponding volume fraction \(V_{CN}\) for each type is

$$\begin{aligned} V_{CN}= & {} 2\left( {\frac{Z-t_0 }{t_1 -t_0 }} \right) V_{CN}^{*} \qquad (\hbox {FG-V}), \nonumber \\ V_{CN}= & {} 2\left( {\frac{t_1 -Z}{t_1 -t_0 }} \right) V_{CN}^{*} \qquad (\hbox {FG}-{\Lambda } ), \end{aligned}$$
(14)

in which \(\hbox {Z}=t_{1}\) and \(\hbox {Z}=t_{0}\), respectively, denote the values in Z-direction at the top surface and bottom surface of a 0-ply. In Eq. (14), \(V_{CN}^*\) depends on the mass densities of CNTs and matrix, and the detailed definition is

$$\begin{aligned} V_{CN}^*=\frac{w_{CN} }{w_{CN} +\left( {{\rho ^{CN}}/{\rho ^{m}}} \right) -\left( {{\rho ^{CN}}/{\rho ^{m}}} \right) w_{CN}} \end{aligned}$$
(15)

in which \(w_{CN}\) is the mass fraction of SWCNTs. For UD-CNTRC 0-plies, \(V_{CN}\) is equal to \(V_{CN}^*\).

In the longitudinal and transverse directions, the thermal expansion coefficients \(\alpha _{11} \)and \(\alpha _{22} \) for an arbitrary layer can be expressed by [40]

$$\begin{aligned} \alpha _{11}= & {} \frac{V_i E_{11}^i \alpha _{11}^i +V_m E^{m}\alpha _m }{V_i E_{11}^i +V_m E^{m}}\qquad (i=f\hbox { or }CN), \nonumber \\ \alpha _{22}= & {} \left( {1+v_{12}^i } \right) \;V_i \alpha _{22}^i +\left( {1+v^{m}} \right) \;V_m \alpha ^{m} \nonumber \\&-v_{12} \alpha _{11} \qquad (i=f\hbox { or }CN), \end{aligned}$$
(16)

in which \(\alpha _{11}^i ,\, \alpha _{22}^i (i=f \hbox { or } CN)\) and \(\alpha ^{m}\) are thermal expansion coefficients, respectively, of the carbon fiber (or carbon nanotube) and the matrix.

The material properties of carbon nanotube and matrix are assumed to be functions of temperature, so that the effective material properties of both FRC and CNTRC plies are functions of temperature.

3 Motion equations of hybrid laminated plate

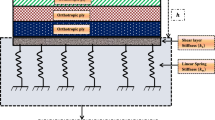
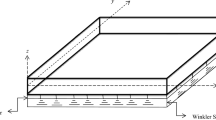
It is assumed that a laminated plate with length a, width b and thickness h rests on an elastomeric substrate with finite depth. This substrate may be modeled as an elastic foundation of Pasternak type. The plate and foundation are assumed to be bonded perfectly, that is, the plate and foundation are not separated after the deformation occurs. This is truly an ideal state. The coupling effect of plate and foundation can be expressed by an interaction force

$$\begin{aligned} p(X,Y)=\bar{{K}}_1 \bar{{W}}-\bar{{K}}_2 \nabla ^{2}\bar{{W}} \end{aligned}$$
(17)

in which p is the force per unit area, \(\nabla ^{2}\) is Laplace operator, \(\bar{{K}}_1 \) is the Winkler stiffness, and \(\bar{{K}}_2\) is the shearing layer stiffness of the foundation. The material of elastomeric substrate is assumed to be temperature dependent. Hence, the Winkler stiffness may be expressed by [41]:

$$\begin{aligned} \bar{{K}}_1 =\frac{E_F [5-(2\gamma _1^2 +6\gamma _1 +5)\exp (-2\gamma _1 )]}{4b(1-\nu _0^2 )(2-c_1 )^{2}} \end{aligned}$$
(18)

where \(c_1 =(\gamma _1 +2)\exp (-\gamma _1 ),\, \gamma _1 ={H_s}/b,\, E_F ={E_s }/{(1-\nu _s^2 )}\) and \(\nu _0 ={\nu _s }/{(1-\nu _s )}\), in which \(E_{s}\) and \(v_{s}\) are Young’s modulus and Poisson’s ratio of the foundation, respectively, and \(H_{s}\) is the depth of the foundation. The shear layer stiffness \(\bar{{K}}_2 \) is assumed to be one-tenth of the Winkler stiffness \(\bar{{K}}_1 \). The initial and additional deflections are expressed by \(\bar{{W}}^{{*}}(X,Y)\) and \(\bar{{W}}(X,Y)\), respectively. The plate is exposed to elevated temperature and is subjected to a transverse dynamic load \(Q(X,\, Y,\, t)\). Based on Reddy’s higher-order shear deformation theory with a von Kármán type of kinematic nonlinearity, Shen [42] derived a set of general von Kármán-type equations which can be expressed in terms of a transverse displacement \(\bar{{W}}\), two rotations \(\bar{{{\varPsi } }}_x\) and \(\bar{{{\varPsi }}}_y \), and stress function \(\bar{{F}}\) as defined by

$$\begin{aligned} \bar{{N}}_X =\frac{\partial ^{2}\bar{{F}}}{\partial Y^{2}}, \bar{{N}}_Y =\frac{\partial ^{2}\bar{{F}}}{\partial X^{2}}, \bar{{N}}_{XY} =-\frac{\partial ^{2}\bar{{F}}}{\partial X\partial Y} \end{aligned}$$
(19)

where \(\bar{{N}}_X ,\bar{{N}}_X\) and \(\bar{{N}}_{XY}\) are stress resultants.

These equations can be expressed by [12]

$$\begin{aligned}&\tilde{L}_{11} (\bar{{W}})-\tilde{L}_{12} (\bar{{\varPsi }}_x )-\tilde{L}_{13} (\bar{{\varPsi }}_y )+\tilde{L}_{14} (\bar{{F}}) \nonumber \\&\qquad -\,\tilde{L}_{15} (\bar{{N}}^{T}) -\tilde{L}_{16} (\bar{{M}}^{T}) \nonumber \\&\quad = \tilde{L}(\bar{{W}},\overline{F} )+\tilde{L}_{17} (\ddot{\bar{{W}}})+I_8 (\ddot{\bar{{\varPsi }}}_{x,X} +\ddot{\bar{{\varPsi }}}_{y,Y} ) \nonumber \\&\qquad -\,(\bar{{K}}_1 \bar{{W}}-\bar{{K}}_2 \nabla ^{2}\bar{{W}})+Q \end{aligned}$$
(20)
$$\begin{aligned}&\tilde{L}_{21} (\bar{{F}})+\tilde{L}_{22} (\bar{{\varPsi }}_x )+\tilde{L}_{23} (\bar{{\varPsi }}_y ) \nonumber \\&\qquad -\,\tilde{L}_{24} (\bar{{W}})-\tilde{L}_{25} (\bar{{N}}^{T})= -\frac{1}{2}\tilde{L}(\bar{{W}},\bar{{W}}) \end{aligned}$$
(21)
$$\begin{aligned}&\tilde{L}_{31} (\bar{{W}})+\tilde{L}_{32} (\bar{{\varPsi }}_x )-\tilde{L}_{33} (\bar{{\varPsi }}_y )+\tilde{L}_{34} (\bar{{F}}) \nonumber \\&\qquad -\,\tilde{L}_{35} (\bar{{N}}^{T})-\tilde{L}_{36} (\bar{{S}}^{T})= I_9 \ddot{\bar{{W}}},_X +I_{10} \ddot{\bar{{\varPsi }}}_x \end{aligned}$$
(22)
$$\begin{aligned}&\tilde{L}_{41} (\bar{{W}})-\tilde{L}_{42} (\bar{{\varPsi }}_x )+\tilde{L}_{43} (\bar{{\varPsi }}_y )+\tilde{L}_{44} (\bar{{F}}) \nonumber \\&\qquad -\,\tilde{L}_{45} (\bar{{N}}^{T}) -\tilde{L}_{46} (\bar{{S}}^{T})= I_9 \ddot{\bar{{W}}},_Y +I_{10} \ddot{\bar{{\varPsi }}}_y \end{aligned}$$
(23)

in which the linear operators \(\tilde{L}_{ij} (\cdot )\) and the nonlinear operators \(L_{ij} (\cdot )\) are defined as in [12]. \(I_{i}\) are defined in Eqs. (31) and (32) below. In the above equations, the superposed dots indicate differentiation with respect to time t. It has been reported that von Kármán-type nonlinearity is accurate for flexural vibration analysis of laminated plates [43]. In the frame work of HSDT, both Green-Lagrange and von Kármán strain-displacement relationships may be used. The complete Green-Lagrange strain expressions make the governing equations nonlinear in all the displacement parameters of the plate. The Green-Lagrange strain expressions are particularly applicable for in-plane vibrational problem [44, 45], whereas the von Kármán strain expressions are simple and convenient to derive governing equations of \(\bar{{W}}-\bar{{F}}\) type which are particularly applicable for a mixed boundary value problem.

Considering the effects of thermal environment, the constitutive relations of the plate are

$$\begin{aligned}&\left[ {{\begin{array}{c} \bar{\varvec{N}} \\ \bar{\varvec{M}} \\ \bar{\varvec{P}} \\ \end{array}}} \right] =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} \varvec{A}&{} \varvec{B}&{} \varvec{E} \\ \varvec{B}&{} \varvec{D}&{} \varvec{F} \\ \varvec{E}&{} \varvec{F}&{} \varvec{H} \\ \end{array} }} \right] \left[ {{\begin{array}{c} \varvec{\varepsilon }^{0} \\ \varvec{\kappa }^{0} \\ \varvec{\kappa }^{2} \\ \end{array}}} \right] +\left[ {{\begin{array}{c} \bar{\varvec{N}}^{T} \\ \bar{\varvec{M}}^{T} \\ \bar{\varvec{P}}^{T} \\ \end{array} }} \right] \end{aligned}$$
(24a)
$$\begin{aligned}&\quad \left[ {{\begin{array}{l} \bar{\varvec{Q}} \\ \bar{\varvec{R}} \\ \end{array}}} \right] =\left[ {{\begin{array}{c@{\quad }c} \varvec{A}&{} \varvec{D} \\ \varvec{D}&{} \varvec{F} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\varvec{\varepsilon }}^{0} \\ {\varvec{\kappa }}^{2} \\ \end{array}}} \right] \end{aligned}$$
(24b)

where \(\varvec{A},\, \varvec{B},\, \varvec{D}\), etc., are plate stiffness, and the detailed definition can be found in Eq. (30) below. \(\varvec{\varepsilon }^{0}\) is the strain of mid-plane, while \(\varvec{\kappa }^{0}\) and \(\varvec{\kappa }^{2}\) are curvatures of mid-plane. \(\bar{\varvec{N}}^{T}\), \(\bar{\varvec{M}}^{T}\) and \(\bar{\varvec{P}}^{T}\) are the thermal forces, moments and higher-order moments caused by the temperature change \(\Delta T(X,Y,Z)\) and are defined by

$$\begin{aligned}&\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\bar{{N}}_x^T }&{} {\bar{{M}}_x^T }&{} {\bar{{P}}_x^T } \\ {\bar{{N}}_y^T }&{} {\bar{{M}}_y^T }&{} {\bar{{P}}_y^T } \\ {\bar{{N}}_{xy}^T }&{} {\bar{{M}}_{xy}^T }&{} {\bar{{P}}_{xy}^T } \\ \end{array}}} \right] =\sum _{i=1}^N {\int \limits _{h_{k-1} }^{h_k } {\left[ {{\begin{array}{l} {A_x } \\ {A_y } \\ {A_{xy} } \\ \end{array} }} \right] } }_k \nonumber \\&\quad (1,Z,Z^{2})\Delta T\hbox {d}Z \end{aligned}$$
(25a)
$$\begin{aligned}&\quad \left[ {{\begin{array}{l} {\bar{{S}}_x^T } \\ {\bar{{S}}_y^T } \\ {\bar{{S}}_{xy}^T } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\bar{{M}}_x^T } \\ {\bar{{M}}_y^T } \\ {\bar{{M}}_{xy}^T } \\ \end{array} }} \right] -\frac{4}{3h^{2}}\left[ {{\begin{array}{l} {\bar{{P}}_x^T } \\ {\bar{{P}}_y^T } \\ {\bar{{P}}_{xy}^T } \\ \end{array} }} \right] \end{aligned}$$
(25b)

In Eq. (25a),

$$\begin{aligned}&\left[ {{\begin{array}{l} {A_x } \\ {A_y } \\ {A_{xy} } \\ \end{array} }} \right] =-\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\bar{{Q}}_{11} }&{} {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{16} } \\ {\bar{{Q}}_{12} }&{} {\bar{{Q}}_{22} }&{} {\bar{{Q}}_{26} } \\ {\bar{{Q}}_{16} }&{} {\bar{{Q}}_{26} }&{} {\bar{{Q}}_{66} } \\ \end{array} }} \right] \left[ {{\begin{array}{cc} {c^{2}}&{} {s^{2}} \\ {s^{2}}&{} {c^{2}} \\ {2cs}&{} {-2cs} \\ \end{array} }} \right] \nonumber \\&\qquad \qquad \qquad \times \left[ {{\begin{array}{l} {\alpha _{11} } \\ {\alpha _{22} } \\ \end{array} }} \right] \end{aligned}$$
(26)

in which \(\alpha _{11}\) and \(\alpha _{22}\) are thermal expansion coefficients of \(k\hbox {th}\) layer in longitudinal and transverse directions.

Partly inversing Eq. (24a), we obtain

$$\begin{aligned} \left[ {{\begin{array}{l} \varvec{\varepsilon }^{0} \\ {\varvec{M}^{{*}}} \\ {\varvec{P}^{{*}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\varvec{A}^{{*}}}&{} {\varvec{B}^{{*}}}&{} {\varvec{E}^{{*}}} \\ {-(\varvec{B}^{{*}})^{\mathrm{T}}}&{} {\varvec{D}^{{*}}}&{} {(\varvec{F}^{{*}})^{\mathrm{T}}} \\ {-(\varvec{E}^{{*}})^{\mathrm{T}}}&{} {\varvec{F}^{{*}}}&{} {\varvec{H}^{{*}}} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\varvec{N}^{{*}}} \\ {\varvec{\kappa }}^{0} \\ \varvec{\kappa }^{2} \\ \end{array}}} \right] \end{aligned}$$
(27)

where the superscript T represents transpose of matrix, and

$$\begin{aligned} \varvec{N}^{{*}}=\bar{\varvec{N}}-\bar{\varvec{N}}^{\mathrm{T}}, \varvec{M}^{{*}}=\bar{\varvec{M}}-\bar{\varvec{M}}^{\mathrm{T}}, \varvec{P}^{{*}}=\bar{\varvec{P}}-\bar{\varvec{P}}^{\mathrm{T}} \end{aligned}$$
(28)

The reduced matrices \(\varvec{A}^{*},\, \varvec{B}^{*}\), etc., are defined by

$$\begin{aligned} \varvec{A}^{{*}}= & {} \varvec{A}^{-1}, \varvec{B}^{{*}}=-\varvec{A}^{-1}\varvec{B}, \varvec{D}^{{*}}=\varvec{D}-\varvec{BA}^{-1}\varvec{B}, \varvec{E}^{{*}} \nonumber \\= & {} -\varvec{A}^{-1}\varvec{E} \nonumber \\ \varvec{F}^{{*}}= & {} \varvec{F}-\varvec{EA}^{-1}\varvec{B}, \varvec{H}^{{*}}=\varvec{H}-\varvec{EA}^{-1}\varvec{E} \end{aligned}$$
(29)

Generally, \(\varvec{A}^{*},\, \varvec{D}^{*}\) and \(\varvec{H}^{*}\) are symmetric matrices, while \(\varvec{B}^{*},\, \varvec{E}^{*}\) and \(\varvec{F}^{*}\) may not always be. The plate stiffnesses \(A_{ij},\, B_{ij}\), \(D_{ij}\), etc., are defined as

$$\begin{aligned}&(A_{ij} ,B_{ij} ,D_{ij} ,E_{ij} ,F_{ij} ,H_{ij} ) \nonumber \\&\quad = \sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {(\bar{{Q}}_{ij} )_k (1,Z,Z^{2},Z^{3},Z^{4},Z^{6})} } \hbox {d}Z, \nonumber \\&\quad (i,j=1,2,6) \end{aligned}$$
(30a)
$$\begin{aligned}&\quad (A_{ij} ,D_{ij} ,F_{ij} ) = \sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {(\bar{{Q}}_{ij} )_k (1,Z^{2},Z^{4})} } \hbox {d}Z, \nonumber \\&\quad (i,j=4,5) \end{aligned}$$
(30b)

and the generalized inertia \(I_{i} \,(i=1,2,3,4,5,7)\) is defined as

$$\begin{aligned}&(I_1 ,I_2 ,I_3 ,I_4 ,I_5 ,I_7 ) \nonumber \\&\quad =\sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {\rho _k (1,Z,Z^{2},Z^{3},Z^{4},Z^{6})} } \hbox {d}Z \end{aligned}$$
(31)

and

$$\begin{aligned}&\bar{{I}}_2 = I_2 -\frac{4}{3h^{2}}I_4 , \bar{{I}}_5 =I_5 -\frac{4}{3h^{2}}I_7 , \bar{{I}}_3 \nonumber \\&\quad =I_3 -\frac{8}{3h^{2}}I_5 +\frac{16}{9h^{4}}I_7 \nonumber \\&I_8 =\frac{I_2 \bar{{I}}_2 }{I_1 }-\bar{{I}}_3 -\frac{4}{3h^{2}}\bar{{I}}_5 , I_9 =\frac{4}{3h^{2}}\left( {\bar{{I}}_5 -\frac{\bar{{I}}_2 I_4 }{I_1 }} \right) , \nonumber \\&\quad I_{10} =\frac{\bar{{I}}_2 \bar{{I}}_2 }{I_1 }-\bar{{I}}_3 \end{aligned}$$
(32)

It is assumed that four edges of plate are simply supported. Based on the in-plane behavior at the edges, two cases of boundary conditions (immovable edges and movable edges) are considered

\(X=0,\, a\);

$$\begin{aligned}&\bar{{W}}=\bar{{{\varPsi } }}_y =0 \end{aligned}$$
(33a)
$$\begin{aligned}&\bar{{M}}_x = \bar{{P}}_x =0 \end{aligned}$$
(33b)
$$\begin{aligned}&\int _0^b {\bar{{N}}_x \hbox {d}Y} = 0\quad (\hbox {movable}) \end{aligned}$$
(33c)
$$\begin{aligned}&\bar{{U}} = 0\quad (\hbox {immovable}) \end{aligned}$$
(33d)

\(Y=0,\, b\);

$$\begin{aligned}&\bar{{W}}=\bar{{{\varPsi } }}_x =0 \end{aligned}$$
(33e)
$$\begin{aligned}&\bar{{M}}_y = \bar{{P}}_y =0 \end{aligned}$$
(33f)
$$\begin{aligned}&\int _0^b {\bar{{N}}_y \hbox {d}X} = 0\quad (\hbox {movable}) \end{aligned}$$
(33g)
$$\begin{aligned}&\bar{{V}} = 0\quad (\hbox {immovable}) \end{aligned}$$
(33h)

In Eq. (33), the in-plane immovable conditions of Eqs. (33d) and (33h) can be expressed, respectively, by

$$\begin{aligned}&\int \limits _0^b {\int \limits _0^a {\left\{ {A_{11}^{*} \frac{\partial ^{2}\bar{{F}}}{\partial Y^{2}}} \right. } } +A_{12}^{*} \frac{\partial ^{2}\bar{{F}}}{\partial X^{2}} \nonumber \\&\quad +\,\left[ {\left( {B_{11}^{*} -\frac{4}{3h^{2}}E_{11}^{*} } \right) \frac{\partial \bar{{{\varPsi }}}_x}{\partial X}+\left( {B_{12}^{*} -\frac{4}{3h^{2}}E_{12}^{*}} \right) \frac{\partial \bar{{{\varPsi }}}_y }{\partial Y}} \right] \nonumber \\&\quad \left. -\,\frac{4}{3h^{2}}\left( {E_{11}^{*} \frac{\partial ^{2}\bar{{W}}}{\partial X^{2}}+E_{12}^{*} \frac{\partial ^{2}\bar{{W}}}{\partial Y^{2}}} \right) -\frac{1}{2}\left( {\frac{\partial \bar{{W}}}{\partial X}} \right) ^{2} \right. \nonumber \\&\quad \left. -\,(A_{11}^{*} \bar{{N}}_x^T +A_{12}^{*} \bar{{N}}_y^T ) \right\} \hbox {d}X\hbox {d}Y=0 \end{aligned}$$
(34a)
$$\begin{aligned}&\quad \int \limits _0^a {\int \limits _0^b {\left\{ {A_{22}^{*} \frac{\partial ^{2}\bar{{F}}}{\partial X^{2}}} \right. } } +A_{12}^{*} \frac{\partial ^{2}\bar{{F}}}{\partial Y^{2}} \nonumber \\&\quad \quad +\,\left[ {\left( {B_{21}^{*} -\frac{4}{3h^{2}}E_{21}^{*} } \right) \frac{\partial \bar{{{\varPsi } }}_x }{\partial X}+\left( {B_{22}^{*} -\frac{4}{3h^{2}}E_{22}^{*} } \right) \frac{\partial \bar{{{\varPsi } }}_y }{\partial Y}} \right] \nonumber \\&\quad \quad \left. -\,\frac{4}{3h^{2}}\left( {E_{21}^{*} \frac{\partial ^{2}\bar{{W}}}{\partial X}+E_{22}^{*} \frac{\partial ^{2}\bar{{W}}}{\partial Y^{2}}} \right) -\frac{1}{2}\left( {\frac{\partial \bar{{W}}}{\partial Y}} \right) ^{2} \right. \nonumber \\&\quad \quad \left. -\,\left( {A_{12}^{*} \bar{{N}}_x^T +A_{22}^{*} \bar{{N}}_y^T } \right) \right\} \hbox {d}Y\hbox {d}X=0 \end{aligned}$$
(34b)

4 Solutions for free and forced vibrations

Before carrying out the solution process, it is convenient to first define the following dimensionless quantities for such plates. Introduce dimensionless coefficients

$$\begin{aligned}&x=\pi \frac{X}{a}, y=\pi \frac{Y}{b}, \beta =\frac{a}{b}, \nonumber \\&\quad W=\frac{W}{[D_{11}^{*} D_{22}^{*} A_{11}^{*} A_{22}^*]^{1/4}}, F=\frac{\bar{{F}}}{[D_{11}^{*} D_{22}^{*} ]^{1/2}}, \nonumber \\&\quad ({\varPsi }_x ,{\varPsi }_y )=\frac{a}{\pi }\frac{(\bar{{{\varPsi } }}_x ,\bar{{{\varPsi }}}_y )}{[D_{11}^{*} D_{22}^{*} A_{11}^{*} A_{22}^{*} ]^{1/4}}, \gamma _{14} =\left[ {\frac{D_{22}^{*} }{D_{11}^{*} }} \right] ^{1/2}, \nonumber \\&\quad \gamma _{24} =\left[ {\frac{A_{11}^{*} }{A_{22}^{*} }} \right] ^{1/2}, \gamma _5 =-\frac{A_{12}^{*} }{A_{22}^*}, \nonumber \\&(\gamma _{T1} ,\gamma _{T2} )=\frac{a^{2}}{\pi ^{2}}\frac{(A_x^T ,A_y^T )}{[D_{11}^{*} D_{22}^{*} ]^{1/2}}, (\gamma _{T3} ,\gamma _{T4} ,\gamma _{T6} ,\gamma _{T7}) \nonumber \\&\quad =\frac{a^{2}}{\pi ^{2}hD_{11}^{*} }\left( {D_x^T ,D_y^T ,\frac{4}{3h^{2}}F_x^T ,\frac{4}{3h^{2}}F_y^T } \right) , \nonumber \\&(K_1 ,K_2 )=\left( {\frac{\bar{{K}}_1 a^{4}}{\pi ^{4}D_{11}^{*} },\frac{\bar{{K}}_2 a^{2}}{\pi ^{2}D_{11}^{*} }} \right) , (M_x ,P_x ) \nonumber \\&\quad =\frac{a^{2}}{\pi ^{2}}\frac{\left( {\bar{{M}}_x ,\frac{4}{3h^{2}}\bar{{P}}_x } \right) }{D_{11}^{*} [D_{11}^{*} D_{22}^{*} A_{11}^*A_{22}^*]^{^{1/4}}}, \tilde{t}=\frac{\pi t}{a}\sqrt{\frac{E_0 }{\rho _0 }}, \nonumber \\&\omega _\mathrm{L} = {\varOmega }_\mathrm{L} \frac{a}{\pi }\sqrt{\frac{\rho _0 }{E_0 }}, \gamma _{170} \nonumber \\&\quad =-\frac{I_1 E_0 a^{2}}{\pi ^{2}\rho _0 D_{11}^{*} }, \gamma _{171} =\frac{4E_0 (I_5 I_1 -I_4 I_2 )}{3\rho _0 h^{2}I_1 D_{11}^{*} } \nonumber \\&(\gamma _{80} ,\gamma _{90} ,\gamma _{10} )=(I_8 ,I_9 ,I_{10} )\frac{E_0 }{\rho _0 D_{11}^{*} }, \lambda _q \nonumber \\&\quad =\frac{qa^{4}}{\pi ^{4}D_{11}^{*} [D_{11}^{*} D_{22}^{*} A_{11}^{*} A_{22}^{*} ]^{1/4}} \end{aligned}$$
(35)

where \(\rho _{0}\) and \(E_{0}\) are, respectively, the values of \(\rho ^{\mathrm{m}}\) and \(E^{\mathrm{m}}\) at the reference temperature (T = 300K). \(A_x^T ,\, D_x^T ,\, F_x^T \), etc., are defined by

$$\begin{aligned}&\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {A_x^T }&{} {D_x^T}&{} {F_x^T } \\ {A_y^T }&{} {D_y^T }&{} {F_y^T } \\ \end{array} }} \right] =-\sum _{k=1}^n \int \limits _{h_{k-1} }^{h_k } \left[ {{\begin{array}{c} {A_x } \\ {A_y } \\ \end{array} }} \right] \nonumber \\&\quad (1,Z,Z^{3})~\hbox {d}Z \end{aligned}$$
(36)

where \(A_{x}\) and \(A_{y}\) are given in Eq. (26).

In uniform temperature field, \(L_{15}(N^{T})=L_{25}(N^{T})=L_{35}(N^{T})=L_{45}(N^{T}) = 0\); then, Eqs. (20)–(23) can be expressed in dimensionless form as

$$\begin{aligned}&L_{11} (W)-L_{12} ({\varPsi }_x )-L_{13} ({\varPsi }_y) \nonumber \\&\quad +\,\gamma _{14} L_{14} (F)-L_{16} (M^{T}) \nonumber \\&\quad =\, \gamma _{14} \beta ^{2}L(W,F)+L_{17} (\ddot{W}) \nonumber \\&\quad +\,\gamma _{80} \left( \frac{\partial \ddot{{\varPsi } }_x }{\partial x}+\beta \frac{\partial \ddot{{\varPsi } }_y }{\partial y}\right) \nonumber \\&\quad -\,(K_1 W-K_2 \nabla ^{2}W)+\lambda _q \end{aligned}$$
(37)
$$\begin{aligned}&L_{21} (F)+\,\gamma _{24} L_{22} ({\varPsi }_x ) \nonumber \\&\quad +\,\gamma _{24} L_{23} ({\varPsi }_y )-\gamma _{24} L_{24} (W) \nonumber \\&\quad = -\frac{1}{2}\gamma _{24} \beta ^{2}L(W,W) \end{aligned}$$
(38)
$$\begin{aligned}&L_{31} (W)+L_{32} ({\varPsi }_x )-L_{33} ({\varPsi }_y) \nonumber \\&\quad +\,\gamma _{14}L_{34} (F)-L_{36} (S^{T}) \nonumber \\&\quad =\,\gamma _{90} \frac{\partial \ddot{W}}{\partial x}+\gamma _{10} \ddot{{\varPsi } }_x \end{aligned}$$
(39)
$$\begin{aligned}&L_{41} (W)-L_{42} ({\varPsi }_x )+L_{43} ({\varPsi }_y) \nonumber \\&\quad \quad +\,\gamma _{14} L_{44} (F)-L_{46} (S^{T}) \nonumber \\&\quad =\, \gamma _{90} \beta \frac{\partial \ddot{W}}{\partial y}+\gamma _{10} \ddot{{\varPsi } }_y \end{aligned}$$
(40)

in which linear operators \(L_{ij}\) (\(\cdot \)) are defined as in [12].

The boundary conditions of Eqs. (33a)–(33h) can be rewritten as

\(x=0,\, \pi \);

$$\begin{aligned}&W={\varPsi }_y =0 \end{aligned}$$
(41a)
$$\begin{aligned}&\quad M_x = P_x =0 \end{aligned}$$
(41b)
$$\begin{aligned}&\quad \int _0^\pi {\beta ^{2}\frac{\partial ^{2}F}{\partial y^{2}}\hbox {d}y} =0\quad (\hbox {movable}) \end{aligned}$$
(41c)
$$\begin{aligned}&\quad \int _0^\pi \int _0^\pi \left[ \gamma _{24}^2 \beta ^{2}\frac{\partial ^{2}F}{\partial y^{2}}-\gamma _5 \frac{\partial ^{2}F}{\partial x^{2}} \right. \nonumber \\&\quad \left. +\,\gamma _{24} \left( {\gamma _{511} \frac{\partial {\varPsi }_x }{\partial x}+\gamma _{233} \beta \frac{\partial {\varPsi }_y }{\partial y}} \right) \right. \nonumber \\&\quad -\,\gamma _{24} \left( {\gamma _{611} \frac{\partial ^{2}W}{\partial x^{2}}+\gamma _{244} \beta ^{2}\frac{\partial ^{2}W}{\partial y^{2}}} \right) \nonumber \\&\quad \left. {-\,\frac{1}{2}\gamma _{24} \left( {\frac{\partial W}{\partial x}} \right) ^{2}+(\gamma _{24}^2 \gamma _{T1} -\gamma _5 \gamma _{T2} )\Delta T} \right] \nonumber \\&\quad \hbox {d}x\hbox {d}y=0\quad (\hbox {immovable}) \end{aligned}$$
(41d)

\(y=0,\,\pi \);

$$\begin{aligned}&W = {\varPsi }_x =0 \end{aligned}$$
(41e)
$$\begin{aligned}&\quad M_y = P_y =0 \end{aligned}$$
(41f)
$$\begin{aligned}&\quad \int _0^\pi {\frac{\partial ^{2}F}{\partial x^{2}}\hbox {d}y} =0\quad (\hbox {movable}) \end{aligned}$$
(41g)
$$\begin{aligned}&\quad \int _0^\pi \int _0^\pi \left[ \frac{\partial ^{2}F}{\partial x^{2}}-\gamma _5 \beta ^{2}\frac{\partial ^{2}F}{\partial y^{2}} \right. \nonumber \\&\quad \left. +\,\gamma _{24} \left( {\gamma _{220} \frac{\partial {\varPsi }_x }{\partial x}+\gamma _{522} \beta \frac{\partial {\varPsi }_y }{\partial y}} \right) \right. \nonumber \\&\quad -\,\gamma _{24} \left( {\gamma _{240} \frac{\partial ^{2}W}{\partial x^{2}}+\gamma _{622} \beta ^{2}\frac{\partial ^{2}W}{\partial y^{2}}} \right) \nonumber \\&\quad \left. -\,\frac{1}{2}\gamma _{24} \beta ^{2}\left( {\frac{\partial W}{\partial y}} \right) ^{2}+(\gamma _{T2} -\gamma _5 \gamma _{T1} )\Delta T \right] \nonumber \\&\hbox {d}y\hbox {d}x=0\quad (\hbox {immovable}) \end{aligned}$$
(41h)

Equations (37)–(40) can be solved by means of a two-step perturbation technique [12]. Because bending–stretching coupling exists in functionally graded CNTRC 0-plies, the initial deflection caused by thermal bending moments should be determined firstly. It is assumed that the solutions of Eqs. (37)–(40) are

$$\begin{aligned} W(x,y,\tilde{t})= & {} W^{{*}}(x,y)+\tilde{W}(x,y,\tilde{t}) \nonumber \\ {\varPsi }_x (x,y,\tilde{t})= & {} {\varPsi }_x^{*} (x,y)+\tilde{{\varPsi } }_x (x,y,\tilde{t}) \nonumber \\ {\varPsi }_y (x,y,\tilde{t})= & {} {\varPsi }_y^{*} (x,y)+\tilde{{\varPsi } }_y (x,y,\tilde{t}) \nonumber \\ F(x,y,\tilde{t})= & {} F^{{*}}(x,y)+\tilde{F}(x,y,\tilde{t}) \end{aligned}$$
(42)
Table 1 Temperature-dependent material properties for (10, 10) SWCNT [47]
Full size table

in which \(W^{*}(x,y)\) is initial deflection caused by thermal bending moments and \(\tilde{W}(x,y,\tilde{t})\) is additional dynamic deflection. \({\varPsi }_x^{*} (x,y),\, {\varPsi }_y^{*} (x,y)\) and \(F^{*}(x,y)\) are rotations and stress function corresponding to \(W^{*}(x,y)\), while \(\tilde{{\varPsi } }_x (x,y,\tilde{t})\), \(\tilde{{\varPsi } }_y (x,y,\tilde{t})\) and \(\tilde{F}(x,y,\tilde{t})\) corresponding to \(\tilde{W}(x,y,\tilde{t})\) have the similar definitions as \({\varPsi }_x^{*} (x,y),\, {\varPsi }_y^{*} (x,y)\) and \(F^{*}(x,y)\). For the conditions of in-plane movable ends, \(W^{*}(x,y)={\varPsi }_x^{*} (x,y)={\varPsi }_y^{*} (x,y)= F^{*}(x,y)=0\), while for the conditions of in-plane immovable ends, \(W^{*}(x,y), {\varPsi }_x^{*} (x,y),\, {\varPsi }_y^{*} (x,y)\) and \(F^{*}(x,y)\) should satisfy nonlinear thermal bending equations. The second set of equations gives the homogeneous solution of vibration characteristics on the initial deflected plate that can be expressed by

$$\begin{aligned}&\tilde{W}(x,y,\tilde{t})=\varepsilon \left[ A_{11}^{(1)} (\tilde{t})\sin \, mx\sin \, ny\right] \nonumber \\&\quad +\,\varepsilon ^{3}\left[ A_{11}^{(3)} (\tilde{t})\sin \, mx\sin my \right. \nonumber \\&\quad + \left. A_{31}^{(3)} (\tilde{t})\sin 3mx\sin \, ny \right. \nonumber \\&\quad \left. +A_{13}^{(3)} (\tilde{t})\sin \, mx\sin 3ny \right] +O(\varepsilon ^{4}) \end{aligned}$$
(43)
$$\begin{aligned}&\tilde{F}(x,y,\tilde{t})={-B_{00}^{(0)} y^{2}}/2{-b_{00}^{(0)} x^{2}}/2 \nonumber \\&\quad +\,\varepsilon \left[ B_{11}^{(1)} (\tilde{t})+\ddot{B}_{11}^{(3)} (\tilde{t})\right] \sin \, mx\sin \, ny \nonumber \\&\quad +\, \varepsilon \left[ {-B_{00}^{(2)} y^{2}}/{2{-b_{00}^{(2)} x^{2}}/2}+B_{02}^{(2)} (\tilde{t})\cos 2ny \right. \nonumber \\&\quad \left. +\, B_{20}^{(2)} (\tilde{t})\cos 2mx\right] \nonumber \\&\quad +\, \varepsilon ^{3}\left[ {-B_{00}^{(2)} y^{2}}/{2{-b_{00}^{(2)} x^{2}}/2}+B_{02}^{(2)} (\tilde{t})\cos 2ny \right. \nonumber \\&\quad \left. +\, B_{20}^{(2)} (\tilde{t})\cos 2mx\right] \nonumber \\&\quad +\, O(\varepsilon ^{4}) \end{aligned}$$
(44)
$$\begin{aligned}&\tilde{{\varPsi }}_x (x,y,\tilde{t})=\varepsilon \left[ C_{11}^{(1)} (\tilde{t})+\ddot{C}_{11}^{(3)} (\tilde{t})\right] \nonumber \\&\quad \times \cos \, mx\sin \, ny+\varepsilon ^{2}C_{20}^{(2)} (\tilde{t})\sin 2mx \nonumber \\&\quad +\, \varepsilon ^{3}\left[ D_{31}^{(3)} (\tilde{t})\cos 3mx\sin \, ny \right. \nonumber \\&\quad \left. +\, D_{13}^{(3)} (\tilde{t})\cos \, mx\sin 3ny\right] +O(\varepsilon ^{4}) \end{aligned}$$
(45)
$$\begin{aligned}&\tilde{{\varPsi }}_y (x,y,\tilde{t})=\varepsilon \left[ D_{11}^{(1)} (\tilde{t})+\ddot{D}_{11}^{(3)} (\tilde{t})\right] \nonumber \\&\quad \sin \, mx\cos \, ny +\varepsilon ^{2}D_{02}^{(2)} (\tilde{t})\sin 2ny \nonumber \\&\quad + \varepsilon ^{3}\left[ D_{31}^{(3)} (\tilde{t})\sin 3mx\cos \, ny \right. \nonumber \\&\quad \left. +D_{13}^{(3)} (\tilde{t})\sin \, mx\cos 3ny\right] +O(\varepsilon ^{4}) \end{aligned}$$
(46)
$$\begin{aligned}&\lambda _q (x,y,\tilde{t})=\varepsilon \left[ g_1 A_{11}^{(1)} (\tilde{t})+g_4 \ddot{A}_{11}^{(1)} (\tilde{t})\right] \nonumber \\&\quad \sin \, mx\sin \, ny \nonumber \\&\quad +\left( \varepsilon A_{11}^{(1)} (\tilde{t})\right) ^{2}(g_{20} \cos 2mx+g_{02} \cos 2ny) \nonumber \\&\quad + \left( \varepsilon A_{11}^{(1)} (\tilde{t})\right) ^{3}g_3 \sin \, mx\sin \, ny+O(\varepsilon ^{4}) \end{aligned}$$
(47)

It is worth noting that t has been replaced back by \(\tilde{t}\) in Eqs. (43)–(47), and all coefficients can be expressed in form of \(A_{11}^{(1)}(\tilde{t})\). In Eq. (44), \(B_{00}^{(0)}\), \(b_{00}^{(0)}\), \(B_{00}^{(2)}\) and \(b_{00}^{(2)}\) are zero-valued when ends are movable, but when ends are immovable, they can be obtained by solving Eqs. (41d) and (41h) and the detailed expressions are given in [31].

In Eq. (47), \((\varepsilon A_{11}^{(1)} )\) is taken as the second perturbation parameter relating to the dimensionless vibration amplitude \(W_{m}\). From Eq. (43), taking \((x,\, y) = ({\uppi }/2m,\, {\uppi }/2n)\) yields

$$\begin{aligned} \varepsilon A_{11}^{(1)} =\tilde{W}_m -{\varTheta }_1 \tilde{W}_m^3 +\cdots \end{aligned}$$
(48)

Substituting Eq. (48) into Eq. (47) and applying Galerkin procedure, for the case of forced vibration, we have

$$\begin{aligned}&g_{40} \frac{d^{2}\left( \varepsilon A_{11}^{(1)}\right) }{\hbox {d}\tilde{t}^{2}}+g_{41}\left( \varepsilon A_{11}^{(1)} \right) +g_{42} \left( \varepsilon A_{11}^{(1)}\right) ^{2} \nonumber \\&\quad +\,g_{43} \left( \varepsilon A_{11}^{(1)}\right) ^{3}=\bar{{\lambda }}_q \end{aligned}$$
(49)

in which

$$\begin{aligned} \bar{{\lambda }}_q (\tilde{t})=\frac{4}{\pi ^{2}}\int \limits _0^\pi {\int \limits _0^\pi {\lambda _q (x,y,\tilde{t})\sin mx\sin ny\hbox {d}x\hbox {d}y}} \end{aligned}$$
(50)

All symbols used in Eqs. (43)–(49) are described in detail in “Appendix”. If zero-valued initial conditions prevail, i.e., \(\tilde{W}_m (0)=\dot{\tilde{W}}_m (0)=0\), Eq. (49) may then be solved by using the Runge–Kutta method [46]. Substituting these solved solutions back into Eqs. (43)–(46), we obtain both displacements and stress function of the plate.

For the case of free vibration, we have \(\lambda _{q}\)=0. That is,

$$\begin{aligned}&\bar{{\lambda }}_q (\tilde{t})=\frac{4}{\pi ^{2}}\int \limits _0^\pi \int \limits _0^\pi \lambda _q (x,y,\tilde{t}) \nonumber \\&\quad \times \sin mx\sin ny\hbox {d}x\hbox {d}y =0 \end{aligned}$$
(51)

In this case, Eq. (49) becomes

$$\begin{aligned}&g_{40} \frac{d^{2}\left( \varepsilon A_{11}^{(1)}\right) }{\hbox {d}\tilde{t}^{2}}+g_{41} \left( \varepsilon A_{11}^{(1)}\right) +g_{42} \left( \varepsilon A_{11}^{(1)}\right) ^{2} \nonumber \\&\quad +\,g_{43} \left( \varepsilon A_{11}^{(1)}\right) ^{3}=0 \end{aligned}$$
(52)

The solution of Eq. (52) can be written as

$$\begin{aligned} \omega _{\mathrm{NL}} =\omega _\mathrm{L} \left[ {1+\frac{9g_{41} g_{43} -10g_{42}^2 }{12g_{41}^2 }A^{2}} \right] ^{1/2} \end{aligned}$$
(53)

where the dimensionless linear frequency is \(\omega _{\mathrm{L}}=[g_{41}/g_{40}]^{1/2}\), A is the maximal dimensionless deflection of plate, and \(A\!=\!W_m \!=\!{\bar{{W}}_{\max } }/{[D_{11}^{*} D_{22}^{*} A_{11}^{*} A_{22}^{*} ]}^{1/2}\).

5 Numerical results and discussion

Numerical results are presented in this section for free and forced vibration of hybrid cross-ply laminated plates in thermal environments. First, it is needed to determine the effective material properties of FRCs and CNTRCs. It is assumed that FRCs and CNTRCs have the same matrix material and the mechanical properties of matrix are assumed to be \(\rho ^{m} = 1150 \hbox { kg}/\hbox {m}^{3}\), \(\nu ^{m} = 0.34,\, \alpha ^{m} = 45(1+0.0005\Delta T)\times 10^{-6} \hbox { K}^{-1}\) and \(E^{m} = (3.52-0.0034T)\) GPa, in which \(T=T_{0}+\Delta T\) and \(T_{0} = 300 \hbox { K}\) (room temperature). The (10, 10) SWCNTs are selected to be reinforcements in CNTRC, and the detailed material properties for different temperatures are listed in Table 1 [47]. The mass density of SWCNTs is taken to be \(1400 \hbox { kg}/\hbox {m}^{3}\). In computation, three volume fractions of CNTs (0.12, 0.17 and 0.28) are considered and the corresponding efficiency parameters are \(\eta _1 =0.137,\, \eta _2=1.022\) and \(\eta _3 =0.715\) for the case of \(V_{CN}^*=0.12\), and \(\eta _1 =0.142,\, \eta _2 =1.626\) and \(\eta _3=1.138\) for the case of \(V_{CN}^*=0.17\), and \(\eta _1=0.141,\, \eta _2 =1.585\) and \(\eta _3 =1.109\) for the case of \(V_{CN}^*=0.28\). For FRC, the volume fraction of graphite fibers is 0.6 and the material properties of which are [48]: \(E_{11}^f = 233.05 \hbox { GPa},\, E_{22}^f = 23.1 \hbox { GPa},\, G_{12}^f = 8.96 \hbox { GPa},\, \nu ^{f} = 0.2,\, \alpha _{11}^f = -0.54\times 10^{-6 }\hbox {K}^{-1},\, \alpha _{22}^f =10.08\times 10^{-6} \hbox { K}^{-1}\) and \(\rho ^{f} = 1750 \hbox { kg}/\hbox {m}^{3}\). The foundation is made of hydrogenated nitrile butadiene rubber (HNBR) filled with 21% carbon black (CB). The temperature-dependent properties of HNBR/CB [49] are \(\nu _{s} = 0.499\) and \(E_{s} = (29.6-0.25 \Delta T+0.0009\Delta T^{ 2})\) MPa. The above values are used in the following examples. In addition, we assume that out-plane shear moduli \(G_{13}=G_{12}\) and \(G_{23} = 1.2G_{12}\). Two layups of hybrid laminated plate (\([0^{C}/90^{F}]_{2}\) and \([0^{C}/90^{F}]_{\mathrm{s}}\)) where the \(0^{C}\)-plies (i.e., CNTRC 0-plies) have different distributions of CNTs are considered. For the type 1, referred to as FG-1, the \(0^{C}\)-plies above the middle plane are FG-V types, while the \(0^{C}\)-plies below the middle plane are FG-\({\Lambda }\) types, whereas for the type 2, referred to as FG-2, the \(0^{C}\)-plies above the mid-plane are FG-\({\Lambda }\) types, while the \(0^{C}\)-plies below the mid-plane are FG-V types. It is assumed that the layers with the same layup angle contain the same matrix density. Then, the matrix crack density is expressed by \((\rho _{crk}^0 ,\,\rho _{crk}^{90})\), in which the superscripts 0 and 90 denote 0-plies and 90-plies, respectively. It is worth noting that the stiffness reduction model presented in Sect. 2 is adopted to UD-CNTRC layer, but not to FG-CNTRC layer.

Table 2 Comparison of the dimensionless fundamental frequency \((\bar{{\omega }}={\varOmega }_\mathrm{L} ({a^{2}}/h)\sqrt{{\rho _0 }/{E_0}})\) of CNTRC plates with simply supported boundary condition \((a/b = 1,\, T = 300\hbox { K})\)
Full size table

5.1 Validation

To validate the present method, four test examples for free and forced vibration of composite laminated plates and CNTRC plates are resolved.

The dimensionless natural frequencies of UD and FG-V CNTRC plates are calculated and compared in Table 2 with the finite element method (FEM) results of Zhu et al. [50] based on the first-order shear deformation plate theory. The dimensionless frequency is defined as \(\bar{{\omega }}={\varOmega }_{\mathrm{L}} ({a^{2}}/h)\sqrt{{\rho _0}/{E_0}}\), where \(\rho _{0}\) and \(E_{0}\) are the reference values of mass density and Young’s modulus of the matrix at room temperature. In this example, the CNT volume fractions and corresponding efficiency parameters \(\eta _j (j=1,2,3)\) are taken to be: \(\eta _1 =0.149,\, \eta _2 =0.934\) and \(\eta _3=0.934\) for the case of \(V_{CN}^*=0.11\), and \(\eta _1=0.150,\, \eta _2 =0.941\) and \(\eta _3 =0.941\) for the case of \(V_{CN}^*=0.14\), and \(\eta _1 =0.149,\, \eta _2 =1.381\) and \(\eta _3 =1.381\) for the case of \(V_{CN}^*\)=0.17. Note that, in this example, \(G_{12}=G_{13}=G_{23}\).

Fig. 2
figure 2

Comparisons of cracked to intact linear frequency ratios \({{\varOmega }_1^\mathrm{c}}/{{\varOmega }_1^0}\) for [0/90/0/90] laminated plates with various values of a / b

Full size image
Fig. 3
figure 3

Comparisons of cracked to intact linear frequency ratios \({{\varOmega }_1^\mathrm{c}}/{{\varOmega }_1^0}\) for [0/90/0/90] laminated plates with various values of \(h_{i}/h\)

Full size image
Fig. 4
figure 4

Comparisons of dynamic response for isotropic square plate subjected to a suddenly applied uniform load

Full size image
Fig. 5
figure 5

Comparisons of dynamic response for laminated plates subjected to a suddenly applied uniform load

Full size image
Table 3 Fundamental frequencies \(\tilde{{\Omega } }={\Omega }_{\mathrm{L}} ({b^{2}}/h)\sqrt{{E_0}/{\rho _0}}\) for \([0^{C}/90^{F}]_{2}\) hybrid laminated plates with different values of \(b/h\, (a/b = 1,\, T = 300\hbox { K})\)
Full size table
Table 4 Fundamental frequencies \(\tilde{{\Omega } }={\Omega }_{\mathrm{L}} ({b^{2}}/h)\sqrt{{E_0}/{\rho _0}}\) for \([0^{C}/90^{F}]_{\mathrm{s}}\) hybrid laminated plates with different values of \(b/h\, (a/b = 1,\, T = 300\hbox { K})\)
Full size table
Table 5 Comparisons of fundamental frequencies \(\tilde{{\Omega }}={\Omega }_\mathrm{L} ({b^{2}}/h)\sqrt{{E_0 }/{\rho _0}}\) for \([0^{C}/90^{F}]_{2}\) hybrid laminated plates with different values of \(b/h\, (a/b = 1, b/h =20,\, T = \hbox {400 and 500 K})\)
Full size table
Table 6 Comparisons of fundamental frequencies \(\tilde{{\Omega } }={\Omega }_{\mathrm{L}} ({b^{2}}/h)\sqrt{{E_0}/{\rho _0}}\) for \([0^{C}/90^{F}]_{\mathrm{s}}\) hybrid laminated plates with different values of \(b/h \, (a/b = 1,\, b/h =20,\, T = \hbox {400 and 500 K})\)
Full size table
Table 7 Comparisons of nonlinear-to-linear ratios \({\omega _{\mathrm{NL}} }/{\omega _\mathrm{L}}\) for \([0^{\mathrm{C}}/90^{\mathrm{F}}]_{\mathrm{S}}\) hybrid laminated plates in thermal environments \((a/b = 1,\, b/h = 20,\, V_{cn}^{*} = 0.12)\)
Full size table

Secondly, the curves of linear fundamental frequency ratios \((\bar{{\omega }}={\varOmega }_\mathrm{L} ({a^{2}}/h)\sqrt{{\rho _0 }/{E_0}})\) for matrix cracking to intact matrix with different values of a / b and hi/h are compared in Figs. 2 and 3 with the theoretical results of Adali and Makins [9] based on the classical laminated thin plate theory. In Figs. 2 and 3, \(h_{i}\) is defined as the thickness of inner layers (the second and third layers) of [0/90/0/90] plate. The plate is made of graphite/epoxy, and the material properties are: \(E_{11} = 132.4 \hbox { GPa}, E_{22}=E_{33} = 10.8 \hbox { GPa},\, G_{12}=G_{13} = 5.65 \hbox { GPa},\, v_{12}=v_{13} =0.24\) while \(v_{23} = 0.49\).

As a comparison for dynamic response, the curves of central deflection as function of time for isotropic square plates subjected to a suddenly applied uniform load \(1.0\times 10^{6}\) Pa are compared in Fig. 4 with the FEM results of Praveen and Reddy [51]. The side length and thickness of the plate are 0.2 m and 0.01 m, respectively. Two kinds of isotropic materials are considered. The material properties are \(E=70\hbox { GPa},\, \nu =0.3\) and \(\rho =2707\hbox {kg}/\hbox {m}^{3}\) for aluminum, and \(E=151\hbox { Gpa},\, \nu =0.3\) and \(\rho =3000\hbox {kg}/\hbox {m}^{3}\) for zirconia. The dimensionless deflection is defined as \({\bar{{W}}E_m h}/{q_0 a^{2}}\), while dimensionless time is defined as \(t\sqrt{{E_m }/{\left( {a^{2}\rho } \right) }}\). Note that the effect of temperature field is not considered in this example.

Finally, the curves of central deflection as function of time for a laminated plate subjected to a suddenly applied uniform load are plotted and compared in Fig. 5 with the analytical results of Reddy [52] and the generalized differential quadrature (GDQ) method results of Maleki et al. [53]. Both the length and width of the plate are 25 cm, and the thickness is 1 cm. Each ply is idealized as a homogeneous orthotropic material and is also assumed to have the same thickness. The mass density of the plate is \(8\times 10^{-6} \hbox { Ns}^{2}/\hbox {cm}^{4}\), and mechanical properties are: \(E_{22} = 2.1\times 10^{-6} \hbox { N}/\mathrm{cm}^{2}, \quad E_{11} = 25E_{22},\, G_{12 }=G_{13} =0.5E_{2},\, G_{23} = 0.2E_{22}\) and \(v_{12} = 0.25\). These four comparison studies show that the results from the present method are in good agreement with the existing results.

5.2 Free vibration

Several numerical examples are provided to investigate the free vibration of hybrid laminated plates with matrix cracking. Tables 3, 4, 5 and 6 show the effects of crack density on the fundamental frequencies of the \([0^{C}/90^{F}]_{2}\) and \([0^{C}/90^{F}]_{\mathrm{s}}\) hybrid laminated plates under both movable and immovable end conditions at T = 300K, 400K and 500K. Two types (FG-1 and FG-2) of FG-CNTRC layers are considered, and UD-CNTRC layers are also considered as a comparator. In the case of movable end conditions, the initial in-plane force is not considered here. Hence, the natural frequency of the plate with movable ends is the same as that of the same plate with immovable ends at T=300 K, as shown in Tables 5 and 6. It can be seen that the natural frequencies are decreased with increase in crack density and temperature, but are increased with increase in CNT volume fraction. The different values of b / h are also considered in Tables 3 and 4. It can be seen that the natural frequencies rise with increase in b / h. From Table 5, it can be seen that the natural frequencies of the unsymmetric cross-ply laminated plate with movable ends are different from those of the same plate with immovable ends when the temperature rise is under consideration. In contrast, from Table 6, for the symmetric cross-ply laminated plate, the thermal bending moments vanish and the results for the symmetric cross-ply laminated plate with either movable or immovable end conditions are identical. It can be seen that the unsymmetric cross-ply laminated plate with movable ends has a higher natural frequency than the same plate with immovable ends does at \(T= 400\) and 500 K. It can also be seen that the natural frequency of the hybrid laminated plate with FG-1 \(0^{\mathrm{C}}\)-plies is higher than that of the hybrid laminated plate with UD \(0^{\mathrm{C}}\)-plies, whereas the hybrid laminated plate with FG-2 \(0^{\mathrm{C}}\)-plies is lower than that of the hybrid laminated plate with UD \(0^{\mathrm{C}}\)-plies.

Table 7 presents the nonlinear-to-linear frequency ratios \({\omega _{\mathrm{NL}}}/{\omega _\mathrm{L}}\) for \([0^{C}/90^{F}]_{2}\) and \([0^{C}/90^{F}]_{\mathrm{s}}\) hybrid laminated square plates at \(T=\hbox {300 K}\), 400 and 500 K. The dimensionless frequency is defined as \(\tilde{\Omega }= \Omega _{\mathrm{L}} ({b^{2}}/h)\sqrt{{E_0}/{\rho _0}}\). The CNT volume fraction is taken to be 0.12, and b / h is taken to be 20. It can be seen that the fundamental frequencies are reduced, but the nonlinear-to-linear frequency ratios are increased with increase in temperature. The results show that the fundamental frequencies of FG-1 CNTRC plate are higher, but the nonlinear-to-linear frequency ratios of the same plate are lower than those of plates with uniform or unsymmetrical distribution of CNTs. Hence, in the following examples, except for Fig. 9, only FG-1-type hybrid laminated plate is considered. The plate end conditions are assumed to be immovable.

Figures 6, 7 and 8 show, respectively, the effects of crack density, CNT volume fraction and foundation stiffness on the nonlinear-to-linear frequency ratios \({\omega _{\mathrm{NL}}}/{\omega _\mathrm{L}}\) of \([0^{C}/90^{F}]_{\mathrm{s}}\) hybrid laminated plates. The plate geometric parameter \(a/b = 1\) and \(b/h= 20\). In Fig. 6, the CNT volume fraction is taken to be 0.12, and the temperature is \(T = \hbox {300K}\). Three crack densities are considered. The crack densities are \((\rho _{crk}^0 ,\rho _{crk}^{90} )=(0.5,0.0)\) for the case of the cracks occurring only in CNTRC 0-plies, \((\rho _{crk}^0 ,\rho _{crk}^{90})=(0.0,0.5)\) for the case of the cracks occurring only in FRC 90-plies, \((\rho _{crk}^0 ,\rho _{crk}^{90})=(0.5,0.5)\) for the case of the cracks occurring in both CNTRC 0-plies and FRC 90-plies and \((\rho _{crk}^0 ,\rho _{crk}^{90} )=(0.0,0.0)\) for the plate without any matrix cracks. It can be found that the nonlinear-to-linear frequency ratio curves become lower when the cracks occur. For UD-type \([0^{C}/90^{F}]_{\mathrm{s}}\) laminated plate, the nonlinear-to-linear frequency ratio curves for the two cases of cracks occurring in 0-plies only and in 90-plies only are close. In Fig. 7, the CNT volume fraction is taken to be 0.12, 0.17 and 0.28, and in Fig. 8, the CNT volume fraction is taken to be 0.28. In Figs. 7 and 8, the temperature is taken \(T= \hbox {400 K}\), and the crack densities are taken to be (0.5, 0.5) for the UD-type CNTRC and (0.0, 0.5) for the FG-1-type CNTRC. Note that in Fig. 8 TD represents the material properties of foundation that are temperature dependent and TID represents the material properties of foundation that are independent of temperature, i.e., \(E_{s} = 29.6 \hbox { MPa}\). The depth of the foundation is taken \(H_{s} = 20 \hbox { mm}\), whereas \(H_{s} = 0\) means the plate without any elastic foundation. Like in the case of intact laminated plate, the nonlinear-to-linear frequency ratio curves are decreased with increase in CNT volume fraction or foundation stiffness. Moreover, when the foundations are TID, the nonlinear-to-linear frequency ratio curves fall further compared with the TD ones.

Fig. 6
figure 6

Effect of crack densities on the frequency–amplitude curves of hybrid laminated plates with doubly matrix cracking

Full size image
Fig. 7
figure 7

Effect of CNT volume fraction on the frequency–amplitude curves of hybrid laminated plates with doubly matrix cracking

Full size image
Fig. 8
figure 8

Effect of foundation stiffness on the frequency–amplitude curves of hybrid laminated plates with doubly matrix cracking

Full size image
Fig. 9
figure 9

Effects of FG-CNTRC types on the dynamic response of matrix-cracked hybrid laminated plate

Full size image
Fig. 10
figure 10

Effects of crack density on the dynamic response of matrix-cracked hybrid laminated plate

Full size image

5.3 Forced vibration

For all cases below, the aspect ratio a / b of laminated plate is 1 and the width to thickness ratio b / h is 10. The deflected mode is taken to be \((m,\, n) = (1, 1)\). The time step for Runge–Kutta method is \(\Delta \tau = 0.5 {\upmu }\hbox {s}\). The dynamic load is assumed to be a suddenly applied uniform load with \(q_{0} = 1 \hbox { MPa}\). The boundary condition is assumed to be immovable ends. The layup of laminate is \([0^{C}/90^{F}]_{2}\).

Figure 9 presents the dynamic response of hybrid laminated plates with two types of FG-CNTRC layers. The results are also compared with those of the plate containing UD-CNTRC layers at \(T = \hbox {400K}\). The CNT volume fraction is taken to be 0.28, and the crack density for \(0^{C}\)-plies and \(90^{F}\)-plies is taken to be (0.0, 0.5). It can be found that the plate with FG-1-type CNTRC layer has the lowest central deflection, while the plate with FG-2-type CNTRC layer has the highest central deflection.

Fig. 11
figure 11

Effects of CNT volume fraction on the dynamic response of matrix-cracked hybrid laminated plate

Full size image

Figure 10 shows the effect of the crack density on the dynamic response of hybrid laminated plates with UD-CNTRC layers at room temperature (\(T = 300\hbox { K}\)). The CNT volume fraction is taken to be 0.12. As expected, the central deflection is higher when the density of matrix cracks is increased. It is worth noting that the crack occurring in 90-plies may have greater influence on the central deflection of the plate than the same crack occurring in 0-plies.

Figures 11, 12 and 13 show, respectively, the effects of the CNT volume fraction, temperature change and foundation stiffness on the central deflection of \([0^{C}/90^{F}]_{2}\) hybrid laminated plates with FG-1-type CNTRC layers. The crack densities are taken to be (0.0, 0.5). From Fig. 11, it can be seen that under the room temperature \((T = 300 \hbox { K})\), the central deflection becomes lower when the CNT volume fraction is increased. In Fig. 12, the CNT volume fraction is taken to be 0.17. The results show that the central deflection becomes higher when temperature rises. In Fig. 13, we study the effect of foundation stiffness on the central deflection of the plate with \(V_{CN}^{*} = 0.17\) at \(T = 400\,\hbox {K}\). The material properties are the same as used in Fig. 8. It can be found that the curve of central deflection versus time becomes lower when foundation stiffness is increased.

Fig. 12
figure 12

Effects of temperature on the dynamic response of matrix-cracked hybrid laminated plate

Full size image
Fig. 13
figure 13

Effects of foundation stiffness on the dynamic response of matrix-cracked hybrid laminated plate

Full size image

6 Conclusions

Nonlinear dynamic responses of matrix-cracked hybrid laminated plates resting on a Pasternak elastic foundation in thermal environments have been presented on the basis of a refined self-consistent model and a higher-order shear deformation plate theory. Two cases of in-plane boundary conditions are considered. The parametric studies have been carried out after four comparison studies which demonstrated the accuracy and effectiveness of the present method. The numerical results illustrate that the matrix crack has a significant effect on the linear frequencies and dynamic responses of hybrid laminated plates, but this effect is less pronounced on the nonlinear-to-linear frequency ratios of the same plate. The crack density also plays an important role on the dynamic deflections of the plate.