1 Introduction

In this article, we discuss the finite time stabilization and the fixed time stabilization for a high-order class of BAM delayed NNs. To investigate the FTSB and the FXTSB of the above-mentioned problem, we consider the following:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\mu }_i(t)&{}=-\,c_i\mu _i(t)+\sum \limits _{j=1}^na^1_{ij}f^{(1)}_{j}\big (\nu _j(t)\big )+\sum \limits _{j=1}^nb^1_{ij}g^{(1)}_{j}\big (\nu _j(t-\tau (t))\big )\\ &{}\quad +\sum \limits _{j=1}^nT_{ijk}g^{(1)}_{k}\big (\nu _k(t-\tau (t))g^{(1)}_{j}\big (\nu _j(t-\tau (t))\big )+u^1_{i},\\ \dot{\nu }_j(t)&{}=-\,d_j\nu _j(t)+\sum \limits _{i=1}^na^2_{ji}f^{(2)}_{i}\big (\mu _i(t)\big )+\sum \limits _{i=1}^nb^2_{ji}g^{(2)}_{i}\big (\mu _i(t-\sigma (t))\big )\\ &{}\quad +\sum \limits _{i=1}^nO_{jik}g^{(2)}_{k}\big (\mu _k(t-\sigma (t))g^{(2)}_{i}\big (\mu _i(t-\sigma (t))\big )+u^2_{j} \end{array}\right. } \end{aligned}$$
(1)

in which \(\mu _i(.)\) and \(\nu _j(.)\) stand for the neuron state, \(C=diag\left( c_1,\ldots ,c_n\right) \) and \(D=diag\left( d_1,\ldots ,d_n\right) \) with \(c_i>0\) and \(d_j>0\) stand respectively for the rate of the reset of the ith and jth unit in the resting state and disconnected of external inputs of network; \(A_1=\left( a^1_{ij}\right) _{n\times n}\), \(A_2=\left( a^2_{ji}\right) _{n\times n}\), \(B_1=\left( b^1_{ij}\right) _{n\times n}\) , \(B_2=\left( b^2_{ji}\right) _{n\times n}\) and \(T_{i}=[T_{ijk}]_{n\times n}\), \(O_{j}=[O_{jik}]_{n\times n}\) stand for the interconnection weight matrices of the neurons and the second-order synaptic weights matrices. \(f_1=\left( f^{(1)}_{1},\ldots ,f^{(1)}_{n}\right) ^T\), \(f_2=\left( f^{(2)}_{1},\ldots ,f^{(2)}_{n}\right) ^T\), \(g_1=\left( g^{(1)}_{1},\ldots ,g^{(1)}_{n}\right) ^T,\) and \(g_2=\left( g^{(2)}_{1},\ldots ,g^{(2)}_{n}\right) ^T\) stand for the neuron activation functions. \(0<\tau (.)\le \bar{\tau }\) and \(0<\sigma (.)\le \bar{\sigma }\) stand for the transmission delays. The initial condition

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _i(s)&{}=\phi _i(s),\quad s\in [-\bar{\tau },~0],\\ \nu _j(s)&{}=\psi _j(s),\quad s\in [-\bar{\sigma },~0]. \end{array}\right. } \end{aligned}$$

where \(\phi _i(.)\in C\left( [-\bar{\tau }, 0],\mathbb {R}^n\right) \) and \(\psi _j(.)\in C\left( [-\bar{\sigma }, 0],\mathbb {R}^n\right) \).

It is well known that the lower-order class of NNs is expected to produce the poorest quality of solution with a great complexity as measured by the order of the network [7]. Also, the high-order class of NNs offers faster convergence rate, higher fault tolerance and greater storage capacity [63] which explains the use of this class in many applications such as robotic manipulator, the resolution of optimization problems and other fields [6, 8,9,10, 13, 27, 33, 35, 44].

In practice, the time delay often occurs in the implementation of NNs [5, 9, 14, 26, 32, 36, 45, 46] and causes a high complexity in the dynamic behaviours of network. Also it can destabilize the system and create some oscillation and bifurcation in NNs which explain the intensity of research around the effect of the delays in the dynamic behaviours of NNs [4, 11, 17, 22, 25, 29, 31, 62].

In 1988, Kosto was introduced the class of bidierctionnel associative memories (BAM) neural networks [21]. Due to its range in many areas such that pattern recognition and combinatorial optimization this class of NNs it becomes one of the most important class of delayed NNs. Recently, many authors has been extensively studied the class of BAM neural networks. In fact, the results around the Lyapunov stability of this class are obtained in [51,52,53]. In [68, 75], the periodic solutions of this class of NNs is investigated bases on the coincidence degree theorem. Moreover, the exponential dichotomy and the fixed point theorems are used for the study of the almost periodic solution [37, 74] and reference therein.

Contrary to the asymptotic convergence that can implies a large time (infinite) for obtaining the desired precision, the FTS ensure that the physical process achieves the convergence in a specific time. Thanks to this proprieties, this concept shows nice features such as robustness to uncertainties [19].

From the practical standpoint such as robotics, the challenge in system theory is the design of suitable controllers able to bring a system back to a desired position as quickly as possible. For example, if the finite time synchronization does not guarantee and only the exponential synchronization is considered, the coupling protocol should exist for ever [38]. Otherwise, for chaotic oscillator, a small error can produce a high difference between nodes. In addition, FTS can lead to better NNs performances in the disturbance rejection [38]. To summarize, the study of FTS is of major interest both in theoretical analysis and real-life applications.

Recently, the FTS problems of NNs has been widely investigated [2, 39,40,41, 57, 60, 61, 64,65,66,67]. However, despite the design of many finite time controllers for different kinds of NNs, there is no general controller able to guarantee the FTSB of a lower order and a high-order class of delayed BAM NNs because it is delicate to design a Lyapunov–Krasovskii functional (LKF) satisfying the derivative condition of the FTS of delayed systems [49].

Despite the contribution that provides the FTS, the time function indicating when the trajectories reach the equilibrium point, variously known as the settling-time depends on the initial conditions of the dynamical systems. On the one hand, the variation of the initial values has a great effect on the estimation of the settling time. On the other hand, in practice, the knowledge in advance of the initial conditions is very difficult [20]. In this context, the concept of fixed time stability occurs naturally where Polyakov was the first to introduce these notation in [55] by imposing the boundedness of the settling time to FTS systems. In practice, the fixed time stability is encountered in control problems such power systems [50], fixed-time observer [47]. In the existing literature, the research around the FXTS has just started and there are few results on the FXTS concept. One of the most important results on this concept is the extension of the results of Polyakov given in [55] to the non-autonomous class of differential equations [56]. Hence, it is urgent establish some new criteria on FXTS.

Motivated by the above discussion, this article deals with the FTSB and FXTSB problems for a lower order and high-order class of delayed BAM NNs. The main aim of this paper is to design a control low able to stabilize in finite time and fixed time the high-order delayed BAM NNs and to obtain a time convergent more accurate and with a high-precision.

The rest of this article is organized as follows. The FTSB and FXTSB of high-order BAM NNs is discussed in Sect. 3 where some sufficient general conditions are included in the control low and two kinds of controller are designed which include a delayed feedback control and a free-delay controller. Then, two numerical examples with graphical illustration are given to appear the effectiveness of our main results in Sect. 4. Finally, some concluding remarks are drawn in Sect. 5.

2 Preliminaries

Throughout this article, the following notations are used.

  • \(\mathbf {C([a,~b],~\mathbb {R}^n)}\) denotes the space formed by the continuous functions \(\phi ~:[a,~b]\rightarrow \mathbb {R}^n\) equipped with uniform norm as follows: \(\Vert \phi \Vert =\sup \nolimits _{a\le s\le b}\Vert \phi (s)\Vert \);

  • \(\langle .,~.\rangle \) stands for the inner product of Euclidean space.

  • For any vector \(x = (x_1,\ldots , x_n)^T\in \mathbb {R}^n\), we define \(Sign(x) = (sign(x_1), \ldots , sign(x_n))^T\);

  • a function \(\nu ~: \mathbb {R}_+\rightarrow \mathbb {R}_+\) is radially unbounded if \(\nu (x)\rightarrow +\infty \), as \(\Vert x\Vert \rightarrow +\infty \);

We also introduce the following assumptions:

  • \((\mathbf {H_1})\): There exist positive constants \(L_i^{f_k},~L_j^{g_{k}},~ k=1,2.\) such that

    $$\begin{aligned} \frac{\left| f^{(1)}_{i}(x)-f^{(1)}_{i}(y)\right| }{|x-y|}&\le L_i^{f_1},\quad \frac{\left| f^{(2)}_{j}(x)-f^{(2)}_{j}(y)\right| }{|x-y|}\le L_j^{f_2};\\ \frac{\left| g^{(1)}_{i}(x)-g^{(1)}_{i}(y)\right| }{|x-y|}&\le L_i^{g_1},\quad \frac{\left| g^{(2)}_{j}(x)-g^{(2)}_{j}(y)\right| }{|x-y|}\le L_j^{g_2}. \end{aligned}$$

    for all \(x,~y\in \mathbb {R}\) and \(1\le i,j\le n\).

  • \((\mathbf {H_2})\): For all \(1\le i\le n,\)

    $$\begin{aligned} f^{(1)}_{i}(0)=g^{(1)}_{i}(0)=f^{(2)}_{i}(0)=g^{(2)}_{i}(0)=0 \end{aligned}$$

    and

    $$\begin{aligned} \left| f^{(1)}_{i}(x)\right|<F^1_{i},~\left| f^{(2)}_{i}(x)\right|<F^2_{i},~\left| g^{(1)}_{i}(x)\right|<G^1_{i},~\left| g^{(2)}_{i}(x)\right| <G^2_{i}. \end{aligned}$$

  • \((\mathbf {H_3})\): For any positive definite matrix P, \(P\bar{B}_i,~i=1,2\) are \(n\times n\) diagonal positive definite matrix where \(\bar{B}_1=\left( B_1+\varGamma ^TT^*\right) \), \(\bar{B}_2=\left( B_2+\varTheta ^TO^*\right) \).

2.1 Model Description

Let \(\mu ^*=(\mu _1^*,~\ldots ,~\mu _n^*)^T\) and \(\nu ^*=(\nu _1^*,~\ldots ,~\nu _n^*)^T\) be an equilibrium point of System (1), by a simple transformation \(x(t) = \mu (t)-\mu ^*\) and \(y(t) = \nu (t)-\nu ^*\), we can shift the equilibrium point \((\mu ^*,\nu ^*)^T\) to the origin and system (1) can be turned into the \((x-y)\) form (see [43])

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)&{}=-\,C\;x(t)+A_1\;F_1\left( y(t)\right) +B_1\;G_1\left( y(t-\tau (t))\right) +\varGamma ^TT^*\; G_1\left( y(t-\tau (t))\right) \\ \dot{y}(t)&{}=-\,D\;y(t)+A_2\;F_2\left( x(t)\right) +B_2\;G_2\left( x(t-\sigma (t))\right) +\varTheta ^TO^* \;G_2\left( x(t-\sigma (t))\right) \end{array}\right. } \end{aligned}$$
(2)

where

$$\begin{aligned} F_1(y)&=f_1(y+\nu ^*)-f_1(\nu ^*),\; F_2(x)=f_2(x+\mu ^*)-f_2(\mu ^*);\\ G_1(y)&=g_1(y+\nu ^*)-g_1(\nu ^*),\; G_2(x)=g_2(x+\mu ^*)-g_2(\mu ^*). \end{aligned}$$
$$\begin{aligned} \xi _{i}&={\left\{ \begin{array}{ll} \frac{T_{ijk}}{T_{ijk}+T_{ikj}}f_k\left( x_k(t-\tau (t)\right) +\frac{T_{ikj}}{T_{ijk}+T_{ikj}}f_k(x_k^*)~&{}\text {if}~T_{ijk}+T_{ikj}\ne 0\\ 0\quad &{} \text {if}~T_{ijk}+T_{ikj}\ne 0 \end{array}\right. }\\ \zeta _{i}&={\left\{ \begin{array}{ll} \frac{O_{ijk}}{O_{ijk}+O_{ikj}}f_k\left( x_k(t-\tau (t)\right) +\frac{O_{ikj}}{O_{ijk}+O_{ikj}}f_k(x_k^*)~&{}\text {if}~O_{ijk}+O_{ikj}\ne 0\\ 0\quad &{} \text {if}~O_{ijk}+O_{ikj}\ne 0 \end{array}\right. } \\ T_i&=[T_{ijk}]_{n\times n},~T^*=[T_1+T_1^T,~\ldots ,~T_n+T_n^T]^T,~ \xi _{ij}=[\xi _{ij1},~\ldots ,~\xi _{ijn}]^T;\\ \xi _i&=[\xi _{i1}^T,~\ldots ,~\xi _{in}^T]^T,~\varGamma =[\xi _1,~\ldots ,~\xi _n]^T;\\ O_i&=[O_{ijk}]_{n\times n},~O^*=[O_1+O_1^T,~\ldots ,~O_n+O_n^T]^T,~ \zeta _{ij}=[\zeta _{ij1},~\ldots ,~\zeta _{ijn}]^T;\\ \zeta _i&=[\zeta _{i1}^T,~\ldots ,~\zeta _{in}^T]^T,~\varTheta =[\zeta _1,~\ldots ,~\zeta _n]^T. \end{aligned}$$

We will use System (2) for the proof of the main results of our article.

2.2 Definitions and Lemmas

Now, we recall some useful lemmas and definitions in what follows.

Lemma 1

([15]) For a positive definite matrix \(Q\in \mathbb {R}^{n\times n}\) and any vectors \(x,~y\in \mathbb {R}^n\) and \(\epsilon >0\), the following inequality holds:

$$\begin{aligned} 2x^Ty\le \epsilon ^{-1}x^TQ^{-1}x+\epsilon y^TQy. \end{aligned}$$

Lemma 2

([18]) If \(a_1,\ldots ,a_n,~r_1,~r_2\in \mathbb {R}\) with \(0<r_1<r_2,\) then the following inequality holds

$$\begin{aligned} \left[ \sum \limits _{i=1}^n|a_i|^{r_2}\right] ^{\frac{1}{r_2}} \le \left[ \sum \limits _{i=1}^n|a_i|^{r_1}\right] ^{\frac{1}{r_1}}, \\ \left[ \frac{1}{n}\sum \limits _{i=1}^n|a_i|^{r_2}\right] ^{\frac{1}{r_2}} \ge \left[ \frac{1}{n}\sum \limits _{i=1}^n|a_i|^{r_1}\right] ^{\frac{1}{r_1}}, \end{aligned}$$

Lemma 3

([64]) If \(b_i\ge ,~i=1,\ldots ,n\) and \(\delta >1\) then the following inequality holds

$$\begin{aligned} \sum \limits _{i=1}^nb_i^\delta \ge n^{1-\delta }\left[ \sum \limits _{i=1}^nb_i\right] ^{\delta }. \end{aligned}$$

Let \(\varOmega _1\) and \(\varOmega _2\) be two open subsets of \(C\left( [-\bar{\tau },~0]\right) \) and \(C\left( [-\bar{\sigma },~0]\right) \) respectively such that \(0\in \varOmega _1\cap \varOmega _2 \).

Now, we introduce the notion of finite time stability and fixed time stability.

Definition 1

([48]): The zero equilibrium point of System (1) is finite time stable (FTS) if:

  1. (i)

    The equilibrium of System (1) is Lyapunov stable;

  2. (ii)

    For any state \(\phi (.)\in \varOmega _1,\) and \(\psi (.)\in \varOmega _2,\) there exists \(0\le T(\phi ,\psi )<+\infty \) such that every solution of System (1) satisfies \(x(t,~\phi )=y(t,~\psi )=0\) for all \(t\ge T(\phi ,\psi ).\)

The functional:

$$\begin{aligned} T_0(\phi ,\psi )&=\inf \left\{ T(\phi ,\psi )\ge 0:~x(t,~\phi )=y(t,~\psi )=0,~~\forall t\ge T(\phi ,\psi )\right\} \end{aligned}$$

is called the settling time of System (1).

Lemma 4

([48]) Consider the non autonomous System

$$\begin{aligned} \dot{x}(t)=f\left( t,x(t)\right) \end{aligned}$$
(3)

with uniqueness of solutions in forward time. If there exist two functions \(\nu \) and r of class \(\mathscr {K}\) and a continuous functional \(V:~\varOmega \rightarrow \mathbb {R}_+\) such that

  1. (i)

    \(\nu \left( \Vert \phi (0\Vert \right) \le V(\phi );\)

  2. (ii)

    \(D^+V(\phi )\le -r\left( V(\phi )\right) \) with

    $$\begin{aligned} \int \limits _0^\epsilon \frac{dz}{r(z)}<\infty ,\quad \forall \epsilon >0,\quad ~\phi \in \varOmega . \end{aligned}$$

then, System (3) is FTS with a settling time satisfying the inequality

$$\begin{aligned} T_0(\phi )\le \int \limits _0^{V(\phi )}\frac{dz}{r(z)}. \end{aligned}$$

In particular, if \(r(V)=\lambda V^\rho \) where \(\lambda >0,~\rho \in (0,~1),\) then the settling time satisfies the inequality

$$\begin{aligned} T_0(\phi )\le \int \limits _0^{V(\phi )}\frac{dz}{r(z)}=\frac{V^{1-\rho }(0,~\phi )}{\lambda (1-\rho )}. \end{aligned}$$
(4)

Definition 2

([55]) The origin of System (1) is said to be fixed time stable if it is FTS and the settling time function \(T_0(\phi )\) is bounded for any \(\phi \in \mathbb {R}^n\), i.e., there exists \(T_{\max }>0\) such that \(T(\phi )\le T_{\max }\) for all \(\phi \in \mathbb {R}^n\).

Lemma 5

([55]) If there exist a continuous, positive definite and radially unbounded functional \(V:~\varOmega \rightarrow \mathbb {R}_+\) such that any solution z(.) of System (1) satisfies

$$\begin{aligned} \dot{V}(z(t))\le -\left( aV^\delta (z(t))+bV^\theta (z(t))\right) ^k \end{aligned}$$
(5)

with \(a,b,\delta ,\theta ,k>0\) and \(\delta k>1,~\theta k<1\), then the origin of System (1) is fixed time stable, and the settling time \(T(\phi )\) is estimated by

$$\begin{aligned} T(\phi )\le T^1_{\max }\triangleq \frac{1}{a^k(\delta k-1)}+\frac{1}{b^k(1-\theta k)}. \end{aligned}$$

Lemma 6

([55]) If there exist a continuous, positive definite and radially unbounded functional \(V:~\varOmega \rightarrow \mathbb {R}_+\) such that any solution z(.) of System (1) satisfies

$$\begin{aligned} \dot{V}(z(t))\le -\left( aV^\delta (z(t))+b\right) ^k \end{aligned}$$
(6)

with \(a,b,\delta ,k>0\) and \(\delta k>1\), then the origin of System (1) is fixed time stable, and the settling time \(T(\phi )\) is estimated by

$$\begin{aligned} T(\phi )\le T^2_{\max }\triangleq \frac{1}{b^k}\left( \frac{b}{a}\right) ^{\frac{1}{\delta }} \left( 1+\frac{1}{\delta k-1}\right) . \end{aligned}$$

3 Main Results

In this section, firstly some sufficient general conditions for the FTSB of the target NNs are established and some new kinds of finite time controller are designed, besides, the problem of fixed time stabilization is solved and a high-precision of the settling time is obtained.

Now, we consider the following state feedback control:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(z)&{}=\hat{u}_1(z)+\check{u}_1(z);\\ u_2(z)&{}=\hat{u}_2(z)+\check{u}_2(z) \end{array}\right. } \end{aligned}$$
(7)

where

$$\begin{aligned}&z(t)=\left( x(t),y(t)\right) ^T,\quad \hat{u}_i(z)=\left( \hat{u}_{i_{1}}(z),~\ldots ,~\hat{u}_{i_{n}}(z)\right) ^T,~ \check{u}_i(z)=\left( \check{u}_{i_{1}}(z),~\ldots ,~\check{u}_{i_{n}}(z)\right) ^T,\;\\&i=1,2. \end{aligned}$$

3.1 Finite Time Stabilization

In the following Theorem, for the first time, sufficient general conditions on the state feedback control are designed to ensure the FTSB of System (1).

Theorem 1

Under assumptions \(\mathbf {(H_1)-(H_2)}\), if there exist symmetric positive matrices \(P,Q_j>0,~j=1,\ldots 4\) and constants \(\epsilon _i>0,~0<\delta _i<1,~i=1,2,~\), \(0\le \mu <1\) such that

$$\begin{aligned}&-\,2PC+\epsilon _1^{-1}PAQ_1^{-1}A^TP+\epsilon _2 {L^{f_2}}^TQ_3L^{f_2}-Q_2<0 \end{aligned}$$
(8)
$$\begin{aligned}&-\,2PD+\epsilon _2^{-1}PA_2Q_3^{-1}A_2^TP+\epsilon _1 {L^{f_1}}^TQ_1L^{f_1}-Q_4<0 \end{aligned}$$
(9)
$$\begin{aligned}&\left\langle P\left( B_1+\varGamma ^TT^*\right) |f_1\left( y(t-\tau (t))\right) |,~|x(t)|\right\rangle +x^T(t)P\hat{u}_1(x(t))\le -\frac{1}{2}x^T(t)Q_2x(t).\nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned}&\left\langle P\left( B_2+\varTheta ^TO^*\right) |f_2\left( x(t-\sigma (t))\right) |,~|y(t)|\right\rangle +y^T(t)P\hat{u}_2(y(t))\le -\frac{1}{2}y^T(t)Q_4y(t).\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned}&x^T(t)P\check{u}_1(t)\le -\frac{\delta _1}{2}\sum \limits _{i=1}^n|x_i(t)|^{\mu +1}. \end{aligned}$$
(12)
$$\begin{aligned}&y^T(t)P\check{u}_2(t)\le -\frac{\delta _2}{2}\sum \limits _{i=1}^n|y_i(t)|^{\mu +1}. \end{aligned}$$
(13)

then the controller (7) stabilize in finite time System (2) with

$$\begin{aligned} T_0(\phi ,\psi )\le \frac{4\lambda _{\max }(P)\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }}{\delta (1-\mu )}. \end{aligned}$$

where \(\delta =\min \{\delta _1,\delta _2\}\).

Proof

Let the following Lyapunov function:

$$\begin{aligned} V(t)=x^T(t)Px(t)+y^T(t)Py(t). \end{aligned}$$
(14)

Taking the derivative of (14) along the solutions of System (1), we have

$$\begin{aligned} \dot{V}(t)&=2x^T(t)P\dot{x}(t)+2y^T(t)P\dot{y}(t)\nonumber \\&\le -\,x^T(t)(PC+CP)x(t)+2\langle PA|f_1(y(t))|,~|x(t)|\rangle \nonumber \\&\quad +2\langle P(B_1+\varGamma ^TT^*)|g_1(y(t-\tau (t)|,~|x(t)|\rangle +2x^T(t)P(u_1(t))\nonumber \\&\quad -y^T(t)(PD+DP)y(t)+2\langle PA_2|f_2(x(t))|,~|y(t)|\rangle \nonumber \\&\quad +2\langle P(B_2+\varTheta ^TO^*)|g_2(x(t-\sigma (t)|,~|y(t)|\rangle +2y^T(t)P(u_2(t)) \end{aligned}$$
(15)

From Lemma 1, the following inequality holds:

$$\begin{aligned} 2\langle PA_1|f_1(y(t))|,~|x(t)|\rangle&\le \epsilon _1^{-1}x^T(t)PA_1Q_1^{-1}A_1^TPx(t)\nonumber \\&\quad +\epsilon _1 f_1(y(t))^TQ_1f_1(y(t))\nonumber \\&\le \epsilon _1^{-1}x^T(t)PA_1Q_1^{-1}A_1^TPx(t)\nonumber \\&\quad +\epsilon _1 y(t)^T{L^{f_1}}^TQ_1L^{f_1}y(t) \end{aligned}$$
(16)

and

$$\begin{aligned} 2\langle PA_2|f_2(x(t))|,~|y(t)|\rangle&\le \epsilon _2^{-1}y^T(t)PA_2Q_3^{-1}A_2^TPy(t)\nonumber \\&\quad +\epsilon _2 x(t)^T{L^{f_2}}^TQ_3L^{f_2}x(t) \end{aligned}$$
(17)

Combining with (8)–(13), and (15)–(17) we deduce that

$$\begin{aligned} \dot{V}(t)&\le x^T(t)[-2PC+\epsilon _1^{-1}PAQ_1^{-1}A^TP+\epsilon _2 {L^{f_2}}^TQ_3L^{f_2}-Q_2]x(t)\nonumber \\&\quad +y^T(t)[-2PD+\epsilon _2^{-1}PA_2Q_3^{-1}A_2^TP+\epsilon _1 {L^{f_1}}^TQ_1L^{f_1}-Q_4]y(t)\nonumber \\&\quad +2x^T(t)P\check{u}_1(t)+2y^T(t)P\check{u}_2(t)\nonumber \\&\le -\,\delta _1\sum \limits _{i=1}^n|x_i(t)|^{\mu +1} -\delta _2\sum \limits _{i=1}^n|y_i(t)|^{\mu +1} \end{aligned}$$
(18)

Since \(0<\mu <1\), from Lemmas 2 and 3, we get the following inequalities:

$$\begin{aligned} \left[ \sum \limits _{i=1}^n|x_i(t)|^{2}+\sum \limits _{i=1}^n|y_i(t)|^{2}\right] ^{\frac{1}{2}}&\le \left[ \left( \sum \limits _{i=1}^n|x_i(t)|+\sum \limits _{i=1}^n|y_i(t)|\right) ^2\right] ^{\frac{1}{2}}\nonumber \\&\le \left[ \left( \sum \limits _{i=1}^n|x_i(t)|+\sum \limits _{i=1}^n|y_i(t)|\right) ^{\mu +1}\right] ^{\frac{1}{\mu +1}}\nonumber \\&\le 2^\mu \left[ \sum \limits _{i=1}^n|x_i(t)|^{\mu +1}+\sum \limits _{i=1}^n|y_i(t)|^{\mu +1}\right] ^{\frac{1}{\mu +1}} \end{aligned}$$
(19)

and consequently \(\dot{V}(t)\le -r\big (V(t)\big )\) where

$$\begin{aligned} r(s)=\frac{\delta }{2\lambda _{max}(P)^{\frac{\mu +1}{2}}}s^{\frac{\mu +1}{2}}. \end{aligned}$$

Since

$$\begin{aligned} \int \limits _0^\epsilon \frac{ds}{r(s)}=\frac{4\epsilon ^{\frac{1-\mu }{2}}}{\delta \lambda _{\max }^{-\frac{(1+\mu )}{2}}(P)(1-\mu )}<+\infty ~~~~\text {for all}~\epsilon >0. \end{aligned}$$
(20)

Based on Lemma 4, we deduce that System (1) is FTSB and the settling time satisfies

$$\begin{aligned} T_0(\phi ,\psi )\le \frac{4\lambda _{\max }(P)\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }}{\delta (1-\mu )} \end{aligned}$$

\(\square \)

Remark 1

The conditions established in Theorem 1 are in the general form and it was necessary to find a correspondent form of the control which satisfied them. In other words, the challenge is to find a correspondent FTS controller that makes these conditions easy to get them. In our paper, under assumptions \((H1-H3)\), we design different kinds of controller which renders these general conditions in the form of standard LMIs where we can easily solve them by using MATLAB LMI toolbox.

It should be pointed out that to the best of the author’s knowledge, there have been no results focused on the FTSB ones and the FXTSB for high-order BAM NNs with time varying coefficients. The approach used here can also be applied to study the FTSB for some other models of NNs, such as BAM Cohen–Grossberg NNs.

In the following, an explicit state feedback control will be designed.

Theorem 2

Under assumptions \(\mathbf {(H_1)-(H_3)}\), if there exist positive constants \(\epsilon _i>0,~i=1,2,~\)\(k_1,~\rho _1>0,~0\le \mu <1\) and three symmetric positives matrices \(P,~Q_1,~Q_3\), such that

$$\begin{aligned} -\,2PC+\epsilon _1^{-1}PAQ_1^{-1}A^TP+\epsilon _2 {L^{f_2}}^TQ_3L^{f_2}-2k_1P<0 \end{aligned}$$
(21)
$$\begin{aligned} -2PD+\epsilon _2^{-1}PA_2Q_3^{-1}A_2^TP+\epsilon _1 {L^{f_1}}^TQ_1L^{f_1}-2\rho _1P<0. \end{aligned}$$
(22)

Then, System (1) is FTSB via controller (23) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)L^{g_1}~sign(y(t))|y\left( t-\tau (t)\right) |\\ &{}\quad -\,k_2~sign(x(t))|x(t)|^\mu \\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)L^{g_2}~sign\left( x(t)\right) |x\left( t-\sigma (t)\right) |\\ &{}\quad -\,\rho _2~sign(y(t))|y(t)|^\mu . \end{array}\right. } \end{aligned}$$
(23)

and the settling time satisfies

$$\begin{aligned} T_0(\phi ,\psi )\le \frac{2\lambda _{\max }(P)\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }}{\alpha \lambda _{\min }(P)(1-\mu )} \end{aligned}$$
(24)

with \(\alpha =\min \{k_2,\rho _2\}\)

Proof

Note that

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{u}_1(t)&{}= -\,k_1x(t)-(B_1+T^*G_1)L^{g_1}~sign\left( y(t)\right) |y\left( t-\tau (t)\right) |\\ \check{u}_1(t)&{}=-\,k_2~sign\left( x(t)\right) |x(t)|^\mu \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{u}_2(t)&{}= -\,\rho _1y(t)-(B_2+O^*G_1)L^{g_2}~sign(x(t))|x(t-\sigma (t))|\\ \check{u}_2(t)&{}=-\,\rho _2~sign(y(t))|y(t)|^\mu \end{array}\right. } \end{aligned}$$

It then follows from \(\mathbf {(H_1)}\) that

$$\begin{aligned}&\left\langle P\bar{B}_1|g_1\left( y(t-\tau (t))\right) |,~|x(t)|\right\rangle +x^T(t)P\hat{u}_1(t)\le -\,k_1x^T(t)Px(t).\\&\left\langle P\bar{B}_2|g_2\left( x(t-\sigma (t))\right) |,~|y(t)|\right\rangle +y^T(t)P\hat{u}_2(t)\le -\,\rho _1y^T(t)Py(t).\\ \end{aligned}$$

and

$$\begin{aligned} 2x^T(t)P\check{u}_1(t)&= -\,2k_2x^T(t)P sign(x(t))|x(t)|^\mu \\&\le -\,2k_2\lambda _{\min }(P)\sum \limits _{i=1}^n|x_i(t)|^{\mu +1}\\ 2y^T(t)P\check{u}_2(t)&=-\,2\rho _2y^T(t)P sign(y(t))|y(t)|^\mu \\&\le -\,2\rho _2\lambda _{\min }(P)\sum \limits _{i=1}^n|y_i(t)|^{\mu +1} \end{aligned}$$

Thus, by choosing \(\delta _1=2k_2 \lambda _{\min }(P),~\delta _2= 2\rho _2\lambda _{\min }(P),~Q_2=2k_1I\), and \(Q_4=2\rho _1I\), (10)–(13) holds and \(T_0(\phi ,\psi )\) satisfies (24) which achieves the proof. \(\square \)

Remark 2

It is possible to use more complex Lyapunov functions. However, when we use more complex Lyapunov functions during the study of the FTS, it is necessary to consider \(\Vert .\Vert _1\) ([12]). Unfortunately, \(\Vert .\Vert _1 \ge \Vert .\Vert _2\), and then the settling time established by using the complex Lyapunov functions may be larger than that obtained based on the Lyapunov–Krasovskii functional.

If we set \(P = pI_n\), we obtain the following Corollary where the settling time is much simpler.

Corollary 1

If there exist constants \(\epsilon _i>0,~i=1,2.,~0\le \mu <1,k_1>0,~\rho _1,~p>0\) such that

$$\begin{aligned}&-\,2pC+\epsilon _1^{-1}p^2A_1A_1^T+\epsilon _2{L^{f_2}}^TL^{f_2}-2k_1p<0 \end{aligned}$$
(25)
$$\begin{aligned}&-\,2pD+\epsilon _2^{-1}p^2A_2A_2^T+\epsilon _1 {L^{f_1}}^TL^{f_1}-2\rho _1P<0. \end{aligned}$$
(26)

then System (1)–(23) is FTS and

$$\begin{aligned} T_0(\phi ,\psi )\le \frac{\left( 2\Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }}{\alpha (1-\mu )} \end{aligned}$$
(27)

In the following proposition, some sufficient conditions in form of LMIs where the control strength are constructed simultaneously are established.

Proposition 1

If there exist constants \(\epsilon _i>0,~i=1,2.,~0\le \mu <1,k_1>0,~\rho _1,~p>0\) such that

$$\begin{aligned} \varPsi =\begin{pmatrix} \varPsi _{11} &{} pA_1 &{} \epsilon _2{L^{f_2}}^T &{} 0 &{} 0 &{} 0 \\ * &{} -\epsilon _1 I &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon _2 I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} \varPsi _{44} &{} pA_2 &{} \epsilon _1 {L^{f_1}}^T \\ * &{} * &{} * &{} * &{} -\epsilon _2 I &{}0 \\ * &{} * &{} * &{} * &{} * &{} -\epsilon _1 I \end{pmatrix}<0 \end{aligned}$$
(28)

with \(\varPsi _{11}=-p(C+C^T)-2kI\), \(\varPsi _{44}=-p(D+D^T)-2\rho I\), \(k_1=p^{-1}k,~\rho _1=p^{-1}\rho \). then System (1) is FTSB via the controller (23) and the settling time satisfies (27).

Proof

Let

$$\begin{aligned} \varXi _1=\begin{pmatrix} -2pC-2kI &{} pA &{} \epsilon _2 {L^{f_2}}^T \\ * &{} -\epsilon _1 I &{} 0 \\ * &{} * &{} -\epsilon _2 I \end{pmatrix} \end{aligned}$$
(29)

and

$$\begin{aligned} \varXi _2=\begin{pmatrix} -2pD-2\rho I &{} pA_2 &{} \epsilon _1 {L^{f_1}}^T \\ * &{} -\epsilon _2 I &{} 0 \\ * &{} * &{} -\epsilon _1 I \end{pmatrix} \end{aligned}$$
(30)

By pre and post multiplying the inequalities (25) and (26) by \(diag(I_n,\frac{1}{\sqrt{\epsilon _1}}I_n,\frac{1}{\sqrt{\epsilon _1}}I_n)\) and , \(diag(I_n,\frac{1}{\sqrt{\epsilon _2}}I_n,\frac{1}{\sqrt{\epsilon _1}}I_n)\) respectively, we obtain from Shur copmlement lemma [16] that \(\varXi _1<0\) and \(\varXi _2<0\), is equivalent respectively to (25) and (26). Since \(\varPsi =diag(\varXi _1,~\varXi _2)<0\), we obtain immediately the result of Corollary 1. \(\square \)

Remark 3

Since \(L_2\subset L_1\), the settling-time established here may be smaller than that considered in the existing literature. In addition, compared with other approach based on the same approach, obviously, the conditions of Corollary 1 are less conservative than that presented in [69, 70] thanks to a positive scalar p added in the Lyapunov function. On the other hand, it should be pointed out that the LKF given in [64] is independent of a matrix P. For reducing the conservatism of conditions, we introduce the matrix P in (14) without influencing on the upper bound \(T(\phi )\).

In the following Corollary a free-delay controller is designed to ensure the FTSB of delayed BAM NNs.

Corollary 2

Under conditions of Theorem 2, System (1) is FTSB via free-delay controller as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)G_1 ~sign(y(t))\\ &{}\quad -\,k_2~sign(x(t))|x(t)|^\mu \\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)G_2 ~sign(x(t))\\ &{}\quad -\,\rho _2~sign(y(t))|y(t)|^\mu . \end{array}\right. } \end{aligned}$$
(31)

and the settling-time satisfies (27).

Proof

By applying \(\mathbf {(H_2)}\) to (10)–(11). The proof will be similar to the proof of Theorem 2.\(\square \)

Remark 4

It is possible to shorten the settling-time based on the approach used in [39]

  • Let the control strength \(r_2=\max \{k_2,\rho _2\}\) be fixed and let

    $$\begin{aligned} T_0(\mu )=\frac{2\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }}{r_2(1-\mu )}, \quad 0\le \mu <1,~r_2>0;. \end{aligned}$$
    (32)

    Since

    $$\begin{aligned} \frac{dT_0^*}{d\mu }=\frac{2\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }\left[ (\mu -1)\ln \left( \Vert \phi \Vert +\Vert \psi \Vert \right) +1\right] }{r_2(1-\mu )^2} \end{aligned}$$

therefore,

  • If \(\left( \Vert \phi \Vert +\Vert \psi \Vert \right) <e\) i.e. \(\ln \left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^{1-\mu }<1\) then \(T_0^*(\mu )\) is strictly increasing for \(0<\mu <1\). Obviously, \(T_0^*(\mu )\) achieves the minimum in \(\mu =0\)

  • Similarly, if \(\left( \Vert \phi \Vert +\Vert \psi \Vert \right) >e\), \(T_0^*(\mu )\) has only one critical point \(u^*=1-\frac{1}{\ln \left( \Vert \phi \Vert +\Vert \psi \Vert \right) }\) at which achieves its minimum value \(\frac{2 e \ln \left( \Vert \phi \Vert +\Vert \psi \Vert \right) }{r_2}\)

Therefore, the following switched controller can be designed for optimizing the settling-time

$$\begin{aligned} u_1(t)= {\left\{ \begin{array}{ll} &{}-\,k_1x(t)-B_1 L^{g_1}~sign\left( y(t)\right) \left| y\left( t-\tau (t)\right) \right| \\ &{}-\,k_2~sign\left( x(t)\right) |x(t)|^{{\mu }^{*}},\quad \Vert x(t)\Vert >e\\ &{}-\,k_1x(t)-B_1 L^{g_1}~sign\left( y(t)\right) \left| y\left( t-\tau (t)\right) \right| \\ &{}-\,k_2~sign\left( x(t)\right) ,\quad 0\le \Vert x(t)\Vert <e. \end{array}\right. } \end{aligned}$$
(33)
$$\begin{aligned} u_2(t)= {\left\{ \begin{array}{ll} &{}-\,\rho _1y(t)-B_2 L^{g_2}~sign\left( x(t)\right) |x\left( t-\sigma (t)\right) |\\ &{}-\,\rho _2~sign\left( y(t)\right) |y(t)|^{{\mu }^{*}}.,\quad \Vert y(t)\Vert >e\\ &{}-\,\rho _1y(t)-B_2 L^{g_2}~sign\left( x(t)\right) |x\left( t-\sigma (t)\right) |\\ &{}-\,\rho _2~sign\left( y(t)\right) |y(t)|.,\quad 0\le \Vert y(t)\Vert <e. \end{array}\right. } \end{aligned}$$
(34)

3.2 Fixed Time Stabilization

In this part, we develop some results on the FXTSB of System (1) where we design different kinds of controller able to ensure the FXTS of the considered class of NNs. Also, the settling time is estimated where a high precision is obtained.

Theorem 3

Under assumptions \(\mathbf {(H_1)-(H_2)}\) and conditions (8)–(11), if there exist symmetric positive matrices \(P,Q_j>0,~j=1,\ldots 4\) and positive constants \(\epsilon _i>0,~\delta _i<1,~i=1,2~\)\(0\le \mu <1\) such that

$$\begin{aligned} x^T(t)P\check{u}_1(t)\le & {} -\frac{\delta _1}{2}\left[ \sum \limits _{i=1}^n|x_i(t)|^{\mu +1} +\sum \limits _{i=1}^n|x_i(t)|^{\beta +1}\right] \end{aligned}$$
(35)
$$\begin{aligned} y^T(t)P\check{u}_2(t)\le & {} -\frac{\delta _2}{2}\left[ \sum \limits _{i=1}^n|y_i(t)|^{\mu +1}+\sum \limits _{i=1}^n|y_i(t)|^{\beta +1}\right] \end{aligned}$$
(36)

then the closed-loop System (2)–(7) is FXTS and the settling time satisfies

$$\begin{aligned} T_0(\phi )&\le T^1_{\max }=\frac{2\lambda _{max}(P)^{\frac{\mu +1}{2}}}{\delta _1 (1-\mu )} +\frac{2\lambda _{max}(P)^{\frac{\beta +1}{2}}}{\delta _2 n^{\frac{1-\beta }{2}}(\beta -1)}. \end{aligned}$$
(37)

Proof

Calculating the derivative of (14) along the trajectories of System (1), similarly to proof of Theorem 1 we obtain that

$$\begin{aligned} \dot{V}(t)&\le -\,\delta \Big (\sum \limits _{i=1}^n|x_i(t)|^{\mu +1} +\sum \limits _{i=1}^n|y_i(t)|^{\mu +1}+\sum \limits _{i=1}^n|x_i(t)|^{\beta +1} \nonumber \\&\quad +\sum \limits _{i=1}^n|y_i(t)|^{\beta +1}\Big ) \end{aligned}$$
(38)

Since \(\beta >1\), from Lemmas 2 and 3, we obtain that:

$$\begin{aligned} \left[ \sum \limits _{i=1}^n|x_i(t)|^{2}+\sum \limits _{i=1}^n|y_i(t)|^{2}\right] ^{\frac{1}{2}}&\le \left[ \left( \sum \limits _{i=1}^n|x_i(t)|+\sum \limits _{i=1}^n|y_i(t)|\right) ^2\right] ^{\frac{1}{2}}\nonumber \\&\le \left[ n^\frac{\beta -1}{2}\left( \sum \limits _{i=1}^n|x_i(t)|+\sum \limits _{i=1}^n|y_i(t)|\right) ^{\beta +1}\right] ^{\frac{1}{\beta +1}}\nonumber \\&\le 2n^\frac{\beta -1}{2}\left[ \sum \limits _{i=1}^n|x_i(t)|^{\beta +1}+\sum \limits _{i=1}^n|y_i(t)|^{\beta +1}\right] ^{\frac{1}{\beta +1}} \end{aligned}$$
(39)

Therefore from (19) and (39) we have

$$\begin{aligned} \dot{V}(t)\le -\frac{1}{2}\left[ \frac{\delta }{\lambda _{max}(P)^{\frac{\mu +1}{2}}}V^{\frac{\mu +1}{2}} + \frac{\delta n^{\frac{1-\beta }{2}}}{\lambda _{max}(P)^{\frac{\beta +1}{2}}}V^{\frac{\beta +1}{2}}\right] \end{aligned}$$
(40)

Therefore, based on Lemma 5, we obtain that the closed-loop system (1)–(7) is fixed time stable and \(T_0(\phi )\) satisfies (37). \(\square \)

Remark 5

This is the first time to study the FXTSB of System (1) for the both cases: lower-order and high-order. Moreover, in Theorem 1 only the FTS is investigated and the established settling time is not of major interest in practice when the initial conditions will be large which is removed in Theorem 2 by establishing a settling time independent of initial conditions and more accurate.

In the following Proposition a practical design procedure for the control strengths \(\rho _i\) and \(k_i\), \(i=1,2,3\) is given based on the LMIs approach.

Proposition 2

Under assumptions \(\mathbf {(H_1)-(H_3)}\), if there exist positive constants \(p,~\epsilon _i>0,~i=1,2,~\)\(k_1,~\rho _1>0,~0\le \mu <1\), \(\beta >1\) such that the following LMI holds

$$\begin{aligned} \varPsi =\begin{pmatrix} \varPsi _{11} &{} pA_1 &{} \epsilon _2{L^{f_2}}^T &{} 0 &{} 0 &{} 0 \\ * &{} -\epsilon _1 I &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon _2 I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} \varPsi _{44} &{} pA_2 &{} \epsilon _1 {L^{f_1}}^T \\ * &{} * &{} * &{} * &{} -\epsilon _2 I &{}0 \\ * &{} * &{} * &{} * &{} * &{} -\epsilon _1 I \end{pmatrix}<0 \end{aligned}$$
(41)

with \(\varPsi _{11}=-2pC-2kI\), \(\varPsi _{44}=-2pD-2\rho I\), \(k_1=p^{-1}k,~\rho _1=p^{-1}\rho \). Then, System (1)–(42) is FXTS via controller (42) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)L^{g_1}~sign(y(t))|y\left( t-\tau (t)\right) |\\ &{}\quad -\,k_2~sign(x(t))|x(t)|^\mu -k_3~sign(x(t))|x(t)|^\beta \\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)L^{g_2}~sign\left( x(t)\right) |x\left( t-\sigma (t)\right) |\\ &{}\quad -\,\rho _2~sign(y(t))|y(t)|^\mu -\rho _3~sign(y(t))|y(t)|^\beta . \end{array}\right. } \end{aligned}$$
(42)

and the settling time satisfies

$$\begin{aligned} T_0(\phi )\le T^1_{\max }=\frac{2}{k_2\sqrt{p}^{1-\mu } (1-\mu )} +\frac{2\sqrt{p}^{\beta -1}}{k_3n^{\frac{1-\beta }{2}}(\beta -1)}. \end{aligned}$$
(43)

Proof

By letting

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{u}_1(t)&{}= -\,k_1x(t)-(B_1+T^*G_1)L^{g_1}~sign\left( y(t)\right) |y\left( t-\tau (t)\right) |\\ \check{u}_1(t)&{}=-\,k_2~sign\left( x(t)\right) |x(t)|^\mu -k_3~sign\left( x(t)\right) |x(t)|^\beta \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{u}_2(t)&{}= -\,\rho _1y(t)-(B_2+O^*G_1)L^{g_2}~sign(x(t))|x(t-\sigma (t))|\\ \check{u}_2(t)&{}= -\,\rho _2~sign(y(t))|y(t)|^\mu -\rho _3~sign(y(t))|y(t)|^\beta \end{array}\right. } \end{aligned}$$

Similarly to the proof of Theorem 2, by choosing \(P=pI_n\)\(\delta _1=2\lambda _{\min }(P)\min \{ k_2 p,~k_3p\}\), \(\delta _2= 2\lambda _{\min }(P)\min \{\rho _2p,~\rho _3p\}\), \(Q_2=2k_1I\), and \(Q_4=2\rho _1I\) , the inequalities (10)–(11) and (35)–(36) hold. Furthermore, from Corollary 1, (8)–(9) are equivalent to condition (41). Therefore, the conditions of Theorem 3 are satisfied which achieves the proof. \(\square \)

In the following Corollary a free-delay controller is presented which is well suitable in practice.

Corollary 3

Under assumptions \(\mathbf {(H_1)-(H_3)}\), if there exist positive constants \(p,~\epsilon _i>0,~i=1,2,~\)\(k_1,~\rho _1>0,~0\le \mu <1\), \(\beta >1\) such that the following LMI holds

$$\begin{aligned} \varPsi =\begin{pmatrix} \varPsi _{11} &{} pA_1 &{} \epsilon _2{L^{f_2}}^T &{} 0 &{} 0 &{} 0 \\ * &{} -\epsilon _1 I &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon _2 I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} \varPsi _{44} &{} pA_2 &{} \epsilon _1 {L^{f_1}}^T \\ * &{} * &{} * &{} * &{} -\epsilon _2 I &{}0 \\ * &{} * &{} * &{} * &{} * &{} -\epsilon _1 I \end{pmatrix}<0 \end{aligned}$$
(44)

with \(\varPsi _{11}=-2pC-2kI\), \(\varPsi _{44}=-2pD-2\rho I\), \(k_1=p^{-1}k,~\rho _1=p^{-1}\rho \). Then, System (1)–(42) is FXTS via free-delay controller (45) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)G_1 ~sign(y(t))\\ &{}\quad -\,k_2~sign(x(t))|x(t)|^\mu -k_3~sign(x(t))|x(t)|^\beta \\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)G_2 ~sign(x(t))\\ &{}\quad -\,\rho _2~sign(y(t))|y(t)|^\mu -\rho _3~sign(y(t))|y(t)|^\beta . \end{array}\right. } \end{aligned}$$
(45)

and the settling time satisfies (43)

Proof

By using \(\mathbf {(H_2)}\) similar arguments to the ones of Corollary 2, we obtain easily the result.\(\square \)

In the following Theorem, some new general conditions for the fixed time stabilization are designed where the obtained settling time is more precise than that given in Theorem 1.

Theorem 4

Under assumptions \(\mathbf {(H_1)-(H_2)}\) and conditions (8)–(11), if there exist symmetric positive matrices \(P,Q_j>0,~j=1,\ldots 4\) and positive constants \(\lambda _i\), \(\epsilon _i>0,~\delta _i<1,~i=1,2,~\), \(0\le \mu <1\) such that

$$\begin{aligned} x^T(t)P\check{u}_1(t)\le & {} -\frac{\delta _1}{2}\left[ \sum \limits _{i=1}^n|x_i(t)|^{\beta +1}\right] -\lambda _1 \end{aligned}$$
(46)
$$\begin{aligned} y^T(t)P\check{u}_2(t)\le & {} -\frac{\delta _2}{2}\left[ \sum \limits _{i=1}^n|y_i(t)|^{\beta +1}\right] -\lambda _2 \end{aligned}$$
(47)

then the closed-loop System (2)–(7) is FXTS and the settling time satisfies

$$\begin{aligned} T_0(\phi )\le T^2_{\max }=(2\lambda )^{-1}\left[ 1+\frac{2}{\beta +1}\right] \left[ \frac{2\lambda \lambda _{max}(P)^{\frac{\beta +1}{2}}}{ \delta n^{\frac{1-\beta }{2}}}\right] ^{\frac{2}{\beta +1}}. \end{aligned}$$

Proof

Consider the same Lyapunov functional (14), similarly to the proof of Theorem 1 we obtain that

$$\begin{aligned} \dot{V}(z(t))\le -\frac{\delta n^{\frac{1-\beta }{2}}}{\lambda _{max}(P)^{\frac{\beta +1}{2}}} V^{\frac{\beta +1}{2}}(z(t))-\lambda . \end{aligned}$$
(48)

Therefore, from Lemma 6 System (1)–(7) is stable in fixed time and \(T_0(\phi )\le T_{\max }^2\). \(\square \)

Based on the results obtained in [20], Theorem 4 complement end extend the recent works around the fixed time stabilization of delayed NNs by establishing a settling time more accurate than that given in the literature. In the following Proposition, an explicitly fixed time controller with a high-precision of a settling time is established

Proposition 3

Under assumptions \(\mathbf {(H_1)-(H_3)}\), if there exist positive constants \(p,~\epsilon _i>0,~i=1,2,~\)\(k_1,~\rho _1>0,~0\le \mu <1\), \(\beta >1\) such that the following LMI holds

$$\begin{aligned} \varPsi =\begin{pmatrix} \varPsi _{11} &{} pA_1 &{} \epsilon _2{L^{f_2}}^T &{} 0 &{} 0 &{} 0 \\ * &{} -\epsilon _1 I &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon _2 I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} \varPsi _{44} &{} pA_2 &{} \epsilon _1 {L^{f_1}}^T \\ * &{} * &{} * &{} * &{} -\epsilon _2 I &{}0 \\ * &{} * &{} * &{} * &{} * &{} -\epsilon _1 I \end{pmatrix}<0 \end{aligned}$$
(49)

with \(\varPsi _{11}=-2pC-2kI\), \(\varPsi _{44}=-2pD-2\rho I\), \(k_1=p^{-1}k,~\rho _1=p^{-1}\rho \). Then, System (1)–(42) is FXTS via controller (50) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)L^{g_1}~sign(y(t))|y\left( t-\tau (t)\right) |\\ &{}\quad -\,k_3~sign(x(t))|x(t)|^\beta -\lambda _1~sign(x(t))\\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)L^{g_2}~sign\left( x(t)\right) |x\left( t-\sigma (t)\right) |\\ &{}\quad -\,\rho _3~sign(y(t))|y(t)|^\beta -\lambda _2 ~sign(y(t)). \end{array}\right. } \end{aligned}$$
(50)

where \(\lambda _i,~i=1,2,~k_3,\rho _3\) are positive constants and \(\lambda =\min \{\lambda _1,\lambda _2\}\), \(\alpha _3=\min \{k_3,~\rho _3\}\). and the settling time satisfies

$$\begin{aligned} T_0(\phi )\le T^2_{\max }=(2\lambda ^{-1})\left[ 1+\frac{2}{\beta +1}\right] \left[ \frac{\lambda p^{\frac{\beta -1}{2}}}{ \alpha _3 n^{\frac{1-\beta }{2}}}\right] ^{\frac{2}{\beta -1}}. \end{aligned}$$
(51)

Proof

Let \(P=pI_n\), the proof of proposition 3 is similar to the one of Corollary 1 so it is omitted here. \(\square \)

Remark 6

The criterion considered in [1, 2, 23,24,25, 28, 73] that ensures the stability of System (1) fails when the function \(\tau (.)\) is not differentiable. The results investigated here overcome these difficulties and extended the existing results to a class of NNs with unknown time-varying delay. In the following Corollary, a free-delay fixed time controller is deduced for better application

Corollary 4

Under conditions of Corollary 3 System (1)–(52) is FXTS via free-delay controller (52) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,k_1x(t)-(B_1+T^*G_1)G_1 ~sign(y(t))\\ &{}\quad -\,k_2~sign(x(t))|x(t)|^\mu -k_3~sign(x(t))|x(t)|^\beta \\ u_2(t)&{}=-\,\rho _1y(t)-(B_2+O^*G_2)G_2 ~sign(x(t))\\ &{}\quad -\,\rho _2~sign(y(t))|y(t)|^\mu -\rho _3~sign(y(t))|y(t)|^\beta . \end{array}\right. } \end{aligned}$$
(52)

and the settling time satisfies (51).

Proof

According to Theorem 4, if we apply the fixed time controller to System (1) then we can easily obtain the result. The details of the proof is left to the reader. \(\square \)

Remark 7

As we known,the same routine as the conventional delayed NNs cannot be utilized to establish sufficient conditions for the FTSB of delayed NNs in the form of LMIs. In fact, the constructed controller in [45, 46] cannot be establish some sufficient LMIs conditions for the the FXTSB. More precisely, with the requirement \(\mu \in ]0,1[\), it is difficult to establish LMIs conditions for the Fixed time stabilization of delayed NNs based on the inequality \(\dot{V}(t)\le - V^\mu -\gamma V^\beta \) . In our paper, based on the Lyapunov-quadratic functional, some FXTSB conditions in the form of LMIs are obtained for the first time.

4 Application

In this section, two numerical examples are designed to appear the effectiveness of our theoretical main results

4.1 Delay-Dependant Controller

Consider the following BAM delayed NNs

$$\begin{aligned} \dot{x}(t)&=-\,cx(t)+a_1f_1\big (y(t)\big )+b_1g_2\big (y(t-\tau (t))\big ) \nonumber \\ \dot{y}(t)&=-\,dy(t)+a_2f_2\big (x(t)\big )+b_2g_2\big (x(t-\sigma (t))\big ) \end{aligned}$$
(53)

where

$$\begin{aligned} f_j(s))&=g_j((s))=\frac{1}{1+\exp ^{s}}-\frac{1}{2},~\tau (.)=\sigma (.)=3,~F_j=G_j=\frac{1}{2}\quad j=1,2. \end{aligned}$$

and

$$\begin{aligned} d&=1.9220,~ a_2=b_2=9.8501,~c=1.1631,~ a_1=8.2311,~ b_1=1.1860. \end{aligned}$$

By using Matlab LMI toolbox [42] for solving (28), we obtain some feasible solutions

$$\begin{aligned} p&=0.2315,~ \epsilon _1=3.2442,~ k=4.1144,~k_1=17.0515;\\ \rho&=3.9475,\quad \rho _1=17.7722,\quad ~\epsilon _2=5.58163. \end{aligned}$$

Hence, from Corollary 1, if we fix \(k_2=\rho _2=2\), system (53) is FTSB via controller (54) as follows.

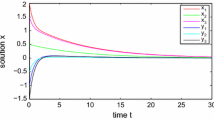
$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05~x(t)-b_1~sign\left( y(t)\right) |y\left( t-3\right) |\\ &{}\quad -\,2sign(x(t))\sqrt{|x(t)|}.\\ u_2(t)&{}=-\,17.77 y(t)-b_2~sign(x(t))|x\left( t-3\right) |\\ &{}\quad -\,2sign(y(t))\sqrt{|y(t)|} \end{array}\right. } \end{aligned}$$
(54)

We plot the state trajectories of System (53) with the initial condition \(y(s)=\phi (s)=-3\), \(x(s)=\psi (s)=3\) for all \(s\in [-3,0)\) without controller and under controller (54) in Fig. 1.

Fig. 1
figure 1

State trajectories of System (53) with initial condition \((3,-3)^T\). a System (53)without controller. b System (53) under controller (54)

Full size image

Remark 8

Many authors studied the global asymptotic stability and exponential stability of System (1) [1, 2, 23, 25]. From Corollary 1, we guarantee the FTSB of System (1) with the initial condition \(y(s)=\phi (s)=-3\), \(x(s)=\psi (s)=3\) for all \(s\in [-3,0)\) via controller (54) with an information about the time for the system to achieve the equilibrium point given by the settling time functional

$$\begin{aligned} T_0(\phi )\le \frac{\left( \Vert \phi \Vert +\Vert \psi \Vert \right) ^\mu }{1-\mu }<4.9890. \end{aligned}$$

where \(\mu =0.5\).

The approach used in [40] fails for System (53) because \(\tau (.)\ne 0\). However, our approach can be stabilize in finite time the class of BAM neural networks in the presence of delay. It should be pointed out that delayed systems have more complex dynamic behaviours compared with systems without delay because it is delicate to design a Lyapunov functional satisfying the derivative condition for FTS of delayed system.

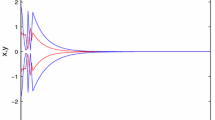
When the initial conditions will be large, on one hand, the established settling time is not of major interest in practice because the knowledge in advance of the initial conditions is very difficult. Motivated by the above-mentioned discussion, we design a fixed time controller where the settling time is independent of initial conditions. In fact, from Corollary 2, if we fix \(k_i=\rho _i=1,~i=2,3\), System (53) is stable in fixed time via controller (55) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05~x(t)-b_1~sign\left( y(t)\right) |y\left( t-3\right) |\\ &{}\quad -\,sign(x(t))\sqrt{|x(t)|}-sign(x(t))|x(t)|^2\\ u_2(t)&{}=-\,17.77 y(t)-b_2~sign(x(t))|x\left( t-3\right) |\\ &{}\quad -\,sign(x(t))\sqrt{|y(t)|}-sign(x(t))|y(t)|^2. \end{array}\right. } \end{aligned}$$
(55)

Corollary 2 guarantees the Fixed time stability of the closed-loop system (53)–(55) but also the following inequality for the settling-time functional

$$\begin{aligned} T^1_{\max } \le 3.2396 . \end{aligned}$$

when \(\mu =0.5\) and \(\beta =2\).

When we fix \(\lambda _1=\lambda _2=0.28\), Corollary 3 can optimize the settling time of System (53) via controller (56) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05~x(t)-b_1~sign\left( y(t)\right) |y\left( t-3\right) |\\ &{}\quad -\,sign(x(t))|x(t)|^2-0.28 ~sign(x(t))\\ u_2(t)&{}=-\,17.77 y(t)-b_1~sign(x(t))|x\left( t-3\right) |\\ &{}\quad -\,sign(y(t))|y(t)|^2-0.28 ~sign(y(t)) \end{array}\right. } \end{aligned}$$
(56)

where the settling-time functional

$$\begin{aligned} T^2_{\max } \le 2.98 \end{aligned}$$

State trajectories of System (53) with initial condition \((6,-5)^T\) with controller (55) and (56) are depicted in Fig. 2.

Fig. 2
figure 2

State trajectories of System (53) with initial condition \((6,-5)^T\). a System (53)with controller (55). b System (53) under controller (56)

Full size image

Remark 9

The concept of FTS invetigated in our paper is based on the classical Lyapunov stability which is associated with an infinite time interval. However, in [7] , only a finite time interval is considered. Dorato reported in [3] that FTB and Lyapunov stability invetigated in our paper are two independent concepts.

4.2 Free-Delay Controller

Now, we consider the following High-order BAM Hopfield NNs

$$\begin{aligned} \dot{x}(t)&=-\,cx(t)+a_1f_1\left( y(t)\right) +b_1g_1\left( y(t-\tau (t))\right) \nonumber \\&\quad + b_3g_1^2\left( y(t-\tau (t))\right) \end{aligned}$$
(57)
$$\begin{aligned} \dot{y}(t)&=-\,dx(t)+a_2f_2\left( x(t)\right) +b_2g_2\left( x(t-\sigma (t))\right) \nonumber \\&\quad +b_4g_2^2\left( y(t-\sigma (t))\right) \end{aligned}$$
(58)

where

$$\begin{aligned} d&=1.9220,\quad a_2=b_2=b_4=9.8501;\\ c&=1.1631,\quad a_1=8.2311,\quad b_1=b_3=1.1860. \end{aligned}$$

and the rest of parameters similar to Sect. 4.1.

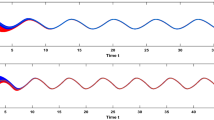
From Corollary 2, the equilibrium point of System (57) is FTSB via controller (59) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05~x(t)-0.5(b_1+0.5b_3) ~sign(y(t))\\ &{}\quad -\,2sign(x(t))\sqrt{|x(t)|}\\ u_2(t)&{}=-\,17.77~y(t)-0.5 (b_2+0.5b_4) ~sign(x(t))\\ &{}\quad -\,2sign(y(t))\sqrt{|y(t)|}\\ \end{array}\right. } \end{aligned}$$
(59)

and the settling-time satisfies \(T(\phi ,\psi )\le 4\). when we fix \(k_2=\rho _2=2\). We plot the state trajectories of System (57) without and under controller (59) in Fig. 3.

Fig. 3
figure 3

State trajectories of System (57) with initial condition \((-2,-2)^T\). a System (57)without controller. b System (57) under controller (59)

Full size image

On the one hand, the following controller (60)

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05 x(t)-0.5 (b_1+0.5b_3) ~sign(y(t))\\ &{}\quad -\,sign(x(t))\sqrt{|x(t)|}-sign(x(t))|x(t)|^2\\ u_2(t)&{}=-\,17.77~y(t)-0.5(b_2+0.5b_4) ~sign(x(t))\\ &{}\quad -\,sign(y(t))\sqrt{|y(t)|}-~sign(y(t))|y(t)|^2. \end{array}\right. } \end{aligned}$$
(60)

can be ensure the fixed time stabilization of System (57).

On the other hand, from corollary 4, the following controller (61)

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(t)&{}=-\,17.05 x(t)-0.5 (b_1+0.5b_3) ~sign(y(t))\\ &{}\quad -\,sign(x(t))|x(t)|^2-0.28 ~sign(x(t))\\ u_2(t)&{}=-\,17.77y(t)-0.5(b_2+0.5b_4) ~sign(x(t))\\ &{}\quad -\,sign(y(t))|y(t)|^2-0.28 ~sign(y(t)). \end{array}\right. } \end{aligned}$$
(61)

can be also ensure the fixed time stability with a high-precision of the settling time such as \(T^2_{\max } \le 2.98\).

We plot the state trajectories of System (57) with controller (60) and (61) in Fig. 4.

Fig. 4
figure 4

State trajectories of System (57). a System (57) under controller (60) with initial condition \((1.2,-1.6)^T\). b System (57) under controller (61) with initial condition \((4,-5)^T\)

Full size image

5 Conclusion and Future Work

Finite time and fixed time stabilization problems for a high-order class of BAM neural networks with time-varying delay is solved. On the one hand, some new general conditions for the FTSB and FXTSB are established. These conditions are in the form of LMIs which can be numerically checked. On the other hand, different kinds of finite time and fixed time control algorithms which contain time delay dependent controller and free-delay controller are designed. Moreover, for the first time, the fixed-settling time is optimized for delayed systems and a high precision for this time is obtained. Compared with the recent work, firstly, we extend the results given in [14, 40, 57, 59, 64, 65] where only the FTSB problem is deals and the fixed time is not considered. Secondly, our approach complement the results of [40] where the time-delay is not taken into account and the fixed time stability is not treated. Thirdly, our analysis offers an improvement compared with [22, 24, 30, 34, 51,52,53,54, 58] where only asymptotic stability concept of high-order BAM neural networks is investigated.

It is well known that the effect of impulses on stabilization is rather scarce, and the topic certainly deserves to be further investigated. At present many research around the impulsive effect on the stabilization of NNs such that the mode-dependent impulsive investigated in [71] and some sufficient conditions are established in [72] that ensure the synchronization of NNs with heterogeneous impulses. However, the approach used in the above mentioned work cannot be extended to solve the problem investigated in our paper. Thus, a variety of impulses will be a real problem to be studied in the near future work. Furthermore, in future work, we would like to extend our results to the BAM neural networks with various kinds of delays, such as infinite distributed delay, time-varying delay in the leakage term, neutral class of delayed NNS. In a word, the BAM neural networks still has some open problems.