1 Introduction

The stability of dynamical neural networks with time delays which have been used in many applications such as optimization, control and image processing has received much attention recently (see, such as [2, 3, 6, 17,18,19,20,21,22, 25,26,27, 43, 44]). For example, the stability of delay Hopfield neural networks [2, 3, 5, 31, 33] and Cohen–Grossberg neural networks [20, 42, 45] has been investigated. In special, BAM neural networks were first proposed by Kosko [29, 30], and since then, the BAM neural system has been extensively studied [9, 11, 13, 27, 28, 34, 35, 37, 39, 41, 46]. As a class of dynamic systems, BAM neural networks are usually featured by either first-order or high-order forms described in continuous or discrete time. The low-order BAM systems have been widely studied (such as [34, 35]) because of its potential for signal and image processing, pattern recognition. Recently, the higher-order BAM systems [12, 27, 28] display nice properties due to the special structure of connection weights. The existence of a globally asymptotically stable equilibrium state has been studied under a variety of assumptions on the activation functions. Generally, the activation functions have been assumed to be continuously differentiable, monotonic and bounded [2, 5, 10, 13, 15, 18, 20, 36, 37, 39, 40]. But in some applications, one is required to use unbounded and non-monotonic activation functions [27, 41, 46]. It has been shown by Crespi [16], Morita [32] that the capacity of an associative memory network can be significantly improved if the sigmoidal functions are replaced by non-monotonic activation functions. On the other hand, the state of electronic networks is often subject to display impulsive effects [7, 22].

To the best of our knowledge, except [27, 28] for higher-order BAM neural networks by using the differential inequality with delay and impulse, the stability analysis for impulsive high-order BAM dynamical systems with time-varying delays has seldom been investigated and remains important and challenging. In this paper, we shall study another generation of high-order BAM dynamical neural networks with impulsive by using Lyapunov–Krasovskii functionals, employing linear matrix inequalities (LMIs) and differential inequalities. The organization of this paper is as follows. In Sect. 2, problem formulation and preliminaries are given. In Sect. 3, several sufficient criteria will be established for the equilibrium of the system to be asymptotical stability in the mean square. In Sect. 4, two examples will be given to demonstrate the effectiveness of our results.

2 Preliminaries and Lemmas

In this paper, we will consider the following impulsive neural networks

$$\begin{aligned} \left\{ \begin{aligned} \frac{\hbox {d}x_i(t)}{\hbox {d}t}&=-d_ix_i(t)+\sum _{j=1}^m a_{ij} f_j(y_j(t))+\sum _{j=1}^m b_{ij} f_j(y_j(t-\tau (t)))\\&\ \ \ \ +\sum _{j=1}^m\sum _{l=1}^mc_{ijl} \int _{t-\tau }^{t}f_j(y_j(t-s))f_l(y_l(s))\hbox {d}s+\sum _{j=1}^{m_1}r_{ij}u_j(t),&t\ne t_k,\\ \frac{\hbox {d}y_j(t)}{\hbox {d}t}&=-\widetilde{d_j}y_j(t)+\sum _{i=1}^n \widetilde{a_{ji}} g_i(x_i(t))+\sum _{i=1}^n \widetilde{b_{ji}} g_i(x_i(t-\sigma (t)))\\ {}&\ \ \ \ \ +\sum _{i=1}^n\sum _{l=1}^n\widetilde{c_{jil}} \int _{t-\sigma }^{t}g_i(x_i(t-s))g_l(x_l(s))\hbox {d}s+\sum _{i=1}^{m_2}\widetilde{r}_{ji}\widetilde{u}_i(t),&t\ne t_k, \\ \triangle x_i(t)&=\sum _{j=1}^n (e_{ij}(t)-\delta _{ij})x_j(t^-)+\sum _{l=1}^{n} m_{il}J_l(t^-),&t= t_k, \\ \triangle y_j(t)&=\sum _{i=1}^m (\widetilde{e_{ji}}(t)-\delta _{ji})y_i(t^-)+\sum _{l=1}^{m} \widetilde{m_{jl}}\widetilde{J}_l(t^-),&t= t_k, \end{aligned} \right. \end{aligned}$$
(1)

or, equivalently,

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\hbox {d}x(t)}{\hbox {d}t}=-Dx(t)+A f(y(t))+B f(y(t-\tau (t)))+ \int _{t-\tau }^{t}\Upsilon ^T_f(s)\Gamma _1f(y(s))\hbox {d}s+Ru(t),\\ {}&\quad \quad t\ne t_k,\\ {}&\frac{\hbox {d}y(t)}{\hbox {d}t}=-\widetilde{D}y(t)+\widetilde{A} g(x(t))+ \widetilde{B} g(x(t-\sigma (t)))+ \int _{t-\sigma }^{t}\Upsilon ^T_g(s)\Gamma _2g(x(s))\hbox {d}s+\widetilde{R}\widetilde{u}(t),\\&\quad \quad t\ne t_k,\\&\triangle x(t)=(E(t)-I)x(t^-)+MJ(t^-), t= t_k,\\&\triangle y(t)= (\widetilde{E}(t)-\widetilde{I})y(t^-)+ \widetilde{M}\widetilde{J}(t^-), t= t_k,\end{aligned}\right. \end{aligned}$$
(2)

where \(t\ge 0;\ i=1,2,\ldots ,n;\ j=1,2,\ldots ,m;~\triangle x_i(t)=x_i(t)-x_i(t^-),~\triangle y_j(t)=y_j(t)-y_j(t^-),~ \triangle x(t)=x(t)-x(t^-)=(\triangle x_1(t),\ldots ,\triangle x_n(t)),~\triangle y(t)=y(t)-y(t^-)=(\triangle y_1(t),\ldots ,\triangle y_m(t)),~0\le t_0<\cdots<t_k<\cdots ,\lim \limits _{k\rightarrow \infty }t_k=\infty \); \(x_i(t), y_j(t)\) denote the potential of the cell i and j at time t. \(x(t)=(x_1(t), x_2(t),\ldots , x_n(t))^T\in R^n,y(t)=(y_1(t), y_2(t),\ldots , y_m(t))^T\in R^m\); \(f(y(t)) = (f_1(y_1(t)),\ldots , f_m(y_m(t)))^T\in R^m\) and \(g(x(t)) = (g_1(x_1(t)), g_2(x_2(t)),\ldots , g_n(x_n(t)))^T\in R^n\) denote the activation functions of the neuron at time t, \(u(t)=(u_1(t), \ldots , u_{m_1}(t))^T\in R^{m_1},\ \widetilde{u}(t)=(\widetilde{u}_1(t), \widetilde{u}_2(t),\ldots , \widetilde{u}_{m_2}(t))^T\in R^{m_2}\) are continuous control input, I and \(\widetilde{I}\) denote the identity matrix of size n and m, respectively. \(J(t) = (J_1(t), \ldots , J_{n}(t))^T\in R^{n},\) \(\widetilde{J}(t) = (\widetilde{J}_1(t), \widetilde{J}_2(t),\ldots , \widetilde{J}_{m}(t))^T \in R^{m}\) are the impulsive control input at time t, \(\Upsilon _f(s) = \mathrm{diag}( f(y(t-s)), f (y(t-s)), \ldots , f (y(t-s)))_{n\times n},\Upsilon _g(s) = \mathrm{diag}(g(x(t-s)), g(x(t-s)), \ldots , g(x(t-s)))_{m\times m};\) \(D = \mathrm{diag}(d_1, \ldots , d_n)> 0,\widetilde{D} = \mathrm{diag}(\widetilde{d_1}, \ldots , \widetilde{d_m}) > 0\) are positive diagonal matrices, and \(d_i\), \(\widetilde{d_j}\) represent the rate of isolation of cells i and j from the other states and inputs, respectively. This means that cells i and j reset their potential to the other state during the isolation. \(A = (a_{ij})_{n\times m}, B = (b_{ij})_{n\times m},~R = (r_{ij})_{n\times m_1},~M = (m_{ij})_{n\times n},~E = (e_{ij}(t))_{n\times n},~\widetilde{A} = (\widetilde{a_{ji}})_{m\times n}, ~\widetilde{B} = (\widetilde{b_{ji}})_{m\times n},~\widetilde{R} = (\widetilde{r}_{ji})_{m\times m_2},~ \widetilde{M} = (\widetilde{m}_{ji})_{m\times m},~\widetilde{E} = (\widetilde{e_{ji}}(t))_{m\times m}\) are the feedback matrix and the delayed feedback matrix, respectively. \(\Gamma _1 = [C^T_1, C^T_2, \ldots , C^T_n]^T,C_i = (c_{ijl})_{m\times m}; \Gamma _2 = [\widetilde{C}^T_1, \widetilde{C}^T_2, \ldots , \widetilde{C}^T_m]^T,\widetilde{C}_j = (\widetilde{c}_{jil})_{n\times n}\). \(E(t), \widetilde{E}(t)\) are matrix functions with time-varying uncertainties, that is, \(E(t)=E+\Delta E,\widetilde{E}(t)=\widetilde{E}+\Delta \widetilde{E}\), where \(E,\widetilde{E}\) are known real constant matrices, \(\Delta E,\Delta \widetilde{E}\) are unknown matrices representing time-varying parameter uncertainties. We assume that the uncertainties are norm-bounded and can be described as

$$\begin{aligned} \Delta E=HF(t)D_1,\quad \Delta \widetilde{E}=\widetilde{H}\widetilde{F}(t)\widetilde{D}_1 \end{aligned}$$
(3)

where \(H,\widetilde{H},D_1, \widetilde{D}_1 \) are known real constant matrices with appropriate dimensions, and the uncertain matrix F(t),  which may be time varying, is unknown and satisfies \(F^T(t)F(t)\le I,\widetilde{F}^T(t)\widetilde{F}(t)\le \widetilde{I}\) for any given t. It is assumed the elements of F(t) are Lebesgue measurable. When \(F(t) = 0,\widetilde{F}(t)=0,\) system (2) is referred to as nominal neural impulsive systems. Time delays \(\tau (t), \sigma (t)\) are continuous functions, which correspond to the finite speed of axonal signal transmission and \(0\le \tau (t)\le \tau , 0 \le \sigma (t) \le \sigma \) and \(0<\sigma '(t)\le \sigma _1<1,0<\tau (t)\le \tau _1<1.\)

The initial conditions associated with (1) or (2) are of the form

$$\begin{aligned} x_i(t)= & {} \phi _i(t), \quad t_0-\sigma \le t\le t_0;\\ y_j(t)= & {} \varphi _j(t),\quad t_0-\tau \le t\le t_0, \end{aligned}$$

in which \(\phi _i (t), \varphi _j (t) (i = 1, 2, \ldots , n; j = 1, 2, \ldots , m)\) are continuous functions. The notations used in this paper are fairly standard. The matrix \(M>\ (\ge ,<,\le )~0\) denotes a symmetric positive definite (positive semidefinite, negative, negative semidefinite) matrix, respectively. For \(x\in R^n,\) denote \(\Vert x\Vert =\sqrt{x^Tx}\) and \(|x| =\sum _{i=1}^n|x_i|.\)

Remark 1

BAM is a type of recurrent neural network. Giving a pattern, it can return another pattern which is potentially of a different size. It is similar to the Hopfield network [2, 3, 5, 31, 33] in that they are both forms of associative memory. However, Hopfield networks return patterns of the same size. As for competitive neural networks [1, 4], they can model the dynamics of cortical cognitive maps with unsupervised synaptic modifications.

Throughout this paper, the activation functions \(f(\cdot ), g(\cdot ), J(\cdot ), \widetilde{J}(\cdot )\) are assumed to possess the following properties:

  1. (H1)

    There exist matrices \(K\in R^{m\times m}, U\in R^{n\times n}\) such that, for all \(y,z\in R^m;x,s\in R^n\),

    $$\begin{aligned} |f(y)-f(z)|\le |K(y-z)|;\ \ |g(x)-g(s)|\le |U(x-s)|. \end{aligned}$$
  2. (H2)

    \(f(0)= g(0)=J(0)= \widetilde{J}(0)=0.\)

  3. (H3)

    There exist positive numbers \(O_{j}, \widetilde{O}_{j}\) such that

    $$\begin{aligned} |f_j(x)|\le O_{j},\ |g_i(x)|\le \widetilde{O}_{i}; \end{aligned}$$

    for all \(x\in R (i = 1, 2, \ldots , n; j = 1, 2, . . . ,m).\)

Remark 2

Under assumption (H2), we have that the equilibrium point of system (2) is the trivial solution of system (2). In fact, when the equilibrium point \((x^*,y^*)\) of system (2) in the engineering background isn’t the trivial solution of system (2), one can transfer the equilibrium point \((x^*,y^*)\) to (0,0) by the transformation \(u=x-x^*,v=y-y^*\). Then, by the transformation \(\widetilde{f}(v)=f(v+y^*)-f(y^*),\widetilde{g}(u)=g(u+x^*)-g(x^*)\), assumption (H2) is always satisfied(see [19,32]), where \(J(0)=0,~\widetilde{J}(0) = 0\) mean that the impulsive control inputs at time 0 do not work in the engineering background.

Let \(x(t; \phi ),\ y(t; \varphi )\) denote the state trajectory of neural network (1) or (2) from the initial data \(x(s) = \phi (s)\in PC([t_0-\sigma , t_0]; R^n),\ y(s) = \varphi (s)\in PC([t_0-\tau , t_0]; R^m)\), respectively, where \(PC([t_0-r, t_0]; R^n)\) denote the set of piecewise right continuous function \(\phi : [-r,0]\rightarrow R^p\) with the norm defined by \(\Vert \phi \Vert _r=\sup _{-r\le \theta \le 0}\Vert \phi (\theta )\Vert .\) It can be easily seen that system (2) admits a trivial solution \(x(t; 0) = 0,\ y(t; 0) = 0\) corresponding to the initial data \(\phi = 0,\ \varphi =0\).

Definition 1

([46]) For system (1) or (2) and every \(\xi _1\in PC([t_0-\sigma , t_0]; R^n)\) and \(\xi _2\in PC([t_0-\tau , t_0]; R^m)\), the trivial solution (equilibrium point) is robustly, globally, asymptotically stable in the mean square if the following holds:

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\left( |x(t;\xi _1)|^2+|y(t;\xi _2)|^2\right) =0. \end{aligned}$$

Lemma 1

For any vectors \(a,b\in R^n,\) the inequality

$$\begin{aligned} 2a^Tb\le \rho a^Ta+\frac{1}{\rho }b^Tb \end{aligned}$$

holds for \(\forall \ \rho >0.\)

Lemma 2

For any vectors \(a,b\in R^n,\) the inequality

$$\begin{aligned} 2a^Tb\le a^TX^{-1}a+b^TXb \end{aligned}$$

holds for any matrices \(X>0.\)

Lemma 3

([9]) Given constant matrices \(\Sigma _1, \Sigma _2, \Sigma _3\) where \(\Sigma _1 = \Sigma _1^T\) and \(0<\Sigma _2 = \Sigma ^T_2\), then

$$\begin{aligned} \Sigma _1 + \Sigma _3^T\Sigma _2^{-1}\Sigma _3<0 \end{aligned}$$

if and only if

$$\begin{aligned} \left( \begin{array}{cc} \Sigma _1 &{} \Sigma _3^T\\ \Sigma _3 &{} -\Sigma _2 \end{array}\right)<0\ \ \mathrm {or}\ \ \left( \begin{array}{cc} -\Sigma _2 &{} \Sigma _3\\ \Sigma _3^T &{} \Sigma _1 \end{array}\right) <0. \end{aligned}$$

Lemma 4

([38]) Let A, D, E, F and P be real matrices of appropriate dimensions with \(P >0\) and F satisfying \(F^TF\le I.\) Then, for any scalar \(\varepsilon >0\) satisfying \(P^{-1}-\varepsilon ^{-1}DD^T >0,\) we have

$$\begin{aligned} (A + DFE)^TP(A + DFE)\le A^T(P^{-1}-\varepsilon ^{-1}DD^T)^{-1}A + \varepsilon E^TE. \end{aligned}$$

3 Impulsively Exponential Stability

Now, we shall present and prove our main results. Our results complement and improve some of the known results found in the literature.

  • \(\widetilde{\Lambda }_1=-Q\widetilde{D}-\widetilde{D}^TQ+Q_1+W_1+W_1^T\),

  • \(\widetilde{\Lambda }_2=-(1-\tau _1)Q_1-W_2-W_2^T+\rho _{Z_2}K^TK,\ \widetilde{\Lambda }_3=-\sigma P_2+\epsilon _1\sigma \lambda _{2}I\),

  • \(\Lambda _1=-PD-D^TP+N_1+N_1^T+P_1\),

  • \(\Lambda _2=-(1-\sigma _1)P_1-N_2-N_2^T+\rho _{Z_1}U^TU,\ \Lambda _3=-\tau Q_2+\epsilon _2\tau \lambda _{1}I\).

where \(\lambda _1=\rho _{\Gamma ^T_1\Gamma _1},\lambda _2=\rho _{\Gamma ^T_2\Gamma _2}.\)

Theorem 1

Consider system (2) with the impulsive control inputs \(J(\cdot )=0,\ \widetilde{J}(\cdot )=0\). Under assumptions (H1)–(H3), the equilibrium point of system (2) is robustly, globally, asymptotically stable in the mean square if there exist some scalars \(\epsilon _i>0(i=1,2,3,4),\rho _X> 0 (X=Q_2,P_2,X_1,X_2,Z_1,Z_2)\) and matrices \(N_i(i=1,2,3),W_i(i=1,2,3),X_1>0,X_2>0,Z_1>0,Z_2>0,P>0,Q>0,P_1>0,Q_1>0,P_2>0,Q_2>0\) such that

$$\begin{aligned}&X<\rho _X I,\end{aligned}$$
(4)
$$\begin{aligned}&\Psi _1= \left[ \begin{array}{cccccccc} \widetilde{\Lambda }_1 &{}-W_1^T+W_2&{} -W_1^T+W_3&{}0&{}Q\widetilde{A}&{}(\rho _{X_2}+\rho _{Q_2})K^T&{}Q\widetilde{B}&{}\sqrt{\sigma \alpha }Q\\ * &{}\widetilde{\Lambda }_2&{}-W_2^T-W_3&{}0&{}0&{}0&{}0&{}0\\ * &{}*&{}-W_3^T-W_3&{}0&{}0&{}0&{}0&{}0\\ * &{}*&{}*&{}\widetilde{\Lambda }_3&{}0&{}0&{}0&{}0 \\ * &{}*&{}*&{}*&{}-X_1&{}0&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}-(\rho _{X_2}+\rho _{Q_2})I&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}-Z_1&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _1I \end{array}\right] \nonumber \\&\quad <0, \end{aligned}$$
(5)
$$\begin{aligned}&\Psi _2= \left[ \begin{array}{cccccccc} {\Lambda }_1 &{}-N_1^T+N_2&{} -N_1^T+N_3&{}0&{}P{A}&{}(\rho _{X_1}+\rho _{P_2})U^T&{}P{B}&{}\sqrt{\tau \widetilde{\alpha }}P\\ * &{}{\Lambda }_2&{}-N_2^T-N_3&{}0&{}0&{}0&{}0&{}0\\ * &{}*&{}-N_3^T-N_3&{}0&{}0&{}0&{}0&{}0\\ * &{}*&{}*&{}{\Lambda }_3&{}0&{}0&{}0&{}0 \\ * &{}*&{}*&{}*&{}-X_2&{}0&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}-(\rho _{X_1}+\rho _{P_2})I&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}-Z_2I&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _2I \end{array}\right] \nonumber \\&\quad <0, \end{aligned}$$
(6)
$$\begin{aligned}&\left[ \begin{array}{cccc} -P &{}E^TP&{}\epsilon _{3}D_1^T&{}0\\ * &{} -P &{} 0&{}PH\\ * &{} * &{} -\epsilon _{3}I &{}0\\ * &{} * &{} * &{}-\epsilon _{3}I \end{array}\right] \le 0, \end{aligned}$$
(7)
$$\begin{aligned}&\left[ \begin{array}{ccccc} -Q &{}\widetilde{E}^TQ&{}\epsilon _{4}\widetilde{D}_1^T&{} \\ * &{} -Q &{} 0&{}Q\widetilde{H}\\ * &{} * &{} -\epsilon _{4}I &{}0\\ * &{} * &{} * &{}-\epsilon _{4}I \end{array}\right] \le 0, \end{aligned}$$
(8)
$$\begin{aligned}&\left[ \begin{array}{cccc} -P &{}PH\\ * &{}-\epsilon _{3}I \end{array}\right] < 0, \end{aligned}$$
(9)
$$\begin{aligned}&\left[ \begin{array}{cccc} -Q &{}Q\widetilde{H}\\ * &{}-\epsilon _{4}I\end{array}\right] < 0, \end{aligned}$$
(10)

hold.

Proof

Let

$$\begin{aligned} V(t)= & {} x^T(t)Px(t)+y^T(t)Qy(t)+\int _{t-\sigma (t)}^tx^T(s)P_1x(s)\hbox {d}s\\&+\int _{t-\tau (t)}^ty^T(s)Q_1y(s)\hbox {d}s+\int _{-\tau }^{0}\int _{t+s}^{t}f^T(y(\eta ))Q_2f(y(\eta ))\hbox {d}\eta \hbox {d}s\\&+\int _{-\sigma }^{0}\int _{t+s}^{t}g^T(x(\eta ))P_2g(x(\eta ))\hbox {d}\eta \hbox {d}s. \end{aligned}$$

(I) We consider the case of \(t\ne t_k.\) Calculate the derivative of V(t) along the solutions of (2), and we obtain

$$\begin{aligned} \dot{ V}(t)= & {} 2x^T(t)P\left( -Dx(t)+A f(y(t))+B f(y(t-\tau (t)))\right. \\&\left. +\,C\int _{t-\tau }^{t}\Upsilon ^T_f\Gamma _1f(y(s))\hbox {d}s\right) \\&+\,2y^T(t)Q\Big (-\widetilde{D}y(t)+\widetilde{A} g(x(t))+ \widetilde{B} g(x(t-\sigma (t)))\\&+\,\widetilde{C}\int _{t-\sigma }^{t}\Upsilon ^T_g\Gamma _2g(x(s))\hbox {d}s\Big )\\&+\,x^T(t)P_1x(t)-(1-\sigma '(t))x^T(t-\sigma (t))P_1x(t-\sigma (t))\\&+\,y^T(t)Q_1y(t)-(1-\tau '(t))y^T(t-\tau (t))Q_1y(t-\tau (t))\\&+\,f^T(y(t))Q_2f(y(t)) -\int _{t-\tau }^{t}f^T(y(s))Q_2f(y(s)) \hbox {d}s\\&+\,g^T(x(t))P_2g(x(t)) -\int _{t-\sigma }^{t}g^T(x(s))P_2g(x(s)) \hbox {d}s. \end{aligned}$$

From Lemmas 1, 2 and 4, we have

$$\begin{aligned}&2y^T(t)Q\widetilde{A}g(x(t))\\&\quad \le y^T(t)Q\widetilde{A}X_1^{-1}\widetilde{A}^TQy(t)+g^T(x(t))X_1g(x(t))\\&\quad \le y^T(t)Q\widetilde{A}X_1^{-1}\widetilde{A}^TQy(t)+\rho _{X_1}x^T(t)U^TUx(t);\\&2x^T(t)P{A}f(y(t))\\&\quad \le x^T(t)P{A}X_2^{-1}{A}^TPx(t)+f^T(y(t))X_2f(y(t))\\&\quad \le x^T(t)P{A}X_2^{-1}{A}^TPx(t)+\rho _{X_2}y^T(t)K^TKy(t);\\&2y^T(t)Q{\widetilde{B}}g(x(t-\sigma (t)))\\&\quad \le y^T(t)Q{\widetilde{B}}Z_1^{-1}{\widetilde{B}}^TQy(t)+g^T(x(t-\sigma (t)))Z_1g(x(t-\sigma (t)))\\&\quad \le y^T(t)Q\widetilde{B}Z_1^{-1}\widetilde{B}^TQy(t)+\rho _{Z_1}x^T(t-\sigma (t))U^TUx(t-\sigma (t));\\&2x^T(t)P{B}f(y(t-\tau (t)))\\&\quad \le x^T(t)P{B}Z_2^{-1}{B}^TPx(t)+f^T(y(t-\tau (t)))Z_2f(y(t-\tau (t)))\\&\quad \le x^T(t)P{B}Z_2^{-1}{B}^TPx(t)+\rho _{Z_2}y^T(t-\tau (t))K^TKy(t-\tau (t));\\&2y^T(t)Q\int _{t-\sigma }^{t}\Upsilon ^T_g\Gamma _2g(x(s))\hbox {d}s\\&\quad \le \int _{t-\sigma }^{t}\left[ \epsilon _1^{-1}y^T(t)Q\Upsilon ^T_g\Upsilon _gQy(t)+ \epsilon _1g^T(x(s))\Gamma ^T_2\Gamma _2g(x(s))\right] \hbox {d}s.\\&2x^T(t)P\int _{t-\tau }^{t}\Upsilon ^T_f\Gamma _1f(y(s))\hbox {d}s\\&\quad \le \int _{t-\tau }^{t}\left[ \epsilon _2^{-1}x^T(t)P\Upsilon ^T_f\Upsilon _fPx(t)+ \epsilon _2f^T(y(s))\Gamma ^T_1\Gamma _1f(y(s))\right] \hbox {d}s. \end{aligned}$$

Since \(\Upsilon ^T_g\Upsilon _g = \Vert g(x(t - s)\Vert ^2 I\) and \(\Vert g(x(t - s)\Vert ^2\le \sum _{j=1}^mO_j=\alpha ,\) it follows that

$$\begin{aligned} y^T(t)Q\Upsilon ^T_g\Upsilon _gQy(t)\le \alpha y^T(t)QQy(t). \end{aligned}$$

Since \(\Upsilon ^T_f\Upsilon _f = \Vert f(y(t - s)\Vert ^2 I\) and \(\Vert f(y(t - s)\Vert ^2\le \sum _{i=1}^n\widetilde{O}_i=\widetilde{\alpha },\) it follows that

$$\begin{aligned} x^T(t)P\Upsilon ^T_f\Upsilon _fPx(t)\le \widetilde{\alpha } x^T(t)PPx(t). \end{aligned}$$

Noting that \(x(t)-x(t-\sigma (t))-\int _{t-\sigma (t)}^t\dot{x}(s)\hbox {d}s=0,\ y(t)-y(t-\tau (t))-\int _{t-\tau (t)}^t\dot{y}(s)\hbox {d}s=0,\) then, there exist matrices \(N_1,N_2,N_3,W_1,W_2,W_3\) such that

$$\begin{aligned}&\left[ 2x^T(t)N^T_1+2x^T(t-\sigma (t))N^T_2+2\left( \int _{t-\sigma (t)}^t\dot{x}(s)\hbox {d}s\right) ^TN^T_3\right] \\&\quad \times \left( x(t)-x(t-\sigma (t))-\int _{t-\sigma (t)}^t\dot{x}(s)\hbox {d}s\right) =0,\\&\left[ 2y^T(t)W^T_1+2y^T(t-\tau (t))W^T_2+2\left( \int _{t-\tau (t)}^t\dot{y}(s)\hbox {d}s\right) ^TW^T_3\right] \\&\quad \times \left( y(t)-y(t-\tau (t))-\int _{t-\tau (t)}^t\dot{y}(s)\hbox {d}s\right) =0. \end{aligned}$$

Moreover,

$$\begin{aligned} f^T(y(t))Q_2f(y(t))\le & {} \rho _{Q_2}y^T(t)K^TKy(t),\, g^T(x(t))P_2g(x(t))\\\le & {} \rho _{P_2}x^T(t)U^TUx(t). \end{aligned}$$

Thus,

$$\begin{aligned} \dot{V}(t)\le \frac{1}{\sigma }\int _{t-\sigma }^{t}\xi ^T_1\Pi _1\xi _1\hbox {d}s+\frac{1}{\tau }\int _{t-\tau }^{t}\xi ^T_2\Pi _2\xi _2\hbox {d}s, \end{aligned}$$

where \(\xi _1=[y^T(t)\ y^T(t-\tau (t))\ (\int _{t-\tau (t)}^t\dot{y}(s)\hbox {d}s)^T\ g^T(x(s))]^T,\xi _2=[x^T(t)\ x^T(t-\sigma (t))\ (\int _{t-\sigma (t)}^t\dot{x}(s)\hbox {d}s)^T\ f^T(y(s))]^T\), and

$$\begin{aligned} \Pi _1= & {} \left[ \begin{array}{llll} \widetilde{\Omega }_1 &{}-W_1^T+W_2&{} -W_1^T+W_3&{}0\\ * &{}\widetilde{\Omega }_2&{}-W_2^T-W_3&{}0\\ * &{}*&{}-W_3^T-W_3&{}0\\ * &{}*&{}*&{}\widetilde{\Omega }_3\end{array}\right] ,\ \Pi _2= \left[ \begin{array}{llll}{\Omega }_1 &{}-N_1^T+N_2&{} -N_1^T+N_3&{}0\\ * &{}{\Omega }_2&{}-N_2^T-N_3&{}0\\ * &{}*&{}-N_3^T-N_3&{}0\\ * &{}*&{}*&{}{\Omega }_3\end{array}\right] .\\ \widetilde{\Omega }_1= & {} -Q\widetilde{D}-\widetilde{D}^TQ+Q_1+W_1+W_1^T+ Q\widetilde{A}X_1^{-1}\widetilde{A}^TQ+(\rho _{X_2}+\rho _{Q_2})K^TK\\&+Q\widetilde{B}Z_1^{-1}\widetilde{B}^TQ+\sigma \epsilon _1^{-1}\alpha QQ,\\ \widetilde{\Omega }_2= & {} -(1-\tau _1)Q_1-W_2-W_2^T+\rho _{Z_2}K^TK,\ \widetilde{\Omega }_3=-\sigma P_2+\epsilon _1\sigma \lambda _{2}I,\\ {\Omega }_1= & {} -PD-D^TP+N_1+N_1^T+P_1+P{A}X_2^{-1}{A}^TP+(\rho _{X_1}+\rho _{P_2})U^TU\\&+P{B}Z_2^{-1}{B}^TP+\tau \epsilon _2^{-1}\widetilde{\alpha }PP,\\ {\Omega }_2= & {} -(1-\sigma _1)P_1-N_2-N_2^T+\rho _{Z_1}U^TU,\ {\Omega }_3=-\tau Q_2+\epsilon _2\tau \lambda _{1}I. \end{aligned}$$

By Lemma 3, it is obvious from (5) and (6) that \(\Pi _1<0,\Pi _2<0\). There must exist scalars \(\eta _1>0,\eta _2>0\) such that

$$\begin{aligned} \Pi _1+\left[ \begin{array}{cccc}\begin{matrix} \eta _1 I &{} 0&{}0&{}0\\ 0 &{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \end{matrix}\end{array}\right]<0;\ \Pi _2+\left[ \begin{array}{cccc} \begin{matrix}\eta _2 I &{} 0&{}0&{}0\\ 0 &{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0 \end{matrix}\end{array}\right] <0. \end{aligned}$$

So

$$\begin{aligned} \dot{V}(t)\le -\eta _1\Vert x(t)\Vert ^2-\eta _2\Vert y(t)\Vert ^2. \end{aligned}$$
(11)

(II) We consider the case of \(t = t_k\). By (4), we have

$$\begin{aligned} V(t_k)-V(t_k^-)= & {} x^T(t_k)Px(t_k)-x^T(t_k^-)Px(t_k^-)+y^T(t_k)Qy(t_k)-y^T(t_k^-)Qy(t_k^-)\\&+\int _{t_k-\sigma (t_k)}^{t_k}x^T(s)P_1x(s)\hbox {d}s-\int _{t_k^--\sigma (t_k^-)}^{t_k^-}x^T(s)P_1x(s)\hbox {d}s\\&+\int _{t_k-\tau (t_k)}^{t_k}y^T(s)Q_1y(s)\hbox {d}s-\int _{t_k^--\tau (t_k^-)}^{t_k^-}y^T(s)Q_1y(s)\hbox {d}s\\&+\,\tau \int _{-\tau }^{0}\int _{t_k+s}^{t_k}f^T(y(t_k-\eta ))\Gamma ^T_1\Upsilon _f(\eta )Q_2\Upsilon ^T_f(\eta )\Gamma _1f(y(t_k\\&\quad -\,\eta ))\hbox {d}\eta \hbox {d}s\\&-\tau \int _{-\tau }^{0}\int _{t_k^-+s}^{t_k^-}f^T(y(t_k^--\eta ))\Gamma ^T_1\Upsilon _f(\eta )Q_2\Upsilon ^T_f(\eta )\Gamma _1f(y(t_k^-\\&\quad -\eta ))\hbox {d}\eta \hbox {d}s\\&+\,\sigma \int _{-\sigma }^{0}\int _{t_k+s}^{t_k}g^T(x(t_k-\eta ))\Gamma ^T_2\Upsilon _g(\eta )P_2\Upsilon ^T_g(\eta )\Gamma _2g(x(t_k\\&\quad -\,\eta ))\hbox {d}\eta \hbox {d}s\\&-\,\sigma \int _{-\sigma }^{0}\int _{t_k^-+s}^{t_k^-}g^T(x(t_k^--\eta ))\Gamma ^T_2\Upsilon _g(\eta )P_2\Upsilon ^T_g(\eta )\Gamma _2g(x(t_k^-\\&\quad -\,\eta ))\hbox {d}\eta \\&\le x^T(t^-_k)[(E+HF(t_k)D_1)^TP(E+HF(t_k)D_1)-P]x(t^-_k)\\&\quad +\,y^T(t^-_k)[(\widetilde{E}+\widetilde{H}\widetilde{F}(t_k)\widetilde{D}_1)^TQ(\widetilde{E}+\widetilde{H}\widetilde{F}(t_k)\widetilde{D}_1)-Q]y(t^-_k)\\&\le x^T(t^-_k)[E^T(P^{-1}-\epsilon _3^{-1}HH^T)^{-1}E+\epsilon _3D_1^TD_1-P]x(t^-_k)\\&\quad +\,y^T(t^-_k)[\widetilde{E}^T(Q^{-1}-\epsilon _4^{-1}\widetilde{H}\widetilde{H}^T)^{-1}\widetilde{E}+\epsilon _4\widetilde{D}_1^T\widetilde{D}_1-Q]y(t^-_k) \end{aligned}$$

By (7)–(10) and combining with Schur complements (Lemma 3) yield

$$\begin{aligned}&E^T(P^{-1}-\epsilon _3^{-1}HH^T)^{-1}E+\epsilon _3D_1^TD_1-P\le 0,\\&\widetilde{E}^T(Q^{-1}-\epsilon _4^{-1}\widetilde{H}\widetilde{H}^T)^{-1}\widetilde{E}+\epsilon _4\widetilde{D}_1^T\widetilde{D}_1-Q\le 0; \end{aligned}$$

then, \(V(t_k)-V(t_k^-)\le 0\), that is,

$$\begin{aligned} V(t_k)\le V(t_k^-). \end{aligned}$$
(12)

This and (I) implie that the equilibrium point of system (2) is robustly, globally, asymptotically stable in the mean square. The proof is complete.

Let us now consider to design a state feedback memory control law of the form

$$\begin{aligned}&u(t)=K_cx(t)+K_{c1}x(t-\sigma (t)),\widetilde{u}(t)=\widetilde{K}_cy(t)+\widetilde{K}_{c1}y(t-\tau (t)),\nonumber \\&J(t_k^-)=K_dx(t_k^-),\nonumber \\&\widetilde{J}(t_k^-)=\widetilde{K}_dy(t_k^-) \end{aligned}$$
(13)

to stabilize system (2), where \(K_c,K_{c1}\in R^{m_1\times n},\ \widetilde{K}_c,\widetilde{K}_{c1}\in R^{m_2\times m}\), \(K_d\in R^{n\times n},\ \widetilde{K}_d\in R^{m\times m}\) are constant gains to be designed.

Substituting (13) into (2) and applying Theorem 1, it is easy to obtain the next theorem.

Theorem 2

Consider system (2). Under assumptions (H1)–(H3), if there exist scalars \(\epsilon _i>0(i=1,2,3,4),\rho _X> 0 (X=Q_2,P_2,X_1,X_2,Z_1,Z_2)\) and matrices \(N_i(i=1,2,3),W_i(i=1,2,3),Y_c,Y_{c1},Y_d,\widetilde{Y}_c,\widetilde{Y}_{c1},\widetilde{Y}_d,X_1>0,X_2>0,Z_1>0,Z_2>0,P>0,Q>0,P_1>0,Q_1>0,P_2>0,Q_2>0\) such that (4), (9), (10) and

$$\begin{aligned}&\left[ \begin{array}{ccccccccc} \widetilde{\varPhi }_1 &{}-W_1^T+W_2+\widetilde{R}\widetilde{Y}_{c1}&{} -W_1^T+W_3&{}0&{}Q\widetilde{A}&{}(\rho _{X_2}+\rho _{Q_2})K^T&{}Q\widetilde{B}&{}\sqrt{\sigma \alpha }Q\\ * &{}\widetilde{\Lambda }_2&{}-W_2^T-W_3&{}0&{}0&{}0&{}0&{}0\\ * &{}*&{}-W_3^T-W_3&{}0&{}0&{}0&{}0&{}0\\ * &{} * &{} * &{}\widetilde{\Lambda }_3&{}0&{}0&{}0&{}0 \\ * &{} * &{} * &{} * &{} -X_1&{}0&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}-(\rho _{X_2}+\rho _{Q_2})I&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}-Z_1&{}0\\ * &{} * &{} * &{} * &{} * &{} * &{} * &{}-\epsilon _1I\end{array}\right] <0,\qquad \end{aligned}$$
(14)
$$\begin{aligned}&\left[ \begin{array}{cccccccc}{\varPhi }_1 &{}-N_1^T+N_2+RY_{c1}&{} -N_1^T+N_3&{}0&{}P{A}&{}(\rho _{X_1}+\rho _{P_2})U^T&{}P{B}&{}\sqrt{\tau \widetilde{\alpha }}P\\ * &{}{\Lambda }_2&{}-N_2^T-N_3&{}0&{}0&{}0&{}0&{}0\\ * &{} * &{} -N_3^T-N_3&{}0&{}0&{}0&{}0&{}0\\ * &{} * &{} * &{}{\Lambda }_3&{}0&{}0&{}0&{}0 \\ * &{} * &{} * &{} * &{} -X_2&{}0&{}0&{}0\\ * &{} * &{} * &{} * &{} * &{} -(\rho _{X_1}+\rho _{P_2})I&{}0&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}-Z_2I&{}0\\ * &{}*&{}*&{}*&{}*&{}*&{}*&{}-\epsilon _2I\end{array}\right] <0,\qquad \end{aligned}$$
(15)
$$\begin{aligned}&\left[ \begin{array}{cccc}-P &{}E^TP+M^TY_d&{}\epsilon _{3}D_1^T&{}0\\ * &{} -P &{} 0&{}PH\\ * &{} * &{} -\epsilon _{3}I &{}0\\ * &{} * &{} * &{}-\epsilon _{3}I \end{array}\right] \le 0, \end{aligned}$$
(16)
$$\begin{aligned}&\left[ \begin{array}{ccccc}-Q &{}\widetilde{E}^TQ+\widetilde{M}^T\widetilde{Y}_d&{}\epsilon _{4}\widetilde{D}_1^T&{} \\ * &{} -Q &{} 0&{}Q\widetilde{H}\\ * &{} * &{} -\epsilon _{4}I &{}0\\ * &{} * &{} * &{}-\epsilon _{4}I \end{array}\right] \le 0, \end{aligned}$$
(17)

hold. Then, for any bounded time delay \(\tau (t),\sigma (t)\), the control law (13) with \(K_c=Y_{c}P^{-1},\widetilde{K}_c=\widetilde{Y}_{c}Q^{-1},K_{c1}=Y_{c1}P^{-1}, \widetilde{K}_{c1}=\widetilde{Y}_{c1}Q^{-1},K_d=Y_{d}P^{-1} \) and \(\widetilde{K}_d=\widetilde{Y}_{d}Q^{-1}\) robustly stabilizes system (1) or (2) in the mean square for any impulsive time sequence \(\{t_k\}\) where

$$\begin{aligned} \widetilde{\varPhi }_1= & {} -Q\widetilde{D}-\widetilde{D}Q+\widetilde{R}\widetilde{Y}_c+\widetilde{Y}_c^T\widetilde{R}^T+Q_1+W_1+W_1^T,\\ \widetilde{\Lambda }_2= & {} -(1-\tau _1)Q_1-W_2-W_2^T+\mu _2K^TK,\ \widetilde{\Lambda }_3=-\tau ^2\lambda _1^2(Q_2-Z_2),\\ {\varPhi }_1= & {} -PD-DP+RY_c+Y_c^TR^T+N_1+N_1^T+P_1,\\ {\Lambda }_2= & {} -(1-\sigma _1)P_1-N_2-N_2^T+\mu _1U^TU,\ {\Lambda }_3=-\sigma ^2\lambda _2^2(P_2-Z_1),\\ \lambda _1= & {} \max \limits _{1\le i\le n}\{\lambda _\mathrm{max}(C_i)\},\lambda _2=\max \limits _{1\le i\le n}\{\lambda _\mathrm{max}(\widetilde{C}_i)\}. \end{aligned}$$

Remark 3

Some stability analysis of higher-order BAM neural networks with delays is presented [12, 27, 28, 37]. However, simple and efficient conditions for the design and robustness analysis of such controllers were missing. The present paper fills this gap through introducing simple LMIs for robust stability analysis of the BAM systems with multiple delays and justifying that these LMIs are always feasible for small enough delays. Moreover, all of these criteria in this paper are easy to verify.

Remark 4

In this paper, the methods are by using Lyapunov–Krasovskii functionals, employing linear matrix inequalities and differential inequalities. In [31, 33], the authors mainly used the differential inequality with delay and impulse, coincidence degree theory as well as a priori estimates and Lyapunov functional, respectively. Moreover, the methods derived in this paper can be used to analyze, design and control some other high-order artificial neural networks.

Remark 5

In this paper, the essential difficulties encountered are how to choose suitable Lyapunov–Krasovskii functionals, and how to design a state feedback memory control law. The first is because that the time-varying delay functions \(\tau (t), \sigma (t)\) exist; the second is because designing the delay feedback impulsive control is a new theory in the impulsive stabilization. And, they were solved by adding the four terms

$$\begin{aligned}&\int _{t-\tau (t)}^ty^T(s)Q_1y(s)\hbox {d}s,~ \int _{-\sigma }^{0}\int _{t+s}^{t}g^T(x(\eta ))P_2g(x(\eta ))\hbox {d}\eta \hbox {d}s,\\&\int _{-\tau }^{0}\int _{t+s}^{t}f^T(y(\eta ))Q_2f(y(\eta ))\hbox {d}\eta \hbox {d}s, ~\int _{t-\sigma (t)}^tx^T(s)P_1x(s)\hbox {d}s \end{aligned}$$

to Lyapunov–Krasovskii functionals and designing a linear delay feedback impulsive control law (13) (since f, g is global Lipschitz continuous), respectively.

Remark 6

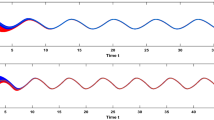
When the system is running with impulses, our results show that impulses make contribution to the stability of differential systems with time delay even if they are unstable, which is shown in Figs. 2 and 3.

4 Numerical Examples

Example 1

Consider system (2) with:

$$\begin{aligned} D= & {} \left[ \begin{array}{lll}2.9 &{}0&{}0\\ 0&{} 3.2&{}0\\ 0&{}0&{}3\end{array}\right] ;\quad A=\left[ \begin{array}{lll}-1 &{}2\\ 2 &{}1\\ -2&{}1 \end{array}\right] ; \quad E=\left[ \begin{array}{ccc}0.3 &{}0&{}0\\ 0 &{}0.3&{}0\\ 0&{}0&{}0.3\end{array}\right] ;\\ C_1= & {} \left[ \begin{array}{lll}0.1210 &{}0.3159\\ 0.3508 &{}0.2028\end{array}\right] ;\quad C_2=\left[ \begin{array}{lll}0.2731 &{}0.3656\\ 0.2548 &{}0.2324\end{array}\right] ;\quad C_3=\left[ \begin{array}{lll}0.1049 &{}0.2319\\ 0.2084 &{}0.2393\end{array}\right] ;\\ B= & {} \left[ \begin{array}{lll}-1&{} 1\\ 1 &{}1\\ 1&{}-1\end{array}\right] ;\quad K=\left[ \begin{array}{ll}0.09&{} 0\\ 0 &{}0.01\end{array}\right] ;\\ U= & {} \left[ \begin{array}{lll}0.3&{} 0&{}0\\ 0 &{}0.1&{}0\\ 0&{}0&{}0.5\end{array}\right] ;\quad D1=\left[ \begin{array}{lll}1&{}-1&{} 0\\ -1&{}-1&{} 0\\ 0&{}-2&{}1\end{array}\right] ;\quad H=\left[ \begin{array}{lll}0.02&{} 0&{}0\\ 0&{} 0.03&{}0\\ 0&{}0&{}0.03\end{array}\right] ;\\ \widetilde{D}= & {} \left[ \begin{array}{ll}2.6&{} 0\\ 0 &{}2.9\end{array}\right] ;\quad \widetilde{B}=\left[ \begin{array}{lll}1&{}0 &{}0.3\\ -0.6&{}0 &{}0.3\end{array}\right] ;\quad \widetilde{C}_1=\left[ \begin{array}{lll}0.0298&{} 0.1800&{} 0.2218\\ 0.1665 &{}0.3139&{} 0.2933\\ 0.5598 &{}0.1536&{} 0.2398\end{array}\right] ;\\ \widetilde{C}_2= & {} \left[ \begin{array}{lll}0.3001 &{}0.3232&{} 0.0321\\ 0.3112 &{}0.3515 &{}0.5586\\ 0.3772 &{}0.2107 &{}0.3361\end{array}\right] ;\quad \widetilde{A}=\left[ \begin{array}{lll}1&{}0&{} -1\\ 0&{} 0&{}1.2\end{array}\right] ;\quad \widetilde{E}=\left[ \begin{array}{ll}0.6 &{}-0.2\\ 0 &{}0.5\end{array}\right] ;\\ \widetilde{D}1= & {} \left[ \begin{array}{ll}0.6&{} 0.5\\ -0.6&{} 0.4\end{array}\right] ;\quad \widetilde{H}=\left[ \begin{array}{ll}0.09&{} 0.06\\ 0.06&{} 0.09\end{array}\right] ;\quad \sigma =\tau =1;\\ \alpha= & {} \widetilde{\alpha }=1. \end{aligned}$$

Then,

$$\begin{aligned} \Gamma _1=\left[ \begin{array}{cccccc}0.1210 &{}0.3159\\ 0.3508 &{}0.2028\\ 0.2731 &{}0.3656\\ 0.2548 &{}0.2324\\ 0.1049 &{}0.2319\\ 0.2084 &{}0.2393\end{array}\right] ; \Gamma _2=\left[ \begin{array}{cccccc}0.0298&{} 0.1800&{} 0.2218\\ 0.1665 &{}0.3139&{} 0.2933\\ 0.5598 &{}0.1536&{} 0.2398\\ 0.3001 &{}0.3232&{} 0.0321\\ 0.3112 &{}0.3515 &{}0.5586\\ 0.3772 &{}0.2107 &{}0.3361\end{array}\right] . \end{aligned}$$

By solving LMIs (3)–(9) for \(\epsilon _i>0(i=1,2,3,4),\rho _X> 0 (X=Q_2,P_2,X_1,X_2,Z_1,Z_2)\) and matrices \(X_1>0,X_2>0,Z_1>0,Z_2>0,P>0,Q>0,P_1>0,Q_1>0,P_2>0,Q_2>0\), we obtain

$$\begin{aligned} P= & {} \left[ \begin{array}{ccc} 0.4654 &{} -0.0064 &{} -0.0340\\ -0.0064 &{} 0.7287 &{} -0.0290\\ -0.0340 &{} -0.0290 &{} 0.4735 \end{array}\right] ;\quad Q=\left[ \begin{array}{cc}0.7960 &{} 0.0238\\ 0.0238 &{} 0.7093\end{array}\right] ;\\ P_1= & {} \left[ \begin{array}{ccc}0.6368 &{} -0.0280 &{} -0.1055\\ -0.0280 &{} 0.7792 &{} 0.2243\\ -0.1055 &{} 0.2243 &{} 0.5100\end{array}\right] ;\quad P_2=\left[ \begin{array}{cc}0.7973&{}0\\ 0 &{} 0.7973 \end{array}\right] ;\\ Q_1= & {} \left[ \begin{array}{cc}0.9273 &{} 0.2330\\ 0.2330 &{} 1.1490\end{array}\right] ;\quad Q_2=\left[ \begin{array}{ccc}1.1561 &{} 0 &{} 0\\ 0 &{} 1.1561 &{} 0\\ 0 &{} 0 &{} 1.1561\end{array}\right] ;\\ X_1= & {} \left[ \begin{array}{ccc}0.9090 &{} 0&{} -0.1013\\ 0 &{} 0.7952 &{} 0\\ -0.1013 &{} 0 &{} 1.0165\end{array}\right] ;\quad X_2=\left[ \begin{array}{cc}2.0404 &{} -0.0182\\ -0.0182 &{} 1.6456\end{array}\right] ;\\ Z_1= & {} \left[ \begin{array}{ccc}1.2089 &{} 0&{} 0.0262\\ 0 &{} 0.9862 &{} 0\\ 0.0262 &{} 0 &{} 1.0117\end{array}\right] ;\quad Z_2=\left[ \begin{array}{cc} 1.4291 &{} -0.0035\\ -0.0035 &{} 1.6198\end{array}\right] ;\\ \epsilon _1= & {} 0.6443;\quad \epsilon _2= 1.1712;\quad \epsilon _3= 0.0945;\quad \epsilon _4= 0.4812. \end{aligned}$$

which implies from Theorem 1 that the above delayed stochastic high-order neural network is robustly, globally, asymptotically stable in the mean square with the impulsive control inputs \(J(\cdot )=0,\ \widetilde{J}(\cdot )=0.\) The time trajectories of Example 1 with initial conditions

$$\begin{aligned} \left\{ \begin{aligned}&\phi _1(s)=2, ~~~ s\in [-5,0];\\ {}&\phi _2(s)=1.5, \ s\in [-5,0];\\ {}&\phi _3(s)=0.5, \ s\in [-5,0]; \end{aligned}\right. ~~~\left\{ \begin{aligned}&\varphi _1(s)=-0.5, ~ s\in [-7,0];\\ {}&\varphi _2(s)=-1, \ \ \ s\in [-7,0];\\ {}&\varphi _3(s)=-1.5, \ s\in [-7,0]; \end{aligned}\right. \end{aligned}$$

and \( \ f_1(x)=\tanh (0.9x),\ f_2(x)=\tanh (0.78x),\ f_3(x)=\tanh (0.96x);\ g_1(x)=\tanh (0.83x),\ g_2(x)=\tanh (0.88x),\ g_3(x)=\tanh (0.93x)\) are shown Fig. 1.

Fig. 1
figure 1

State of system Example 1

Full size image

Example 2

Consider impulsive neural networks (2) with:

$$\begin{aligned} D= & {} \left[ \begin{array}{ccc}2.9 &{}0&{}0\\ 0&{} 3.2&{}0\\ 0&{}0&{}3\end{array}\right] ;\quad A=\left[ \begin{array}{ccc}-1 &{}2\\ 2 &{}1\\ -2&{}1 \end{array}\right] ;\quad E=\left[ \begin{array}{ccc}0.3 &{}0&{}0\\ 0 &{}0.3&{}0\\ 0&{}0&{}0.3\end{array}\right] ;\\ C_1= & {} \left[ \begin{array}{ccc}0.1210 &{}0.3159\\ 0.3508 &{}0.2028\end{array}\right] ;\quad C_2=\left[ \begin{array}{ccc}0.2731 &{}0.3656\\ 0.2548 &{}0.2324\end{array}\right] ;\quad C_3=\left[ \begin{array}{ccc}0.1049 &{}0.2319\\ 0.2084 &{}0.2393\end{array}\right] ;\\ B= & {} \left[ \begin{array}{ccc}-1&{} 1\\ 1 &{}1\\ 1&{}-1\end{array}\right] ;\quad K=\left[ \begin{array}{cc}0.9&{} 0\\ 0 &{}0.8\end{array}\right] ;\\ U= & {} \left[ \begin{array}{ccc}0.3&{} 0&{}0\\ 0 &{}0.1&{}0\\ 0&{}0&{}0.5\end{array}\right] ;\quad D1=\left[ \begin{array}{ccc}1&{}-1&{} 0\\ -1&{}-1&{} 0\\ 0&{}-2&{}1\end{array}\right] ;\\ H= & {} \left[ \begin{array}{ccc}0.02&{} 0&{}0\\ 0&{} 0.03&{}0\\ 0&{}0&{}0.03\end{array}\right] ;\quad \widetilde{D}=\left[ \begin{array}{cc}2.9&{} 0\\ 0 &{}2.9\end{array}\right] ;\\ \widetilde{B}= & {} \left[ \begin{array}{ccc}1&{}0 &{}0.3\\ -0.6&{}0 &{}0.3\end{array}\right] ;\quad \widetilde{C}_1=\left[ \begin{array}{ccc}0.0298&{} 0.1800&{} 0.2218\\ 0.1665 &{}0.3139&{} 0.2933\\ 0.5598 &{}0.1536&{} 0.2398\end{array}\right] ;\\ \widetilde{C}_2= & {} \left[ \begin{array}{ccc}0.3001 &{}0.3232&{} 0.0321\\ 0.3112 &{}0.3515 &{}0.5586\\ 0.3772 &{}0.2107 &{}0.3361\end{array}\right] ;\quad \widetilde{A}=\left[ \begin{array}{ccc}1&{}0&{} -1\\ 0&{} 0&{}1.2\end{array}\right] ;\quad \widetilde{E}=\left[ \begin{array}{cc}0.6 &{}-0.2\\ 0 &{}0.5\end{array}\right] ;\\ \widetilde{D}1= & {} \left[ \begin{array}{cc}0.6&{} 0.5\\ -0.6&{} 0.4\end{array}\right] ;\quad \widetilde{H}=\left[ \begin{array}{cc}0.09&{} 0.06\\ 0.06&{} 0.09\end{array}\right] ;\quad {M}=\left[ \begin{array}{ccc}1 &{}1&{} 1\\ 1 &{} 0.2 &{}0.8\\ 0 &{}1&{} 1\end{array}\right] ;\\ \widetilde{M}= & {} \left[ \begin{array}{cc}0.6 &{}1\\ 0.7 &{}0.8\end{array}\right] ;\quad \widetilde{R}=\left[ \begin{array}{cc}3.9\\ 3\end{array}\right] ;\quad {R}=\left[ \begin{array}{cc}3\\ 3\\ 3.5\end{array}\right] ;\quad \sigma =\tau =1;\\ \alpha= & {} \widetilde{\alpha }=1. \end{aligned}$$

Then,

$$\begin{aligned} \Gamma _1=\left[ \begin{array}{cccccc}0.1210 &{}0.3159\\ 0.3508 &{}0.2028\\ 0.2731 &{}0.3656\\ 0.2548 &{}0.2324\\ 0.1049 &{}0.2319\\ 0.2084 &{}0.2393\end{array}\right] ;\quad \Gamma _2=\left[ \begin{array}{cccccc}0.0298&{} 0.1800&{} 0.2218\\ 0.1665 &{}0.3139&{} 0.2933\\ 0.5598 &{}0.1536&{} 0.2398\\ 0.3001 &{}0.3232&{} 0.0321\\ 0.3112 &{}0.3515 &{}0.5586\\ 0.3772 &{}0.2107 &{}0.3361\end{array}\right] . \end{aligned}$$

By solving LMIs (3)–(9) for \(\epsilon _i>0(i=1,2,3,4),\rho _X> 0 (X=Q_2,P_2,X_1,X_2,Z_1,Z_2)\) and matrices \(X_1>0,X_2>0,Z_1>0,Z_2>0,P>0,Q>0,P_1>0,Q_1>0,P_2>0,Q_2>0\), we obtain

$$\begin{aligned} P= & {} \left[ \begin{array}{ccc} 0.2257 &{} -0.0169 &{} -0.0391\\ -0.0169 &{} 0.3624 &{} 0.0212\\ -0.0391 &{} 0.0212 &{} 0.2539 \end{array}\right] ;\quad Q=\left[ \begin{array}{cc}0.3316 &{} 0.1228\\ 0.1228 &{} 0.5125\end{array}\right] ;\\ P_1= & {} \left[ \begin{array}{ccc} 0.3605 &{} -0.0005 &{} -0.0016\\ -0.0005 &{} 0.1667 &{} 0.0474\\ -0.0016 &{} 0.0474 &{} 0.1246\end{array}\right] ;\quad P_2=\left[ \begin{array}{cc}0.3239 &{} 0\\ 0 &{} 0.3239 \end{array}\right] ;\\ Q_1= & {} \left[ \begin{array}{cc}0.5007 &{} 0.0097\\ 0.0097 &{} 0.2897\end{array}\right] ;\quad Q_2=\left[ \begin{array}{ccc}0.4190 &{} 0&{} 0\\ 0 &{} 0.4190 &{}0\\ 0 &{} 0 &{} 0.4190\end{array}\right] ;\\ X_1= & {} \left[ \begin{array}{ccc}0.3861 &{} 0&{} -0.0057\\ 0 &{} 0.3290 &{} 0\\ -0.0057 &{} 0 &{} 0.4381\end{array}\right] ;\quad X_2=\left[ \begin{array}{cc}0.7768 &{} 0.0136\\ 0.0136 &{} 0.6089\end{array}\right] ;\\ Z_1= & {} \left[ \begin{array}{ccc}0.4788 &{} 0 &{}-0.0014\\ 0 &{} 0.4079 &{} 0\\ -0.0014 &{} 0 &{} 0.4400\end{array}\right] ;\quad Z_2=\left[ \begin{array}{cc} 0.6490 &{} -0.0223\\ -0.0223 &{} 0.6819\end{array}\right] ;\\ \epsilon _1= & {} 0.6443;\quad \epsilon _2= 1.1712;\quad \epsilon _3= 0.0945;\quad \epsilon _4= 0.4812 \end{aligned}$$

which implies from Theorem 2 that the above neural network is robustly, globally, asymptotically stable in the mean square by designing a state feedback memory control law and a impulsive feedback control law of the form

$$\begin{aligned} u(t)= & {} [0.1151 0.3782 -0.9017]x(t)+[9.5251 -5.6552 1.9394]x(t-\sigma (t)),\nonumber \\ \widetilde{u}(t)= & {} [-13.7069 10.9838]y(t)+[3.2767 -2.4000]y(t-\tau (t)),\nonumber \\ J(t_k^-)= & {} \left[ \begin{array}{ccc} -0.2118 &{} -0.0994 &{} 0.3143\\ -0.1684 &{} 0.2283 &{} -0.4115\\ 0.3271 &{} -0.2291 &{} -0.2115\end{array}\right] x(t_k^-),\nonumber \\ \widetilde{J}(t_k^-)= & {} \left[ \begin{array}{cc} 2.4283 &{} -2.0264\\ -2.8833 &{} 1.7573\end{array}\right] y(t_k^-) \end{aligned}$$
(18)

The time trajectories of Example 2 with initial conditions

$$\begin{aligned} \left\{ \begin{aligned}&\phi _1(s)=2, ~~~ s\in [-2.5,0];\\ {}&\phi _2(s)=1.5, \ s\in [-2.5,0];\\ {}&\phi _3(s)=0.5, \ s\in [-2.5,0]; \end{aligned}\right. ~~~\left\{ \begin{aligned}&\varphi _1(s)=-0.5, ~ s\in [-3,0];\\ {}&\varphi _2(s)=-1, \ \ \ s\in [-3,0];\\ {}&\varphi _3(s)=-1.5, \ s\in [-3,0]; \end{aligned}\right. \end{aligned}$$

and \( \ f_i(x)=\tanh (x) (i=1,2,3);\ g_j(x)=\tanh (x) (j=1,2,3)\) are shown in Figs. 2 [without impulsive controller (18)] and 3 [with impulsive controller (18)].

Fig. 2
figure 2

State of system Example 2 without impulsive control

Full size image
Fig. 3
figure 3

State of system Example 2 with impulsive controller (18)

Full size image

5 Conclusion and Future Works

In this article, we have investigated some high-order bidirectional neural networks with time-varying delays and impulsive, established a new globally asymptotical stability and designed a state feedback memory controller to robustly stabilize this network. Due to the development of the fractional-order calculus and its applications [23, 24], some results on fractional-order neural networks have been obtained [8, 14]. To the best of our knowledge, the model of the high-order fractional-order BAM neural networks has not been investigated until now. The corresponding results will appear in the near future.