1 Introduction

Image moments in the field of image processing are essentially weighted digital measurements of the intensity of the pixels in the image. These moments form functions that inherit special properties to specify a particular set of image characteristics. These moments and the functions of the moments have been widely used in pattern recognition (Flusser and Suk 1993; Heywood and Noakes 1995), fingerprint recognition (Qader et al. 2007), object representation and retrieval (Karakasis et al. 2015; Höschl and Flusser 2016), medical image analysis (Dai et al. 2010; Daoui et al. 2019), texture analysis (Bharathi and Ganesan 2008), and image watermarking (Yamni et al. 2020; Xiao et al. 2020; Yuan et al. 2013). There are popular non-orthogonal moments, such as moments of rotation (RM), complex moments (CM) and geometric moments (GM) (Teh and Chin 1988). These are not as effective as orthogonal moments due to redundancy of information and robustness to noise due to non-orthogonality. Teague (1980) gave the idea to use orthogonal moments for image analysis that give better results than non-orthogonal moments, with very little information redundancy and increased noise resistance. Teague was the pioneer of image reconstruction from a moment on, pointing out that the image can be reconstructed from a set of orthogonal moments (Zhu et al. 2010). Several works of the literature treat the methods of extraction of the invariant moments and their uses for the classification of 2D images. Hu presented the theory of algebraic invariants to define seven invariants of linear transformations based on geometric moments (Hu 1962). These descriptors are widely used in several applications thanks to their invariance to the geometric transformations of rotation, translation and scaling. So far, several continuous orthogonal moments have been introduced, Legendre (Shu et al. 2000; Rao et al. 2010), Chebyshev (Yang et al. 2018; Yap et al. 2001), Gegenbauer (Hosny 2014; Liao et al. 2002), Jacobi (Ping et al. 2007), Zernike (Qader et al. 2007; Khotanzad and Hong 1990), Gaussian-Hermite (Yang et al. 2015; Hosny 2012) and Fourier-Mellin (Shao et al. 2016). However, these moments generally involve several major problems such as the numerical approximation of continuous integrals, the transformation of the coordinate space, high computation costs, etc.… Recently, a set of new types of discrete orthogonal moments based on discrete orthogonal polynomials, the Tchebichef (Xiao et al. 2020; Pee et al. 2017), Krawtchouk (Xiao et al. 2016; Sayyouri et al. 2015), Charlier (Yamni et al. 2020; Karmouni et al. 2019), Meixner (Karmouni et al. 2019; Sayyouri et al. 2015), Hahn (Sayyouri et al. 2016; Sayyouri et al. 2013) and Racah (Zhu et al. 2007) polynomials, has been successfully introduced as alternatives to continuous orthogonal moments. In addition, we can construct different moments in other spaces like Radon transform invariant moments (Xiao et al. 2015) and histogram invariant moments in the Radon transform space (Tabbone et al. 2008). Note that all the above orthogonal moments are limited to a traditional first order integer. However, since these polynomials use series of integer powers to approximate fractions, it cannot accurately represent the properties of fractional computation. Further experimental results showed that the fractional order orthogonal moments were better than the traditional orthogonal moments based on the integer order in image reconstruction, noise robustness, and image recognition. Xiao et al. (2017) introduced two types of fractional orthogonal moments defined in polar and Cartesian coordinates, based on Legendre polynomials shifted to the fractional order. Although Legendre’s rotation invariants of fractional moments have been studied in Xiao et al. (2017). Zhang et al. (2016) presented the fractional orthogonal Fourier-Mellin moments for pattern recognition. Hosny et al. (2020) derived fractional-order shifted Gegenbauer moments for image analysis and recognition. Pandey et al. (2018) defined the fractional order Tchebichef moment and its invariants. Bhrawy et al. (2012, 2014) and Baleanu et al. (2013) presented the fractional-order modified generalized Laguerre functions (FMGLFs) based on fractional order generalized Laguerre polynomials to find the numerical solution of fractional differential equations (FDEs) and concluded that their method is accurate, efficient and easy to implement. This type of orthogonal polynomials implies the introduction of a fractional parameter \( \lambda \succ 0 \), in order to generalize the notion of integer order \( n \) with \( n \in {\mathbb{N}} \) to fractal order \( n\lambda \). In such cases, we have to consider the fractional-order generalized Laguerre approximation with weight function \( w^{(\alpha ,\lambda )} (x) = x^{(\alpha + 1)\lambda - 1} e^{{ - x^{\lambda } }} \,\,,\alpha > - 1\,\,,\lambda \succ 0 \). Indeed, from both theoretical and computational points of view, it is more interesting to consider an fractional-order orthogonal system with a more general weight function: \( w^{(\alpha ,\beta ,\lambda )} (x) = x^{(\alpha + 1)\lambda - 1} e^{{ - \beta x^{\lambda } }} ,\;\alpha \succ - 1,\beta \succ 0,\;\lambda \succ 0 \). One obvious advantage is that it can provide us a variety of choices of polynomial bases to fit exact solutions of underlying differential equations with various asymptotic behaviors at infinity. Moreover, as we will see later, some other good by-products can be obtained using this new family of orthogonal polynomials. Unfortunately, to our knowledge, the 3D invariants of the generalized, fractional modified geometric transformations of the Laguerre moment have not yet been studied. The attractive characteristics of FMGLMIs motivated the authors to generalize the generalized Laguerre functions to be defined with a fractional-order, and then, utilizing the successful the image cuboid representation approach to derived a novel set of FMGLMIs based on image cuboid representation for 3D image analysis.

In this paper, we present a new set of FMGLMIs up to any of their parameter values, with respect to geometric transformations (RST). These new invariant fractional moments can be used effectively in object recognition, 3D image classification, region of interest (ROI) extraction and very robust to image noise. To summarize, the main motivation of this paper contains three aspects: (1) Introduce a new set of fractional-order modified generalized Laguerre moment invariants for 3D pattern recognition based on Laguerre polynomials of fractional-order using the 3D image cuboid representation (ICR). (2) Provide the theoretical framework for the derivation of FMGLMIs, which are independent to the change of shape’s orientation, size and position, are efficiently evaluated through several appropriate experiments concerning the invariability property and the 3D image classification performance. (3) Propose a fast and accurate algorithm to compute the FMGLMIs based on the cuboid representation of 3D images. This new algorithm is very efficient to maintain numerical stability and considerably reduces computation time of the moment invariants 3D, because the computation of FMGLMIs by the proposed method depends only on the number of cuboids instead of the size of the 3D image. The performance of the newly proposed fractional-order moment invariants is effectively evaluated through several appropriate experiments, with regard to the computational time, the 3D pattern recognition, the invariability property and the 3D image classification performance. Consequently, the experimental results conclusively prove the effectiveness of this new technique, which can be considered as a new algorithm for calculating 3D invariants.

This article is organized as follows: In “Classical 3D generalized Laguerre moments” section, we will present the classical Laguerre continuous orthogonal moments. In “Fractional-order modified generalized Laguerre moments” section, we will define new fractional-order modified generalized Laguerre orthogonal moments. In “Proposed fractional-order modified generalized Laguerre moment invariants” section, will provide the proposed method for the fast and accurate computation of the 3D fractional order modified generalized Laguerre moment invariant based on the algorithm ICR for obtaining fractional order generalized Laguerre moment invariants (FC-FMGLMI-ICR) of rotation, scale and translation, validates the property of invariability, noise resistance and 3D images recognition. The experimental analyses are carried out in “Experimental results and discussions” and “Conclusion” sections summarizes the conclusion.

2 Classical 3D generalized Laguerre moments

In this section, we present a brief study of classical generalized Laguerre polynomials and Laguerre continuous orthogonal moments of two and three dimensions.

2.1 Generalized Laguerre polynomials

The generalized Laguerre polynomials, \( L_{n}^{\alpha } (x) \), have the following Gauss hypergeometric representation (Koekoek et al. 2010):

$$ L_{n}^{\alpha } (x) = \frac{{(\alpha + 1)_{n} }}{n!}{}_{1}F_{1} ( - n;\alpha + 1;x){ ; }n = 0,1,2, \ldots {\text{ and }}\alpha \succ - 1 $$
(1)

where \( (\alpha + 1)_{n} \) is Pochhammer’s symbol given by:

$$ (\alpha + 1)_{n} = (\alpha + 1)(\alpha + 2) \cdots (\alpha + n),\,\,\,\,n \ge 1\,\,\,\,{\text{and}}\,\,\,\,(\alpha + 1)_{0} = 1 $$
(2)

where the hypergeometric function \( {}_{1}F_{1} \) is defined as:

$$ {}_{1}F_{1} (a;b;x) = \sum\limits_{k = 0}^{\infty } {\frac{{(a)_{k} }}{{(b)_{k} }}} \frac{{x^{k} }}{k!} $$
(3)

The finite power series of the shifted Laguerre polynomials \( L_{n}^{\alpha } (x) \) of degree n is given by:

$$ L_{n}^{\alpha } (x) = \sum\limits_{k = 0}^{n} {B_{n,k}^{(\alpha )} x^{k} } \;\;{\text{with}}\;\;B_{n,k}^{(\alpha )} = \frac{{( - 1)^{k} \varGamma (\alpha + n + 1)}}{(n - k)!k!\varGamma (\alpha + k + 1)} $$
(4)

The calculation of generalized Laguerre polynomial values from Eq. (4) is very expensive in terms of computation time. To overcome this problem, it is proposed to use the recursive form of Laguerre polynomials.

The recurrence relation with respect to n of the generalized orthogonal Laguerre polynomials is defined as (Koekoek and Meijer 1993):

$$ L_{n + 1}^{\alpha } (x) = \frac{(2n + \alpha + 1 - x)}{(n + 1)}L_{n}^{\alpha } (x) - \frac{(n + \alpha )}{(n + 1)}L_{n - 1}^{\alpha } (x) ;\;\;\;n = 1,2, \ldots $$
(5)

The first two polynomials are defined as:

$$ L_{0}^{\alpha } (x) = 1, \, L_{1}^{\alpha } (x) = 1 + \alpha - x $$
(6)

The orthogonality relation of the generalized Laguerre polynomials with respect to the weight function \( w(x) = x^{\alpha } e^{ - x} \), is defined as follows:

$$ \int_{0}^{ + \infty } {w(x)L_{n}^{\alpha } (x)L_{m}^{\alpha } (x)dx = h_{n}^{\alpha } } \delta_{nm} , $$
(7)

with respect to the weight function and the squared norm \( h_{n}^{\alpha } = \frac{\varGamma (n + \alpha + 1)}{n!}, \) where \( \delta_{nm} \) denotes the Kronecker symbol.

Then, the generalized normalized Laguerre polynomials are defined by:

$$ \tilde{L}_{n}^{\alpha } (x) = \sqrt {\frac{w(x)}{{h_{n}^{\alpha } }}} L_{n}^{\alpha } (x) $$
(8)

The generalized normalized Laguerre polynomials satisfy the following orthogonality property:

$$ \int_{0}^{ + \infty } {\tilde{L}_{n}^{\alpha } (x)\tilde{L}_{m}^{\alpha } (x)dx} = \delta_{nm} $$
(9)

2.2 Generalized Laguerre moments

For an image \( f\left( {x,y,z} \right) \) with size \( N \times M \times K \), the classical 3D Generalized Laguerre moments (CGLMs) of order \( (n,m,p) \) are defined as follows:

$$ CGLM_{nmp}^{\alpha } = \int_{0}^{ + \infty } {\int_{0}^{ + \infty } {\int_{0}^{ + \infty } {\tilde{L}_{n}^{\alpha } (x)\tilde{L}_{m}^{\alpha } (y)\tilde{L}_{p}^{\alpha } (z)f(x,y,z)dxdydz} } } $$
(10)

where \( n,m,p = 0,1,2, \ldots \infty \)

For a digital image of size \( N \times M \times K \), the approximated classical 3D generalized Laguerre moments are computed by using the following formula:

$$ CGLM_{{_{nmp} }}^{\alpha } = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\tilde{L}_{n}^{\alpha } (x_{i} )} \tilde{L}_{m}^{\alpha } (y_{j} )\tilde{L}_{p}^{\alpha } (z_{k} )} } f(x_{i} ,y_{j} ,z_{k} )\Delta x\Delta y\Delta z $$
(11)

where \( \tilde{L}_{n}^{(\alpha )} (x_{i} ,N) \) is the nth order generalized orthonormal polynomials of Laguerre and \( \Delta x = x_{i} - x_{i - 1} \), \( \Delta y = y_{j} - y{}_{j - 1} \) end \( \Delta z = z_{k} - z_{k - 1} \) are sampling intervals in the ‘x’, ‘y’ and ‘z’ directions respectively, \( \left( {x_{i} ,y_{j} ,z_{k} } \right) \) is the centre of \( \left( {i,j,k} \right) \) voxel. The image has to be mapped inside the \( \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \) with \( x_{i} = \frac{b \times i}{N}; \, y_{j} = \frac{b \times j}{M} \, ; \, z_{k} = \frac{b \times k}{K} \, \), with \( b = 1,2,3, \ldots ;\;\;i = 1,2, \ldots ,N;\;\;j = 1,2, \ldots ,M\;\;{\text{and}}\;\;k = 1,2, \ldots ,K \).

Based on the orthogonality of classical generalized Laguerre polynomials \( \tilde{L}_{n}^{\alpha } (x) \), image reconstruction only adds the individual components of each order to generate the reconstructed image. The 3D image function \( f\left( {x,y,z} \right) \) can be written as an infinite expansion series in terms of the classical generalized Laguerre polynomials over the cube \( \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \):

$$ f\left( {x,y,z} \right)f(x,y,z) = \sum\limits_{n = 0}^{\infty } {\sum\limits_{m = 0}^{\infty } {\sum\limits_{p = 0}^{\infty } {CGLM_{{_{nmp} }}^{\alpha } \tilde{L}_{n}^{\alpha } (x)} \tilde{L}_{m}^{\alpha } (y)\tilde{L}_{p}^{\alpha } (z)} } $$
(12)

where the classical generalized Laguerre moments \( CGLM_{{_{nmp} }}^{\alpha } \), are calculated on the maximum order. If only generalized Laguerre moments of order smaller than or equal to the order \( \left( {n_{\hbox{max} } ,m_{\hbox{max} } ,p_{\hbox{max} } } \right) \) are given, then the function \( f\left( {x,y,z} \right) \) in Eq. (12) can be reconstructed as follows:

$$ f(x,y,z) = \sum\limits_{n = 0}^{{n_{max} }} {\sum\limits_{m = 0}^{{m_{max} }} {\sum\limits_{p = 0}^{{p_{max} }} {CGLM_{nmp}^{\alpha } \tilde{L}_{n}^{\alpha } (x)} \tilde{L}_{m}^{\alpha } (y)\tilde{L}_{p}^{\alpha } (z)} } $$
(13)

The triple integration in Eq. (10) is replaced by triple summations, which results in numerical error. Based on the basis of mathematical analysis, triple summation is identical to the triple integration only when the indices are reaching to infinity. In computing environment, this is not possible. Therefore, numerical instabilities could be encountered when the moment order reaches a cretin value. The optimum way to overcome this problem is the accurate evaluation of the triple integration in Eq. (10). The classical generalized Laguerre moments above are defined only for integer orders. In the next section, we propose a new type of moments that are fractional-order modified generalized Laguerre moments, which is a generalization of the traditional integer order one. These are extended to orthogonal moments of real order (or fractional-order) using fractional-order generalized Laguerre moments.

3 Fractional-order modified generalized Laguerre moments

This section presents a description of the proposed fractional-order modified generalized Laguerre moments (FMGLMs) more interesting to consider an orthogonal system with a more general weighting function: \( w^{(\alpha ,\beta )} (x) = x^{\alpha } e^{ - \beta \,x} ,\;\alpha \succ - 1,\;\beta \succ 0 \). Novel fractional-order modified generalized Laguerre polynomials are derived. Then, the new FMGLMs for 3D images derived.

3.1 Fractional-order Modified Generalized Laguerre Polynomials

This subsection, we have introduced a new functions based on the fractional-order modified generalized Laguerre polynomials (FMGLPs) to obtain the solution of some fractional differential equations more simply and efficiently (Bhrawy et al. 2014; Baleanu et al. 2013; Yan and Guo 2011). Next, let \( w^{(\alpha ,\beta )} (x) = x^{\alpha } e^{ - \beta \,x} \) with \( \alpha \succ - 1\,{\text{and}}\,\beta \succ 0 \). The modified generalized Laguerre polynomial of degree \( n \) is defined by

$$ L_{n}^{(\alpha ,\beta )} (x) = \frac{1}{n!}x^{ - \alpha } e^{\beta \,x} \partial_{x}^{n} \left( {x^{n + \alpha } e^{ - \beta \,x} } \right)\;\;\;n = 0,1, \ldots $$
(14)

Let \( L_{n}^{(\alpha ,\beta )} (x) \) be the usual generalized Laguerre polynomials that are mutually orthogonal with the weight function \( w(x) = x^{\alpha } e^{ - x} \). It is noted that \( L_{n}^{(\alpha )} (x) = L_{n}^{(\alpha ,1)} (x) \), and

$$ L_{n}^{(\alpha ,\beta )} (x) = L_{n}^{(\alpha )} (y) = L_{n}^{(\alpha )} (\beta x),\;\;y = \beta x $$
(15)

The FMGLPs can be defined by introducing the change of variable \( x = t^{\lambda } \) and \( \lambda \succ 0 \) on generalized Laguerre polynomials as:

$$ FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) = L_{n}^{{\left( {\alpha ,\beta } \right)}} (t^{\lambda } ),\;\;t \in \left[ {0, + \infty } \right[ $$
(16)

Moreover, for \( \alpha \succ - 1\,{\text{and}}\,\beta \succ 0 \), we have (Hosny et al. 2020)

$$ \partial_{x} FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) = - \beta \times FL_{n - 1}^{{\left( {\alpha + 1,\beta ,\lambda } \right)}} (t)\,, $$
(17)
$$ FL_{n + 1}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) = \frac{{\left( {2n + \alpha + 1 - \beta \,t^{\lambda } } \right)}}{{\left( {n + 1} \right)}}FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) - \frac{{\left( {n + \alpha } \right)}}{{\left( {n + 1} \right)}}FL_{n - 1}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t)\,, $$
(18)
$$ {\text{where}}\;\;n = 1,2, \ldots $$

The first two polynomials are defined as:

$$ FL_{0}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) = 1\,\,\,\,{\text{and}}\,\,\,\,FL_{1}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) = - \beta \,t^{\lambda } + \frac{{\varGamma \left( {\alpha + 2} \right)}}{{\varGamma \left( {\alpha + 1} \right)}} $$
(19)

The polynomials \( FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) \) forms an orthogonal basis on the interval \( t \in \left[ {0, + \infty } \right[ \) with respect to the weight function \( w^{(\alpha ,\beta ,\lambda )} (t) = t^{(\alpha + 1)\lambda - 1} e^{{ - \beta \,t^{\lambda } }} \) and the squared norm \( h_{n}^{(\alpha ,\beta ,\lambda )} \), where the orthogonality relation is given by:

$$ \int_{0}^{ + \infty } {FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t)FL_{m}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t)\,w^{(\alpha ,\beta ,\lambda )} (t)dt = h_{n}^{(\alpha ,\beta ,\lambda )} } \delta_{nm} , $$
(20)

where \( \delta_{nm} \) is the Kronecker function and \( h_{n}^{(\alpha ,\beta ,\lambda )} = \frac{\varGamma (n + \alpha + 1)}{{\lambda \,\beta^{(\alpha + 1)} n!}} \).

The FMGLPs \( FL_{n}^{{\left( {\alpha ,\beta ,\lambda } \right)}} (t) \) of degree \( n \) on the interval \( t \in \left[ {0, + \infty } \right[ \), are given by:

$$ FL_{n}^{(\alpha ,\beta ,\lambda )} (t) = \sum\limits_{k = 0}^{n} {B_{n,k}^{(\alpha ,\beta )} t^{\lambda k} } \,\,{\text{with}}\,\,B_{n,k}^{(\alpha ,\beta )} = ( - 1)^{k} \frac{{\varGamma (\alpha + n + 1)\beta^{k} }}{\varGamma (\alpha + k + 1)(n - k)!k!} $$
(21)

We can define the normalized FMGLPs, denoted by \( \widetilde{FL}_{n}^{(\alpha ,\beta ,\lambda )} (t) \), by using the weight function and the squared norm as:

$$ \widetilde{FL}_{n}^{(\alpha ,\beta ,\lambda )} (t) = \sqrt {\frac{{w^{(\alpha ,\beta ,\lambda )} (t)}}{{h_{n}^{(\alpha ,\beta ,\lambda )} }}} FL_{n}^{(\alpha ,\beta ,\lambda )} (t) ;\;\;n = 0,1,2, \ldots $$
(22)

Therefore, the orthogonality relation of the normalized FMGLPs is given by:

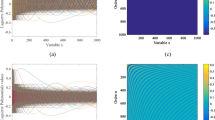
$$ \int_{0}^{ + \infty } {\widetilde{FL}_{n}^{(\alpha ,\beta ,\lambda )} (t)\widetilde{FL}_{m}^{(\alpha ,\beta ,\lambda )} (t)dt = } \delta_{nm} , $$
(23)

Figure 1 shows the graphs of \( \widetilde{FL}_{n}^{(\alpha ,\beta ,\lambda )} (t) \) with \( n = 0,1, \ldots , 6 \), for different values of the fractional parameter \( \lambda \) and polynomials parameter \( \alpha \,{\text{and}}\,\beta \). The FMGLPs control the distribution of zeros and their positions, based on fractional parameter \( \lambda \). As shown in Fig. 1.

Fig. 1
figure 1

Plot of FMGLPs for different values of \( \lambda = 0.8 \), \( \lambda = 1 \), \( \lambda = 1.5 \), \( \lambda = 2 \) and for: \( \alpha = 1\,,\,\beta = 0.5 \), \( \alpha = 0\,,\,\beta = 1 \) and \( \alpha = 0.5\,,\,\beta = 1.5 \) up to order 6, with \( t \in \left[ {0,1} \right] \)

Full size image

  • for \( \lambda = 1 \), one can obtain modified generalized classical Laguerre polynomials.

  • for \( \lambda \prec 1 \), the distribution of the FMGLPs zeros is shifted up and down within the definition range.

  • for the case where \( \lambda \succ 1 \), the distribution of the FMGLPs zeros is shifted up and down outside the definition range.

3.2 Fractional-order modified 3D generalized Laguerre moments

Generally, the image moment is considered as an integral transform, which aims to map an image intensity function from the image domain into the moment domain, where the dimensionality of moment domain is usually very small in comparison with the original domain (Xiao et al. 2017). In this respect, the FMGLMs noted by \( FLM_{nmp}^{(\alpha ,\beta ,\lambda )} \) of order \( (\lambda_{\,x} n + \lambda_{\,y} m + \lambda_{\,z} p) \) with \( n,m,p \in {\mathbb{N}} \) and \( (\lambda_{\,x} \,,\,\lambda_{\,y} \,,\,\lambda_{\,z} \succ 0) \), for a function \( f\left( {x,y,z} \right) \) defined in the square region \( \left[ { 0 , { + }\infty } \right[ \times \left[ { 0 , { + }\infty } \right[ \times \left[ { 0 , { + }\infty } \right[ \), is given by:

$$ FLM_{nmp}^{(\alpha ,\beta ,\lambda )} = \int_{0}^{ + \infty } {\int_{0}^{ + \infty } {\int_{0}^{ + \infty } {f(x,y,z)\widetilde{FL}_{n}^{{(\alpha ,\beta ,\lambda_{x} )}} (x)\widetilde{FL}_{m}^{{(\alpha ,\beta ,\lambda_{y} )}} (y)\widetilde{FL}_{p}^{{(\alpha ,\beta ,\lambda_{z} )}} (z)dxdydz} } } $$
(24)

where \( n,m,p = 0,1,2, \ldots \infty \).

Therefore, the FMGLMs of order \( (\lambda_{\,x} n + \lambda_{\,y} m + \lambda_{\,z} p) \) for the digital image \( f\left( {i,j,k} \right) \) with the size \( N \times M \times K \), can be computed by using a suitable transformation of the discrete coordinates \( \left( {i,j,k} \right) \) into the square region \( \left[ { 0 , { + }\infty } \right[ \times \left[ { 0 , { + }\infty } \right[ \times \left[ { 0 , { + }\infty } \right[ \), as follows:

$$ FLM_{nmp}^{(\alpha ,\beta ,\lambda )} = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {f(i,j,k)\widetilde{FL}_{n}^{{(\alpha ,\beta ,\lambda_{x} )}} (x_{i} )\widetilde{FL}_{m}^{{(\alpha ,\beta ,\lambda_{y} )}} (y_{j} )\widetilde{FL}_{p}^{{(\alpha ,\beta ,\lambda_{z} )}} (z_{k} )\Delta x} } } \Delta y\Delta z $$
(25)

where \( \widetilde{FL}_{n}^{{(\alpha ,\beta ,\lambda_{x} )}} (x_{i} ,N - 1) \) is the nth order generalized orthonormal polynomials of Laguerre. The image has to be mapped inside the \( \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \times \left[ { 0 {\text{ b}}} \right] \) with \( x_{i} = \frac{b \times i}{N}; \, y_{j} = \frac{b \times j}{M};\;z_{k} = \frac{b \times k}{K};\;b = 1,2,3, \ldots ;\;\;i = 1,2, \ldots ,N;\;\;j = 1,2, \ldots ,M\;\;{\text{and}}\;\;k = 1,2, \ldots ,K \).

Even if \( FLM_{nmp}^{(\alpha ,\beta ,\lambda )} \) is defined as a fractional-order moment \( (\lambda_{\,x} n + \lambda_{\,y} m + \lambda_{\,z} p) \), using the base function \( \left\{ {FL_{n}^{{(\alpha ,\beta ,\lambda_{x} )}} (x)FL_{m}^{{(\alpha ,\beta ,\lambda_{y} )}} (y)FL_{p}^{{(\alpha ,\beta ,\lambda_{z} )}} (z)} \right\} \). It is important to specify that the integer variables \( n,m\,\,{\text{and}}\,\,p \) are related to the number of roots of the polynomials basis function. In fact, the lower values of \( n,m\,\,{\text{and}}\,\,p \) allow to capture lower frequency components of the image, while the higher values can capture higher frequencies, like edges and small image details (Xiao et al. 2010). Conversely, using the orthogonality property, the function of the original image \( f\left( {i,j,k} \right) \) can be reconstructed as follows:

$$ \tilde{f}(i,j,k) = \sum\limits_{i = 0}^{\hbox{max} } {\sum\limits_{j = 0}^{\hbox{max} } {\sum\limits_{k = 0}^{\hbox{max} } {FLM_{nmp}^{(\alpha ,\beta ,\lambda )} \widetilde{FL}_{n}^{{(\alpha ,\beta ,\lambda_{x} )}} (x_{i} )\widetilde{FL}_{m}^{{(\alpha ,\beta ,\lambda_{y} )}} (y_{j} )\widetilde{FL}_{p}^{{(\alpha ,\beta ,\lambda_{z} )}} (z_{k} )} } } $$
(26)

Moments have become important and frequently used as form descriptors for classification and pattern recognition. The properties of these moments aroused the interest of finding their invariants in terms of translation, scale and rotation. The most efficient method for obtaining the invariant moments with respect to translation, scaling and rotation is to express them as a linear combination of geometric moments, then to use rotation invariants, scaling and translation instead of geometric moments.

In the next section, we propose a new fast computation method of 3D invariant moments for obtaining FMGLMIs with respect to translation and scaling and rotation using the invariants of the corresponding fractional-order generalized geometric moments.

4 Proposed fractional-order modified generalized Laguerre moment invariants

In this section, we propose a precise (ICR) method for the calculation of fractional-order modified generalized Laguerre moment invariants (FMGLMIs) (Karmouni et al. 2019; Jahid et al. 2019). In fact, the FMGLMs are not precisely designed for pattern recognition, in the sense that FMGLMs are not invariants with respect to the geometric transformation, like rotation, scaling and translation. In this method, the 3D image is decomposed into a set of 3D sub-image of single intensity and each intensity is represented by a set of cuboid, and each cuboid corresponding to an object. These cuboids are defined as a set of connected voxels. This method has the advantage of accelerating the process of extraction of the invariant moments of FMGLMs, and it allows us to improve the classification result without affecting the property of invariance compared to the classical method. For this, to obtain the rotation, scale and translation invariants of the FMGLMs, we first need to define the Fractional-order Generalized Geometric Moment Invariants (FGGMIs), which is a modified form of the traditional geometric moments invariants, by introducing three positive fractional parameters \( \lambda_{\,x} \,,\,\lambda_{\,y} \,,\,\lambda_{\,z} \, \succ 0 \) in the geometric basis function \( \left\{ {x^{{\lambda_{x} n}} y^{{\lambda_{y} m}} z^{{\lambda_{z} k}} } \right\} \), with \( n,m,p \in {\mathbb{N}} \). Then, we establish algebraic relation between the FMGLMs and the generalized geometric moments. Finally, we can express the FMGLMIs through the set of FGGMIs.

4.1 Fractional-order generalized geometric invariant moments

The three-dimensional fractional-order generalized geometric moments (FGGMs) of order \( \left\{ {\lambda_{x} n + \lambda_{y} m + \lambda_{z} k} \right\} \) for a given image function \( f\left( {i,j,k} \right) \) of the size \( N \times M \times K \), are defined as follows:

$$ m_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1} {x_{i}^{{\lambda_{x} p}} y_{j}^{{\lambda_{y} q}} } } } z_{k}^{{\lambda_{z} r}} f\left( {i,j,k} \right) $$
(27)

where \( \lambda_{x} ,\;\lambda_{y} ,\;\lambda_{z} \succ 0,\;x_{i} = \frac{i}{N},\;y_{j} = \frac{j}{M},\;z_{k} = \frac{k}{K},\;i = 0,2, \ldots ,N - 1;\;\;j = 0,2, \ldots ,M - 1 \), and \( k = 0,2, \ldots ,K - 1 \).

We can define the centroids of the x, y and z-coordinates, respectively \( \hat{x},\hat{y}\,{\text{and }}\hat{z} \) by:

$$ \hat{x} = \frac{{m_{100}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }}{{m_{000}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }},\,\,\,\hat{y} = \frac{{m_{010}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }}{{m_{000}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }},\,\,\,\hat{z} = \frac{{m_{001}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }}{{m_{000}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} }} $$
(28)

After the definition of 3D fractional-order generalized geometric moments as a function of the 3D geometric moments. Due to the fact that the expressions \( x_{i} - \hat{x},y_{i} - \hat{y} \) and \( z_{i} - \hat{z} \) may take negative values, and since we are limited to work with real numbers in the computation of moment invariants, we assume that \( \lambda_{\,x} \,,\,\lambda_{\,y} \,{\text{and}}\,\lambda_{\,z} \) have an odd denominators and can be written as \( {\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {2b + 1}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2b + 1}$}} \) with \( a,b \in {\mathbb{N}} \) and \( a \ne 0 \) For this, we will define the central moments of 3D fractional-order generalized geometric moments noted \( \mu_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} \) that are invariant to the translation as follows:

$$ \mu_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1} {(x_{i} - \hat{x})^{{\lambda_{x} p}} (y_{j} - \hat{y})^{{\lambda_{y} q}} (z_{k} - \hat{z})^{{\lambda_{z} r}} f(i,j,k)} } } $$
(29)

The rotation transformation of a 3D image is usually done as a series of three bi-dimensional rotations around each axis. For this fact, we will use Euler angle sequences conventions by matrix multiplication. For this analysis, we will rotate first about the x-axis, then the y-axis, and finally the z-axis. Such a sequence of rotations can be represented as the matrix product (Flusser et al. 2016; Batioua et al. 2017):

$$ R_{xyz} \left( {\theta ,\phi ,\psi } \right) = R_{x} \left( \theta \right)R_{y} \left( \phi \right)R_{z} \left( \psi \right) $$
(30)
$$ R_{xyz} \left( {\theta ,\phi ,\psi } \right) = \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \theta } & {\sin \theta } \\ 0 & { - \sin \theta } & {\cos \theta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \phi } & 0 & { - \sin \phi } \\ 0 & 1 & 0 \\ {\sin \phi } & 0 & {\cos \phi } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \psi } & {\sin \psi } & 0 \\ { - \sin \psi } & {\cos \psi } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right) $$
(31)

with \( R_{x} \left( \theta \right) \) the rotation matrix around x-axis by angle \( \theta \), \( R_{y} \left( \phi \right) \) the rotation matrix around y-axis by angle \( \phi \) and \( R_{z} \left( \psi \right) \) the rotation matrix around z-axis by angle \( \psi \).where

$$ R_{xyz} \left( {\theta ,\phi ,\psi } \right) = \left( {\begin{array}{*{20}c} {\cos \phi \cos \psi } & {\cos \phi \sin \psi } & { - \sin \phi } \\ {\sin \theta \sin \phi \cos \psi - \cos \theta \sin \psi } & {\sin \theta \sin \phi \sin \psi + \cos \theta \cos \psi } & {\cos \phi \sin \theta } \\ {\cos \theta \sin \phi \cos \psi + \sin \theta \sin \psi } & {\cos \theta \sin \phi \sin \psi - \sin \theta \cos \psi } & {\cos \theta \cos \phi } \\ \end{array} } \right) $$
(32)

More generally, the translation and rotation in 3D can be considered as a linear transformation of the 3D object coordinates, which can be described in a matrix form as

$$ \left( {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ {z^{\prime}} \\ \end{array} } \right) = R_{xyz} \left( {\theta ,\phi ,\psi } \right)\left( {\begin{array}{*{20}c} {x - \hat{x}} \\ {y - \hat{y}} \\ {z - \hat{z}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{13} } \\ {A_{21} } & {A_{22} } & {A_{23} } \\ {A_{31} } & {A_{32} } & {A_{33} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x - \hat{x}} \\ {y - \hat{y}} \\ {z - \hat{z}} \\ \end{array} } \right) $$
(33)

with \( \left( {A_{ij} } \right){}_{\begin{subarray}{l} 1 \le i \le m \\ 1 \le j \le n \end{subarray} } \) are the elements of \( R_{xyz} \left( {\theta ,\phi ,\psi } \right) \) matrix.

The FGGMIs, denoted \( v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} \), which are independent of rotation, scaling and translation transforms, can be written as:

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \eta^{ - \gamma } \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1} {\left\{ \begin{aligned} \left( {A_{11} \left( {x_{i} - \hat{x}} \right) + A_{12} \left( {y_{j} - \hat{y}} \right) + A_{13} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{x} p}} \hfill \\ \times \left( {A_{21} \left( {x_{i} - \hat{x}} \right) + A_{22} \left( {y_{j} - \hat{y}} \right) + A_{23} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{y} q}} \hfill \\ \times \left( {A_{31} \left( {x_{i} - \hat{x}} \right) + A_{32} \left( {y_{j} - \hat{y}} \right) + A_{33} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{z} r}} \hfill \\ \end{aligned} \right\}} } } \,f\left( {i,j,k} \right) $$
(34)

By applying the ICR algorithm (Jahid et al. 2019), the 3D image is decomposed into a set of 3D sub-image of single intensity and each intensity is represented by a set of cuboid, and each cuboid corresponding to an object. These cuboids are defined as a set of connected voxels, the 3D image \( f\left( {i,j,k} \right) \) containing \( L \) cuboids can be defined as:

$$ f\left( {i,j,k} \right) = \sum\limits_{s = 1}^{{n_{f} }} {f_{s} \left( {i,j,k} \right)} $$
(35)

with \( \left\{ {f_{s} ,\;{\text{s}} = 1,2, \ldots ,n_{f} } \right\} \) is the \( s^{th} \) intensity \( S \) of 3D image, and \( n_{f} \) is the number of intensity values. By using the ICR algorithm, the proposed FGGMIs of order \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right)^{th} \) of a 3D image \( f\left( {i,j,k} \right) \) of size \( N \times M \times K \) in Eq. (34), can be rewritten as:

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \eta^{ - \gamma } \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1} {\left\{ \begin{aligned} \left( {A_{11} \left( {x_{i} - \hat{x}} \right) + A_{12} \left( {y_{j} - \hat{y}} \right) + A_{13} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{x} p}} \hfill \\ \times \left( {A_{21} \left( {x_{i} - \hat{x}} \right) + A_{22} \left( {y_{j} - \hat{y}} \right) + A_{23} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{y} q}} \hfill \\ \times \left( {A_{31} \left( {x_{i} - \hat{x}} \right) + A_{32} \left( {y_{j} - \hat{y}} \right) + A_{33} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{z} r}} \hfill \\ \end{aligned} \right\}} } } \,\sum\limits_{s = 1}^{{n_{f} }} {f_{s} } $$
(36)

The 3D FGGMIs Eq. (36), can be computed as follows:

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \sum\limits_{s = 1}^{{n_{f} }} {v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s)} $$
(37)

where \( v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s) \) are the proposed FGGMIs computed by considering an intensity \( \, f_{s} \) of the 3D image, are given by

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s) = f_{s} \left\{ {\eta^{ - \gamma } \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {\sum\limits_{k = 0}^{K - 1} {\left[ \begin{aligned} \left( {A_{11} \left( {x_{i} - \hat{x}} \right) + A_{12} \left( {y_{j} - \hat{y}} \right) + A_{13} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{x} p}} \hfill \\ \times \left( {A_{21} \left( {x_{i} - \hat{x}} \right) + A_{22} \left( {y_{j} - \hat{y}} \right) + A_{23} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{y} q}} \hfill \\ \times \left( {A_{31} \left( {x_{i} - \hat{x}} \right) + A_{32} \left( {y_{j} - \hat{y}} \right) + A_{33} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{z} r}} \hfill \\ \end{aligned} \right]} } } } \right\} $$
(38)

The \( v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s) \) FGGMIs corresponding to an intensity \( \, f_{s} \) are calculated from the cuboids of each intensity. Then the \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right)^{th} \) order of the \( L_{s} \) cuboid, having coordinates \( \left\{ {x_{{1,Cub_{l}^{{f_{s} }} }} ,x_{{2,Cub_{l}^{{f_{s} }} }} } \right\} \), \( \left\{ {y_{{1,Cub_{l}^{{f_{s} }} }} ,y_{{2,Cub_{l}^{{f_{s} }} }} } \right\} \) and \( \left\{ {z_{{1,Cub_{l}^{{f_{s} }} }} ,z_{{2,Cub_{l}^{{f_{s} }} }} } \right\} \), can be computed using the following formula:

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s) = \sum\limits_{l = 1}^{{L_{s} }} {\,f_{s} \left\{ {\eta^{ - \gamma } \sum\limits_{{i = x_{{1,Cub_{l}^{{f_{s} }} }} }}^{{x_{{2,Cub_{l}^{{f_{s} }} }} }} {\sum\limits_{{j = y_{{1,Cub_{l}^{{f_{s} }} }} }}^{{y_{{2,Cub_{l}^{{f_{s} }} }} }} {\sum\limits_{{k = z_{{1,Cub_{l}^{{f_{s} }} }} }}^{{z_{{2,Cub_{l}^{{f_{s} }} }} }} {\left[ \begin{aligned} \left( {A_{11} \left( {x_{i} - \hat{x}} \right) + A_{12} \left( {y_{j} - \hat{y}} \right) + A_{13} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{x} p}} \hfill \\ \times \left( {A_{21} \left( {x_{i} - \hat{x}} \right) + A_{22} \left( {y_{j} - \hat{y}} \right) + A_{23} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{y} q}} \hfill \\ \times \left( {A_{31} \left( {x_{i} - \hat{x}} \right) + A_{32} \left( {y_{j} - \hat{y}} \right) + A_{33} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{z} r}} \hfill \\ \end{aligned} \right]} } } } \right\}} $$
(39)
$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (s) = \sum\limits_{l = 1}^{{L_{s} }} {\,v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (Cub_{l}^{{f_{s} }} )} $$
(40)

where \( Cub_{l}^{{f_{s} }} \) is the cuboid \( l \) of intensity \( \, f_{s} \), \( l = 1, \ldots ,L_{s} \) and \( L = \sum\limits_{s = 1}^{{n_{f} }} {L_{s} } \), \( L_{s} \) the number of cuboid for each intensity \( \, f_{s} \).

Whereas \( v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (Cub_{l}^{{f_{s} }} ) \) are the FGGMIs for each cuboids \( Cub_{l}^{{f_{s} }} \), the computation of the \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right)^{th} \) order, they are defined as

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (Cub_{l}^{{f_{s} }} ) = \eta^{ - \gamma } \sum\limits_{{i = x_{{1,Cub_{l}^{{f_{s} }} }} }}^{{x_{{2,Cub_{l}^{{f_{s} }} }} }} {\sum\limits_{{j = y_{{1,Cub_{l}^{{f_{s} }} }} }}^{{y_{{2,Cub_{l}^{{f_{s} }} }} }} {\sum\limits_{{k = z_{{1,Cub_{l}^{{f_{s} }} }} }}^{{z_{{2,Cub_{l}^{{f_{s} }} }} }} {f_{s} \times \left[ \begin{aligned} \left( {A_{11} \left( {x_{i} - \hat{x}} \right) + A_{12} \left( {y_{j} - \hat{y}} \right) + A_{13} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{x} p}} \hfill \\ \times \left( {A_{21} \left( {x_{i} - \hat{x}} \right) + A_{22} \left( {y_{j} - \hat{y}} \right) + A_{23} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{y} q}} \hfill \\ \times \left( {A_{31} \left( {x_{i} - \hat{x}} \right) + A_{32} \left( {y_{j} - \hat{y}} \right) + A_{33} \left( {z_{k} - \hat{z}} \right)} \right)^{{\lambda_{z} r}} \hfill \\ \end{aligned} \right]} } } $$
(41)

Therefore, the 3D proposed FGGMIs under translation, scaling and rotation of the 3D image can be obtained from this is the sum of 3D geometric moments of each cuboid \( v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (Cub_{l}^{{f_{s} }} ) \) of each intensity \( \, f_{s} \) of the order \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right)^{th} \), can be computed as

$$ v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} = \sum\limits_{s = 1}^{{n_{f} }} {\sum\limits_{l = 1}^{{L_{s} }} {\,v_{pqr}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} (Cub_{l}^{{f_{s} }} )} } $$
(42)

The appropriate values for the parameters \( \theta ,\phi ,\psi ,\gamma {\text{ and }}\eta \), are already defined in the literature (Flusser et al. 2016; Batioua et al. 2017). Hence, they can be determined by using the special case \( \left( {\lambda_{x} = \lambda_{y} = \lambda_{z} = 1} \right) \) as follows:

$$ \theta = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\mu_{011}^{{}} }}{{\mu_{020}^{{}} - \mu_{002}^{{}} }}} \right)\,\,,\,\,\phi = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\mu_{001}^{{}} }}{{\mu_{200}^{{}} - \mu_{002}^{{}} }}} \right)\,\,,\,\,\psi = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\mu_{110}^{{}} }}{{\mu_{200}^{{}} - \mu_{020}^{{}} }}} \right) $$
(43)
$$ \gamma = \frac{{\lambda_{x} p + \lambda_{y} q + \lambda_{z} r + 3}}{3}\,\,\,\,{\text{and}}\,\,\,\,\eta = m_{000}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} $$
(44)

At last, we can obtain the translation, scaling and rotation of 3D FMGLMIs of the order \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right)^{th} \), from the equations Eq. (42).

4.2 Fractional-order modified generalized Laguerre 3D invariant moments

The fractional-order modified generalized Laguerre polynomials are orthogonal over the interval \( \left[ {0, + \infty } \right[ \) according to Eq. (23). To compute the Laguerre polynomial matrix, one must work on a finite order \( N \) which will affect the property of orthogonality of the FMGLPs. In addition, the method that we used, based on Laguerre polynomials of fractional-order using the 3D image cuboid representation, ensured the numerical value in an optimal minimal order of moments to compute the moment invariants of the image function, it is enough that \( i,j \) and \( k \) between \( 1 \prec i \prec N \), \( 1 \prec j \prec M \) and \( 1 \prec k \prec K \). In this sub-section, we can derive the RST invariants of FMGLMIs, based on the algebraic relation between the FMGLPs and the geometric basis \( \left\{ {x^{{\lambda_{\,x} n}} y^{{\lambda_{\,y} m}} z^{{\lambda_{\,z} l}} } \right\} \).

First, we define FMGLMIs of order \( \left( {\lambda_{x} p + \lambda_{y} q + \lambda_{z} r} \right) \) for a given weighted image function \( \tilde{f}(i,j,k) = \left[ {w^{{(\alpha ,\beta ,\lambda_{x} )}} (x)\,w^{{(\alpha ,\beta ,\lambda_{y} )}} (y)\,w^{{(\alpha ,\beta ,\lambda_{z} )}} (z)} \right]^{ - 1/2} f(i,j,k) \), of size \( N \times M \times K \) voxels, with \( w^{(\alpha ,\beta ,\lambda )} \) is the weight function of FMGLPs, as follows:

$$ FLM_{pqr}^{(\alpha ,\beta ,\lambda )} = \frac{{b^{3} }}{NMK}\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\widetilde{FL}_{p}^{{(\alpha ,\beta ,\lambda_{x} )}} (x_{i} )\widetilde{FL}_{q}^{{(\alpha ,\beta ,\lambda_{y} )}} (y_{j} )\widetilde{FL}_{r}^{{(\alpha ,\beta ,\lambda_{z} )}} (z_{k} )} } } \tilde{f}(i,j,k) $$
(45)

By the help of Eq. (22) and (45), we can express the FMGLMs:

$$ \begin{aligned} FLM_{pqr}^{(\alpha ,\beta ,\lambda )} & = \frac{{b^{3} \chi_{p}^{{(\alpha ,\beta ,\lambda_{x} )}} \chi_{q}^{{(\alpha ,\beta ,\lambda_{y} )}} \chi_{r}^{{(\alpha ,\beta ,\lambda_{z} )}} }}{NMK} \\ & \quad \times \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {FL_{p}^{{(\alpha ,\beta ,\lambda_{x} )}} (x_{i} )FL_{q}^{{(\alpha ,\beta ,\lambda_{y} )}} (y_{j} )FL_{r}^{{(\alpha ,\beta ,\lambda_{z} )}} (z_{k} )} } } f(i,j,k) \\ \end{aligned} $$
(46)

with \( \chi_{p}^{(\alpha ,\beta ,\lambda )} = \frac{1}{{\sqrt {h_{p}^{(\alpha ,\beta ,\lambda )} } }}\,\,\,\,{\text{and}}\,\,\,\, \, b = 1,2,3, \ldots \)

By substituting the FMGLPs expansion Eqs. (21) and (27) in the previous equation, we can express the FMGLMs as a linear combination of FGGMs of the image \( f(i,j,k) \) by:

$$ FLM_{pqr}^{(\alpha ,\beta ,\lambda )} = \frac{{b^{3} \chi_{p}^{{(\alpha ,\beta ,\lambda_{x} )}} \chi_{q}^{{(\alpha ,\beta ,\lambda_{y} )}} \chi_{r}^{{(\alpha ,\beta ,\lambda_{z} )}} }}{NMK}\sum\limits_{n = 0}^{p} {\sum\limits_{m = 0}^{q} {\sum\limits_{l = 0}^{r} {B_{p,n}^{(\alpha ,\beta )} B_{q,m}^{(\alpha ,\beta )} B_{r,l}^{(\alpha ,\beta )} } } } m_{nml}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} $$
(47)

In order to obtain the the invariants of rotation, scaling and translation of fractional-order generalized Laguerre moment invariants, which will be designated by FMGLMIs in this article noted by \( FLM_{pqr}^{(\alpha ,\beta ,\lambda )} \), the terms \( m_{nml}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} \) in the previous equation will be replaced by the FGGMIs \( v_{nml}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} \) of Eq. (47):

$$ FLMI_{pqr}^{(\alpha ,\beta ,\lambda )} = \frac{{b^{3} \chi_{p}^{{(\alpha ,\beta ,\lambda_{x} )}} \chi_{q}^{{(\alpha ,\beta ,\lambda_{y} )}} \chi_{r}^{{(\alpha ,\beta ,\lambda_{z} )}} }}{NMK}\sum\limits_{n = 0}^{p} {\sum\limits_{m = 0}^{q} {\sum\limits_{l = 0}^{r} {B_{p,n}^{(\alpha ,\beta )} B_{q,m}^{(\alpha ,\beta )} B_{r,l}^{(\alpha ,\beta )} \,} } } v_{nml}^{{\lambda_{x} \lambda_{y} \lambda_{z} }} $$
(48)

where the fractional parameters \( \lambda_{\,x} \,,\,\lambda_{\,y} \,{\text{and}}\,\lambda_{\,z} \) must satisfy the condition that they have odd denominators. Finally, it is worth noting that the direct computation of the coefficients \( B_{n,k}^{(\alpha ,\beta )} \) defined in Eq. (21) involves the evaluation of factorial terms for each value of \( n\,{\text{and}}\,k \), thereby, this can increase the computational time of FMGLMIs and affect their numerical accuracy, especially at the computation of higher-order moment invariants (Camacho-Bello et al. 2014; Hmimid et al. 2015).

Based on the property that \( n! = \left( {n - 1} \right)!n \), the coefficients \( B_{n,k}^{(\alpha ,\beta )} \) of Eq. (21) can be easily computed using the following recursive method:

$$ \begin{aligned} \, B_{n,0}^{{\left( {\alpha ,\beta } \right)}} & = \frac{\alpha + n}{n} \, B_{n - 1,0}^{{\left( {\alpha ,\beta } \right)}} ;\;\;B_{0,0}^{{\left( {\alpha ,\beta } \right)}} = 1 \\ \\ \, B_{n,k}^{{\left( {\alpha ,\beta } \right)}} & = - \frac{{\beta \left( {n - k + 1} \right)}}{{\left( {\alpha + k} \right)k}} \, B_{n,k - 1}^{{\left( {\alpha ,\beta } \right)}} ,\;\;1 \le k \le n \\ \end{aligned} $$
(49)

It is clearly seen from Eq. (39) that the proposed recursive method is free from factorial terms and it is more adequate for the computation of the polynomial coefficients \( B_{n,k}^{(\alpha ,\beta )} \).

The following algorithm summarizes the calculation steps of the fractional-order modified generalized Laguerre moment 3D invariants from the proposed fractional-order generalized geometric moment invariants using ICR algorithm.

figure a

The FMGLMIs based on image cuboid representation algorithm, it’s a new type generic of continuous orthogonal moments with real order have been defined for image classification and object recognition applications. It has considered modified generalized Laguerre moments and converted them to FMGLMs, while comparing with integer order moments. A new real number \( \alpha \) is introduced to make fractional moments from integer one. After extensive experimentation, it is found that fractional moments are highly robust to image noise, capable of Region of Interest feature extraction and are better than conventional integer order moments in both image reconstruction and face recognition. In the next section, we tested the effectiveness of the proposed new method, FMGLMIs based on the ICR algorithm, will describe the shape characteristics independently of the geometric transformations and desirable in the field of image recognition.

5 Experimental results and discussions

In this section, several experiments are performed to validate the performance and effectiveness of the new FMGLMIs as well as to evaluate the accuracy of the invariance and the newly introduced FMGLMIs recognition performance. It is important to note that all the algorithms are implemented in Matlab and that all the experiments are carried out under Microsoft Windows environment on PC with Intel i5 2.4 GHz processor and 8 GB RAM. Thanks to these experiments, we will test: (1) Invariance of FMGLMs with respect to RST of 3D images. (2) Invariability property of the proposed FMGLMIs against different geometric transformations and noise degradations of 3D images. (3) Classification and recognition of 3D images. (4) The calculation time of the proposed fractional order invariants.

5.1 Invariants 3D of different geometric transformations of the FMGLMIs

In this subsection, we test the invariability of the proposed FMGLMIs introduced in this paper against different geometric transformations. For that, we will compare the invariability of the fractional-order modified generalized Laguerre moment invariants by two methods: the classical method and the proposed method of fractional parameters \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 0.8 \) and \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8 \) based on Eq. (48). Three 3D images “ Four “,” Octopus “ and “ Cup “ of size 300 × 300 × 300 voxels also extracted from McGill 3D Shape Benchmark database are used as test images and the fourth test image, 3D image medical (IRM) of size 512 × 512 × 512 voxels shown in the figure (Fig. 2). In order to measure the ability of the proposed invariants to remain unchanged under translation, scaling and rotation of the 3D image. The accuracy of the invariant descriptors is measured by the Relative Standard Deviation (RSD) with percentage spread, that is,

$$ RSD\,(\% ) = \frac{\sigma }{\left| \mu \right|} \times (100\,\% ) $$
(50)

where \( \sigma \) and \( \mu \) denotes the standard deviation and the mean of the FMGLMIs respectively. All invariant moments of FMGLMIs is calculated up to order three for each transformation.

Fig. 2
figure 2

The 3D test images: a Four, b Octopus c Cup, of size 300 × 300 × 300 voxels d medical image IRM of size 512 × 512 × 512voxels

Full size image

In the first experiment, we verify the efficiency of the translation invariant descriptors FMGLMIs. The 3D original “Four “ image shown in Fig. 2a is shifted with a set of translation vectors along x, y and z-axes. The figure (Fig. 3) shows a set of translated images. The numerical values of FMGLMIs are presented in Table 1, from this table, it can be seen that the invariant moments FMGLMIs remain unchanged for all the translations and the ratio of \( RSD\,(\% ) \) is very low whatever the values of the parameter fractional \( (\lambda_{x} ,\lambda_{y} ,\lambda_{z} ) \), which proves the invariability of the proposed 3D FMGLMIs moments concerning translation.

Fig. 3
figure 3

Set of translated 3D “Four” image

Full size image
Table 1 The translation 3D invariants of fractional-order modified generalized Laguerre moment
Full size table

In the second experiment, we verify the efficiency of the scaling invariant descriptors FMGLMIs. The original “ Octopus “ image shown in Fig. 2b scaled with a set of scaling factors along x, y and z-directions. The figure (Fig. 4) shows a set of scaled “ Octopus “ images. The Table 2 shows the numerical values of FMGLMIs, it can be seen from this Table that the moment invariants FMGLMIs remain unchanged under different non-uniform scale and the ratio of \( RSD\,(\% ) \) is very low whatever the values of the parameter fractional \( (\lambda_{x} ,\lambda_{y} ,\lambda_{z} ) \), which proves the invariability of the proposed 3D FMGLMIs moments concerning by scaling.

Fig. 4
figure 4

Set of scaled 3D “ Octopus “ image

Full size image
Table 2 The Scaling 3D invariants of Fractional-order Modified Generalized Laguerre moment
Full size table

In the third experiment, we verify the efficiency of the rotation invariant descriptors FMGLMIs. The original “ Cup “ image shown in Fig. 2c in rotation with a set of the images is rotated about each axis (x-axis, y-axis and z-axis) by an angle of rotation varying. The figure (Fig. 5) shows a set of in rotation “ Cup “ images. The Table 3 shows the numerical values of FMGLMIs, it can be seen from this Table that the moment invariants FMGLMIs remain unchanged under different non-uniform scale and the ratio of \( RSD\,(\% ) \) is very low whatever the values of the parameter fractional \( (\lambda_{x} ,\lambda_{y} ,\lambda_{z} ) \), which proves the invariability of the proposed 3D FMGLMIs moments concerning by rotation.

Fig. 5
figure 5

Set of “ Cup “ 3D images in rotation

Full size image
Table 3 The rotation 3D invariants of fractional-order modified generalized Laguerre moment
Full size table

In the last experiment, we will compare the invariability of the FMGLMIs by two methods: the classical method and the proposed method of fractional parameters \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 0.8 \) and \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8 \). The 3D “IRM” medical image shown in Fig. 2d is transformed by a set of mixed transformations of translation vectors, scale factors and rotation angles. A set of transformed 3D “IRM” medical images are shown in Fig. 6. The Table 4 shows the values of moment invariants obtained by the two methods. It is clear that our proposed method works better than the classical method that gives the largest deviation. Therefore, we can confirm again the robustness of the descriptors proposed for the translation, the scaling and the rotation of the 3D images.

Fig. 6
figure 6

Set of 3D “IRM” medical images transformed by a set of mixed transformations of translation vectors, scale factors and rotation angle

Full size image
Table 4 A comparison of the classical and proposed translation, scale and rotation invariant (FMGLMIs)
Full size table

5.2 Invariability property

After having tested the invariance of the FMGLMIs moments for each RST geometric transformation, we will investigate the invariability property of the proposed FMGLMIs against different geometric transformations. Therefore, we are conducted to use the 3D image « birds » , of size 300 × 300 × 300 voxels, selected from the database PSB (http://www.cim.mcgill.ca/~shape/benchMark/) and shown in the figure (Fig. 7). The test image is firstly translated by vector varying from \( \left( { - 15, - 15, - 15} \right) \) to \( \left( {15,15,15} \right) \) with step \( \left( {1,1,1} \right) \). Then, scaled by factors starting from 0.4 to 1.4 with an interval of 0.05 and finally they are images is rotated about each axis (x-axis, y-axis and z-axis) by an angle of rotation varying between 0 and 360 with a step equal to 10. In addition, it is worth noting that we have used Eq. (48) with \( \alpha = 0 \) and \( \beta = 1 \) for the computation of FMGLMIs, and also we have considered six testing fractional parameters values of \( FLMI_{pqr}^{(\alpha ,\beta ,\lambda )} \): (A) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 0.8 \), (B) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1 \), (C) \( \lambda_{x} = 0.8\,,\,\lambda_{y} = 0.8\,,\,\lambda_{z} = 1 \), (D) \( \lambda_{x} = 1.8\,,\,\lambda_{y} = 1\,,\,\lambda_{z} = 0.8 \), (E) \( \lambda_{x} = 1\,,\,\lambda_{y} = 1.8\,,\,\lambda_{z} = 1.8 \) and (F) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8 \). Subsequently, the relative error between the FMGLMIs coefficients, up to the order \( \left( {n, \, m\,\,{\text{and}}\,\,p \, = \, 3} \right) \), of the original and the transformed images is calculated as follow:

$$ {\text{R}}E\left( {f,f^{d} } \right) = \frac{{\left\| {FLMI(f) - FLMI(f^{d} )} \right\|}}{{\left\| {FLMI(f)} \right\|}} $$
(51)

where ∥ ∥, \( f\,\,{\text{and}}\,\,f^{d} \) respectively designate the Euclidean norm, the original images and the deformed images. It should be emphasized that a very small relative error leads to a good invariance.

Fig. 7
figure 7

3D image « birds » of size 300 × 300 × 300 voxels

Full size image

Examining the results presented in Fig. 8a–c, it can be seen that the proposed FMGLMIs exhibit very low relative errors (\( 10^{ - 15} \)), under geometric transformations, which shows the invariance of the FMGLMIs in relation to the geometric transformations for any order fractional.

Fig. 8
figure 8

Relative error of the proposed FMGLMIs using 3D image « birds » by: a translation transformation, b scaling transformation, c rotation transformation

Full size image

In this experiment we studied the effect of different kinds of noise on the numerical accuracy of the proposed invariants FMGLMIs, the test image has been corrupted by different types of noise. First, affected by Salt and-Pepper noise with a varying density from 0 to 5% with step 0.25%. Second, distorted by Gaussian noise with zero mean and standard deviation varying from 0 to 0.5 with step 0.05, the noisy images are shown in the figure (Fig. 9).

Fig. 9
figure 9

Noisy 3D image of « birds » by “Salt & Peppers (1% until 5%)” and “Gaussian” (mean = 0 and variance = 0.1% until variance = 0.5%)

Full size image

Figure 10a, b show the relative errors between the original and the distorted images, he relative error rate is very low (\( 10^{ - 13} \)) for all the fractional orders, the values of the relative errors are clearly seen to increase with the increase of the noise densities. Finally, these important results, depict respectively the robustness of FMGLMIs against Salt-and-Pepper and Gaussian noise.

Fig. 10
figure 10

Relative error of the proposed FMGLMI using 3D image « birds » by: a Salt-and-Pepper noise and b Gaussian noise

Full size image

It is clear from figure (Figs. 8 and 10) that the relative error FMGLMIs rate is very low \( (10^{ - 15} ) \), which indicate that the proposed moment invariants exhibit good performance and express high numerical stability under different geometric trans formations, as well as, in the presence of noisy effects. Moreover, these experiment, can help us to choose the appropriate parameters values for image classification applications, where the special case (F) with the higher parameters values \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8 \) gives the best numerical accuracy. As a result, this new set of invariants is very stable and show sufficient numerical accuracy to describe shape features independently of rotation, scale and translation transforms Therefore, new Invariants moment type FMGLMIs based on FC-FMGLMI-ICR algorithm will be desirable in the field of image classification and object recognition.

5.2.1 3D object recognition using FMGLMIs

In this subsection, we study the performance of the FC-FMGLMI-ICR for the invariant pattern recognition of 3D objects and the classification ability of the invariant moments studied in this paper, on a 3D images database in both noise-free and noisy conditions. The vector \( FLMI_{pqr}^{(\alpha ,\beta ,\lambda )} \) (Eq. 48) is used as feature vector in this test up to the order \( \left( {p,{\text{ q}}\,\,{\text{and}}\,\,r \, = { 4}} \right) \). For that, we use the base of Princeton Shape Benchmark (PSB) (http://www.cim.mcgill.ca/~shape/benchMark/), we have selected 25 images of (PSB) database have size 128 × 128 × 128 voxels, which are shown in Fig. 11, each selected image will be affected by different transformations (10 translations + 10 scale + 10 rotations + 10 mixed transformations), in order to generate 1000 objects per base (PSB). Moreover, to depict the noise robustness of the proposed invariant descriptors, we are conducted to add Salt-and-Pepper noise with densities {1%, 2%, 3%, 4%, 5%} to the base of 3D database to construct noisy testing sets. In fact, the features vector \( FLMI_{pqr}^{(\alpha ,\beta ,\lambda )} \) is constructed by moment invariants up to the fourth order. To perform the classification of the objects to their appropriate classes, Euclidean distance \( d_{1} \) (Eq. 52) and Correlation distance \( d_{2} \) (Eq. 53) are used as simple classifiers (Mukundan and Ramakrishnan 1998). they are defined by:

$$ d_{1} (x_{s} ,y_{t}^{(k)} ) = \sqrt {\sum\nolimits_{j = 1}^{n} {(x_{sj} - y_{tj} )^{2} } } $$
(52)
$$ d_{2} (x_{s} ,y_{t}^{(k)} ) = 1 - \frac{{\sum\nolimits_{j = 1}^{n} {x_{sj} y_{tj} } }}{{\sqrt {\sum\nolimits_{j = 1}^{n} {(x_{sj} )^{2} } } \sqrt {\sum\nolimits_{j = 1}^{n} {(y_{tj} )^{2} } } }} $$
(53)
Fig. 11
figure 11

Collection of 25 objects extracted from the PSB database used as learning set

Full size image

If the two vectors \( x_{s} \) and \( y_{t} \) are equal, then the distances \( d_{1} \), and \( d_{2} \), tend to 0.

We define the recognition accuracy as:

$$ \xi = \frac{\text{Number of correctly classified 3D objects}}{\text{The total of 3D objects used in the test }} \times 100 \, \% $$
(54)

Tables 5 and 6 present respectively a comparison in terms of object recognition accuracy on the Princeton Shape Benchmark (PSB) database, between the proposed FC-FMGLMI-ICR and the traditional Geometric Moment Invariants (GMI) (Teague 1980), Chebychev Moment Invariants (CMI) (Yang et al. 2018), Jacobi Moment Invariants (JMI) (Ping et al. 2007), Gegenbauer Moment Invariants (GegMI) (Hosny 2014), Gauss–Hermite Moment Invariants (GHMI) (Yang et al. 2015). Finally, it is worth noting that we have used Eq. (48) with \( \alpha = 0 \) and \( \beta = 1 \) for the computation of FMGLMIs, and also it is important to note that we have used six parameterization settings for \( FLMI_{pqr}^{(\alpha ,\beta ,\lambda )} \): (A) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 0.8 \), (B) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1 \), (C) \( \lambda_{x} = 0.8\,,\,\lambda_{y} = 0.8\,,\,\lambda_{z} = 1 \), (D) \( \lambda_{x} = 1.8\,,\,\lambda_{y} = 1\,,\,\lambda_{z} = 0.8 \), (E) \( \lambda_{x} = 1\,,\,\lambda_{y} = 1.8\,,\,\lambda_{z} = 1.8 \) and (F) \( \lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8 \).

Table 5 Comparative analysis of object recognition accuracy (%) on PSB database, by using FLMI, CMI, JMI, GegMI, GHMI and GMI based on Euclidean distance \( d_{1} \)
Full size table
Table 6 Comparative analysis of object recognition accuracy (%) on PSB database, by using FLMI, CMI, JMI, GegMI, GHMI and GMI based on correlation distance \( d_{2} \)
Full size table

By examining the results presented in Tables 5 and 6, we can observe that the best performance of the proposed FC-FMGLMI-ICR, is approximately 93.87% for noise-free images. Moreover, the obtained recognition results by the FMGLMIs are significantly higher than those obtained by the other methods, especially for high noise densities. Also, it should be emphasized that the average correct recognition improvement of the FC-FMGLMI-ICR in comparison with other methods. Finally, the best recognition accuracies for the 3D database, was achieved by the FC-FMGLMI-ICR for (F) with \( (\,\lambda_{x} = \lambda_{y} = \lambda_{z} = 1.8\,) \). As a conclusion of the provided results, it is evident that the FC-FMGLMI-ICR proposed invariants could be a highly useful tool in the field of pattern recognition, especially when the shape of the object undergoes several deformations and 3D image classification.

5.3 Computational time

Computation time is very crucial issue. For explicit computation time, a number of numerical experiments are performed. We will compare the computational time of FMGLMIs by two methods: the method FMGLMIs computed from the 3D geometric invariants moments based on Eq. (34) and the proposed method FC-FMGLMI-ICR computed from the 3D geometric invariants moments based on algorithm ICR usage Eq. (42). The execution-time improvement ratio (ETIR) is used as a criterion to compare the different computation methods and defined as (Hosny 2012):

$$ ETIR(\% ) = \left( {1 - \frac{Time\,1}{Time\,2}} \right) \times 100 $$
(55)

where Time1 and Time2 are the execution-times of the first and the second methods, \( ETIR = 0 \) if both execution times are identical. This ratio is defined as are the average time of the proposed FC-FMGLMI-ICR method and the FMGLMIs one, respectively. Three 3D images “Four”, “Octopus “ and “Cup” of sizes 300 300 300 voxels extracted from McGill 3D Shape Benchmark database (Koekoek et al. 2010) (Fig. 2a–c), and Magnetic Resonance Image medical (MRI) with size of 512 512 512 voxels (Fig. 2d), are used as test images. The process of calculating the invariant moments is performed 10 times for orders ranging from 6 to 30 for of the three images 3D and medical image 3D.

In this experiment, we will evaluate the computational performance of the proposed FMGLMIs by ICR algorithm. The Tables 7 and 8 represent the average calculation time and \( ETIR(\% ) \) of the FMGLMIs as well Fig. 12a shows the elapsed CPU times in seconds for the average invariant moments computation of the 3D images “Four”, “Octopus “ and “Cup” and Fig. 12b 3D medical image (MRI) invariant moments and shown in Fig. 2, by using the method FMGLMIs and the fast method FC-FMGLMI-ICR, for an increasing maximum moments order from 6 to 30. It can be clearly seen from these tables and from the figure that the computation of the FMGLMIs invariant moments based on FC-FMGLMI-ICR algorithm is much faster than that obtained by method invariant moments FMGLMIs.

Table 7 Average times in seconds and reduction percentage using the proposed FC-FMGLMI-ICR method and the FMGLMIs one, for selected moment orders: 3D images “Four”, “Octopus “ and “Cup”
Full size table
Table 8 Average times in seconds and reduction percentage using the proposed FC-FMGLMI-ICR method and the FMGLMIs one, for selected moment orders: magnetic resonance image (MRI) medical 3D
Full size table
Fig. 12
figure 12

Comparative results of the elapsed CPU time in (second) for an increasing order from 6 to 30 between the computation methods, FMGLMI and FC-FMGLMI-ICR: a 3D images moments “Four”, “Octopus “ and “Cup”. b 3D medical image moments (Magnetic Resonance Image (MRI))

Full size image

In a similar way, the 3D images “Four”, “Octopus “ and “Cup” as test images of size 300 × 300 × 300 voxels, shown in Fig. 2 is used for the computation of moment invariants FC-FMGLMI-ICR, FCMI, FJMI, FGegMI and GHMI, where the computation process has been repeated 10 times and the average of the elapsed CPU times are calculated for each method with an increasing moment invariants order starting from 6 to 30, the corresponding results are presented in Fig. 13.

Fig. 13
figure 13

Comparative results of the elapsed CPU time in (second) for an increasing order from 6 to 30 between the computation of image moment invariants FC-FMGLMI-ICR, FCMI, FJMI, FGegMI and GHMI

Full size image

It can be seen from Fig. 13, that the computation of the FC-FMGLMI-ICR invariant moments is much faster than that obtained by invariant moments FCMI, FJMI, FGegMI and GHMI. However, the FC-FMGLMI-ICR can greatly reduce the computation time in comparison with FCMI, FJMI, FGegMI and GHMI. These results show that our method considerably reduces the calculation time of the invariant moments, because of the computation of FMGLMIs by the proposed method depend only on the number of cuboids instead of the 3D image’s size. Therefore, new Invariants moment type FMGLMI based on FC-FMGLMI-ICR algorithm is not only fast, but also provide accurate computation, as demonstrated in the previous experiments.

6 Conclusion

A new set of adaptive characteristics by adjusting the fractional parameters of continuous orthogonal moments invariants based on the invariant moments of FMGLMIs has been proposed in this paper. And I have added to the field of research, a new algorithm based on the improved calculation of the moment 3D invariants by the proposed method. These algorithms, which minimize the execution time, improve the calculation and facilitate the analysis method of the different 3D images. Then, a creation of new mathematical tools for image processing and analysis, and new definitions and properties of invariant moments. Therefore, the experimental results conclusively prove that the efficiency of the invariant moments of FMGLMIs as descriptors of analysis elements, compared to classical generalized Laguerre moments and geometric moments, a detailed comparative analysis with the invariants of moments, concerning the recognition of shapes and the classification of 3D images. The result shows that FMGLMIs moments are effective in improving the invariability of geometric transformations and their recognition of noisy and noiseless objects.