1 Introduction

Description of images invariant to geometric transformations such as rotation, scaling and translation is useful in image analysis, object recognition and classification [1, 2]. Moments, as a popular class of the global invariant features, have been widely used in different applications of pattern recognition, image analysis and computer vision applications, such as object recognition [3], optical character recognition [2], pattern classification [4], image watermarking [5], content-based image retrieval [6], image reconstruction [7], image compression [8, 9], edge detection [10] and template matching [11].

The moments can be divided into two groups: orthogonal moments and non-orthogonal moments. Non-orthogonal moments such as geometric moments, complex moments and rotational moments have a certain degree of information redundancy and high sensitivity to noise, and the reconstruction of image from these moments is also quite difficult [12, 13]. On the contrary, orthogonal moments defined in terms of a set of orthogonal polynomials have received more attentions recently owing to their ability in representing images with minimal information redundancy and high noise robustness and image intensity functions could be reconstructed by using a finite number of orthogonal moments [14].

Depending on the kernel polynomials orthogonal on a rectangle or on a disk, orthogonal moments can be further divided into orthogonal moments defined in polar coordinate or Cartesian coordinate. The orthogonal moments defined in polar coordinate mainly include Zernike moments [15, 16], pseudo-Zernike moments [17], Bessel–Fourier moments [18], orthogonal Fourier–Mellin moments [19] and the remarkable advantage of these moments is easily to achieve rotation invariance. The orthogonal moments defined in the Cartesian coordinate mainly include Legendre [15], Tchebichef [20], Krawtchouk [21] and Hahn moments [22].

Gegenbauer–Chebyshev moments [23,24,25] as classical orthogonal moments defined in the Cartesian coordinates have been widely used in the field of image analysis. It is known that the rotation, scaling and translation invariant property of image moments has a high significance in image recognition. Unfortunately, to the best of our knowledge, both rotation, scaling and translation invariant of the Gegenbauer–Chebyshev moments have not been studied until now. Indeed, in Sect. 6 of the paper cited in [25], Zhu was able to construct moment invariants from Tchebichef–Krawtchouk moment, Tchebichef–Hahn moment and Krawtchouk–Hahn moment, but he could not extract the invariants from Gegenbauer–Chebyshev moment.

The extraction of invariant features of an image from the orthogonal moments defined in the Cartesian coordinate is a very difficult task. In this context, many authors have used the technique of expressing the orthogonal invariant moments as a linear combination of geometric invariant moments with the later are invariants under translation, scaling and rotation of the image they describe. It is used by Hosny [23, 24] to extract the invariants of orthogonal Gegenbauer Moment, by Papakostas et al. [26] to derive of invariants of the Krawtchouk orthogonal moments, by Zhu [25] to obtain the invariants of Tchebichef moments (TMI), Krawtchouk moments (KMI), Hahn moments (HMI), Tchebichef–Krawtchouk moments (TKMI), Tchebichef–Hahn moments (THMIs), Krawtchouk–Hahn moments (KHMI), it is used also by Hmimid et al. [27] to build the invariants of Meixner–Tchebichef moments (MTMIs), Meixner Krawtchouk moments (MKMIs) and Meixner–Hahn moments (MHMIs) etc.

In this paper, we use this technique to construct a new set of invariants of adapted Gegenbauer–Chebyshev moments (AGCMIs). This technique is based on the explicit formulation \(\sum\nolimits_{i = 0}^{n} {\alpha_{i} x^{i} }\) of the used orthogonal polynomials. On the other hand, the explicit formulations of the Gegenbauer and the Chebyshev polynomials, which are defined in Eqs. (10) and (12), are written in the form \(\sum\nolimits_{i = 0}^{n} {a_{i} \left( {\frac{x - 1}{2}} \right)^{i} }\). This obstructs the extraction of invariants from the orthogonal moments (AGCMs). For this reason, we introduce in this paper a new series of orthogonal polynomials, based on Gegenbauer and Chebyshev polynomials. We call them “the orthogonal adapted Gegenbauer–Chebyshev polynomials (OAGCP)”. This set of orthogonal polynomials is used to define a new type of orthogonal moments called adapted orthogonal Gegenbauer–Chebyshev moments (AGCMs). This helps to create a set of orthogonal moments (AGCMIs) invariant to translation, rotation and scale. These moment invariants (AGCMIs) are written in terms of geometric moment invariants presented by Hu [2]. We also apply a new 2D image classification technique using the invariant features extracted from the proposed invariant moments (AGCMIs and fuzzy K-means (FKM) [28, 29]. The performance of these new orthogonal moment invariants is compared with the existing orthogonal moments in terms of quantitative and qualitative measures. The comparison clearly shows the superiority of the proposed AGCMIs over the existing orthogonal moment invariants.

The other sections of the paper are organized as follows. The basic equations of the Gegenbauer–Chebyshev polynomials are briefly described in Sect. 2. All aspects of the proposed orthogonal moments for images are presented in Sect. 3. The computation of orthogonal adapted Gegenbauer–Chebyshev moment invariants is presented in Sect. 4. Experiments and the discussion of the obtained results are presented in Sect. 5. Conclusion is presented in Sect. 5.

2 The adapted Gegenbauer–Chebyshev polynomials

In this work, the image features are extracted using Gegenbauer–Chebyshev orthogonal moments for image representation and recognition. These orthogonal moments are based on the composition of two sets of orthogonal polynomials: Gegenbauer and Chebyshev polynomials. The theoretical aspect of these polynomials will be presented in the following subsections. In the first subsection, the equations governing orthogonal Jacobi polynomials are presented. The Gegenbauer polynomials are defined in the second subsection. In the third subsection the Chebyshev polynomials are presented. Finally, based on the last two sets of polynomials a new series of separable polynomials \(\psi_{n,m} \left( {x,y} \right)\) with two variable \(x\) and \(y\) are proposed in the fourth subsection. These polynomials are defined and orthogonal over the rectangle \(\left[ {0,N} \right] \times \left[ {0,M} \right],\) where \(N \times M\) is the size of the described image.

2.1 Orthogonal Jacobi polynomials

The \(n^{th}\) order Jacobi polynomial \(P_{n}^{\alpha ,\beta } \left( x \right)\) with parameters \(\alpha ,\beta\) is defined by the hypergeometric function as follows [25]:

$$P_{n}^{\alpha ,\beta } \left( x \right) = \frac{{\left( {\alpha + 1} \right)_{n} }}{n!}\;_{2} F_{1} \left( { - n,1 + \alpha + \beta + n; \alpha + 1; \frac{1}{2}\left( {1 - x} \right)} \right)$$
(1)

where \(\left( {\alpha + 1} \right)_{n}\) is a Pochhammer symbol defined as:

$$\left( m \right)_{n} = m\left( {m + 1} \right) \ldots \left( {m + n - 1} \right)$$
(2)

The hypergeometric function \({}_{2}^{{}} F_{1} \left( {a,b; c; x} \right)\) is defined for \(\left| x \right| < 1\) by the power series

$${}_{2}^{{}} F_{1} \left( {a,b; c; x} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{\left( a \right)_{n} \left( b \right)_{n} }}{{\left( c \right)_{n} }}\frac{{x^{n} }}{n!}.$$
(3)

More explicitly, Jacobi polynomial of the nth order is defined as follows:

$$P_{n}^{\alpha ,\beta } \left( x \right) = \frac{{\varGamma \left( {\alpha + n + 1} \right)}}{{n!\varGamma \left( {\alpha + \beta + n + 1} \right)}}\mathop \sum \limits_{i = 0}^{n} \left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)\frac{{\varGamma \left( {\alpha + \beta + n + i + 1} \right)}}{{\varGamma \left( {\alpha + i + 1} \right)}}\left( {\frac{x - 1}{2}} \right)^{i}$$
(4)

where \(\varGamma \left( z \right)\) is the Gamma function.

For \(\alpha > - 1\) and \(\beta > - 1,\) the set of Jacobi polynomials satisfy the orthogonality condition:

$$\mathop \int \limits_{ - 1}^{1} P_{n}^{\alpha ,\beta } \left( x \right)P_{m}^{\alpha ,\beta } \left( x \right)w_{\alpha ,\beta } \left( x \right){\text{d}}x = \rho \left( { n,\alpha ,\beta } \right)\delta_{nm}$$
(5)

where \(\delta_{nm}\) is the Kronecker delta and \(w_{\alpha ,\beta } \left( x \right)\) is the weight function defined by

$$w_{\alpha ,\beta } \left( x \right) = \left( {1 - x} \right)^{\alpha } \left( {1 + x} \right)^{\beta }$$
(6)

And

$$\rho \left( { n,\alpha ,\beta } \right) = \frac{{2^{n + \beta + 1} }}{2n + \alpha + \beta + 1}\frac{{\varGamma \left( {n + \alpha + 1} \right)}}{{\varGamma \left( {n + \alpha + \beta + 1} \right)n!}}$$
(7)

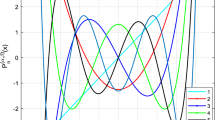
Figures 1 and 2 show the graphs of the first six Jacobi polynomials with \(\alpha = 3, \beta = 3\) and with \(\alpha = 1, \beta = 2\), respectively.

Fig. 1
figure 1

The graphs of the first six Jacobi polynomials of degree n = 1,2,..,6 with \(\alpha = 3, \beta = 3\)

Full size image
Fig. 2
figure 2

The graphs of the first six Jacobi polynomials of degree \(n = 1,2, \ldots ,6\) with \(\alpha = 1, \beta = 2\)

Full size image

2.2 Orthogonal Gegenbauer polynomials

The Gegenbauer polynomials [30] \(G_{n}^{\left( \lambda \right)} \left( x \right)\) are given in terms of the Jacobi polynomial \(P_{n}^{\alpha ,\beta } \left( x \right)\) with \(\alpha = \beta = \lambda - \frac{1}{2}(\lambda > - \frac{1}{2},\lambda \ne 0)\) by

$$\begin{aligned} G_{n}^{\left( \lambda \right)} \left( x \right) & = \frac{{\left( {2\lambda } \right)_{n} }}{{\left( {\lambda + \frac{1}{2}} \right)_{n} }}P_{n}^{{\lambda - \frac{1}{2}, \lambda - \frac{1}{2}}} \left( x \right) \\ & = \left( {\begin{array}{*{20}c} {n + 2\lambda - 1} \\ n \\ \end{array} } \right)\mathop \sum \limits_{k = 0}^{n} \frac{{\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)\left( {n + 2\lambda } \right)_{k} }}{{\left( {\lambda + \frac{1}{2}} \right)_{k} }}\left( {\frac{x - 1}{2}} \right)^{k} \\ \end{aligned}$$
(8)

We define \(c_{k} \left( \lambda \right)\) as follows

$$c_{k} \left( \lambda \right) = \left( {\begin{array}{*{20}c} {n + 2\lambda - 1} \\ n \\ \end{array} } \right)\frac{{\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)\left( {n + 2\lambda } \right)_{k} }}{{\left( {\lambda + \frac{1}{2}} \right)_{k} }}$$
(9)

The polynomial \(G_{n}^{\left( \lambda \right)} \left( x \right)\) can be written as

$$G_{n}^{\left( \lambda \right)} \left( x \right) = \mathop \sum \limits_{k = 0}^{n} c_{k} \left( \lambda \right)\left( {\frac{x - 1}{2}} \right)^{k}$$
(10)

2.3 Orthogonal Chebyshev polynomials

The Chebyshev polynomials of the first kind are a special case of the Jacobi polynomials \(P_{n}^{{\left( {\alpha ,\beta } \right)}} \left( x \right)\) with \(\alpha = \beta = - 1/2\)

$$T_{n} \left( x \right) = \frac{{P_{n}^{ - 1/2, - 1/2} \left( x \right)}}{{P_{n}^{ - 1/2, - 1/2} \left( 1 \right)}} = \frac{{2^{2n} \left( {n!} \right)^{2} }}{{\left( {2n} \right)!}}P_{n}^{ - 1/2, - 1/2} \left( x \right)$$
(11)

Therefore, the Chebyshev polynomial \(T_{n} \left( x \right)\) can be written as follows

$$T_{n} \left( x \right) = \mathop \sum \limits_{k = 0}^{n} d_{k} \left( {\frac{x - 1}{2}} \right)^{k}$$
(12)

Where \(d_{k}\) is defined as

$$d_{k} = \frac{{2^{2n} \left( {n!} \right)^{2} }}{{\left( {2n} \right)!}}\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)\frac{{\varGamma \left( {n + \frac{1}{2}} \right)\varGamma \left( {n + k} \right)}}{{n!\varGamma \left( n \right)\varGamma \left( {k + \frac{1}{2}} \right)}}$$
(13)

2.4 Orthogonal adapted Gegenbauer–Chebyshev polynomials

For \(N,M \ge 1.\) According to Sects. 2.2 and 2.3, we can define the adapted Gegenbauer polynomials \(\bar{G}_{n}^{\left( \lambda \right)} \left( t \right)\) of size \(N\) as

$$\bar{G}_{n}^{\left( \lambda \right)} \left( t \right) = G_{n}^{\left( \lambda \right)} \left( {\frac{N - 2t}{N}} \right), 0 \le t \le N$$
(14)

And the adapted Chebyshev polynomials \(\bar{T}_{n} \left( t \right)\) of size \(M\) as

$$\bar{T}_{n} \left( t \right) = T_{n} \left( {\frac{M - 2t}{M}} \right), 0 \le t \le M$$
(15)

According to Eq. (10), the adapted Gegenbauer polynomial \(\bar{G}_{n}^{\left( \lambda \right)} \left( t \right)\) of size \(N\) can be written as:

$$\bar{G}_{n}^{\left( \lambda \right)} \left( t \right) = G_{n}^{\left( \lambda \right)} \left( {\frac{N - 2t}{N}} \right) = \mathop \sum \limits_{k = 0}^{n} c_{k} \left( \lambda \right)\left( {\frac{ - t}{N}} \right)^{k} = \mathop \sum \limits_{k = 0}^{n} c'_{k} \left( \lambda \right)t^{k}$$
(16)

Where \(c'_{k} \left( \lambda \right) = c_{k} \left( \lambda \right)\left( {\frac{ - 1}{N}} \right)^{k}\).

And the adapted Chebyshev polynomial \(\bar{T}_{n} \left( t \right)\) of size \(M\) can be written as

$$\bar{T}_{n} \left( t \right) = T_{n} \left( {\frac{M - 2t}{M}} \right) = \mathop \sum \limits_{k = 0}^{n} d_{k} \left( {\frac{ - t}{M}} \right)^{k} = \mathop \sum \limits_{k = 0}^{n} d'_{k} t^{k}$$
(17)

Where \(d'_{k} = d_{k} \left( {\frac{ - 1}{N}} \right)^{k}\).

Definition 1

The adapted Gegenbauer–Chebyshev polynomials of size \(\left( {N,M} \right)\) are defined as follows

$$\psi_{n,m} \left( {x,y} \right) = \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right), \forall \left( {x,y} \right) \in \left[ {0,N} \right] \times \left[ {0,M} \right]$$
(18)

We use Eqs. (16) and (17); the polynomial \(\psi_{n,m} \left( {x,y} \right)\) is written as

$$\psi_{n,m} \left( {x,y} \right) = \mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} c'_{i} \left( \lambda \right)d'_{j} x^{i} y^{j}$$
(19)

Where \(c'_{k} \left( \lambda \right) = c_{k} \left( \lambda \right)\left( {\frac{ - 1}{N}} \right)^{k}\) and \(d'_{k} = d_{k} \left( {\frac{ - 1}{N}} \right)^{k}\)

Theorem 1

The adapted Gegenbauer–Chebyshev polynomials of size \(\left( {N,M} \right)\) are orthogonal over on the rectangle \(\left[ {0,N} \right] \times \left[ {0,M} \right]\) with the weighting function

$$v\left( {x,y} \right) = x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2} }}$$
(20)

and

$$\mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \psi_{n,m} \left( {x,y} \right)\psi_{pq} \left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y = C\left( { n,m,\lambda } \right)\delta_{np} \delta_{mq}$$
(21)

Where \(C\left( { n,m,\lambda } \right)\) is the normalization constant defined as:

$$C\left( { n,m,\lambda } \right) = \left( {\frac{N}{2}} \right)^{2\lambda } \left[ {\frac{{\left( {2\lambda } \right)_{n} }}{{\left( {\lambda + \frac{1}{2}} \right)_{n} }}\frac{{2^{2m} \left( {m!} \right)^{2} }}{{\left( {2m} \right)!}}} \right]^{2} \rho \left( { n,\lambda - \frac{1}{2},\lambda - \frac{1}{2}} \right)\rho \left( { m, - \frac{1}{2}, - \frac{1}{2}} \right)$$
(22)

Proof of Theorem 1

By substituting

$$\begin{aligned} \psi_{n,m} \left( {x,y} \right) & = \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right) = G_{n}^{\left( \lambda \right)} \left( {\frac{N - 2x}{N}} \right)T_{m} \left( {\frac{M - 2y}{M}} \right) \\ \psi_{p,q} \left( {x,y} \right) & = \bar{G}_{P}^{\left( \lambda \right)} \left( x \right)\bar{T}_{q} \left( y \right) = G_{p}^{\left( \lambda \right)} \left( {\frac{N - 2x}{N}} \right)T_{q} \left( {\frac{M - 2y}{M}} \right) \\ \end{aligned}$$

And

$$v\left( {x,y} \right) = x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2} }}$$

And with the help of Eq. (5) and with the change of variables \(x' = \frac{N - 2x}{N}\) and \(y' = \frac{M - 2y}{M},\) we have

$$\begin{aligned} & \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \psi_{n,m} \left( {x,y} \right)\psi_{pq} \left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ & = \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right)\bar{G}_{p}^{\left( \lambda \right)} \left( x \right)\bar{T}_{q} \left( y \right)x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2}}} {\text{d}}x{\text{d}}y \\ & = \mathop \int \limits_{0}^{N} \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{G}_{p}^{\left( \lambda \right)} \left( x \right)x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} {\text{d}}x \times \mathop \int \limits_{0}^{M} \bar{T}_{m} \left( y \right)\bar{T}_{q} \left( y \right) y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2}}} {\text{d}}y \\ & = \mathop \int \limits_{0}^{N} G_{n}^{\left( \lambda \right)} \left( {\frac{N - 2x}{N}} \right)G_{p}^{\left( \lambda \right)} \left( {\frac{N - 2x}{N}} \right)x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} {\text{d}}x \\ & \quad \times \mathop \int \limits_{0}^{M} T_{m} \left( {\frac{M - 2y}{M}} \right)T_{q} \left( {\frac{M - 2y}{M}} \right) y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2} }} {\text{d}}y \\ & = \left( {\frac{N}{2}} \right)^{2\lambda } \mathop \int \limits_{ - 1}^{1} G_{n}^{\left( \lambda \right)} \left( {x'} \right)G_{p}^{\left( \lambda \right)} \left( {x'} \right)\left( {1 - x'} \right)^{{\lambda - \frac{1}{2}}} \left( {1 + x'} \right)^{{\lambda - \frac{1}{2} }} {\text{d}}x' \\ & \quad \times \mathop \int \limits_{ - 1}^{1} T_{m} \left( {y'} \right)T_{q} \left( {y'} \right) y^{{ - \frac{1}{2}}} \left( {1 - y'} \right)^{{ - \frac{1}{2}}} \left( {1 + y'} \right)^{{ - \frac{1}{2} }} {\text{d}}y' \\ \end{aligned}$$

Using Eqs. (8), (11) and (5), we get

$$\begin{aligned} & \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \psi_{n,m} \left( {x,y} \right)\psi_{pq} \left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ & = \left( {\frac{N}{2}} \right)^{2\lambda } \frac{{\left( {2\lambda } \right)_{n} }}{{\left( {\lambda + \frac{1}{2}} \right)_{n} }}\frac{{\left( {2\lambda } \right)_{p} }}{{\left( {\lambda + \frac{1}{2}} \right)_{p} }}\frac{{2^{2m} \left( {m!} \right)^{2} }}{{\left( {2m} \right)!}}\frac{{2^{2q} \left( {q!} \right)^{2} }}{{\left( {2q} \right)!}} \\ & \quad \times \mathop \int \limits_{ - 1}^{1} P_{n}^{{\lambda - \frac{1}{2}, \lambda - \frac{1}{2}}} \left( {x^{\prime}} \right)P_{p}^{{\lambda - \frac{1}{2}, \lambda - \frac{1}{2}}} \left( {x^{\prime}} \right)\left( {1 - x^{\prime}} \right)^{{\lambda - \frac{1}{2}}} \left( {1 + x^{\prime}} \right)^{{\lambda - \frac{1}{2} }} {\text{d}}x' \\ & \quad \times \mathop \int \limits_{ - 1}^{1} P_{m}^{{ - \frac{1}{2}, - \frac{1}{2}}} \left( {y^{\prime}} \right)P_{q}^{{ - \frac{1}{2}, - \frac{1}{2}}} (y^{\prime})\left( {1 - y^{\prime}} \right)^{{ - \frac{1}{2}}} \left( {1 + y^{\prime}} \right)^{{ - \frac{1}{2} }} {\text{d}}y^{\prime} \\ & = \left( {\frac{N}{2}} \right)^{2\lambda } \left[ {\frac{{\left( {2\lambda } \right)_{n} }}{{\left( {\lambda + \frac{1}{2}} \right)_{n} }}\frac{{2^{2m} \left( {m!} \right)^{2} }}{{\left( {2m} \right)!}}} \right]^{2} \rho \left( { n,\lambda - \frac{1}{2},\lambda - \frac{1}{2}} \right)\rho \left( { m, - \frac{1}{2}, - \frac{1}{2}} \right)\delta_{np} \delta_{mq} \\ & = C\left( { n,m,\lambda } \right)\delta_{np} \delta_{mq} \\ \end{aligned}$$
(22)

3 Orthogonal adapted Gegenbauer–Chebyshev moments

The orthogonal Gegenbauer–Chebyshev moments (AGCMs) of a gray-level image \(f\left( {x,y} \right)\) are defined as follows:

$$\begin{aligned} {\text{AGC}}_{nm} & = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \psi_{n,m} \left( {x,y} \right)f\left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ & = \frac{1}{{C\left( { n,m,\lambda } \right)}} \\ \end{aligned}$$
(23)
$$\times \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right)f\left( {x,y} \right)x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2} }} {\text{d}}x{\text{d}}y$$
(24)

Equation (24) can be approximated by:

$$\begin{aligned} {\text{AGC}}_{nm} & = \frac{1}{{C\left( { n,m,\lambda } \right)}} \\ & \quad \times \mathop \sum \limits_{x = 0}^{N - 1} \mathop \sum \limits_{y = 0}^{M - 1} \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right)f\left( {x,y} \right)x^{{\lambda - \frac{1}{2}}} \left( {N - x} \right)^{{\lambda - \frac{1}{2}}} y^{{ - \frac{1}{2}}} \left( {M - y} \right)^{{ - \frac{1}{2} }} \\ \end{aligned}$$
(25)

The relation (25) makes it possible to construct a descriptor vector of an image \(f\left( {x, y} \right)\) of size \(N \times M\) in the form of a matrix \(V\left( f \right) = \left( {AGC_{ij} } \right)\) for a given size \(\left( {p + 1} \right) \times \left( {q + 1} \right)\) as follows:

$$\begin{aligned} V\left( f \right) & = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{AGC}}_{00} } & {{\text{AGC}}_{01} } \\ {{\text{AGC}}_{10} } & {{\text{AGC}}_{11} } \\ \end{array} } & {\begin{array}{*{20}c} { \ldots .} & {{\text{AGC}}_{0q} } \\ { \ldots .} & {{\text{AGC}}_{1q} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {{\text{AGC}}_{p0} } & {{\text{AGC}}_{p1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots & \vdots \\ { \ldots .} & {{\text{AGC}}_{pq} } \\ \end{array} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{T}_{0} \left( 0 \right)} & {\bar{T}_{0} \left( 1 \right)} \\ {\bar{T}_{1} \left( 0 \right)} & {\bar{T}_{1} \left( 1 \right)} \\ \end{array} } & {\begin{array}{*{20}c} { \ldots .} & {\bar{T}_{0} \left( {M - 1} \right)} \\ { \ldots .} & {\bar{T}_{1} \left( {M - 1} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {\bar{T}_{p} \left( 0 \right)} & {\bar{T}_{p} \left( 1 \right)} \\ \end{array} } & {\begin{array}{*{20}c} \vdots & \vdots \\ { \ldots .} & {\bar{T}_{p} \left( {M - 1} \right)} \\ \end{array} } \\ \end{array} } \right) \\ & \quad \times \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {h_{00} } & {h_{01} } \\ {h_{10} } & {h_{11} } \\ \end{array} } & {\begin{array}{*{20}c} { \ldots .} & {h_{0,N - 1} } \\ { \ldots .} & {h_{1,N - 1} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {h_{M - 1,0} } & {h_{M - 1,1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots & \vdots \\ { \ldots .} & {h_{M - 1,N - 1} } \\ \end{array} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{G}_{0}^{\left( \lambda \right)} \left( 0 \right)} & { \bar{G}_{1}^{\left( \lambda \right)} \left( 0 \right)} \\ {\bar{G}_{0}^{\left( \lambda \right)} \left( 1 \right)} & { \bar{G}_{1}^{\left( \lambda \right)} \left( 1 \right)} \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {\bar{G}_{q}^{\left( \lambda \right)} \left( 0 \right)} \\ \ldots & {\bar{G}_{q}^{\left( \lambda \right)} \left( 1 \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {\bar{G}_{0}^{\left( \lambda \right)} \left( {N - 1} \right)} & {\bar{G}_{1}^{\left( \lambda \right)} \left( {N - 1} \right)} \\ \end{array} } & {\begin{array}{*{20}c} \vdots & \vdots \\ \ldots & {\bar{G}_{q}^{\left( \lambda \right)} \left( {N - 1} \right)} \\ \end{array} } \\ \end{array} } \right) \\ \end{aligned}$$
(26)

where \(h_{ij} = f\left( {j,i} \right)i^{{\lambda - \frac{1}{2}}} \left( {N - i} \right)^{{\lambda - \frac{1}{2}}} j^{{ - \frac{1}{2}}} \left( {M - j} \right)^{{ - \frac{1}{2} }} .\)

Based on the orthogonality property of the adapted Gegenbauer–Chebyshev polynomials, the image function \(f \left( {x, y} \right)\) defined on the rectangle \(\left[ {0,N} \right] \times \left[ {0,M} \right]\) can be written as:

$$f\left( {x,y} \right) = \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{m = 0}^{\infty } {\text{AGC}}_{nm} \bar{G}_{n}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right)$$
(27)

where the orthogonal adapted Gegenbauer–Chebyshev moments, \(AGC_{nm}\), are calculated over the rectangle \(\left[ {0,N} \right] \times \left[ {0,M} \right]\). If moments are limited to an order \(Max\), we can approximate \(f\) with \(\tilde{f}\):

$$\tilde{f}\left( {x,y} \right) \approx \mathop \sum \limits_{n = 0}^{Max} \mathop \sum \limits_{m = 0}^{n} {\text{AGC}}_{n - m} \bar{G}_{n - m}^{\left( \lambda \right)} \left( x \right)\bar{T}_{m} \left( y \right)$$
(28)

where the number of adapted Gegenbauer–Chebyshev moment \(AGC_{ij}\) used in Eq. (28) is computed as follows:

$${\text{NT}} = \frac{{\left( {{\text{Max}} + 1} \right)\left( {{\text{Max}} + 2} \right)}}{2}$$
(29)

4 Computation of adapted Gegenbauer–Chebyshev moment invariants

To use the proposed Gegenbauer–Chebyshev moments (AGCMs) in 2D image classification, we need to construct invariant features under the three geometric transformations: translation, rotation and scale of the image. Therefore, to obtain the translation, scale and rotation invariants of adapted Gegenbauer–Chebyshev orthogonal moments (AGCMs), we adopt the same strategy used by Papakostas et al. for Krawtchouk moments [26]. So, we derive the adapted Gegenbauer–Chebyshev moment invariants (AGCMIs) through the geometric invariant moments.

4.1 Geometric invariant moments

Given an image function \(h \left( {x, y} \right)\) defined on the rectangle \(\left[ {0,N} \right] \times \left[ {0,M} \right].\) The geometric moment of order \(\left( {n + m} \right)\) is defined as:

$${\text{GM}}_{nm} \left( h \right) = \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} x^{n} y^{m} h\left( {x,y} \right){\text{d}}x{\text{d}}y$$
(30)

The set of geometric moments, which are invariant under rotation, scaling and translation are defined as [25,26,27]:

$$\begin{aligned} {\text{GMI}}_{nm} & = {\text{GM}}_{00}^{ - \gamma } \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \left[ {\left( {x - \bar{x}} \right)\cos \theta + \left( {y - \bar{y}} \right)\sin \theta } \right]^{n} \\ & \quad \times \left[ {\left( {y - \bar{y}} \right)\cos \theta - \left( {x - \bar{x}} \right)\sin \theta } \right]^{m} h\left( {x,y} \right){\text{d}}x{\text{d}}y \\ \end{aligned}$$
(31)

With

$$\gamma = \frac{n + m}{2} + 1;\quad \bar{x} = \frac{{{\text{GM}}_{10} }}{{ {\text{GM}}_{00} }};\quad \bar{y} = \frac{{ {\text{GM}}_{01} }}{{ {\text{GM}}_{00} }}$$
(32)

And

$$\theta = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2\mu_{11} }}{{\mu_{20} - \mu_{02} }}} \right)$$
(33)

The central geometric moment of order \(\left( {n + m} \right)\) is defined as

$$\mu_{nm} \left( h \right) = \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \left( {x - \bar{x}} \right)^{n} \left( {y - \bar{y}} \right)^{m} h\left( {x,y} \right){\text{d}}x{\text{d}}y$$
(34)

By using the binomial formula with Eq. (31), the set of geometric moments, which are invariant to the three geometric transformations, are defined as follows:

$${\text{GMI}}_{nm} = {\text{GM}}_{00}^{ - \gamma } \mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} \left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)\left( { - 1} \right)^{j} \left( {\sin \theta } \right)^{i + j} \left( {\cos \theta } \right)^{n + m - i - j} \mu_{n - i + j, m - j + i}$$
(35)

4.2 Adapted Gegenbauer–Chebyshev moment invariants

Using Eqs. (23) and (19), we get

$$\begin{aligned} {\text{AGC}}_{nm} & = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \psi_{n,m} \left( {x,y} \right)f\left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ & = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} \mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} c'_{i} \left( \lambda \right)d'_{j} x^{i} y^{j} f\left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ & = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} c'_{i} \left( \lambda \right)d'_{j} \mathop \int \limits_{0}^{N} \mathop \int \limits_{0}^{M} x^{j} y^{j} f\left( {x,y} \right)v\left( {x,y} \right){\text{d}}x{\text{d}}y \\ \end{aligned}$$
(36)

We consider the new image function \(h\left( {x, y} \right)\) defined as:

$$h\left( {x,y} \right) = f\left( {x,y} \right)v\left( {x,y} \right)$$
(37)

Substituting Eqs. (37) and (30) into (36) yields:

$${\text{AGC}}_{nm} = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} c'_{i} \left( \lambda \right)d'_{j} GM_{ij} \left( h \right)$$
(38)

The adapted Gegenbauer–Chebyshev moment invariants (AGCMIs) can be expanded in terms of GMIs as follows:

$${\text{AGCI}}_{nm} = \frac{1}{{C\left( { n,m,\lambda } \right)}}\mathop \sum \limits_{i = 0}^{n} \mathop \sum \limits_{j = 0}^{m} c'_{i} \left( \lambda \right)d'_{j} V_{ij} \left( h \right)$$
(39)

Where \(V_{ij} \left( h \right)\) are the parameters defined as

$$V_{nm} \left( h \right) = \mathop \sum \limits_{q = 0}^{n} \mathop \sum \limits_{p = 0}^{m} \left( {\begin{array}{*{20}c} n \\ p \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ q \\ \end{array} } \right)\left( {\frac{N \times M}{2}} \right)^{{\frac{p + q}{2} + 1}} \left( {\frac{N}{2}} \right)^{n - p} \left( {\frac{M}{2}} \right)^{m - q} {\text{GMI}}_{pq} \left( h \right)$$
(40)

According to all the aforementioned about the theoretical framework, we have succeeded in constructing orthogonal invariant features of the images, which are invariant to the three geometric transformations defined as follows:

$$V = \left( {{\text{AGCI}}_{\text{ij}} } \right),\;i = 0, \ldots ,p;\;j = 0, \ldots ,q$$
(41)

To evaluate the performance of this feature vectors, we will present an experimental study in the next section.

5 Experimental results

Experiments are performed to evaluate the ability of the proposed orthogonal moments in representation and recognition of gray-level images and objects. The performance of the proposed, AGCMs, is compared with the performance of the existing orthogonal moments such as the orthogonal Chebyshev rational moments (CRMs) [31], the weighted radial shifted Legendre moment (WRSLMs) [32], the fractional-order Orthogonal Chebyshev moments (FrCbMs) [33], the orthogonal fractional discrete Tchebyshev moments (FrDTMs) [34], the Fractional-Order Polar Harmonic Transform moments (FrPHTMs) [35], the Legendre moments (LMs) [36], the Tchebichef (TMs) moments [25] and the Gegenbauer moments (GegMs) [23, 24].

This section is divided into five subsections. Experiments for testing the invariance to geometric transformations are presented in the first subsection. Tests in the second subsection are performed to evaluate the ability of the proposed AGCMs method in reconstructing the gray-level images. The accuracy of the reconstructed images is an indicator that reflects the accuracy of the proposed method. An image retrieval system based on the proposed feature vectors is presented in the third subsection. In the fourth subsection, we present an evaluation on the accuracy of the proposed descriptor vector for the recognition of object and the classification of image databases. Experiments to estimate the CPU times are presented in the in the fifth subsection.

5.1 Invariance to geometric transformations

Geometric transformations of digital images include rotation, scaling and translation (RST). These spatial transformations sometimes called similarity transformations. Invariance with respect to RST is required in most pattern recognition applications, because the object should be correctly recognized, regardless of its position, orientation in the scene, and the object-to-camera distance. In other words, the computed moment invariants must be unchanged if the original images are rotated with any angle, scaled with any scaling factor and translated with any translation vectors.

However, the accuracy of the orthogonal moment invariants is negatively affected by the accumulated errors. In this section, the accuracy of the proposed moment invariants is evaluated and compared with the moment invariants of the existing methods [31,32,33,34,35]. Three experiments are performed using the gray-scale image of Lena of size \(128 \times 128\) pixels as displayed in Fig. 3.

Fig. 3
figure 3

The gray-scale image of Lena

Full size image

To measure the degree of the invariability of adapted Gegenbauer–Chebyshev invariant moments (AGCMIs) to remain unchanged under different image transformations, we use the relative error between the two sets of invariant moments corresponding to the original image \({\text{f}}\left( {{\text{x}},{\text{y}}} \right)\) and the transformed image \({\text{f}}^{\text{t}} \left( {{\text{x}},{\text{y}}} \right)\) as

$${\text{MSE}}\left( {{\text{f}},{\text{f}}^{\text{t}} } \right) = \frac{{{\text{AGCI}}\left( {\text{f}} \right) - {\text{AGCI}}\left( {{\text{f}}^{\text{t}} } \right)}}{{{\text{AGCI}}\left( {\text{f}} \right)}},$$
(42)

where \({\text{p}}\) is the number of transformed images, \(||. ||\) is the Euclidean norm, \({\text{AGCI}}\left( {\text{f}} \right)\) is the adapted Gegenbauer–Chebyshev orthogonal invariant moments for the original image and \({\text{AGCI}}\left( {{\text{f}}^{\text{t}} } \right)\) is the adapted Gegenbauer–Chebyshev orthogonal invariant moment for the transformed image.

The first experiment is performed to test the rotation invariance of the proposed orthogonal moments. The image Lena (Fig. 3) is rotated with different angles ranging from 0o to 180o with fixed increment 30o where the original and rotated images are displayed in Fig. 4.

Fig. 4
figure 4

Original and rotated images of Lena

Full size image

The proposed AGCMIs, the existing orthogonal moments [31,32,33,34,35] are computed for original and rotated images with moment order 20. The MSE values for of these moments are presented in Table 1. It is observed that the values of the MSE measure for the proposed method are much smaller than their corresponding values for the existing orthogonal methods [31,32,33,34,35] that ensures the accuracy of the proposed method.

Table 1 MSE for the rotated images of “image Lena” using the proposed method, AGCMIs, and the existing orthogonal moments [31,32,33,34,35]
Full size table

The second experiment is performed to test the scaling invariance of the proposed orthogonal moments (AGCMIs). The image “Baboon” presented in Fig. 5 is uniformly scaled with 7 different scaling factors \(\lambda = 0,5, 0.75, 1, 1.25, 1.5, 1.75, 2\).

Fig. 5
figure 5

The gray-level image “Baboon”

Full size image

The original image and the scaled ones are displayed in Fig. 6. The proposed AGCMIs and the existing orthogonal moments [31,32,33,34,35] are computed for original image, \({\text{M}}_{\text{pq}} \left( {\text{f}} \right)\), and the scaled images, \({\text{M}}_{\text{pq}} \left( {{\text{f}}^{\text{scaled}} } \right),\) with moment order. The MSE values of these moments are presented in Table 2. It is clear that the proposed method is outperformed all other methods.

Fig. 6
figure 6

Scaled images of the image “Baboon”

Full size image
Table 2 MSE for the scaled images of image Baboon using the proposed method, AGCMIs, and the existing orthogonal moments [31,32,33,34,35]
Full size table

The third experiment is performed to evaluate the translation invariance of the proposed moments. The image Barbara, illustrated in Fig. 7, is translated with the five different vectors (− 3, − 3), (− 1, − 1), (1, 1), (3, 3), (5, 5) and (8, 8). The original image and the translated images of image “Barbara” are displayed in Fig. 8.

Fig. 7
figure 7

The gray-level image “Barbara”

Full size image
Fig. 8
figure 8

Translated images of the image “Barbara”

Full size image

The proposed AGCMIs and the existing orthogonal are computed for original image, \({\text{M}}_{{{\text{p}},{\text{q}}}} \left( {\text{f}} \right),\) and the translated images, \({\text{M}}_{{{\text{p}},{\text{q}}}} \left( {{\text{f}}^{\text{trans}} } \right),\) with moment order 20. The MSE values of the translation invariants are presented in Table 3. It is observed that the trend of the results obtained from the three performed experiments is the same and ensures the superiority of the proposed method over all other exiting methods.

Table 3 MSE for the translated images of image Barbara using the proposed method, AGCMIs, and the existing orthogonal moments [31,32,33,34,35]
Full size table

5.2 Image reconstruction

In this section, we will discuss the ability of the adapted Gegenbauer–Chebyshev for the reconstruction of 2D images using Eq. (28). The accuracy of the reconstructed images usually evaluated using quantitative and qualitative measures. The quantitative measure is the normalized image reconstruction error (NIRE) [37]:

$${\text{NIRE}} = \frac{{\mathop \sum \nolimits_{x = 0}^{N - 1} \mathop \sum \nolimits_{y = 0}^{M - 1} \left[ {f\left( {x,y} \right) - \hat{f}\left( {x,y} \right)} \right]^{2} }}{{\mathop \sum \nolimits_{x = 0}^{N - 1} \mathop \sum \nolimits_{y = 0}^{M - 1} \left[ {f\left( {x,y} \right)} \right]^{2} }}$$
(43)

The value of is zero when the reconstructed image,\({\hat{\text{f}}}\left( {{\text{x}},{\text{y}}} \right)\), is identical to the original image, \({\text{f}}\left( {{\text{x}},{\text{y}}} \right)\) which is impossible in practice. The value of the \({\text{NIRE}}\) decreased as the accuracy of the computational method increased. The proposed method is highly accurate when the value of the quantitative measure \({\text{NIRE}}\) approaches zero. The quality of the reconstructed image is evaluated quantitatively using the human eye observation, where the normal human eye could easily measure the degree of similarity between the original and the reconstructed images.

The six images displayed in Fig. 9 are used as the test images in this study. This section presents three experiments. In the first experiment, we perform experimental tests in the two gray-scale images “Dog” and “House” presented in Fig. 9a, b of sizes 200 ×200 pixels. Knowing that the maximum order of the orthogonal ranging is 40, 60, 80, 100, 140, 160 and 200. The MSE‟s values of the proposed (AGCMs) are compared with their corresponding values of the Legendre moments (LMs) [36], the Tchebichef (TMs) moments [25] and the Gegenbauer moments (GegMs) [23, 24], where these values are presented in Tables 4 and 5.

Fig. 9
figure 9

Test images: a Dog, b House, c Girl, d Barbara, e Baboon and f Cameramen

Full size image
Table 4 Reconstruction error MSE of adapted Gegenbauer–Chebyshev moments (AGCMs), Legendre moments (LMs), Tchebichef moments (TMs) and Gegenbauer orthogonal moments (GegMs) for image “House”
Full size table
Table 5 Reconstruction error MSE of adapted Gegenbauer–Chebyshev moments (AGCMs), Legendre moments (LMs), Tchebichef moments (TMs) and Gegenbauer orthogonal moments (GegMs) for image “Dog”
Full size table

It is clear that the MSE values decrease and approach zero as the order of the moment increases. The proposed adapted Gegenbauer–Chebyshev orthogonal moment is highly accurate and stable for all moment orders compared with the other tested orthogonal moments.

In the second experiment, we perform visual tests for the reconstruction of two images “Girl” and “Barbara” presented in Fig. 9c, d using three types of orthogonal moments. The reconstructions of images based on the proposed orthogonal moments (AGCMs), Legendre orthogonal moment (LMs), Tchebichef orthogonal moments (TMs) and Gegenbauer orthogonal moments (GegMs) of order 50, 100, 150 are illustrated in Figs. 10 and 11. The first analysis of the results illustrated in these figures shows the quality of the reconstruction of (AGCMs) and indicates that the reconstructed image is closer to the original when the order of the maximum moment reaches a certain value. We observe that the reconstruction results based on the proposed orthogonal moments (AGCMs) are better than the other orthogonal moments tested.

Fig. 10
figure 10

Reconstructed images of image “Barbara” using our orthogonal moments (AGCMs), Legendre moments (LMs) and Tchebichef moments (TMs)

Full size image
Fig. 11
figure 11

Reconstructed images of image “Girl” using our orthogonal moments (AGCMs), Legendre moments (LMs) and Tchebichef moments (TMs)

Full size image

In the third experiment, we test the capacity of noisy image reconstruction using the proposed orthogonal moments (AGCMs). In this context, we use two images “Baboon” and “Cameramen” (Fig. 9e, f). We add two types of noise: Gaussian noise (mean: 0, variance: 0.01) and salt-and-pepper noise (3%). The reconstructions of the images are performed by three types of orthogonal moments: (AGCMs), (LMs) and (TMs) with the maximal order 200. We represent the results of this experiment in Fig. 12. Other times, the results of this experiment show the superiority of our orthogonal moments (AGCMs) in the reconstruction of noisy images.

Fig. 12
figure 12

a Are reconstructed images using Gaussian noise-contaminated images and b are reconstructed images using salt-and-pepper noise-contaminated images. The maximum order used is 200 for each algorithm

Full size image

5.3 Proposed image retrieval system

This section presents a new image retrieval system based on the features extracted by the proposed AGCMIs and the similarity measure. In the proposed retrieval scheme, the distances between the query image and the images present in the database are calculated using the Euclidean distance

$$d\left( {X,Y} \right) = \sqrt {\left( {X - Y} \right)^{T} \left( {X - Y} \right)}$$
(44)

where \(X = \left( {{\text{AGCI}}_{ij} \left( Q \right)} \right), i = 0, \ldots ,p\; {\text{and}} \;j = 0, \ldots ,q\) is a descriptor vector of query image Q and \(Y = \left( {{\text{AGCI}}_{ij} \left( I \right)} \right), i = 0, \ldots ,p\;{\text{and}}\;j = 0, \ldots ,q\) the descriptor vector of image \(I\) in the database. To measure the performance of our image retrieval system, we use the recall and precision criteria defined by

$${\text{Recal}} = \frac{{{\text{Number}}\;{\text{of}}\; {\text{retrieved}}\;{\text{relevant}}\;{\text{images }}}}{{{\text{Total}}\;{\text{number}}\;{\text{of}}\;{\text{relevant}}\;{\text{images}}\;{\text{in}}\;{\text{the}}\;{\text{collection}}}}$$
(45)
$${\text{Precision}} = \frac{{{\text{Number}}\;{\text{of}}\;{\text{retrieved}}\;{\text{relevant}}\;{\text{images }}}}{{{\text{Retrieved}}\;{\text{images}} }}$$
(46)

To show the effectiveness of our image retrieval approach, we have performed tests on COLL-100 image database. Our system proceeds in two phases: The first is the indexing phase, in this step the descriptor vectors of the images are automatically extracted; using the orthogonal adapted Gegenbauer–Chebyshev moment invariants AGCMIS and stored in a database of vectors. These features are recovered quickly and efficiently. The second is the research phase; it consists of extracting the feature vector of the query image using our AGCMIs and comparing it with the feature vectors of the images of the database using the Euclidean distance. The system returns the result of the search in a list of ordered images according to the distance between their descriptors vectors and the descriptor vector of the query image. The distances are arranged in ascending order and the first images are retrieved. The results to retrieve the query image “object13_0” (Fig. 13) from COIL-100 database are compared with those obtained using very recent invariant moments such as CRMs [31], WRSLMs [32], FrCbMs [33], FrDTMs [34] and FrPHTMs [35].

Fig. 13
figure 13

image of “object13_0”

Full size image

The performance is tested with the measures precision and recall, which are defined in Eqs. (45) and (46). Knowing that, the conditions of these experiences are satisfied; the precision and recall are calculated and the results obtained are presented in the form of recall–precision graphs in Fig. 14. The comparison results show the superiority of our orthogonal invariant moments. Finally, the proposed AGCMIs are robust to image transformations.

Fig. 14
figure 14

Precision and recall obtained with the proposed invariant moments AGCMI the moment invariants CRMs [31], WRSLMs [32], FrCbMs [33], FrDTMs [34] and FrPHTMs [35] for COIL-100 image database

Full size image

5.4 Image classification

2D Image classification is a system in computer vision, which can classify a 2D image according to its content. This system can be divided into two main phases: The first is the feature extraction step, which consists in calculating the descriptor vectors of the images and storing them in a database. The second phase consists of applying a classification algorithm.

The extraction of descriptor vectors of the image is an operation that makes it possible to convert an image into a vector of real or complex values that can serve as a signature for an image. That is to say, for an accurate system of classification, the used descriptor vector must be invariant to the three image transformations (translation, rotation and scale), which means that, the descriptor vectors of the image and the transformed image by translation, rotation or scale must be equal. In the proposed classification system, we use the proposed orthogonal adapted Gegenbauer–Chebyshev invariant moments (AGCMIs) presented in Eq. (39) to extract the descriptor vectors of the images as follows:

$$V\left( f \right) = \left( {{\text{AGCI}}_{ij} } \right), i = 0, \ldots ,p\; {\text{and}}\;j = 0, \ldots ,q$$
(47)

For the second phase, we use the fuzzy K-means (FKM) algorithm [29, 38] to classify image databases such the number of its classes is predefined in advance. This technique is based on the notion of measure of similarity or distance between two descriptor vectors. In this approach, we use the Euclidean distance. Note \(X = \left\{ {X_{j} \left( {f_{j} } \right),j = 1, \ldots ,N} \right\}\) is the set of the descriptor vectors of the considered images, where \(X_{j} \left( {f_{j} } \right) = \left( {x_{1j} ,x_{2j} , \ldots ,x_{dj} } \right) ^{t}\) is the descriptor vector of an image \(f_{j}\) of the database and \(C = \left\{ {C_{i} ;i = 1, \ldots ,c} \right\}\) is a set of vector unknown prototypes, where \(C_{i} = \left( {c_{i1} ,x_{i2} , \ldots ,x_{id} } \right) ^{t}\) characterizes the class. In this method an element of X is assigned to a class and only one of the proposed \(C\). In this case, the functional to be minimized is:

$$J\left( {C,U,X} \right) = \mathop \sum \limits_{i = 1}^{c} \mathop \sum \limits_{j = 1}^{N} \left( {u_{ij} } \right)^{m} d^{2} \left( {X_{j} ,C_{i} } \right).$$
(48)

where m is any real number greater than 1, \(X_{i}\) is the \(i^{th}\) of p-dimensional measured data, \(C_{j}\) is the p-dimension center of the cluster and the fuzzy partition matrix \(U = \left( {u_{ij} } \right)_{c \times N}\) satisfies the following conditions.

$$u_{ik} \in \left[ {0,1} \right];\quad 1 \le i \le c;1 \le k \le N$$
(49)
$$\mathop \sum \limits_{i = 1}^{c} u_{ik} = 1;\quad k = 1, \ldots ,N$$
(50)
$$0 < \mathop \sum \limits_{k = 1}^{N} u_{ik} < N,\quad 1 \le i \le c$$
(51)

The optimal points of the objective function (48) can be found by adjoining the constraint (50) to J by means of Lagrange multipliers:

$$J\left( {C,U,X,\lambda } \right) = \mathop \sum \limits_{i = 1}^{c} \mathop \sum \limits_{j = 1}^{N} \left( {u_{ij} } \right)^{m} d_{A}^{2} \left( {X_{j} ,C_{i} } \right) + \mathop \sum \limits_{j = 1}^{N} \lambda_{j} \left( {\mathop \sum \limits_{i = 1}^{c} u_{ij} - 1} \right).$$
(52)

Where \(\lambda = \left( {\lambda_{j} } \right), j = 1, \ldots , N\) are the Lagrange multipliers for the N constraints in Eq. (50). By differentiating \(J\left( {C,U,X,\lambda } \right)\) to all its inputs arguments, the necessary conditions for J to reach its minimum are

$$u_{ij} = \frac{1}{{\mathop \sum \nolimits_{k = 1}^{c} \left( {\frac{{d_{ij} }}{{d_{kj} }}} \right)^{{\frac{2}{m - 1}}} }}$$
(53)
$$C_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} \left( {u_{ij} } \right)^{m} X_{j} }}{{\mathop \sum \nolimits_{j = 1}^{N} \left( {u_{ij} } \right)^{m} }}$$
(54)

This iteration will stop when

$$U_{k + 1} - U_{k} = \max_{i,j} \left| {u_{ij}^{{\left( {k + 1} \right)}} - u_{ij}^{\left( k \right)} } \right| < \varepsilon ,$$
(55)

where \(\varepsilon\) is a termination criterion between 0 and 1, whereas k are the iteration steps. This procedure converges to a local minimum or a saddle point of \(J\left( {C, U, X} \right)\).

figure a

Our objective is to focus on using the invariant moments to classify an image into one of many classes based on shape.

According to algorithm 1, the degree of membership of each image to the clusters is given randomly in the initial step (iteration \(l = 0\)) such as \(U^{\left( 0 \right)} = \left( {U_{ij}^{0} } \right)\) satisfies the conditions (49), (50) and (51) and in each iteration \(l \left( {l = 1,2 \ldots} \right),\) we calculate, simultaneously, the cluster centers \(C_{i}^{\left( l \right)}\) and the degrees of membership \(u_{ij}^{\left( l \right)}\) as follows

  1. 1
    $$\left\{ {C_{i}^{\left( l \right)} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} \left( {u_{ij}^{{\left( {l - 1} \right)}} } \right)^{m} X_{j} }}{{\mathop \sum \nolimits_{j = 1}^{N} \left( {u_{ij}^{{\left( {l - 1} \right)}} } \right)^{m} }} , \quad 1 < i < c} \right..$$
  2. 2
    $$d_{ij}^{2} = d^{2} \left( {X_{j} , C_{i}^{\left( l \right)} } \right)^{t} ;\quad 1 < i < c , 1 < j < N.$$
  3. 3
    $$u_{ij}^{\left( l \right)} = \frac{1}{{\mathop \sum \nolimits_{k = 1}^{c} \left( {\frac{{d_{ij} }}{{d_{kj} }}} \right)^{{\frac{2}{{\left( {m - 1} \right)}}}} }}$$

The algorithm stops when the condition \({\text{U}}^{{\left( {\text{l}} \right)}} - {\text{U}}^{{\left( {{\text{l}} - 1} \right)}} = max_{i,j} \left| {u_{ij}^{\left( l \right)} - u_{ij}^{{\left( {l - 1} \right)}} } \right| < \varepsilon\) is satisfied.

If the value of \(k\) equals the number of classes in the database, the application of the FKM algorithm presents the results as \(k\) homogeneous classes (each class contains the same object). Therefore, in this case, the FKM behaves brilliantly as a method of classification.

To test our image classification system presented in Fig. 15, which is based on the proposed orthogonal invariant moments and fuzzy K-means algorithm (FKM), we use the three image databases: The first database is “MPEG7-CE Shape” [39]. This database contains images of the objects geometrically deformed. In this experiment, we have considered ten classes of objects and each class contains 20 images. The second is the Columbia “Object Image Library (COIL-20) database” [40], which consists of 1440 images of size \(128 \times 128\) distributed as 72 images for each object. The third image database is the “ORL-faces database” [41]. This database contains ten different images for the face of each person. The total number of images is equal to 400. All images of this database have the size \(92 \times 112\).

Fig. 15
figure 15

Algorithm-Flowchart of our classification system

Full size image

We tested the performance of the adapted Gegenbauer–Chebyshev orthogonal moment invariants (AGCMIs) and we performed a comparative study with the performance of the existing orthogonal moments such as the Chebyshev rational moments (CRMs) [31], the weighted radial shifted Legendre moment (WRSLMs) [32], the fractional-order Chebyshev moments (FrCbMs) [33], the fractional discrete Tchebyshev moments (FrDTMs) [34] and the Fractional-Order Polar Harmonic Transform moments (FrPHTMs) [35]. This study was done on the three previous databases by adding different densities of salt-and-pepper noise densities 1%, 2%, 3%, and 4%. We use the precision defined in Eq. (56) to measure the performance of each image classification system.

$$\eta = \frac{{{\text{Number}}\;{\text{of}}\;{\text{correcty}}\;{\text{classified}}\;{\text{images}}}}{{{\text{Number}} \;{\text{of}}\;{\text{images}}\;{\text{used}}\;{\text{in}}\;{\text{the}}\;{\text{test}}}} \times 100\%$$
(56)

Tables 6, 7 and 8 present the results of image classification for the three databases. From these results, we can see our classification system based on orthogonal invariant moments (AGCMIs) and the fuzzy k-means algorithm (FKM) better than the systems based on the other invariant moments. See that, the accuracy of the recognition is decreasing according to the density of noise.

Table 6 Classification results of the “MPEG7-CE shape database” with the salt-and-pepper noise
Full size table
Table 7 Classification results of the “COIL-20 database” with the salt-and-pepper noise
Full size table
Table 8 Classification results of the “ORL-faces database” with the salt-and-pepper noise
Full size table

In addition, our proposed orthogonal invariant moments (AGCMIs) are robust for the three geometric transformations, despite the noisy conditions and the accuracy of the recognition compared with the other tested descriptors.

5.5 CPU time

CPU times are a quantitative measure used to evaluate the rapidity of any algorithm. In this subsection, we performed two experiments with both datasets of images. All our numerical experiments are performed in MATLAB 2018 on a PC HP, Intel(R) Core(TM) I5-5200U CPU @ 2.20 GHz, 4 GB of RAM, Operating system windows 7. The first experiment is performed with the COIL-20 database. In this experiment, the proposed orthogonal moment invariants AGCMIs, the orthogonal Chebyshev rational moments (CRMs) [31], the weighted radial shifted Legendre moment (WRSLMs) [32], the fractional-order orthogonal Chebyshev moments (FrCbMs) [33], the orthogonal fractional discrete Tchebyshev moments (FrDTMs) [34] and the fractional-order polar harmonic transform moments (FrPHTMs) [35] are used to compute the moments of the images of the COIL-20 dataset for moment orders ranging from 0 to 40 with fixed increment 10. We present the results as the average time needed for a single image, by dividing the overall time by the number of images in the dataset. The average CPU times for these methods are presented in Table 9. In the second experiment, we used the test set of the MPEG7-CE Shape database. We follow the same steps of the first experiment to estimate the processing times of each of this set. The average CPU times for this experiment are presented in Table 10. It is clear that the proposed moment invariants AGCMIs are very fast than the other tested methods.

Table 9 CPU times in seconds for each image in the test set of COIL-20
Full size table
Table 10 CPU times in seconds for each image in the test set of MPEG7-CE
Full size table

6 Conclusion

A new set of orthogonal adapted Gegenbauer–Chebyshev moments for image representation and recognition is presented. The performed experiments clearly show that the proposed image descriptors have many useful characteristics. First, the new adapted Gegenbauer–Chebyshev polynomials are invariant under the three geometric transformations and orthogonal over the rectangular domain \(\left[ {0, N} \right] \times \left[ {0,M} \right]\) of the image, which significantly increase the recognition capabilities of the proposed image descriptors. Second, these descriptors are computed using a highly accurate and numerically stable method. Third, the proposed image descriptors are robust against the different kinds of noise. Fourth, fast computation of the proposed image descriptors is suitable for real-time applications. Based on these characteristics, the recognition performance of the proposed image descriptors is outperformed the existing moments-based image descriptors. Also, the proposed descriptors are almost unchanged with rotation, scaling and translation transformations which ensure the usefulness of these descriptors in pattern recognition applications.

The proposed orthogonal Gegenbauer–Chebyshev moments show a significant improvement in image reconstruction capabilities and stabilities for either lower or higher moment orders. This is very attractive property for image processing applications. Based on their characteristics, the proposed orthogonal moments AGCMs and their image descriptors constitute promising tools for many pattern recognition and images processing applications.