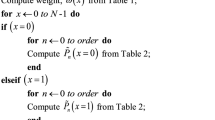1 Introduction

The dynamic development of 3D imaging technology has prompted researchers to improve methods of analysis and processing of 3D images, including those based on the theory of moments. Indeed, the latter has been applied for image reconstruction, compression, watermarking, classification, and indexing as well as pattern recognition [5, 10, 20, 24, 25, 31, 41].

Theoretically, moments can be classified into three main categories:

(a) Nonorthogonal moments such as geometric and complex moments, which have been applied by several researchers for reconstruction and classification of two-dimensional (2D) images [7,8,9,10,11,12,13,14,15], although they are limited by two major problems, namely information redundancy and noise sensitivity [30].

(b) Continuous orthogonal moments such as those of Legendre [30, 34, 39], Zernike [3, 30, 40], Hermite [3, 14], Gegenbauer [13], and Jacobi [32], which have been applied by many researchers. Their advantageous feature of orthogonality can solve the problems of information redundancy and noise sensitivity, but they are limited to problems that can be spatially discretized on domains defined by polynomials and suffer from divergence of the values of moments, especially those of high order.

(c) Discrete orthogonal moments such as those of Tchebichef [2, 33], Krawtchouk [38], Hahn [25, 36, 37], Charlier [8, 19], and Meixner [10, 26]. The main advantage of these moments is that they do not require spatial discretization, thereby addressing the problems encountered when using continuous orthogonal moments, albeit at the cost of increased time consumption. Indeed, computation of such moments is a complex and costly task in terms of time, limiting their application, especially for large image sizes and in the case of calculations online. This slowness is mainly due to two factors: the computation of a set of complex quantities for each order of moments, and the evaluation of the values of the polynomial for each pixel of the image.

To reduce the cost of such moment computations, several algorithms have been introduced in literature for 2D images [1, 6, 10, 11, 22, 26, 28]; Most of these algorithms are based on either:

  • Acceleration of the time required to calculate the values of the polynomials using new approaches such as recursive or matrix computations [6, 11, 17, 19, 33]

  • Use of new image representations based, e.g., on blocks or slices, to reduce the amount of the image that must be processed [28, 29]

However, no work has been dedicated to acceleration of the calculation of Charlier discrete orthogonal moments to make them usable for 3D images, especially for 3D objects of large size and for processing in real time.

We propose herein, for the first time, a new algorithm to accelerate the calculation of Charlier discrete orthogonal moments for 3D images. The algorithm is based on a new representation called image cuboid representation (ICR), in which a 3D image is decomposed into a set of cuboids of the same gray level instead of voxels, allowing a considerable reduction in both the quantity of voxels to be processed and thus the computation time of the moments.

In addition, we adopt and compare three methods for calculating the Charlier moments of a 3D image, viz. direct, recursive, and matrix, then choose the fastest. Simulation results confirm the efficiency of the proposed method in terms of reducing the time required to calculate the Charlier moments.

These results encouraged us to apply this representation for reconstruction of 3D objects using Charlier moments. We therefore also propose a new method for reconstruction of 3D images using Charlier moments, based on partial reconstruction of 3D images from the cuboids instead of global reconstruction. The proposed method offers two advantages: acceleration of the computation and enhanced reconstruction quality.

The remainder of this manuscript is organized as follows: Section 2 defines the three-dimensional Charlier moments and presents the three methods to calculate the Charlier polynomial values. Section 3 presents the new 3D image representation based on cuboids, called image cuboid representation (ICR). Section 4 presents the novel algorithm to calculate the 3D Charlier moments rapidly based on the ICR and the matrix calculation of the moments. Then, Sect. 5 presents the new 3D image reconstruction method based on the cuboids extracted using the ICR algorithm. Section 6 presents simulation results that confirm the efficiency and speed of the proposed algorithm. Finally, Sect. 7 concludes the paper.

2 3D Charlier Moments

The three-dimensional Charlier moments are defined as the projections of a 3D image onto the orthogonal basis of the Charlier discrete orthogonal polynomials. Therefore, for a 3D digital image f(x, y, z) with size N × M × K, that is, \( x \in [0, N - 1], \)\( y \in [0, M - 1] \), \( {\text{and}}\;z \in [0, K - 1] \), the \( \left( {n + m + k} \right) \)th-order Charlier moment is defined as

$$ \mathrm{CM}_{nmk} = \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)f\left( {x,y,z} \right)} } } $$
(1)

where \( \tilde{C}_{n}^{{a_{1} }} (x) \) is the nth Charlier normalized polynomial.

Calculation of the 3D Charlier moments proceeds by calculation of the values of the Charlier polynomials for each voxel of the 3D image. We present herein three methods for calculating the values of the Charlier polynomials: the direct and recursive methods with respect to the order n, and the recursive method with respect to the variable x.

2.1 Direct Method

The nth Charlier polynomials can be represented using the hypergeometric function as [21]

$$ C_{n}^{{a_{1} }} (x) = {}_{2}F_{0} \left( { - n, - x; - \frac{1}{{a_{1} }}} \right), $$
(2)

where \( x,n = 0,1,2, \ldots ,N - 1, N > 0,\quad {\text{and}}\quad a_{1} > 0 \).

The normalized form of the Charlier polynomials is defined by [21]

$$ \tilde{C}_{n}^{{a_{1} }} \left( x \right) = C_{n}^{{a_{1} }} \left( x \right)\sqrt {\frac{\omega \left( x \right)}{\rho \left( n \right)}}, $$
(3)

where ω(x) is the weight function of the Charlier discrete orthogonal polynomials, viz.

$$ \omega \left( x \right) = \frac{{\mathrm{e}^{{ - a_{1} }} a_{1}^{x} }}{x!}, $$
(4)

and ρ(n) is the squared norm of the Charlier discrete orthogonal polynomials, defined as

$$ \rho \left( n \right) = \frac{n!}{{a_{1}^{n} }}. $$
(5)

Calculation of the Charlier polynomial values using Eq. (2) is very demanding in terms of time, requiring excessive operations including a certain number of multiplications and additions (factorials, powers, sums, etc.). To address this problem, we introduce the recursive computation method.

2.2 Recursive Method with Respect to the Order n

The Charlier polynomials satisfy a recurrence relation between three successive terms, defined by the following relation [8]:

$$ \tilde{C}_{n}^{{a_{1} }} \left( x \right) = \frac{{a_{1} - x + n - 1}}{{a_{1} }}\sqrt {\frac{{a_{1} }}{n} } \tilde{C}_{n - 1}^{{a_{1} }} \left( x \right) - \sqrt {\frac{n - 1}{n}} \tilde{C}_{n - 2}^{{a_{1} \,}} \left( x \right) $$
(6)

with n = 2, 3, …

\( \tilde{C}_{0}^{{a_{1} }} \left( x \right) \) and \( \tilde{C}_{1}^{{a_{1} }} \left( x \right) \) are the initial values, defined as

$$ \tilde{C}_{0}^{{a_{1} }} \left( x \right) = \sqrt {\frac{\omega \left( x \right)}{\rho \left( 0 \right)}} \quad {\text{and}}\quad \tilde{C}_{1}^{{a_{1} }} \left( x \right) = \frac{{a_{1} - x}}{{a_{1} }}\sqrt {\frac{\omega \left( x \right)}{\rho \left( 1 \right)}}. $$
(7)

The calculation of the Charlier polynomial values using this recurrence relation with respect to the order n is limited by the numerical fluctuation problem of polynomial values and for large values. To solve this problem, Hmimid et al. [9] suggested using the recurrence relation with respect to the variable x instead of the order n to calculate the values of the Charlier polynomials.

2.3 Recursive Method with Respect to the Variable x

The Charlier discrete orthogonal polynomials satisfy the following recurrence relation between three successive terms with respect to the variable x:

$$ C_{n}^{{a_{1} }} \left( x \right) = \frac{{x - 1 + a_{1} - n}}{{a_{1} }}C_{n}^{{a_{1} }} \left( {x - 1} \right) - \frac{x - 1}{{a_{1} }}C_{n}^{{a_{1} }} \left( {x - 2} \right). $$
(8)

According to Eq. (3), the normalized form can be expressed by substitutions as follows:

$$ \tilde{C}_{n}^{{a_{1} }} \left( x \right) = \frac{{\sqrt {\omega \left( x \right)} }}{{a_{1} }} \left[ { \frac{{x - 1 + a_{1} - n}}{{\sqrt {\omega \left( {x - 1} \right)} }}\tilde{C}_{n}^{{a_{1} }} \left( {x - 1} \right) - \frac{x - 1}{{\sqrt {\omega \left( {x - 2} \right)} }}\tilde{C}_{n}^{{a_{1} }} \left( {x - 2} \right) } \right], $$
(9)

where \( x = 2, \ldots , N - 1. \).

The initial values are defined by

$$ \tilde{C}_{n}^{{a_{1} }} \left( 0 \right) = \sqrt {\frac{\omega \left( 0 \right)}{\rho \left( n \right)}} \quad {\text{and}}\quad \tilde{C}_{n}^{{a_{1} }} \left( 1 \right) = \frac{{a_{1} - n}}{{a_{1} }}\sqrt {\frac{\omega \left( 1 \right)}{\rho \left( n \right)}}. $$
(10)

This section has presented the different types of calculations for the 3D Charlier moments, namely the direct and recursive methods with respect to the variable x and order n. The resulting definitions and properties are used throughout the work. However, these calculations of the moments are very slow and complex, limiting their wide use for 3D images. To address these problems, we propose, in the next section, a new method based on the 3D image cuboid representation (ICR).

3 3D Image Cuboid Representation (ICR)

A 3D image is a three-dimensional representation of an object or set of objects in the real or digital domain. In the case of a discrete representation, the 3D image is often projected into a three-dimensional space with the three axes x, y, z. The notion of a voxel in 3D images is the equivalent of a pixel in 2D images.

Therefore, a voxel represents the elementary unit of volume, defined by its position in space, its dimensions, and its intensity. In addition, voxels are often considered as elements that have the same dimensions, although there may be cases where voxels of the same image are of different dimensions, as in magnetic resonance imaging (MRI) medical images. In the case of voxels having the same dimensions, we consider that the volume can be represented by a discrete function f(x, y, z) where each voxel at coordinates (x, y, z) is represented by an intensity fi; alternatively, this function can be represented as a 3D matrix (Fig. 1).

Fig. 1
figure 1

Representation of a 3D image

Full size image

Herein, we suggest a new method for representing a 3D image using cuboids that include voxels of the same intensity (homogeneous), considering the work of Spiliotis [29] and Papakostas [23], who presented the concept of representing a 2D image using a set of homogeneous pixel blocks.

Using this representation, called the image cuboid representation (ICR), an image is defined by a set of cuboids, each of which contains a single gray level. This also allows the image to be divided into larger elements than simple voxels but with homogeneous intensity, thus reducing the number of elements that must be treated. Based on this proposal, for 3D binary images, one no longer needs to describe the voxels of level 0, but only those of level 1. However, for gray level images, the intensity takes values between 0 and 255, which results in cuboids represented by n (1 ≤ n ≤ 255) values of intensity, while cuboids of zero intensity are neglected. Thus, to represent a binary or grayscale 3D image of size N × M × K, we propose the following algorithm, called image cuboid representation (ICR):

ICR algorithm

Step 1: Divide the image f(x, y, z) such that \( x \in \left[ {1,N} \right], \, y \in \left[ {1,M} \right] \, and \, z \in \left[ {1,K} \right] \) into a matrix K of size N × M

Step 2: Consider each line y of Kz with \( z = 0, \ldots \, K - 1 \) and find object-level intervals for each intensity value that exists in line y

Step 3: Compare intervals and blocks having the same intensity in line y − 1

Step 4: If an interval does not match with any block of the same intensity, it is the beginning of a new block. If a block matches with an interval of the same intensity, the end of the block is in line y

Step 5: Compare blocks having the same intensity in the matrix Kz−1. If a block does not correspond to any cuboid of the same intensity, then it is the beginning of a new cuboid

Step 6: Output the L cuboids described by their intensities fi and positions (x1, x2, y1, y2, z1, z2)

To illustrate the proposed algorithm, we apply it to a 3D image taken from the McGill database [16], which represents a 3D “Airplane” with size of 128 × 128 × 128 (Fig. 2). Applying the ICR algorithm to this image, we obtain the different cuboids that form the image, as shown in Fig. 2.

Fig. 2
figure 2

Several views of the representation of the “Airplane” image using cuboids

Full size image

The number of cuboids in this image is 586, thus one can treat these 586 elements instead of the \( 128 \times 128 \times 128 = 2 \, 097 \, 152 \) pixels, which shows the importance of this new representation for image processing.

In the next sections, a new method for calculating the 3D Charlier discrete orthogonal moments and their inverse based on the 3D ICR is suggested, to reduce the computation time and thereby accelerate the process of 3D image analysis (reconstruction, shape recognition, classification, etc.).

4 Fast Computation of 3D Charlier Discrete Orthogonal Moments

In this section, we propose a new method to compute the 3D Charlier moments based on the new representation presented in the previous section. Applying the ICR algorithm, the 3D Charlier moments can be calculated using two methods:

  • Direct calculation from the cuboids instead of the whole image

  • Calculation as the product of the matrices for each cuboid

4.1 Direct Computation of 3D Charlier Moments

For a 3D image f(x, y, z) containing L cuboids extracted using the ICR algorithm,

$$ f\left( {x,y,z} \right) = \sum\limits_{i = 1}^{255} {f_{i} \left( {x,y,z} \right)}, $$
(11)

where \( \left\{ {f_{i} , i = 1,2, \ldots ,255} \right\} \) is the ith intensity of the 3D image and

$$ f_{i} \left( {x,y,z} \right) = \mathrm{Cub}_{j}^{{f_{i} }}, $$
(12)

where \( \mathrm{Cub}_{j}^{{f_{i} }} \) is cuboid j of intensity fi, j = 1, ···, and Li is the jth cuboid of intensity fi, while \( L = \sum\limits_{i = 1}^{255} {L_{i} } \), where Li is the number of cuboids of each intensity fi.

Using the ICR algorithm, the 3D Charlier moments of order \( \left( {n + m + k} \right) \) for a 3D image f(x, y, z) of size N × M × K in Eq. (1) can be computed as

$$ \begin{aligned} \mathrm{CM}_{nmk} & = \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)f\left( {x,y,z} \right)} } } \\ & = \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)\sum\limits_{i = 1}^{255} {f_{i} \left( {x,y,z} \right)} } } } \\ & = \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)} f_{1} \left( {x,y,z} \right)} } \\ & \quad + \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)} f_{2} \left( {x,y,z} \right) + \cdots \cdots } } \\ & \quad + \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)} f_{255} \left( {x,y,z} \right)} }. \\ \end{aligned} $$
(13)

Since a cuboid is determined by the coordinates \( \left( {x_{1} ,x_{2} ,y_{1} ,y_{2} ,z_{1} ,z_{2} } \right) \), Eq. (13) can be written as

$$ \begin{aligned} \mathrm{CM}_{nmk} & = f_{1} \sum\limits_{{x_{1} }} {\sum\limits_{{y_{1} }} {\sum\limits_{{z_{1} }} {\tilde{C}_{n}^{{a_{1} }} \left( {x_{1} } \right)\tilde{C}_{m}^{{a_{1} }} \left( {y_{1} } \right)\tilde{C}_{k}^{{a_{1} }} \left( {z_{1} } \right)} } } \\ &\quad + f_{2} \sum\limits_{{x_{2} }} {\sum\limits_{{y_{2} }} {\sum\limits_{{z_{2} }} {\tilde{C}_{n}^{{a_{1} }} \left( {x_{2} } \right)\tilde{C}_{m}^{{a_{1} }} \left( {y_{2} } \right)\tilde{C}_{k}^{{a_{1} }} \left( {z_{2} } \right)} } } \\ & \quad + \cdots f_{255} \sum\limits_{{x_{255} }} {\sum\limits_{{y_{255} }} {\sum\limits_{{z_{255} }} {\tilde{C}_{n}^{{a_{1} }} \left( {x_{255} } \right)\tilde{C}_{m}^{{a_{1} }} \left( {y_{255} } \right)\tilde{C}_{k}^{{a_{1} }} \left( {z_{255} } \right)} } } \\ & = f_{1} \mathrm{CM}_{nmk}^{1} + f_{2} \mathrm{CM}_{nmk}^{2} + \cdots f_{255} \mathrm{CM}_{nmk}^{255} \\ & = \sum\limits_{i = 1}^{255} {f_{i} \mathrm{CM}_{nmk}^{i} }, \\ \end{aligned} $$
(14)

where \( \mathrm{CM}_{nmk}^{i} \) is the \( \left( {n + m + k} \right) \)th-order 3D Charlier discrete orthogonal moment of intensity \( f_{i} \).

The moments corresponding to an intensity \( f_{i} \) can be calculated from the cuboids of each intensity using the relation

$$ \begin{aligned} \mathrm{CM}_{nmk}^{i} & = \sum\limits_{j = 1}^{{L_{i} }} {f_{i} \sum\limits_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\sum\limits_{{y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{m}^{{a_{1} }} \left( y \right)\sum\limits_{{z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{k}^{{a_{1} }} \left( z \right)} } } } \\ & = \sum\limits_{j = 1}^{{L_{i} }} {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} }, \\ \end{aligned} $$
(15)

where \( \mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \) is the \( (n + m + k) \)th-order 3D Charlier discrete orthogonal moment of intensity fi for each cuboid.

Thus, the 3D Charlier discrete orthogonal moments can be written as

$$ \begin{aligned} \mathrm{CM}_{nmk} & = \sum\limits_{i = 1}^{255} {\sum\limits_{j = 1}^{{L_{i} }} {\sum\limits_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)f_{i} (x,y,z)} } } } } \\ & = \sum\limits_{i = 1}^{255} {\sum\limits_{j = 1}^{{L_{i} }} {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } } \\ \end{aligned} $$
(16)

with

$$ \mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} = \sum\limits_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)f_{i} (x,y,z)} } }. $$
(17)

4.2 Matrix Computation of 3D Charlier Moments

In this section, to accelerate the computation of the 3D Charlier moments, we combine the ICR algorithm with that based on matrix multiplication proposed by Wu et al. [35].

After specifying the cuboids of a 3D image using the ICR algorithm, we first apply the matrix calculation of the Charlier moments as follows: First, for each matrix of cuboid j of size Nj × Mj × Kj with \( N_{j} = x_{2} - x_{1} + 1, \quad M_{j} = y_{2} - y_{1} + 1,{\text{ and }}K_{j} = z_{2} - z_{1} + 1 \) by the coordinates (x1, x2, y1, y2, z1, z2) that are based on the decomposition of this cuboid j in Kj matrix, which represents the blocks \( b_{ij}^{z} \), \( z_{1} \le z \le z_{2} \). Then, for each block in the following step. Thus, it is evident that each block is determined by the coordinates (x1, x2, y1, y2).

The 3D Charlier orthogonal moments for each cuboid in Eq. (17) can thus be expressed as

$$ \begin{aligned} \mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} & = \sum\limits_{{z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{k}^{{a_{1} }} \left( z \right)\left[ {\sum\limits_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)f_{i} (x,y,z)} } } \right]} \\ & = \sum\limits_{{z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{k}^{{a_{1} }} \left( z \right)} \mathrm{CM}_{nm}^{{b_{ij}^{z} }} \\ \end{aligned} $$
(18)

where \( \mathrm{CM}_{nm}^{{b_{ij}^{z} }} \) are the Charlier moments in each block of cuboid j, which can also be written as

$$ \mathrm{CM}_{nm}^{{b_{ij}^{z} }} = \sum\limits_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\sum\limits_{{y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} {\tilde{C}_{n}^{{a_{1} }} \left( x \right)} \tilde{C}_{m}^{{a_{1} }} \left( y \right)f_{i} (x,y,z)}, $$
(19)

which can be reexpressed as a matrix product thus

$$ \mathrm{CM}_{nm}^{{b_{ij}^{z} }} = P_{1} IP_{2}^{\mathrm{T}}, $$
(20)

where

$$ \begin{array}{*{20}l} {\mathrm{CM}^{{b_{ij}^{z} }} = \left\{ {\mathrm{CM}_{nm}^{{b_{ij}^{z} }} } \right\}_{n,m = 0}^{n = M - 1,m = N - 1} ,} \hfill & {0 \le n \le M - 1,} \hfill & {0 \le m \le N - 1} \hfill \\ {P_{1} = \left\{ {\tilde{C}_{n}^{{a_{1} }} \left( x \right)} \right\}_{{n = 0,x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{n = M - 1,x = x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} ,} \hfill & {0 \le n \le M - 1,} \hfill & {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \hfill \\ {P_{2} = \left\{ {\tilde{C}_{m}^{{a_{1} }} \left( y \right)} \right\}_{{m = 0,y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{m = N - 1,y = y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} ,} \hfill & {0 \le m \le N - 1,} \hfill & {y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \hfill \\ {I = \left\{ {f_{i} \left( {x,y,z} \right)} \right\}_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} ,y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x = x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} ,y = y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} ,} \hfill & {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} ,} \hfill & {y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }. \hfill \\ \end{array} $$

The calculation of the 3D Charlier moments for each cuboid proceeds through the two following steps:

  • Step 1. Compute the matrix Kj along the z-direction using Eq. (20) to yield temporary matrices of the Charlier moments at each block of cuboid j, where \( \mathrm{CM}_{nm}^{{b_{ij}^{z} }} \) denotes the element in the nth row and mth column of the kth plane in the z-direction.

  • Step 2. Rearrange the matrices obtained in step 1 and multiply by the polynomial matrices \( P_{3} = \left\{ {\tilde{C}_{k}^{{a_{1} }} \left( z \right)} \right\}_{{k = 0,z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{k = K - 1,z = z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} , \, 0 \le k \le K - 1 \, , \, z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} \) to obtain a (n + 1) matrix of size (m + 1) × (k + 1) and thereby the 3D Charlier moments of order (n, m, k) for each cuboid.

The 3D Charlier moments of order n = 0 can then be written for each cuboid as the following matrix:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {\mathrm{CM}_{000}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{001}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{00k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {\mathrm{CM}_{010}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{011}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{01k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {\mathrm{CM}_{0m0}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{0m1}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{0mk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \end{array} } \right] \\ & \quad \times \left[ {\begin{array}{*{20}l} {\mathrm{CM}_{00}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & {\mathrm{CM}_{01}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{0m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill \\ {\mathrm{CM}_{00}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill & {\mathrm{CM}_{01}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{0m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\mathrm{CM}_{00}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & {\mathrm{CM}_{01}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{0m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill \\ {\quad \quad \quad \quad \quad \vdots } \hfill & {} \hfill & {} \hfill & {} \hfill \\ \end{array} } \right]. \\ \end{aligned} $$

Meanwhile, for order n = 1, the 3D Charlier moments for each cuboid can be written as the following matrix:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {\mathrm{CM}_{100}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{101}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{10k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {\mathrm{CM}_{110}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{111}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{11k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {\mathrm{CM}_{1m0}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{1m1}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{1mk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \end{array} } \right] \\ &\quad \times \left[ {\begin{array}{*{20}l} {\mathrm{CM}_{10}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & {\mathrm{CM}_{11}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{1m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill \\ {\mathrm{CM}_{10}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill & {\mathrm{CM}_{11}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{1m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\mathrm{CM}_{10}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & {\mathrm{CM}_{11}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill & \cdots \hfill & {\mathrm{CM}_{1m}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \hfill \\ \end{array} } \right] \\ & \quad \quad \quad \;\begin{array}{*{20}l} \vdots \hfill \\ \vdots \hfill \\ \vdots \hfill \\ \end{array} \\ \end{aligned} $$

For order n, the 3D Charlier moments for each cuboid can be written as the following matrix:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {\mathrm{CM}_{n00}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{n01}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{n0k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {\mathrm{CM}_{n10}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{n11}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{n1k}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {\mathrm{CM}_{nm0}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & {\mathrm{CM}_{nm1}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } & \cdots & {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{0}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{1}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\tilde{C}_{k}^{{a_{1} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \end{array} } \right] \\ & \quad \times \left[ {\begin{array}{*{20}c} {\mathrm{CM}_{n0}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\mathrm{CM}_{n1}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & \cdots & {\mathrm{CM}_{nm}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ {\mathrm{CM}_{n0}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & {\mathrm{CM}_{n1}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} & \cdots & {\mathrm{CM}_{nm}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} + 1} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\mathrm{CM}_{n0}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & {\mathrm{CM}_{n1}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} & \cdots & {\mathrm{CM}_{nm}^{{b_{ij}^{{z_{1} }} }} \left( {z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \right)} \\ \end{array} } \right]. \\ \end{aligned} $$

Then, having calculated the 3D Charlier moments for each cuboid using the blocks in each, one sums the resulting matrices for each cuboid to finally compute the 3D Charlier moments using Eq. (16).

The direct and matrix calculations based on the 3D ICR require less computational time. The significant reduction in the time required to calculate the 3D Charlier discrete orthogonal moments when using these two computational methods encouraged us to apply them for several image processing tasks such as reconstruction and classification.

5 Fast 3D Image Reconstruction Using 3D Charlier Moments

In this section, we present a fast and accurate approach for 3D image reconstruction using Charlier discrete orthogonal moments. The approach is based on the new ICR algorithm. Thus, the acceleration of the reconstruction process for a 3D image is due to two factors:

  • The rapid calculation of the Charlier moments using the cuboids extracted from each image

  • The partial reconstruction of the image from the cuboids instead of the whole image

Two versions of the proposed reconstruction method are presented:

  • A local reconstruction of the 3D image using a direct computation on the cuboids

  • A method based on the matrix calculation for each block at each cuboid, to calculate the local Charlier 3D moments

5.1 Local Reconstruction of 3D Image by Direct Computation of 3D Charlier Moments

In theory, an original 3D image function f(x, y, z) of size N × M × K can be represented by an infinite series of 3D moments:

$$ f\left( {x,y,z} \right) = \sum\limits_{n = 0}^{\infty } {\sum\limits_{m = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\mathrm{CM}_{nmk} \tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right),} } } \quad \quad \left\{ {\begin{array}{*{20}c} {0 \le x \le N - 1} \\ {0 \le y \le M - 1} \\ {0 \le z \le K - 1} \\ \end{array} } \right. $$
(21)

The local reconstruction of a 3D image f(x, y, z) of size N × M × K can be obtained by direct calculation from the 3D image cuboid representation (ICR), using the definition of the 3D Charlier moments in Eq. (17):

$$ \begin{aligned} f(x,y,z) & = \sum\limits_{i = 1}^{255} {\sum\limits_{j = 1}^{{L_{i} }} {\sum\limits_{n = 0}^{\infty } {\sum\limits_{m = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right) ,\quad \quad \left\{ {\begin{array}{*{20}c} {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right.} } } } } \\ & = \sum\limits_{i = 1}^{255} {\sum\limits_{j = 1}^{{L_{i} }} {f^{{\mathrm{Cub}_{j}^{{f_{i} }} }} (x,y,z)} }, \\ \end{aligned} $$
(22)

where \( f^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \left( {x,y,z} \right) \) is the partial reconstruction for each cuboid:

$$ f^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \left( {x,y,z} \right) = \sum\limits_{n = 0}^{\infty } {\sum\limits_{m = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{m}^{{a_{1} }} \left( y \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right),\quad \left\{ {\begin{array}{*{20}c} {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right.} } }. $$
(23)

5.2 Local Reconstruction of 3D Image by Matrix Computation of 3D Charlier Moments

In this subsection, we present a new method for reconstructing the 3D image, called the local reconstruction method; it allows reconstruction of the 3D image using the Charlier 3D matrix calculation of the blocks of each cuboid j. If the 3D moments are limited to one order, the partial reconstruction of the 3D Charlier moments for each cuboid using Eq. (23) can be rewritten as

$$ \begin{aligned} f^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \left( {x,y,z} \right) & = \sum\limits_{m = 0}^{\text{Max}} {\tilde{C}_{m}^{{a_{1} }} \left( y \right) \times \left[ {\sum\limits_{n = 0}^{\text{Max}} {\sum\limits_{k = 0}^{\text{Max}} {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)} } } \right]} ,\quad \quad \left\{ {\begin{array}{*{20}c} {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right. \\ & = \sum\limits_{m = 0}^{\text{Max}} {\tilde{C}_{m}^{{a_{1} }} \left( y \right) \times } F^{{b_{ij}^{z} }} \left( {x,z} \right), \\ \end{aligned} $$
(24)

where \( F^{{b_{ij}^{z} }} \) is the partial reconstruction of the 2D Charlier moments in each block of cuboid j.

\( F^{{b_{ij}^{z} }} \) can also be written as

$$ F^{{b_{ij}^{z} }} \left( {x,z} \right) = \sum\limits_{n = 0}^{\text{Max}} {\sum\limits_{k = 0}^{\text{Max}} {\mathrm{CM}_{nmk}^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \tilde{C}_{n}^{{a_{1} }} \left( x \right)\tilde{C}_{k}^{{a_{1} }} \left( z \right)} }. $$
(25)

We calculate \( F^{{b_{ij}^{z} }} \) in Eq. (25) by using a matrix form for a 2D image, which can be reexpressed as

$$ F^{{b_{ij}^{z} }} = Q_{1}^{\mathrm{T}} \mathrm{CM}^{{b_{ij}^{z} }} Q_{2}, $$
(26)

where \( F^{{b_{ij}^{z} }} \), \( \mathrm{CM}^{{b_{ij}^{z} }} \), \( Q_{1}^{\mathrm{T}} \), and \( Q_{2} \) are defined as

$$ \begin{array}{*{20}l} {F^{{b_{ij}^{z} }} = \left\{ {F_{xz}^{{b_{ij}^{z} }} } \right\}_{{x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} ,z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{x = x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} ,z = z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} ,} \hfill & {\left\{ {\begin{array}{*{20}c} {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ \end{array} } \right.} \hfill & {} \hfill \\ {\mathrm{CM}^{{b_{ij}^{z} }} = \left\{ {\mathrm{CM}_{nk}^{{b_{ij}^{z} }} } \right\}_{n,k = 0}^{{n,k = {\text{Max}}}} ,} \hfill & {0 \le n,k \le {\text{Max}},} \hfill & {{\text{for}}\;{\text{each}}\;m\;{\text{with}}\;0 \le m \le \;{\text{Max}}} \hfill \\ {Q_{1} = \left\{ {\tilde{C}_{n}^{{a_{1} }} \left( x \right)} \right\}_{{n = 0,x = x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{n = {\text{Max}},x = x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} ,} \hfill & {\left\{ {\begin{array}{*{20}c} {x_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le x \le x_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {0 \le n \le {\text{Max}}} \\ \end{array} } \right.} \hfill & {} \hfill \\ {Q_{2} = \left\{ {\tilde{C}_{k}^{{a_{1} }} \left( z \right)} \right\}_{{k = 0,z = z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{k = {\text{Max}},z = z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} , { }} \hfill & {\left\{ {\begin{array}{*{20}c} {z_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le z \le z_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} } \\ {0 \le k \le {\text{Max}}} \\ \end{array} } \right.} \hfill & {} \hfill \\ \end{array} $$

The local reconstruction of a 3D image using the matrix computation of the 3D Charlier moments for each cuboid proceeds through the following three-step algorithm:

Algorithm for the local reconstruction of 3D Charlier moments

Step 1: Compute the matrix Kj along the m-direction using (26) to obtain temporary matrices of the partial reconstruction of the 2D Charlier moments in each block of cuboid j, where \( F_{xz}^{{b_{ij}^{z} }} \) denotes the element in the xth row and zth column in the yth plane of m-direction. \( F_{{_{xz} }}^{{b_{ij}^{z} }} \left( m \right){ , }m = 0,1, \ldots ,{\text{ Max}}. \)

Step 2. Rearrange the matrices obtained in step 1 and multiply by the polynomial matrices \( Q_{3} = \left\{ {\tilde{C}_{m}^{{a_{1} }} \left( y \right)} \right\}_{{m = 0,y = y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} }}^{{m = {\text{Max}},y = y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} }} , \, y_{{1,\mathrm{Cub}_{j}^{{f_{i} }} }} \le y \le y_{{2,\mathrm{Cub}_{j}^{{f_{i} }} }} , \, 0 \le m \le {\text{Max}} \) to obtain a matrix Nj of size Mj × Kj, which yields the local reconstruction of the 3D Charlier moments for each cuboid \( f^{{\mathrm{Cub}_{j}^{{f_{i} }} }} \) of size (Nj, Mj, Kj).

Step 3. Merge the partial reconstruction of the 3D Charlier moments of each cuboid to reconstruct a 3D image with the same size as the original 3D image.

Figure 3 shows the flowchart for calculating the 3D Charlier moments and their inverse using the matrix computation via the ICR algorithm.

Fig. 3
figure 3

3D image reconstruction process diagram

Full size image

The proposed method focuses on reducing the computation time required to obtain the 3D Charlier discrete orthogonal moments of a 3D image, vastly enhancing the quality of the 3D image reconstruction. Clearly, our method is based on two main concepts:

  • The image cuboid representation (ICR)

  • The matrix calculation of the 3D Charlier moments and their inverse

The 3D image decomposition therefore starts with the extraction of cuboids for which only weak-order moments are needed, based on the ICR algorithm. The extracted cuboids are then applied to calculate the 3D Charlier moments using the matrix calculation for each cuboid. Each cuboid is then rebuilt using the 3D Charlier moments computed for each cuboid. Finally, the matrices of the reconstructed cuboid are summed to complete the 3D image reconstruction.

6 Simulations and Results

To validate the theoretical results developed in the previous sections and test the performance of the proposed method in terms of time and reconstruction performance, several simulations were carried out. This section is divided into two subsections:

  • Firstly, we compare the calculation time of the 3D Charlier moments and their inverse using the recurrence calculation method with respect to the variable x and the two versions of the proposed method, viz. based on direct and matrix calculations.

  • Secondly, we test the ability of the 3D Charlier discrete orthogonal moments to reconstruct 3D images when using the global and the proposed local methods. We also test the proposed method for other types of 3D discrete orthogonal moments such as those of Tchebichef, Krawtchouk, and Hahn, and compare the four types of moments in terms of computation time and image reconstruction performance.

6.1 Computation Time of 3D Charlier Moments

In this subsection, we compare the time required to compute the Charlier discrete orthogonal moments using the recursive and the two versions of the proposed method based on the 3D image representation using cuboids according to the ICR algorithm presented in Sect. 3.

In the first test, we present the simulation results obtained in terms of the number of cuboids extracted from each 3D image. We use images of size 128 × 128 × 128 voxels, viz. four 3D images extracted from from the McGill 3D shape benchmark database CVonline [16] (Fig. 4) and three MRI images (Fig. 5), as a three-dimensional matrix, where each image is composed of a different number of cuboids.

Fig. 4
figure 4

Image cuboid representation (ICR) of 3D images

Full size image
Fig. 5
figure 5

Image cuboid representation (ICR) of 3D MRI images

Full size image

After extracting the cuboids from each 3D image using the ICR algorithm, the ICR and the number of cuboids in each image are shown in Figs. 4 and 5; this new representation of the 3D images effectively reduces the number of elements to be processed, as the number of cuboids in a 3D image is much smaller than the number of voxels.

In the second test, we compare the time required to calculate the 3D Charlier discrete orthogonal moments using both the recursive and the proposed methods based on the 3D ICR with either the direct or matrix calculations. The process of calculating the 3D Charlier moments is performed for orders ranging from 0 to 90 for two 3D images (“Ant” and “Bird”) of size 128 × 128 × 128 (Fig. 4).

Figure 6 shows the time required to compute the Charlier moments using the three methods, viz. the recursive, direct, and matrix approaches, revealing that the two proposed methods are faster than the recursive one, with the matrix version being faster than the direct one. These results confirm the importance of the proposed method for calculating the 3D Charlier moments compared with the recursive method. Note that the time required for cuboid extraction from each 3D image is approximately 0.1 ms, being much shorter than the time required to calculate the 3D Charlier moments by the recursive method.

Fig. 6
figure 6

Time required to compute the 3D Charlier moments for the 3D images “Ant” (a) and “Bird” (b) using the recursive method and the proposed direct and matrix methods

Full size image

In the third test, we compare the time required to reconstruct a 3D image using the 3D Charlier moments computed by the three methods presented above. The reconstruction process is performed using the 3D Charlier moments of order from 0 to 90 for the two previous 3D images (“Ant” and “Bird”) of size 128 × 128 × 128 (Fig. 4).

Figure 7 shows the reconstruction times for the two images using the 3D Charlier moments computed by the three methods, viz. recursive, direct, and matrix. The results in this figure confirm that the reconstruction time using the moments calculated by the two proposed methods is shorter compared with the recursive method, and that the proposed matrix method is faster than the direct version. These results confirm the importance of the two methods proposed for 3D image reconstruction.

Fig. 7
figure 7

Reconstruction time for 3D images “Ant” (a) and “Bird” (b) using the 3D Charlier moments obtained by the recursive method and the proposed direct and matrix methods

Full size image

In the fourth test, we test our proposed method but with other types of 3D discrete orthogonal moments, namely those of Tchebichef [35], Krawtchouk [12], and Hahn [4]. We compare the computation time for the 3D image “Bird” when using the Tchebichef, Krawtchouk, and Hahn moments with the reconstruction time for this image using the three methods presented above. The calculation and reconstruction processes were performed using moments of order from 0 to 90. To compare the three computational methods, the execution time improvement ratio (ETIR) is used as a criterion [27], defined as \( {\text{ETIR = (1}} - {\text{Time1/Time2)}} \times {1}00 \), where Time1 and Time2 are the execution times of the recursive and the proposed methods. ETIR = 0 if both execution times are identical.

Tables 1 and 2 present the average computation time for the 3D moments of Tchebichef, Krawtchouk, Hahn, and Charlier of order from 0 to 90 for the 3D “Bird” image using the three methods presented above. Note that ETIR1 [11] is calculated between the direct method and the recursive method, while ETIR2 [11] is computed between the matrix method and the recursive method.

Table 1 Average calculation time for the 3D moments using the three methods and the reduction percentage for the 3D image “Bird”
Full size table
Table 2 Average 3D image reconstruction time using 3D moments obtained by the three methods and the reduction percentage for the 3D image “Bird”
Full size table

The simulation results in Tables 1 and 2 show that the computation time for the moments and the reconstruction of the two images by the two methods (direct and matrix) is much shorter than when using the moments obtained by the recursive method. This confirms the speed and robustness of the two proposed methods for the calculation of the 3D moments and the reconstruction of 3D images, compared with the recursive method. The computational time required for the 3D moments of Tchebichef, Krawtchouk, Hahn, and Charlier is considerably shortened, where the acceleration reaches 99 %.

Note that the results in Figs. 6 and 7 and Tables 1 and 2 were obtained for the case a1 = 80 for the Charlier polynomials, for the case p = 0.5 for the Krawtchouk polynomials, and for the case \( a = 10{\text{ and }}b = 1 0 \) for the Hahn polynomials.

6.2 3D Image Reconstruction by Global and Local Methods Using 3D Charlier Moments

In this section, we discuss the capacity of 3D Charlier moments for 3D image reconstruction using the proposed local and global methods presented in Sect. 5, applying objective criteria commonly used in literature to measure the quality of reconstructed 3D images. To evaluate the performance of the two methods, we calculate the mean squared error (MSE) between the original and reconstructed image, a criterion that is widely used in the field of image analysis as a quantitative measure of reconstruction accuracy.

The mean squared error for a 3D image of size N × M × K is defined as

$$ \text{MSE} = \frac{1}{N \times M \times K}\sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\sum\limits_{z = 0}^{K - 1} {\left( {f(x,y,z) - \mathop f\limits^{ \wedge } (x,y,z)} \right)^{2} } } \,\,}, $$
(27)

where \( \mathop f\limits^{ \wedge } (x,y,z) \) is the reconstructed version of the 3D original image function f(x, y, z) for each voxel (x, y, z).

In Ref. [18], the peak signal-to-noise ratio is defined in decibels (dB) as

$$ \text{PSNR} = 10\log_{10} \left( {\frac{{k^{2} }}{\text{MSE}}} \right), $$
(28)

where k is the maximum value in each voxel of the 3D original image.

To illustrate the performance of the proposed local method, we tested our algorithm on two 3D images of size 128 × 128 × 128 voxels, viz. “Crab” and “Image 1” shown in Figs. 4 and 5, respectively. The reconstruction test was performed using the two methods on the different 3D images: the proposed local method and the global one using the 3D Charlier discrete orthogonal moments of order from 0 to 90.

Figures 8 and 9 show the mean squared error (MSE) and the peak signal-to-noise ratio obtained for the 3D image “Crab” using both methods. Note that the mean squared error (MSE) decreases as the number of orders of Charlier 3D moments is increased, approaching zero.

Fig. 8
figure 8

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) obtained using 3D Charlier moments for the 3D image “Crab” with the global and proposed local methods

Full size image
Fig. 9
figure 9

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) obtained using 3D Charlier moments for the 3D image “Image of MRI” with the global and proposed local methods

Full size image

When the maximum order of the moments reaches a certain value, the reconstructed image becomes very similar to the original image. The PSNR ratio increases with increase of the Charlier moment order, until reaching a stable value where the reconstructed image becomes closest to the original image.

Moreover, this figure also shows that the proposed local method is efficient in terms of the quality of the 3D image reconstruction in comparison with the global method, illustrating the power of this method for different 3D images.

In the second test, we test the 3D image reconstruction capability of the proposed method using other types of 3D discrete orthogonal moments, viz. those of Tchebichef, Krawtchouk, and Hahn. The reconstruction test is performed on the same 3D image (“Crab”) using the three sets of moments obtained using the proposed local methods and the global one.

The simulation results in Figs. 10, 11, and 12 further demonstrate the effectiveness of the proposed method for 3D image reconstruction using the different types of 3D discrete orthogonal moments. Having shown the robustness of the local method for 3D image reconstruction, these results confirm its image reconstruction capability when using the moments of Tchebichef, Krawtchouk, Hahn, and Charlier.

Fig. 10
figure 10

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) when using 3D Tchebichef moments for the 3D image “Crab” with the global and proposed local methods

Full size image
Fig. 11
figure 11

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) when using 3D Krawtchouk moments for the 3D image “Crab” with the global and proposed local methods

Full size image
Fig. 12
figure 12

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) when using 3D Hahn moments for the 3D image “Crab” with the global and proposed local methods

Full size image

The simulation results in Fig. 13 confirm the capacity of these moments for reconstruction of 3D images with a slight advantage for Charlier and Krawtchouk moments compared with those of Tchebichef or Hahn.

Fig. 13
figure 13

a Mean squared error (MSE) and b peak signal-to-noise ratio (PSNR) when using 3D moments of Tchebichef, Krawtchouk, Hahn, and Charlier for the 3D image “Crab” with the proposed local method

Full size image

Finally, Figs. 14, 15, 16, and 17 show the original 3D images “Airplane” and “Table,” chosen from the McGill database [16], with size of 128 × 128 × 128 voxels and the original 3D MRI images “Image 2” and “Image 3,” reconstructed from the 3D Charlier moments using the two methods, viz. the proposed local and global method, at orders 10, 20, 30, 50, and 80.

Fig. 14
figure 14

Columns 1 to 5 show reconstructed 3D “Airplane” images up to order 10, 20, 30, 50, and 80, respectively

Full size image
Fig. 15
figure 15

Columns 1 to 5 show reconstructed 3D “Table” images up to order 10, 20, 30, 50, and 80, respectively

Full size image
Fig. 16
figure 16

Columns 1 to 5 show reconstructed 3D “Image 2” images up to order 10, 20, 30, 50, and 80, respectively

Full size image
Fig. 17
figure 17

Columns 1 to 5 show reconstructed 3D “Image 3” images up to order 10, 20, 30, 50, and 80, respectively

Full size image

With increasing order of the moments, the quality of the reconstruction increases, and the proposed local method presents better reconstruction quality than the global method for the different 3D images, confirming its effectiveness.

7 Conclusions

A fast and efficient method to calculate the 3D Charlier discrete orthogonal moments for a 3D image is proposed based on a new representation of the 3D image and a matrix computation of the 3D Charlier discrete orthogonal moments from cuboids of the 3D image. The method has been applied for local reconstruction of 3D images from Charlier moments extracted from the cuboids of the 3D image. The simulation results confirm the speed and quality of the 3D image reconstruction using the proposed method. In the future, we plan to apply this method for classification of 3D images using invariant Charlier moments.