1 Introduction

A multibody system is mainly considered as the combination of two parts, bodies and joints, which restrict the relative motion between the components of the system. Due to clearances at the joints, collision phenomena can frequently take place [1–4] and must be considered for an accurate analysis of the dynamic behavior of a multibody mechanical system since it has a significant influence on the response of the system [5–7]. Thus, a lot of researches [8–12] for impact have been carried out over the last few decades.

The contact force model plays a key role in the dynamic analysis of contact-impact events in multibody mechanical systems, which is obtained based on the neglect of external forces reflected in the multibody system by supporting force, torque, inertial force, etc. These external forces can affect the collisions that occur in a multibody system and cannot be ignored when this influence is large enough. In addition, the impact pair can eventually enter the stable contact state when the collision takes place; however, there is a lack of judgment for this case. Therefore, it is necessary to carry out the investigation on the contact force model considering external forces and the collision end state for the accurate analysis of multibody dynamics.

As a crucial property of the contact force model, the damping characterized by the dissipative energy from the system is classified as external or internal sources. Generally, the external source in a mechanical system mainly includes friction forces between sliding surfaces in contact, whereas the internal damping is treated as the dissipative energy mechanism of the contact material itself [13]. For the joint interfaces with roughness, the damping is mainly caused by the external source under normal dynamic load [14, 15], and it usually affected by the excitation frequency, contact pressure, friction, etc. [14, 16]. Meanwhile, Rayleigh damping, which is a linear combination of the mass and stiffness damping, is applied frequently in the finite element analysis of this joint [13, 16]. However, the friction is usually ignored during the contact-impact process between smooth surfaces, and the internal damping is utilized to describe the dissipative energy during collision. This contact-impact process has been analyzed by a collision tests between steel ball and cylindrical specimen [17, 18], and the law of the energy loss is also validated for low-speed impact.

Focusing on the frictionless contact and low-speed collision in this paper, the internal damping is used to model the contact force for the contact-impact analysis in multibody dynamics. This contact force model is based on the hypothesis of local deformation and can be expressed as a continuous function of the relative deformation and the deformation velocity between the contact surfaces of two bodies during collision. Several different continuous contact force models have been published in the literature. A simple one is the Kelvin–Voigt model, and Khulief and Shabana [19] applied it to the impact analysis in multibody system; then more researches are carried out [20–23] based on this model. However, the Kelvin–Voigt model is not very accurate since it does not consider the overall nonlinear nature of contact, and it also cannot represent the energy transfer process during the impact process. Instead, Hunt and Crossley [24] proposed a nonlinear contact force model written in the terms of Hertz contact force and damping force. Due to the derivation method of the hysteresis damping factor, the Hunt and Crossley model and several other similar models, such as the Lee and Wang model [25], the Lankarani and Nikravesh model [26], etc., are only suitable for hard materials. Thus the models for both soft and hard materials are proposed, for instance, the Gonthier et al. model [27], the Zhang and Sharf model [28], the Gharib and Hurmuzlu model [29], the Flores et al. model [3], the Shiwu Hu and Xinglin Guo model [4], etc. As simple methods applicable to solve the impact force, these nonlinear models are widely applied to engineering problems.

In general, the impact force is considered far greater than other forces, so that external forces are often ignored in impact dynamic analysis; hence the important parameter of contact force model, namely hysteresis damping factor, is derived in the light of the momentum theorem and the momentum conservation theorem. In fact, the equations of motion of a multibody mechanical system include the balance equations between contact force and external forces (such as torque, supporting force, inertial force, etc.) [30–38]. In other words, the impact contact force is affected by external forces during simulation. When this influence is large enough, the errors of the dynamic response of collision system obtained by these continuous model are obvious. Moreover, the repeated or sustained collision phenomenon can frequently take place in multibody system, which can be concluded from the dynamic analysis in [30, 33–35, 37, 38], so the accumulation of these errors can lead to the distortion simulation in multibody dynamics.

The purpose of this paper is to develop the contact force model of impact system where external forces cannot be ignored. This study begins with a description of the collision dynamic response under the influence of constant external forces, and then proposes an influence factor of external forces and the judgment criterion of impact end state for the following derivation and analysis. In fact, an important boundary condition, the separation velocity, which is used to deduce the hysteresis damping factor, cannot be derived due to the influence of external forces, and therefore a numerical approach is utilized to obtain the parametric surface of this factor. Based on this, a contact force model under constant external forces is established by the methodology shown in [3, 4] and the fitting method. Furthermore, the advantages and limitations of this model are analyzed with a simulation of a special bouncing ball problem.

2 Description of the impact under constant external forces

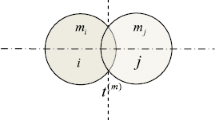
A direct central impact model under constant external forces \(F_{i}\) and \(F_{j}\) in the direction of normal contact force is considered for the impact analysis between two smooth (frictionless) spheres, as shown in Fig. 1, where the masses of two spheres are \(m_{i}\) and \(m_{j}\), respectively. The equivalent external force of these external forces can be evaluated by

$$ F_{e} = m_{e} a, $$
(1)

where \(m_{e} = m_{i} m_{j} /( m_{i} + m_{j} )\) is the equivalent mass of these two spheres, and \(a = F_{i} / m_{i} - F_{j} / m_{j}\) denotes the relative acceleration under these constant external forces. As Fig. 1 shows, three effects of external forces may occur, including \(a > 0\), \(a = 0\), and \(a < 0\), which indicate strengthening impact, no influence, and weakening collision, respectively. In this paper, the case of \(a \geq 0\) is analyzed, and the other situation can be discussed by the same method presented in this study.

Fig. 1
figure 1

Impact process between two solid spheres under constant external forces

Full size image

Under the condition \(a > 0\), the collision process between these bodies can be separated as two phases, namely the compression and restitution phases. When these two bodies come in contact with initial velocities \(\dot{v}_{i}^{(-)}\) and \(\dot{v}_{j}^{(+)}\), deformation takes place in the local contact area, and this denotes the start of the first phase. From this time, the contact force between these colliding bodies begins to increase but is smaller than the equivalent external force \(F _{e}\), so that the relative acceleration is greater than zero, and the deformation velocity continues to accelerate until to \(t_{a}\), as shown in Fig. 2. At this moment, the contact force is equal to the equivalent external force, and the deformation acceleration is reduced to zero, whereas the deformation velocity and the deformation are increased to \(\dot{\delta}_{\max}\) and \(\delta_{a}\), respectively. After the instant of time \(t_{a}\), the deformation continues to increase due to the conversion of relative kinetic energy to elastic strain energy. Therefore, the deformation acceleration begins to be negative and decreases continuously, whereas the deformation velocity keeps decreasing until to the final instant of compression phase \(t_{m}\), and the deformation is increased to the maximum value \(\delta_{m}\). At this time, the deformation acceleration and the deformation velocity are reduced to \(\ddot{\delta}_{\mathrm{min}}\) and zero, respectively. In turn, the inverse process, known as the restitution phase, starts and lasts to the end of impact. Moreover, the collision pair may not be separated at the end of impact due to the effect of external forces, and this is discussed in Sect. 3.

Fig. 2
figure 2

Dynamic response of a collision under constant external forces

Full size image

3 Influence assessment of constant external forces on collision

As analyzed before, the external forces have effect on the dynamic response of collision; however, there is a lack of quantitative indicator to measure the role of external force. In this section, an influence factor is proposed to further discuss this influence based on the Hertz contact law. Moreover, the termination of collision, which is usually judged to occur when these two bodies separate, is analyzed according to the energy loss during impact. Then, a judgment criterion is also proposed for this end state. It should be noted that the influence factor and the judgment criterion are important and fundamental conditions for the numerical computation of hysteresis damping factor, the derivation of contact force model, and the comparative analysis of different contact force model in this paper.

3.1 Influence factor of external forces

The classical force model for the contact between two spheres is the Hertz contact force

$$ F_{n} = k \delta^{\frac{3}{2}}, $$
(2)

where \(\delta\) indicates the local deformation, and \(k\) denotes the contact stiffness.

When two bodies are in contact, the contact force \(F_{n}\) starts to change the state of motion, so that the force balance of these bodies can be expressed as

$$ m_{i} \frac{d v_{i}}{dt} = F_{i} - F_{n},\qquad m_{j} \frac{d v_{j}}{dt} = F_{j} + F_{n}, $$
(3)

and the relative velocity between bodies is

$$ \dot{\delta} = v_{i} - v_{j}. $$
(4)

From (2), (3), and (4), the dynamic equivalent equation of the impact system shown in Fig. 1 can be written in the form

$$ m_{e} \frac{d^{2} \delta}{d t^{2}} + k \delta^{\frac{3}{2}} = m_{e} a. $$
(5)

Multiplying both sides of (5) by \(d\delta\) [39] results in

$$ \frac{1}{2} m_{e} d \biggl[ \biggl( \frac{d\delta}{d t} \biggr)^{2} \biggr] + k \delta^{\frac{3}{2}} d\delta = m_{e} ad\delta. $$
(6)

Then integrating three terms of (6), we derive the energy balance during collision process as

$$ \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( - )} \bigr)^{2} + m_{e} a \delta= \frac{2}{5} k \delta^{\frac{5}{2}} + \frac{1}{2} m_{e} \dot{ \delta}^{2}, $$
(7)

where \(\dot{\delta}^{ ( - )} = \dot{v}_{i}^{(-)} - \dot{v}_{j}^{(-)}\) denotes the initial relative velocity, and \(\dot{\delta}\) represents the deformation velocity.

Equation (7) represents that the deformation is the absorbed energy by the contact force from the initial relative kinetic energy and the work done by the equivalent external force in the compression phase, and it reaches the maximum value \(\delta_{m}\) when the deformation velocity is reduced to zero. Thus, substituting \(\dot{\delta} =0\) into (7) yields the relation between the initial relative kinetic energy and the maximum elastic strain energy as follows:

$$ \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( - )} \bigr)^{2} = \frac{2}{5} k \delta_{m}^{\frac{5}{2}} - m_{e} a \delta_{m}. $$
(8)

Both sides of (7) are divided by the initial relative kinetic energy shown in (8); then the relationship between the deformation velocity and the deformation is deduced as follows:

$$ \dot{\delta} = \dot{\delta}^{ ( - )} \sqrt{1 - \frac{\frac{2}{5} k \delta^{\frac{5}{2}} - m_{e} a\delta}{\frac{2}{5} k \delta_{m}^{\frac{5}{2}} - m_{e} a \delta_{m}}.} $$
(9)

Let \(\xi\) denote the influence factor of the equivalent external force given by

$$ \xi= \frac{m_{e} a \delta_{m}}{\frac{1}{2} m_{e} ( \dot{\delta}^{ ( - )} )^{2} + m_{e} a \delta_{m}} = \frac{1}{\frac{1}{2} m_{e} ( \dot{\delta}^{ ( - )} )^{2} / ( m_{e} a \delta_{m} ) +1}, $$
(10)

where the value range of this factor \(\xi\) is taken as \(0\leq \xi<1\) according to the condition \(a \geq\) 0 shown in Sect. 2.

Substituting (10) into (8) and (9), respectively, results in

$$\begin{aligned} \frac{2}{5} k \delta_{m}^{\frac{5}{2}} =& \frac{1}{2 ( 1 - \xi )} m_{e} \bigl( \dot{\delta}^{ ( - )} \bigr)^{2}, \end{aligned}$$
(11)
$$\begin{aligned} \dot{\delta} =& \dot{\delta}^{ ( - )} \sqrt{1- x^{\frac{5}{2}} + \frac{\xi}{1 - \xi} \bigl( x- x^{\frac{5}{2}} \bigr)}, \end{aligned}$$
(12)

where \(x\) is the ratio of \(\delta\) and \(\delta_{m}\), and its value range is \(0\leq x \leq1\).

Equation (11) shows that the maximum elastic strain energy increases as \(\xi\) increases when the initial relative velocity, contact stiffness, and equivalent mass are fixed. Meanwhile, (12) represents that the deformation velocity is also increased with the increase of the influence factor \(\xi\). It should be noted that this factor \(\xi\) is associated with the conditions of contact stiffness \(k\), equivalent mass \(m _{e}\), relative acceleration \(a\) under constant external forces, and initial relative velocity \(\dot{\delta}^{ ( - )}\), which can be drawn from (8) and (10). In other words, this factor \(\xi\) can reflect the comprehensive assessment of the influence of external forces on collision. Hence, the influence factor \(\xi\) is used to estimate the influence of constant external forces on the impact dynamic response.

3.2 Impact end state

The Hertz contact force model does not include the damping effect, and scholars have extended its application to include energy dissipation. A classical dissipative contact force model proposed by Hunt and Crossley is

$$ F_{n} = k \delta^{\frac{3}{2}} + \mu \delta^{\frac{3}{2}} \dot{\delta}, $$
(13)

where \(\mu\) is called the hysteresis damping factor, and the second term on the right side denotes the damping force.

Considering the work done by damping force, the balance of energy shown in (8) can be rewritten as

$$ \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( - )} \bigr)^{2} + m_{e} a \delta_{m} = \frac{2}{5} k \delta_{m}^{\frac{5}{2}} + \int_{0}^{\delta_{m}} \mu \delta^{\frac{3}{2}} \dot{\delta}\, d \delta, $$
(14)

where the integral term represents the work done by damping force.

For the case of separation state right after impact, the energy balance during restitution phase can be given by

$$ \frac{2}{5} k \delta_{m}^{\frac{5}{2}} = \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( + )} \bigr)^{2} + m_{e} a \delta_{m} + \int_{0}^{\delta_{m}} \mu \delta^{\frac{3}{2}} \vert \dot{ \delta} \vert \, d\delta, $$
(15)

where \(\dot{\delta}^{ ( + )} = \dot{v}_{i}^{(+)} - \dot{v}_{j}^{(+)}\) is the separation velocity at the end of impact. This expression indicates that the maximum elastic strain energy has three different destinations in restitution phase, which are in turn the final relative kinetic energy, the work done by the equivalent external force, and the work done by the damping force.

Usually, the work done by the damping force during the impact process is considered as the energy dissipation of collision; hence, subtracting (14) from (15) yields

$$ \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( + )} \bigr)^{2} = \frac{1}{2} m_{e} \bigl( \dot{ \delta}^{ ( - )} \bigr)^{2} - \Delta E, $$
(16)

where \(\Delta E\) denotes the dissipated energy.

To obtain the separation velocity \(\dot{\delta}^{ ( + )}\), the Newton model of restitution coefficient is frequently used [3, 4, 24–29]. However, the momentum is not conserved when the impact event considers the action of external forces, and thus the Newton model is not suitable for the impact issue discussed in this paper. In fact, it is indicated in the literature [40] that in addition to the energy model, which is called Stronge’s model, the Newton model and Poisson models cannot obey the law of energy conservation when the energy is lost during impact from sources other than friction. Therefore, this study employs the energy model to analyze the separation velocity or the final relative kinetic energy.

The Stronge model is defined as the square root of the ratio \(\varepsilon\) of the elastic strain energy released during restitution to the energy absorbed by deformation in compression [40]. In terms of the work done by the normal force during the two phases, the restitution coefficient is

$$ \varepsilon^{2} =- \frac{W_{r}}{W_{c}}, $$
(17)

where \(W_{c}\) and \(W_{r}\) represent the works done by the contact force during the compression and restitution phases, respectively. With the aid of (13), the work done by the contact force can be expressed as

$$\begin{aligned} W_{c} =& \int_{0}^{\delta_{m}} F_{n}\, d\delta = \frac{2}{5} k_{m} \delta_{m}^{\frac{5}{2}} + \int_{0}^{\delta_{m}} \mu \delta^{\frac{3}{2}} \dot{\delta}\, d \delta, \end{aligned}$$
(18)
$$\begin{aligned} W_{r} =& \int_{\delta_{m}}^{\delta_{o}} F_{n} \,d\delta =- \biggl( \frac{2}{5} k_{m} \delta_{m}^{\frac{5}{2}} - \frac{2}{5} k_{m} \delta_{o}^{\frac{5}{2}} \biggr) - \int_{\delta_{m}}^{\delta_{o}} \mu \delta^{\frac{3}{2}} \vert \dot{ \delta} \vert \, d\delta, \end{aligned}$$
(19)

where \(\delta_{o}\) denotes the deformation at the end of impact.

According to (17) and (18), the energy loss can be given by

$$ \Delta E = \bigl( 1- \varepsilon^{2} \bigr) W_{c} = \bigl( 1- \varepsilon^{2} \bigr) \biggl( \frac{2}{5} k_{m} \delta^{\frac{5}{2}} + \int_{0}^{\delta_{m}} \mu \delta^{\frac{3}{2}} \dot{\delta}\, d \delta \biggr), $$
(20)

and then, substituting (14) into (20) yields the relation

$$ \Delta E = \bigl( 1- \varepsilon^{2} \bigr) \biggl[ \frac{1}{2} m_{e} \bigl( \dot{\delta}^{ ( - )} \bigr)^{2} + m_{e} a \delta_{m} \biggr]. $$
(21)

The final relative kinetic energy and the initial relative kinetic energy are denoted as \(E_{r}^{+}\) and \(E_{r}^{-}\), respectively, so (16) can be rewritten in the simple form

$$ E_{r}^{+} = E_{r}^{-} - \Delta E. $$
(22)

It should be highlighted that the energy loss shown in (21) is affected not only by the initial relative velocity, but also by the equivalent external force. Hence the relative kinetic energy \(E_{r}^{+}\) is larger than zero when the initial relative kinetic energy \(E_{r}^{-}\) can satisfy the energy loss, which means that the collision pair enters the separation state at the end of impact. When \(E_{r}^{+}\) is equal to zero (\(E_{r}^{+}\) cannot be negative) and the impact pair still does not separate, the collision pair enters the nonseparation state. The judgment criterion of the impact end state can be described as follows:

(1) During the restitution phase, the separation state occurs when \(\delta=0\) and \(E_{r}^{+} >0\).

(2) During the restitution phase, the nonseparation state occurs when \(\delta>0\) and \(E_{r}^{+} =0\).

4 Numerical computation of hysteresis damping factor

The hysteresis damping factor \(\mu\) shown in (13) is the key for modeling contact force and can be written in a common form [4]:

$$ \mu= \alpha \frac{k}{\dot{\delta}^{ ( - )}}, $$
(23)

where \(\alpha\) is a factor associated with the coefficient of restitution when the external forces are ignored.

For this factor, which must be determined, two main approaches are often utilized in the literature, including the energy-based method [3, 4, 24, 26] and the regularized method [27, 28]. The Newton law of restitution, also known as the kinematical coefficient of restitution, is used in these two methods. Based on this coefficient, an important boundary condition, the separation velocity at the end of impact, can be calculated with the initial condition. However, as mentioned before, only the Stronge model of restitution coefficient is suitable for the impact analysis considering external forces. This means that the separation velocity is not related to the initial approach velocity by a constant under the influence of external forces, and the factor \(\alpha\) is hard to be derived directly with these two methods. Hence we propose a numerical method for \(\alpha\) and then obtain the parametric surface of \(\alpha\).

4.1 Numerical method

To obtain a parametric surface of the factor \(\alpha\) in the entire ranges of the restitution coefficient and the external forces influence factor, we carry out a continuous contact analysis based on the dynamic equivalent equation written in the form

$$ m_{e} \ddot{\delta} +\mu \delta^{\frac{3}{2}} \dot{\delta} +k \delta^{\frac{3}{2}} = m_{e} a. $$
(24)

As an example, the values of \(m_{e}\) and \(k\) are taken as 5 kg and \(5.4 \times 10^{9}~\mbox{N}/\mbox{m}^{1.5}\), respectively, and the initial approach velocity \(\dot{\delta}^{ ( - )}\) is equal to 1 m/s. For the value range of the influence factor, which is \(0\leq \xi \leq 0.99\), the corresponding value of \(a\) is taken as \(0\leq a \leq 23\,000\) m/s2. In addition, the initial factor \(\alpha\) is calculated by (25) [4], and the restitution coefficient value is \(0.01\leq \varepsilon \leq0.99\). Then, the numerical computation process is represented as shown in Fig. 3.

$$ \alpha_{\mathrm{initial}} = \frac{3 ( 1-\varepsilon )}{ 2\varepsilon}. $$
(25)
Fig. 3
figure 3

Computation process of factor \(\alpha\)

Full size image

4.2 Parametric surface of hysteresis damping factor

The results of the factor \(\alpha\) are shown in Fig. 4, where \(\varepsilon\) illustrates the coefficient of restitution, and \(\xi\) denotes the influence factor of external forces. It appears that \(\alpha\) is sensitive to the influence of external forces when \(0< \varepsilon<0.1\) and \(0< \xi<0.1\). Moreover, the smaller the restitution coefficient, the greater the factor \(\alpha\) when the influence factor \(\xi\) is fixed, as shown in Fig. 5, which is the curve of Sect. A in Fig. 4.

Fig. 4
figure 4

Parametric surface of \(\alpha\)

Full size image
Fig. 5
figure 5

Factor curve of \(\alpha\) when \(\xi=0.2\)

Full size image

Figure 5 also illustrates that the curve in region I is close to the result of (26), whereas the curve during region III is approximate to the value calculated by (25), and the region II could be the mixed result of them. Therefore the expression of factor \(\alpha\) considering external forces can be obtained by combining these two equations when \(\xi=0.2\), and this approach can be expanded to the entire domain of the influence factor \(\xi\):

$$ \mathrm{EXP} = \frac{1}{\beta} e^{- \frac{ ( \varepsilon+\tau )^{2}}{\sigma}}, $$
(26)

where \(\tau=0.01\), \(\sigma=0.011\), and \(\beta=0.113\) when \(\xi=0.2\).

5 Normal contact force

The numerical computation of the factor \(\alpha\) would take a long time for collision, which is not conducive to the simulation of multibody system, and thus an approximate function for contact force is derived in this section. According to the energy-based method adopted for (25) and the parametric surface, the expression of the factor \(\alpha\) in region III is first derived. Then, based on EXP shown in (26), the expression for region I is fitted with the parametric surface. Finally, the approximate contact force model is given by the weighted combination of these two expressions.

From (17)–(19) it is possible to obtain the following formulas:

$$\begin{aligned} \varepsilon^{2} \Delta E_{c} + \Delta E_{r} =& \bigl( 1- \varepsilon^{2} - \lambda^{\frac{5}{2}} \bigr) \frac{2}{5} k \delta_{m}^{\frac{5}{2}}, \end{aligned}$$
(27)
$$\begin{aligned} \Delta E_{c} =&\mu \int_{0}^{\delta_{m}} \delta^{\frac{3}{2}} \dot{\delta} \,d \delta, \end{aligned}$$
(28)
$$\begin{aligned} \Delta E_{r} =& \mu \int_{\lambda \delta_{m}}^{\delta_{m}} \delta^{\frac{3}{2}} \vert \dot{ \delta} \vert \, d\delta, \end{aligned}$$
(29)

where \(\lambda\) is the ratio of \(\delta_{o}\) and \(\delta_{m}\). Substituting (12) into (28), the expression of \(\Delta E_{c}\) is rewritten as

$$ \Delta E_{c} =\mu \delta_{m}^{\frac{5}{2}} \dot{ \delta}^{ ( - )} s_{1}, $$
(30)

where

$$ s_{1} = \int_{0}^{1} f(x,\xi)\,dx = \int_{0}^{1} x^{\frac{3}{2}} \sqrt{1- x^{\frac{5}{2}} + \frac{\xi}{1 - \xi} \bigl( x- x^{\frac{5}{2}} \bigr)} \,dx, $$
(31)

\(f(x,\xi)\) is the destiny function of \(s_{1}\), and the value range of the influence factor is \(0\leq \xi<1\).

Based on the numerical approach, the value of \(s_{1}\) can be evaluated by the following relation, and the compared result between (31) and (32) is plotted in Fig. 6:

$$ s_{21} =0.851 \sqrt{0.5 s_{2}}, $$
(32)

where

$$ s_{2} = \int_{0}^{1} x^{\frac{3}{2}} \biggl[ 1- x^{\frac{5}{2}} + \frac{\xi}{1 - \xi} \bigl( x- x^{\frac{5}{2}} \bigr) \biggr]\, dx. $$
(33)
Fig. 6
figure 6

Relation of \(\xi\) and \(s\)

Full size image

Integrating (33) and then substituting it into (32) yield

$$ s_{21} = 0.851 \sqrt{\frac{7-4 \xi}{70 ( 1 - \xi )}}. $$
(34)

In fact, \(s_{1}\) calculated by (31) has an error due to the neglect of damping force influence, as shown in Fig. 7, where \(s_{a}\) denotes the similar value considering damping force. Moreover, this error would be obvious when the restitution coefficient is low, which is also shown in the literature [3, 4]. To reduce this error, the expression of \(s_{1}\) is rewritten as

$$ s_{1} = 0.851 \eta_{c} \sqrt{\frac{7-4 \xi}{70 ( 1 - \xi )}}, $$
(35)

where the coefficient \(\eta_{c}\) is related to the restitution coefficient and the influence factor. Hence, the energy loss during the compression phase can be given by

$$ \Delta E_{c} =0.851\mu \delta_{m}^{\frac{5}{2}} \dot{ \delta}^{ ( - )} \eta_{c} \sqrt{\frac{7-4 \xi}{70 ( 1 - \xi )}}. $$
(36)
Fig. 7
figure 7

Relation between \(x\) and \(f(x,\xi)\)

Full size image

Assuming that the energy loss during the compression and restitution phases performs a similar function, equation (29) is rewritten as

$$ \Delta E_{r} =0.851\mu \delta_{m}^{\frac{5}{2}} \dot{ \delta}^{ ( - )} \eta_{r} \sqrt{\frac{7-4 \xi}{70 ( 1 - \xi )}} \bigl( 1- \lambda^{\frac{5}{2}} \bigr). $$
(37)

Combining (23), (27), (36), and (37), the factor \(\alpha\) for region III can be evaluated by

$$ \alpha= \frac{0.47 ( 1- \varepsilon^{2} - \lambda^{\frac{5}{2}} )}{\sqrt{\frac{7-4 \xi}{70 ( 1 - \xi )}} [ \eta_{c} \varepsilon^{2} + \eta_{r} ( 1- \lambda^{\frac{5}{2}} ) ]}, $$
(38)

where the coefficients of \(\lambda\), \(\eta_{c}\), and \(\eta_{r}\) must be determined.

It can be observed from Fig. 5 that the value of EXP is close to zero in region III, whereas the result of multiplying (25) by the square of \(\varepsilon\) is also close to zero during region I, and hence, the expression of \(\alpha\) is assumed as

$$ \alpha= \frac{e^{- \frac{ ( \varepsilon+\tau )^{2}}{\sigma}} ( 1-\varepsilon )^{a}}{\beta} + \frac{0.47 ( 1- \varepsilon^{2} - \lambda^{\frac{5}{2}} ) \varepsilon^{b}}{ \sqrt{\frac{7-4\xi}{70 ( 1-\xi )}} [ \eta_{c} \varepsilon^{2} + \eta_{r} ( 1- \lambda^{\frac{5}{2}} ) ]}, $$
(39)

where the coefficients of \(\tau\), \(\sigma\), \(\beta\), \(a\), \(\lambda\), \(b\), \(\eta_{c}\), and \(\eta_{r}\) can be obtained by fitting the parametric surface of \(\alpha\). The fitting results are shown in Fig. 8, and the factor \(\alpha\) is finally expressed as

$$ \alpha= \left \{ \textstyle\begin{array}{l} \frac{e^{- \frac{ ( \varepsilon+1- \xi^{0.05} )^{2}}{0.1568 \xi^{0.9}}} ( 1-\varepsilon )^{\varepsilon^{0.4}}}{S \xi^{ ( 1.2 \xi^{2} +0.0165 \xi^{-1.17} +2.02 )}} + \frac{0.47 ( 1- \varepsilon^{2} - \lambda^{\frac{5}{2}} )}{S \varepsilon^{ ( \varepsilon^{\xi^{1.3}} +0.1\xi-0.97 )} [ \varepsilon^{2} +\eta ( 1- \lambda^{\frac{5}{2}} ) ]}, \quad 0< \xi< 1,\\ \frac{3 ( 1-\varepsilon )}{2 \varepsilon^{0.89}}, \quad \xi=0, \end{array}\displaystyle \right . $$
(40)

with

$$\left \{ \textstyle\begin{array}{l} S = \sqrt{\frac{7-4\xi}{70 ( 1-\xi )}},\\ \eta= \varepsilon^{0.86+2.6\xi+ \xi^{3.5} -1.5\varepsilon\xi},\\ \lambda = 1- ( \frac{\varepsilon}{\xi^{0.59}} )^{1+ \xi^{0.3} [ 1-\varepsilon ( 1-\xi ) ]}, \end{array}\displaystyle \right . $$

where \(\xi\) is obtained by solving (8) and (10), whereas the value of \(\lambda\) is taken as zero when the expression of \(\lambda\) is less than zero. Finally, the normal contact force considering external forces is expressed as

$$ F_{n} =k \delta^{\frac{3}{2}} \biggl( 1+\alpha \frac{\dot{\delta}}{ \dot{\delta}^{ ( - )}} \biggr). $$
(41)
Fig. 8
figure 8

Fitting results of \(\alpha\)

Full size image

The fitting curves shown in Fig. 8 also have errors, and its accuracy can be measured by the difference between the prerestitution coefficient represented in (40) and the postrestitution coefficient obtained by (17) with a continuous contact analysis. This measurement approach presented by Lankarani and Nikravesh [25] is also utilized in this paper, and the plots of the post and prerestitution coefficient for five models are obtained. According to the analysis of these plots in the full range of \(\xi\), this paper sets three levels of the influence of constant external forces, including the small (\(0\leq \xi<0.1\)), moderate (\(0.1\leq \xi <0.5\)), and large (\(0.5\leq \xi <0.1\)) effects. Meanwhile, these plots related to the three levels are shown in Fig. 9, in which the straight line represents the same value for post- and prerestitution coefficients, used as a reference. From the plots of Fig. 9(a, b) it can be drawn that the errors of the dissipated energy described by classical models are obvious during the range of low restitution coefficient. Conversely, the described model has a better performance for the entire range of restitution coefficient when \(\xi\) is small or equal to zero. Furthermore, these errors are great when the influence factor is large enough, as shown in Fig. 9(c–f). This indicates that the external forces should be considered carefully for the dynamic analysis of the impact between softer material bodies. Meanwhile, it can also be observed from (25) that \(\alpha\) is just related to the coefficient of restitution; in other words, the classical contact force models have fixed hysteresis damping factors when \(\dot{\delta}^{ ( - )}\) and \(\varepsilon\) are constant while \(\xi\) is variable. These fixed factors lead to an incorrect description of energy dissipation even if the restitution coefficient closes to unity, as shown in Figs. 9(e, f), and the incorrect description may cause wrong impact end state.

Fig. 9
figure 9

Relation between the postrestitution and prerestitution coefficients: (a) \(\xi=0\); (b) \(\xi=0.016\); (c) \(\xi=0.227\); (d) \(\xi=0.429\); (e) \(\xi=0.665\); (f) \(\xi=0.91\)

Full size image

6 Application to a bouncing ball

Since collisions are often affected by external forces, we use a special bouncing ball as an example for application in this paper and then analyze the specific influence of the constant external forces on the contact-impact response, namely deformation, deformation velocity, energy loss, and impact end state. As Fig. 10 shows, an elastic ball is acted by a constant force \(F\), and the gravity hits the ground perpendicularly at an initial velocity \(\dot{\delta}_{0}^{ ( - )}\) of 0.5 m/s. The mass \(m\) of the ball is 0.5 kg, whereas the radius \(R\) and the equivalent stiffness \(k\) are equal to 0.08 m and \(1.4 \times 10 ^{8}~\mbox{N}/\mbox{m}^{1.5}\), respectively. When the ball collides with the ground, which is considered to be rigid and stationary, the impact occurs, and the ball rebounds, and then it jumps to a height. After that, the ball falls down until it collides with the ground again. Finally, the ball rests on the ground after repeated collisions, jumps, and drops.

Fig. 10
figure 10

Special bouncing ball example

Full size image

During the collision process, the response of the ball is obtained by the equivalent dynamic equation of impact system, in which the deformation \(\delta\) between the ball and ground is evaluated as

$$ \delta=R-y, $$
(42)

where \(R \) represents the ball radius, and \(y\) denotes the ball center of mass. Additionally, the ball motion between two adjacent collisions is solved by the Newtonian equations of motion.

To evaluate the influence of the collision affected by constant external forces on the ball motion, two cases of the ball motion are obtained under the same conditions of restitution coefficient (0.8) and constant external force (5.1 N), and the results are plotted in Fig. 11. The ball motion marked as “case A” is solved by the equivalent dynamic equation (24) and Newtonian equations of motion, whereas (43) and the same Newtonian equations are used for “case B”. In other words, the external forces consisting of the constant force \(F\) and gravity are taken into account for the computation of each collision in case A; however, the same computation does not consider the influence of external forces in case B. In addition, the straight line shown in Fig. 11(a) indicates the ball position where the collisions start or end.

$$ m_{e} \ddot{\delta} +\mu \delta^{\frac{3}{2}} \dot{\delta} +k \delta^{\frac{3}{2}} = 0. $$
(43)

It appears that the difference of the ball motion between cases A and B increases firstly and then decreases. This trend is also represented in Fig. 12(a), which illustrates the total energy of the ball, including kinetic energy, elastic potential energy, gravity potential energy, and the potential work done by constant force \(F\). One step reduction of the total energy means one collision, and \(\Delta E_{10i}\) and \(\Delta E_{0i}\) denote the energy loss of the \(i\)th collision in cases A and B, respectively. It can be drawn from Fig. 11(a) and Fig. 12(a) that 10 collisions occur in case A, whereas more collisions are needed for case B. In fact, these different responses are caused by the accumulative error in the dissipative energy of each collision between cases A and B, as shown in Fig. 12(b). It can be observed that the first collision energy loss calculated by (21) in case A is greater than in case B. Since the dissipative energy errors of the next two collisions are also larger than zero, the accumulation of this error reaches the maximum value right after the third collision. From the fourth collision, the initial approach velocity of each impacts in case B is significantly greater than the same velocity in case A, and thus the cumulative error of the energy loss is decreased constantly. Moreover, the more collisions required in case B are due to the consumption of the cumulative error during the first three impacts.

Fig. 11
figure 11

Kinematic results of a ball hits the ground: (a) Ball position; (b) Ball velocity

Full size image
Fig. 12
figure 12

Development of energy: (a) Total energy of the ball; (b) Accumulative error of energy loss per collision

Full size image

According to this analysis, the first collision has a large influence on the dynamic response of the ball, so a detailed analysis of this collision is carried out. In the case studies presented here, four different contact force models, including the Hunt and Crossley model, the Flores et al. model, the Shiwu Hu and Xinglin Guo model, and the model described in this paper, are utilized to obtain the impact response. Three values (0.1 N, 60 N, 495 N) of the constant external force \(F\), and four values (0.3, 0.5, 0.7, 0.9) of the restitution coefficient are also considered in the four different contact force models. It is worth noting that the influence factors of the three values of \(F\) are equal to 0.021, 0.233, and 0.799, respectively, which represent the small, moderate, and large effects of constant external forces.

Figures 13, 16, and 19, respectively, show the deformation–time curves, velocity–time curves, and hysteresis loop curves of the ball when the influence factor \(\xi\) is equal to 0.021. It appears that the results obtained by the Flores et al. model, the Shiwu Hu and Xinglin Guo model, and the model described in this paper are close to each other. Moreover, these results are also similar to the same outcomes shown in [4], where the external forces are not considered.

Fig. 13
figure 13

Relation of deformation and time in different models when \(\xi=0.021\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image

The same impact responses of the ball are plotted in Figs. 14, 17, and 20 when \(\xi=0.233\). By analyzing the curves in Fig. 14 it can be observed that the deformations at the end of collision obtained by all models except the Hunt and Crossley model are greater than zero when the restitution coefficient is equal to 0.3. This means that the ball enters nonseparation state at the end of collision. Meanwhile, only the postimpact deformation obtained by the described model in this paper exhibits the nonseparation state when \(\varepsilon=0.5\). It should be noted that the nonseparation state results in the zero separation velocity and incomplete hysteresis loop, as shown in Figs. 17 and 20. When the restitution coefficient is 0.7 or 0.9, the Flores et al. model and the Shiwu Hu and Xinglin Guo model exhibit similar responses compared to the case simulated with the model described in this paper.

Fig. 14
figure 14

Relation of deformation and time in different models when \(\xi=0.233\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image

Furthermore, the large influence of the constant external forces on the dynamic behavior of the collision between the ball and ground are illustrated in Figs. 15, 18, and 21. Under the condition of \(\xi=0.799\), most all the results obtained by the four models represent the nonseparation state. All the responses obtained by the Hunt and Crossley model, the Flores et al. model, and the Shiwu Hu and Xinglin Guo model have obvious errors compared to the described models, even if the coefficient of restitution is close to unity.

Fig. 15
figure 15

Relation of deformation and time in different models when \(\xi=0.799\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 16
figure 16

Relation of deformation velocity and time in different models when \(\xi=0.021\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 17
figure 17

Relation of deformation velocity and time in different models when \(\xi=0.233\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 18
figure 18

Relation of deformation velocity and time in different models when \(\xi=0.799\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 19
figure 19

Relation of contact force and deformation in different models when \(\xi=0.021\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 20
figure 20

Relation of contact force and deformation in different models when \(\xi=0.233\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image
Fig. 21
figure 21

Relation of contact force and deformation in different models when \(\xi =0.799\): (a) \(\varepsilon =0.3\); (b) \(\varepsilon =0.5\); (c) \(\varepsilon =0.7\); (d) \(\varepsilon =0.9\)

Full size image

In conclusion, the larger the value of influence factor or the smaller the restitution coefficient, the harder the ball separates from the ground. The influence of external forces on collision can be ignored when the influence factor is small (\(0\leq \xi <0.1\)) and the Flores et al. model, the Shiwu Hu and Xinglin Guo model, and the model described in this paper are suitable for soft and hard contacts. However, the external forces should be considered carefully for soft contact when the influence of external forces is moderate (\(0.1\leq \xi<0.5\)), and all the models shown in this paper except the Hunt and Crossley model present the approximate response when the restitution coefficient is high or moderate. When the influence factor is large (\(0.5\leq \xi<1\)), the collision analysis for both soft and hard contact needs to take the external forces into account carefully.

7 Conclusions

In this paper, the issue of contact force model considering constant external forces is analyzed for collision in multibody dynamics. As the basic problem, the collision evolution associated with fundamental contact mechanics was discussed. Furthermore, the influence of constant external forces on contact-impact event was also estimated, especially for the impact end state. Based on the energy model of restitution coefficient and the judgment criterion of impact end state defined in this paper, a numerical computation method for hysteresis damping factor was proposed due to the lack of an important boundary condition, and then a parametric surface related to the hysteresis damping factor was obtained. Combining the curve fitting method and the parametric surface, a contact force model was derived for analyzing the dynamic response of impact system under external forces. In addition, the advantages and limitations of the new model together with three classical models were analyzed by comparing the post- and prerestitution coefficient. Finally, a simple problem was utilized to analyze and compare four contact force models. The results indicate that the external forces and the energy loss are the main reasons for the multibody system to enter a steady contact state from repeated impact state. The larger influence of external forces or the smaller the restitution coefficient, the easier the occurrence of the nonseparation state. The influence of the constant external forces can be divided into the small, moderate, and large levels, which correspond to the values 0–0.1, 0.1–0.5 and 0.5–1 of \(\xi\), respectively. Except the small value of \(\xi\), the constant external forces should be considered carefully for collision. The described model is more suitable for impact analysis in multibody dynamics.