A dissipative contact force model for impact analysis in multibody dynamics

Abstract

In this work, a new dissipative contact force model, based on the foundation of Hertz contact law, is presented for impact analysis in multibody dynamics. A hysteresis damping force is introduced in the model for capturing the energy loss during the contact process. An approximate function, representing the relationship between the deformation velocity and deformation, is used to calculate the energy loss due to the damping force. The difference between the compression phase and restitution phase during the contact process is taken into account in the energy loss calculation. For illustration, four different contact force models are applied in a numerical example to compare their behaviors. The results are presented in the form of dynamic simulations in a multibody system, which allow comparison of the differences and similarities among the four contact models. They show the validity of our model for soft or hard contact problems.

1 Introduction

A multibody mechanical system mainly contains two parts, that is, bodies and joints, which restrict the relative motion of the various bodies of the system. Contact–impact events can frequently occur in mechanisms that have clearances at their joints, and the constraint equations of motion are based on them. The analysis of contact between two bodies can be extended to the analysis of impact in a multibody system. Therefore, the contact force model that can describe the contact–impact event is used to represent the interaction among the different bodies that comprise the multibody system.

The contact–impact phenomenon is important and must be considered for an accurate analysis of the dynamic behavior of a multibody mechanical system since it has negligible influences on the responses of the multibody system. However, the contact–impact problem is challenging and complex to model because it depends on several factors, such as the geometry of contacting surfaces, material properties, friction, and the contact law involving the interaction among different bodies that make up the multibody system. Over the last few decades, the contact problem has been studied by many researchers [1–4], and the interest on this topic is still arising [5–17].

In general, two main approaches are often used to model the contact–impact events in a multibody system, including the nonsmooth dynamics formulation and the regularized approach [13, 14]. The first approach is known as a rigid approach since it assumes that the impact effect occurs instantaneously [18]. In the nonsmooth dynamics approach, there are two ways to treat the contact–impact problem in a multibody system, namely the linear complementarity problem (LCP) [4, 19] and the differential variational inequality (DVI) [20, 21]. For the LCP, the unilateral constraints are used to compute the contact forces in the contact dynamics problem with the purpose of preventing penetration. For the DVI, simpler integrator schemes are employed to directly deal with nonsmooth phenomena [16, 20]. Although the nonsmooth approach is relatively efficient for the contact analysis in a multibody system, the unknown duration of the contact problem limits its application since the assumption of instantaneity for the impact effect is invalid if the duration of the contact is large enough [22].

In turn, the regularized approach, based on the contact force, can be expressed as a continuous function of the relative deformation between the compliant surfaces of the contact bodies, so it is often named as a compliant contact force function or model. This approach can be understood as if each contact region of the two contact bodies is covered with some spring–damper elements scattered over their surfaces. In contrast to the nonsmooth formulation, the regularized approach is referred to as the continuous analysis, which requires the evaluation of the contact force during the contact period. Over the last few decades, several different contact force models have been published in the literature to calculate the contact force [23, 24]. The simple model is the linear Kelvin–Voigt viscoelastic model [25]. However, the linear model is not very accurate since it does not consider the overall nonlinear nature during the impact process. A more suitable model is the nonlinear Hertz contact law [26]. The model is purely elastic in nature and does not account for the energy dissipation process associated with the damping of materials. Thus, a large number of studies, based on the Hertz theory, have been performed to accommodate the energy dissipation in the form of internal damping. The classical dissipative contact force models are the Hunt and Crossley model [27], the Lankarani and Nikravesh model [22], and the Flores et al. model [15]. Some other models of the dissipative contact force can be found in the previous studies by Herbert and McWhannell [28], Lee and Wang [29], Gonthier et al. [30], and Zhiying and Qishao [31]. In short, these models have inherently advantages and disadvantages for each particular application, which have been listed in the paper [24].

Two approaches make it possible to obtain the energy loss during the contact process. In the first approach, the energy loss is controlled by the coefficient of restitution. This parameter is, in general, assumed to be constant; however, it depends on several factors such as the geometry of the contacting surfaces, pre-impact velocity, local material properties, contact duration, temperature, and frictions [32, 33]. In the other approach, the energy loss is obtained from a damping force, which is a function of the deformation velocity. In the present work, based on the above method, different deformation velocity formulations are presented and discussed to calculate energy loss and also to account for the difference of the energy loss in the compression phase and the restitution phase during the contact process. Furthermore, a new dissipative contact force model is proposed, which is based on the analysis of the energy loss calculated separately by the two approaches. The differences and similarities in several dissipative contact force models are analyzed, and their limitations are also discussed.

This new dissipative contact force model is based on the Hertz elastic contact equations because one advantage of the Hertz contact law is that it considers the geometric and material characteristics of the contacting surfaces, which are of paramount importance in the contact dynamic responses. Meanwhile, the contact force model is only valid for low impact velocity, that is, impacts slowly enough so that no plastic deformation occurs and the damping force component is the prime factor for energy dissipation. For steel–steel system, Braccesi and Landi (2007) [34] have proposed a so-called yield velocity (below this velocity, no plastic deformation occurs), that is, 0.519 m/s. This yield velocity has been described by Vu-Quoc and Zhang (2002) [35].

In this work, we are interested in developing models involving contact events between soft materials. The soft materials are characterized by low or medium values of the coefficient of restitution in the case of biomechanical systems and bushing elements. The methodology adopted in this work follows closely that of [15], in which an explicit relation between the coefficient of restitution and a hysteresis damping factor is derived.

This paper is organized as follows. Section 2 presents the model of two solid spheres in contact. The energy loss calculated by two different approaches are separately presented in Sects. 3 and 5. The fundamental issues associated with the deformation velocity are discussed in Sect. 4. Then, the new dissipative contact force model and its application range are presented in Sect. 6. In Sect. 7, four dissipative contact force models are used in a numerical example to investigate their behaviors. Finally, Sect. 8 ends the paper with the concluding remarks.

2 Modeling of two solid spheres in contact

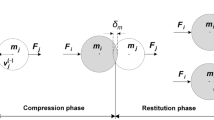
A direct central normal impact between two solid spheres is considered to analyze the general situation of the impact process between two bodies [15, 22]. When two solid spheres are in contact, a contact force occurs in the local contact zone due to the local deformation. In general, the contact process can be separated as two phases, namely, the compression phase and the restitution phase. The compression phase starts when the two spheres begin contact and ends when the deformation reaches the maximum value or the deformation velocity is zero. The restitution phase starts at the instant of the maximum deformation and lasts until the two spheres separate.

In Fig. 1, let the two solid spheres i and j have masses m _i and m _j , velocities $v_{i}^{ ( - )}$ and $v_{j}^{ ( - )}$ at the time t ⁽⁻⁾of the initial contact of the local contact surfaces, and velocities $v_{i}^{ ( + )}$ and $v_{j}^{ ( + )}$ at the time t ⁽⁺⁾of separation of the local contact surfaces. Also, t ^(m) denotes the time when the maximum deformation reaches with the velocity zero.

Fig. 1

Impact process between two solid spheres

With radii R _i and R _j of the two spheres, the Hertz contact law relates the contact force as [22]

$$ F_{N} = K\delta^{n}, $$

(1)

where δ is the local relative normal deformation between the contacting spheres, and the exponent n is equal to 3/2. The generalized parameter K depends on the material properties and the radii of the spheres, that is,

$$ K = \frac{4}{3\pi ( h_{i} + h_{j} )} \biggl[ \frac{R_{i}R_{j}}{R_{i} + R_{j}} \biggr]^{\frac{1}{2}}, $$

(2)

where the material parameters h _i and h _j are

$$ h_{l} = \frac{1 - \lambda_{l}^{2}}{\pi E_{l}}\quad (l = i,j ), $$

(3)

and the variables E _l and λ _l are, respectively, the Young modulus and Poisson ratio associated with each sphere.

3 The energy loss associated with the coefficient of restitution

In this section, the energy loss associated with the coefficient of restitution is determined. Let T ⁽⁻⁾ and T ⁽⁺⁾, respectively, denote the kinetic energies of the two spheres before and after impact.

Considering the law of the energy balance, the energy loss during the impact process can be expressed as [22]

$$ \Delta E = T^{ ( - )} - T^{ ( + )} = \frac{1}{2}m_{i} \bigl[ \bigl( v_{i}^{ ( - )} \bigr)^{2} - \bigl( v_{i}^{ ( + )} \bigr)^{2} \bigr] + \frac{1}{2}m_{j} \bigl[ \bigl( v_{j}^{ ( - )} \bigr)^{2} - \bigl( v_{j}^{ ( + )} \bigr)^{2} \bigr]. $$

(4)

The linear momentum balance between times t ⁽⁻⁾ and t ⁽⁺⁾ gives

$$ m_{i} \bigl( v_{i}^{ ( - )} - v_{i}^{ ( + )} \bigr) + m_{j} \bigl( v_{j}^{ ( - )} - v_{j}^{ ( + )} \bigr) = 0. $$

(5)

The coefficient of restitution, denoted e, is defined as the ratio between the relative velocity at separation and the relative velocity at initial contact of the two spheres:

$$ e = - \frac{v_{i}^{ ( + )} - v_{j}^{ ( + )}}{v_{i}^{ ( - )} - v_{j}^{ ( - )}}. $$

(6)

Substituting Eq. (6) into Eqs. (4), (5) and solving these equations, we obtain

$$ \Delta E = \frac{1}{2}\frac{m_{i}m_{j}}{m_{i} + m_{j}} \bigl( v_{i}^{ ( - )} - v_{j}^{ ( - )} \bigr)^{2} \bigl( 1 - e^{2} \bigr). $$

(7)

Equation (7) can be simplified as

$$ \Delta E = \frac{1}{2}m \bigl( \dot{\delta}^{ ( - )} \bigr)^{2} \bigl( 1 - e^{2} \bigr) $$

(8)

where m and $\dot{\delta}^{ ( - )}$ are the equivalent mass of the two spheres and the initial deformation velocity:

$$\begin{aligned} m =& \frac{m_{i}m_{j}}{m_{i} + m_{j}}, \end{aligned}$$

(9)

$$\begin{aligned} \dot{\delta}^{ ( - )} =& v_{i}^{ ( - )} - v_{j}^{ ( - )}. \end{aligned}$$

(10)

Thus, using the coefficient of restitution and the deformation velocity, Eq. (8) represents the energy loss during the impact process of the two solid spheres.

4 The relationship between the deformation velocity and deformation

An equivalent system of the contact process between the two solid spheres is considered to get the relationship between the deformation velocity and deformation. The two spheres are materialized by a single-degree-of-freedom dynamic system, as shown in Fig. 2. In this figure, D, t ⁽⁻⁾, and t ^(m), respectively, denote the damping coefficient, the time of the initial contact, and the time of the maximum deformation.

Fig. 2

Equivalent system to the contact process: (a) initial contact phase; (b) the maximum indentation phase

In this model, two phases, the compression phase and the restitution phase, are included during the impact process between the two spheres. During the compression phase, the indentation deformation δ increases from zero to the maximum compression deformation δ _m , and the initial indentation velocity $\dot{\delta}^{ ( - )}$ reduces to zero. The contact force consists of the spring force and damping force, which can be expressed as

$$ F_{N} = K\delta^{n} + D\dot{\delta}, $$

(11)

where the exponent n is usually set to 3/2 in the well-known Hertz contact law [26]. The damping coefficient D is proposed by Hunt and Crossley as [27]

$$ D = c\delta^{n}. $$

(12)

So, the contact force may be written as

$$ F_{N} = K\delta^{\frac{3}{2}} + c\delta^{\frac{3}{2}}\dot{\delta}. $$

(13)

The mathematical representation of the dynamic equivalent system can be expressed as

$$ m\ddot{\delta} + D\dot{\delta} + K\delta^{n} = 0 $$

(14)

or

$$ m\ddot{\delta} + c\delta^{\frac{3}{2}}\dot{\delta} + K\delta^{\frac{3}{2}} = 0, $$

(15)

in which m is the equivalent mass given by (9), c is called the “hysteresis damping factor,” and K represents the equivalent stiffness given by (2). This equation is a second-order nonlinear ordinary differential equation with variable coefficients. It is difficult to get an analytical solution of this dynamic equation, so the numerical solution may be obtained by using Matlab software.

In order to get an effective numerical value, we consider a steel sphere as the impact body and choose two groups of initial conditions to solve Eq. (15), that is,

• (1) R=0.01 m, E=2.07×10¹¹ N/m², λ=0.3, K=1.07×10¹⁰ N/m^1.5, m=0.033 kg, e=0.9, c=2.0×10⁹ Ns/m^2.5, $\dot{\delta}^{ ( - )} = 0.8~\mathrm{m}\mbox{/}\mathrm{s}$, δ(0)=0;

• (2) R=0.01 m, E=2.07×10¹¹ N/m², λ=0.3, K=1.07×10¹⁰ N/m^1.5, m=0.033 kg, e=0.9, c=2.0×10¹⁰ Ns/m^2.5, $\dot{\delta}^{ ( - )} = 0.1~\mathrm{m}\mbox{/}\mathrm{s}$, δ(0)=0.

Figure 3 shows the deformation velocity–time diagram and the deformation-time diagram in the whole impact process. It is apparently observed that the variation of the deformation velocity–time is not a straight line, and the variation of the deformation velocity with its corresponding deformation is quite clear by comparison.

Fig. 3

Variations of deformation velocity and deformation with time for different impact velocities: (a) $\dot{\delta}^{ ( - )} = 0.8~\mathrm{m}\mbox{/}\mathrm{s}$; (b) $\dot{\delta}^{ ( - )} = 0.1~\mathrm{m}\mbox{/}\mathrm{s}$

During the period of compression, the relationship between the deformation velocity and deformation has been considered. Lankarani and Nikravesh [22] assumed that the contact force is represented by the Hertz contact model F _N =Kδ ⁿ. Thus, the mathematical representation of the dynamic equivalent system can expressed as

$$ m\ddot{\delta} + K\delta^{n} = 0. $$

(16)

The relationship between the deformation velocity and the deformation can be obtained by (16), that is,

$$ \dot{\delta} = \dot{\delta}^{ ( - )}\sqrt{1 - \biggl( \frac{\delta}{\delta_{m}} \biggr)^{\frac{5}{2}}}. $$

(17)

Flores et al. [15] assumed that the contact force is represented by the ideal Kelvin–Voigt viscoelastic model $F_{N} = D\dot{\delta} + K\delta$. Thus, the mathematical representation of the dynamic equivalent system can expressed as

$$ m\ddot{\delta} + D\dot{\delta} + K\delta= 0. $$

(18)

In the case that the damping effect ($D\dot{\delta}$) is neglected, the relationship between the deformation velocity and deformation can be obtained by (18), that is,

$$ \dot{\delta} = \dot{\delta}^{ ( - )}\sqrt{1 - \biggl( \frac{\delta}{\delta_{m}} \biggr)^{2}}. $$

(19)

In addition, with the purpose of comparing with the two models above, the relationship can also be assumed as a linear model and a step model, that is,

$$ \dot{\delta} = \dot{\delta}^{ ( - )} \biggl( 1 - \frac{\delta}{ \delta_{m}} \biggr), $$

(20)

$$ \dot{\delta} = \dot{\delta}^{ ( - )} - \dot{\delta}^{ ( - )} \biggl( \frac{\delta}{\delta_{m}} \biggr)^{2} \biggl( 3 - \frac{2\delta}{\delta_{m}} \biggr). $$

(21)

Based on the maximum deformation values of δ _m in Fig. 3, Fig. 4 shows the relationship between the deformation velocity and deformation for the purpose of comprising these formulas (17), (19), (20), and (21) with the numerical solution of Eq. (15).

Fig. 4

Deformation velocity–deformation relationship described by models of Lankarani and Nikravesh, Flores et al., Line, Step, and the numerical solution for different impact velocities: (a) $\dot{\delta}^{ ( - )} = 0.8~\mathrm{m}\mbox{/}\mathrm{s}$; (b) $\dot{\delta}^{ ( - )} = 0.1~\mathrm{m}\mbox{/}\mathrm{s}$

From Fig. 4 we can observe that Matlab solution gives the relation curves between the Lankarani and Nikravesh model and the Flores et al. model. In order to obtain a corresponding function of the fitting curve given by Matlab codes, it is necessary to assume a functional formula with a factor β, which can expressed as

$$ \dot{\delta} = \dot{\delta}^{ ( - )}\sqrt{1 - \biggl( \frac{\delta}{\delta_{m}} \biggr)^{\beta}}. $$

(22)

The result shows that β=2.408 $(\dot{\delta}^{ ( - )} = 0.8~\mathrm{m}\mbox{/}\mathrm{s})$ and β=2.395 $(\dot{\delta}^{ ( - )} = 0.1~\mathrm{m}\mbox{/}\mathrm{s})$, which are quite close to β=5/2 in (17) presented by Lankarani and Nikravesh. Moreover, it must be highlighted that the value of the factor β given by Lankarani and Nikravesh (β=5/2) is much closer to the true fitting value than the one given by Flores et al. (β=2), as it can be clearly observed in the diagrams plotted in Fig. 4.

In conclusion, Eq. (17) provides a good description of the relationship between the deformation velocity and deformation, and it will be utilized in the next section.

5 The energy loss associated with the damping force

In this section, the energy losses during the compression and restitution phases are determined. From Eq. (11), the total energy loss can be evaluated through the work done by the damping force $D\dot{\delta}$, which can be expressed as

$$ \Delta E = \oint D\dot{\delta}\,\mathrm{d}\delta= \oint c\delta^{\frac{3}{2}} \dot{\delta}\,\mathrm{d}\delta, $$

(23)

where ∮ refers to the integration around a hysteresis loop for the damping force.

The integral loop contains the compression and restitution phases. In the compression phase, the deformation velocity $\dot{\delta}$ can be obtained from Eq. (17). Based on the assumption that the relations between the deformation velocities and deformation during the two phases are performed by the same function, we can express the deformation velocity $\dot{\delta}$ in the restitution phase as

$$ \dot{\delta} = \dot{\delta}^{ ( + )}\sqrt{1 - \biggl( \frac{\delta}{\delta_{m}} \biggr)^{\frac{5}{2}}}. $$

(24)

It should be noted that the postimpact velocity $\dot{\delta}^{ ( + )}$ is negative because the spheres are separated from each other.

Thus, the energy loss can divide into two phases, that is,

$$\begin{aligned} \Delta E_{c} =& \int_{0}^{\delta_{m}} c \delta^{\frac{3}{2}}\dot{\delta}^{ ( - )} \sqrt{1 - \biggl( \frac{\delta}{\delta_{m}} \biggr)^{\frac{5}{2}}} \,\mathrm{d}\delta, \end{aligned}$$

(25)

$$\begin{aligned} \Delta E_{r} =& \int_{0}^{\delta_{m}} c \delta^{\frac{3}{2}}\bigl\vert \dot{\delta}^{ ( + )} \bigr\vert \sqrt{1 - \biggl( \frac{\delta}{ \delta_{m}} \biggr)^{\frac{5}{2}}} \,\mathrm{d}\delta. \end{aligned}$$

(26)

Similar to Flores et al. [15], Eqs. (25) and (26) can be evaluated as

$$\begin{aligned} \Delta E_{c} =& \frac{4}{15}c\dot{\delta}^{ ( - )} \delta_{m}^{\frac{5}{2}}, \end{aligned}$$

(27)

$$\begin{aligned} \Delta E_{r} =& \frac{4}{15}c\bigl\vert \dot{ \delta}^{ ( + )} \bigr\vert \delta_{m}^{\frac{5}{2}}. \end{aligned}$$

(28)

The energy loss may be evaluated by introducing Eqs. (27) and (28) as

$$ \Delta E = \Delta E_{c} + \Delta E_{r} = \frac{4}{15}c\dot{\delta }^{ ( - )}\delta_{m}^{\frac{5}{2}} + \frac{4}{15}c\bigl\vert \dot{\delta}^{ ( + )} \bigr\vert \delta_{m}^{\frac{5}{2}}. $$

(29)

Taking into account the coefficient of restitution

$$ e = - \frac{\dot{\delta}^{ ( + )}}{\dot{\delta}^{ ( - )}}, $$

(30)

the energy loss can be simplified as

$$ \Delta E = \frac{4}{15}c ( 1 + e )\dot{\delta}^{ ( - )} \delta_{m}^{\frac{5}{2}}. $$

(31)

It should be noted that, similarly to (31), there is an error in Eq. (40) of the paper by Flores et al. (2010) [15], which should be (1+c _r ), not (1−c _r ).

6 The hysteresis damping factor and the normal contact force model

In this section, the hysteresis damping factor c is evaluated, and the normal contact force model is presented. An energy balance between the start and end of the compression phase was taken into account to get the relationship between the maximum deformation δ _m and the initial deformation velocity $\dot{\delta}^{ ( - )}$:

$$ T^{ ( - )} = T^{ ( m )} + U^{ ( m )} + \Delta E_{c}, $$

(32)

where T ^(m) is the kinetic energy at the end of compression phase, and U ^(m) is the stored elastic strain energy during the compression phase:

$$ U^{ ( m )} = \int_{0}^{\delta_{m}} K \delta^{\frac{3}{2}}\,\mathrm{d}\delta= \frac{2}{5}K\delta_{m}^{\frac{5}{2}}. $$

(33)

Substituting Eqs. (27) and (33) into Eq. (32), the energy balance may be expanded as

$$ \frac{1}{2}m_{i} \bigl( v_{i}^{ ( - )} \bigr)^{2} + \frac{1}{2}m_{j} \bigl( v_{j}^{ ( - )} \bigr)^{2} = \frac{1}{2} ( m_{i} + m_{j} ) \bigl( v_{ij}^{ ( m )} \bigr)^{2} + \frac{2}{5}K\delta_{m}^{\frac{5}{2}} + \frac{4}{15}c\dot{\delta}^{ ( - )}\delta_{m}^{\frac{5}{2}}. $$

(34)

The momentum balance between times t ⁽⁻⁾ and t ^(m) is given by

$$ m_{i}v_{i}^{ ( - )} + m_{j}v_{j}^{ ( - )} = ( m_{i} + m_{j} )v_{ij}^{ ( m )}. $$

(35)

Substituting Eqs. (9), (10), and (35) in Eq. (34), the relationship between $\dot{\delta}^{ ( - )}$ and δ _m is expressed as

$$ \delta_{m}^{\frac{5}{2}} = \frac{15m}{4 ( 2c\dot{\delta}^{ ( - )} + 3K )}\dot{ \delta}^{ ( - )^{2}}. $$

(36)

Combining Eqs. (8), (31), and (36), the hysteresis damping factor c can be finally evaluated as

$$ c = \frac{3K ( 1 - e )}{2e\dot{\delta}^{ ( - )}}. $$

(37)

If the contact material is purely elastic, that is,e=1, the hysteresis damping factor equals to zero; if the contact material is purely plastic, that is,e=0, the hysteresis damping factor tends to be infinite from the view of physics. Finally, the normal contact force in conjunction with the hysteresis damping factor may be described in an alternative form:

$$ F_{N} = K\delta^{n} \biggl[ 1 + \frac{3 ( 1 - e )}{2e} \frac{\dot{\delta}}{\dot{\delta}^{ ( - )}} \biggr]. $$

(38)

This is a direct relationship between the contact force and the coefficient of restitution. It is important to point out that this relationship is valid for direct central and frictionless impacts. The reason is that the coefficient of restitution is invalid when friction or multiple points appear in impacts.

Equation (37) shows that the damping factor c depends on different parameters such as the initial deformation velocity and the coefficient of restitution. In order to show the variations of damping factors associated with different coefficients of restitution, some damping factor models were developed by Lankarani and Nikravesh [26], Flores et al. [15], Hunt and Crossley [27], and in this paper, as shown in Table 1. These damping factor models can be written in a common form:

$$ c = \alpha\frac{K}{\dot{\delta}^{ ( - )}}, $$

(39)

where α is a factor changed with the coefficient of restitution. It is provided as the input to Eq. (38) and is denoted as e _in. The damping factor c can be determined by α since K and $\dot{\delta}^{ ( - )}$ are set values on the initial condition. Hence, the variation of α represents the variation of c.

Table 1 Different damping factor models

Figure 5 shows this relationship between α and e _in. It can be observed that, for a perfectly elastic contact (e _in=1), the damping factors from the four models above have the same zero value, whereas for a perfectly plastic contact (e _in=0), the damping factors from the Lankarani and Nikravesh model and the Hunt and Crossley model have not infinite values as expected. This fact is not surprising because they have derived their models for high values of the coefficient of restitution, being, therefore, valid for hard contacts, such as metals. On the other hand, it is clearly observed that the α–e _in curves given by the model in this paper are in good agreement with the one given by Flores et al. model. This is in accordance with the actual situation that the damping factor should rapidly increase with the reducing input coefficient e _in and indicates that they can be valid for soft materials. Therefore, the damping factor and the contact force model (38) are valid for the entire interval of values (0–1) of the input coefficient e _in.

Fig. 5

Relation between α and e _in for different contact models

The same result can be obtained by another way as follows. First, the input coefficient e _in is used for the contact force model. Next, the deformation velocity at separation time $\dot{\delta}^{ ( + )}$ is obtained by using the contact force model to perform a continuous analysis. Thus, the actual measure of restitution e _out is evaluated as

$$ e_{\mathrm{out}} = - \frac{\dot{\delta}^{ ( + )}}{\dot{\delta}^{ ( - )}}. $$

(40)

It can be found that this actual measure of restitution e _out differs from the input coefficient e _in, but they should theoretically be the same value. Figure 6 shows the plots of e _out versus e _in for different contact force models. Clearly, the Lankarani and Nikravesh model and the Hunt and Crossley model are suitable for high values of e _in. However, the Flores et al. model and the contact force model described in this paper can be valid for the values of the input coefficient of restitution e _in between 0 and 1. It is highlighted that the solution for the present model is much closer to the actual situation from the view of physical point, as presented in Fig. 6.

Fig. 6

Relation between e _out and e _in for different contact models

7 Numerical examples

A classical bouncing ball problem is a simple contact system selected as an example of application, as shown in Fig. 7 [15]. This bouncing ball problem is considered here to study the influence of the use of different contact force models. The physical data for this example are listed in Table 2.

Fig. 7

An example of a bouncing ball

Table 2 Data for the bouncing ball example

The ball falls from the initial position until it collides with the ground, which is assumed to be rigid and stationary. During the contact process between the ball and ground, the contact force model is used to calculate the contact force, output velocity, deformation, and contact time. The output velocity v ⁽⁺⁾ can especially help to calculate the displacement of the ball after the ball rebounds.

When the ball contacts with the ground, the initial contact velocity v ⁽⁻⁾ can be evaluated as

$$ v^{ ( - )} = \sqrt{2g ( h_{0} - R )}. $$

(41)

Since the velocity of ground is zero, the relative contact velocity $\dot{\delta}^{ ( - )}$ can be expressed as

$$ \dot{\delta}^{ ( - )} = v^{ ( - )} - 0 = \sqrt {2g ( h_{0} - R )}. $$

(42)

Therefore, the relative contact velocity would be used in the contact force model to calculate relevant parameters. This problem was analyzed by using Matlab codes.

Figures 8, 9, 10, respectively, show the deformation–time curves, velocity–time curves, and contact force–deformation curves of the ball obtained by four different contact force models developed by Lankarani and Nikravesh, Hunt and Crossley, Flores et al., and the model described in this work. Five difference values (1.0, 0.8, 0.6, 0.4, and 0.2) for the coefficient of restitution are considered in the four different contact force models.

Fig. 8

Deformation–time relation in different coefficients of restitution for different contact force models: (a) Lankarani and Nikravesh; (b) Hunt and Crossley; (c) Flores et al.; (d) described model

Fig. 9

Deformation velocity–time relation in different coefficients of restitution for different contact force models: (a) Lankarani and Nikravesh; (b) Hunt and Crossley; (c) Flores et al.; (d) described model

Fig. 10

Contact force-deformation relation in different coefficients of restitution for different contact force models: (a) Lankarani and Nikravesh; (b) Hunt and Crossley; (c) Flores et al.; (d) described model

By analyzing the curves in Fig. 8(a–d), we can observe that the maximum deformation value reduces with the decreasing coefficient of restitution. This fact is not surprising because the less amount of energy dissipated during the contact process. Furthermore, it is worth noting that when the coefficient of restitution is high enough (e.g.,e=1), the four contact force models exhibit very similar responses. However, when the coefficient of restitution is low enough (e.g., e=0.1), the Lankarani and Nikravesh model and the Hunt and Crossley model do not work adequately. This means that the two models are valid for the case in which the dissipated energy is small when compared to the maximum absorbed elastic energy, that is, the relation is valid for the values of the coefficient of restitution close to unity.

In turn, the Flores et al. model and the model described in this work present superior responses for low values of the coefficient of restitution because the two models were developed to take into account the differences of the energy dissipation during both phases of contact (the compression and restitution phases). From Figs. 9 and 10 we also concluded that the Flores et al. model and the present model are suitable for the low and high values of the coefficient of restitution (e.g., 0<e≤1). In general, the global data produced here are corroborated by similar analysis available in the thematic literature [22, 26, 30, 36].

From the plots of Fig. 9(a–d) we can observe that if the coefficient of restitution decreases, then the velocity value is reduced, and the time of the contact process is increased. Furthermore, the velocity values obtained by the Flores et al. model and the model described in this work are obviously close to null if the coefficient of restitution is close to zero. This indicated that the model described in this work presents a superior response mainly for low values of the coefficient of restitution, which means that it can perform well for perfectly inelastic contacts. Moreover, for moderate and high values of the coefficient of restitution (higher than 0.5), the four models present a close response. This means that the model described in this work can perform well for the entire range of the coefficient of restitution.

Figure 10(a–d) shows the relationship between the contact force and the deformation. Again, we observe that the Lankarani and Nikravesh model and the Hunt and Crossley model dissipate less energy and exhibit smaller hysteresis loops. In contrast, the Flores et al. model and the model described in this work dissipate more energy and exhibit larger hysteresis loops. This fact is not surprising because these two models were developed taking into account that the compression and restitution phased of the contact process are not equal to each other due to the differences in the energy loss between these two phases. Moreover, it must be highlighted that for lower values of the coefficient of restitution, the latter two models reflect the energy dissipation during the contact process that is better than in the former two models.

In conclusion, the contact force models can be grouped into two main classes, one for the higher values of the coefficient of restitution, including the Lankarani and Nikravesh model and the Hunt and Crossley model, and the other for the entire range of the coefficient of restitution, including the Flores et al. model and the model described in this work.

8 Conclusions

In this work, a new continuous contact force model for impact analysis in multibody dynamics has been developed to take the energy balance during the contact process into account. The energy loss during the impact process was evaluated separately based on the classical kinetic energy principle and the work done by damping force for the two-sphere impact. Furthermore, a relationship between the deformation velocity and deformation was proposed to calculate the dissipated energy due to the damping force. In particular, a direct approximate mathematical expression of the relationship was obtained by comparing with the relevant models, which was difficult to get by the form of analytical function.

The advantages and limitations of the new model together with three classical contact force models were analyzed by comparing the output and input values of the coefficient of restitution. Comparisons indicated that the result by the new model was closer to the actual value for the entire range of the coefficient of restitution (0–1). Finally, numerical examples were used to analyze and compare the four continuous contact force models. For high values of the coefficient of restitution, these contact force models exhibited quite similar responses. In sharp contrast, for the low or moderate values of the coefficient of restitution, the new model and the Flores et al. model presented very close responses, which were different from the case simulated with the Lankarani and Nikravesh model and the Hunt and Crossley model. Thus, the new model is valid for soft and hard contact problems. Also, the model, as an independent formula, can be extended directly for impact analysis of a multibody mechanical system.