1 Introduction

While eigenfrequencies and mode shapes of assembled structures can be predicted reliably with the finite element method, the incorporation of damping is subject to ongoing research. The key to valid damping predictions of assembled structures is accurate representation of joint damping caused by friction on mechanical interfaces. A proposed modeling technique for joint damping is the thin-layer element (TLE) approach which has shown promising results in previous work [1, 2]. Thereby, a thin layer of finite elements is placed on the joint interface. These TLEs contain a linear, phenomenological model of the joint behavior. The major advantage of this approach is that the main contributions to energy dissipation in assembled structures are incorporated spatially correct, while efficient evaluation of the model through eigenvalue analysis is still possible. Additionally, the linear approach facilitates comparison with data from experimental modal analysis. On the other hand, experimental investigations clearly show the nonlinear behavior of bolted joints [3]. Thus, the accuracy of the linear TLE approach is limited. The main source of inaccuracy is parameter and model uncertainty connected to the joint loss factor. To mitigate the effects of these inaccuracies, model updating [4] or uncertainty analysis [5] is employed. That, however, requires a large number of model evaluations with varying loss factors.

In this work, a model reduction technique for the TLE modeling approach and an application to model updating are presented. The reduction is based on a sensitivity analysis of the eigenvalues and takes advantage of the particularly simple formulation of joint damping in the form of constant hysteretic damping. The result is a single, linear equation for each eigenvalue. The resulting cost advantage is utilized for a model updating application on an engine.

2 Thin-layer element joint model

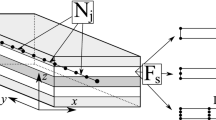
This section covers the basic approach of joint modeling using TLEs. Further details can be found in [2, 6]. As mentioned above, the basic idea of the TLE modeling approach is to place a layer of elements with a linear, orthotropic material model on all joint interfaces (Fig. 1).

Fig. 1
figure 1

FE model of an engine block oil pan assembly with exposed thin-layer elements on the joint interface

Full size image

The TLEs reproduce the localized occurrence of joint damping in assembled structures in contrast to, e.g., Rayleigh Damping where the energy dissipation is distributed over the entire structure. The TLEs are implemented as finite elements with a height to width ratio of up to 1:100. As joints have distinct behavior in normal and tangential direction with respect to the interface, an orthotropic material is model employed. Stiffness and damping parameters of the joint are experimentally identified on a specialized experimental setup [6].

Joint damping shows only weak dependence on frequency. Therefore, the model of constant hysteretic damping is applied [7]. The starting point for the implementation of constant hysteretic damping is the discrete equation of motion of a free, undamped system

$$\begin{aligned} \varvec{M \ddot{u}} + \varvec{K u} = \varvec{0}. \end{aligned}$$
(1)

Here, \(\varvec{M}\) is the mass matrix, \(\varvec{K}\) the real-valued stiffness matrix and \(\varvec{u}\) the displacement vector. Constant hysteretic damping can now be incorporated by replacing the real-valued stiffness matrix \(\varvec{K}\) with a complex-valued stiffness matrix \(\varvec{K}^*\) with

$$\begin{aligned} \varvec{K}^* = \varvec{K} + j \, \sum _{i=1}^n \alpha _i \varvec{K}_i^\text {(Material)} + j \sum _{i=1}^m \beta _i \varvec{K}_i^\text {(Joint)}, \end{aligned}$$
(2)

where \(\varvec{K}_i^\text {(Material)}\) are the regular element stiffness matrices, \(\varvec{K}_i^\text {(Joint)}\) are the TLE stiffness matrices and j is the complex unit. The material loss factor is represented by \(\alpha _i\) and the joint loss factor by \(\beta _i\). While material and joint damping are accounted for by this approach, joint damping is decisive for accurate damping predictions. Thus, further elaboration is limited to the joint loss factor \(\beta _i\).

Replacing \(\varvec{K}\) in Eq. (1) by \(\varvec{K}^*\) from Eq. (2), the eigenvalue problem can be formulated

$$\begin{aligned} (\lambda _k^2 \varvec{M} + \varvec{K}^* ) \varvec{{\psi }}_k = \varvec{0}, \end{aligned}$$
(3)

with eigenvalues \(\lambda _k\) and eigenvectors \(\varvec{\psi }_k\).

3 Thin-layer element model reduction

3.1 Derivation

As mentioned above, models with TLEs often require multiple evaluations of Eq. (3) for systems that are equivalent in all respects but the joint loss factors \(\beta _i\). In this chapter, a more efficient way to calculate the resulting eigenvalues in the sense of a model reduction is presented. For the sake of brevity, all derivations will be shown for \(\lambda _k^2\). The modal damping \(\chi _k \) can be calculated from \(\lambda _k^2\):

$$\begin{aligned} \chi = \frac{\text {Re}(\lambda _k)}{\text {Im}(\lambda _k)} \approx \frac{\text {Im}(\lambda _k^2)}{2 \cdot \text {Re} (\lambda _k^2)}. \end{aligned}$$
(4)

Starting point of the derivation is the eigenvalue problem Eq. 3. Eigensensitivity analysis is now employed to find a relation between the change of the ith loss factor \(\Delta \beta _i\) and the kth squared eigenvalue \(\lambda _k^2\).

Rearranging Eq. (3) into its Rayleigh Quotient [8] form and scaling \(\varvec{\psi }_k\) such that

$$\begin{aligned} \varvec{\psi }_k^T \varvec{M} \varvec{\psi }_k = 1, \end{aligned}$$
(5)

one obtains

$$\begin{aligned} \lambda _k^2 = - \varvec{\psi }_k^T \varvec{K}^* \varvec{\psi }_k. \end{aligned}$$
(6)

Using the definition of the complex-valued stiffness matrix \(\varvec{K}^*\) in Eq. (2), the partial derivative of Eq. (6) with respect to \(\beta _i\) yields the eigensensitivity \(J_{ik}\)

$$\begin{aligned} \frac{\partial \lambda _k^2}{\partial \beta _i}= & {} {-} \varvec{\psi }_k^T \left( \varvec{K} + j \, \sum _{i=1}^n \alpha _i \varvec{K}_i^\text {(Material)} + j \sum _{i=1}^m \beta _i \varvec{K}_i^\text {(Joint)} \right) \varvec{\psi }_k^T = \nonumber \\= & {} - \varvec{\psi }_k^T \left( j \varvec{K}_i^\text {(Joint)}\right) \varvec{\psi }_k = \nonumber \\= & {} J_{ik}. \end{aligned}$$
(7)

A more detailed derivation of this result can be found in [9–11]. Equation (7) reveals that the derivative of \(\lambda _k^2\) with respect to a joint loss factor \(\beta _i\) only depends on the corresponding (constant) stiffness matrix \(\varvec{K}_i^\text {Joint}\) and eigenvector \(\varvec{\psi }_k \). In typical applications, the TLEs have negligible influence on the mode shape since they constitute only a small fraction of the overall structure. Hence it is feasible to assume

$$\begin{aligned} \frac{\partial \varvec{\psi }_k}{\partial \beta _i} \approx \varvec{0}. \end{aligned}$$
(8)

Therefore, \(J_{ik}\) is independent of \(\beta _i\). Equation (7) can therefore be used to calculate the eigenvalues \(\hat{\lambda }_k^2\) of a model with joint loss factors \(\hat{\beta }_i\):

$$\begin{aligned} \hat{\lambda }_k^2 = \lambda _k^2 + \sum _{i=1}^m J_{ik} (\hat{\beta }_i - \beta _i). \end{aligned}$$
(9)

With Eq. (9), eigenvalues of an augmented system can be calculated from a single, linear equation. One full model evaluation is necessary to calculate \(\lambda _k^2\) and \(\varvec{\psi _k}\). During this evaluation, all TLE stiffness matrices \(\varvec{K}_i^{\text {Joint}}\) are assembled as well and can be stored for the calculation of \(\varvec{J}_{ik}\).

As long as Eq. (8) is a sufficiently exact approximation, Eq. (9) is valid for all reasonable values of \(\ \hat{\beta }_i\). One can further assume that the eigenvectors, though in reality complex, are approximately real-valued. Therefore, \(J_{ik}\) is purely imaginary and Eq. (9) reveals that a change of the loss factor \(\beta _i\) only affects the imaginary part of \(\hat{\lambda }_k^2\). This is equivalent with the intuitive assumption that a variation of the loss factor mainly affects modal damping ratios without significantly altering eigenfrequencies.

3.2 Validation

The reduced model is validated by examining the first eight eigenvalues of the test structure depicted in Fig. 1. To that end, the eigenvalues of the system are calculated for different loss factors by evaluating the full model [Eq. (3)] and by using the reduced model [Eq. (9)]. It is important to note that here, in contrast to the model updating example in Sect. 4, all TLEs have identical loss factors \(\beta _i\). Figure 2 shows the modal damping for the first eight modes for loss factors ranging between 0 and 0.5. The solid line depicts the simulation with the reduced model and the dots represent values from full model evaluations. The base system used for the model reduction has a loss factor of \(\beta _i = 0.05\) which is close to the lower limit of the parameter range. Nonetheless, the largest deviation from the reference values calculated with the full model is \({<}3\) % of the corresponding modal damping value.

Fig. 2
figure 2

Validation of the reduced model by comparison of modal damping \(\chi \) calculated by full model evaluations \((+)\) and reduced model evaluations (solid line)

Full size image

4 Model updating with reduced model

The TLE modeling approach was introduced as an efficient way to predict damping in assembled structures before a physical prototype exists. The original approach [2] employs an uniform loss factor parametrization across the joint surface. While this approach is effective for damping predictions, it is not well suited for model updating because only a single design parameter exists.

With the reduced model, a more numerically compliant TLE approach can be devised. Instead of a single parameter for the entire joint interface, each element can be allocated an independent loss factor parameter. This increases the number of design variables for the optimization from one in the original approach to several hundreds (1042 in the presented example). An optimization with such a high number of variables requires a large number of iterations which is only feasible under the utilization of the reduced model.

In the presented example, parameters for 1042 TLEs are to be found such that the experimentally determined modal damping ratios for the first eight modes are reproduced in an optimal way. Due to the large number of design variables, this problem has various solutions with most of them being physically not feasible. Therefore, a set of boundary conditions has to be defined which reduces the set of solutions to physically reasonable ones. In previous work [12] it was shown that this leads to the identification of an optimal TLE parametrization which is closely correlated to the average relative displacement \(\Delta \bar{u}_i\) of the considered modes. The relative displacement of each element can be calculated during the initial full model evaluation which is necessary to determine the reduced model. The relative displacement is defined as the difference between the displacement of the top and the bottom of a TLE Fig. 3.

(10)

It is scaled such that

$$\begin{aligned} {\text {max}}(\Delta \bar{u}_i) = 1. \end{aligned}$$
(11)

A more efficient formulation of the boundary conditions is possible assuming a direct proportionality between the relative displacement and the loss factor. Thus the lower and upper bounds \(\eta _{i,lb}\) and \(\eta _{i,ub}\) of the allowable parameter interval for the optimization are set to be proportional to the average relative displacement

$$\begin{aligned} \eta _{i,lb}= & {} c_{lb} \cdot \Delta \bar{u}_i \end{aligned}$$
(12)
$$\begin{aligned} \eta _{i,ub}= & {} c_{ub} \cdot \Delta \bar{u}_i \end{aligned}$$
(13)

Through experimental investigations and some trial and error, reasonable values for the proportionality factors are found to be \(c_{lb}=0.035\) and \(c_{ub}=0.7\). As this parameter choice allows rather large intervals, it is necessary to additionally limit the maximum step size \(\Delta \beta _\text {max}\) of the loss factor parameter between neighboring elements. This is implemented as an inequality boundary condition. For two elements, i and j, which have at least one common node, the following inequalities are enforced:

$$\begin{aligned} | \beta _i - \beta _j| < \Delta \beta _\text {max}. \end{aligned}$$
(14)
Fig. 3
figure 3

Relative displacement in a TLE

Full size image

With these boundary conditions, the loss factor parameters are optimized such that the first eight experimentally determined modal damping ratios of the test structure are reproduced optimally in a least-squares sense. The algorithm converges after 7146 iterations in 565 s. At approximately 30 min per full model evaluation and numerous model evaluations per iteration, the cost advantage of the reduced model is significant. As base line, model updating with uniform parametrization is performed. This optimization with a single degree of freedom is representative of the performance of the original TLE modeling approach.

Fig. 4
figure 4

Comparison of the first eight modal damping values of the engine oil pan assembly obtained experimentally and by optimization with uniform and individual loss factor parametrization

Full size image

In Fig. 4 the results of the two different optimized parametrizations are compared to experimental reference values. It is evident that the much larger number of design variables of the element-wise, individual parametrization allows a much better representation of the reference values. Yet, for some modes, e.g., Mode 5, discrepancies between numerical and experimental results remain after the model updating. These discrepancies indicate the existence of additional damping mechanisms outside of the investigated joint area, for example, at pressed-in valve bearings. The inclusion of material damping as parameter for the model updating might also reduce the residual error.

While previous work [6] shows that for simple structures a homogeneous loss factor distribution is sufficient to attain acceptable accuracy, more complex machines require a non-homogeneous loss factor distribution.

5 Conclusions

The existing thin-layer element modeling approach is extended by a model reduction. The reduced model is derived through an eigensensitivity analysis and provides a single, linear equation for each eigenvalue. Validation on a engine block oil pan assembly shows the high accuracy and significant cost reduction achieved through the proposed model reduction.

The TLE modeling approach can be augmented for better performance in model updating applications by taking advantage of the reduced computational effort. The presented approach reproduces experimental data more accurately by providing a very large number of design variables to the optimization algorithm. Physically unreasonable solutions are avoided by defining the interval bounds proportionally to the relative displacement in the joint. While the original TLE approach localizes joint damping at mechanical interfaces but does not consider variations over the area of the interface, the new model updating approach identifies areas of high and low energy dissipation on the interface. Thus complex machines in particular can be modeled more accurately.