A new perspective towards decomposition of the generalized inertia matrix of multibody systems

Abstract

This paper presents a new perspective into the decomposition of the Generalized Inertia Matrix (GIM) of multibody systems with open kinematic architecture, serial or tree-type. Links and kinematic pairs are the two constituting elements of multibody systems. In this work, we propose to decompose a multi-branch multibody system into several kinematic modules. Each module is a set of serially connected links like a serial-chain system. Such a description allows one to obtain a block decomposition $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ of the GIM where $\bar{\mathbf{U}}$ and $\bar{\mathbf{D}}$ are the block upper-triangular and diagonal matrices, respectively. The results provide a recursive inverse of the GIM on module-level. Many new perspectives leading to macroscopic purview of the complex multibody systems are provided. Empowered with the proposed decomposition, an inter- and intra-modular efficient and numerically stable recursive dynamics algorithm for forward dynamics and simulation was possible. While recursive expressions are derived for a four degree-of-freedom gripper, numerical results are shown for a spatial biped.

Notational rules followed in this paper are as follows:

• (1) Scalars are in lightface italics font.

• (2) Column matrices and algebraic vectors are in boldface lower-case letters.

• (3) Matrices are in boldface upper-case letters.

• (4) A ‘−’ over an entity, e.g., $\bar{\mathbf{M}}_{i}$, signifies that it is associated with a module.

• (5) Superscript over an entity, e.g., $k^{i}$, specifies module number.

1 Introduction

Over the last two decades multibody dynamics has been applied in the areas of robotics, automobile, aerospace, bio-mechanics, molecular modeling, and many more [1]. With continuous development and evolution of complex systems, multibody dynamics has still wider scope of research. Complex multibody systems, mainly those with closed kinematic loops, are commonly analyzed by representing them as equivalent open tree-type systems subjected to constraints and/or external forces [2]. The inertia matrix of these tree-type systems plays a key role in the study of their overall dynamic behavior, particularly, in the forward dynamics which is essential for simulation of the multibody system under study. In forward dynamics, the main objective is to find the joint accelerations as $\ddot{\mathbf{q}} = \mathbf{I}^{ - 1}\boldsymbol{\varphi }$, where $\mathbf{I}$ is the generalized inertia matrix (GIM) of the tree-type system, whereas $\boldsymbol{\varphi }$ contains the Coriolis, centripetal, and gravity terms, along with the external forces. The joint accelerations $\ddot{\mathbf{q}}$ are subsequently integrated to find the corresponding joint velocities and positions. Note that the calculation of the joint accelerations does not generally require explicit inversion of the GIM. However, the way $\ddot{\mathbf{q}}$ is solved, not only the computational efficiency but also the numerical stability of the algorithm get affected. The role of the GIM in the analysis of multibody systems was demonstrated in [3, 4].

Interestingly, the forward dynamics algorithms can be categorized based on explicit or implicit solutions of the associated linear equations derived from the dynamic equations of motion, namely, $\mathbf{I}\ddot{\mathbf{q}} = \boldsymbol{\varphi }$. In the explicit solution methods, the GIM $\mathbf{I}$ is formulated first numerically or analytically [5, 6] before it is decomposed numerically using Cholesky decomposition or Gaussian elimination (GE) [7]. It is followed by the backward and forward substitutions to obtain the joint accelerations $\ddot{\mathbf{q}}$. This method leads to a forward dynamics algorithm which is of $\mathit{Order}(n^{3})$ or simply $O(n^{3})$ complexity, where $n$ is the degree-of-freedom (DOF) or the number of joint variables present in a tree-type system. On the contrary in the implicit solution methods [8–10], the joint accelerations are obtained directly. It means that no numerical values need be found explicitly either for the computations of the elements of the GIM nor for the steps involved during the substitution processes. Rather the process of decomposition and substitutions evolves using several recursive expressions of the GIM available from the systematic modeling approach, e.g., using the concept of the Decoupled Natural Orthogonal Complement (DeNOC) matrices proposed in [10]. Such steps exhibit recursive relations leading to $O(n)$ computational complexity for the forward dynamics algorithm which is not only efficient but also numerically stable. The latter requirement is very important from a realistic simulation point of view. In relation to explicit calculations, the implicit steps are more involved resulting in complex expressions, which of course pay off in terms of algorithmic efficiency and numerical stability. The explicit and implicit methods were referred in [8] as inertia matrix and propagation methods, respectively. In the implicit solution approach of [8], the terms of the equations of motion were made available at the link-level. They were then used to write the same for the adjacent links till a solvable link is obtained to find an expression for the joint acceleration associated with that solvable link. The process was then reversed to find the joint accelerations associated with the previous adjacent links. In the implicit approach of [10], the GIM was first decomposed into three matrices using the rules of the Reverse Gaussian Elimination (RGE) [3], and then solved for the joint accelerations recursively using the forward and backward substitutions instead of the backward–forward substitutions of the GE. The advantages of the latter approach using the RGE plus forward-backward substitutions were demonstrated in [10]. The approach in [10] provided several advantages, for example, one can very easily evaluate the condition number of the GIM from the diagonal elements of the GIM, which contain the “composite masses.” This aspect was demonstrated in [11], which was not so obvious from the derivations of [8]. In this work, the DeNOC based approach is extended to provide macroscopic view of the system’s dynamics rather than the microscopic view of [8–10]. Motivated by the work in [10] applied to a single serial-chain system, a block decomposition on the GIM of a tree-type multibody system is attempted in this paper. For this purpose, we use a module-level description of the tree-type kinematic architecture shown in [12, 13], and we propose the module-level decomposition of the GIM. Their benefits are enumerated through examples.

Many times simple delineation of a system in terms of a set of bodies does not provide macroscopic purview of the several kinematic and dynamic properties, thereby increasing the complexity of analyses in many instances. In the module-based description, instead of considering a serial or tree-type system composed of several links or bodies (classical approach), the complete system is considered to have several kinematic modules. A kinematic module is defined here as a collection of one or more than one serially connected links. Hence, a more comprehensive macroscopic purview is possible based on the simpler serial-chain module which is well developed in the domain of serial robot dynamics. One needs not analyze the complete GIM of the tree-type system. Instead, the GIMs of the constituent modules can be monitored whose condition could infer the overall condition of the complete system.

This paper augments the work presented earlier in [3, 10, 14, 15] and introduces a decomposition and analytical inverse of the GIM expressed using the module-level description of a complex multi-branched multibody system. The earlier work in the literature, e.g., in [8] and others or by one of the authors of this paper, say, in [10], exploited discretization of a multibody system into several links or bodies. In the proposed work, however, a more systematic and comprehensive view is proposed, where even a serial-chain system can be considered consisting of several smaller serial-chain modules instead of only links or bodies. In fact, in that sense, the views taken by [8] or [10] is the special or limiting case of what is proposed here. Each smaller serial-chain module has only one link. The present representation now allows one to extend the proposed module concept to multi-branched system where each branch is a set of modules or serial-chains. It leads to an elegant inter- and intra-modular representations of many mathematical terms appear during the derivation of the dynamic equations of motion of a complex multi-branched multibody system. These expressions provide a step-by-step understanding of the complete system, i.e., in the first-level one understands how each module, which is like a serial-chain system, affects the overall system, followed by the second-level understanding of how each link affects the dynamics of a module. Alternatively, one studies the effects of links on the module, followed by the effects of modules on the complete system. The concept of the kinematic module is central to the complete development of the dynamics of any complex multi-branched multibody system and plays a crucial role in the derivations of the dynamic equations of motion. The derivations performed in this paper builds on the recursive relationships between several modules in contrast to the links used in [10]. This has led to the generalization of the concept of the Reverse Gaussian Elimination (RGE) of the GIM proposed in [3, 10] for the decomposition and analytical inverse of the GIM. Note that the notion of the kinematic module was introduced in [13], where it was used only for the development of recursive algorithms of legged robots. Here, the proposed work explains new perspectives towards the decomposition of the GIM for any general multibody systems, which was not reported earlier.

The modular approach leads to the following advantages: (1) compact representation of a system’s kinematic and dynamic model; (2) Provision of module-level analytical expressions for the matrices and vectors appearing in the equations of motion. One can use such expressions in predicting instability of a module rather than only having the global picture; (3) Possibility of repeating the computations of a module to another module having similar module architecture; (4) Possibility of the development of hybrid recursive-parallel algorithms, where modules are solved in parallel, whereas the links inside the modules are solved in a recursive manner. It is worth pointing out that the main objective of this work is to exploit the module-level expressions of the GIM for a tree-type multibody system, and then use it for module-level decomposition of the GIM and its analytical recursive inverse which provide many physical interpretations. The decomposed GIM itself suggests a recursive inter- and intra-modular forward dynamics algorithm which is not only efficient but also numerically stable. The salient contributions of the paper, not reported earlier, are summarized here:

• The module-level block decomposition of the GIM introducing the Elementary Block Upper Triangular Matrices (EBUTMs) and the Block Reverse Gaussian Elimination (BRGE) of the GIM.

• Attaining analytical expressions for the product of the two neighboring EBUTMs and the consequent derivation of the analytical inverse of the GIM.

• Ascertaining new module level properties such as the composite and articulated modules, the inertia matrix of the articulated-module, the articulated-module transformation matrix and the articulated module-twist propagation matrix.

• Numerical studies of tree-type systems, namely, a planar tree-type gripper and a spatial biped, to investigate the numerical stability of the recursive inter- and intra-modular forward dynamics algorithms developed based on the proposed BRGE and its comparison with the algorithms based on GE and RGE.

The rest of the paper is organized as follows: Sect. 2 presents the derivation of the GIM using the concept of kinematic modules and the module-level DeNOC matrices, while its module-level decomposition is shown in Sect. 3. The module-level analytical inverse of the GIM is shown in Sect. 4. An application of the proposed concept in deriving the inter- and intra-modular recursive algorithms is discussed in Sect. 5 along with numerical simulation of a spatial biped. Numerical stability of the proposed algorithm is presented in Sect. 6. Finally, conclusions are given in Sect. 7.

2 Generalized inertia matrix (GIM): a macroscopic purview

Conventionally, a serial- or tree-type system is considered to have a set of links connected by kinematic pairs, as shown in Fig. 1(a). However, in this work a more generic approach is undertaken where a serial or tree-type architecture is considered to have a set of kinematic modules instead of links. This is shown in Fig. 1(b), where the modules are depicted by dotted lines. It is assumed that each module, other than the base, is a child module, e.g., $M_{i}$ in Fig. 1(b), which contains serially connected links and emerges from the last link of its parent module $M_{\beta}$. Obviously the child module bears a higher module number than its parent, i.e., $i> \beta$. As a result, the conventional approach, Fig. 1(a), turns out to be the special case of the proposed architecture shown in Fig. 1(b) where each module has only one link. Referring to Fig. 2, the links in module $M_{i}$ are denoted $1^{i}, \ldots,k^{i}, \ldots, n^{i}$, where superscript $i$ is the module number. The total number of modules, the number of links in each module and the total number of links in all the modules are designated by $s$, $n^{i}$, and $n$, respectively. The set of all modules originating from $M_{i}$ is denoted by $\boldsymbol{\gamma}_{i}$, as shown in Fig. 3.

Fig. 1

Microscopic and macroscopic purview of open kinematic architectures

Fig. 2

Module $M_{i}$ and its parent $M_{\beta}$

Fig. 3

Definition of $\boldsymbol{\gamma}_{i}$

Next, the elements of the GIM, $\mathbf{I}$, for the multi-modular tree-type system will be derived. These will not only provide interpretations of several module-level properties but also enable one to decompose the GIM. For the system shown in Fig. 1(b), the $6n \times6n$ generalized mass matrix, resulting out of the $6n$ uncoupled Newton–Euler equations (written with respect to the origin of each body) of $n$ free bodies in $s$ modules, can be written as [13]

$$ \mathbf{M} \equiv \mathrm{diag}\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{M}}_{1} & \bar{\mathbf{M}}_{2} & \cdots& \bar{\mathbf{M}}_{i} &\cdots & \bar{\mathbf{M}}_{s} \end{array}\displaystyle \right] $$

(1)

where

$$ \bar{\mathbf{M}}_{i} \equiv \mathrm{diag} \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{M}_{1^{i}} & \cdots &\mathbf{M}_{k^{i}}& \cdots & \mathbf{M}_{n^{i}} \end{array}\displaystyle \right] \quad\mbox{and} \quad \mathbf{M}_{k^{i}} \equiv \left[ \textstyle\begin{array}{c@{\quad}c} \mathbf{I}_{k^{i}} & m_{k^{i}}\tilde{\mathbf{d}}_{k^{i}} \\ - m_{k^{i}}\tilde{\mathbf{d}}_{k^{i}} & m_{k^{i}}\mathbf{1} \end{array}\displaystyle \right]. $$

(2)

In Eq. (2), $\bar{\mathbf{M}}_{i}$ and $\mathbf{M}_{k^{i}}$ are the mass matrices of the $i$th module and $k$th link in the $i$th module, respectively. A bar (‘−’) over an entity signifies that it is related to a module and the superscript, $i$, identifies the module. Moreover, $\mathbf{I}_{k^{i}}$ is the inertia tensor about the origin of the $k$th link ($O_{k^{i}}$ of Fig. 4), $m_{k^{i}}$ is mass of the $k$th link, $\tilde{\mathbf{d}}_{k^{i}}$ is the $3\times3$ cross-product tensor associated with the vector $\mathbf{d}_{k^{i}}$ (shown in Fig. 4) and $\mathbf{1}$ represents the $3\times3$ identity matrix.

Fig. 4

Link $k^{i}$ in module $M_{i}$ ($\mathbf{f}_{k^{i}}$: force; $\mathbf{n}_{k^{i}}$: moment; $\dot{\mathbf{o}}_{k^{i}}$: linear velocity; $\boldsymbol{\omega}_{k^{i}}$: angular velocity; $\mathbf{d}_{k^{i}}$, $\mathbf{r}_{k^{i}}$, $\mathbf{a}_{(k + 1)^{i},k^{i}}$: position vectors)

If the set of rigid bodies in $s$ modules is constrained to move due to the joint adjoining any two links, then the $6n$-dimensional generalized twist vector $\mathbf{t}$ containing angular and linear velocities of the links of all constituent modules can be written in terms of the $n$-dimensional generalized joint-rate vector $\dot{\mathbf{q}}$ of the multi-modular tree-type system as

$$ \mathbf{t} \equiv \mathbf{N}\dot{\mathbf{q}}, \quad\mbox{where}\ \mathbf{N} \equiv \bar{\mathbf{N}}_{l}\bar{\mathbf{N}}_{d}. $$

(3)

In Eq. (3), $\bar{\mathbf{N}}_{l}$ and $\bar{\mathbf{N}}_{d}$ are the $6n \times6n$ and $6n \times n$ module-level decoupled form of the Natural Orthogonal Complement (NOC) matrix [6] or simply the decoupled NOC (DeNOC) matrices [10]. The matrices $\bar{\mathbf{N}}_{l}$ and $\bar{\mathbf{N}}_{d}$ for the tree-type system were obtained in [13] and their detailed derivations are given in Appendices A.1 and A.2. The matrices $\bar{\mathbf{N}}_{l}$ and $\bar{\mathbf{N}}_{d}$ are reproduced as

$$\begin{aligned} \bar{\mathbf{N}}_{l} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & & & & \\ \bar{\mathbf{A}}_{2,1} & \mathbf{1}_{2} & & \mathbf{O}'\mathrm{s} & \\ \bar{\mathbf{A}}_{3,1} & \bar{\mathbf{A}}_{3,2} & \mathbf{1}_{3} & & \\ \vdots & \vdots & \ddots & \ddots & \\ \bar{\mathbf{A}}_{s,1} & \bar{\mathbf{A}}_{s,2} & \cdots & \bar{\mathbf{A}}_{s,s - 1} & \mathbf{1}_{s} \end{array}\displaystyle \right], \quad\mbox{and}\quad \bar{\mathbf{N}}_{d} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{N}}_{1} & && & \mathbf{O}'\mathrm{s} \\ & \ddots& &&\\ &&\bar{\mathbf{N}}_{i} & &\\ &&& \ddots &\\ \mathbf{O}'\mathrm{s} & & && \bar{\mathbf{N}}_{s} \end{array}\displaystyle \right]. \end{aligned}$$

(4)

In Eq. (4), $\bar{\mathbf{A}}_{i,j}$ and $\bar{\mathbf{N}}_{i}$ are the $6n^{i} \times6n^{j}$ module-twist propagation and the $6n^{i} \times n^{i}$ module-joint-motion propagation matrices, as derived in Appendix A.2. The term $\bar{\mathbf{A}}_{j,i} \equiv \mathbf{O}$ if module $M_{j}$ does not belong to the set $\boldsymbol{\gamma}_{i}$ of all modules originating from $M_{i}$, as shown in Fig. 3. The module-level DeNOC matrices form the foundation of this paper aiming to obtain the macroscopic purview of the GIM.

Now, using Eqs. (1) and (4), the $n \times n$ GIM $\mathbf{I}$ can be expressed as an extension of what was proposed in [10] for a serial-chain system, i.e.,

$$ \mathbf{I} \equiv (\bar{\mathbf{N}}_{l}\bar{\mathbf{N}}_{d})^{T} \mathbf{M}(\bar{\mathbf{N}}_{l}\bar{\mathbf{N}}_{d}) \equiv \bar{\mathbf{N}}_{d}^{T} \tilde{\mathbf{M}}\bar{\mathbf{N}}_{d} $$

(5a)

where

$$ \tilde{\mathbf{M}} \equiv \bar{\mathbf{N}}_{l}^{T}\mathbf{M}\bar{\mathbf{N}}_{l}. $$

(5b)

In Eq. (5b), the matrix $\tilde{\mathbf{M}}$ is referred here as the generalized mass matrix of the composite modules. Substituting the expressions for $\bar{\mathbf{N}}_{l}$ and the mass matrix $\mathbf{M}$ from Eq. (4) and Eq. (1) into Eq. (5b) and simplifying the terms, the symmetric matrix $\tilde{\mathbf{M}}$ is obtained:

$$ \tilde{\mathbf{M}} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \tilde{\bar{\mathbf{M}}}_{1} & & & & \mathit{sym} \\ \tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} & \tilde{\bar{\mathbf{M}}}_{2} & & & \\ \tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1} & \tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,2} & \tilde{\bar{\mathbf{M}}}_{3} & & \\ \vdots & \vdots & \ddots & \ddots & \\ \tilde{\bar{\mathbf{M}}}_{s}\bar{\mathbf{A}}_{s,1} & \tilde{\bar{\mathbf{M}}}_{s}\bar{\mathbf{A}}_{s,2} & \cdots & \tilde{\bar{\mathbf{M}}}_{s}\bar{\mathbf{A}}_{s,s - 1} & \tilde{\bar{\mathbf{M}}}_{s} \end{array}\displaystyle \right]\quad (\tilde{\bar{\mathbf{M}}}_{j}\bar{\mathbf{A}}_{j,i} \equiv \mathbf{O},\ \mbox{if}\ M_{j} \notin \boldsymbol{\gamma}_{i}) $$

(6)

where

$$ \tilde{\bar{\mathbf{M}}}_{i} = \bar{\mathbf{M}}_{i} + \sum_{j \in \gamma_{i}} \bar{\mathbf{A}}_{j,i}^{T}\bar{\mathbf{M}}_{j}\bar{\mathbf{A}}_{j,i}. $$

(7)

The $6n^{i} \times6n^{i}$ matrix $\tilde{\bar{\mathbf{M}}}_{i}$ is referred to as the mass matrix of the $i$th composite-module. It represents the mass and inertia properties of the system comprising rigidly connected links of modules which are upstream from the $i$th module, as depicted in Fig. 3 by the dotted boundary line. Note that $\bar{\mathbf{A}}_{i,j}$ in Eq. (7) is the $6n^{i} \times6n^{j}$ module-twist-propagation matrix defined in Appendix A.2. In Eq. (7), $\tilde{\bar{\mathbf{M}}}_{i}$ is expressed in terms of the module mass matrix $\bar{\mathbf{M}}_{j}$ of all the modules upstream from module $M_{i}$, i.e., $\bar{\mathbf{M}}_{j}$ for all $j \in \boldsymbol{\gamma}_{i}$. Due to introduction of the concept of kinematic module and the parent-child relationships explained in Sect. 2, it can be shown that $\tilde{\bar{\mathbf{M}}}_{i}$can be expressed recursively in terms of the already computed mass matrices of the composite-modules that are immediate children ($\boldsymbol{\xi}_{i}$) of the $i$th module, as shown in Fig. 3. If these composite modules are denoted by $\tilde{\bar{\mathbf{M}}}_{j}$, then for all $j \in \boldsymbol{\xi}_{i}$

$$ \tilde{\bar{\mathbf{M}}}_{i} = \left\{ \textstyle\begin{array}{l@{\quad}l} \bar{\mathbf{M}}_{i} + \sum_{j \in \boldsymbol{\xi}_{i}} \bar{\mathbf{A}}_{j,i}^{T}\tilde{\bar{\mathbf{M}}}_{j}\bar{\mathbf{A}}_{j,i} & \mbox{if}\ \boldsymbol{\xi}_{i} \ne \{\, \}, \\ \bar{\mathbf{M}}_{i} & \mbox{if}\ \boldsymbol{\xi}_{i} = \{\, \}, \end{array}\displaystyle \right. $$

(8)

where $\boldsymbol{\xi}_{i}$ denotes the array of children of module $M_{i}$. Note that the summation in Eq. (8) for $j \in \boldsymbol{\xi}_{i}$ is computationally more efficient in comparison to Eq. (7) for $j \in \boldsymbol{\gamma}_{i}$. If a module has no child, i.e., $\boldsymbol{\xi}_{i} = \{\,\}$, it is referred to as a leaf or terminal module. For the terminal modules, the mass matrix of the composite-module is simply equal to the module mass matrix, i.e., $\tilde{\bar{\mathbf{M}}}_{i} \equiv \bar{\mathbf{M}}_{i}$. Here the concept of composite-module is the generalization over a similar concept of composite body used in [8–10]. It may be shown that the mass matrix of the composite-body is a special case of Eq. (8), where each module has only one link, i.e., $n^{i} =1$, for $i =1, \ldots, s$. Finally, using the expression in Eq. (5a), i.e., $\mathbf{I} \equiv \bar{\mathbf{N}}_{d}^{T}\tilde{\mathbf{M}}\bar{\mathbf{N}}_{d}$, the block elements of the GIM are given by

$$ \mathbf{I} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{I}}_{1,1} & & & & \mathit{sym} \\ \bar{\mathbf{I}}_{2,1} & \bar{\mathbf{I}}_{2,2} & & & \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} & & \\ \vdots & \vdots & \ddots & \ddots & \\ \bar{\mathbf{I}}_{s,1} & \bar{\mathbf{I}}_{s,2} & \cdots & \bar{\mathbf{I}}_{s,s - 1} & \bar{\mathbf{I}}_{s,s} \end{array}\displaystyle \right] $$

(9)

where the $n^{i} \times n^{j}$ block element $\bar{\mathbf{I}}_{i,j}$ is given, for $i=1, \ldots, s$ and $j=1, \ldots, i$, as

$$ \bar{\mathbf{I}}_{i,j} \equiv \bar{\mathbf{I}}_{j,i} = \left\{ \textstyle\begin{array}{l@{\quad}l} \bar{\mathbf{N}}_{i}^{T}\tilde{\bar{\mathbf{M}}}_{i}\bar{\mathbf{A}}_{i,j}\bar{\mathbf{N}}_{j}, &\mbox{if}\ M_{i} \in \boldsymbol{\gamma}_{j}\ (\mbox{for}\ i = j,\ \bar{\mathbf{A}}_{i,j} = \mathbf{1}) ,\\ \mathbf{O}, &\mbox{otherwise}. \end{array}\displaystyle \right. $$

(10)

The analytical expression derived in Eq. (10) is the foundation for obtaining the analytical block decomposition of the GIM at module-level, and enables one to find analytical module-level inverse of the GIM and the inter- and intra-modular recursive forward dynamics algorithm. These will be presented in the subsequent sections.

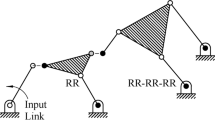
2.1 An illustration: the GIM of a tree-type gripper

For clearer understanding, the module-level expression of the GIM is derived for a tree-type 4-DOF gripper shown in Fig. 5. The gripper is divided into three modules, $M_{1}$, $M_{2}$, and $M_{3}$ whereas $M_{0}$ is the fixed-base. Using Eqs. (9) and (10), the GIM $\mathbf{I}$ is expressed as

$$ \mathbf{I} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{N}}_{1}^{T}\tilde{\bar{\mathbf{M}}}_{1}\bar{\mathbf{N}}_{1} & & \mathit{sym} \\ \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} & \\ \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{N}}_{3} \end{array}\displaystyle \right]. $$

(11)

Here $\mathbf{I}$ is the $4\times4$ GIM and $\bar{\mathbf{I}}_{3,2} = 0$ as $M_{3}$ does not belong to tree upstream from $M_{2}$, i.e., $M_{3} \notin \boldsymbol{\gamma}_{2}$. In Eq. (11), the block elements $\bar{\mathbf{N}}_{i}$ and $\bar{\mathbf{A}}_{j,i}$ are obtained using Eq. (A.7) in Appendix A.2:

$$ \begin{gathered} \bar{\mathbf{N}}_{1} \equiv \mathbf{p}_{1^{1}}, \qquad \bar{\mathbf{N}}_{2} \equiv \left[ \textstyle\begin{array}{c@{\quad}c} \mathbf{p}_{1^{2}} & \mathbf{0} \\ \mathbf{A}_{2^{2}1^{2}}\mathbf{p}_{1^{2}} & \mathbf{p}_{2^{2}} \end{array}\displaystyle \right], \qquad \bar{\mathbf{N}}_{3} \equiv \mathbf{p}_{1^{3}},\\ \bar{\mathbf{A}}_{2,1} \equiv \left[ \textstyle\begin{array}{c} \mathbf{A}_{1^{2}1^{1}} \\ \mathbf{A}_{2^{2}1^{1}} \end{array}\displaystyle \right],\quad \mbox{and}\quad \bar{\mathbf{A}}_{3,1} \equiv \mathbf{A}_{1^{3}1^{1}}. \end{gathered} $$

(12)

Moreover, the $6\times6$, $12\times12$ and $6\times6$ mass matrices of the composite-module $\tilde{\bar{\mathbf{M}}}_{3}$, $\tilde{\bar{\mathbf{M}}}_{2}$ and $\tilde{\bar{\mathbf{M}}}_{1}$, respectively, are obtained by using Eq. (8) as

$$ \tilde{\bar{\mathbf{M}}}_{3} = \bar{\mathbf{M}}_{3},\qquad \tilde{\bar{\mathbf{M}}}_{2} = \bar{\mathbf{M}}_{2},\qquad \tilde{\bar{\mathbf{M}}}_{1} = \bar{\mathbf{M}}_{1} + \sum_{j = 3,2} \bar{\mathbf{A}}_{j,1}^{T}\tilde{\bar{\mathbf{M}}}_{j}\bar{\mathbf{A}}_{j,1} $$

(13)

where the module mass matrices $\bar{\mathbf{M}}_{1}$, $\bar{\mathbf{M}}_{2}$ and $\bar{\mathbf{M}}_{3}$ are obtained from Eq. (2), i.e.,

$$ \bar{\mathbf{M}}_{1} \equiv \mathbf{M}_{1^{1}},\qquad \bar{\mathbf{M}}_{2} \equiv \left[ \textstyle\begin{array}{c@{\quad}c} \mathbf{M}_{1^{2}} & \mathbf{O} \\ \mathbf{O} & \mathbf{M}_{2^{2}} \end{array}\displaystyle \right], \qquad \bar{\mathbf{M}}_{3} \equiv \mathbf{M}_{1^{3}} . $$

(14)

Fig. 5

A robotic gripper and its modularization

3 Block decomposition of the GIM

The $\mathbf{UDU}^{T}$ decomposition, where $\mathbf{U}$ and $\mathbf{D}$ are the upper triangular and diagonal matrices, respectively, of the GIM of a serial-chain system was shown in [14]. A similar $\mathbf{L}^{T}\mathbf{DL}$ factorization for branched kinematic tree, where $\mathbf{L}$ is the lower triangular matrix, and hence $\mathbf{L}^{T}\equiv\mathbf{U}$, was proposed in [16]. Note here that the approach followed in [17] was numerical in contrast to the analytical approach taken in [14]. In both approaches the decomposition was carried out on link-level. More recently, a factorization was proposed in [17] for a tree consisting of a single main chain with short side branches for an optimal serial-parallel algorithm. As compared to link-level approaches in [14, 16], the module-level decomposition in the form of $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ is presented in this work for a tree-type multibody system. This provides suitable recursive module-level expressions to obtain the implicit inverse of the GIM resulting in a recursive forward dynamics algorithm. In contrast to [17], the proposed approach builds on the concept of kinematic module presented earlier in [12, 13], and emphasizes on analytical block decomposition and related physical interpretation.

The proposed $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition is based on the Block Reverse Gaussian Elimination (BRGE) of the GIM that generalizes the concept of the Reverse Gaussian Elimination (RGE) of the GIM proposed in [3]. The term “reverse” was used with the well-known Gaussian Elimination (GE), where the annihilation starts from the first column [7], because of starting of the annihilation from the $n$th (last) column of the matrix. In this paper, another adjective “block” is added to emphasize the point that the rules of annihilation are applied to the block matrices of the GIM arising out of the masses and inertia tensors of the links belonging to composite-module instead of the scalar terms of a serial-chain system arising out of the masses and inertias of a composite-body [10]. It actually helps in obtaining various element of the decomposed matrix by establishing recursive relationships from the terminal module or link to the zeroth module or link, a process otherwise is not possible with the conventional GE. The RGE or BRGE also preserves the sparsity pattern of the elements of the GIM into its factor $\bar{\mathbf{U}}$, and results into numerically stable algorithms. The BRGE of the GIM given by Eq. (9) starts with the annihilation of the $s$th block column and proceeds to the second block column by using Elementary Block Upper Triangular Matrices (EBUTMs), similar to the Elementary Upper Triangular Matrices (EUTMs) of [3], which in turn were adopted from the Elementary Lower Triangular Matrices used in the conventional process of GE [7].

3.1 The $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition of the GIM of a tree-type gripper

For the 3-module robotic gripper explained in Sect. 2.1, the GIM was obtained in Eq. (11), which is reproduced here:

$$ \mathbf{I} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{N}}_{1}^{T}\tilde{\bar{\mathbf{M}}}_{1}\bar{\mathbf{N}}_{1} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{N}}_{3} \\ \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} & \mathbf{O} \\ \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{N}}_{3} \end{array}\displaystyle \right] \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}_{1,1} & \bar{\mathbf{I}}_{1,2} & \bar{\mathbf{I}}_{1,3} \\ \bar{\mathbf{I}}_{2,1} & \bar{\mathbf{I}}_{2,2} & \bar{\mathbf{I}}_{2,3} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]. $$

(15)

As $M_{2}$ and $M_{3}$ are terminal modules, $\tilde{\bar{\mathbf{M}}}_{2} = \bar{\mathbf{M}}_{2}$ and $\tilde{\bar{\mathbf{M}}}_{3} = \bar{\mathbf{M}}_{3}$ from Eq. (8). In BRGE, the above GIM is converted into a lower block triangular matrix in two stages shown below:

$$ \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}_{1,1} & \bar{\mathbf{I}}_{1,2} & \bar{\mathbf{I}}_{1,3} \\ \bar{\mathbf{I}}_{2,1} & \bar{\mathbf{I}}_{2,2} & \bar{\mathbf{I}}_{2,3} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}} \stackrel{1\text{st stage}}{\Rightarrow} \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}^{(3)}_{1,1} & \bar{\mathbf{I}}^{(3)}_{1,2} & \mathbf{O} \\ \bar{\mathbf{I}}^{(3)}_{2,1} & \bar{\mathbf{I}}^{(3)}_{2,2} & \mathbf{O} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(3)}} \stackrel{2\text{nd stage}}{\Rightarrow} \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}^{(2)}_{1,1} & \mathbf{O} & \mathbf{O} \\ \bar{\mathbf{I}}^{(3)}_{2,1} & \bar{\mathbf{I}}^{(3)}_{2,2} & \mathbf{O} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(2)}} $$

(16)

where $\mathbf{I}^{(2)}$ is the resulting lower block triangular matrix, and $\bar{\mathbf{I}}_{3,3}$, $\bar{\mathbf{I}}^{(3)}_{2,2}$ and $\bar{\mathbf{I}}_{1,1}^{(2)}$ are the block pivots for the BRGE. The matrix $\mathbf{I}^{(2)}$ represents the matrix whose above block-diagonal elements till column 2 have been annihilated. The first stage of the BRGE started with $\bar{\mathbf{I}}_{3,3}$ as the block pivot which annihilated the block elements above it using the following matrix operations:

$$ \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & - \bar{\mathbf{U}}_{1,3} \\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{U}}_{2,3} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}_{3}} \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}_{1,1} & \bar{\mathbf{I}}_{1,2} & \bar{\mathbf{I}}_{1,3} \\ \bar{\mathbf{I}}_{2,1} & \bar{\mathbf{I}}_{2,2} & \bar{\mathbf{I}}_{2,3} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}} = \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}^{(3)}_{1,1} & \bar{\mathbf{I}}^{(3)}_{1,2} & \mathbf{O} \\ \bar{\mathbf{I}}^{(3)}_{2,1} & \bar{\mathbf{I}}^{(3)}_{2,2} & \mathbf{O} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(3)}} $$

(17)

where $\bar{\mathbf{U}}_{2,3} \equiv \bar{\mathbf{I}}_{2,3}\bar{\mathbf{I}}_{3,3}^{ - 1}$ and $\bar{\mathbf{U}}_{1,3} \equiv \bar{\mathbf{I}}_{1,3}\bar{\mathbf{I}}_{3,3}^{ - 1}$ are the block coefficient matrices applied for annihilation of $(2,3)$rd and $(1,3)$rd block elements of the GIM $\mathbf{I}$. Matrix $\bar{\mathbf{U}}_{3}$ is nothing but the EBUTM and $\bar{\mathbf{U}}_{2,3}$ and $\bar{\mathbf{U}}_{1,3}$ are obtained using block elements of $\mathbf{I}$ in Eq. (15) as

$$ \textstyle\begin{array}{l} \bar{\mathbf{U}}_{2,3} = \bar{\mathbf{I}}_{2,3}\bar{\mathbf{I}}_{3,3}^{ - 1} = \mathbf{O} \quad (\mbox{because}\ \bar{\mathbf{I}}_{2,3} = \mathbf{O}), \\ \bar{\mathbf{U}}_{1,3} = \bar{\mathbf{I}}_{1,3}\bar{\mathbf{I}}_{3,3}^{ - 1} = \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{N}}_{3} \bar{\mathbf{I}}_{3,3}^{ - 1} = \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \end{array} $$

(18)

where $\bar{\boldsymbol{\Psi}}_{3} \equiv \tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{N}}_{3}$ and $\hat{\bar{\mathbf{I}}}_{3} \equiv \bar{\mathbf{I}}_{3,3}$. The block elements $\bar{\mathbf{I}}^{(3)}_{2,2}$ and $\bar{\mathbf{I}}^{(3)}_{21}$are then obtained from Eqs. (15) and (17):

$$ \bar{\mathbf{I}}^{(3)}_{2,2} = \bar{\mathbf{I}}_{2,2} - \bar{\mathbf{U}}_{2,3}\bar{\mathbf{I}}_{3,2} = \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} \quad\mbox{because}\quad \bar{\mathbf{I}}_{3,2} = \mathbf{O} $$

(19)

and

$$ \bar{\mathbf{I}}^{(3)}_{2,1} = \bar{\mathbf{I}}_{2,1} - \bar{\mathbf{U}}_{2,3}\bar{\mathbf{I}}_{3,1} = \bar{\mathbf{N}}_{2}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} = \bar{\boldsymbol{\Psi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} $$

(20)

where $\bar{\boldsymbol{\Psi}}_{2} = \tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2}$. Next, $\bar{\mathbf{I}}^{(3)}_{1,2}$ and $\bar{\mathbf{I}}^{(3)}_{1,1}$ are obtained:

$$ \bar{\mathbf{I}}^{(3)}_{1,2} = \bar{\mathbf{I}}_{1,2} - \bar{\mathbf{U}}_{1,3}\bar{\mathbf{I}}_{3,2} = \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} = \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} $$

(21)

and

$$ \bar{\mathbf{I}}^{(3)}_{1,1} = \bar{\mathbf{I}}_{1,1} - \bar{\mathbf{U}}_{1,3}\bar{\mathbf{I}}_{3,1} = \bar{\mathbf{N}}_{1}^{T}\tilde{\bar{\mathbf{M}}}_{1}\bar{\mathbf{N}}_{1} - \bigl\{ \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \bigr\} \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1}. $$

(22)

Substituting $\tilde{\bar{\mathbf{M}}}_{1} = \bar{\mathbf{M}}_{1} + \bar{\mathbf{A}}_{2,1}^{T}\tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} + \bar{\mathbf{A}}_{3,1}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1}$ one obtains

$$\begin{aligned} \bar{\mathbf{I}}^{(3)}_{1,1} & = \bar{\mathbf{N}}_{1}^{T} \bigl\{ \bar{\mathbf{M}}_{1} + \bar{\mathbf{A}}_{2,1}^{T} \tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} + \bar{ \mathbf{A}}_{3,1}^{T}\tilde{\bar{\mathbf{M}}}_{3}\bar{ \mathbf{A}}_{3,1} \bigr\} \bar{\mathbf{N}}_{1} - \bigl\{ \bar{ \mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1} \bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \bigr\} \bar{\mathbf{N}}_{3}^{T}\tilde{\bar{\mathbf{M}}}_{3} \bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} \\ &= \bar{\mathbf{N}}_{1}^{T} \bigl[ \bigl\{ \bar{ \mathbf{M}}_{1} + \bar{\mathbf{A}}_{2,1}^{T}\tilde{ \bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} \bigr\} + \bar{ \mathbf{A}}_{3,1}^{T} \bigl\{ \mathbf{1} - \bar{\boldsymbol{\Psi}}_{3}\hat{ \bar{\mathbf{I}}}_{3}^{ - 1} \bar{\mathbf{N}}_{3}^{T} \bigr\} \tilde{\bar{\mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1} \bigr]\bar{\mathbf{N}}_{1} \\ &= \bar{\mathbf{N}}_{1}^{T} \bigl[ \bigl\{ \bar{ \mathbf{M}}_{1} + \bar{\mathbf{A}}_{2,1}^{T}\tilde{ \bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} \bigr\} + \bar{ \mathbf{A}}_{3,1}^{T}\bar{\boldsymbol{\Phi}}_{3}\tilde{\bar{ \mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1} \bigr]\bar{ \mathbf{N}}_{1} \end{aligned}$$

(23)

where

$$ \bar{\boldsymbol{\Phi}}_{3} \equiv \mathbf{1} - \bar{\boldsymbol{\Psi}}_{3}\hat{\bar{\mathbf{I}}}_{3}^{ - 1} \bar{\mathbf{N}}_{3}^{T}. $$

(24)

The second stage of the BRGE started with $\bar{\mathbf{I}}^{(3)}_{2,2}$ of Eq. (19) as the block pivot element which annihilated the block elements of the second column above it. The following matrix operation was used:

$$ \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & - \bar{\mathbf{U}}_{1,2} & \mathbf{O} \\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}_{2}} \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}^{(3)}_{1,1} & \bar{\mathbf{I}}^{(3)}_{1,2} & \mathbf{O} \\ \bar{\mathbf{I}}^{(3)}_{2,1} & \bar{\mathbf{I}}^{(3)}_{2,2} & \mathbf{O} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(3)}} = \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \bar{\mathbf{I}}^{(2)}_{1,1} & \mathbf{O} & \mathbf{O} \\ \bar{\mathbf{I}}^{(3)}_{2,1} & \bar{\mathbf{I}}^{(3)}_{2,2} & \mathbf{O} \\ \bar{\mathbf{I}}_{3,1} & \bar{\mathbf{I}}_{3,2} & \bar{\mathbf{I}}_{3,3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(2)}} $$

(25)

where

$$ \bar{\mathbf{U}}_{1,2} = \bar{\mathbf{I}}_{1,2}^{(3)} \bigl\{ \bar{\mathbf{I}}_{2,2}^{(3)} \bigr\} ^{ - 1} = \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1} \bar{\boldsymbol{\Psi}}_{2} \bigl\{ \bar{\mathbf{N}}_{2}^{T} \tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{N}}_{2} \bigr\} ^{ - 1} = \bar{\mathbf{N}}_{1}^{T}\bar{ \mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1}. $$

(26)

In Eq. (26), $\hat{\bar{\mathbf{I}}}_{2} \equiv \bar{\mathbf{I}}_{3,3}^{(3)}$ was used for simplicity in notation. The recursive expression to calculate $\bar{\mathbf{I}}^{(2)}_{1,1}$ is given by

$$\begin{aligned} \bar{\mathbf{I}}^{(2)}_{11} =& \bar{\mathbf{I}}^{(3)}_{11} - \bar{\mathbf{U}}_{12}\bar{\mathbf{I}}^{(3)}_{21} \\ =& \bar{\mathbf{N}}_{1}^{T} \bigl[ \bigl\{ \bar{ \mathbf{M}}_{1} + \bar{\mathbf{A}}_{2,1}^{T}\tilde{ \bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} \bigr\} + \bar{ \mathbf{A}}_{3,1}^{T}\bar{\boldsymbol{\Phi}}_{3}\tilde{\bar{ \mathbf{M}}}_{3}\bar{\mathbf{A}}_{3,1} \bigr]\bar{ \mathbf{N}}_{1} - \bigl\{ \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1} \bigr\} \bar{\mathbf{N}}_{2}^{T} \tilde{\bar{\mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1}\bar{ \mathbf{N}}_{1} \\ =& \bar{\mathbf{N}}_{1}^{T} \bigl[ \bar{ \mathbf{M}}_{1} + \bar{\mathbf{A}}_{3,1}^{T}\bar{ \boldsymbol{\Phi}}_{3}\tilde{\bar{\mathbf{M}}}_{3}\bar{ \mathbf{A}}_{3,1} + \bar{\mathbf{A}}_{2,1}^{T} \bigl\{ \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2}\hat{\bar{\mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bigr\} \tilde{\bar{ \mathbf{M}}}_{2}\bar{\mathbf{A}}_{2,1} \bigr]\bar{ \mathbf{N}}_{1} \\ =& \bar{\mathbf{N}}_{1}^{T} \bigl[ \bar{ \mathbf{M}}_{1} + \bar{\mathbf{A}}_{3,1}^{T}\bar{ \boldsymbol{\Phi}}_{3}\tilde{\bar{\mathbf{M}}}_{3}\bar{ \mathbf{A}}_{3,1} + \bar{\mathbf{A}}_{2,1}^{T}\bar{ \boldsymbol{\Phi}}_{2}\tilde{\bar{\mathbf{M}}}_{2}\bar{ \mathbf{A}}_{2,1} \bigr]\bar{\mathbf{N}}_{1}\quad \bigl( \mbox{where}\ \bar{\boldsymbol{\Phi}}_{2} \equiv \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2}\hat{ \bar{\mathbf{I}}}_{2}^{ - 1}\bar{\mathbf{N}}_{2}^{T} \bigr) \\ =& \bar{\mathbf{N}}_{1}^{T}\hat{\bar{\mathbf{M}}}_{1} \bar{\mathbf{N}}_{1} \equiv \hat{\bar{\mathbf{I}}}_{1} \end{aligned}$$

(27)

where $\hat{\bar{\mathbf{I}}}_{1}$ is the third block pivot-element and

$$ \hat{\bar{\mathbf{M}}}_{1} \equiv \bar{\mathbf{M}}_{1} + \sum_{j = 3,2} \bar{\mathbf{A}}_{j,1}^{T}\bar{\boldsymbol{\Phi}}_{j}\hat{\bar{\mathbf{M}}}_{j}\bar{\mathbf{A}}_{j,1}. $$

(28)

Note that, for the terminal modules $M_{2}$ and $M_{3}$, $\hat{\bar{\mathbf{M}}}_{2} = \tilde{\bar{\mathbf{M}}}_{2} = \bar{\mathbf{M}}_{2}$, $\hat{\bar{\mathbf{M}}}_{3} = \tilde{\bar{\mathbf{M}}}_{3} = \bar{\mathbf{M}}_{3}$. We have now obtained a block lower triangular matrix as a result of the BRGE of $\mathbf{I}$ as

$$ \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & - \bar{\mathbf{U}}_{1,2} & \mathbf{O} \\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}_{2}} \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & - \bar{\mathbf{U}}_{1,3} \\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{U}}_{2,3} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}_{3}}\mathbf{I} = \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1} & \mathbf{O} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \hat{\bar{\mathbf{I}}}_{2} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{3}^{T}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \hat{\bar{\mathbf{I}}}_{3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(2)}} $$

(29)

where

$$ \textstyle\begin{array}{l} \bar{\mathbf{U}}_{1,j} \equiv \bar{\mathbf{N}}_{i}^{T}\bar{\mathbf{A}}_{j,i}^{T}\bar{\boldsymbol{\Psi}}_{j}\hat{\bar{\mathbf{I}}}_{j}^{ - 1}\quad (\mbox{for}\ j = 2,3) \quad\mbox{and}\quad \bar{\mathbf{U}}_{2,3} \equiv \mathbf{O}, \\ \hat{\bar{\mathbf{I}}}_{i} \equiv \bar{\mathbf{N}}_{i}^{T}\hat{\bar{\mathbf{M}}}_{i}\bar{\mathbf{N}}_{i} \quad(\mbox{for}\ i = 1,2,3) . \end{array} $$

(30)

Equation (29) can be rewritten in terms of $\mathbf{I}$ using the inverses of the EBUTMs $\bar{\mathbf{U}}_{2}$ and $\bar{\mathbf{U}}_{3}$ as

$$ \mathbf{I} = \bar{\mathbf{U}}_{3}^{ - 1}\bar{\mathbf{U}}_{2}^{ - 1}\underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1} & \mathbf{O} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \hat{\bar{\mathbf{I}}}_{2} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{3}^{T}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \hat{\bar{\mathbf{I}}}_{3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(2)}} . $$

(31)

It is a simple matter to observe that the EBUTMs in Eq. (29) have the following trivial inverses:

$$ \bar{\mathbf{U}}_{2}^{ - 1} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \bar{\mathbf{U}}_{1,2} & \mathbf{O} \\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right], \qquad \bar{\mathbf{U}}_{3}^{ - 1} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & \bar{\mathbf{U}}_{1,3} \\ \mathbf{O} & \mathbf{1} & \bar{\mathbf{U}}_{2,3} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(32)

Substitution of Eq. (32) into Eq. (31) yields

$$ \mathbf{I} = \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2}\hat{\bar{\mathbf{I}}}_{2}^{ - 1} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}} = \bar{\mathbf{U}}_{3}^{ - 1}\bar{\mathbf{U}}_{2}^{ - 1}}\underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1} & \mathbf{O} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \hat{\bar{\mathbf{I}}}_{2} & \mathbf{O} \\ \bar{\boldsymbol{\Psi}}_{3}^{T}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \hat{\bar{\mathbf{I}}}_{3} \end{array}\displaystyle \right]} _{\mathbf{I}^{(2)}}. $$

(33)

Now, the lower block triangular matrix $\mathbf{I}^{(2)}$ in Eq. (33) for the symmetric GIM, $\mathbf{I}$, can be shown to be equal to $\mathbf{I}^{(2)} = \bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$. As a result, $\mathbf{I}$ is decomposed as $\mathbf{I} = \bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$, i.e.,

$$ \mathbf{I} = \underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2}\hat{\bar{\mathbf{I}}}_{2}^{ - 1} & \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}}\underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1} & \mathbf{O} & \mathbf{O} \\ \mathbf{O} & \hat{\bar{\mathbf{I}}}_{2} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \hat{\bar{\mathbf{I}}}_{3} \end{array}\displaystyle \right]} _{\bar{\mathbf{D}}}\underbrace{\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & \mathbf{O} \\ \hat{\bar{\mathbf{I}}}_{2}^{ - 1}\bar{\boldsymbol{\Psi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}\bar{\mathbf{N}}_{1} & \mathbf{1} & \mathbf{O} \\ \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\bar{\boldsymbol{\Psi}}_{3}^{T}\bar{\mathbf{A}}_{3,1}\bar{\mathbf{N}}_{1} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]} _{\bar{\mathbf{U}}^{T}}. $$

(34)

The derivation of Eq. (34) on the modular level is one of the main contributions of this paper, which is generalized in the next sub section.

3.2 The $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition of multi-module tree-type system

In this subsection, we build on the results of the previous subsection to obtain the $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition of an $n-$DOF multi-module tree-type system. As an extension of Eq. (16), a tree-type system with $s$ modules will require annihilation from the $s$th block column to the second block column using EBUTMs. This is expressed as

$$ \bar{\mathbf{U}}_{2} \cdots \bar{\mathbf{U}}_{i} \cdots \bar{\mathbf{U}}_{s}\mathbf{I} = \mathbf{I}^{(2)}. $$

(35)

The $n \times n$ matrices $\bar{\mathbf{U}}_{i}$ and $\mathbf{I}^{(2)}$ are the upper and lower block triangular matrices, as demonstrated in Eq. (29). The matrix $\mathbf{I}^{(2)}$ is the one whose block elements above the diagonal elements were annihilated. The expression of the $n \times n$ EBUTM $\bar{\mathbf{U}}_{i}$, similar to Eqs. (17) and (25), is derived:

$$ \bar{\mathbf{U}}_{i} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} &\mathbf{O}&\cdots & - \bar{\mathbf{U}}_{1,i} & { \cdots} & \mathbf{O}\\ & { \ddots} & \vdots & \vdots&&{ \vdots}\\ && \mathbf{1}_{i - 1} &- \bar{\mathbf{U}}_{i - 1,i} & \cdots&\mathbf{O} \\ &&& \mathbf{1}_{i} & {\cdots} &\mathbf{O}\\ &&&&\ddots&\vdots\\ & \mathbf{O}'\mathrm{s} &&& & \mathbf{1}_{s} \end{array}\displaystyle \right] \equiv \mathbf{1} - \bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T}. $$

(36)

Here the $n \times n^{i}$ matrices $\bar{\mathbf{U}}'_{i}$ and $\bar{\mathbf{V}}_{i}$ have the following representation:

$$\begin{aligned} \bar{\mathbf{U}}'_{i} \equiv &\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{U}}_{1,i}^{T} & \cdots & \bar{\mathbf{U}}_{i - 1,i}^{T} & \mathbf{O} & \cdots & \mathbf{O} \end{array}\displaystyle \right]^{T} , \end{aligned}$$

(37)

$$\begin{aligned} \bar{\mathbf{V}}_{i} \equiv &\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{O} & \cdots & \mathbf{O} & \mathbf{1}_{i} & \cdots & \mathbf{O} \end{array}\displaystyle \right]^{T}. \end{aligned}$$

(38)

In Eq. (36) $\bar{\mathbf{U}}_{j,i}$ is the $n^{j} \times n^{i}$ block coefficient matrix applied for the annihilation of ($j,i$)th block element of the updated GIM obtained as a result of the annihilation of the ($i+1$)th block column. Note that $\bar{\mathbf{U}}_{j,i}$ is nothing but the ($j,i$)th block element times the inverse of the ($i,i$)th block element (or pivot) of the updated GIM. Equation (35) can then be re-written as

$$ \mathbf{I} = \bar{\mathbf{U}}\mathbf{I}^{(2)}\quad \mbox{where}\ \bar{\mathbf{U}} \equiv \bar{\mathbf{U}}_{s}^{ - 1} \cdots \bar{\mathbf{U}}_{i}^{ - 1} \cdots \bar{\mathbf{U}}_{2}^{ - 1} $$

(39)

where $\bar{\mathbf{U}}_{i}^{ - 1}$ is the inverse of the EBUTM $\bar{\mathbf{U}}_{i}$ which can easily be obtained:

$$ \bar{\mathbf{U}}_{i}^{ - 1} = \bigl(\mathbf{1} - \bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T}\bigr)^{ - 1} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & \mathbf{O}&{ \cdots} & \bar{\mathbf{U}}_{1,i} & \cdots& \mathbf{O} \\ & { \ddots} &\vdots&\vdots&&\vdots\\ && \mathbf{1}_{i - 1}& \bar{\mathbf{U}}_{i - 1,i} & \cdots &\mathbf{O} \\ & & &\mathbf{1}_{i} & { \cdots}& \mathbf{O} \\ &&&&\ddots&\vdots\\ & \mathbf{O}'\mathrm{s} & & && \mathbf{1}_{s} \end{array}\displaystyle \right] \equiv \mathbf{1} + \bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T}. $$

(40)

The multiplication of the two inverses of the neighboring EBUTM is simply

$$ \bar{\mathbf{U}}_{i}^{ - 1}\bar{\mathbf{U}}_{i - 1}^{ - 1} = \bigl(\mathbf{1} + \bar{\mathbf{U}}'_{i}\bar{ \mathbf{V}}_{i}^{T}\bigr) \bigl(\mathbf{1} + \bar{\mathbf{U}}'_{i - 1} \bar{\mathbf{V}}_{i - 1}^{T}\bigr) = \mathbf{1} + \bar{ \mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T} + \bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{V}}_{i - 1}^{T}. $$

(41)

It is worth noting that in Eq. (41), the term $\bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T}\bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{V}}_{i - 1}^{T}$ vanishes as $\bar{\mathbf{V}}_{i}^{T}\bar{\mathbf{U}}'_{i - 1} = \mathbf{O}$. This is evident from Eqs. (37) and (38). Similarly, it can be shown that the product of $\bar{\mathbf{U}}_{s}^{ - 1} \cdots \bar{\mathbf{U}}_{2}^{ - 1}$ is obtained:

$$ \bar{\mathbf{U}} = \mathbf{1} + \bar{\mathbf{U}}'_{s}\bar{\mathbf{V}}_{s}^{T} +\cdots + \bar{\mathbf{U}}'_{2}\bar{\mathbf{V}}_{2}^{T}. $$

(42)

Substituting Eqs. (37) and (38) into Eq. (42), the inverse of the EBUTMs, namely, $\bar{\mathbf{U}}$, can be represented in the matrix form as

$$ \bar{\mathbf{U}} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & \bar{\mathbf{U}}_{1,2}&{ \cdots} & \bar{\mathbf{U}}_{1,i} & { \cdots}& \bar{\mathbf{U}}_{1,s} \\ & { \ddots}&\vdots&\vdots&&\vdots\\ &&\mathbf{1}_{i - 1} & \bar{\mathbf{U}}_{i - 1,i} & \cdots& \bar{\mathbf{U}}_{i - 1,s} \\ & & &\mathbf{1}_{i} & { \cdots} &\bar{\mathbf{U}}_{i,s} \\ &&&&\ddots&\vdots\\ & \mathbf{O}'\mathrm{s} & & && \mathbf{1}_{s} \end{array}\displaystyle \right]. $$

(43)

Since the GIM $\mathbf{I}$ is a symmetric matrix [7], similar to Eq. (34), the lower block triangular matrix $\mathbf{I}^{(2)}$ can be shown to be equal to $\mathbf{I}^{(2)} = \bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$. Hence, the GIM for the $n$-DOF tree-type system with $s$ module is decomposed as

$$ \mathbf{I} = \bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T} $$

(44)

where the expression for the block upper triangular matrix $\bar{\mathbf{U}}$ is obtained in (43) and the block diagonal matrix $\bar{\mathbf{D}}$ has the representation

$$ \bar{\mathbf{D}} = \mathrm{diag}\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1} & \hat{\bar{\mathbf{I}}}_{2} & \cdots & \hat{\bar{\mathbf{I}}}_{s} \end{array}\displaystyle \right]. $$

(45)

Note that the $n^{i} \times n^{i}$ matrix $\hat{\bar{\mathbf{I}}}_{i}$ is essentially the block pivot of the BRGE.

It is worth noting that the elements of the matrices $\mathbf{U}$ and $\mathbf{D}$ resulting from the UDU ^T decomposition of the GIM of a serial system [10] are scalars, whereas the elements of the matrices $\bar{\mathbf{U}}$ and $\bar{\mathbf{D}}$, i.e., $\bar{\mathbf{U}}_{i,j}$ and $\hat{\bar{\mathbf{I}}}_{i}$, in Eqs. (43) and (45), respectively, are matrices. Their recursive expressions are obtained by performing the BRGE analytically, similar to Sect. 3.1, as

$$ \begin{aligned} \bar{\mathbf{U}}_{i,j} &\equiv \left\{ \textstyle\begin{array}{l@{\quad}l} \bar{\mathbf{N}}_{i}^{T}\bar{\mathbf{A}}_{j,i}^{T}\bar{\boldsymbol{\Psi}}_{j}\hat{\bar{\mathbf{I}}}_{j}^{ - 1}, &\mbox{if}\ j \in \boldsymbol{\gamma}_{i}, \\ \mathbf{O}, &\mbox{otherwise}, \end{array}\displaystyle \right. \\ \hat{\bar{\mathbf{I}}}_{i} &\equiv \bar{\mathbf{N}}_{i}^{T}\hat{\bar{\mathbf{M}}}_{i}\bar{\mathbf{N}}_{i}. \end{aligned} $$

(46)

For the $i$th module, the $6n^{i} \times n^{i}$ matrices $\bar{\boldsymbol{\Psi}}_{i}$ needed in Eq. (46) is given by

$$ \bar{\boldsymbol{\Psi}}_{i} = \hat{\bar{\mathbf{M}}}_{i}\bar{\mathbf{N}}_{i} $$

(47)

where the $6n^{i} \times6n^{i}$ matrix $\hat{\bar{\mathbf{M}}}_{i}$ in Eq. (47) contains the mass and inertia properties of the articulated-module $i$, which is obtained similar to Eq. (28) as

$$ \hat{\bar{\mathbf{M}}}_{i} = \left\{ \textstyle\begin{array}{l@{\quad}l} \bar{\mathbf{M}}_{i} + \sum_{j \in \boldsymbol{\xi}_{i}} \bar{\mathbf{A}}_{j,i}^{T}\bar{\boldsymbol{\Phi}}_{j}\hat{\bar{\mathbf{M}}}_{j}\bar{\mathbf{A}}_{j,i} & \mbox{if}\ \boldsymbol{\xi}_{i} \ne \{\, \}, \\ \bar{\mathbf{M}}_{i} & \mbox{if}\ \boldsymbol{\xi}_{i} = \{ \,\}, \end{array}\displaystyle \right. $$

(48)

the articulated-module corresponding to $\hat{\bar{\mathbf{M}}}_{i}$ is nothing but the composite-module of Fig. 3 in which fixed joints are replaced with the actual joints. The $n^{i} \times n^{i}$ matrix $\hat{\bar{\mathbf{I}}}_{i}$ of Eq. (46), on the other hand, may be interpreted as the generalized inertia matrix of the articulated-module. The relationship between the matrices $\hat{\bar{\mathbf{M}}}_{i}$ and $\hat{\bar{\mathbf{I}}}_{i}$ can be viewed similar to that between $\mathbf{M}$ and $\mathbf{I}$ of Eqs. (1) and (9), respectively. Moreover, the $6n^{i} \times6n^{i}$ matrix $\bar{\boldsymbol{\Phi}}_{j}$ in Eq. (48) is obtained:

$$ \bar{\boldsymbol{\Phi}}_{j} \equiv \mathbf{1} - \bar{\boldsymbol{\Psi}}_{j}\hat{\bar{\mathbf{I}}}_{j}^{ - 1} \bar{\mathbf{N}}_{j}^{T}. $$

(49)

Matrix $\bar{\boldsymbol{\Phi}}_{j}$ is referred to as the matrix of the articulated-module transformation. Similar matrix, however, at link-level was also derived in [3, 10]. The one proposed here is more generic as it is applicable to any multi-module tree-type system. Comparing Eqs. (8) and (48), it may be seen that it is $\bar{\boldsymbol{\Phi}}_{j}$, which distinguishes mass matrix of the articulated module $\hat{\bar{\mathbf{M}}}_{i}$ from the mass matrix of the composite-module $\tilde{\bar{\mathbf{M}}}_{i}$. Again the concept of the articulated-body inertia [8–10] is generalized here to a tree-type multibody system consisting of several kinematic modules. If each module of a tree-type system has only one link, the matrix of the articulated-module degenerates to the articulated-body inertia of [3].

4 Analytical block inversion of the GIM

The block $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition of the GIM of a tree-type multibody system presented in the previous section also facilitates its block analytical inversion. According to Eq. (44) the inverse is given by

$$ \mathbf{I}^{ - 1} = \bar{\mathbf{U}}^{ - T}\bar{\mathbf{D}}^{ - 1}\bar{\mathbf{U}}^{ - 1} $$

(50)

where $\bar{\mathbf{D}}^{ - 1}$ is block diagonal matrix and $\bar{\mathbf{U}}^{ - 1} \equiv \bar{\mathbf{U}}_{2} \cdots \bar{\mathbf{U}}_{i} \cdots \bar{\mathbf{U}}_{s}$ is the block upper triangular matrix given by Eq. (35). Using the definition of the EBUTM given by Eq. (36), the multiplication of the two neighboring EBUTMs is obtained:

$$ \begin{aligned}[b] \bar{\mathbf{U}}_{i - 1}\bar{\mathbf{U}}_{i} &= \bigl(\mathbf{1} - \bar{\mathbf{U}}'_{i - 1}\bar{ \mathbf{V}}_{i - 1}^{T}\bigr) \bigl(\mathbf{1} - \bar{\mathbf{U}}'_{i} \bar{\mathbf{V}}_{i}^{T}\bigr) \\ &= \mathbf{1} - \bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{V}}_{i - 1}^{T} - \bigl(\bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T} - \bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{V}}_{i - 1}^{T} \bar{\mathbf{U}}'_{i}\bar{\mathbf{V}}_{i}^{T} \bigr) \\ &= \mathbf{1} - \bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{V}}_{i - 1}^{T} - \hat{\bar{\mathbf{U}}}_{i}\bar{\mathbf{V}}_{i}^{T} \end{aligned} $$

(51)

where $\hat{\bar{\mathbf{U}}}_{i} \equiv \bar{\mathbf{U}}'_{i} - \bar{\mathbf{U}}'_{i - 1}(\bar{\mathbf{V}}_{i - 1}^{T}\bar{\mathbf{U}}'_{i})\bar{\mathbf{V}}_{i}^{T} = \bar{\mathbf{U}}'_{i} - \bar{\mathbf{U}}'_{i - 1}\bar{\mathbf{U}}_{i - 1,i}\bar{\mathbf{V}}_{i}^{T}$ in which unlike in Eq. (41) where $\bar{\mathbf{V}}_{i}^{T}\bar{\mathbf{U}}'_{i - 1} = \mathbf{O}$, the term $\bar{\mathbf{V}}_{i - 1}^{T}\bar{\mathbf{U}}'_{i}$ does not vanish, i.e., $\bar{\mathbf{V}}_{i - 1}^{T}\bar{\mathbf{U}}'_{i} \ne \mathbf{O}$. However, its expression can easily be obtained from Eqs. (37) and (38) as $\bar{\mathbf{V}}_{i - 1}^{T}\bar{\mathbf{U}}'_{i} = \bar{\mathbf{U}}_{i - 1,i}$, which is the last non-zero block element of $\bar{\mathbf{U}}'_{i}$. The non-vanishing $\bar{\mathbf{V}}_{i - 1}^{T}\bar{\mathbf{U}}'_{i}$ makes the calculations for Eq. (51) more involved. The product of the EBUTMs, Eq. (51), is then generalized to

$$ \bar{\mathbf{U}}^{ - 1} = \bar{\mathbf{U}}_{2}\cdots \bar{\mathbf{U}}_{i}\cdots \bar{\mathbf{U}}_{s} = \mathbf{1} + \hat{\bar{\mathbf{U}}}_{2}\bar{\mathbf{V}}_{2}^{T} + \cdots \hat{\bar{\mathbf{U}}}_{i}\bar{\mathbf{V}}_{i}^{T} \cdots + \hat{\bar{\mathbf{U}}}_{s}\bar{\mathbf{V}}_{s}^{T} $$

(52)

where $\hat{\bar{\mathbf{U}}}_{i}$, for $i=2,\ldots, s$, is given by

$$ \hat{\bar{\mathbf{U}}}_{i} = - (\bar{\mathbf{U}}'_{i} - \hat{\bar{\mathbf{U}}}_{i - 1}\bar{\mathbf{U}}_{i - 1,i} -\cdots - \hat{\bar{\mathbf{U}}}_{2}\bar{\mathbf{U}}_{2,i});\quad \hat{\bar{\mathbf{U}}}_{2} = \bar{\mathbf{U}}'_{2} \ \mbox{and}\ \bar{\mathbf{U}}_{j,i} = \mathbf{O} \ \mbox{if}\ i \notin \boldsymbol{\gamma}_{j}. $$

(53)

Based on Eqs. (52) and (53), the $n \times n$ block upper-triangular and diagonal matrices $\bar{\mathbf{U}}^{ - 1}$ and $\bar{\mathbf{D}}^{ - 1}$ have the following representation:

$$ \bar{\mathbf{U}}^{ - 1} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & \hat{\bar{\mathbf{U}}}_{1,2} & \cdots & \hat{\bar{\mathbf{U}}}_{1,s} \\ & \mathbf{1}_{1} & & \vdots \\ & & \ddots & \hat{\bar{\mathbf{U}}}_{s - 1,s} \\ \mathbf{O}'\mathrm{s} & & & \mathbf{1}_{s} \end{array}\displaystyle \right], \quad\mbox{and}\quad \bar{\mathbf{D}}^{ - 1} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1}^{ - 1} & & \mathbf{O}'\mathrm{s} & \\ & \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & & \\ & & \ddots & \\ & \mathbf{O}'\mathrm{s} & & \hat{\bar{\mathbf{I}}}_{s}^{ - 1} \end{array}\displaystyle \right] $$

(54)

where the block elements $\hat{\bar{\mathbf{U}}}_{i,j}$ and $\hat{\bar{\mathbf{I}}}_{i}^{ - 1}$ are obtained by performing analytical steps, for inverse similar to the one used to obtain Eq. (46), i.e.,

$$ \begin{aligned} \hat{\bar{\mathbf{U}}}_{i,j} &\equiv \left\{ \textstyle\begin{array}{l@{\quad}l} - \bar{\mathbf{N}}_{i}^{T}\hat{\bar{\mathbf{A}}}_{j,i}^{T}\bar{\boldsymbol{\Psi}}_{j}\hat{\bar{\mathbf{I}}}_{j}^{ - 1}, &\mbox{if}\ j \in \boldsymbol{\gamma}_{i}, \\ \mathbf{O}, &\mbox{otherwise} , \end{array}\displaystyle \right. \\ \hat{\bar{\mathbf{I}}}_{i}^{ - 1} &\equiv \bigl(\bar{\mathbf{N}}_{i}^{T}\hat{\bar{\mathbf{M}}}_{i}\bar{\mathbf{N}}_{i}\bigr)^{ - 1}. \end{aligned} $$

(55)

In Eq. (55), note that the second term $\hat{\bar{\mathbf{A}}}_{j,i}$ is different from $\bar{\mathbf{A}}_{j,i}$ in Eq. (46). The matrix $\hat{\bar{\mathbf{A}}}_{j,i}$ may be interpreted as the articulated module-twist propagation matrix and has the following representation:

$$ \hat{\bar{\mathbf{A}}}_{j,i} \equiv \hat{\bar{\mathbf{A}}}_{j,h}\hat{\bar{\boldsymbol{\Phi}}}_{h}^{T}\hat{\bar{\mathbf{A}}}_{h,i} \quad\mbox{where}\ \hat{\bar{\boldsymbol{\Phi}}}_{h} = \mathbf{1} - \bar{\boldsymbol{\Psi}}_{h} \hat{\bar{\mathbf{I}}}_{h}^{ - 1}\bar{\mathbf{N}}_{h}^{T}. $$

(56)

In Eq. (56), $h$ is any intermediate serially connected module between modules $j$ and $i$. The proof of Eqs. (55) and (56) is given in Appendix A.3.

Interestingly, the module-twist propagation matrix $\bar{\mathbf{A}}_{j,i}$ has the property of $\bar{\mathbf{A}}_{j,i} = \bar{\mathbf{A}}_{j,h}\bar{\mathbf{A}}_{h,i}$, whereas the matrix of the articulated module transformation $\bar{\boldsymbol{\Phi}}_{h}$ makes the property of matrix $\hat{\bar{\mathbf{A}}}_{j,i}$ different which is shown in Eq. (56). For any two adjoining modules, say, module $j$ and its parent $\boldsymbol{\beta}_{j}$, the articulated module-twist propagation matrix $\hat{\bar{\mathbf{A}}}_{j,\beta}$ is simply equal to the module-twist propagation matrix, i.e.,

$$ \hat{\bar{\mathbf{A}}}_{j,\beta} = \bar{\mathbf{A}}_{j,\beta}. $$

(57)

4.1 An illustration: analytical inversion of the GIM of the gripper

The $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition of the GIM for the Gripper, shown in Fig. 5, is derived in Eq. (34). The analytical inverse of the decomposed GIM in terms of the $4\times4$ $\bar{\mathbf{U}}^{ - 1}$ and the $4\times4$ $\bar{\mathbf{D}}^{ - 1}$ is obtained from Eqs. (54) and (55):

$$ \begin{aligned} \bar{\mathbf{U}}^{ - 1} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1}_{1} & - \bar{\mathbf{N}}_{1}^{T}\hat{\bar{\mathbf{A}}}_{2,1}^{T}\bar{\boldsymbol{\Psi}}_{2}\hat{\bar{\mathbf{I}}}_{2}^{ - 1} & - \bar{\mathbf{N}}_{1}^{T}\hat{\bar{\mathbf{A}}}_{3,1}^{T}\bar{\boldsymbol{\Psi}}_{3}\hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ & \mathbf{1}_{2} & \mathbf{O} \\ \mathbf{O}'\mathrm{s} & & \mathbf{1}_{3} \end{array}\displaystyle \right] \quad\mbox{and}\\ \bar{\mathbf{D}}^{ - 1} &= \mathrm{diag}\left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \hat{\bar{\mathbf{I}}}_{1}^{ - 1} & \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & \cdots & \hat{\bar{\mathbf{I}}}_{s}^{ - 1} \end{array}\displaystyle \right] \end{aligned} $$

(58)

where the $12\times6$ and the $6\times6$ matrices $\hat{\bar{\mathbf{A}}}_{2,1}^{T}$ and $\hat{\bar{\mathbf{A}}}_{3,1}^{T}$, respectively, are available from Eq. (56), namely,

$$ \hat{\bar{\mathbf{A}}}_{2,1} \equiv \bar{\mathbf{A}}_{2,1}, \quad\mbox{and}\quad \hat{\bar{\mathbf{A}}}_{3,1} \equiv \bar{\mathbf{A}}_{3,1}. $$

(59)

In Eq. (59), module $M_{1}$ is the parent of modules $M_{2}$ and $M_{3}$. Hence, the expressions for $\hat{\bar{\mathbf{A}}}_{2,1}$ and $\hat{\bar{\mathbf{A}}}_{3,1}$ are simplified to their corresponding module twist-propagation matrices, i.e., $\bar{\mathbf{A}}_{2,1}$ and $\bar{\mathbf{A}}_{3,1}$, respectively.

A numerical validation of Eqs. (34) and (58) is provided in Appendix A.4.

5 Intra- and inter-modular recursive forward dynamics

One of the purposes of inverting the GIM was to perform forward dynamics calculations as $\ddot{\mathbf{q}} = \mathbf{I}^{ - 1}\boldsymbol{\varphi }$, where $\ddot{\mathbf{q}}$ is the vector of joint accelerations, $\mathbf{I}$ is the GIM, and $\boldsymbol{\varphi }$ is the vector of all external and other generalized forces. As mentioned in Introduction, a straight-forward numerical inversion leads to $O(n^{3})$ algorithm. However, due to the existence of the recursive expressions of the decomposed matrices of the GIM, one can easily derive a set of recursive relations which have complexity of $O(n)$, thus, making it extremely efficient when $n$ is very large [18]. Besides, it was shown in [15] how the RGE based algorithm can provide numerically stable results.

It is pointed out here that the recursive algorithms are also available in the literature, e.g., [8–10], which use only body-level recursions. However, in the present work, the recursion is obtained first amongst the modules, followed by the body- or link-level recursions inside a module. In fact, the latter approach encapsulates the former. As result, the problem is solved in a much more elegant manner where a tree-type system has several modules, which in turn have several bodies or links in them. This was possible, mainly due to the existence of several module-level expressions in the matrices $\bar{\mathbf{U}}$, $\bar{\mathbf{D}}$, and $\bar{\mathbf{U}}^{ - 1}$. Using Eq. (50), the joint accelerations $\ddot{\mathbf{q}}$ are solved in three steps, namely,

$$ \textstyle\begin{array}{l@{\quad}l} (\mathrm{i}) &\hat{\bar{\boldsymbol{\varphi }}} \equiv \bar{\mathbf{U}}^{ - 1}\boldsymbol{\varphi }, \\ (\mathrm{ii}) &\tilde{\bar{\boldsymbol{\varphi }}} = \bar{\mathbf{D}}^{ - 1}\hat{\bar{\boldsymbol{\varphi }}}, \\ (\mathrm{iii}) &\ddot{\mathbf{q}} = \bar{\mathbf{U}}^{ - T}\tilde{\bar{\boldsymbol{\varphi }}}. \end{array} $$

(60)

Equation (60) involves backward and forward recursions, which are explained in [12]. For a general tree-type multibody system, Appendix A.5 highlights the necessary steps. Based on the forward dynamics calculations given in Appendix A.5, computation complexity was found and compared in Fig. 6 with other algorithms reported in the literature. The details of the computation complexity are provided in [12] and avoided here for brevity. It was found that the proposed analytical inversion leads to much superior algorithm, both in terms of efficiency [20] and numerical stability [15]. Whereas Fig. 6 demonstrates the superiority of the computational efficiency, Sect. 6 elaborates on the numerical stability of the proposed $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ based simulation algorithm.

Fig. 6

Performance of the proposed forward dynamics algorithm

5.1 Simulation of spatial biped

As a numerical example, simulation results of a spatial biped shown in Fig. 7 were generated whose geometrical and inertial parameters are given in Table 1. The biped has spherical joints at the hips, revolute joints at the knees, and universal joints at the ankles. Biped motion was analyzed for a single support phase where one of the feet (the supporting foot during walking) is assumed to have no relative motion with respect to the ground. This is indicated in the figure with hatched lines. Hence, the biped dynamics can be solved as an open tree-type system. The biped is divided into three modules, $M_{0}$, $M_{1}$ and $M_{2}$, as shown in Fig. 7(b). Such modularization helps one to treat module $M_{1}$ and $M_{2}$ in a similar manner as each module consists of three links, one spherical joint, one revolute joint, and one universal joint. Hence computationally one can use the same instructions. This results in a more elegant approach.

Fig. 7

A 7-link biped and its module architecture

Table 1 Model parameters for the biped

In order to perform dynamic analysis, the desired trajectories of the swing foot $(x_{h}, y_{h})$ and the Center-of-Mass (COM) $(x_{0}, y_{0})$ of the trunk were synthesized first. The trunk’s COM trajectories were designed based on the Inverted Pendulum Model [22]. For $0 \le t \le T$,

$$ \begin{aligned} x_{0}(t) = x_{0}(0)\cosh ( wt ) + \biggl( \frac{\dot{x}_{0}(0)}{w} \biggr)\sinh ( wt ), \\ y_{0}(t) = y_{0}(0)\cosh ( wt ) + \biggl( \frac{\dot{y}_{0}(0)}{w} \biggr)\sinh ( wt ) \end{aligned} $$

(61)

where $w = \sqrt{g / z_{0}}$ and $g = 9.81~\mbox{m}/\mbox{s}^{2}$. Equation (61) assumes that the mass of the biped is concentrated at the trunk, the feet remain horizontal throughout the robot’s motion and the trunk moves horizontally with constant height from the ground. For the spatial biped under study, the co-ordinates of COM $x_{0} (0)$, $y_{0} (0)$ at $t=0$ and $z_{0}$, and $T$ are assumed to be −0.15 m, 0.10 m, and 0.80 m, and 1 s, respectively. In order to obtain the periodic and symmetric biped pattern, the following repeatability conditions were used:

$$ \begin{aligned} &x_{h}(0) = - x_{h}(T);\qquad\dot{x}_{h}(0) = \dot{x}_{h}(T), \\ &y_{h}(0) = y_{h}(T);\qquad\dot{y}_{h}(0) = - \dot{y}_{h}(T) . \end{aligned} $$

(62)

The above repeatability conditions help in obtaining the values of the initial velocities $\dot{x}_{h}(0)$ and $\dot{y}_{h}(0)$, i.e.,

$$ \dot{x}_{h}(0) = \frac{1 + e^{ - wT}}{1 - e^{ - wT}}wx_{h}(0) \quad\mbox{and}\quad \dot{y}_{h}(0) = \frac{1 - e^{ - wT}}{1 + e^{ - wT}}wy_{h}(0). $$

(63)

The trajectories of the ankle of the swing foot $(x_{a}, y_{a})$ were defined as cosine functions, namely,

$$ x_{a}(t) = - \frac{l_{s}}{2}\cos \biggl( \frac{\pi}{T}t \biggr),\qquad z_{a}(t) = \frac{h_{f}}{2} \biggl[ 1 - \cos \biggl( \frac{2\pi}{T}t \biggr) \biggr] $$

(64)

where stride length ($l_{s}$) and maximum foot height ($h_{f}$) were assumed to be 0.60 m and 0.15 m, respectively. The resulting trajectories of the COM of the trunk and the ankle of the swing foot are shown in Fig. 8.

Fig. 8

Designed trajectories of the trunk’s COM and the ankle of the spatial biped

Based on the motion of the trunk and ankles, the desired joint trajectories, i.e., $\boldsymbol{\theta}_{1^{1}} \equiv [\begin{array}{c@{\ }c} \theta_{1_{1}^{1}} & \theta_{1_{2}^{1}} \end{array}]^{T}$, $\theta_{2^{1}}$, $\boldsymbol{\theta}_{3^{1}} \equiv [\begin{array}{c@{\ }c@{\ }c} \theta_{3_{1}^{1}} & \theta_{3_{2}^{1}} & \theta_{3_{3}^{1}} \end{array}]^{T}$, $\boldsymbol{\theta}_{1^{2}} \equiv [\begin{array}{c@{\ }c@{\ }c} \theta_{1_{1}^{2}} & \theta_{1_{2}^{2}} & \theta_{1_{3}^{2}} \end{array}]^{T}$, $\theta_{2^{2}}$, $\boldsymbol{\theta}_{3^{2}} \equiv [\begin{array}{c@{\ }c} \theta_{3_{1}^{2}} & \theta_{3_{2}^{2}} \end{array}]^{T}$, were calculated using the inverse kinematics relationships. The joint trajectories thus obtained are shown in Fig. 9 as desired trajectories.

Fig. 9

Simulated and desired joint angles for the biped

Forced simulation was performed next, where the motion of the biped was studied under the application of the joint torques calculated using the computed torque control approach to track the above trajectories. Note that the values of the proportional and derivative gains were taken as $K_{p} = 225$ and $K_{d} = 30$ for all the joints. The joint motions were calculated using the forward dynamics module of ReDySim [19]. The plots for the simulated joint angles are shown in Fig. 9 along with the desired one. It can be seen that the simulated joint angles match with the desired joint angles.

6 Numerical stability

As explained in the previous section, the block $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition lends its utility in developing efficient forward dynamics algorithms. Numerical stability of the forward dynamics algorithm is an important issue, and it directly affects the accuracy of the results [23]. An algorithm is called numerically stable, if it is stable in the mixed forward–backward error sense [24]. It is worth noting that the numerical stability mainly depends on the method of solving a problem rather than the order of computational complexity of the solver. It will be shown in this section that the algorithms developed based on the proposed BRGE is more stable than the algorithm based on the conventional GE [7]. As is evident from (60), the forward dynamics problem requires computation of the joint accelerations from the set of constrained equations of motion, i.e.,

$$ \ddot{\mathbf{q}} = \mathbf{I}^{ - 1}\boldsymbol{\varphi }. $$

(65)

If the GIM $\mathbf{I}$ is ill-conditioned, small perturbations in the system of equations can produce relatively large changes in the numerical solutions of $\ddot{\mathbf{q}}$. Mathematically, the solution must satisfy the following:

$$ (\ddot{\mathbf{q}} + \boldsymbol{\delta} \ddot{\mathbf{q}}) = \mathbf{I}^{ - 1}(\boldsymbol{\varphi } + \boldsymbol{\delta \varphi } ) $$

(66)

where $\boldsymbol{\delta} \ddot{\mathbf{q}}$ denotes the errors in solutions due to errors in the input denoted with $\boldsymbol{\delta \varphi }$. Then the relative error in the computation of the joint accelerations is given by [24]

$$ \frac{ \Vert \boldsymbol{\delta} \ddot{\mathbf{q}} \Vert }{ \Vert \ddot{\mathbf{q}} \Vert } \le \kappa (\mathbf{I})\frac{ \Vert \boldsymbol{\delta} \boldsymbol{\varphi } \Vert }{ \Vert \boldsymbol{\varphi } \Vert } $$

(67)

where $\kappa (\mathbf{I}) = \Vert \mathbf{I}^{ - 1} \Vert \Vert \mathbf{I} \Vert$ and $\Vert \mathbf{I} \Vert$ represents the norm of the GIM $\mathbf{I}$. The term $\kappa (\mathbf{I})$is defined as the condition number of the GIM which determines the scale factor by which the relative change in $\ddot{\mathbf{q}}$ is magnified. With the increase in the number of bodies or link ($n$), the increase in condition number of the GIM is of order $n^{4}$ [25]. If the condition number of the GIM is very high, it is ill-conditioned or close to singular and there can be a loss of accuracy in the computation of the joint accelerations. In order to investigate the numerical stability of the proposed algorithm based on the $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition, a comparative study of three different methods to calculate the joint accelerations was undertaken. They are:

• 1. Gaussian Elimination (Numerical) or GE-N.

• 2. Reverse Gaussian Elimination (Numerical) or RGE-N.

• 3. Block Reverse Gaussian Elimination (Analytical) or BRGE-A.

Note that ‘N’ and ‘A’ are used to emphasize the fact that the steps were performed numerically and analytically, respectively.

In order to test the stability of GE-N, RGE-N, and BRGE-A based solvers, gripper and biped were considered. Since all the above three methods performed well with the double-precision accuracy, the floating-point accuracy was considered to stress upon the numerical errors, leading to clear differentiation between the results generated by the different methods. This is justified as actual computations at the hardware-level are generally performed with the floating-point accuracy. The results of $\ddot{\mathbf{q}}(0)$, were generated first using MATLAB’s command ‘$\mathbf{I}(0)\backslash \boldsymbol{\varphi}(0)$’, with double precision accuracy. These were assumed to be “correct” for the comparison of other results with floating point accuracy. The values of $\mathbf{I}(0)$, $\boldsymbol{\varphi}(0)$, and $\ddot{\mathbf{q}}(0)$ (obtained with double precision accuracy) for the gripper are shown in Table 3 for the model parameters given in Table 2.

Table 2 Model parameters for the robotic gripper

Table 3 Solution of $\ddot{\mathbf{q}}(0)$ with double precision accuracy for the gripper

The effect of varying floating point accuracy on the solution of the joint accelerations using GE-N, RGE-N and BRGE-A based solvers was studied and the results are reported in Table 4. Similar studies were performed in [15] for long-chain up to 1,00,000 DOF. The table shows the joint accelerations obtained using the corresponding solvers and the percentage errors relative to $\ddot{\mathbf{q}}(0)$. For a given floating point accuracy, the percentage errors, denoted by $\boldsymbol{\delta}_{\ddot{\mathbf{q}}}$ are defined as

$$ \boldsymbol{\delta}_{\ddot{\mathbf{q}}} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \delta_{\ddot{q}_{1}} & \delta_{\ddot{q}_{2}} & \delta_{\ddot{q}_{3}} \end{array}\displaystyle \right]^{T} $$

(68)

where

$$ \delta_{\ddot{q}_{i}} = \frac{\ddot{q}_{iF}(0) - \ddot{q}_{i}(0)}{\ddot{q}_{i}( 0 )} \times 100 $$

(69)

for $i = 1, 2, 3$. The $i$th joint acceleration, $\ddot{q}_{iF}(0)$, was obtained with different floating-point round-offs, and $\ddot{q}_{i}(0)$ is the solution obtained using MATLAB with double-precision accuracy. Here, the absolute error is avoided to emphasize on how $\ddot{q}_{iF}(0)$ varies around $\ddot{q}_{i}(0)$. It is evident from Table 4 that the percentage error is lower for the BRGE-A and RGA-N based solvers while the GE-N-based solver showed higher deviations. As the floating point accuracy of the computing system was made higher, the solution for joint accelerations obtained from the RGE-N- and RGE-A-based solvers converged faster to the desired solution $\ddot{\mathbf{q}}(0)$ than the GE-N-based solver. Table 5 shows the norm of $\boldsymbol{\delta}_{\ddot{\mathbf{q}}}$ for both the gripper and the biped with varying floating point accuracy. It is evident that the BRGE-A based solver converges faster even for lower floating point accuracy in comparison to GE-N. Finally, Figs. 10(a–b) show the change in total instantaneous energy per unit mass.

Fig. 10

Change in total instantaneous energy per unit mass, $\delta_{M}( t )$, using GE-N, RGE-N and BRGE-A

Table 4 Comparison of GE-N, RGE-N and RGE-A with variable floating point round off for the gripper

Table 5 Comparison of norm ($\boldsymbol{\delta}_{\ddot{\mathbf{q}}}$) for GE-N, RGE-N and RGE-A

It is clearly evident that RGE-N- and BRGE-A-based solvers perform better than the GE-N-based solver, while the BRGE-A-based solver performs even better than RGE-N-based solver. This proves the efficacy of the proposed approach.

7 Conclusions

The module-level analytical expressions of the inverted inertia matrix of a tree-type multibody system are presented with its application in forward dynamics and simulation purposes. The expressions were possible due to the introduction of the concept of kinematic modules, and subsequently the module-level Decoupled Natural Orthogonal Complement (DeNOC) matrices. At the end, the extension of the $\mathbf{UDU}^{T}$ decomposition applied to serial-chain systems has been demonstrated with the tree-type systems, in which case the module-level decomposition of the GIM is referred as $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$ decomposition.

Hence, a new perspective towards the decomposition of the GIM is given which provides a framework to model a complex multi-branched multibody system, namely, a tree-type, by decomposing it into a set of smaller serial modules. These serial modules can then be treated using the vast knowledge available in the open literature for their forward dynamics. In this paper, the one based on the DeNOC matrices for the serial-chain systems was used. While investigating the performances of the numerical algorithms it was observed that the proposed simulation algorithms using the $\bar{\mathbf{U}}\bar{\mathbf{D}}\bar{\mathbf{U}}^{T}$decomposition is not only efficient but also numerically stable. In conclusion, what has been proposed and shown in this paper is the generalization of the earlier work in this domain [8, 10] where even a complex system was considered consisting of many links instead of a smaller set of serial-chain modules. It is much more convenient to deal with a smaller set of modules which in turn has a smaller set of links or bodies. Hence, the gradual development of the dynamics has been possible in this paper with their possible interpretations, and level-by-level, namely, link-to-module and module-to-system, interactions. As shown in the literature earlier, the present concept is equally applicable to closed-loop multibody systems where appropriate joints are cut to make the closed-loop system open in order to be able to treat it as a tree-type open architecture for which the methodology presented in this paper is applicable. The future work would focus on the use of the proposed block decomposition in obtaining hybrid parallel-recursive algorithm and predicating stability of the system of multibody systems.

Appendix A

The inter- and intra-modular kinematic constraints leading to the module-level DeNOC matrices are obtained in Appendices A.1 and A.2, respectively. Appendix A.3 provides an illustration of the recursive block inverse of $\bar{\mathbf{U}}$. Appendix A.4 presents a numerical validation of the decomposed GIM, whereas the steps of the forward dynamics algorithm are provided in Appendix A.5.

1.1 A.1 Intra-modular velocity constraints

As mentioned in the beginning of Sect. 2, module $i$, for $i= 1, \ldots, s$, in a tree-type system contains only serially connected links. Let us consider the $k$th link in the $i$th module, denoted #$k^{i}$, connected to the link #$(k -1)^{i}$, by a 1-DOF revolute or prismatic joint $k^{i}$, as shown in Fig. 11. The six-dimensional vector of twist associated with the angular velocity, $\boldsymbol{\omega}_{k^{i}}$, and linear velocity, $\dot{\mathbf{o}}_{k^{i}}$, of the origin of #$k^{i}$ is defined as $\mathbf{t}_{k^{i}} \equiv [\begin{array}{c@{\ }c} \boldsymbol{\omega}_{k^{i}}^{T} & \dot{\mathbf{o}}_{k^{i}}^{T} \end{array}]^{T}$. Next, the twist of #$k^{i}$, $\mathbf{t}_{k^{i}}$, can be written in terms of the twist of #$(k-1)^{i}$, $\mathbf{t}_{(k - 1)^{i}}$, as

$$ \mathbf{t}_{k^{i}} = \mathbf{A}_{k^{i},(k - 1)^{i}}\mathbf{t}_{(k - 1)^{i}} + \mathbf{p}_{k^{i}}\dot{\theta}_{k^{i}}. $$

(A.1)

In Eq. (A.1), $\dot{\theta}_{k^{i}}$ is the time rate of change of the angular or translational displacement of the $k$th joint depending on the type of joint, i.e., revolute or prismatic, respectively. The matrix $\mathbf{A}_{k^{i},(k - 1)^{i}}$ is the $6\times6$ twist-propagation matrix, and $\mathbf{p}_{k^{i}}$ is the six-dimensional join motion-propagation vector. They are given by

$$ \mathbf{A}_{k^{i},(k - 1)^{i}} \equiv \left[ \textstyle\begin{array}{c@{\quad}c} \mathbf{1} & \mathbf{O} \\ \tilde{\mathbf{a}}_{k^{i},(k - 1)^{i}} & \mathbf{1} \end{array}\displaystyle \right], \quad\mbox{and}\quad \mathbf{p}_{k^{i}} \equiv \left\{ \textstyle\begin{array}{l@{\quad}l} \left[ \textstyle\begin{array}{c} \mathbf{e}_{k^{i}}\\ \mathbf{0} \end{array}\displaystyle \right], &\mbox{if joint is revolute}, \\ \left[ \textstyle\begin{array}{c} \mathbf{0} \\ \mathbf{e}_{k^{i}} \end{array}\displaystyle \right], & \mbox{if joint is prismatic} \end{array}\displaystyle \right. $$

(A.2)

where $\tilde{\mathbf{a}}_{k^{i},(k - 1)^{i}}$ is the $3\times3$ cross-product tensor associated with vector $\mathbf{a}_{k^{i},(k - 1)^{i}}$, and $\mathbf{e}_{k^{i}}$ is the unit vector along the axis of rotation or translation of the joint $k^{i}$. Next, the vectors of module-twist and the independent module-joint-rates for the $n^{i}$-coupled links of the $i$th serial module are defined as

$$ \bar{\mathbf{t}}_{i} \equiv \left[ \textstyle\begin{array}{c} \mathbf{t}_{1^{i}} \\ \vdots\\ \mathbf{t}_{k^{i}} \\ \vdots\\ \mathbf{t}_{n^{i}} \end{array}\displaystyle \right] \quad\mbox{and}\quad \dot{\bar{\mathbf{q}}}_{i} \equiv \left[ \textstyle\begin{array}{c} \dot{\theta}_{1^{i}}\\ \vdots\\ \dot{\theta}_{k^{i}} \\ \vdots\\ \dot{\theta}_{n^{i}} \end{array}\displaystyle \right] $$

(A.3)

where $\bar{\mathbf{t}}_{i}$ and $\dot{\bar{\mathbf{q}}}_{i}$ are the $6n^{i}$- and $n^{i}$-dimensional vectors, respectively. Substituting Eq. (A.1) into Eq. (A.3), for $k^{i} =1^{i}, \ldots,n^{i}$, the expression for the generalized twist of a serial module, $\bar{\mathbf{t}}_{i}$, is obtained [10]:

$$ \bar{\mathbf{t}}_{i} = \bar{\mathbf{N}}_{i}\dot{\bar{\mathbf{q}}}_{i} \quad \mbox{where}\ \bar{\mathbf{N}}_{i} = \bar{\mathbf{N}}_{i,l}\bar{\mathbf{N}}_{i,d}. $$

(A.4)

In Eq. (A.4), $6n^{i} \times6n^{i}$ and $6n^{i} \times n^{i}$ matrices $\bar{\mathbf{N}}_{i,l}$ and $\bar{\mathbf{N}}_{i,d}$ are given by

$$ \begin{aligned} \bar{\mathbf{N}}_{i,l} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1} & &\mathbf{O} & &\cdots & \mathbf{O} \\ \mathbf{A}_{2^{i},1^{i}} & { \ddots} &\mathbf{1} & &\ddots & \vdots\\ &\ddots&&&&\\ \vdots && \mathbf{A}_{k^{i},(k - 1)^{i}} && \ddots & \mathbf{O}\\ &&&\ddots&&\\ \mathbf{A}_{n^{i},1^{i}} & &\cdots & &\mathbf{A}_{n^{i},(n - 1)^{i}} & \mathbf{1} \end{array}\displaystyle \right] \quad\mbox{and}\\ \bar{\mathbf{N}}_{i,d} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{p}_{1^{i}} & &&& \mathbf{0}'\mathrm{s}\\ & { \ddots}&&&\\ && \mathbf{p}_{k^{i}} &&\\ &&&{ \ddots}&\\ \mathbf{0}'\mathrm{s}&&& & \mathbf{p}_{n^{i}} \end{array}\displaystyle \right]. \end{aligned} $$

(A.5)

The matrices $\bar{\mathbf{N}}_{i,l}$ and $\bar{\mathbf{N}}_{i,d}$ are referred here as the Decoupled Natural Orthogonal Complement (DeNOC) matrices of the serial-module, which are nothing but those reported in [10] for a serial robot.

Fig. 11

Links #$k^{i}$ and $\#(k-1)^{i}$ coupled by joint $k^{i}$ in $i$th module

1.2 A.2 Inter-modular velocity constraints

It is worth noting that Eq. (A.4) represents the twists of the links in the $i$th module if it emanates from the ground. However, in a tree-type system, each module, other than the base, is a child module, e.g., $M_{i}$ in Fig. 1(b), which contains serially connected links and emerges from the last link of its parent module $M_{\beta}$. Hence, the velocity constraints between the modules, i.e., at inter-modular level, will be derived in this section as an extension of the expression derived in Eq. (A.4). For the module $M_{i}$, the $6n^{i}$-dimensional vector of module-twist, $\bar{\mathbf{t}}_{i}$, which has $n^{i}$ link twists, and the $n^{i}$-dimensional vector of module-joint-rate, $\dot{\bar{\mathbf{q}}}_{i}$, having $n^{i}$ joint rates are defined in Eq. (A.3). Next, it is shown that the module-twist $\bar{\mathbf{t}}_{i}$, for $M_{i}$, can be written in terms of the module-twist $\bar{\mathbf{t}}_{\beta}$ (or $\bar{\mathbf{t}}_{\beta_{i}}$) of its parent $M_{\beta}$ as

$$ \bar{\mathbf{t}}_{i} = \bar{\mathbf{A}}_{i,\beta} \bar{\mathbf{t}}_{\beta_{i}} + \bar{\mathbf{N}}_{i}\dot{\bar{\mathbf{q}}}_{i} $$

(A.6)

where $\bar{\mathbf{A}}_{i,\beta}$ and $\bar{\mathbf{N}}_{i}$ are the $6n^{i} \times6n^{\beta}$ module-twist propagation and $6n^{i} \times n^{i}$ module-joint-motion propagation matrices, respectively, which are given by

$$ \begin{aligned} \bar{\mathbf{A}}_{i,\beta} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{O}& \cdots & \mathbf{O} & \mathbf{A}_{1^{i},n^{\beta}} \\ \vdots&&\vdots&\vdots\\ \mathbf{O}& & \mathbf{O}&\mathbf{A}_{k^{i},n^{\beta}} \\ \vdots&&\vdots&\vdots\\ \mathbf{O} & \cdots & \mathbf{O} & \mathbf{A}_{n^{i},n^{\beta}} \end{array}\displaystyle \right] \quad\mbox{and}\\ \bar{\mathbf{N}}_{i} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{p}_{1^{i}} && \mathbf{0} & &\cdots & \mathbf{0} \\ &\ddots&&&&\\ \mathbf{A}_{2^{i},1^{i}}\mathbf{p}_{1^{i}} & & \mathbf{p}_{(k - 1)^{i}} & &\ddots & \vdots \\ &\ddots&&&&\\ \vdots & & \mathbf{A}_{k^{i},(k - 1)^{i}}\mathbf{p}_{(k - 1)^{i}} && \ddots & \mathbf{0} \\ &&&\ddots&&\\ \mathbf{A}_{n^{i},1^{i}}\mathbf{p}_{1^{i}} & &\cdots & & \mathbf{A}_{n^{i},(n - 1)^{i}}\mathbf{p}_{(n - 1)^{i}} & \mathbf{p}_{n^{i}} \end{array}\displaystyle \right]. \end{aligned} $$

(A.7)

In Eq. (A.7), $\bar{\mathbf{A}}_{i,\beta}$ propagates the twist of the parent module ($\beta$th) to the child module ($i$th); the last column contains the twist propagation matrix from the $n$th link of the $\beta$th module wherefrom the $i$th module emanates, to the different links of the $i$th module. Matrix $\mathbf{A}_{k^{i},n^{\beta}}$ in the expression of $\bar{\mathbf{A}}_{i,\beta}$ denotes the $6\times6$ twist-propagation matrix from the twist of link #$n^{\beta}$ (last link in the $\beta$th module) in module $M_{\beta}$ to the twist of link #$k^{i}$ in module $M_{i}$. Moreover, $\mathbf{A}_{k^{i},(k - 1)^{i}}$ and $\mathbf{p}_{k^{i}}$ are defined in Eq. (A.2). Next, considering the links and joints of all the modules, the generalized twist vector, $\mathbf{t}$, consisting of all module-twists, and the generalized joint-rate vector, $\dot{\mathbf{q}}$, consisting of all module-joint-rates are defined as

$$ \mathbf{t} \equiv \left[ \textstyle\begin{array}{c} \bar{\mathbf{t}}_{1}\\ \vdots \\ \bar{\mathbf{t}}_{s} \end{array}\displaystyle \right] \quad\mbox{and}\quad \dot{\mathbf{q}} \equiv \left[ \textstyle\begin{array}{c} \dot{\bar{\mathbf{q}}}_{1} \\ \vdots \\ \dot{\bar{\mathbf{q}}}_{s} \end{array}\displaystyle \right]. $$

(A.8)

In Eq. (A.8), the vector of module-twists $\bar{\mathbf{t}}_{i}$ and module-joint-rates $\dot{\bar{\mathbf{q}}}_{i}$ contain link twists and joint rates, respectively, as defined in Eq. (A.3). Substituting Eq. (A.6) into Eq. (A.8), for $i = 1, \ldots, s$, the generalized twist $\mathbf{t}$ is expressed as

$$ \mathbf{t} = \bar{\mathbf{A}}\mathbf{t} + \bar{\mathbf{N}}_{d}\dot{\mathbf{q}} $$

(A.9)

where $\bar{\mathbf{A}}$ and $\bar{\mathbf{N}}_{d}$ are the $6n \times6n$ and $6n \times n$ matrices, and they are given as

$$ \begin{aligned} \bar{\mathbf{A}} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{O} & &&& & \mathbf{O}'\mathrm{s} \\ &\ddots&&&&\\ \bar{\mathbf{A}}_{2,\beta} & & \mathbf{O} & & &\\ &\ddots&&&&\\ && \bar{\mathbf{A}}_{i,\beta} && \ddots & \\ &&&\ddots&&\\ \mathbf{O}'\mathrm{s} & & && \bar{\mathbf{A}}_{s,\beta} & \mathbf{O} \end{array}\displaystyle \right], \quad\mbox{and}\\ \bar{\mathbf{N}}_{d} &\equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \bar{\mathbf{N}}_{1} & && &\mathbf{O}'\mathrm{s} \\ & { \ddots}&&&\\ && \bar{\mathbf{N}}_{i} &&\\ &&&\ddots&\\ \mathbf{O}'\mathrm{s} & & && \bar{\mathbf{N}}_{s} \end{array}\displaystyle \right]. \end{aligned} $$

(A.10)

In Eq. (A.10), $\beta$ in $\bar{\mathbf{A}}_{i,\beta}$ corresponds to the parent of $i$, for $i=1, \ldots,s$. Rearranging Eq. (A.10), the $6n$-dimensional generalized twist is given by

$$ \mathbf{t} = \bar{\mathbf{N}}_{l}\bar{\mathbf{N}}_{d}\dot{\mathbf{q}},\quad \mbox{where}\ \bar{\mathbf{N}}_{l} = (1 - \bar{\mathbf{A}})^{ - 1}. $$

(A.11)

The $6n \times6n$ matrix $\bar{\mathbf{N}}_{l}$ can easily be obtained

$$ \bar{\mathbf{N}}_{l} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1}_{1} & & & &\\ \bar{\mathbf{A}}_{2,1} & \mathbf{1}_{2} & & \mathbf{O}'\mathrm{s}& \\ \bar{\mathbf{A}}_{3,1} & \bar{\mathbf{A}}_{3,2} & \mathbf{1}_{3} & &\\ \vdots & \vdots & \ddots & \ddots& \\ \bar{\mathbf{A}}_{s,1} & \bar{\mathbf{A}}_{s,2} & \cdots & \bar{\mathbf{A}}_{s,s - 1} & \mathbf{1}_{s} \end{array}\displaystyle \right] $$

(A.12)

where $1_{i}$ represents the $6n^{i} \times6n^{i}$ identity matrix, and $\mathbf{O}$ is the null matrix of compatible dimension. Moreover, $\bar{\mathbf{A}}_{i,j}$ and $\bar{\mathbf{N}}_{i}$ are the $6n^{i} \times6n^{j}$ module-twist propagation and the $6n^{i} \times n^{i}$ module-joint-motion propagation matrices, in line with the twist-propagation matrix and joint-motion propagation vector from one link to the neighboring link connected by a single-degree-of-freedom joint [10]. The term $\bar{\mathbf{A}}_{i,j}$, defined similar to $\bar{\mathbf{A}}_{i,\beta}$ in Eq. (A.7), propagates the twist of the $j$th module relative to the $i$th one, where $\bar{\mathbf{A}}_{j,i} \equiv \mathbf{O}$ if module $M_{j}$ does not belong to the set $\boldsymbol{\gamma}_{i}$ of all modules originating from $M_{i}$, as shown in Fig. 3. The matrices $\bar{\mathbf{N}}_{l}$ and $\bar{\mathbf{N}}_{d}$ of Eq. (A.11) are nothing but the DeNOC matrices for the multi-modular tree-type system under study, rather than the multi-link system.

1.3 A.3 An illustration of recursive block inverse of $\bar{\mathbf{U}}$

The inverse of the block upper triangular matrix $\bar{\mathbf{U}}$ can be obtained from Eq. (39) as

$$ \bar{\mathbf{U}}^{ - 1} \equiv \bar{\mathbf{U}}_{2} \cdots \bar{\mathbf{U}}_{i} \cdots \bar{\mathbf{U}}_{s} \equiv \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{1} & \hat{\bar{\mathbf{U}}}_{1,2} & \cdots & \hat{\bar{\mathbf{U}}}_{1,s} \\ \mathbf{O} & \mathbf{1} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \hat{\bar{\mathbf{U}}}_{s - 1,s} \\ \mathbf{O} & \cdots & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.13)

In order to comprehend recursive relationship for the block elements $\hat{\bar{\mathbf{U}}}_{i,j}$, the tree-type system should have at least three serially connected modules. The example of gripper is simple enough as it contains only two serially connected module sets, i.e., ($M_{1}, M_{2}$) and ($M_{1}, M_{3}$). Therefore, let us consider a simplest system with three serially connected modules $M_{1}$, $M_{2}$ and $M_{3}$. For such a three module system $\bar{\mathbf{U}}^{ - 1}$ is expressed as

$$ \bar{\mathbf{U}}^{ - 1} \equiv \bar{\mathbf{U}}_{2}\bar{\mathbf{U}}_{3} $$

(A.14)

where the elements of EBUTM $\bar{\mathbf{U}}_{2}$ and $\bar{\mathbf{U}}_{3}$ are obtained from Eq. (30) and the resulting matrices $\bar{\mathbf{U}}_{2}$ and $\bar{\mathbf{U}}_{3}$ are given by

$$ \bar{\mathbf{U}}_{2} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & \mathbf{O}\\ \mathbf{O} & \mathbf{1} & \mathbf{O} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right] \quad\mbox{and}\quad \bar{\mathbf{U}}_{3} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & \mathbf{O} & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.15)

Substituting Eq. (A.15) into Eq. (A.14) $\mathbf{U}^{ - 1}$ is expressed as

$$ \mathbf{U}^{ - 1} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & - \bar{\mathbf{N}}_{1}^{T}\bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} & - \bar{\mathbf{N}}_{1}^{T}\hat{\bar{\mathbf{A}}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1}\\ \mathbf{O} & \mathbf{1} & - \bar{\mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ \mathbf{O} & \mathbf{O} & \mathbf{1} \end{array}\displaystyle \right]. $$

(A.16)

The $(1,3)$ block element in Eq. (A.16) denoted $\hat{\bar{\mathbf{U}}}_{1,3}$ is the simplified expression which is obtained as follows:

$$\begin{aligned} \hat{\bar{\mathbf{U}}}_{1,3} =& - \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{3,1} \bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} + \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1}\bar{\mathbf{N}}_{2}^{T} \bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{\mathbf{A}}^{T}_{3,1} - \bar{\mathbf{A}}^{T}_{2,1} \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1}\bar{ \mathbf{N}}_{2}^{T}\bar{\mathbf{A}}^{T}_{3,2} \bigr)\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{ \mathbf{A}}^{T}_{2,1}\bar{\mathbf{A}}^{T}_{3,2} - \bar{\mathbf{A}}^{T}_{2,1}\bar{\boldsymbol{\Psi}}_{2} \hat{\bar{ \mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bar{\mathbf{A}}^{T}_{3,2} \bigr)\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bar{\mathbf{A}}^{T}_{2,1} \bigl( \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bigr)\bar{\mathbf{A}}^{T}_{3,2}\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1} \\ =& - \bar{\mathbf{N}}_{1}^{T} \bigl( \bar{\mathbf{A}}_{3,2}\bar{\boldsymbol{\Phi}}_{2}^{T}\bar{ \mathbf{A}}_{2,1} \bigr)^{T}\bar{\boldsymbol{\Psi}}_{3} \hat{\bar{ \mathbf{I}}}_{3}^{ - 1} \quad \bigl( \mbox{where}\ \bar{ \boldsymbol{\Phi}}_{2} = \mathbf{1} - \bar{\boldsymbol{\Psi}}_{2} \hat{\bar{\mathbf{I}}}_{2}^{ - 1} \bar{\mathbf{N}}_{2}^{T} \bigr) \\ =& - \bar{\mathbf{N}}_{1}^{T} \hat{\bar{\mathbf{A}}}^{T}_{3,1}\bar{\boldsymbol{\Psi}}_{3} \hat{ \bar{\mathbf{I}}}_{3}^{ - 1}\quad \bigl( \mbox{where}\ \hat{\bar{ \mathbf{A}}}_{3,1} = \bar{\mathbf{A}}_{3,2}\bar{ \boldsymbol{\Phi}}_{2}^{T}\bar{\mathbf{A}}_{2,1} \bigr) \end{aligned}$$

(A.17)

where

$$ \hat{\bar{\mathbf{A}}}_{3,1} = \bar{\mathbf{A}}_{3,2}\bar{\boldsymbol{\Phi}}_{2}^{T}\bar{\mathbf{A}}_{2,1}. $$

(A.18)

It may be noted that, for the adjoining modules sets ($M_{2}, M_{3}$) and ($M_{1},M_{2}$), $\hat{\bar{\mathbf{A}}}_{3,2} = \bar{\mathbf{A}}_{3,2}$ and $\hat{\bar{\mathbf{A}}}_{2,1} = \bar{\mathbf{A}}_{2,1}$.

1.4 A.4 Numerical validation of the decomposed GIM of gripper

For the set of numerical values of the link masses and inertias, as given in Table 2, the GIM can be obtained for the configuration $\theta_{1^{1}} = \theta_{1^{2}} = \theta_{2^{2}} = 0$ and $\theta_{1^{3}}=90$, as

$$ \mathbf{I} = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 113.3333 & 33.3333 & 9.1667 & 1.6667 \\ \hline & 13.3333 & 4.1667 & 0 \\ & & 1.6667 & 0 \\ \hline \mathit{sym} & & & 1.6667 \end{array}\displaystyle \right] \times 10^{ - 4}. $$

(A.19)

Its decomposed block matrices $\bar{\mathbf{U}}$ and $\bar{\mathbf{D}}$, and the corresponding block inverses $\bar{\mathbf{U}}^{ - 1}$ and $\bar{\mathbf{D}}^{ - 1}$, respectively, are obtained from Eq. (34) and Eq. (58) as follows:

$$ \begin{aligned} \bar{\mathbf{U}} &= \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 1 & 3.571 & - 3.428 & 1\\ \hline 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0\\ \hline 0 & 0 & 0 & 1 \end{array}\displaystyle \right], \\ \bar{\mathbf{D}} &= \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 24.047 & 0 & 0 & 1 \\ \hline 0 & 13.333 & 4.166 & 0\\ 0 & 4.166 & 1.666 & 0\\ \hline 0 & 0 & 0 & 1.666 \end{array}\displaystyle \right] \times 10^{ - 4} \end{aligned} $$

(A.20)

and

$$ \begin{aligned} \bar{\mathbf{U}}^{ - 1}& = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 1 & - 3.5714 & 3.4286 & - 1 \\ \hline 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \hline 0 & 0 & 0 & 1 \end{array}\displaystyle \right], \\ \bar{\mathbf{D}}^{ - 1}& = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 0.0416 & 0 & 0 & 1 \\ \hline 0 & 0.3429 & - 0.8571 & 0 \\ 0 & - 0.8571 & 2.7429 & 0 \\ \hline 0 & 0 & 0 & 0.6 \end{array}\displaystyle \right] \times 10^{4}. \end{aligned} $$

(A.21)

It is now a simple matter to verify the correctness of the inverses by computing $\mathbf{I}^{ - 1} = \bar{\mathbf{U}}^{ - 1}\bar{\mathbf{D}}^{ - 1}\bar{\mathbf{U}}^{ - T}$ as

$$ \mathbf{I}^{ - 1} = \left[ \textstyle\begin{array}{c|c@{\quad}c|c} 0.0416 & - 0.1485 & 0.1426 & - 0.0416 \\ \hline & 0.8733 & - 1.3663 & 0.1485\\ & & 3.2317 & - 0.1426 \\ \hline \mathit{sym} & & & 0.6416 \end{array}\displaystyle \right] \times 10^{4}. $$

(A.22)

Equation (A.22) was checked against numerical result obtained using MATLAB command “inv.”

1.5 A.5 Forward dynamics algorithm for a tree-type multibody system

Steps for recursive forward dynamics algorithm [12] are shown in Table 6.

Table 6 Recursive ${O}(n)$ forward dynamics algorithm for a tree-type multibody systems [12]