On the Dynamic Equivalence of Planar Mechanisms, an Inertia Decomposition Method

Abstract

In this paper the dynamic equivalence of planar mechanisms is investigated by decomposition of inertia into point masses. For a planar rigid body, two point masses can fully describe its dynamic behavior. The location of one these points can be chosen freely, fixing the second point. By locating one of the two point masses of a link on a revolute joint, this link can be fully described by the one remaining point mass. By applying this approach throughout the mechanism’s chain, a reduced parameterization of the dynamics is found. The inverse process—inertia recomposition—gives a range of dynamic equivalent mechanisms. This paper gives the bounds for the selection of such equivalent mechanisms. Simulations of two dynamically equivalent 4-bar mechanisms, derived using this method, show equal base reaction forces and moments, confirming the dynamic equivalence.

1 Introduction

Mechanical systems are said to be dynamically equivalent or equimomental [1] if for all motions the same linear and angular momentum is generated. This means that its time derivative—the external forces and moments—are equal for equal motion, even though the internal forces, such as joint forces, generally are different. Equimomental bodies are usually defined by replacing an inertia—spatial or planar—by a set of point masses. For spatial inertias at least four point masses are required [5]. For planar bodies two points are sufficient [6].

The concept of equimomental bodies is used to model dynamics [5], optimize mass distribution [6], and design mechanisms with reduced shaking forces and moments [2]. This method has also been used for dynamic balance, which is the full elimination of base shaking forces and moments [1, 10]. Wu and Gosselin [9] used a point mass representation to describe a set of spatial platforms which is balanced by chains consisting of dynamic balanced four-bar mechanisms. Van der Wijk used mass equivalent dyads [7] and triads [8] considering linear momentum equality for the synthesis of force balanced mechanisms.

In dynamic balance, a set of dynamic variables are sought for which the momentum equations are equal to zero for all motion. These momentum equations usually employ a full set of dynamic variables [4], without eliminating for equimomental mechanisms. Therefore, if the variables that do not affect the momentum can be found and excluded beforehand, the dynamics equations simplify, speeding up the process of dynamic balancing.

The contribution of this paper is twofold. Firstly, the point mass representation of bodies is extended to planar mechanisms giving a reduced set of parameters to fully describe its momentum. Secondly, this point mass representation can be used to find a range of equimomental mechanisms, paving the way for better understanding and synthesis of dynamically balanced mechanisms. In this paper we confine ourself to the redistribution of the mass and inertia and do not undertake the adaption of the kinematics. Currently only serial and single loop mechanism with revolute joints are considered. The method is exemplified on a 4-bar mechanism.

2 Method

The presented method to find dynamic equivalence consist of two phases. In the first phase, the inertia and mass of the bodies in a mechanism are described in terms of point masses. In the second phase, a set of inertias is recomposed from these point masses such that a range of dynamic equivalent mechanisms for a given geometry is found. However, not all resulting mechanisms are feasible as some of the masses and inertias can become negative. Therefore, the bounds on inertia recomposition are investigated with a graphical an algebraic method for serial and single loop mechanisms. The phases of this approach are shown in Fig. 1a, b.

A planar body is usually described with four parameters: a mass ($m_t$), an x and y location of the center of mass (COM, $\varvec{c}_{}^{}$) and an inertia around this COM (g). The inertia of a rigid body can be understood as a collection of points fixed at a distance with each other. For set of point masses $m_i$ located at $\varvec{r}_{i}^{}$, the total mass, COM, and inertia of a body is:

$$\begin{aligned} m_t&= \sum _{i=1}^{n}m_i&\varvec{c}_{}^{}&= \sum _{i=1}^{n} \frac{m_i}{m_t} \varvec{r}_{i}^{}&g&= \sum _{i=1}^{n}m_i \Vert \varvec{r}_{i}^{} \Vert ^2 - m_t \Vert \varvec{c}_{}^{} \Vert ^2 \end{aligned}$$

(1)

Fig. 1

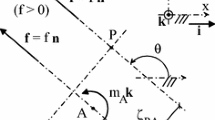
The inertia decomposition and recomposition of simple pendulum. a shows the initial COM ($\varvec{c}_{}^{}$), mass ($m_t$), and inertia (g) of the body. b This can be decomposed into two points ($\varvec{r}_{1}^{},\varvec{r}_{2}^{}$) with a certain mass distribution ($m_1$, $m_2$). c As $\varvec{r}_{2}^{}$ is at the base joint, it does not contribute to the inertia and can be disregarded, leaving us with a 1-point representation. d Inertia recomposition gives us a set of dynamic equivalent mechanisms by adding an arbitrary amount of mass at the base joint (indicated with a$'$)

2.1 Inertia Decomposition of a Body

Rearrangement of Eq. 1 shows that any planar inertia can be represented by at least two point masses. The location of one of these point masses ($\varvec{r}_{2}^{}$) can be selected freely, fixing the mass distribution ($m_1$, $m_2$) and the location of the other point ($\varvec{r}_{1}^{}$).

$$\begin{aligned} m_1&= \frac{m_t^2\Vert \varvec{c}_{}^{} - \varvec{r}_{2}^{} \Vert ^2}{m_t \Vert \varvec{c}_{}^{} - \varvec{r}_{2}^{} \Vert ^2 +g}&m_2&= \frac{m_t g}{m_t \Vert \varvec{c}_{}^{} - \varvec{r}_{2}^{} \Vert ^2 +g}&\varvec{r}_{1}^{}&= \varvec{c}_{}^{} + \frac{g\left( \varvec{c}_{}^{} - \varvec{r}_{2}^{}\right) }{m_t \Vert \varvec{c}_{}^{} - \varvec{r}_{2}^{} \Vert ^2} \end{aligned}$$

(2)

Similarly, any inertia can be decomposed into more than two point masses. It should be noted that in those cases, some of the point masses can obtain a negative value.

$$\begin{aligned} m_1&= - \frac{ \Vert \sum _{i=3}^{n}m_i(\varvec{r}_{2}^{} - \varvec{r}_{i}^{}) - m_t (\varvec{r}_{2}^{} - \varvec{c}_{}^{}) \Vert ^2}{\sum _{i=3}^{n}m_i \Vert \varvec{r}_{2}^{} - \varvec{r}_{i}^{} \Vert ^2 - m_t \Vert \varvec{r}_{2}^{} - \varvec{c}_{}^{} \Vert ^2 - g} \end{aligned}$$

(3)

$$\begin{aligned} m_2&= m_t - m_1 - \sum _{i=3}^{n}m_i \end{aligned}$$

(4)

$$\begin{aligned} \varvec{r}_{1}^{}&= \frac{m_t}{m_1} \varvec{c}_{}^{} - \sum _{i=3}^{n}\frac{m_i}{m_1} \varvec{r}_{i}^{} \end{aligned}$$

(5)

The decomposition into three points (see Fig. 2-left) has special geometric properties which shall be used later on. When the location of two points $\varvec{r}_{2}^{}$ and $\varvec{r}_{3}^{}$ are chosen (e.g. on the body’s joints), the $\varvec{r}_{1}^{}$ is fixed to a circumscribed circle of the triangle $\varvec{r}_{2}^{}$, $\varvec{r}_{3}^{}$ and the 2-point solution for $\varvec{r}_{1}^{}$. This follows from the fact that the radius of the circumscribed circle is invariant to the choice of $m_3$. When the point mass locations are expressed with respect to the origin of the circle $\varvec{d}_{}^{}$ ($\varvec{r}_{i}^{d} = \varvec{r}_{i}^{} - \varvec{d}_{}^{}$) it can be seen that $m_3$ vanishes in the inertia constraint (Eq. 1c). This is done by applying $\Vert \varvec{r}_{1}^{d} \Vert ^2 = \Vert \varvec{r}_{2}^{d} \Vert ^2 = \Vert \varvec{r}_{3}^{d} \Vert ^2$ and Eq. 1.

$$\begin{aligned} g&= m_1 \Vert \varvec{r}_{1}^{d} \Vert ^2 + m_2 \Vert \varvec{r}_{2}^{d} \Vert ^2 + m_3 \Vert \varvec{r}_{3}^{d} \Vert ^2 - m_t \Vert \varvec{c}_{}^{d} \Vert ^2\end{aligned}$$

(6)

$$\begin{aligned} g&=( m_1 + m_2 + m_3) \Vert \varvec{r}_{1}^{d} \Vert ^2 - m_t \Vert \varvec{c}_{}^{d} \Vert ^2\end{aligned}$$

(7)

$$\begin{aligned} g&=m_t (\Vert \varvec{r}_{1}^{d} \Vert ^2 - \Vert \varvec{c}_{}^{d} \Vert ^2) \end{aligned}$$

(8)

Fig. 2

The left figure shows the 3-point decomposition of inertia at $\varvec{c}_{}^{}$. This allows point mass ($\varvec{r}_{1}^{}$) to be placed on a circle by choosing the $m_3$. Right shows the constraint propagation of a dynamic equivalent mechanism

2.2 Inertia Decomposition of a Mechanism

We have seen that two or more point masses sufficiently describe the inertia of a planar body. The location of all but one point masses can be selected freely. For a mechanism with revolute joints, these free point masses can be placed on the joints. These revolute joints ($\varvec{u}_{i,j}^{}$) are the only points for which the linear velocities are equal for both the original (i) and connecting body (j). Therefore the mechanism’s momentum does not change when this point mass is considered as attached to the connecting body (j), leaving the original body (i) with one point mass ($m_i$, $\varvec{r}_{i}^{}$). Applying this strategy throughout the mechanism, we can reduce the number of dynamic parameters from 4 to 3 per body.

For serial mechanisms this approach is straightforward. Starting from the most distal link, the point mass distribution can be calculated with the free point placed at the joint. Sequentially, this point mass is added to inertia of second link and the process is repeated down the chain. To this end, the equation for the three point mass inertia decomposition, Eq. 3 till 5 is used. This recursive nature gives a unique point mass representation per set of dynamic equivalent serial mechanisms.

A parallel mechanism can be seen as multiple serial chains connected together. Therefore, the process described for serial mechanism can also be applied to a parallel mechanism by cutting the loop at an arbitrary body. The loop closure at coupler link allows an extra freedom to select how the mass is distributed over the connecting bodies. Therefore, the point mass decomposition gains a freedom with each loop closure.

2.3 Inertia Recomposition of a Mechanism

Based on a given set of point masses we can calculate the possible dynamic equivalent COMs, masses, and inertias. To convert this point mass representation into feasible inertias we recognize that we can exchange a point mass ($a_{i,j}$) in revolute joint ($\varvec{u}_{i,j}^{}$), between body i and j. For mass continuity there must hold:

$$\begin{aligned} a_{i,j} = - a_{j,i} \end{aligned}$$

(9)

Applying this mass transportations to the mechanism we use Eq. 1 to calculate the mass, COM and inertia of each body.

2.3.1 Constraints

By selection of the joint masses ($a_{i,j}$) the dynamic equivalent properties of the links are fixed. However, not all of these parameters are feasible. We must guarantee that the resulting inertias and masses in the system are positive. This precludes the a range of joint masses, and therefore COM locations of the mechanism. For bodies with maximally two revolute joints these constraints on COM location can be interpreted geometrically:

• 1. $m_t > 0$. Positive mass occurs if the COM is placed on one side of the line trough $\varvec{u}_{1}^{}$ and $\varvec{u}_{2}^{}$. By increasing the masses at the joints simultaneous, the COM moves towards the $\varvec{u}_{1}^{}\varvec{u}_{2}^{}$-line. When the COM approaches this line, the total mass goes to infinity. Passing over this line the total mass switches sign. Therefore if $m_i$ is positive, $m_t$ is positive when the COM is placed on the same half-side. If $m_i$ is negative, COM has to be on the opposite half-side.

• 2. $g > 0$. The limit where COM can be placed to ensure positive inertia is given by the circle of 3-point decomposition solution. If the COM is placed on this circle the corresponding inertia is zero. Outside this circle the mass becomes negative, as can be seen in Eq. 8.

The previous two constraints limit the COMs of each body to a circle segment. Since the mass continuity relationship (Eq. 9), also constraints on a body are inherited over to the adjacent bodies. In Fig. 2-right an example is shown how these constraints are propagated through a single chain mechanism.

• 1. Starting at body 1, connected to the base, the point mass $a_{1,2}$—placed at the second joint ($\varvec{u}_{1,2}^{}$)—has a minimal value for which the mass at joint 1 ($\varvec{u}_{1,0}^{}$) can compensate to pull the COM ($\varvec{c}_{1}^{}$) inside this circle. If this value becomes too negative no point mass at $\varvec{u}_{1,0}^{}$ results in a positive inertia ($g_{1}$). This minimal value ($a_{1,2,min}$) is given by the line which is tangential to the circle at joint 1.

• 2. This limit on the point mass $a_{1,2}$ also acts on the second body as $a_{1,2,min} = - a_{2,1,max}$. Therefore, the second COM ($\varvec{c}_{2}^{}$) can only be placed on a smaller circle segment, defined by the $a_{2,1,max}$ line.

• 3. Similarly, the point mass constraint on joint 3 ($a_{2,3,max}$)—inherited from the rest of the linkage—takes a slice from the pie, limiting the second COM ($\varvec{c}_{2}^{}$) to a intersection of two circle segments.

• 4. Now we can see that also $a_{2,1}$ has a lower limit on the intersection of $a_{3,2,max}$—line with the circle. Again this $a_{2,1,min}$ value gives a constraint on COM of body 1.

Using this approach, the constraints can be propagated in the two directions for a single loop mechanism.

To find the values for these limits, we consider a generic link i with a free point mass at $\varvec{r}_{i}^{}$ and revolute joints at $\varvec{u}_{1}^{}$ and $\varvec{u}_{2}^{}$ with associated masses $m_i$, $a_1$ and $a_2$. The limit values for $a_1$ and $a_2$ are given when $\varvec{c}_{i}^{}$ intersect with the zero-inertia circle which has its origin in $\varvec{d}_{}^{}$.

$$\begin{aligned} \Vert \varvec{c}_{i}^{d} \Vert ^2 = \Vert \varvec{r}_{i}^{d} \Vert ^2 = \Vert \varvec{u}_{1}^{d} \Vert ^2 = \Vert \varvec{u}_{2}^{d} \Vert ^2 \end{aligned}$$

(10)

Expansion of $\Vert \varvec{c}_{i}^{d} \Vert ^2$ with Eq. 1b gives us the following limit condition:

$$\begin{aligned} ( m_i ( a_{1} + a_{2} ) + a_{1} a_{2})\Vert \varvec{r}_{i}^{d} \Vert ^2 = \varvec{r}_{i}^{d} \cdot ( a_{1} \varvec{u}_{1}^{d} + a_{2} \varvec{u}_{1}^{d} ) + a_{1} a_{2}\varvec{u}_{2}^{d} \cdot \varvec{u}_{2}^{d} \end{aligned}$$

(11)

The the following lower bound on $a_1$, can be obtained as functions of the other two parameters $a_2$, and $m_i$.

$$\begin{aligned} a_{1,min} = -\frac{a_{2} m_i ( \varvec{u}_{2}^{d} \cdot \varvec{r}_{i}^{d} - \Vert \varvec{r}_{i}^{d} \Vert ^2 ) }{ ( m_i \varvec{r}_{i}^{d} + a_{2}\varvec{u}_{2}^{d}) \cdot \varvec{u}_{1}^{d} - (m_i+ a_{2}) \Vert \varvec{r}_{i}^{d} \Vert ^2 } \end{aligned}$$

(12)

When selecting the maximal value for $a_{2}$, the corresponding global minimal values for $a_{1}$ are found. Similarly, by swapping the indexes on a and on $\varvec{u}_{}^{}$, the lower bound on $a_{2}$ is given.

When there is no maximal value for $a_2$, (e.g. when the joint is connecting to the base) the minimal value for $a_{1,min}$ can be calculated from the limit case of Eq. 12.

$$\begin{aligned} a_{1,min} = - m_i \frac{ \varvec{u}_{2}^{d} \cdot \varvec{r}_{i}^{d} - \Vert \varvec{r}_{i}^{d} \Vert ^2 }{ \varvec{u}_{2}^{d} \cdot \varvec{u}_{1}^{d} - \Vert \varvec{r}_{i}^{d} \Vert ^2 } \end{aligned}$$

(13)

When the limits on all the a’s are determined, the dynamic parameters can be chosen to our liking to give a range of dynamically equivalent mechanisms.

Fig. 3

Two equimomental mechanism #1 (left) and #2 (right). The shaded area represent feasible locations for the COMs

Table 1 Geometrical parameters, and reduced point mass parameters

3 Results

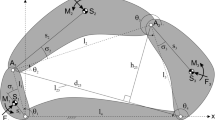
To show the effectiveness of the proposed procedure, a four bar mechanism (#1) is decomposed into point mass representation. From this point mass representation a second dynamic equivalent mechanism (#2) is recomposed. The geometry of the 4-bar mechanism of Fig. 3 is given in Table 1. In Table 2 the mass, COM, and inertia of both mechanisms are given side by side for comparison.

The inertia decomposition of mechanism #1 is done by recursive application of Eq. 3 till 5. Starting at the coupler (link 3) the mass is distributed over joint $\varvec{u}_{3,1}^{}$ and $\varvec{u}_{3,2}^{}$. The point mass $a_{3,1}$ is chosen to be 0.15 kg. This fixes $\varvec{r}_{3}^{} = [0.0, 1.3]^T$, $m_3 = 0.25$ kg, and $a_{3,2} = - 0.03$ kg. Another choice of $a_{3,1}$ would give another mass distribution and location of the points $\varvec{r}_{}^{}$. Now we can now calculate the point mass representation of body 1. For mass continuity there must hold that $a_{3,1} = -a_{1,3}$. We can again use Eq. 3 till 5 to calculate point mass representation of body 1. Similar approach is applied to body 2. This gives us the reduced set of point mass parameters of Table 2. We reduced the number of variables regarding dynamics from 12 to 9.

From this point mass representation a range of dynamically equivalent mechanisms can be recomposed. The feasible locations of the COMs are determined using the procedure as described in Sect. 2.3.1, giving the shaded area of Fig. 3. The inertia properties of equivalent mechanism #2 are calculated by addition of the joint masses ($a_{i,j}$) to the point mass representation using Eq. 1. The resulting COM, mass and inertia are shown in Fig. 3-right and Table 2.

The two equimomental four-bar mechanisms are evaluated in dynamic simulation software SPACAR [3]. An arbitrary motion with a maximal velocity and acceleration of joint 1 of respectively 10 rad/s and 20 rad/s$^2$ is applied to both mechanisms. The base reaction forces and moments are reported to be maximally 126.4 N and 45.0 Nm. The difference between the base reaction forces and moments of mechanism $\#1$ and $\#2$ is maximally $6.0\times 10^{-9}$ N and $5.1\times 10^{-9}$ Nm. These differences can be explained by computational round-off errors, confirming dynamic equivalence of the two mechanism.

Table 2 Dynamic parameters of mechanisms #1 and #2

4 Conclusion

In this paper a methodology to find dynamic equivalent mechanisms has been presented. Mechanisms for which this method does not directly apply—containing prismatic joints, or with multiple closed loop—fall outside the scope of this paper. The method relies on the decomposition of a given inertia into a point mass representation, resulting in a reduced set of dynamic parameters. For a planar mechanism with only revolute joints, the dynamics can be described by three parameters ($\varvec{r}_{i}^{}$ and $m_i$) per body i. Based on this point mass representation a range of dynamic equivalent mechanisms can be found. The bounds on the COMs are given both graphically and algebraically. The method is confirmed by applying it to find two dynamically equivalent 4-bar mechanisms, showing equal ground reaction forces and moments.