Abstract
This paper describes a new factorization of the inverse of the joint-space inertia matrix M. In this factorization, M −1 is directly obtained as the product of a set of sparse matrices wherein, for a serial chain, only the inversion of a block-tridiagonal matrix is needed. In other words, this factorization reduces the inversion of a dense matrix to that of a block-tridiagonal one. As a result, this factorization leads to both an optimal serial and an optimal parallel algorithm, that is, a serial algorithm with a complexity of O(N) and a parallel algorithm with a time complexity of O(logN) on a computer with O(N) processors. The novel feature of this algorithm is that it first calculates the interbody forces. Once these forces are known, the accelerations are easily calculated. We discuss the extension of the algorithm to the task of calculating the forward dynamics of a kinematic tree consisting of a single main chain plus any number of short side branches. We also show that this new factorization of M −1 leads to a new factorization of the operational-space inverse inertia, Λ −1, in the form of a product involving sparse matrices. We show that this factorization can be exploited for optimal serial and parallel computation of Λ −1, that is, a serial algorithm with a complexity of O(N) and a parallel algorithm with a time complexity of O(logN) on a computer with O(N) processors.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This paper describes a new algorithm for calculating the forward dynamics of a kinematic tree (a rigid-body system having tree topology). It is applicable to any kinematic tree, but is best suited to a tree consisting of a single main chain with short side branches. However, as this algorithm employs inverse inertias in its calculations, it does require that every body in the system have a nonsingular inertia matrix.
The algorithm is based on a new factorization of the inverse of the joint-space inertia matrix M. In this factorization, M −1 is directly obtained as the product of a set of sparse matrices wherein only the inversion of a block-tridiagonal matrix is needed. In other words, this factorization reduces the inversion of the dense matrix M to that of a block-tridiagonal one. As a result, this factorization leads to both an optimal serial and an optimal parallel algorithm, that is, a serial algorithm with a complexity of O(N) and a parallel algorithm with a time complexity of O(logN) on O(N) processors, where N is the number of bodies. These figures assume that none of the side branches contain more than O(logN) bodies.
The new algorithm resembles the Constraint Force Algorithm (CFA) [6, 10] in that the key step involves solving a system of linear equations of size O(N), in which the coefficient matrix is block-tridiagonal. On a serial computer, such a system can be solved in O(N) operations using standard matrix methods. On a parallel computer having O(N) processors, such a system can be solved in O(logN) time using a technique called cyclic reduction [10, 11].
The CFA was the first algorithm to achieve O(logN) time complexity with O(N) processors, which is the theoretical minimum parallel complexity for the forward-dynamics problem. It was based on a new factorization of M −1, in the form of a Schur Complement. The original CFA applied only to an unbranched chain, but was later extended in [6] to allow short side branches. A few other algorithms have subsequently matched or slightly outperformed the CFA. These include: the divide-and-conquer algorithm [3, 4], the assembly-disassembly algorithm [23], and a hybrid direct/iterative algorithm described in [1]. The divide-and-conquer algorithm has subsequently been extended to nonrigid bodies in [17], and to adaptive dynamics in [18], wherein the active subset of joints in an articulated body is determined adaptively as a function of the applied forces and the desired level of realism. The assembly-disassembly algorithm, as described in [23], is practically identical to the divide-and-conquer algorithm.
The point of departure between the CFA and the new algorithm presented here is that the CFA calculates the constraint forces acting at the joints, whereas the new algorithm calculates the total forces acting at the joints—the sum of active and constraint forces. For this reason, we call it the Total Force Algorithm (TFA). The theoretical advantage of calculating the total force transmitted across each joint, rather than only the constraint forces, is that the former are uniquely defined by the joint force variables and the dynamics of the tree, whereas the latter depend on assumptions about how the joints are being driven (e.g., see Example 3.2 in [5]). Having calculated the total force transmitted across each joint, it is a trivial matter to calculate the net force on each body, followed by the acceleration of each body, and then the acceleration at each joint. The TFA also differs from the CFA in the way that the factorization of M −1 is obtained. In the TFA, a novel factorization of M −1 is obtained in the form of a product involving sparse matrices wherein only the inversion of a block-tridiagonal matrix is needed. This factorization is multiplicative in nature, and quite different from any previously discovered factorization.
The TFA has two more points in common with the CFA. First, it assumes that the forces due to gravity, Coriolis and centrifugal terms, and any other forces that do not depend on accelerations, have already been calculated by means of an inverse dynamics algorithm. Second, it delegates the processing of the short side branches to the articulated-body algorithm in exactly the same manner as the improved CFA described in [6].
The TFA has been tested numerically on chains of up to 1,000 bodies, and the accuracy compared with other dynamics algorithms. It has been found to have the same accuracy as the CFA, slightly better accuracy than the divide-and-conquer algorithm (DCA), but worse accuracy than the pivotted DCA, the articulated-body algorithm and the composite-rigid-body algorithm.Footnote 1
This paper is organized as follows. In Sect. 2, we present notation and preliminaries, as well as a derivation of the equation of motion and a factorization of M by using compact global notation. In Sect. 3, we present the derivation of the new factorization of M −1 as a basis for the TFA. We also present yet another novel, though less efficient, factorization of M −1. The serial and parallel computational complexities of the TFA are discussed in Sect. 4. In Sect. 5, we discuss the extension of the TFA to systems with tree topology. We also show that this new factorization of M −1 leads to a new factorization of the Operational-Space Inverse Inertia, Λ −1, in a the form of a product involving sparse matrices. Finally, some concluding remarks are made in Sect. 6.
2 Notation and preliminaries
Throughout this paper, we assume that the forces due to gravity and velocity-dependent effects have already been calculated, using an inverse dynamics algorithm, and have been subtracted from the vector of active joint forces (τ). Thus, the equations below do not contain any gravity or velocity-dependent terms. This tactic is originally due to Walker and Orin [21]. Physically, such equations can be regarded as those of a rigid-body system in a zero-gravity field, in which the velocities of the bodies happen to be zero at the current instant. For computing the inverse dynamics, there are suitable O(N) serial algorithms [5, 7, 8] and O(logN) parallel algorithms [15, 16].
To facilitate the derivation of the TFA, we initially assume that all 3D vectors and matrices are expressed in a single common Cartesian coordinate system. However, Sect. 4 will introduce a set of link coordinate systems, and will derive the serial and parallel computational costs of the link-coordinates version of the TFA.
This paper uses the global notation (spatial operator algebra) of Rodriguez et al., which is built upon a kind of spatial vector notation [19, 20]. The subsections below describe this notation only to the minimum extent necessary to understand the TFA.
The notation in this paper adopts the following conventions: bold symbols denote vectors and matrices; calligraphic letters denote global quantities; vectors are denoted by lower-case letters, and matrices by upper-case letters. Two exceptions to the lower-case rule are that spatial vectors and global vectors are denoted by upper-case letters. Individual symbols are described in the nomenclature table, and some quantities are illustrated in Fig. 1.
2.1 Equation of motion
The equation of motion for a rigid-body system without any constraints on the joint acceleration variables can be expressed in the form
where \(\ddot {\boldsymbol {q}}\) is the vector of joint acceleration variables, M is the joint-space inertia matrix, and τ is given by
where τ in is the vector of input joint forces and b is the vector of forces due to gravity, Coriolis and centrifugal effects, and any other forces that do not depend on acceleration. We assume that b has already been calculated using an inverse dynamics algorithm, and that τ is therefore already known. The objective of the TFA is to calculate \(\ddot {\boldsymbol {q}}\) from τ.
2.2 Spatial vectors
We use spatial vectors in the format shown in the nomenclature table (i.e., angular component above linear). Descriptions of spatial vectors can be found in [5, 8]. Referring to Fig. 1, acceleration and force vectors can be shifted from one reference point to another using the following formulae:


where \(\dot {\boldsymbol {V}}_{\!\!i}\) and F i here stand for any acceleration and force vector referred to point O i , and \(\dot {\boldsymbol {V}}_{\!\!i+1}\) and F i+1 are the same vectors referred to point O i+1. The matrix P i is given by
where \({\bf 0}\) and \({\bf U}\) stand for zero and identity matrices of appropriate size (which is 3×3 in this case), and p i+1,i is a 3D vector giving the position of O i+1 relative to O i . For any vector v, a 3×3 skew-symmetric matrix \(\tilde{\boldsymbol {v}}\) is defined as
\(\tilde{\boldsymbol {p}}_{i+1,i}\) is the 3×3 skew-symmetric matrix associated to the vector p i+1,i . The P matrices have the following properties:
where i, j and k denote link numbers. The spatial inertia and inverse inertia of link i are

and

where J i is the rotational inertia of the link about its center of mass, m i is its mass, and s i locates the center of mass relative to O i . Equation (7) is an expression of the parallel-axes theorem. We will also make use of the identity
which is the inverse inertia of link i−1 expressed at O i .
2.3 System model
We consider a rigid-body system consisting of N bodies connected together to form an unbranched chain. One end of the chain is connected to a fixed base, and the other end (the tip) is free. The bodies are numbered 1 to N from base to tip, and the base is regarded as body number 0. The joints are numbered such that joint i connects from body i−1 to body i. Joints can have any number of degrees of freedom (DOF) from 1 to 6. If joint 1 allows 6 DOF, then the system is a floating structure. We define n i to be the DOF of joint i, and \(n=\sum_{i=1}^{N}n_{i}\) to be the DOF of the whole system. A point O i is fixed in each body i, and is used as the reference point for all spatial quantities pertaining to body i and joint i. We assume that the bodies are all at rest at the current instant, and that there are no forces acting on the system other than the joint force variables τ i .
The equation of motion for body i can now be written
where F i is the force transmitted from body i−1 to body i across joint i, F i+1 is likewise the force transmitted from body i to body i+1 across joint i+1, I i and \(\dot {\boldsymbol {V}}_{\!\!i}\) are the inertia and acceleration of body i, and \(\boldsymbol {P}_{\!i}^{\mathrm {T}}\) maps F i+1 from O i+1 to O i (cf. Eq. (4)) so that every quantity in this equation is referred to O i .
Joint i is characterized by a 6×n i matrix H i , which maps the vector of joint-i acceleration variables (\(\ddot {\boldsymbol {q}}_{i}\)) to the spatial acceleration across the joint. With this matrix, the relationship between body accelerations and joint accelerations can be written
Joint i is further characterized by a 6×n i matrix \(\boldsymbol {W}_{\!\!{\rm a}\,i}\) and a 6×(6−n i ) matrix W i . The former maps the vector of active joint forces (τ i ) to a spatial vector, and the latter spans the space of constraint forces at joint i. More details on this kind of joint model can be found in [6, 8, 10]). These matrices satisfy
and they allow the force across joint i to be expressed as the sum of an active force and a constraint force:
where λ i is a vector of constraint force variables. (If n i =6, then we define W i λ i to be zero.) Three equations that follow immediately from Eqs. (12), (13), and (11) are
and
2.4 Global notation
It is possible to collect together all of the equations of motion given by Eq. (10) into a single “global” equation of the form
where \(\dot {\boldsymbol {\mathcal {V}}}=\mathrm {col}\{ \dot {\boldsymbol {V}}_{\!\!i}\}\), \(\boldsymbol {\mathcal {F}}=\mathrm {col}\{ \boldsymbol {F}_{\!i}\}\), and \(\boldsymbol {\mathcal {I}}=\mathrm {diag}\{ \boldsymbol {I}_{i}\}\), for i=1⋯N, and
Likewise, it is possible to collect all of Eqs. (11), (13), (14), (15), and (16) into five global equations
and
where



Note that these matrices satisfy
which represents the global version of Eq. (12). Note, also, that \(\boldsymbol {\mathcal {P}}\) is invertible, and that its inverse is the upper-triangular matrix
Physically, \(\boldsymbol {\mathcal {P}}\) is the matrix that transforms the global vector of inter-body forces to the global vector of net forces acting on the bodies, while \(\boldsymbol {\mathcal {P}}^{\mathrm {T}}\) transforms the global vector of body accelerations to the global vector of accelerations across the joints (i.e., interbody accelerations).
The global notation of Rodriguez et al. is not the only notation based on collections of 6D vectors and 6×6 matrices. In particular, a similar notation can be found in [22], and many of the equations in this section can be found in that paper. They can also be found in [10] and elsewhere. The novel contributions of our paper begin in Sect. 3.
2.5 Mass matrix factorization
To illustrate the use of global notation, we derive here the simplest factorization of the joint-space inertia matrix, which is known as the Newton–Euler factorization [19, 20]. Starting with Eq. (21), and applying Eqs. (17) and (19), we get

On comparing this with Eq. (1), and taking into account the fact that both equations hold for all values of τ and \(\ddot {\boldsymbol {q}}\), we get
As the expression \(\boldsymbol {\mathcal {P}}^{\mathrm {T}}\boldsymbol {\mathcal {I}}^{-1}\boldsymbol {\mathcal {P}}\) will appear later on, let us define
so that
The physical significance of \(\boldsymbol {\mathcal {G}}\) is that it maps the global vector of joint forces to the global vector of joint accelerations. In comparison, \(\boldsymbol {\mathcal {I}}^{-1}\) maps the global vector of body forces to the global vector of body accelerations. The computational significance of \(\boldsymbol {\mathcal {G}}\) is that it is block-tridiagonal.
3 The new algorithm
3.1 Derivation
Starting with Eq. (10), the first step is to substitute for \(\dot {\boldsymbol {V}}_{\!\!i}\) using Eq. (11), resulting in
Substituting this equation into Eq. (14) gives
from which \(\ddot {\boldsymbol {q}}_{i}\) can be calculated as
Note that, as shown in Appendix A, the matrix \(\boldsymbol {H}_{i}^{\mathrm {T}} \boldsymbol {I}_{i} \boldsymbol {H}_{i}\) is positive definite, and hence invertible. Replacing \(\ddot {\boldsymbol {q}}_{i}\) in Eq. (11) with the expression in Eq. (35), we get
where
This equation can be written in global form as
where




\(\boldsymbol {\mathcal {L}}\) is an upper bidiagonal matrix having the form
and \(\boldsymbol {\mathcal {K}}\) is a lower bidiagonal matrix having the form
where
We now substitute for \(\dot {\boldsymbol {\mathcal {V}}}\) in Eq. (38) using Eq. (17). This gives
which can be expressed as
where

Appendix A proves that \(\boldsymbol {\mathcal {A}}\) is nonsingular. The special property of Eq. (44) that makes it interesting for dynamics calculations is that the coefficient matrix, \(\boldsymbol {\mathcal {A}}\), is block tridiagonal. Thus, it can be used as the basis for an O(N) serial algorithm for calculating \(\boldsymbol {\mathcal {F}}\), and also a parallel algorithm having O(logN) time complexity on a parallel computer with O(N) processors.
The nonzero block elements of \(\boldsymbol {\mathcal {A}}\) are given as follows:




The second step in Eq. (47) follows from Eq. (9).
The final step is to obtain an expression for \(\ddot {\boldsymbol {q}}\) in terms of τ. We accomplish this by applying Eqs. (17), (31), and (44) to Eq. (22) as follows:

On comparing Eq. (50) with Eq. (1), it can be seen that we have obtained a new factorization of the inverse of the joint-space inertia matrix:
The correctness of this factorization can be proved simply by showing that it is the inverse of the factorization in Eq. (30). This is shown in Appendix B.
Equation (50) is the basis of the TFA. It supports both the optimal serial O(N) and optimal parallel O(logN) computation of \(\ddot {\boldsymbol {q}}\). This optimal efficiency for both serial and parallel computation results from the fact that Eq. (51) represents a new direct factorization of the inverse of the dense matrix M in terms of products of sparse matrices wherein only the inversion of a block-tridiagonal matrix \(\boldsymbol {\mathcal {A}}\) is required.
From Eq. (50), the computational steps of the new algorithm can be summarized as:
-
Step 1. Calculate \(\dot {\boldsymbol {\mathcal {V}}}{}'\) from
$$ \dot {\boldsymbol {\mathcal {V}}}{}'= \boldsymbol {\mathcal {H}}\bigl(\boldsymbol {\mathcal {H}}^\mathrm {T}\boldsymbol {\mathcal {I}}\boldsymbol {\mathcal {H}}\bigr)^{-1} \boldsymbol {\tau }$$(52)\(\dot {\boldsymbol {\mathcal {V}}}{}'\) is just an intermediate variable: the output of Step 1 and the input to Step 2. It’s physical interpretation is given below in Sect. 3.2.
-
Step 2. Calculate \(\boldsymbol {\mathcal {F}}\) from
$$ \boldsymbol {\mathcal {A}}\boldsymbol {\mathcal {F}}= \dot {\boldsymbol {\mathcal {V}}}{}'$$(53) -
Step 3. Calculate \(\ddot {\boldsymbol {q}}\) from
$$ \ddot {\boldsymbol {q}}= \boldsymbol {\mathcal {W}}_{\!\rm a}^\mathrm {T}\boldsymbol {\mathcal {G}}\boldsymbol {\mathcal {F}}. $$(54)
As can be seen, in Step 2 of the computation, the total force \(\boldsymbol {\mathcal {F}}\) is calculated; hence the designation of the algorithm as TFA.
It should be noted that a different (and to our knowledge new) factorization of M −1 can be derived as follows. By substituting \(\boldsymbol {\mathcal {F}}\) from Eq. (17) into Eq. (38), we get
and by substituting into Eq. (22), we then get
On comparing Eq. (56) with Eq. (1), it can be seen that we have obtained yet another new factorization of the inverse of the joint-space inertia matrix as
From the structure of matrix \(\boldsymbol {\mathcal {P}}^{-1}\) in Eq. (28), it can be seen that the matrix \((\boldsymbol {\mathcal {K}}+\boldsymbol {\mathcal {L}}\boldsymbol {\mathcal {P}}^{-1}\boldsymbol {\mathcal {I}})\) is an upper-Hessenberg matrix. (A matrix is upper-Hessenberg if a ij =0 for i>j+1 [11].) Therefore, Eq. (57) represents a factorization of the inverse of the dense matrix M in terms of sparse factors wherein the inversion of an upper-Hessenberg matrix is needed. This leads to a serial computational complexity of O(N 2), and hence less efficiency, of the algorithm based on Eq. (57).
It is rather interesting to note that the better efficiency of the TFA, which is based on Eq. (51), compared with an algorithm based on Eq. (57), results from the different sequence of intermediate variables in each case. In the TFA, first one calculates \(\dot {\boldsymbol {\mathcal {V}}}{}'\), then the total force, \(\boldsymbol {\mathcal {F}}\), and then the total acceleration, \(\dot {\boldsymbol {\mathcal {V}}}\) (buried inside Step 3—see Step 3.2 in Sect. 4.1). In contrast, an algorithm based on Eq. (57) never calculates the total force, but proceeds to calculate the total acceleration, \(\dot {\boldsymbol {\mathcal {V}}}\), via an alternative sequence of intermediate variables.
3.2 Physical interpretation
The physical interpretation of our new factorization of the inverse of the joint-space inertia matrix can be better described by considering the three steps in its implementation given by Eqs. (52), (53), and (54). In Step 1, the acceleration vector \(\dot {\boldsymbol {\mathcal {V}}}{}'\), given by Eq. (52), can be interpreted as the acceleration response of a hypothetical rigid-body system obtained by dismantling the given system and connecting every body directly to the fixed base through its inboard joint. In Step 2, \(\boldsymbol {\mathcal {A}}\) can be regarded as the matrix that maps the acceleration of the hypothetical system to the total joint forces of the given system. The physical interpretation of Step 3 is straightforward since, given the global force \(\boldsymbol {\mathcal {F}}\), it first calculates the global link accelerations and then joint accelerations (see also Sect. 4.1 for more details).
A more detailed interpretation of Eq. (44) can be obtained by multiplying both sides by the square, nonsingular matrix \([\boldsymbol {\mathcal {I}}\boldsymbol {\mathcal {H}}\;\;\boldsymbol {\mathcal {W}}]^{\mathrm {T}}\) (see Appendix A). This operation is equivalent to a change of basis (i.e., a coordinate transform) as defined in [6]. The result, after some algebraic simplification, is
The top row of this equation is clearly just a copy of Eq. (21), and the bottom row is a combination of Eq. (23) and Eq. (17), which has been simplified using Eq. (31). The physical interpretation can now be stated as follows: the solution to Eq. (44) is the unique force \(\boldsymbol {\mathcal {F}}\) that satisfies the n force constraints in Eq. (21), and that produces an acceleration (via the equation of motion Eq. (17)) that satisfies the 6N−n acceleration constraints in Eq. (23).
3.3 Symmetry of the factorizations
One obvious peculiarity of Eq. (51) is that the expression for M −1 does not look symmetric. In fact, the middle portion of this expression really is asymmetric, but the asymmetry is eliminated when we premultiply by \(\boldsymbol {\mathcal {W}}_{\!\rm a}^{\mathrm {T}}\) and post-multiply by \(\boldsymbol {\mathcal {B}}\). Starting from the equations in Appendix A, it is possible to show that
Thus, \(\boldsymbol {\mathcal {G}}\boldsymbol {\mathcal {A}}^{-1}\) is not a symmetric matrix. However, it becomes symmetric under the action of \(\boldsymbol {\mathcal {W}}_{\!\rm a}^{\mathrm {T}}\) and \(\boldsymbol {\mathcal {B}}\):

3.4 Comparison with CFA factorization of mass matrix
It is rather instructive to compare this new factorization of the inverse of the mass matrix, given by Eq. (51), with that of the CFA [6, 10]. The factorization in the CFA is in the form of a Schur complement, and is given as
wherein, according to our notation, \(\boldsymbol {M}_{1}=\boldsymbol {\mathcal {W}}^{\mathrm {T}}\boldsymbol {\mathcal {G}}\boldsymbol {\mathcal {W}}\), \(\boldsymbol {M}_{2}=\boldsymbol {\mathcal {W}}^{\mathrm {T}}\boldsymbol {\mathcal {G}} \boldsymbol {\mathcal {W}}_{\!\rm a}\), and \(\boldsymbol {M}_{3}= \boldsymbol {\mathcal {W}}_{\!\rm a}^{\mathrm {T}}\boldsymbol {\mathcal {G}} \boldsymbol {\mathcal {W}}_{\!\rm a}\). For a serial chain system, the matrices M 1, M 2, and M 3 are block-tridiagonal and, furthermore, M 1 and M 3 are symmetric positive-definite.
As can be seen from Eq. (51) and Eq. (60), both TFA and CFA are based on the derivation of explicit factorizations of the inverse of the mass matrix, M −1, though in two quite different forms. Furthermore, both factorizations reduce the inversion of the dense mass matrix to that of block tridiagonal matrices. In fact, the key to the optimal serial and particularly parallel efficiency of both algorithms result from this reduction.
4 Serial and parallel computational complexity analysis
In this section, we evaluate the serial and parallel computational complexity of the algorithm. To do so, and starting from the three steps of the algorithm given in Sect. 3.1, we first give a more detailed description of the computation of the algorithm, and then consider the serial and parallel implementations.
This section is chiefly concerned with floating-point operation counts. It is well known that such counts do not give a precise indication of execution time on specific computer hardware because they do not take into account special properties of the hardware, such as vector processing capability, or the efficiencies of available libraries implementing operations such as basic matrix arithmetic. Nevertheless, operation counts have been published for many dynamics algorithms, and they are an accepted standard measure for comparing algorithms.
4.1 A step-by-step description of the algorithm
The computational steps involved in the implementation of the algorithm can be further broken up as follows.
Step 1. Calculate \(\dot {\boldsymbol {\mathcal {V}}}{}'\) from \(\dot {\boldsymbol {\mathcal {V}}}{}'=\boldsymbol {\mathcal {H}}(\boldsymbol {\mathcal {H}}^{\mathrm {T}}\boldsymbol {\mathcal {I}}\boldsymbol {\mathcal {H}})^{-1}\boldsymbol {\tau }\)
-
Step 1.1. Calculate \(\boldsymbol {\varTheta }_{i}=( \boldsymbol {H}_{i}^{\mathrm {T}} \boldsymbol {I}_{i} \boldsymbol {H}_{i})\) for i=1,…,N
-
Step 1.2. Calculate \(\boldsymbol {\varPhi }_{i}=\boldsymbol {\varTheta }_{i}^{-1}\boldsymbol {\tau }_{i}\) for i=1,…,N
-
Step 1.3. Calculate \(\dot {\boldsymbol {V}}{}'_{\!\!i}= \boldsymbol {H}_{i}\boldsymbol {\varPhi }_{i}\) for i=1,…,N.
Step 2. Calculate \(\boldsymbol {\mathcal {F}}\) from \(\boldsymbol {\mathcal {A}}\boldsymbol {\mathcal {F}}= \dot {\boldsymbol {\mathcal {V}}}{}'\)
-
Step 2.1. Calculate matrix \(\boldsymbol {\mathcal {A}}\) from Eqs. (49)–(52).
-
Step 2.2. Calculate \(\boldsymbol {\mathcal {F}}\) by solving \(\boldsymbol {\mathcal {A}}\boldsymbol {\mathcal {F}}= \dot {\boldsymbol {\mathcal {V}}}{}'\).
Step 3. Calculate \(\ddot {\boldsymbol {q}}\) from \(\ddot {\boldsymbol {q}}= \boldsymbol {\mathcal {W}}_{\!\rm a}^{\mathrm {T}}\boldsymbol {\mathcal {P}}^{\mathrm {T}}\boldsymbol {\mathcal {I}}^{-1}\boldsymbol {\mathcal {P}}\boldsymbol {\mathcal {F}}\)
-
Step 3.1. Calculate \(\boldsymbol {\varPsi }_{\!i}= \boldsymbol {F}_{\!i}- \boldsymbol {P}_{\!i}^{\mathrm {T}} \boldsymbol {F}_{\!i+1}\) for i=N,…,1 with \(\boldsymbol {F}_{\!N+1}={\bf 0}\)
-
Step 3.2. Calculate \(\dot {\boldsymbol {V}}_{\!\!i}= \boldsymbol {I}_{i}^{-1} \boldsymbol {\varPsi }_{\!i}\) for i=N,…,1
-
Step 3.3. Calculate \(\boldsymbol {\varUpsilon }_{\!\;\!\!i}= \dot {\boldsymbol {V}}_{\!\!i}- \boldsymbol {P}_{\!i-1}\, \dot {\boldsymbol {V}}_{\!\!i-1}\) for i=1,…,N with \(\dot {\boldsymbol {V}}_{\!\!0}={\bf 0}\)
-
Step 3.4. Calculate \(\ddot {\boldsymbol {q}}_{i}= \boldsymbol {W}_{\!\!{\rm a}\,i}^{\mathrm {T}} \boldsymbol {\varUpsilon }_{\!\;\!\!i}\) for i=1,…,N.
4.2 Serial computational complexity
Thus far, the computation procedure has been presented without explicit reference to any coordinate frame. For the implementation, however, the vectors and tensors involved in the computation need to be projected onto suitable reference frames. The choice of the appropriate frame and the way that the projection is performed can affect the efficiency of the algorithm for both serial and parallel computation. The computation of the algorithm involves spatial inertias and inverse inertias of the links. Our choice of coordinate frame is then to optimize the efficiency in calculating such operations. Note that, according to our notation, and as shown in Fig. 1, frame i+1 is fixed in link i and, therefore, all the parameters of link i are constant in frame i+1. Also, in evaluating the computational cost, we assume joints with one revolute DOF. The computational cost of each step is then given as follows.
Step 1. The cost of this step is mN obtained as follows. Note that, with 1 DOF joints, Θ i is a scalar. \(\boldsymbol {\varTheta }_{i}^{-1}\) is calculated as
According to our notation, the terms H i and I i are constant in frame i+1 and can be precomputed. Therefore, the term \(\boldsymbol {\varTheta }_{i}^{-1}\) is also constant and can be precomputed. The computation of Φ i requires one scalar multiplication. The vector \(\dot {\boldsymbol {V}}{}'_{\!\!i}\) is calculated in frame i as
which, given the sparse structure of i H i , does not require any operation but replacing the only nonzero element of i H i by Φ i .
Step 2 The cost of this step is (1154m+977a)N−(868m+763a) obtained as follows.
-
Step 2.1. The block elements of row i of matrix \(\boldsymbol {\mathcal {A}}\) are computed in frame i, as
$$ \boldsymbol {\mathcal {A}}_{\,i,i} = {}^{i} \boldsymbol {I}_{i}^{-1} + \bigl({\bf U}- {}^{i}\boldsymbol {C}_i {}^{i} \boldsymbol {I}_{i}\bigr) {}^{i} \boldsymbol {I}_{i-1,i}^{-1}, $$(63)$$ \boldsymbol {\mathcal {A}}_{\,i,i-1} = \bigl({}^{i}\boldsymbol {C}_i {}^{i} \boldsymbol {I}_{i} - {\bf U}\bigr) {}^{i} \boldsymbol {P}_{\!i-1} {}^{i} \boldsymbol {I}_{i-1}^{-1} \boldsymbol {R}_{\;\!i-1}^\mathrm {T}, $$(64)$$ \boldsymbol {\mathcal {A}}_{\,i,i+1} = \boldsymbol {R}_{\;\!i} \bigl({}^{i+1}\boldsymbol {C}_i - {}^{i+1} \boldsymbol {I}_{i}^{-1}\bigr) {}^{i+1} \boldsymbol {P}_{\!i}. $$(65)For the computation of Eqs. (63), (64), and (65), first the matrices i I i and \({}^{i} \boldsymbol {I}_{i}^{-1}\) are computed by exploiting their special structure as shown in Eqs. (7) and (8). To this end, first i+1 J i and i+1 s i (which are constant link parameters) and \({}^{i+1} \boldsymbol {J}_{\!i}^{-1}\) (which can be precomputed) are projected onto frame i. Then, Eqs. (7) and (8) are computed with all tensors and vectors projected onto frame i, leading to the cost of computing i I i and \({}^{i} \boldsymbol {I}_{i}^{-1}\) as (63m+48a)N and (117m+81a)N, respectively.
For computation of Eq. (63), note that the term \({}^{i} \boldsymbol {I}_{i-1,i}^{-1}\) is constant in frame i, and hence can be precomputed. Also, given the sparse structure of i H i , the matrix i C i is highly sparse with actually only one nonzero element. As a consequence of this sparsity, the evaluation of the term i C i i I i reduces to forming a sparse matrix with only one non-zero row (third row) of elements wherein this row is simply a scalar multiple of the third row of i I i . Taking advantage of the sparse structure of the matrix \(({\bf U}-{}^{i}\boldsymbol {C}_{i} {}^{i} \boldsymbol {I}_{i})\), the cost of computing Eq. (63) is obtained as (42m+66a)N−(42m+66a).
For computation of Eq. (64), since both i P i−1 and \({}^{i} \boldsymbol {I}_{i-1}^{-1}\) are constant and can be precomputed, therefore, the term \({}^{i} \boldsymbol {P}_{\!i-1}{}^{i} \boldsymbol {I}_{i-1}^{-1}\) can be also precomputed. Taking advantage of the sparse structure of matrices \(({\bf U}-{}^{i}\boldsymbol {C}_{i} {}^{i} \boldsymbol {I}_{i})\) and \(\boldsymbol {R}_{\;\!i-1}\), the cost of computing Eq. (64) is then obtained as (144m+102a)N−(144m+102a).
For computation of Eq. (65), since the terms i+1 C i , \({}^{i+1} \boldsymbol {I}_{i}^{-1}\), and i+1 P i are all constant, therefore the matrix \(({}^{i+1}\boldsymbol {C}_{i}-{}^{i+1} \boldsymbol {I}_{i}^{-1}) {}^{i+1} \boldsymbol {P}_{\!i}\) can be precomputed. Taking advantage of the sparse structure of matrix \(\boldsymbol {R}_{\;\!i}\), the cost of computing Eq. (65) is then obtained as (108m+72a)N−(108m+72a).
-
Step 2.2. By using block LU decomposition algorithm, the cost of calculating \(\boldsymbol {\mathcal {F}}\) by solving \(\boldsymbol {\mathcal {A}}\boldsymbol {\mathcal {F}}= \dot {\boldsymbol {\mathcal {V}}}{}'\) is (680m+608a)N−(574m+523a).
Step 3. The cost of this step is (84m+78a)N−(48m+48a) which is obtained as follows.
-
Step 3.1. The term Ψ i is computed in frame i as
$$ {}^{i} \boldsymbol {\varPsi }_{\!i} = {}^{i} \boldsymbol {F}_{\!i} - \boldsymbol {R}_{\;\!i} {}^{i+1}\! \boldsymbol {P}_{\!i}^\mathrm {T}\ {}^{i+1}\! \boldsymbol {F}_{\!i+1} $$(66)with a cost of (24m+24a)N−(24m+24a).
-
Step 3.2. The vector \(\dot {\boldsymbol {V}}_{\!\!i}\) is computed in frame i as
$$ {}^{i} \dot {\boldsymbol {V}}_{\!\!i} = {}^{i} \boldsymbol {I}_{i}^{-1}\ {}^{i} \boldsymbol {\varPsi }_{\!i} $$(67)with a cost of (36m+30a)N.
-
Step 3.3. The term \(\boldsymbol {\varUpsilon }_{\!\;\!\!i}\) is computed in frame i as
$$ {}^{i} \boldsymbol {\varUpsilon }_{\!\;\!\!i} = {}^{i} \dot {\boldsymbol {V}}_{\!\!i} - {}^{i} \boldsymbol {P}_{\!i-1} \boldsymbol {R}_{\;\!i-1}^\mathrm {T}{}^{i-1} \dot {\boldsymbol {V}}_{\!\!i-1} $$(68)with a cost of (24m+24a)N−(24m+24a).
-
Step 3.4. Joint i acceleration is computed as
$$ \ddot {\boldsymbol {q}}_i = {}^{i} \boldsymbol {W}_{\!\!{\rm a}\,i}^\mathrm {T}\ {}^{i} \boldsymbol {\varUpsilon }_{\!\;\!\!i} $$(69)which given the sparse structure of \({}^{i} \boldsymbol {W}_{\!\!{\rm a}\,i}\) does not require any operation but a proper selection of an element of \({}^{i} \boldsymbol {\varUpsilon }_{\!\;\!\!i}\).
The total computation cost of the algorithm is then obtained as (1239m+1055a)N−(916m+811a). Note that, as can be seen from the costs of different steps, the most computation intensive part of the algorithm is Step 2, that is, forming matrix \(\boldsymbol {\mathcal {A}}\) and solving \(\boldsymbol {\mathcal {A}}\boldsymbol {\mathcal {F}}= \dot {\boldsymbol {\mathcal {V}}}{}'\).
4.3 Parallel computational complexity
The optimal efficiency of the TFA for parallel computation can be easily assessed by examining the steps involved in its implementation. In fact, in terms of parallel implementation, the TFA is very similar to the CFA, which is discussed in detail in [10]. Therefore, much of the detailed analysis in [10] can be used for parallel implementation of the TFA. In particular, the detailed analysis in [10] concerning the connectivity of the processors, the data communication requirements, and the details of implementing the cyclic reduction algorithm for Step 2.2, can all be carried over to the TFA. In the following, we briefly discuss the parallel efficiency of the TFA.
We consider a parallel implementation by using N processors, denoted as PR i for i=1,…,N. The computation for each link is assigned to a specific processor, i.e., the computation of link i is assigned to PR i . The computations for each link in Step 1 are fully decoupled and hence can be performed in parallel with a cost of O(1). For Step 2.1, the computation of each row of matrix \(\boldsymbol {\mathcal {A}}\) can be performed in a fully decoupled fashion, leading to a cost of O(1) for this step. For Step 2.2, by using the block cyclic reduction algorithm [12] the block tridiagonal system can be solved with a cost of O(logN)+O(1). The computations in Step 3 are either fully decoupled (Steps 3.2 and 3.4) or require a local nearest neighbor communication (Steps 3.1 and 3.3), leading to a cost of O(1) for this step.
The parallel complexity of the TFA algorithm is therefore of O(logN)+O(1) by using N processors, indicating an optimal parallel efficiency in terms of time and processors. Note that, most of the computations of the TFA algorithm are fully decoupled and data dependency only exists in the solution of the block tridiagonal system in Step 2.2, resulting in the O(logN) complexity.
5 Extensions of the TFA
5.1 Extension to tree topology systems
Strictly speaking, the algorithm embodied in Eq. (50) will work for any tree-topology system, not only an unbranched chain—the only quantity that needs to be modified is \(\boldsymbol {\mathcal {P}}\). However, branches do spoil the tridiagonal structure of \(\boldsymbol {\mathcal {A}}\), leading to a loss of efficiency and a loss of O(N) complexity. An alternative method for dealing with branches, which was originally proposed as an extension to the constraint force algorithm, is to replace the original set of N rigid bodies with a set of N articulated bodies [6]. This results in a system consisting of a single main chain containing N rigid bodies, plus any number of side branches. The idea is that the articulated-body algorithm can be used to process the side branches, while the TFA processes the main chain. The complete algorithm works as follows:
-
1.
Perform the inverse-dynamics calculation, as explained in Sect. 2.1.
-
2.
Run the articulated-body algorithm on each articulated body, up to the end of the main pass (i.e., up to the end of Pass 2 in Table 7.1 of [5], or the end of the second ‘for’ loop in Table 2.8 of [8], or the end of Step 1 in [2, Chap. 6]).
-
3.
Run the TFA, using the articulated-body inertia of articulated body number i in place of the rigid-body inertia I i in Eq. (10).
-
4.
Complete the execution of the articulated-body algorithm, so as to calculate the accelerations of the bodies on the side branches.
The important point here is that the articulated bodies can all be processed in parallel. Thus, if no articulated body contains more than O(logN) rigid bodies, then Step 2 above can be performed in O(logN) time on a parallel computer with O(N) processors.
5.2 Computation of operational-space inverse inertia
The fact that our method is based on a new explicit factorization of M −1 can be exploited to derive a new factorization for computation of the Operational-Space Inverse Inertia, Λ −1 [13, 14], which is needed to control robots directly in task space. In [9], the Schur complement factorization of M −1 in the CFA [10] was used to derive a Schur complement factorization of Λ −1. In the following, we show that the new factorization of M −1 leads to a new factorization of Λ −1 in the form of a product, resulting in optimal serial and parallel algorithms.
The Operational-Space Inverse Inertia, Λ −1, is defined as
where J∈ℜ6×N is the Jacobian matrix. Note that, if Rank(J)≥6 then Λ −1 is nonsingular and Λ can be obtained by inverting a 6×6 matrix with a flat cost. In the following, we discuss the factorization of Λ −1.
Using our notation, and Eq. (19), the acceleration of the end-effector can be written as
where \(\boldsymbol {\varDelta }=[{\bf 0}\ {\bf 0}\ \cdots\ \boldsymbol {P}_{\!N}]\in \Re^{6\times6N}\). On comparing this with the definition of the Jacobian as \(\dot {\boldsymbol {V}}_{\!\!N+1} = \boldsymbol {J}\ddot {\boldsymbol {q}}\), it can be seen that a factorization of the Jacobian is obtained as
Substituting the factorization of M −1, given by Eq. (51), and that of J, given by Eq. (72), into Eq. (70), a factorization of Λ −1 is then obtained as
Note that, as can be seen from (28), \(\boldsymbol {\mathcal {P}}^{-1}\) and \(\boldsymbol {\mathcal {P}}^{-\mathrm {T}}\) are dense upper and lower triangular matrices. A simpler and particularly more computationally efficient factorization of Λ −1 can be obtained by exploiting the sparse structure of Δ and is given as
where


and


The factorization of Λ −1 given by Eq. (74) can be used for optimal serial O(N) and parallel O(logN) computation. In the following, we briefly discuss these serial and parallel complexities.
For both serial and parallel computation of Eq. (74), we only discuss the asymptotic complexity. Furthermore, it can be easily shown that all the required projections for implementation of Eq. (74) as well as the computation of the elements of matrices Ω, \(\boldsymbol {\mathcal {G}}\), \(\boldsymbol {\mathcal {A}}\), and Π can be done with a serial complexity of O(N) and a parallel complexity of O(logN).
For serial implementation, the computation of \(\boldsymbol {\varGamma }=\boldsymbol {\mathcal {A}}^{-1}\boldsymbol {\varPi }\), where Γ∈ℜ6N×6, corresponds to the solution of a block-tridiagonal linear system with six right-hand sides and can be performed in O(N). Given the block-tridiagonal structure of matrix \(\boldsymbol {\mathcal {G}}\), the computation of \(\boldsymbol {\varXi }=\boldsymbol {\mathcal {G}}\boldsymbol {\varGamma }\), where Ξ=col{Ξ i }∈ℜ6N×6, can be performed in O(N). Finally, Λ −1 is computed as \(\boldsymbol {\varLambda }^{-1}=\boldsymbol {\varOmega }\boldsymbol {\varXi }=\sum_{i=1}^{N}\boldsymbol {\varOmega }_{i}\boldsymbol {\varXi }_{i}\), with a cost of O(N). Note that each evaluation of the products Ω i Ξ i involves the multiplication of two 6×6 matrices.
For parallel computation by using O(N) processors, the computation of \(\boldsymbol {\varGamma }=\boldsymbol {\mathcal {A}}^{-1}\boldsymbol {\varPi }\) can be performed in O(logN) by using the block cyclic reduction algorithm [12]. Given the block-tridiagonal structure of matrix \(\boldsymbol {\mathcal {G}}\), the computation of \(\boldsymbol {\varXi }=\boldsymbol {\mathcal {G}}\boldsymbol {\varGamma }\) can be performed in O(logN). Finally, for computation of Λ −1 first all the products Ω i Ξ i , for i=1⋯N, can be computed in parallel in O(1) and then the summation of these products represent a linear recurrence that can be computed in O(logN) [12]. Therefore, the complexity of the parallel computation of Λ −1 is O(logN) by using N processors, indicating an optimal parallel efficiency in terms of both time and processors.
6 Conclusion
In this paper, we presented a new explicit factorization of M −1 as a product of a set of sparse matrices wherein only the inversion of a block-tridiagonal matrix is needed. Such a sparse factorization led to an algorithm, which we called the TFA, for both optimal serial and optimal parallel solution of the problem. We also showed that the TFA can be efficiently applied for optimal serial and parallel computation of the forward dynamics of a kinematic tree consisting of a single main chain plus any number of short side branches. We also presented yet another novel, though less efficient, factorization of M −1 in terms of the product of a set of sparse matrices wherein only the inversion of an upper-Hessenberg matrix is required. We showed that, interestingly, the better efficiency of our first factorization over the second one is a direct result of the choice of intermediate variables for the computation. That is, while our first factorization calculates the total force and then the total acceleration, in the second factorization the total acceleration is directly calculated without calculation of the total force.
We also show that this new factorization of M −1 leads to a new factorization of the operational-space inverse inertia, Λ −1, in the form of a product involving sparse matrices. We show that this factorization can be exploited for optimal serial and parallel computation of Λ −1, that is, a serial algorithm with a complexity of O(N) and a parallel algorithm with a time complexity of O(logN) on a computer with O(N) processors.
It should be noted that the TFA is less efficient, in terms of total number of operations, than other known algorithms for serial computation, such as the articulated body algorithm [2]. However, it achieves optimal parallel efficiency, with rather simple practical parallel implementation requirements (particularly in terms of data communication pattern), for both computation of M −1 and Λ −1. This is a definite advantage of the TFA for computation of very large serial chain systems or kinematic tree systems consisting of a large single main chain plus any number of short side branches.
To our knowledge, the CFA and the TFA are the only known algorithms that are based on explicit factorizations of M −1, involving sparse matrices and leading to similar explicit factorizations of Λ −1. However, while in the CFA these factorizations are in the form of Schur complements, in the TFA they are in the form of direct products of sparse matrices. An interesting question is then whether there are other possible factorizations of M −1, resulting in an even better efficiency for serial computation, in terms of actual number of operations.
Notes
These results are reported in an ANU M.Phil. thesis “Numerical Analysis of Robot Dynamics Algorithms” by Mingxu Li, which is currently under examination.
Abbreviations
- n :
-
Total number of Degrees of Freedom (DOF) of the system
- n i :
-
DOF of joint i
- N :
-
Number of bodies in the system
- m,a :
-
Cost of multiplication and addition
- O i :
-
Reference point fixed in body i
- P i,j :
-
Matrix to shift reference point from O j to O i
- P i :
-
Shorthand for P i+1,i
- \(\boldsymbol {\mathcal {P}}\in\Re^{6N\times6N}\) :
-
Global mapping from joint forces to body forces, or from body accelerations to joint accelerations (\(\boldsymbol {\mathcal {P}}^{\mathrm {T}}\))
- Q i :
-
3×3 rotational coordinate transform matrix from the frame located at O i+1 to the frame located at O i
-
 :
: -
6×6 rotational coordinate transform constructed from Q i
- m i :
-
Mass of body i
- s i :
-
Location of center of mass of body i relative to O i
- J i :
-
Second moment of mass of body i about its center of mass
- I i ∈ℜ6×6 :
-
Spatial inertia of body i referred to point O i
-
 :
: -
Global matrix of body inertias (\(\boldsymbol {\mathcal {I}}\in\Re^{6N\times6N}\))
- M∈ℜn×n :
-
Joint-space inertia matrix
- \(\ddot {\boldsymbol {q}}_{i} \in \Re^{n_{i}}\) :
-
Acceleration variables of joint i
- \(\ddot {\boldsymbol {q}}= \mathrm {col}\{\ddot {\boldsymbol {q}}_{i}\} \in \Re^{n}\) :
-
Global vector of joint acceleration variables
- \(\boldsymbol {\tau }_{i} \in \Re^{n_{i}}\) :
-
Force variables of joint i
- τ=col{τ i }∈ℜn :
-
Global vector of joint force variables
- \(\boldsymbol {\omega }_{i}, \dot{\boldsymbol {\omega }}_{i} \in \Re^{3}\) :
-
Angular velocity and acceleration of body i
- \(\boldsymbol {v}_{i}, \dot{\boldsymbol {v}}_{i} \in \Re^{3}\) :
-
Linear velocity and acceleration of body i (point O i )
-
 :
: -
Spatial acceleration of body i (assuming zero velocity)
- \(\dot {\boldsymbol {\mathcal {V}}}= \mathrm {col}\{ \dot {\boldsymbol {V}}_{\!\!i}\}\in \Re^{6N}\) :
-
Global vector of body accelerations
- f i ∈ℜ3 :
-
Force applied from body i−1 to body i at O i
- n i ∈ℜ3 :
-
Moment applied from body i−1 to body i about O i
-
 :
: -
Spatial force transmitted from body i−1 to body i
- \(\boldsymbol {\mathcal {F}}= \mathrm {col}\{ \boldsymbol {F}_{\!i}\} \in \Re^{6N}\) :
-
Global vector of interbody forces
-
 :
: -
Matrix describing the motion freedom of joint i (maps \(\ddot {\boldsymbol {q}}_{i}\) to spatial acceleration of joint i, assuming zero velocity)
-
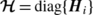 :
: -
Global matrix of joint motion freedoms (\(\boldsymbol {\mathcal {H}}\in \Re^{6N \times n}\))
- \(\boldsymbol {W}_{\!\!i} \in \Re^{6 \times (6-n_{i})}\) :
-
Matrix describing the constraint force space of joint i
-
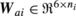 :
: -
Matrix that maps τ i to a spatial force at joint i
- \(\boldsymbol {\mathcal {W}}= \mathrm {diag}\{ \boldsymbol {W}_{\!\!i}\}\) :
-
Global constraint force matrix (\(\boldsymbol {\mathcal {W}}\in \Re^{6N \times (6N-n)}\))
-
 :
: -
Global mapping from τ to joint spatial forces (\(\boldsymbol {\mathcal {W}}_{\!\rm a}\in \Re^{6N \times n}\))
References
Anderson, K.S., Duan, S.: Highly parallelizable low order dynamics algorithm for complex multi-rigid-body systems. AIAA J. Guidance Control Dyn. 23(2), 355–364 (2000)
Featherstone, R.: Robot Dynamics Algorithms. Kluwer, Boston (1987)
Featherstone, R.: A divide-and-conquer articulated-body algorithm for parallel O(log(n)) calculation of rigid-body dynamics. Part 1: Basic algorithm. Int. J. Robot. Res. 18(9), 867–875 (1999)
Featherstone, R.: A divide-and-conquer articulated-body algorithm for parallel O(log(n)) calculation of rigid-body dynamics. Part 2: Trees, loops and accuracy. Int. J. Robot. Res. 18(9), 876–892 (1999)
Featherstone, R.: Rigid Body Dynamics Algorithms. Springer, New York (2008)
Featherstone, R., Fijany, A.: A technique for analyzing constrained rigid-body systems, and its application to the constraint force algorithm. IEEE Trans. Robot. Autom. 15(6), 1140–1144 (1999)
Featherstone, R., Orin, D.E.: Robot dynamics: equations and algorithms. In: Proc. IEEE Int. Conf. Robotics & Automation, San Francisco, CA, April 2000, pp. 826–834 (2000)
Featherstone, R., Orin, D.E.: Dynamics. In: Siciliano, B., Khatib, O. (eds.) Springer Handbook of Robotics, pp. 35–65. Springer, Berlin (2008)
Fijany, A.: Schur complement factorizations and parallel O(logn) algorithms for computation of operational space mass matrix and its inverse. In: Proc. IEEE Int. Conf. on Robotics & Automation, San Diego, May 1994, pp. 2369–2376 (1994)
Fijany, A., Sharf, I., D’Eleuterio, G.M.T.: Parallel O(logN) algorithms for computation of manipulator forward dynamics. IEEE Trans. Robot. Autom. 11(3), 389–400 (1995)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 2nd edn. The Johns Hopkins Univ. Press, Baltimore (1989)
Hockney, R.W., Jesshope, C.R.: Parallel Computers. Adam Hilger, London (1981)
Khatib, O.: A unified approach to motion and force control of robot manipulators: the operational space formulation. IEEE J. Robot. Autom. 3(1), 43–53 (1987)
Khatib, O.: Inertial properties in robotic manipulation: an object-level framework. Int. J. Robot. Res. 14(1), 19–36 (1995)
Lathrop, R.H.: Parallelism in manipulator dynamics. Int. J. Robot. Res. 4(2), 80–102 (1985)
Lee, C.S.G., Chang, P.R.: Efficient parallel algorithms for robot inverse dynamics computation. IEEE Trans. Syst. Man Cybern. 16(4), 532–542 (1986)
Mukherjee, R.M., Anderson, K.S.: A logarithmic complexity divide-and-conquer algorithm for multi-flexible articulated body systems. J. Comput. Nonlinear Dyn. 2(1), 10–21 (2007)
Redon, S., Galoppo, N., Lin, M.C.: Adaptive dynamics of articulated bodies. ACM Trans. Graph. 24(3), 936–945 (2005) (SIGGRAPH 2005)
Rodriguez, G., Jain, A., Kreutz-Delgado, K.: A spatial operator algebra for manipulator modelling and control. Int. J. Robot. Res. 10(4), 371–381 (1991)
Rodriguez, G., Kreutz-Delgado, K.: Spatial operator factorization and inversion of the manipulator mass matrix. IEEE Trans. Robot. Autom. 8(1), 65–76 (1992)
Walker, M.W., Orin, D.E.: Efficient dynamic computer simulation of robotic mechanisms. J. Dyn. Syst. Meas. Control 104, 205–211 (1982)
Wehage, R.A.: Solution of multibody dynamics using natural factors and iterative refinement—Part I: Open kinematic loops. In: Proc. Advances in Design Automation, Montreal, Quebec, Canada, Sept. 1989. ASME, New York, ASME Publication DE 19-3, pp. 125–132 (1989)
Yamane, K., Nakamura, Y.: Comparative study on serial and parallel forward dynamics algorithms for kinematic chains. Int. J. Robot. Res. 28(5), 622–629 (2009)
Acknowledgements
The first author would like to dedicate this paper to the memory of his dear friend, Ms. Bahareh Butterfly, for her courage, passion, and love.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Nonsingularity of \(\boldsymbol {H}_{i}^{\mathrm {T}} \boldsymbol {I}_{i} \boldsymbol {H}_{i}\) and \(\boldsymbol {\mathcal {A}}\)
If a matrix is positive definite, then it is nonsingular. According to Theorem 4.2.1 in [11], if A∈ℜn×n is positive definite, and X∈ℜn×k has rank k, then the matrix B=X T AX is positive definite. Now, I i is positive definite, and H i has full rank, so \(\boldsymbol {H}_{i}^{\mathrm {T}} \boldsymbol {I}_{i} \boldsymbol {H}_{i}\) is positive definite and, therefore, nonsingular.
To prove that \(\boldsymbol {\mathcal {A}}\) is nonsingular, we make use of the following result: if A∈ℜn×n is positive definite, and if X∈ℜn×(n−k) and Y∈ℜn×k have full rank and satisfy \(\boldsymbol {Y}^{\mathrm {T}}\boldsymbol {X}={\bf 0}\), then B=[AX Y]∈ℜn×n is nonsingular. The proof of this result is as follows. If B is singular, then there must exist a linear dependency between the columns of AX and the columns of Y. In other words, there must exist a vector \(\boldsymbol {z}\ne {\bf 0}\) that satisfies both z=AXx and z=Yy for some vectors x and y. However, this implies that \(\boldsymbol {z}^{\mathrm {T}}\boldsymbol {A}^{-1}\boldsymbol {z}=\boldsymbol {y}^{\mathrm {T}}\boldsymbol {Y}^{\mathrm {T}}\boldsymbol {X}\boldsymbol {x}={\bf 0}\), which is impossible because A is positive definite. Therefore, B must be nonsingular.
Consider the product \(\boldsymbol {\mathcal {A}}^{\mathrm {T}}\boldsymbol {B}\), where \(\boldsymbol {B}=[\boldsymbol {\mathcal {I}}\boldsymbol {\mathcal {H}}\quad \boldsymbol {\mathcal {W}}]\in\Re^{6N\times6N}\). It evaluates to

Now, \(\boldsymbol {\mathcal {G}}\) is positive definite (for the same reason that \(\boldsymbol {H}_{i}^{\mathrm {T}} \boldsymbol {I}_{i} \boldsymbol {H}_{i}\) is positive definite), and \(\boldsymbol {\mathcal {H}}\) and \(\boldsymbol {\mathcal {W}}\) are full-rank matrices satisfying \(\boldsymbol {\mathcal {H}}^{\mathrm {T}}\boldsymbol {\mathcal {W}}={\bf 0}\), so the right-hand side of this equation is nonsingular, therefore, the left-hand side is also nonsingular, and so \(\boldsymbol {\mathcal {A}}\) must be nonsingular.
Appendix B: Correctness of symbolic factorization of M −1
The correctness of the factorization of M −1 given in Eq. (51) can be proved by showing that \(\boldsymbol {M}^{-1}\boldsymbol {M}= {\bf U}\), where M −1 is taken from Eq. (51) and M is taken from Eq. (32). The first step is to simplify the expression in Eq. (51):

where
We now have

Rights and permissions
About this article
Cite this article
Fijany, A., Featherstone, R. A new factorization of the mass matrix for optimal serial and parallel calculation of multibody dynamics. Multibody Syst Dyn 29, 169–187 (2013). https://doi.org/10.1007/s11044-012-9313-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-012-9313-z




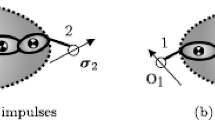

 :
: :
: :
: :
: :
: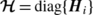 :
: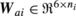 :
: :
: