1 Introduction

Functionally graded (FG) foams have attracted great attention due to the remarkable simultaneous properties of FG and viscoelastic materials (Altenbach and Eremeyev 2009, 2008a,b,c). Functionally graded materials have degraded properties that avoid severe variations of properties and thermo-mechanical stresses, and viscoelastic materials have high damping capability and phase delay (Brinson and Brinson 2008). Viscoelastic materials also can provide safe and quick ophthalmic surgery (Buratto et al. 2000). These foams are generally known as FG viscoelastic (FGV) foams and are categorized based on their inner connections, the open-cell with interconnected networks of cells, and close-cell without interconnections of cells (Ashby et al. 2000; Taraz Jamshidi et al. 2015; Hedayati and Sadighi 2016; Sadeghnejad et al. 2017; Sarrafan and Li 2022).

The mentioned properties of FGV foams provide an opportunity to use them in beam, plate, and shell structures, as a whole or as a constituent of composites (Jahwari and Naguib 2016; Zamani 2021a; Montgomery et al. 2021). From this point of view, FGV plates under dynamic loads are newly at the center of the attentions of researchers. Hosseini-Hashemi et al. (2015) used first-order shear deformation theory (FSDT) to derive natural frequency and damping ratios of cylindrical panels under Levy-type boundary conditions. Shariyat and Jahangiri (2020) studied the impact behavior of partially supported plates under bending-induced fluid flow based on the Galerkin finite element method (FEM) and the Hertz law. Zamani (2021b) applied the Galerkin, least squares, Ritz, and point collocation weighted residual methods to derive complex frequencies of foam plates. Alavi et al. (2022) studied transient and dynamic responses of porous standard solid plates using FSDT and the perturbation method. Dogan (2022) investigated quasi-static and dynamic responses of plates based on modified Durbin’s algorithm and Navier approach. Zamani (2022) considered thickness-stretching effect for free vibrations of thick foam plates using the Galerkin method with various shear and normal deformation theories (SNDT). Singh et al. (2023) applied power series EKM for standard solid piezoelectric plates with Levy-type boundary conditions.

In many practical circumstances, interactions of the foundation are inevitable (Kerr 1964). Therefore FGV plates may face various loads such as elastic and viscoelastic foundations. In this outline, Alimirzaei et al. (2019) investigated wave propagation of FGV plates on the visco-Pasternak foundation using a quasi-3D shear deformation theory. Sofiyev et al. (2019) analyzed the dynamic buckling of plates resting on an elastic foundation based on the CPT and the Galerkin method. Also, Sofiyev (2023) extended the dynamic buckling investigation for plates on viscoelastic foundation under different initial conditions. Besides FGV plates, vibration behavior of FGV foams on foundations is taken into consideration in recent years. Zamani et al. (2018) studied the free vibration of thin foam plates on an orthotropic foundation based on the classical plate theory (CPT), the Galerkin method, and various boundary conditions. Recently, Zamani et al. (2022) studied large-amplitude vibrations and mechanical buckling of foam beams on a nonlinear elastic foundation. They concluded that the viscoelasticity of foams enhances the differences of linear and nonlinear frequencies and buckling loads. Obviously, vibration analysis of FGV foam plates on the viscoelastic foundation is limited to the thin plates and CPT, whereas in many practical circumstances, analysis of thick plates using SNDT considering thickness-stretching effects are necessary. Furthermore, the main aim of this study is the implementation of viscoelastic foundation for vibrations of thick foam plates considering thickness stretching.

In accordance with the literature review, it is revealed that dynamic analysis of FGV plates is restricted to the CPT (Shariyat and Jahangiri 2020; Dogan 2022), FSDT (Hosseini-Hashemi et al. 2015; Alavi et al. 2022), refined FSDT (Zamani 2021b), quasi-3D theories (Singh et al. 2023), and SNDT (Zamani 2022). Moreover, dynamic analysis of FGV plates on foundations (Sofiyev et al. 2019; Sofiyev 2023) and FGV foams on foundations (Zamani et al. 2018, 2022) is limited to the CPT and wave propagation with quasi-3D (Alimirzaei et al. 2019) approach. Overall, there is no study for the application of SNDT for vibrations of thick shear-and-normal deformable FGV foam plates resting on the viscoelastic foundations.

In this paper, SNDT is applied to study the complex frequency behavior of foam plates. Shear and normal deformation theory includes in-plane and out-of-plane displacements, whereas normal strain through the thickness direction is also considered. Simple power law, separable kernels framework, and Boltzmann–Volterra superposition integral are adapted for constitutive relations. The Hamilton principle is used to derive the governing equations of motions with frequency-dependent coefficients. The Galerkin method in conjunction with \(\mathit{QZ}\) iterative numerical algorithm is implemented to derive natural frequencies and modal loss factors. Some numerical examples are carried out to assess the accuracy of the present method. Then the impacts of material model, geometrical parameters, and foundation coefficients are investigated through parametric studies.

2 Basic formulation

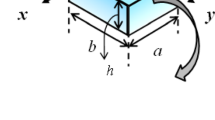
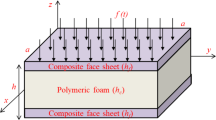
Consider a rectangular plate as depicted by Fig. 1. Variables \(x\), \(y\), and \(z\) stand for orthogonal coordinate systems, and the origin is placed at the corner of the midsurface of the plate. The parameters \(a\), \(b\), and \(h\) denote the length, width, and total thickness, respectively. Moreover, \(K_{w}\), \(K_{p}\), and \(K_{d}\) represent the Winkler, Pasternak, and damping coefficients of foundation, respectively.

Fig. 1
figure 1

The geometry and coordinates of a functionally graded viscoelastic plate (a) and schematic of a polymeric open-cell foam (b) (Altenbach and Eremeyev 2008c)

Full size image

2.1 Constitutive equations

In the present work, we adapt the Boltzmann–Volterra superposition integral is adapted for linear viscoelastic behavior of the open-cell foam plate as follows (Brinson and Brinson 2008):

$$\begin{aligned} &\left \{ \textstyle\begin{array}{c} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{zz}\\ \sigma _{yz}\\ \sigma _{xz}\\ \sigma _{xy} \end{array}\displaystyle \right \} \\ &\quad = \int _{-\infty}^{t} \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \lambda _{1} (t - t ' ) & \lambda (t - t ' ) & \lambda (t - t ' ) & 0 & 0 & 0\\ & \lambda _{1} (t - t ' ) & \lambda (t - t ' ) & 0 & 0 & 0\\ & & \lambda _{1} (t - t ' ) & 0 & 0 & 0\\ Sym. & & & \mu (t - t ' ) & 0 & 0\\ & & & & \mu (t - t ' ) & 0\\ & & & & & \mu (t - t ' ) \end{array}\displaystyle \right ] \\ &\qquad {}\times\left \{ \textstyle\begin{array}{c} \varepsilon _{x, t '} ( t ' )\\ \varepsilon _{y, t '} ( t ' )\\ \varepsilon _{z, t '} ( t ' )\\ \varepsilon _{yz, t '} ( t ' )\\ \varepsilon _{xz, t '} ( t ' )\\ \varepsilon _{xy, t '} ( t ' ) \end{array}\displaystyle \right \} dt ', \end{aligned}$$
(1)

where \(\sigma \), \(\varepsilon \), \(t\), \(t '\), and “ , ” stand for the stress, strain, time, Boltzmann integral variable, and differential operator, respectively. Moreover, \(\lambda \), \(\lambda _{1}\), and \(\mu \) represent frequency-dependent viscoelastic Lame coefficients (Brinson and Brinson 2008; Altenbach and Eremeyev 2008b,c):

$$\begin{gathered} \lambda (z,\omega )=K(z\omega ) - \frac{2}{3} G(z,\omega )= \frac{\nu (z,\omega )E(z,\omega )}{\left ( 1 - 2\nu (z,\omega ) \right ) \left ( 1+\nu (z,\omega ) \right )}, \\ \lambda _{1} (z,\omega )=K(z,\omega )+ \frac{4}{3} G(z,\omega )= \frac{(1 - \nu (z,\omega ))}{v(z,\omega )} \lambda (z,\omega ), \\ \mu (z,\omega )=G(z,\omega )= \frac{E(z,\omega )}{2(1+\nu (z,\omega ))}, \\ \lambda \left ( \omega ,z \right ) +2\mu \left ( \omega ,z \right ) = \lambda _{1} \left ( \omega ,z \right ), \\ \hat{C}_{12} \left ( \omega \right ) +2 \hat{C}_{66} \left ( \omega \right ) = \hat{C}_{11} \left ( \omega \right ), \\ \hat{C}_{11} \left ( \omega \right ) = \hat{C}_{22} \left ( \omega \right ) = \hat{C}_{33} \left ( \omega \right ), \\ \hat{C}_{13} \left ( \omega \right ) = \hat{C}_{23} \left ( \omega \right ) = \hat{C}_{12} \left ( \omega \right ), \\ \hat{C}_{44} \left ( \omega \right ) = \hat{C}_{55} \left ( \omega \right ), \end{gathered}$$
(2)

where \(\omega \), \(K\ G\), \(E\), \(C\), and \(\nu \) stand for the frequency, bulk, shear, Young moduli, viscoelastic stiffness coefficients, and Poisson ratio, respectively. Generally, the mentioned properties are frequency-dependent or time-dependent, and in the present study, we consider the frequency-dependent one. Also, frequency-dependent properties and viscoelastic stiffness coefficients could be derived directly using the Alfrey correspondence principle (Alfrey 1944). Other effective properties could be written as (Srinivas and Rao 1971; Hatami et al. 2008)

$$\begin{gathered} \rho \left ( z,\omega \right ) = \rho _{s} V \left ( z \right ), \end{gathered}$$
(3)
$$\begin{gathered} K \left ( z,\omega \right ) = K_{0} V^{2} \left ( z \right ), \end{gathered}$$
(4)
$$\begin{gathered} G \left ( z,\omega \right ) = G_{0} \frac{1+i c_{1} \omega}{1+i\beta c_{1} \omega} V^{2} \left ( z \right ), c_{1} = h \sqrt{\frac{\rho}{G_{0}}}, \end{gathered}$$
(5)
$$\begin{gathered} V(z)= \frac{\rho _{p}}{\rho _{s}} +(1 - \frac{\rho _{p}}{\rho _{s}} )( \frac{1}{2} - \frac{z}{h} )^{p}, \end{gathered}$$
(6)

where \(\rho \), \(\rho _{s}\), \(\rho _{p} / \rho _{s}\), \(p\), \(\beta \), \(K_{0}\), and \(G_{0}\) stand for the density, minimum density, minimal relative density, power index, parameter of constitutive relation, elastic dilatation, and distortion moduli, respectively. Also, \(\beta =0.5, 1\) and \(p=0, 1, 2\) represent standard solid and elastic models, and homogenous, linear, and quadratic distributions of porosity through the thickness direction, respectively. It is worth mentioning that homogenous and linear distributions of porosity are particular cases, and in this study, we also consider other values of \(p\). Generally, power index represents the order of variations of volume fraction and eventually other properties. Moreover, for illustration, in Fig. 2, we present the effects of power index on volume fraction for \(\rho _{p} / \rho _{s} =0.3\).

Fig. 2
figure 2

The effects of power index on volume fraction (Zamani et al. 2018)

Full size image

2.2 Kinematic formulation

In this work, consider the displacement field in three different directions (Mantari 2015; Mantari and Guedes Soares 2014):

$$\begin{gathered} u_{1} \left ( x,y,z,t \right ) =u \left ( x,y,t \right ) - z \left [ w_{b,x} + \left ( f ' \left ( \frac{h}{2} \right ) +g \left ( \frac{h}{2} \right ) \right ) w_{s,x} \right ] +f \left ( z \right ) w_{s,x}, \\ u_{2} \left ( x,y,z,t \right ) =v \left ( x,y,t \right ) - z \left [ w_{b,y} + \left ( f ' \left ( \frac{h}{2} \right ) +g \left ( \frac{h}{2} \right ) \right ) w_{s,y} \right ] +f \left ( z \right ) w_{s,y}, \\ u_{3} \left ( x,y,z,t \right ) = w_{b} \left ( x,y,t \right ) +g \left ( z \right ) w_{s} \left ( x,y,t \right ), \\ f(z)= \frac{h}{m} \tan h ( \frac{mz}{h} )+ z^{3}, \\ g(z)=nf(z), \\ n=2/15,m=0.4, \end{gathered}$$
(7)

where \(u\), \(v\), \(w_{b}\), and \(w_{s}\) stand for midplane displacements in the \(x\), \(y\), \(z\) directions, bending the component and shear components of transverse displacements, respectively. Also, \(f (z)\) and \(g(z)\) are obtained using stress-free edge conditions on the top of the plate, and for details, we refer to Mantari and Guedes Soares (2014) and Mantari (2015). It is worth mentioning that the number of unknowns is four, which is less than in FSDT and higher-order shear deformation theory (HSDT).

The linear strain-displacement components are expressed as (Mantari and Guedes Soares 2014; Mantari 2015)

$$\begin{gathered} \begin{aligned}[t] &\left \{ \textstyle\begin{array}{c} \varepsilon _{x}\\ \varepsilon _{y}\\ \gamma _{xy} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} u_{,x}\\ v_{,y}\\ u_{,y} + v_{,x} \end{array}\displaystyle \right \} - z \left ( \left \{ \textstyle\begin{array}{c} w_{b,xx}\\ w_{b,yy}\\ 2 w_{b,xy} \end{array}\displaystyle \right \} + \left ( f ' ( \frac{h}{2} )+g( \frac{h}{2} ) \right ) \left \{ \textstyle\begin{array}{c} w_{s,xx}\\ w_{s,yy}\\ 2 w_{s,xy} \end{array}\displaystyle \right \} \right ) \\ &\hphantom{\left \{ \textstyle\begin{array}{c} \varepsilon _{x}\\ \varepsilon _{y}\\ \gamma _{xy} \end{array}\displaystyle \right \} ={}}{}- f(z) \left \{ \textstyle\begin{array}{c} w_{s,xx}\\ w_{s,yy}\\ 2 w_{s,xy} \end{array}\displaystyle \right \}, \end{aligned} \\ \varepsilon _{z} =g ' (z) w_{s}, \\ \left \{ \textstyle\begin{array}{c} \gamma _{yz}\\ \gamma _{xz} \end{array}\displaystyle \right \} = \left \{ \begin{aligned} &\left ( - f ' ( \frac{h}{2} )+g( \frac{h}{2} )+g(z)+f ' (z) \right ) w_{s,y}\\ &\left ( - f ' ( \frac{h}{2} )+g( \frac{h}{2} )+g(z)+f ' (z) \right ) w_{s,x} \end{aligned} \right \}, \end{gathered}$$
(8)

where \(\varepsilon _{i} \ (i=x,y,z)\) and \(\gamma _{i} \ (i=xy,yz,xz)\) stand for the normal and shear strains, respectively. Clearly, the normal strain through the thickness direction is proportional to the shear component of transverse displacement, a polynomial and trigonometric hyperbolic function in the thickness direction.

3 Governing equations

In this section, we derive the governing equations of motions of FGV open-cell foam plates on visco-Pasternak foundation considering thickness-stretching effect. To this aim, we implement the dynamic version of virtual displacement or Hamilton principle:

$$\begin{gathered} \int _{t_{1}}^{t_{2}} (\delta U+\delta V - \delta T)dt=0, \\ \delta U= \int _{A} \int _{- {h} / {2}}^{{h} / {2}} \left ( \textstyle\begin{array}{l} \sigma _{xx} (\omega )\delta \varepsilon _{x} + \sigma _{yy} (\omega )\delta \varepsilon _{y} + \sigma _{zz} (\omega )\delta \varepsilon _{z} \\ + \sigma _{xy} (\omega )\delta \varepsilon _{xy} + \sigma _{yz} (\omega )\delta \varepsilon _{yz} + \sigma _{xz} (\omega )\delta \varepsilon _{xz} \end{array}\displaystyle \right ) dzdA, \\ \delta V= \int _{A} \int _{{-h} / {2}}^{{h} / {2}} ( K_{w} \delta u_{3} - K_{p} \left ( u_{3,x} \delta u_{3,x} + u_{3,y} \delta u_{3,y} \right ) + K_{d} u_{3,t} \delta u_{3,t} )dzdA, \\ \delta T= \int _{A} \int _{{-h} / {2}}^{{h} / {2}} \rho (z,\omega )( u_{1,t} \delta u_{1,t} + u_{2,t} \delta u_{2,t} + u_{3,t} \delta u_{3,t} )dzdA, \\ \delta u_{i} =0, \left ( u_{i} =u,v, w_{b}, w_{s} \right ), \end{gathered}$$
(9)

where \(A\), \(t_{1}\), \(t_{2}\), \(\delta u_{i}\), \(\delta U\), \(\delta V\), and \(\delta T\) denote the area, initial time, terminal time, virtual displacement, virtual strain energy, potential energy of foundation, and virtual kinematic energy, respectively. Substituting Eqs. (1)–(8) into Eqs. (9), integrating in the thickness direction, and integrating by parts, we can extract the virtual displacements and write the resulting equations of motions as

$$\begin{gathered} \begin{aligned} & \delta u: N_{x,x} \left ( \omega \right ) + N_{xy,y} \left ( \omega \right ) \\ &\quad = I_{0} \left ( \omega \right ) u_{,tt} - I_{1} \left ( \omega \right ) w_{b,xtt} \\ &\qquad {}+ \left ( I_{3} \left ( \omega \right ) - \left ( f ' \left ( \frac{h}{2} \right ) +g \left ( \frac{h}{2} \right ) \right ) I_{1} \left ( \omega \right ) \right ) w_{s,xtt}, \end{aligned} \end{gathered}$$
(10)
$$\begin{gathered} \begin{aligned} & \delta v: N_{xy,x} \left ( \omega \right ) + N_{y,y} \left ( \omega \right ) \\ &\quad = I_{0} \left ( \omega \right ) v_{,tt} - I_{1} \left ( \omega \right ) w_{b,ytt} \\ &\qquad {}+ \left ( I_{3} \left ( \omega \right ) - \left ( f ' \left ( \frac{h}{2} \right ) +g \left ( \frac{h}{2} \right ) \right ) I_{1} \left ( \omega \right ) \right ) w_{s,ytt}, \end{aligned} \end{gathered}$$
(11)
$$\begin{gathered} \begin{aligned} & \delta w_{b}: M_{x,xx} (\omega )+2 M_{xy,xy} (\omega )+ M_{y,yy} (\omega ) \\ &\quad = I_{0} (\omega ) w_{b,tt} + I_{1} (\omega ) \left ( u_{,x} + v_{,y} \right )_{,tt} - I_{2} (\omega ) \nabla ^{2} w_{b,tt} \\ &\qquad {}+ \left ( I_{4} (\omega ) - I_{2} (\omega )(f ' ( h /2)+g( h /2) \right ) \nabla ^{2} w_{s,tt} + I_{6} (\omega ) w_{s,tt} \\ &\qquad {}+ K_{w} \left ( w_{b} +g( h /2) w_{s} \right ) - K_{p} \left ( \nabla ^{2} w_{b} +g \left ( \frac{h}{2} \right ) \nabla ^{2} w_{s} \right ) \\ &\qquad {}+ K_{d} \left ( w_{b,t} +g \left ( \frac{h}{2} \right ) w_{s,t} \right ), \end{aligned} \end{gathered}$$
(12)
$$\begin{gathered} \begin{aligned} & \delta w_{s}: \left ( f ' ( h /2)+g( h /2) \right ) \bigl( M_{x,xx} (\omega )+2 M_{xy,xy} (\omega )+ M_{y,yy} (\omega ) \\ &\qquad {}- N_{xz,x} (\omega ) - N_{yz,y} (\omega ) \bigr) - P_{x,xx} (\omega ) - 2 P_{xy,xy} (\omega ) - P_{y,yy} (\omega )+ Q_{yz,y} (\omega ) \\ &\qquad {}+ Q_{xz,x} (\omega )+ K_{yz,y} (\omega )+ K_{xz,x} (\omega ) - R_{z} (\omega ) \\ &\quad = - \left ( I_{3} (\omega ) - I_{1} (\omega )(f ' ( h /2)+g( h /2) \right ) \left ( u_{,x} + v_{,y} \right )_{,tt} \\ &\qquad {}+ \left ( I_{4} (\omega ) - I_{2} (\omega )(f ' ( h /2)+g( h /2) \right ) \nabla ^{2} w_{b,tt} \\ &\qquad {} + \left ( - \left ( f ' ( h /2)+g( h /2) \right )^{2} I_{2} +2 \left ( f ' ( h /2)+g( h /2) \right ) I_{4} - I_{5} \right ) \nabla ^{2} w_{s,tt} \\ &\qquad {}+ I_{6} w_{b,tt} + I_{7} w_{s,tt} \\ &\qquad {}+g \left ( \frac{h}{2} \right ) K_{w} \left ( w_{b}+g \left ( \frac{h}{2} \right ) w_{s} \right ) - g \left ( \frac{h}{2} \right ) K_{p} \left ( \nabla ^{2} w_{b} +g \left ( \frac{h}{2} \right ) \nabla ^{2} w_{s} \right ) \\ &\qquad {} +g \left ( \frac{h}{2} \right ) K_{d} \left ( w_{b,t} +g \left ( \frac{h}{2} \right ) w_{s,t} \right ), \end{aligned} \end{gathered}$$
(13)

where \(N\), \(M\), \(Q\), \(K\), \(R\), and \(I_{i} \ ( i =0,\ldots,6)\) stand for the frequency-dependent stress resultants and frequency-dependent mass inertia, respectively, which are defined as

$$\begin{gathered} \left \{ \textstyle\begin{array}{c} N_{i} (\omega ), M_{i} (\omega ), P_{i} (\omega )\\ Q_{j} (\omega ), K_{j} (\omega )\\ R_{z} (\omega ) \end{array}\displaystyle \right \} = \int _{- \frac{h}{2}}^{\frac{h}{2}} \left \{ \textstyle\begin{array}{c} \sigma _{i} \left ( 1,z,f \right )\\ \sigma _{j} (g,f ' (z))\\ \sigma _{z} g_{,z} \end{array}\displaystyle \right \} dz \quad \left ( \textstyle\begin{array}{l} i=x,y,xy,yz,xz\\ j=xz,yz \end{array}\displaystyle \right ), \\ \left \{ \textstyle\begin{array}{c} I_{i} (\omega )\\ I_{j} (\omega )\\ I_{k} (\omega ) \end{array}\displaystyle \right \} = \int _{- \frac{h}{2}}^{\frac{h}{2}} \left \{ \textstyle\begin{array}{c} \rho z^{i}\\ \rho (f,zf, f^{2} )\\ \rho (g, g^{2} ) \end{array}\displaystyle \right \} dz\quad \left ( \textstyle\begin{array}{l} i=0,1,2\\ j=3,4,5\\ k=6,7 \end{array}\displaystyle \right ). \end{gathered}$$
(14)

For the case of stress resultants, the extended form is rewritten as

$$\begin{gathered} \left \{ \textstyle\begin{array}{c} N_{x}\\ N_{y}\\ N_{xy}\\ M_{x}\\ M_{y}\\ M_{xy}\\ P_{x}\\ P_{y}\\ P_{xy}\\ R_{z} \end{array}\displaystyle \right \} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} A_{11} & A_{12} & 0 & B_{11} & B_{12} & 0 & C_{11} & C_{12} & 0 & F_{12}\\ A_{12} & A_{11} & 0 & B_{12} & B_{11} & 0 & C_{12} & C_{11} & 0 & F_{12}\\ 0 & 0 & A_{66} & 0 & 0 & B_{66} & 0 & 0 & C_{66} & 0\\ B_{11} & B_{12} & 0 & G_{11} & G_{12} & 0 & H_{11} & H_{12} & 0 & K '_{12}\\ B_{12} & B_{11} & 0 & G_{12} & G_{11} & 0 & H_{12} & H_{11} & 0 & K '_{12}\\ 0 & 0 & B_{66} & 0 & 0 & G_{66} & 0 & 0 & H_{66} & 0\\ C_{11} & C_{12} & 0 & H_{11} & H_{12} & 0 & L_{11} & L_{12} & 0 & O_{12}\\ C_{12} & C_{11} & 0 & H_{12} & H_{11} & 0 & L_{12} & L_{11} & 0 & O_{12}\\ 0 & 0 & C_{66} & 0 & 0 & H_{66} & 0 & 0 & L_{66} & 0\\ F_{12} & F_{12} & 0 & K '_{12} & K '_{12} & 0 & O_{12} & O_{12} & 0 & U_{11} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{0}\\ \varepsilon _{yy}^{0}\\ \varepsilon _{xy}^{0}\\ \varepsilon _{xx}^{1}\\ \varepsilon _{yy}^{1}\\ \varepsilon _{xy}^{1}\\ \varepsilon _{xx}^{2}\\ \varepsilon _{yy}^{2}\\ \varepsilon _{xy}^{2}\\ \varepsilon _{zz} \end{array}\displaystyle \right \}, \end{gathered}$$
(15)
$$\begin{gathered} \left \{ \textstyle\begin{array}{c} N_{yz}\\ N_{xz}\\ K_{yz}\\ K_{xz}\\ Q_{yz}\\ Q_{xz} \end{array}\displaystyle \right \} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} A_{66} & 0 & D_{66} & 0 & E_{66} & 0\\ 0 & A_{66} & 0 & D_{66} & 0 & E_{66}\\ E_{66} & 0 & Q_{66} ' & 0 & S_{66} & 0\\ 0 & E_{66} & 0 & Q_{66} ' & 0 & S_{66}\\ D_{66} & 0 & P_{66} ' & 0 & Q_{66} ' & 0\\ 0 & D_{66} & 0 & P_{66} ' & 0 & Q_{66} ' \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} \varepsilon _{yz}^{0}\\ \varepsilon _{xz}^{0}\\ \varepsilon _{yz}^{3}\\ \varepsilon _{xz}^{3}\\ \varepsilon _{yz}^{4}\\ \varepsilon _{xz}^{4} \end{array}\displaystyle \right \}, \end{gathered}$$
(16)

where the matrix coefficients and strains are defined as

$$\begin{gathered} \left ( A_{i}, B_{i}, C_{i}, D_{i}, E_{i}, F_{i}, G_{i} \right ) = \int _{-h /2}^{h /2} Q_{ij} (z) \left ( 1,z,f(z),g(z), f ' (z), g ' (z), z^{2} \right ) dz, \\ \left ( H_{i}, K_{i} ', L_{i}, O_{i}, U_{i} \right ) = \int _{- \frac{h}{2}}^{\frac{h}{2}} Q_{ij} \left ( z \right ) \left ( zf \left ( z \right ),z g ' \left ( z \right ), f^{2} \left ( z \right ),f \left ( z \right ) g ' \left ( z \right ), g^{\prime \, 2} \left ( z \right ) \right ) dz, \end{gathered}$$
(17)
$$\begin{gathered} \left ( Q_{i} ', S_{i}, P_{i} ' \right ) = \int _{-h /2}^{h /2} Q_{ij} (z) \left ( g(z) f ' (z), f^{\prime \, 2} (z), g^{2} (z) \right ) dz, \\ \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{0}\\ \varepsilon _{yy}^{0}\\ \varepsilon _{xy}^{0}\\ \varepsilon _{xx}^{1}\\ \varepsilon _{yy}^{1}\\ \varepsilon _{xy}^{1}\\ \varepsilon _{xx}^{2}\\ \varepsilon _{yy}^{2}\\ \varepsilon _{xy}^{2}\\ \varepsilon _{z} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} u_{,x}\\ v_{,y}\\ u_{,y} + v_{,x}\\ - w_{b,xx} - \left ( f ' ( h /2)+g( h /2) \right ) w_{s,xx}\\ - w_{b,yy} - \left ( f ' ( h /2)+g( h /2) \right ) w_{s,yy}\\ - 2 w_{b,xy} - 2 \left ( f ' ( h /2)+g( h /2) \right ) w_{s,xy}\\ w_{s,xx}\\ w_{s,yy}\\ 2 w_{s,xy}\\ w_{s} \end{array}\displaystyle \right \}, \end{gathered}$$
(18)
$$\begin{gathered} \left \{ \textstyle\begin{array}{c} \varepsilon _{yz}^{0}\\ \varepsilon _{xz}^{0}\\ \varepsilon _{yz}^{3}\\ \varepsilon _{xz}^{3}\\ \varepsilon _{yz}^{4}\\ \varepsilon _{xz}^{4} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} - \left ( f ' ( h /2)+g( h /2) \right ) w_{s,y}\\ - \left ( f ' ( h /2)+g( h /2) \right ) w_{s,x}\\ w_{s,y}\\ w_{s,x}\\ w_{s,y}\\ w_{s,x} \end{array}\displaystyle \right \}. \end{gathered}$$
(19)

Also, the displacement field variables are expressed based on harmonic functions as (Rao 2004)

$$\begin{aligned} \begin{aligned} u(x,y,t)&=u(x,y) e^{i\omega t}, \\ v \left ( x,y,t \right ) &=v \left ( x,y \right ) e^{i\omega t}, \\ w_{b} \left ( x,y,t \right ) &= w_{b} \left ( x,y \right ) e^{i\omega t}, \\ w_{s} \left ( x,y,t \right ) &= w_{s} \left ( x,y \right ) e^{i\omega t}. \end{aligned} \end{aligned}$$
(20)

By substitution of strains (18)–(19) into the resultant equations (15)–(16), using harmonic functions, we can rewrite the governing equations (10)–(13) as

$$\begin{aligned} & A_{11} u_{,xx} + A_{66} u_{,yy} + \left ( A_{12} + A_{66} \right ) v_{,xy} - B_{11} \nabla ^{2} w_{b,x} + \left ( B_{11} q_{11} + C_{11} \right ) \nabla ^{2} w_{s,x} \end{aligned}$$
(21)
$$\begin{aligned} &\quad {}+ F_{12} w_{s,x} - \omega ^{2} \left ( - I_{0} u+ I_{1} w_{b,x} + \left ( I_{3} - I_{1} q_{11} \right ) w_{s,x} \right ) =0, \\ & \left ( A_{12} + A_{66} \right ) u_{,xy} + A_{66} v_{,xx} + A_{11} v_{,yy} - B_{11} \nabla ^{2} w_{b,y} + \left ( B_{11} q_{11} + C_{11} \right ) \nabla ^{2} w_{s,y} \end{aligned}$$
(22)
$$\begin{aligned} &\quad {}+ F_{12} w_{s,y} - \omega ^{2} \left ( - I_{0} v+ I_{1} w_{b,y} + \left ( I_{3} - I_{1} q_{11} \right ) w_{s,y} \right ) =0, \\ & B_{11} \nabla ^{2} u_{,x} + B_{11} \nabla ^{2} v_{,y} + G_{11} \left ( q_{11} \nabla ^{4} w_{s} - \nabla ^{4} w_{b} \right ) + H_{11} \nabla ^{4} w_{s} + K_{12} ' \nabla ^{2} w_{s} \end{aligned}$$
(23)
$$\begin{aligned} &\quad {}- \left ( K_{w} +i\omega K_{d} \right ) \left ( w_{b} +g( {h} / {2} ) w_{s} \right ) + K_{p} \left ( \nabla ^{2} w_{b} +g( {h} / {2} ) \nabla ^{2} w_{s} \right ) \\ &\quad {}- \omega ^{2} \left ( - I_{0} w_{b} - I_{1} u_{,x} - I_{1} v_{,y} + I_{2} \nabla ^{2} w_{b} + \left ( I_{4} - q_{11} I_{2} \right ) \nabla ^{2} w_{s} - I_{6} w_{s} \right ) =0, \\ &{-} C_{11} \nabla ^{2} \left ( u_{,x} + v_{,y} \right ) - F_{12} \left ( u_{,x} + v_{,y} \right ) + q_{11} B_{11} \nabla ^{2} \left ( u_{,x} + v_{,y} \right ) \end{aligned}$$
(24)
$$\begin{aligned} &\quad {}+ \left ( H_{11} - G_{11} q_{11} \right ) \nabla ^{4} w_{b}+ K_{12} ' \nabla ^{2} w_{b} - g( h /2) \bigl( \left ( K_{w} +i\omega K_{d} \right ) \left ( w_{b} +g( h /2) w_{s} \right ) \\ &\quad {}- K_{p} \left ( \nabla ^{2} w_{b} +g( h /2) \nabla ^{2} w_{s} \right ) \bigr) \\ &\quad {} + \left ( - q_{11}^{2} A_{66} +2 Q_{66} ' + P_{66} ' - 2 O_{12} ' + S_{66} ' \right ) \nabla ^{2} w_{s} + \left ( q_{11}^{2} G_{11} - L_{11} \right ) \nabla ^{4} w_{s} - U_{11} w_{s} \\ &\quad {}- \omega ^{2} \bigl( \left ( I_{3} - I_{1} q_{11} \right ) \left ( u_{,x} + v_{,y} \right ) + \left ( q_{11} I_{2} - I_{4} \right ) \nabla ^{2} w_{b} - I_{6} w_{b} \\ &\quad {}+ I_{5} \nabla ^{2} w_{s} - I_{7} w_{s} + \left ( q_{11}^{2} I_{2} - 2 q_{11} I_{4} \right ) \nabla ^{2} w_{s} \bigr) =0, \\& \nabla ^{2} \left ( \right ) = \left ( \right )_{,xx} + \left ( \right )_{,yy}, \\ &\nabla ^{4} \left ( \right ) = \nabla ^{2} \left ( \nabla ^{2} \left ( \right ) \right ) = \left ( \right )_{,xxxx} +2 \left ( \right )_{,xxyy} + \left ( \right )_{,yyyy}, \end{aligned}$$
(25)

where \(\nabla ^{2} \left ( \right )\) and \(\nabla ^{4} \left ( \right )\) stand for the Nabla and biharmonic operators, respectively.

4 Semianalytical solution

In this section, we resolve the mentioned governing equations of motions using the Bubnov–Galerkin method and \(QZ\) eigenvalue solver (Golub and Van Loan 2013) to obtain fundamental frequencies and modal loss factors of foam plates with simply supported boundary conditions. The introduced edge conditions are defined as

$$ \begin{aligned} N_{x} &= M_{x} = P_{x} =v= w_{b} = w_{s} = w_{s,y} =0, \quad x =0, a, \\ N_{y} &= M_{y} = P_{y} =u= w_{b} = w_{s} = w_{s,x} =0, \quad y =0, b. \end{aligned} $$
(26)

By applying the Galerkin weighed residual method, we discretize four-coupled PDEs of motion in the spatial domain. The applied functions of movable simply supported edge conditions are (Mantari 2015)

$$\begin{gathered} u(x,y)= \cos ( \frac{m\pi}{a} x) \sin ( \frac{n\pi}{b} y), \\ v(x,y)= \sin ( \frac{m\pi}{a} x) \cos ( \frac{n\pi}{b} y), \\ w_{b} (x,y)= \sin ( \frac{m\pi}{a} x) \sin ( \frac{n\pi}{b} y), \\ w_{s} (x,y)= \sin ( \frac{m\pi}{a} x) \sin ( \frac{n\pi}{b} y). \end{gathered}$$
(27)

The degraded PDEs of motions convert to a system of complex algebraic equations with frequency-dependent coefficients. The system of equations can be rewritten as

$$ \left ( \boldsymbol{C} (\omega ) - \omega ^{2} \boldsymbol{M} (\omega )+ \boldsymbol{C} ' (\omega ) \right ) \boldsymbol{q} =0, $$
(28)

where \(\mathbf{C}\), \(\boldsymbol{C} '\), M, and \(\mathbf{q}\) stand for the square matrices of frequency-dependent stiffness, damping, inertia, and vector of displacement, respectively. By applying \(QZ\) eigenvalue solver the outcomes are complex roots, which are written as (Zamani and Aghdam 2016)

$$ \begin{gathered} \omega = \omega ^{\operatorname{Re}} + i\omega ^{\operatorname{Im}}, \\ \omega _{mn} = \omega ^{\operatorname{Re}}, \\ \eta = \frac{2\omega ^{\operatorname{Re}} \omega ^{\operatorname{Im}}}{(\omega ^{\operatorname{Re}} )^{2} - (\omega ^{\operatorname{Im}} )^{2}}, \end{gathered} $$
(29)

where \(\eta \) and superscripts \(\operatorname{Re}\), \(\operatorname{Im}\) stand for the modal loss factor and real and imaginary parts of frequencies, respectively. Furthermore, the real and imaginary parts of complex frequencies refer to the natural frequency and damping capability, respectively. In this study, damping emanates from two sources: first, material damping due to viscoelasticity, and the second is external damping of foundations.

5 Results and discussion

In this part, the presented method is verified and the impacts of various parameters are evaluated through numerical examples. First, the present method is verified for available results of elastic \(\mathrm{Al}/\mathrm{A} \mathrm{l}_{2} \mathrm{O}_{3}\) plate on an elastic foundation (Thai and Choi 2012; Akavci 2014; Mantari et al. 2014b,a; Alazwari and Zenkour 2022) and laminated viscoelastic composite plate (Koo and Lee 1993). Then the impacts of geometry and foundation on complex frequencies are studied with numerical examples. We further assume the following properties of FGV open-cell foam plates: \(\rho _{p} / \rho _{s} =0.65\), \(\rho _{s} =200~{\mathrm{kg}} / {\mathrm{m}^{3}}\), \(G_{0} =2\ \mathrm{GPa}\), \(K_{0} =2 G_{0}\), \(h = 1\), \(\beta =0.5\), \({b} / {a} =1\), \({a} / {h} =10\), \(p = 1\), \((m,n) = (1, 1)\).

5.1 Comparative studies

In this section, we compare the nondimensional fundamental frequency parameters of elastic \(\mathrm{Al}/\mathrm{A} \mathrm{l}_{2} \mathrm{O}_{3}\) plates with available results reported by Thai and Choi (2012), Akavci (2014), Mantari et al. (2014a), Mantari et al. (2014b), and Alazwari and Zenkour (2022). For this case, the assumed properties and parameters are as follows: \(E_{m} = 70\text{ GPa}\), \(\rho _{m} = 2702\text{ kg}/\text{m}^{3}\), \(E_{c} = 380 \text{ GPa}\), \(\rho _{c} = 3800\text{ kg/m}^{3}\), \(\nu =0.3\), \(\bar{K}_{w} = \frac{K_{w} a^{4}}{D_{m}}\), \(\bar{K}_{s} = \frac{K_{s} a^{4}}{D_{m}}\), \(D_{m} = \frac{E_{m} h^{3}}{12(1- \nu ^{2} )}\), \(\bar{\omega} = \frac{\omega a^{2}}{h} \sqrt{{\rho _{m}} / {E}_{m}}\). The obtained results are compared in Table 1. As we can see, by increment of side-to-thickness ratio and aspect ratio the frequencies increase. Also, by adding the elastic foundation frequencies enlarge, whereas by increment of power index frequencies decrease. Moreover, it is revealed that the aspect ratios have more impacts on frequencies than the side-to-thickness ratios.

Table 1 A comparison of the frequency parameters \(\bar{\omega} \) of Al/Al2O3 plates on elastic foundation
Full size table

The next example studies the nondimensional natural frequencies \(\omega ' = a^{2} /h(\rho / E_{2} )^{1/2}\) and modal loss factors of laminated viscoelastic composite plates with \(\left [ 0 \right ]_{8T}\) layers, and material properties are (Koo and Lee 1993): \(\rho =1566\text{ kg}/\text{m}^{3}\), \(V_{f} =0.516\), \(h = 1.58\text{ mm}\), \(a = b = 200\text{ mm}\), \(\nu _{12} = 0.3\), \(E_{1} =172.7(1+0.0007162i)\), \(E_{2} =7.2(1+0.0067816i)\), \(G_{12} = G_{23} =3.76(1+0.01122i)\). The results are collated in Fig. 3, and a reliable correlation is observed between the present result and those obtained via Mindlin plate theory. It should be mentioned that the present study represents lower natural frequencies and higher loss factors than Mindlin theory due to greater flexibility of SNDT than Mindlin theory. Also, the presented results have no significant differences because the considered composite plates are very thin. After verification in elastic and viscoelastic domains, the effects of parameters on vibrational characteristics could be evaluated via a set of parametric study.

Fig. 3
figure 3

A comparison of fundamental frequencies and loss factors of laminated composite plates versus side-to-thickness ratio

Full size image

5.2 Parametric studies

In this part, we study the effects of parameters of aspect ratio (\(b/a\)), thickness ratio (\({a} / {h}\)), power index, and foundation coefficients via numerical examples.

First, the fundamental frequencies and loss factors versus aspect ratio of FGV foam plates with different power indices are depicted in Fig. 4.

Fig. 4
figure 4

Vibrational characteristics of plates with different aspect ratios and power indices

Full size image

As we can see, both frequencies and loss factors decrease as the aspect ratio increases. Also, long rectangular narrow foam plates have lower values of stiffness and damping capability. However, the maximum and minimum reductions of frequencies are 49.07% and 40.46%, which refer to plates with \(p = 1\), 5, respectively. In other words, plates with linear distribution of porosity are more sensitive to the aspect ratios. The counterpart values of loss factors are 48% and 38% for \(p = 0\), 5, respectively. In other words, the loss factors of homogenous plates are the most affected by the aspect ratio. Moreover, foam plates with long aspect ratios have lower damping capability.

Second, the effects of thickness ratio on natural frequencies and loss factors are presented in Fig. 5. By increment of thickness ratio fundamental frequencies increase; in other words, frequencies of thin plates are larger than those of thick plates. However, thin plates have lower loss factor or damping capability than that of thick plates. Among considered plates, the plates with linear and parabolic distributions of porosities have the maximum fundamental vibrational characteristics. On the contrary, foam plates with drastic variations of properties or higher values of power index have lower natural frequencies and damping capability.

Fig. 5
figure 5

Vibrational characteristics of plates with different side-to-thickness ratios and power indices

Full size image

Third, the impacts of power index and material models are investigated by Fig. 6. As depicted, both models have the maximum frequencies at \(p = 2\), whereas the material model has no significant effects on natural frequencies. On the contrary, the material model has remarkable effects on loss factors. Indeed, the Kelvin–Voigt model predicts higher loss factor than the standard solid model. Also, the maximum loss factor of Kelvin–Voigt refers to \(p = 1\), and the maximum loss factor of standard solid refers to \(p = 2\). In other words, the material model is the key factor for damping analysis, regardless the functions of porosity distribution.

Fig. 6
figure 6

Vibrational characteristics of plates with different power index and model

Full size image

Fourth, the effects of foundation are considered in Fig. 7 for plates in three cases. For the first case, \(K_{w} =0, 1 0^{2}, 1 0^{3}, 5000\), \(K_{p} = K_{d} =0\), for the second case, \(K_{w} =1 0^{3}\), \(K_{p} =0, 50, 1 0^{2}, 250\), \(K_{d} =0\), for the last case, \(K_{w} =1 0^{3}\), \(K_{p} =1 0^{2}\), \(K_{d} =0, 1 0^{- 3}, 5 \times 1 0^{- 3}, 1 0^{- 2}\) are assumed. As we can observe, the fundamental frequencies increase as the thickness ratio increases. However, based on the assumed values of foundation stiffness, the Pasternak coefficients lead to remarkable distinction of frequencies, whereas the Winkler coefficients have lower impacts.

Fig. 7
figure 7

Vibrational characteristics versus side-to-thickness ratio of plates on the viscoelastic foundation

Full size image

In addition, these values of damping coefficients result in no remarkable change of frequencies. For the loss factor, some interesting remarks are observed. Although it is mentioned that thin plates without foundation have lower damping capability, this remark is reliable to some extent for plates on viscoelastic foundation. Indeed, this behavior is true for elastic foundations, whereas, as both thickness ratio and viscoelastic coefficients promote, thin plates show an incremental approach of loss factors. The main reason refers to the fact that external damping outweighs material damping. So the loss factors reach their minimum points and then follow an incremental approach. It is worth mentioning that the minimum points refer to \(a/h = 10, 12, 20, \text{and }40 \) for \(K_{d} =1 0^{- 2}, 5 \times 1 0^{- 3}, 1 0^{- 3} \), and 0, respectively.

Fifth, the behaviors of higher-mode of vibrations are studied in Fig. 8. For this case, \(K_{w} =1 0^{3}\), \(K_{p} =1 0^{2}\), and \(K_{d} =1 0^{- 3}\) are assumed. For this example, the minimum value of loss factors of \((1, 1)\). \((1, 2)\), \((2, 2)\), \((1, 3)\), and \((2, 3)\) modes refer to \(a/h = 18, 28, 40, 44, \text{and }50\), respectively. From damping capability point of view, fundamental modes are the most important modes due to remarkable variations of loss factors. In addition, it is clear that higher modes of plates on viscoelastic foundation are less sensitive to the thickness ratio variation. Besides, fundamental modes display thoroughly obvious behavior in comparison with higher mode of vibrations. Moreover, the curves of loss factors pass each other, which is known as the crossing phenomenon (Leissa 1974; Perkins and Mote 1986). Therefore here the crossing phenomenon of FGV foam plates on viscoelastic foundation is reported for the first time.

Fig. 8
figure 8

The higher modes of plates on the viscoelastic foundations

Full size image

6 Conclusions

The free vibration behavior of FGV open-cell foam plate on viscoelastic foundations is studied based on thickness-stretching effect. Boltzmann superposition principle, separable kernel framework, and simple power law are used to derive constitutive relations, and the Hamilton principle is implemented to obtain integro-PDEs of motion. The Galerkin method and the iterative numerical algorithm are applied to derive complex frequencies. For comparison, elastic FG plates on Pasternak foundation and laminated viscoelastic composite plates are studied. Based on new results, some conclusions are derived:

  • Long rectangular narrow foam plates have smaller frequencies and loss factors than wide plates.

  • Aspect ratios are the most effective on plates with linear distribution of porosity and on loss factors of homogenous plates.

  • FGV plates with linear and parabolic distributions of porosities have the maximum fundamental frequencies and loss factors.

  • Regardless of the porosity distribution, the material model is the key factor for damping analysis.

  • Based on the values, Pasternak, Winkler, and damping coefficients are the most remarkable factor on frequencies.

  • Loss factors of thin plates display an incremental approach as both thickness ratio and viscoelastic coefficients increase due to outweighing external damping over structural damping.

  • The crossing phenomenon of FGV foam plates on viscoelastic foundation is observed.