1 Introduction

Lightweight structures have been encountered with steadily growing demands over the last decades [1,2,3]. These growing demands are mainly observed in the aerospace industry which is one of the most promising industries [4, 5]. To address such demands, different types of materials include but not limited to fiber-reinforced composites, laminates, foams, and nanocomposite [6,7,8,9,10]. The performance of an engineering structure can be intensified by a suitable use of such materials [11]. Sandwich structures as promising engineering structures usually involve two thin but stiff outer layers to stand against normal loads, whereas a thick and usually soft material/structure is utilized as the core layer to ensure the stability of the structure against shear loads [12,13,14]. Due to the layer arrangements of sandwich panels, they enjoy a high ratio of structural stiffness to weight, and also their energy absorption is relatively high [15,16,17]. Given these facts about the sandwich structures, it can be anticipated that the use of composite and polymeric foam materials could be great selections to come up with a lightweight structure that is able to address so many requirements of an aerospace structure. The key design parameters for such sandwich structures could be fiber orientations of composite layers and geometrical dimensions. Moreover, in advanced foams, the distribution of voids can be controlled to follow FG patterns and adjust the mechanical or thermal performance of such structures [18,19,20]. However, the design of such functionally graded porous composite sandwich structures necessitates precise but simple mechanical analyses [21,22,23,24].

Because of the vast applications of composites, there have been so many works on the thermomechanical behaviors of composites structures. Mantari et al. [25] employed trigonometric theory and presented a Navier’ solution for composite plates under static loads. In a dynamic study, Malekzadeh et al. [26] presented the response of a composite plate under moving loads by implementing a layerwise theory. Setoodeh [27] implemented three-dimensional theory of plates in a layerwise FE solution and studied low velocity impact response of composite plates. Thai et al. [28] investigated the stresses and static deflections of circular and rectangular composite plates using an isogeometric FE solution based on layerwise deformation theory which employed FSDT for each layer to avoid the use of shear correction factor. For composite plates with different shapes of holes, Yu et al. [29] presented buckling resistances and frequencies using an isogeometric FE solution and FSDT which was able to rectify the shear locking issue. Tornabene et al. [30] presented a differential quadrature (DQ) technique which captured the zig-zag effect between layers and presented stresses of curved shells consisted of different composite layers rested on elastic foundations. The static response [31] and free vibration behavior [32] of multilayered composite plates were also studied by Xiaohui et al. using a refined plate theory. Bisheh and Wu [33] studied the wave propagation behavior of composite shells which were activated by an outer piezoelectric layer using Cooper-Naghdi shell theory.

Polymeric foams or metal porous structures have been also widely utilized as the core layer of sandwich structures. However, before the use of these materials, their material properties need to be characterized. In this regard, Wang et al. [34] managed to simulate 3D voids in a media by developing an extended FEM modeling. Nguyen et al. [35] considered FG plates made of a mixture of metal and ceramic materials which had FG patterns of porosity distribution and characterized their mechanical behaviors using a nonlinear polygonal FE solution. Yang et al. [36] considered graphene enhanced plates with FG patterns of porosity distribution and presented vibration and buckling responses of such plates using an FSDT method. Dong et al. [37] proposed the use of the same material for rotary cylindrical shells and characterized vibrations of such porous nanocomposite shells. Barati and Zenkour [38] conducted a nonlinear free vibration analysis FG plates made of two piezoceramics with embedded porosities in FG patterns using a refined plate theory. Askari et al. [39] considered an FG porous metal circular plate located between two piezoceramic layers and presented the fundamental frequencies of such active plates Mindlin plate theory. Mohammadi et al. [40] also considered two piezoelectric layers attached to the faces of an FG porous metal cylinder and presented static electro-mechanical stresses of these active cylinders. Moradi et al. [41,42,43] considered FG patterns of porosity distributions in CNT enhanced plates which were activated by piezoceramic layers and presented vibrations, static and buckling responses using a mesh-free method. Nguyen et al. [44] also used piezoceramic to activate a graphene enhanced metal plate with embedded porosities in FG patterns, and conducted active control study for such plates using FE model. Zhao et al. [45] developed a semi-analytical technique based on Fourier series to characterize the vibrations of axisymmetric shells with embedded porosities in FG patterns. Zargar et al. [46] conducted an analytical study to investigate heat transfer behavior of porous metal fins using an axisymmetric model. By employing 3D elasticity theory in a framework of an analytical solution, Babaei et al. [47] studied the frequencies and transient responses of disks and panels made of an FG porous metallic material. For FG porous silicon beams in nanoscale, Xie et al. [1] studied resonance phenomenon through a nonlinear analysis using surface elasticity theory.

Due to the structural benefits of foams and composite materials, researchers have been greatly convinced to apply them separately or jointly in sandwich structures. Sobhani and Yas [48] presented the fundamental frequencies of a sandwich shell which involved an FG metal/ceramic core and two fiber reinforced faces. They assumed FG patterns for the variation of fiber orientation in the plies of composite layers. Moradi et al. [49, 50] considered an FG polymeric porous plate sandwiched between two graphene enhanced layers, whereas whole these three layers activated by two more layers of a piezoceramic. They presented the fundamental frequencies and damped forced vibrations of such sandwich plates using a meshless technique. Setoodeh et al. [51] also considered curved sandwich shells with the same layer arrangement while they utilized CNT enhanced nanocomposite instead of graphene one, and presented the fundamental frequencies of such sandwich shells using DQ technique. Safaei et al. [52] presented dynamic behavior of FG porous plates sandwiched between CNT enhanced nanocomposite layers using a third-order theory. Amiri et al. [53] considered a flexible porous cylindrical micropanel sandwiched between two CNT enhanced nanocomposite faces, and presented buckling resistance as well as stresses of the resulting micro-sandwich panel. Li et al. [54] enhanced a rectangular FG porous metal plate with graphene nanosheets and presented the dynamic stability resistance of the resulting sandwich structure through a nonlinear analysis. In a dynamic analysis framework, the propagation of stress waves in FG porous cylinders sandwiched by graphene enhanced layers was analyzed using a mesh-free method in [55]. Safaei [56] studied the impact of adding a thick FG polymeric foam in the middle of composite plies on the fundamental frequencies of the resulting sandwich plate while it was rested on an elastic foundation.

This paper investigates the natural frequencies and damped forced vibrations of an advanced and lightweight sandwich plate under a periodic load within a limited time. This sandwich plate includes a thick FG/UD polymeric core which is sandwiched by two thin layers of laminate composites. The governing equations for the study of dynamic behavior of the proposed PCSPs are developed using FSDT, and then these equations were treated using an FE solution. Using the mentioned solution approach, an extensive sensitivity analysis has been performed to examine the effects of fiber orientation in composite layers, void’s volume and dispersion in core, and geometrical dimensions on the vibrational behavior of PCSPs.

2 Modeling of PCSP

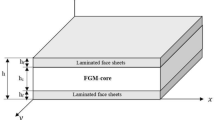
As illustrated in Fig. 1, a sandwich plate with outer layers made of fiber-reinforced composite and a core made of a polymeric foam with FG/UD distributions of porosities have been considered. In addition, this PCSP is subjected to a sinusoidal periodic load i.e., f(t) = f0 sin (2π ωt t) with the load amplitude f0 and load frequency ωt in a limited time (t < t0) as shown in Fig. 2. The composite layers are assumed to be two layers composed of 2p plies which are indicated as [α1, α2,]p. The considered PCSPs have side length a, thickness h, core thickness hc and composite thickness hf.

Fig. 1
figure 1

The schematic of PLCSP with an FG foam sandwiched by two composite layers under a uniform load

Full size image
Fig. 2
figure 2

Time history of the applied uniform load

Full size image

2.1 Governing equations

By employing the first-order shear deformation theory which is capable of treating such sandwich plates when they are thin to moderately thick, the displacement field can be described only with five unknowns as follows ([57, 58]):

$$ \begin{gathered} u = u_{0} (x,y) + z\varphi_{x} (x,y) \hfill \\ v = v_{0} (x,y) + z\varphi_{y} (x,y) \hfill \\ w = w_{0} (x,y) \hfill \\ \end{gathered} $$
(1)

where u, v and w show components of the displacement field in Cartesian coordinates. Moreover, \(\varphi\) and the subscribe 0 show normal rotations and deflections of the midline of PCSP, respectively.

According to Eq. (1), the linear components of strain vector for the proposed PCSP are presented below [57]:

$$ \varepsilon_{xx} = \frac{\partial u}{{\partial x}}\,,\,\varepsilon_{yy} = \frac{\partial v}{{\partial y}}\,\,,\,\,\gamma_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}\,\,,\,\,\gamma_{xz} = \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}\,\,,\,\,\gamma_{yz} = \frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}} $$
(2)

To make the equations easier, the in-plane \({{\varvec{\upvarepsilon}}}_{b}\) and out-of-plane \({{\varvec{\upgamma}}}\) components of the strain vector can be distinguished as follow:

$$ \varepsilon_{b} = \left\{ {\begin{array}{*{20}c} {{{\partial u_{0} } \mathord{\left/ {\vphantom {{\partial u_{0} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial v_{0} } \mathord{\left/ {\vphantom {{\partial v_{0} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ {{{\partial u_{0} } \mathord{\left/ {\vphantom {{\partial u_{0} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} + {{\partial v_{0} } \mathord{\left/ {\vphantom {{\partial v_{0} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {{{\partial \varphi_{x} } \mathord{\left/ {\vphantom {{\partial \varphi_{x} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial \varphi_{y} } \mathord{\left/ {\vphantom {{\partial \varphi_{y} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ {{{\partial \varphi_{x} } \mathord{\left/ {\vphantom {{\partial \varphi_{x} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} + {{\partial \varphi_{y} } \mathord{\left/ {\vphantom {{\partial \varphi_{y} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ \end{array} } \right\}\,\,\gamma = \left\{ {\begin{array}{*{20}c} {\varphi_{x} + {{\partial w_{0} } \mathord{\left/ {\vphantom {{\partial w_{0} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {\varphi_{y} + {{\partial w_{0} } \mathord{\left/ {\vphantom {{\partial w_{0} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ \end{array} } \right\} $$
(3)

or in the vector form, they are rewritten as:

$$ {{\varvec{\upvarepsilon}}}_{b} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{yy} } & {\gamma_{xy} } \\ \end{array} } \right\}^{T} = {{\varvec{\upvarepsilon}}}_{{\mathbf{0}}} + z{{\varvec{\upvarepsilon}}}_{1} \,\,\,,\,\,{{\varvec{\upgamma}}} = \left\{ {\begin{array}{*{20}c} {\gamma_{xz} } & {\gamma_{yz} } \\ \end{array} } \right\}^{T} $$
(4)

In the same manner, the in-plane \({{\varvec{\upsigma}}}\) and out-of-plane \({{\varvec{\uptau}}}\) stress vectors of PCSPs are also distinguished in the constitutive equation as follows [57]:

$$ {{\varvec{\upsigma}}} = {\mathbf{D}}_{{\mathbf{b}}} {{\varvec{\upvarepsilon}}}_{b} \,\,,\,\,\,{{\varvec{\uptau}}} = \frac{5}{6}{\mathbf{D}}_{s} {{\varvec{\upgamma}}}\,\,,\,\,{\mathbf{D}} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{\mathbf{b}}} } & 0 \\ 0 & {{\mathbf{D}}_{s} } \\ \end{array} } \right] $$
(5)

where 5/6 is for the shear correction factor as it is needed in FSDT, and D is the elastic constant matrix. D and stress vectors are defined below:

$$ \left\{ {\begin{array}{*{20}l} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{16} } \\ {D_{12} } & {D_{22} } & {D_{26} } \\ {D_{26} } & {D_{26} } & {D_{66} } \\ \end{array} } \right]\,\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\}\left\{ \begin{gathered} \tau_{xz} \hfill \\ \tau_{yz} \hfill \\ \end{gathered} \right\} = \frac{5}{6}\left[ {\begin{array}{*{20}l} {D_{55} } & {D_{45} } \\ {D_{45} } & {D_{44} } \\ \end{array} } \right]\left\{ \begin{gathered} \gamma_{xz} \hfill \\ \gamma_{yz} \hfill \\ \end{gathered} \right\} $$
(6)

Given the aforementioned equations for the displacement field, strains and stresses, the energy function U of the proposed PCSP which includes the energy of external work, kinetic energy and strain energy are defined as follows:

$$ \Pi = \frac{1}{2}\int\limits_{\Omega }^{{}} {\left[ { - \rho (z)(\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} ) + {{\varvec{\upvarepsilon}}}_{b}^{T} {{\varvec{\upsigma}}} + {{\varvec{\upgamma}}}^{T} {{\varvec{\uptau}}}} \right]\,\,d\Omega } + \int\limits_{A} {w{\mathbf{f}}\,dA} $$
(7)

where \(\rho\) is density, A is the area of PCSP that load is applied on it, and V is the volume of PCSP and is \({\mathbf{f}}\) the load vector.

2.2 Materials properties of foam layer

In order to define the components of D described in Eqs. (5) and (6), the material properties of each layer need to be defined. As mentioned before, one uniform pattern and two FG patterns including a symmetric (FG-S) and an asymmetric (FG-A) one for the distributions of porosity inside the foam layer have been considered. For further illustration, Fig. 3 generally compares such patterns along the thickness of the foam layer. According to Ref. [45], the density \(\rho^{p}\) and elasticity modulus \(E^{p}\) of such foams with these three distribution patterns can be estimated as:

$$ UD:E^{p} = \left( {\frac{2}{\pi }\sqrt {1 - e_{0} } - \frac{2}{\pi } + 1} \right)^{2} E^{m} \rho^{p} = \left( {\frac{2}{\pi }\sqrt {1 - e_{0} } - \frac{2}{\pi } + 1} \right)\rho^{m} $$
(8)
$$ FG - S:E^{p} (z) = \left( {1 - e_{0} \cos \left( {\frac{\pi z}{{h_{c} }}} \right)} \right)E^{m} \rho^{p} (z) = \left( {1 - e_{m} \cos \left( {\frac{\pi z}{{h_{c} }}} \right)} \right)\rho^{m} $$
(9)
$$ FG - A:E^{p} (z) = \left( {1 - e_{0} \cos \left( {\frac{\pi z}{{4h_{c} }} + \frac{\pi }{4}} \right)} \right)E^{m} \rho^{p} (z) = \left( {1 - e_{m} \cos \left( {\frac{\pi z}{{4h_{c} }} + \frac{\pi }{4}} \right)} \right)\rho^{m} $$
(10)
Fig. 3
figure 3

Comparison between the three porosity patterns with e0 = 0.6

Full size image

in which Poisson’s ratio of such foams \(\upsilon^{p}\) is estimated as:

$$ \upsilon^{p} (z) = 0.221\beta + \upsilon^{m} \left( {0.342\beta^{2} - 1.21\beta + 1} \right) $$
(11)

where \(e_{0}\) and superscript m indicate porosity parameter a non-porous material (i.e., \(e_{0} = 0\)). Moreover, \(e_{m} = 1 - \sqrt {1 - e_{0} }\), \(\beta = 1 - {{\rho^{p} } \mathord{\left/ {\vphantom {{\rho^{p} } {\rho^{m} }}} \right. \kern-\nulldelimiterspace} {\rho^{m} }}\). It should be noted that the overall volume fraction of porosity for these three patterns is equal when the same \(e_{0}\) is considered.

Given the fact that the foam layer is an isotropic material, the components of elasticity matrix \(D_{ij}\) are determined as follows:

$$ \begin{gathered} D_{11} = D_{22} = \frac{{E^{p} }}{{1 - \left( {\upsilon^{p} } \right)^{2} }}\,,D_{44} = D_{55} = D_{66} = \frac{{E^{p} }}{{2\left( {1 + \upsilon^{p} } \right)}}\,\,,\,\, \hfill \\ \,\,D_{12} = \upsilon^{p} D_{11} \,,D_{16} = D_{26} = D_{45} = 0 \hfill \\ \end{gathered} $$
(12)

2.3 Elasticity matrix of composite layers

The fiber-reinforced composite materials are usually a transverse isotropic material. Therefore, the elasticity matrix for such materials when the components of z direction are reduced can be defined as:

$$ D_{ij} = \left\{ {\begin{array}{*{20}l} {\overline{Q}_{ij} - \left( {\overline{Q}_{i3} \cdot \overline{Q}_{ij} } \right)/Q_{33} \,\,\,i,j = 1,\,2,\,6} \\ {\overline{Q}_{ij} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i,j = 4,\,5} \\ \end{array} } \right.\,\,\, $$
(13)

where

$$ \begin{gathered} Q_{11} = E_{1} \frac{{1 - \nu_{23} \,\nu_{32} }}{\,\Delta }\,\,\,,\,\,\,Q_{22} = E_{2} \frac{{1 - \nu_{13} \,\nu_{31} }}{\,\Delta }\,\,,\,\,Q_{12} = E_{1} \frac{{\nu_{21} + \nu_{31} \,\nu_{32} }}{\,\Delta }\,\,,\, \hfill \\ Q_{13} = E_{3} \frac{{\nu_{13} + \nu_{12} \,\nu_{23} }}{\,\Delta }\,\,,\,\,Q_{23} = E_{3} \frac{{\nu_{23} + \nu_{13} \,\nu_{21} }}{\,\Delta }\,,\,\,Q_{33} = E_{3} \frac{{1 - \nu_{12} \,\nu_{21} }}{\,\Delta } \hfill \\ Q_{44} = G_{23} \,\,,\,\,Q_{55} = G_{13} \,\,,\,\,Q_{66} = G_{12} \, \hfill \\ \Delta = \frac{{1 - \nu_{32} \nu_{23} - \nu_{21} \nu_{12} - \nu_{13} \nu_{31} - 2\,\nu_{32} \nu_{21} \nu_{13} }}{{E_{1} E_{2} E_{3} }} \hfill \\ \end{gathered} $$
(14)

In order to take into account the effect of fiber orientation, another elasticity matrix \(\overline{Q}_{ij}\) should be determined as follows [57]:

$$ \begin{aligned} &\overline{Q}_{11} = \,\,m^{4} Q_{11} + 2m^{2} n^{2} \left( {Q_{12} + 2Q_{66} } \right) + n^{4} Q_{22} ,\\ & \overline{Q}_{22} = \,\,n^{4} Q_{11} + 2m^{2} n^{2} \left( {Q_{12} + 2Q_{66} } \right) + m^{4} Q_{22} \hfill \\ &\overline{Q}_{44} = \,\,m^{2} Q_{44} + n^{2} Q_{55} ,\;\overline{Q}_{55} = \,\,m^{2} Q_{55} + n^{2} Q_{44} ,\\ & \overline{Q}_{66} = \,\, - m^{2} n^{2} \left( {Q_{11} + Q_{22} - 2Q_{12} } \right) + \left( {m^{4} - n^{4} } \right)Q_{66} \hfill \\ &\overline{Q}_{12} = \,\,m^{2} n^{2} \left( {Q_{11} + 4Q_{22} Q_{66} } \right) + \left( {m^{4} + n^{4} } \right)Q_{12} ,\\ & \overline{Q}_{13} = \,\,m^{2} Q_{13} + n^{2} Q_{23} ,\;\overline{Q}_{23} = \,\,n^{2} Q_{13} + m^{2} Q_{23} \hfill \\ &\overline{Q}_{36} = \,\,\left( {Q_{32} - Q_{31} } \right)mn,\;\overline{Q}_{45} = \,\,\left( {Q_{45} - Q_{55} } \right)mn,\\ & \overline{Q}_{16} = \,\, - mn\left[ {n^{2} Q_{11} - m^{2} Q_{22} - \left( {m^{2} - n^{2} } \right)\left( {Q_{12} + 2Q_{66} } \right)} \right] \hfill \\ &\overline{Q}_{26} = \,\, - mn\left[ {m^{2} Q_{11} - n^{2} Q_{22} - \left( {m^{2} - n^{2} } \right)\left( {Q_{12} + 2Q_{66} } \right)} \right] \hfill \\ \end{aligned} $$
(15)

where \(m = \cos \alpha\) and \(n = \sin \alpha\).

3 FEM Formulations

By employing a proper shape function N, the real values of displacement vector ui can be estimated in an element as follows:

$$ {\mathbf{u}} = \sum\limits_{i = 1}^{n} {N_{i} u_{i} } $$
(16)

where u is the estimated displacement field by FE method, Ni is value of shape functions at each node, n is node number in each element. Due to employing FSDT, each node has five degrees of freedom and accordingly the components of displacement field are defined as:

$$ u_{i} = \left[ {u_{0i} ,v_{0i} ,w_{0i} ,\varphi_{xi} ,\varphi_{yi} } \right]^{T} $$
(17)

By substituting Eq. (16) into Eq. (4), strain vectors in FE forms are developed as follows:

$$ {{\varvec{\upvarepsilon}}}_{b} = \left\{ {{\mathbf{P}}_{m} + z\,{\mathbf{P}}_{b} \,} \right\}\,{\mathbf{u}}\,\,\,\,,\,\,\,{{\varvec{\upgamma}}} = {\mathbf{P}}_{s} \,{\mathbf{u}} $$
(18)

where:

$$ \begin{gathered} {\mathbf{P}}_{s} = \left[ {\begin{array}{*{20}c} 0 & 0 & {N_{i,x} } & {N_{i} } & 0 \\ 0 & 0 & {N_{i,y} } & 0 & {N_{i} } \\ \end{array} } \right],{\mathbf{P}}_{m} = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ {N_{i,y} } & {N_{i,x} } & 0 & 0 & 0 \\ \end{array} } \right]\, \hfill \\ {\mathbf{P}}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {N_{i,x} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i,y} } \\ 0 & 0 & 0 & {N_{i,y} } & {N_{i,x} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(19)

The FE form of energy function can be obtained by substituting strain and stress vectors into total energy function (Eq. 7) which results in:

$$ \begin{aligned} U &= \frac{1}{2}\int\limits_{\Omega } {\delta \left( {\mathbf{u}} \right)^{T} \left\{ {{\mathbf{P}}_{m}^{T} {\mathbf{AP}}_{m} + {\mathbf{P}}_{m}^{T} {\overline{\mathbf{B}}\mathbf{P}}_{b} + {\mathbf{P}}_{b}^{T} {\overline{\mathbf{B}}\mathbf{P}}_{m} + {\mathbf{P}}_{b}^{T} {\mathbf{DB}}_{b} + {\mathbf{P}}_{s}^{T} {\mathbf{A}}_{s} {\mathbf{P}}_{s} } \right\}\,{\mathbf{u}}\,dA} \hfill \\ &\quad\, + \frac{1}{2}\int\limits_{A} {\delta \left( {\mathbf{u}} \right)^{T} } \int\limits_{z} {\left[ {{\mathbf{I}}_{i}^{T} {\overline{\mathbf{M}}\mathbf{I}}_{j} } \right]} \,{\mathbf{\ddot{u}}}dA - \delta \left( {\mathbf{u}} \right)^{T} \int\limits_{\Omega } {{\mathbf{P}}_{w} \,{\mathbf{f}}_{w} \,dA} \hfill \\ \end{aligned} $$
(20)

where

$$ ({\mathbf{A}},\,{\overline{\mathbf{B}}},\,{\mathbf{D}}) = \int\limits_{ - h/2}^{h/2} {{\mathbf{D}}_{b} (1,\,z,\,z^{2} )dz\,\,,\,\,} {\mathbf{A}}_{s} = \frac{5}{6}\int\limits_{ - h/2}^{h/2} {{\mathbf{D}}_{s} dz} $$
(21)
$$ {\mathbf{P}}_{w} = \left[ {\begin{array}{*{20}c} 0 & 0 & {N_{i} } & 0 & 0 \\ \end{array} } \right]\, $$
(22)
$$ {\mathbf{I}}_{i} = \left[ {\begin{array}{*{20}c} {N_{i} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i} } & 0 & 0 & 0 \\ 0 & 0 & {N_{i} } & 0 & 0 \\ 0 & 0 & 0 & {N_{i} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i} } \\ \end{array} } \right] $$
(23)
$$ {\overline{\mathbf{M}}} = \left[ {\begin{array}{*{20}c} {I_{0} } & 0 & 0 & {I_{1} } & 0 \\ 0 & {I_{0} } & 0 & 0 & {I_{1} } \\ 0 & 0 & {I_{0} } & 0 & 0 \\ {I_{1} } & 0 & 0 & {I_{2} } & 0 \\ 0 & {I_{1} } & 0 & 0 & {I_{2} } \\ \end{array} } \right] $$
(24)

In addition, \(I_{0}\), \(I_{1}\) and \(I_{2}\) are the coefficient of inertia which are defined as:

$$ (I_{0} ,\,I_{1} ,\,I_{2} ) = \int\limits_{ - h/2}^{h/2} {\rho (z)(1,\,z,\,z^{2} )dz\,} $$
(25)

Equation (20) should be satisfied for every value of \(\delta \left( {\mathbf{u}} \right)\); therefore this equation can be rearranged as:

$$ {\mathbf{M\ddot{u}}} + {\mathbf{Ku}} = {\mathbf{f}} $$
(26)

where \({\mathbf{f}}\), M and K are the global force vector, stiffness matrix and mass matrix as described below:

$$ {\mathbf{f}} = \int\limits_{\Omega } {{\mathbf{P}}_{w} \,{\mathbf{f}}_{w} \,dA} $$
(27)
$$ {\mathbf{M}} = \int\limits_{A} {{\mathbf{I}}_{i}^{T} {\overline{\mathbf{M}}\mathbf{I}}_{j} } dA $$
(28)
$$ {\mathbf{K}} = \int\limits_{\Omega } {\left\{ {{\mathbf{B}}_{m}^{T} {\mathbf{AB}}_{m} + {\mathbf{B}}_{m}^{T} {\overline{\mathbf{B}}\mathbf{B}}_{b} + {\mathbf{B}}_{b}^{T} {\overline{\mathbf{B}}\mathbf{B}}_{m} + {\mathbf{B}}_{b}^{T} {\mathbf{DB}}_{b} + {\mathbf{B}}_{s}^{T} {\mathbf{A}}_{s} {\mathbf{B}}_{s} } \right\}d\Omega } $$
(29)

By involving structural damping with mass Rm and stiffness Rk coefficients, Eq. (26) is rearranged as follows:

$$ {\mathbf{M\ddot{u}}} + {\mathbf{C\dot{u}}} + {\mathbf{Ku}} = {\mathbf{f}} $$
(30)

where \({\mathbf{C}} = Rm \times {\mathbf{M}} + Rk \times {\mathbf{K}}\).

4 Results and discussions

After the elaboration of the problem and its solution procedure in previous sections, the free and forced vibration behaviors of the proposed lightweight sandwich plates as well as the reliability of the developed FE approach are presented in this section. Regarding the utilized materials in PCSP, a neat epoxy foam is considered for the core, whereas composite layers made of graphite–epoxy (Gr/Ep) is utilized for the face layers. The employed material properties for the nonporous epoxy and Gr/Ep are as follows [59]:

$$ \begin{gathered} {\text{Epoxy}}:E = 4.5\;{\text{GPa}},\upsilon = 0.4,\rho = 1150\;{\text{Kg}}/{\text{m}}^{3} \hfill \\ Gr/Ep:E_{11} = 132.38\;{\text{GPa}},E_{12} = E_{13} = 10.756\;{\text{GPa}},\upsilon_{23} = 0.49,\upsilon_{12} = \upsilon_{13} = 0.24, \hfill \\ G_{23} = 3.606e9\;{\text{GPa}},G_{12} = G_{13} = 5.6537\;{\text{GPa}},\rho = 1578\;{\text{Kg}}/{\text{m}}^{3} \hfill \\ \end{gathered} $$

4.1 Validation of models

To establish the precision of the obtained FE results, we first modeled square simply supported plates made of an isotropic material with E = 380 GPa, ρ = 3800 kg/m3 and υ = 0.3 and compared the obtained normalized natural frequency of such plates at different thickness values with those available in Refs. [60, 61]. This comparison study has been summarized in Table 1, whereas the normalized natural frequency is determined by \(\Omega = \omega h_{0} \sqrt {{{\rho^{m} } \mathord{\left/ {\vphantom {{\rho^{m} } {E^{m} }}} \right. \kern-\nulldelimiterspace} {E^{m} }}}\) where h0 = 0.1 m. It is evident from the agreement between the results that the precision of the developed FE solution is successfully verified especially for thinner plates i.e., h/a < 0.2.

Table 1 comparison study for the normalized natural frequency of square isotropic plates
Full size table

As a further establishment of the precision of the developed FE solution, we have examined the convergence of the results by studying time history of vibrations at the midpoint of a PCSP. Therefore, a simply supported (SSSS) square PCSP with a = 1 m, hc/a = 0.01 and hf/hc = 0.1, whereas the PCSP has an FG-S core with e0 = 0.7, and two composite faces with four plies as [45,-45]2. Figure 4 shows the undamped vibrations of this PCSP under a periodic load with f0 = 500 N/m2, t0 = 100 ms and ωt = 50 Hz for different node arrangements. This figure illustrates that the dynamic response of this plate is perfectly converged such that there is a slight difference between the results of models employed at higher nodes. Therefore, for the following modelings, PCSPs with 15 × 15 nodes have been considered.

Fig. 4
figure 4

midpoint undamped vibrations of a PCSP with different node arrangements (convergence study)

Full size image

4.2 Free vibration of PCSPs

This subsection concerns the study of the fundamental natural frequency of PCSPs. In the first analysis, the effect of fiber orientations is investigated. In this regard, SSSS square PCSPs with a = 1 m, hc/a = 0.01, hf/hc = 0.1, e0 = 0.7, FG-S porosity patterns and with composite faces with different fiber orientations and ply number have been considered. Table 2 summarizes the results of this study and shows that although the number of ply slightly improves the fundamental frequency, fiber orientation has a significant impact on it such that the fundamental frequency of PCSP with [0,90]2 is only 67.02 Hz while this number for the same PCSP with [45,-45]2 is 86.61 Hz. This shows fiber orientation can remarkably change the structural stiffness of PCSPs.

Table 2 Fundamental frequencies (Hz) of PCSPs with different fiber orientations and ply numbers
Full size table

Considering the same PCSPs but with [45, − 45]2 and different porosity parameters and distribution patterns, Figs. 5a and b study the effect of different porosity states for PCSPs with hc/a = 0.01 and 0.02, respectively. The most important observation is that the increase in embedding porosity enhances the fundamental frequency of PCSPs due to the significant reduction of the weight of PCSPs. Moreover, the results show that PCSPs with FG-S foams in core offer the higher fundamental frequencies while those with UD foam have the lowest natural frequencies. Furthermore, as anticipated, the comparison between Figs. 5a and b discloses that the natural frequencies of PCSPs with thicker cores have greatly higher natural frequencies.

Fig. 5
figure 5

Fundamental frequency of PCSPs with a hc/a = 0.01 b hc/a = 0.02 versus porosity parameter for different porosity distribution patterns

Full size image

4.3 Forced vibrations of PCSPs

In this subsection, the forced vibration response of PCSPs is investigated. In the following modeling, SSSS square PCSP with geometrical dimensions as a = 1 m, hc/a = 0.01 and hf/hc = 0.1, porosity states as FG-S core with e0 = 0.7, composite faces with fiber orientation as [45,-45]2, damping status as Rm = 10 and Rk = 5e-5, and loading conditions as f0 = 500 N/m2, t0 = 100 ms and ωt = 50 Hz have been considered unless otherwise clearly mentioned.

To begin with, the effect of fiber orientation is investigated in Fig. 6 where the midpoint vibrations of PCSPs with different fiber orientations for two values of composite layers’ thicknesses are shown. Figure 6 shows that PCSPs with [45,-45]2 have the lowest vibration amplitudes while their frequencies of vibrations in the free vibration zone are the highest. On the other side, PCSPs with [0, 90]2 can be observed whose vibrations have the highest amplitudes and the lowest frequencies of vibrations in the free vibration zone. These observations are absolutely supported by the results reported in Table 2. Moreover, the comparison between the vibrations of PCSPs with hf/hc = 0.1 and hf/hc = 0.2 reveals that the thickness of composite faces has a remarkable impact on both amplitudes and frequencies of vibrations.

Fig. 6
figure 6

Midpoint’s vibrations of PCSPs with a hf/hc = 0.1 b hf/hc = 0.2 and different fiber orientations

Full size image

Figures 7a and b also explore the effect of porosity distribution patterns and porosity parameters on the vibrations of the proposed PCSPs, respectively. Figure 7a shows that the pattern of porosity distribution does not have a considerable impact on the vibrations of PCSPs although PCSPs with UD core have vibrations with the highest amplitudes and the lowest frequency. On the other side, Fig. 7b illustrates that the amount of porosity embedded in the core layer has a great impact on the vibrations of PCSPs such that the PCSP with nonporous core has the lowest frequency of vibrations as this observation is supported with the results of Fig. 5. Moreover, it can be seen that PCSPs with porous cores have the lowest amplitudes of vibrations. This could be due the beats phenomena observed in forced vibration zone as the vibrations of PCSPs with porous core are entered into the free vibration zone with much lower amplitudes of vibrations.

Fig. 7
figure 7

Midpoint’s vibrations of PCSPs with different a porosity distribution patterns b porosity parameter

Full size image

Figure 8 also investigates the effect of structural damping coefficients on the vibrations of the PCSP. As expected, the application of each coefficient smoothly reduces the vibrations amplitudes. It also observed that the frequency of vibrations is slightly reduced by increasing these coefficients. This figure also gives a good understanding about the range of structural damping coefficients.

Fig. 8
figure 8

Midpoint’s vibrations of PCSPs with different a mass coefficient b stiffness coefficient of structural damping

Full size image

Finally, the effects of core and face thicknesses on the vibrations are investigated in Figs. 9a and b, respectively. It can be seen the use of thicker layers either in core or faces leads to significant reductions in vibration amplitudes as well as a considerable increase in vibration frequencies as the structural stiffness of PCSPs improves.

Fig. 9
figure 9

Midpoint’s vibrations of PCSPs with different a core thicknesses b composite layer thicknesses

Full size image

5 Conclusions

Lightweight sandwich plates consist of two thin composite layer faces, and a thick polymeric foam core was considered. UD and FG patterns were considered for the distribution of porosities inside the thick foam layer. The natural frequency and damped forced vibration behavior of such advanced PCSPs under a periodic load within a limited time were investigated by developing an FE solution based on FSDT. By performing an extensive sensitivity analysis on the considered PCSP, it was found that simply supported PCSPs with the fiber orientation of [45,− 45]2 offer the highest natural frequency and the lowest amplitude of vibrations. Moreover, the results showed that the amount of porosity has a significant impact on both fundamental frequency and transient response of PCSPs such that embedding porosity reduces the amplitude of vibrations and improves the fundamental frequency. Furthermore, it was shown that the use of thicker layers leads to PCSPs with lower vibrations amplitudes and higher frequency of vibrations.