1 Introduction

In recent years, engineering applications of foams have received increasing attention due to their remarkable characteristics such as high specific strength, low weight, and high energy absorption (Zamani 2021a,b). By proper material design, some issues such as delamination, abrupt change of properties, and undesired thermal stresses can be avoided using functionally graded (FG) properties with continuous variations of properties through the thickness direction. These capabilities led to the application of FG foams in various fields such as acoustic control (Gibson and Ashby 1997; Ashby et al. 2000), shock and energy absorption (Hedayati and Sadighi 2016; Shimazaki et al. 2016; Sadeghnejad et al. 2017), automobile industries (Patten et al. 1998; Zhang et al. 2015), and biomedical instruments (Gibson et al. 2010). Moreover, viscoelastic damping of composites plays a fundamental role to reduce the amplitude of vibrations, to bring about phase delay, and to decrease the time duration of vibrations (Zhou et al. 2016). Furthermore, FG viscoelastic (FGV) foams have an extraordinary characteristic, frequency-dependent or complex damping, which would be a vital property for beam-like structures that possess a lightweight constituent, acceptable strength, and damping simultaneously, especially under static (Altenbach and Eremeyev 2008a,b,c, 2009) and dynamic loads (Higuchi and Adachi 2014; Al Jahwari et al. 2016; Montgomery et al. 2021; Zamani 2022). However, it is worth noting that considering the viscoelasticity of FG beams provides computational complexities for vibration analysis in the frequency or the time domain and this remark may be modified using various computational approaches.

From the computational point of view, the Bubnov–Galerkin (BG) weighted residual method has been used to solve nonlinear vibration of Kelvin–Voigt FGV beams with von Karman geometrical nonlinearity or small strains and moderate rotations. Ghayesh (2018) applied the BG method with a parameter-continuation technique to analyze forced vibrations of FG microbeams. The same author extended this method for imperfect Timoshenko beams (Ghayesh 2019c), imperfect Timoshenko microbeams (Ghayesh 2019d), and fully clamped imperfect axially graded Euler–Bernoulli beams (Ghayesh 2019a). In the mentioned works, it should be noted that the Kelvin–Voigt viscoelastic model is applied explicitly in the constitutive relations of FGV beams via a simple differential operator. However, numerical approaches should be applied for other forms of viscoelastic models such as fractional derivatives. In this outline, Loghman et al. (2021) used fractional derivatives of FGV beams. They implemented a finite-element method (FEM) and a finite-difference method to study nonlinear free and forced vibrations of Euler–Bernoulli microbeams. Although a simple differential operator or the Kelvin–Voigt model is common in the literature, viscoelastic behavior could also be represented through constitutive relations via frequency-dependent properties that are suitable for vibration analysis in the frequency domain.

Kelvin–Voigt FGV beams with nonlinear geometry may face distributed forces or external excitations in practical circumstances. Generally, these forces are simulated via an elastic medium or foundation. Although the linear and nonlinear coefficients of an elastic medium complicate computations, investigations of these coefficients will improve the accuracy and the reliability of the design and the analyses of geometrically nonlinear vibrations of FGV beams. For this case, Ghayesh (2019b) studied nonlinear vibrations of microbeams resting on a nonlinear elastic support applying BG to achieve nonlinear responses of cantilevered (clamped–free) Euler–Bernoulli beams. Gholipour et al. (2020) scrutinized nonlinear vibrations of clamped–clamped axially graded beams resting on a nonlinear elastic foundation using the BG method, von Karman strains and the Euler–Bernoulli assumption. Recently, Yee et al. (2022) used a modal decomposition approach, third-order shear deformation theory, and a Gaussian random field model to analyze nonlinear vibrations of imperfect FGV beams reinforced with graphene nanosheets on a viscoelastic foundation. It is worth mentioning that various combinations of clamped and simply supported edge conditions have remarkable importance from both practical and mathematical points of view. Obviously, simultaneous study of geometrical nonlinear vibrations, a nonlinear elastic medium, frequency-dependent constitutive relations, and general boundary conditions of FGV beams are rarely studied in the literature.

Based on the literature survey, it is observed that the main concentration of the literature is located on the geometrically nonlinear vibrations of FGV beams (Ghayesh 2018, 2019a,c,d; Loghman et al. 2021), while nonlinear vibrations of FGV foam beams have attracted less attention from researchers. In addition, the study of nonlinear vibrations of FGV beams on nonlinear elastic/viscoelastic foundations is merely restricted to the single cantilevered, fully clamped, and simply supported edge conditions of beams (Ghayesh 2019b; Gholipour et al. 2020; Yee et al. 2022), and implementation of other edge conditions seems to be missing from the literature. Moreover, the studied papers only considered the Kelvin–Voigt model via a simple differential operator, while other viscoelastic models such as Boltzmann–Volterra superposition principles that have the capability to produce frequency-dependent representations of properties are neglected.

In the present study, large-amplitude free vibration and mechanical buckling of FGV open-cell foam Euler–Bernoulli beams resting on a Pasternak medium are investigated using the BG approach, the He variational method, and an iterative numerical algorithm for integropartial differential equations of motion. The nonlinearity of deformation and medium are formulated via von Karman strains and a cubic coefficient, respectively. A simple power law and separable kernel framework are used to define porosity and constitutive equation, respectively. The presented method is examined for linear vibrational characteristics of viscoelastic composite beams, critical buckling loads, and nonlinear frequencies of homogeneous and FG elastic beams, while for the latter, the effect of a neutral surface is also investigated. Eventually, the impacts of medium, amplitude, constitutive relation, and edge condition on the critical buckling load and nonlinear frequency are studied via numerical examples.

2 Basic equations

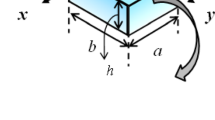
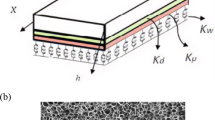
Consider a nonhomogeneous viscoelastic beam with rectangular cross section resting on a nonlinear Pasternak medium, as depicted in Fig. 1. Parameters \(L\) and \(h\) stand for length and thickness, respectively. The Cartesian coordinate system (\(x,z\)) is placed on the middle surface of the beam. Also, \(K_{w}\), \(K_{s}\), \(K_{nl}\), and \(P\) denote Winkler, Pasternak, nonlinear coefficients of the medium, and the external axial force, respectively.

Fig. 1
figure 1

(a) The coordinate system of a FGV foam beam on a nonlinear elastic medium, (b) schematic of a polymeric open-cell foam (Altenbach and Eremeyev 2008c).

Full size image

2.1 Constitutive equations

Due to the nonlinear nonsymmetric distribution of properties through the thickness direction and around the midplane, there are bending–extensional couplings in the constitutive relations. These couplings could be neglected using a neutral physical surface (Abrate 2008). However, in order to retain the generality of the analysis, a common approach that considers couplings is applied through this section. Based on the classical beam theory and nonlinear von Karman strains, strain–displacement relations are assumed as (Ghayesh 2019a; Daya et al. 2004):

$$ \left \{ \textstyle\begin{array}{c} \varepsilon _{x} \\ \kappa _{x} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} u_{,x} + \frac{1}{2}w_{,x}^{2} \\ w_{,xx} \end{array}\displaystyle \right \}, $$
(1)

where \(u\), \(w\), \(\varepsilon _{x}\), \(\kappa _{x}\), and subscript “,” stand for displacement components in the \(x\) and \(z\) directions, normal strain, curvature, and the differential operator, respectively. The constitutive equation of the plane stress state of FGV materials can be written as (Zamani 2021b, 2022; Zamani et al. 2018; Brinson and Brinson 2008):

$$\begin{aligned} \sigma _{x} &= Q_{11}(\omega )\varepsilon _{x} \end{aligned}$$
(2)
$$\begin{aligned} \left \{ \textstyle\begin{array}{c} N_{x}(\omega ) \\ M_{\mathrm{x}}(\omega ) \end{array}\displaystyle \right \} &= \int _{ - h/2}^{h/2} \sigma _{x}\left \{ \textstyle\begin{array}{c} 1 \\ z \end{array}\displaystyle \right \} dz \\ &= \left [ \textstyle\begin{array}{c@{\quad}c} A_{11}(\omega ,z) & B_{11}(\omega ,z) \\ B_{11}(\omega ,z) & D_{11}(\omega ,z) \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} \varepsilon _{x} \\ \kappa _{x} \end{array}\displaystyle \right \}, \end{aligned}$$
(3)

where \(\sigma _{x}\), \(N_{x}\), \(M_{x}\), and \(\omega \) stand for stress, stress resultant, bending moment per unit length, and frequency, respectively. Also, \(A_{11}\), \(B_{11}\), \(D_{11}\), and \(Q_{11}\) denote spatial/frequency-dependent extensional stiffness, bending–extensional coupling, bending stiffness, and reduced stiffness, respectively, which are all defined as (Zamani 2021b, 2022; Zamani et al. 2018):

$$\begin{aligned} \left \{ \textstyle\begin{array}{c} A_{11}(\omega ,z) \\ B_{11}(\omega ,z) \\ D_{11}(\omega ,z) \end{array}\displaystyle \right \} &= \int _{ - h/2}^{h/2} Q_{11}(\omega ,z) \left \{ \textstyle\begin{array}{c} 1 \\ z \\ z^{2} \end{array}\displaystyle \right \}dz \end{aligned}$$
(4)
$$\begin{aligned} Q_{11}(\omega ,z) &= \frac{4G(\omega ,z) ( 3K(\omega ,z) + G(\omega ,z) )}{3K(\omega ,z) + G(\omega ,z)}, \end{aligned}$$
(5)

where \(G\) and \(K\) stand for the distortion and dilatation moduli, respectively. The stiffness coefficients in Eq. (4) are similar to those that are represented for general elastic composites, while these coefficients are spatially dependent like FG materials and frequency dependent like viscoelastic materials, simultaneously. In addition, Eq. (5) can be derived from the elastic domain using the Alfrey correspondence principle (Alfrey 1944), which transfers properties from the elastic to the viscoelastic domain. Furthermore, the effective properties of FGV open-cell foam beams are defined as (Hatami et al. 2008; Gibson and Ashby 1997):

$$\begin{aligned} \rho (z,\omega ) &= \rho _{s}V(z) \end{aligned}$$
(6)
$$\begin{aligned} K(z,\omega ) &= K_{0}V^{2}(z) \end{aligned}$$
(7)
$$\begin{aligned} G(z,\omega ) &= G_{0}\frac{1 + ic_{1}\omega}{1 + i\beta c_{1}\omega} V^{2}(z) \\ c_{1} &= h\sqrt{\rho /G_{0}} \end{aligned}$$
(8)
$$\begin{aligned} V(z) &= \frac{\rho _{p}}{\rho _{s}} + \biggl(1 - \frac{\rho _{p}}{\rho _{s}}\biggr) \biggl( \frac{1}{2} + \frac{z}{h}\biggr)^{p}, \end{aligned}$$
(9)

where \(\rho \), \(\rho _{s}\), \(\rho _{p}/\rho _{s}\), \(V(z)\), \(\beta \), \(p\), \(K_{0}\), and \(G_{0}\) stand for density, minimum density, minimal relative density, volume fraction, parameter of constitutive relation, power index, elastic dilatation, and distortion moduli, respectively. Furthermore, \(\beta = 0\), 0.5, and 1 refer to Kelvin–Voigt, standard solid, and elastic materials, respectively. It is worth mentioning that \(p = 0\), 1 denote homogeneous and linear distributions of porosity, respectively (Gibson and Ashby 1997).

2.2 Governing equations

The dynamic version of the principle of virtual displacements or the Hamilton principle can be expressed as:

$$ \begin{gathered} \int _{t_{1}}^{t_{2}} (\delta T_{k} + \delta V_{w} - \delta U)dt = 0 \\ \delta u = \delta w = 0, \end{gathered} $$
(10)

where \(t\), \(\delta \), \(U\), \(V_{w}\), and \(T_{k}\) stand for time, variational operator, strain energy, work of external load, and kinetic energy, respectively, which are all defined as:

$$\begin{aligned} \delta U &= \int _{\vartheta} \sigma _{x}\delta \varepsilon _{x}d\vartheta \end{aligned}$$
(11)
$$\begin{aligned} \delta V_{w} &= \int _{A} q_{w}(x)\delta wdA \end{aligned}$$
(12)
$$\begin{aligned} \delta T_{k} &= \int _{\vartheta} \rho (u_{,t}\delta u_{,t} + w_{,t}\delta w_{,t})d\vartheta , \end{aligned}$$
(13)

where \(\vartheta \), \(A\), and \(q_{w}\) stand for volume element, area element, and transverse applied load, respectively. The transverse load or interaction of a Pasternak medium is presented as (Gholipour et al. 2020):

$$ q_{w}(x) = - K_{w}w - K_{nl}w^{3} + K_{s}w_{,xx}. $$
(14)

Application of integration by parts and revealing virtual displacements lead to the governing equations of motion with frequency-dependent coefficients as:

$$\begin{aligned} \delta u:\ N_{x,x}(\omega ) &= I(\omega )u_{,tt} - P \end{aligned}$$
(15)
$$\begin{aligned} \delta w:\ M_{x,xx}(\omega ) + N_{x}(\omega )w_{,xx} &= I(\omega )w_{tt} + K_{w}w + K_{nl}w^{3} - K_{s}w_{,xx}, \end{aligned}$$
(16)

where \(I\) stands for an inertia term that is defined as:

$$ I(\omega ) = \int _{ - h/2}^{h/2} \rho (z,\omega )bdz, $$
(17)

where \(b\) stands for the width of the FGV beam. In order to simplify the governing equations of motion, some assumptions are applied as (Emam and Nayfeh 2009; Fallah and Aghdam 2011; Emam and Lacarbonara 2021, 2022):

  • Inertia and a distributed axial force in the inplane direction are neglected and therefore, the axial force or axial stress resultant \(N_{x}\) is assumed constant.

  • The FGV beam is restricted at \(x = 0\), while a compressive axial load, \(P\) is applied at \(x = L\).

  • The FGV beam is axially restrained and the ends cannot slide axially. Therefore, midplane stretching and the definite integral will appear in the governing equations of motions.

Using these assumptions together with some mathematical manipulations, the governing equations of motion and their initial conditions can be expressed respectively, as (Emam and Nayfeh 2009; Fallah and Aghdam 2011; Emam and Lacarbonara 2021, 2022):

$$\begin{aligned} & \begin{aligned} &b \biggl( D_{11}(\omega ) - \frac{B_{11}^{2}(\omega )}{A_{11}(\omega )} \biggr)w_{,xxxx} \\ &\quad{}+ \biggl( P - \frac{bA_{11}(\omega )}{2L} \int _{0}^{L} (w_{,x})^{2}dx - \frac{bB_{11}(\omega )}{L} \bigl( w_{,x}(L,t) - w_{,x}(0,t) \bigr) \biggr)w_{,xx} \\ &I(\omega )w_{,tt} + K_{w}w + K_{nl}w^{3} - K_{s}w_{,xx} = 0 \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned} &w \biggl(\frac{L}{2},0\biggr) = a,\quad w_{,x}\biggl( \frac{L}{2},0\biggr) = 0, \end{aligned}$$
(19)

where \(a\) stands for the nondimensional maximum amplitude of vibration at the center of the beam. It is worth mentioning that the governing equations have similarities with their counterparts in the elastic domain, whereas, the frequency-dependent coefficients are distinctive points. To maintain the generality of the solution, some nondimensional parameters are introduced as:

$$ \bar{x} = \frac{x}{L},\quad \bar{w} = \frac{w}{r},\quad \bar{t} = t\sqrt{\frac{b\Theta (\omega )}{I(\omega ) L^{4}}},\quad \Theta (\omega ) = D_{11}(\omega ) - \frac{B_{11}^{2}(\omega )}{A_{11}(\omega )},\quad r = \sqrt{ \frac{I(\omega )}{A}}, $$
(20)

where \(\bar{x}\), \(\bar{w}\), \(\bar{t}\), \(\Theta \), and \(r\) stand for nondimensional longitudinal and transverse coordinates, time, stiffness, and radius of gyration, respectively. Using Eq. (18) together with the nondimensional parameters in Eq. (20), the governing equation of motion can be rewritten as:

$$ \begin{aligned} & \biggl( \bar{P}(\omega ) - \frac{1}{2}\Lambda ( \omega ) \int _{0}^{1} (\bar{w}_{,\bar{x}})^{2}d \bar{x} - B(\omega ) \bigl( \bar{w}_{,\bar{x}}(1, t) - \bar{w}_{,\bar{x}}(0, t) \bigr) \biggr)\bar{w}_{,\bar{x}\bar{x}} \\ &\bar{w}_{,\bar{t}\bar{t}} + \bar{w}_{,\bar{x}\bar{x}\bar{x}\bar{x}} + \bar{K}_{w}( \omega )\bar{w} + \bar{K}_{nl}(\omega ) \bar{w}^{3} - \bar{K}_{s}(\omega )\bar{w}_{,\bar{x}\bar{x}} = 0 \end{aligned}, $$
(21)

where a separable function and the nondimensional parameters are expressed as:

$$\begin{aligned} \begin{aligned} &\bar{w}(\bar{x},\bar{t}) = W(\bar{x})q(\bar{t}),\quad\bar{P}( \omega ) = \frac{PL^{2}}{b\Theta (\omega )},\quad \Lambda (\omega ) = \frac{A_{11}(\omega )r(\omega )^{2}}{\Theta (\omega )} \\ &B(\omega ) = \frac{B_{11}(\omega )r}{\Theta (\omega )},\quad \bar{K}_{w}(\omega ) = \frac{K_{w}L^{4}}{b\Theta (\omega )},\quad \bar{K}_{nl}(\omega ) = \frac{K_{nl} r^{2}L^{4}}{b\Theta (\omega )},\quad \bar{K}_{s}(\omega ) = \frac{K_{s}L^{2}}{b\Theta (\omega )}, \end{aligned} \end{aligned}$$
(22)

where \(W(\bar{x})\) and \(q(\bar{t})\) stand for spatial and temporal functions, respectively. It should be noted that Emam and Nayfeh (2009), Fallah and Aghdam (2011) derived the governing equations in the elastic domain, while the governing equations are extended for the viscoelastic domain in the present study. Moreover, \(CC\), \(CS\), and \(SS\) denote fully clamped, clamped–simply supported, and simply supported boundary conditions, respectively; while the first and the second letters refer to edge conditions at \(\bar{x} = 0\) and 1, respectively. The considered edge conditions are expressed as:

$$ \begin{aligned} &CC:\ W(0) = W'(0) = W(1) = W'(1) = 0 \\ &CS:\ W(0) = W'(0) = W(1) = W''(1) = 0 \\ &SS:\ W(0) = W''(0) = W(1) = W''(1) =0. \end{aligned} $$
(23)

3 Method of solution

In this section, Eq. (21) is solved via a two-step procedure. First, the BG method with an appropriate shape function is implemented to discretize Eq. (21) in the spatial domain. The considered shape functions are presented in Table 1 (Rao 2004). Next, the resulted nonlinear ordinary differential equation (ODE) with frequency-dependent coefficients is determined by a variational method. To gain more details of the method, one may refer to other studies, see for instance (He 2007). The resultant equation and initial conditions take a novel form using BG and variational methods as:

$$\begin{aligned} & \ddot{q}(t) + \bigl( \alpha _{1}(\omega ) + \alpha _{p}(\omega )\bar{P}(\omega ) + \alpha _{kl}(\omega ) + \alpha _{ks}(\omega ) \bigr)q(t) \\ &\quad{} + \alpha _{2}(\omega )q^{2}(t) + \bigl( \alpha _{Knl}(\omega ) + \alpha _{3}(\omega ) \bigr)q^{3}(t) \\ \end{aligned}$$
(24)
$$\begin{aligned} &q (0) = a,\quad \dot{q}(0) = 0, \end{aligned}$$
(25)

where the frequency-dependent coefficients are defined as:

$$\begin{aligned} \begin{aligned} & \alpha _{1} = \frac{\int _{0}^{1} W_{,\bar{x}\bar{x}\bar{x}\bar{x}}Wd\bar{x}}{ \int _{0}^{1} W^{2}d\bar{x}},\quad \alpha _{p} = \frac{\int _{0}^{1} W_{,\bar{x}\bar{x}}Wd\bar{x}}{\int _{0}^{1} W^{2}d\bar{x}},\quad \alpha _{2} = - B(\omega ) \bigl( W_{,\bar{x}}(1) - W_{,\bar{x}}(0) \bigr)\alpha _{p} \\ &\alpha _{kl} = \bar{K}_{w},\quad \alpha _{ks} = - \bar{K}_{s}\alpha _{p},\quad \alpha _{knl} = \bar{K}_{nl}\frac{\int _{0}^{1} W^{4}d\bar{x}}{\int _{0}^{1} W^{2}d\bar{x}},\quad \alpha _{3} = - \frac{1}{2}\Lambda \alpha _{p} \int _{0}^{1} (W_{,\bar{x}})^{2}d \bar{x}. \end{aligned} \end{aligned}$$
(26)

It should be noted that the physical neutral surface vanishes at \(\alpha _{2}\) or a quadratic nonlinearity. However, a nonlinear eigenvalue solver is required to solve the ODE with frequency-dependent coefficients. Indeed, the He variational method is used as (He 2007):

$$\begin{aligned} & \ddot{q} + f(q) = 0 \\ \end{aligned}$$
(27)
$$\begin{aligned} & \begin{aligned} &J(q) = \int _{0}^{T / 4} \biggl\{ - \frac{1}{2} \dot{q}^{2} + F(q) \biggr\} dt = 0 \\ &T = 2\pi /\omega \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned} & q = a\cos (\omega t), \end{aligned}$$
(29)

where \(T \) stands for period of vibration. Equations (27)–(29) refer to a homogeneous second-order ODE, a functional equation, and an approximate solution, respectively. Substitution of Eq. (29) into Eq. (28) leads to (He 2007):

$$\begin{aligned} &J(a,\omega ) = \frac{1}{\omega} \int _{0}^{\pi / 2} \biggl\{ - \frac{1}{2} \bigl( a\omega \sin (\tau ) \bigr)^{2} + F \bigl( a\cos (\tau ) \bigr) \biggr\} d\tau = 0 \\ &\quad\tau = \omega t. \end{aligned}$$
(30)

Implementation of \(\partial J / \partial a = 0\) results in a nonlinear algebraic equation as (He 2007):

$$ \frac{1}{\omega} \biggl( \frac{1}{8}\pi a^{2}(\alpha _{1} + \alpha _{p}\bar{P} + \alpha _{kl} + \alpha _{ks}) + \frac{2}{9}a^{3}\alpha _{2} + \frac{3}{64}\pi a^{4}(\alpha _{Knl} + \alpha _{3}) - \frac{1}{8}\pi a^{2}\omega ^{2} \biggr) = 0. $$
(31)

For a linear frequency, an ODE with nonlinear frequency-dependent coefficients should be solved for \(a = 0\). Equation (31) will be solved in the complex frequency domain via the \(QZ\) iterative algorithm (Golub and Van Loan 2013) in the following computations. The outcomes of Eq. (31) are expressed as (Zamani and Aghdam 2015):

$$\begin{aligned} \begin{aligned} \omega &= \omega ^{\operatorname{Re}} + i\omega ^{\operatorname{Im}} \\ \omega _{n} &= \omega ^{\operatorname{Re}} \\ \eta &= \operatorname{Im} \bigl(\omega ^{2}\bigr) / \operatorname{Re} \bigl(\omega ^{2}\bigr), \end{aligned} \end{aligned}$$
(32)

where \(\omega \), \(\omega _{n}\), \(\eta \) stand for complex frequency, natural frequency, and loss factor, respectively.

Table 1 Spatial functions of plates (Rao 2004)
Full size table

4 Results and discussion

In this section, first, the accuracy of the present solution is verified via different examples. Finally, the impacts of various parameters are analyzed via parametric studies. For the first part, three examples compare nonlinear to linear frequency ratios of homogeneous elastic \(SS\) (Qaisi 1993; Ke et al. 2010), \(CS\), and \(CC\) (Qaisi 1993) beams, frequency ratio, and the critical buckling load of FG beams (Fallah and Aghdam 2011; Ke et al. 2010; Gunda et al. 2011; Yaghoobi and Torabi 2013). Also, frequencies and loss factors of viscoelastic beams are compared with the results of FEM (Bilasse et al. 2010) and exact solutions (Rao 1978). For the final part, the impacts of a Pasternak medium, a constitutive relation, the amplitude of vibration, the nonhomogeneity of the material, and edge conditions on the frequency ratio, buckling load ratio (BLR), and loss factor are scrutinized elaborately.

4.1 Comparative study

The first example is assigned to the nonlinear to linear frequency ratio (\(\omega _{nl} / \omega _{l}\)) of homogeneous beams with \(L / h = 20\), \(h = 0.1\). In this example, the present results are compared with those reported by Qaisi (1993) based on an analytical or harmonic balance method (HBM), Ke et al. (2010) based on a direct numerical integration method (DNIM) for \(SS\) beams in Table 2 and \(CS\), \(CC\) beams in Table 3. As can be observed, a reliable correlation is observed, however, it should be noted that weighted residual methods naturally overestimate the eigenvalues of eigenvalue problem (Leissa 1969). Therefore, the present results demonstrate higher values than the results of HBM and DNIM. In addition, the frequency ratios in Table 3 demonstrate the remark that \(CC\) beams or stiff edge conditions display more resistance than \(CS\) beams against geometrical nonlinearity.

Table 2 A comparison of the frequency ratios of \(SS\) beams
Full size table
Table 3 A comparison of the frequency ratios of beams
Full size table

The second example compares the nonlinear frequency and BLRs of FG beams resting on a nonlinear elastic medium with reported results based on DNIM (Ke et al. 2010), an iterative FEM (IFEM) (Gunda et al. 2011), the He variational method (HVM) (Fallah and Aghdam 2011), and the variational iteration method (VIM) (Yaghoobi and Torabi 2013). It should be noted that Fallah and Aghdam (2011) applied HVM via a ODE45 command in MATLAB software, while the present variational method is applied based on the \(QZ\) iterative algorithm that is used for complex eigenvalue problems (Golub and Van Loan 2013). Also, the considered parameters are \(p = 2\), \(P = 1\), \(\bar{K}_{w} = \bar{K}_{nl} = \bar{K}_{s} = 50\), and other material properties are given by Table 4 (Gunda et al. 2011). Table 5 expresses comparisons between the nonlinear ratios of the general approach considering coupling, neutral surface approach neglecting coupling, and other results. As can be seen, acceptable accuracy is depicted by the present results. Moreover, \(SS\) beams without coupling presents the upper bound of frequency ratios, while the general approach presents the lower bound of ratios. Furthermore, both approaches approximately result in the same frequency and BLRs of fully clamped beams.

Table 4 Material properties of FG beams (Gunda et al. 2011)
Full size table
Table 5 A comparison of frequency/buckling ratios of FG beams on a nonlinear elastic medium
Full size table

The third example investigates the first six frequencies and loss factors of sandwich beams with isotropic elastic face sheets and a viscoelastic core. The geometrical and mechanical properties of face sheets and core are \(L = 177.8~\text{mm}\), \(b = 12.7~\text{mm}\), \(\rho _{c} = 968.1~\text{Kg/m}^{3}\), \(E_{c} = 1.794(1 + 0.1i)~\text{MPa}\), \(v_{c} = 0.3\), \(h_{c}= 0.127~\text{mm}\), \(\rho _{f} = 2766~\text{Kg/m}^{3}\), \(E_{f} = 69~\text{GPa}\), \(v_{f} = 0.3\), \(h_{f} = 1.524~\text{mm}\). Results are assessed by comparison with the results of Bilasse et al. (2010) based on FEM and Rao (Rao 1978) based on exact solutions in Table 6. The obtained results are in good agreement with other predictions. As mentioned previously, the present method overestimates natural frequencies and loss factors due to the nature of the weighted residual method; however, the differences from the exact solution are acceptable.

Table 6 The first six modes of sandwich beams with a viscoelastic core
Full size table

4.2 Parametric study

In this section, a parametric study is conducted on FGV foam beams on an elastic medium. The considered parameters include Winker, Pasternak, and nonlinear coefficients of the elastic medium, axial load, edge conditions, vibration amplitude, and foam nonhomogeneity.

4.2.1 Constitutive relation parameters

The effects of a standard solid, Kelvin–Voigt, and elastic models of constitutive relations are taken into consideration in Table 7. In this case, the assumed values are \(\bar{K}_{w} = 50\), \(\bar{K}_{nl} = 10\), \(\bar{K}_{s} = 5\), \(P = 1\), \(\gamma = K_{0} / G_{0} = 2\), \(\rho _{p}/\rho _{s} = 0.65\). It is worth mentioning that linear frequency \(\omega _{l}\) and linear buckling load \(P_{l}\) refer to \(a = 0\). As can be observed, by an increment of the amplitude, three parameters show increases regardless of edge conditions and material models. Also, to some extent, BLRs present a sharp increase as the amplitude increases. In other words, by comparisons of the ratios, the stability of beams is the most affected, as the amplitude increases. For the loss factor, an interesting point can be extracted from the results. Although loss factors amplify by increments of the amplitude, a jump can be seen from \(a = 0\) to 0.5. Moreover, the range of the frequency and BLRs are approximately similar to each other while Kelvin–Voigt beams have higher loss factors than standard solid beams. For the case of \(CC\) edge conditions, elastic beams have lower frequency ratios and BLRs than viscoelastic beams. In other words, the viscoelasticity of foams increases the discrepancies of the linear and nonlinear parameters of \(CC\) beams. Therefore, the influences of viscoelastic behavior come to the fore in the nonlinear regime of clamped beams.

Table 7 Frequency ratio, buckling load, and loss factor of elastic and FGV foam beams with various amplitudes and boundary conditions
Full size table

The next studied parameter is the power index that demonstrates the degree of nonhomogeneity or the distribution of properties through the thickness direction. Frequency ratios and BLRs of beams with various power indices and viscoelastic models are presented in Table 8. For this example, \(\bar{K}_{w} = 100\), \(\bar{K}_{nl} = 100\), \(\bar{K}_{s} = 50\), \(P = 5\), \(a = 2\), \(\gamma = 2\), \(\rho _{p}/\rho _{s} = 0.65\) are assumed. Clearly, the frequency and critical buckling load are decreased via the increment of power index due to stiffness reduction. Also, both ratios of \(CC\) beams have lower values than \(CS\) beams. To clarify, some interpretation should be declared. First, the mean values of the linear and nonlinear parameters of \(CS\) beams are lower than those of \(CC\) beams. In other words, the discrepancies of linear and nonlinear values of the mentioned parameters of \(CC\) beams are not increased, as the amplitude increases. Secondly, \(CS\) beams are more sensitive to the amplitude rather than \(CC\) beams, which show an ascending trend, as the amplitude increases. These remarks are similar to those observed in the first comparative example of elastic beams.

Table 8 Frequency/buckling load ratios of FGV foam beams with various porosities
Full size table

4.2.2 Medium coefficients

In order to scrutinize the influences of the medium, simply supported FGV foam beams on a nonlinear medium are studied. The considered parameters are \(P = 2\), \(\gamma = 2\), \(\rho _{p}/\rho _{s} = 0.65\), \(\beta = 0.5\), \(\bar{K}_{w} = 10\), \(\bar{K}_{s} = 5\), \(\bar{K}_{nl} = 10\). The effects of the Winkler coefficient on the BLRs and frequency ratios are depicted in Fig. 2. As depicted, the considered ratios of beams resting on a soft Winkler medium show significant variations as the amplitude increases, while for the case of a stiff Winkler medium, these ratios display smooth variations. In other words, as the Winkler coefficient increases, the sensitivity of beams to the amplitude diminishes. Also, the effect of the medium comes to the fore, while the impact of geometrical nonlinearity wanes, as the Winkler coefficient increases. In spite of the same manner of BLRs, the frequency ratios represent smoother treatment than BLRs, as the amplitude increases. Indeed, they reach 2.269, while BLRs reach 5.864 with \(\bar{K}_{w} = 0\). It should be noted that beams resting on media with various Winkler coefficients show similar behaviors, while the shear (Pasternak) coefficient leads to the distinctive discrepancies of the frequency ratios and BLRs, as depicted in Fig. 3. In other words, the mentioned ratios demonstrate more sensitivity to the shear coefficients than the Winkler coefficient. These discrepancies are remarkable especially for beams with \(\bar{K}_{s} = 0, 10\). Furthermore, by the increment of Winkler and Pasternak coefficients, the rates of increment of the mentioned ratios reduce significantly.

Fig. 2
figure 2

The effect of the Winkler coefficient on the frequency and the buckling load ratios.

Full size image
Fig. 3
figure 3

The effect of the Pasternak coefficient on the frequency and the buckling load ratios.

Full size image

The nondimensional nonlinear coefficients of a medium result in a different treatment of beams, as demonstrated in Fig. 4. As can be observed, the studied ratios with high values of this coefficient represent remarkable variation, as the amplitude increases. Also, the curves of the frequency ratios and the BLRs of beams without nonlinear coefficients locate at the bottom of graphs; significantly, which is in clear contrast to the Winkler and Pasternak coefficients in Figs. 2 and 3. Furthermore, the ratios of beams with various nonlinear coefficients show smooth behaviors, but they are not similar to those displayed by beams with various Winkler coefficients. The nonlinear coefficients have significant influences on the BLRs so that the highest values of ratios reach 16.32 for \(\bar{K}_{nl} = 100\), \(a = 5\), whereas the maximum values for \(\bar{K}_{s} = \bar{K}_{w} = 0\), are 7.64 and 5.86, as depicted in Fig. 3 and Fig. 2, respectively.

Fig. 4
figure 4

The effect of the nonlinear coefficient of the medium on the frequency and the buckling load ratios.

Full size image

4.2.3 Boundary conditions

The influences of boundary conditions and the amplitude on the frequency ratios and BLRs of \(CC\) and \(CS\) beams are illustrated in Fig. 5. In this example, FGV foam beams with \(\beta = 0\), \(P = 3\), \(\bar{K}_{w} = 50\), \(\bar{K}_{s} = 20\), \(\bar{K}_{nl} = 50\) are investigated. The sensitivity of the ratios of \(CS\) beams to the amplitude is more than clamped edge conditions so that the relevant curves of clamped beams locate under \(CS\) beams. The same behavior of beams is observed previously in Tables 7 and 8.

Fig. 5
figure 5

The effect of the edge condition on the frequency and the buckling load ratios.

Full size image

The effects of the amplitude on the frequency ratios versus the critical buckling load of beams are depicted in Fig. 6. For this example, \(\omega _{ref}\) refers to \(a = 0\), \(P = 0\) and the zero frequency ratio relies on the critical buckling load. As can be observed, first, \(CC\) beams have the highest values of the critical buckling loads in comparison with \(CS\) and \(SS\) beams, in other words, the fully clamped beams are the most resistant beams against the mechanical buckling load. Secondly, \(CS\) and \(SS\) beams show the highest and the lowest frequency ratios, respectively. Thirdly, the critical buckling loads and the frequency ratios show increments, as the amplitude increases. This behavior is approximately similar to the curves of the frequency ratios versus the critical buckling load with various amplitudes. Indeed, the maximum frequency ratios are 2.22, 2.51, and 2.04 for \(CC\), \(CS\), and \(SS\) edge conditions, respectively. Furthermore, the minimum and the maximum nondimensional buckling loads refer to \(a = 0, 5\), and their relevant values are 64.75 and 405.26 for \(CC\) beams, 44.99 and 363.89 for \(CS\) beams, and 34.93 and 183.26 for \(SS\) beams.

Fig. 6
figure 6

The effect of amplitude on the frequency ratio–buckling load of FGV foam beams with various edge conditions.

Full size image

5 Conclusions

In this paper, a multiple-step semianalytical approach consisting of decoupling of PDEs, the BG and the He variational methods together with an iterative numerical algorithm are implemented to analyze nonlinear mechanical buckling and vibrations of FGV foam beams resting on nonlinear elastic foundations. The separable kernel and power-law relationships are adapted for constitutive relations. After verification, the influences of edge conditions, material, and geometrical properties on the nonlinear frequency and buckling trend are scrutinized via numerical studies and some of the conclusions are expressed concisely. First, the viscoelasticity of foams intensifies discrepancies of the linear and nonlinear parameters of \(CC\) beams. Also, as the amplitude increases, the ratios of the frequency, buckling load, and loss factor ratios of \(CC\) beams display increases, while the latter show a smoother trend. Moreover, the buckling load ratios show a high level of sensitivity to the nonlinear coefficients of the medium so that the maximum value is 16.32 for \(a = 5\), \(\bar{K}_{nl} = 100\), while the maximum values for \(\bar{K}_{s} = 0\) and \(\bar{K}_{w} = 0\) are 7.64 and 5.86, respectively. In addition, the minimum critical buckling loads refer to \(a = 0\) and their corresponding values for \(CC\), \(CS\), and \(SS\) beams are 64.75, 44.99, and 34.93, respectively. The maximum critical buckling loads of beams at \(a = 5\) are 405.26, 363.89, and 183.26, respectively. Furthermore, as the Winkler coefficient increases, the impact of the medium comes to the fore, while the influences of nonlinear geometry wane. Eventually, the nonlinear, Pasternak, and Winkler coefficients are the most influential coefficients of a medium, respectively.