1 Introduction

Autogenous mobile systems have been widely employed, either in large sizes for pipeline inspection[1,2,3,4], impact moling [5,6,7], or in micro-scale such as in capsule endoscopy [8,9,10]. Of such movable dynamical systems, vibration-driven platforms are a new kind which is propelled by the periodic motion of internal masses or the periodic deformation of their bodies. Conventional wheeled and legged mobile robots would face with many restrictions in terms of mechanical complexity, controllability, physical size, failure of moving parts, and causing hazard to surrounding environment. To address these challenges, crawling robots have received significant attention, whose inspirations are obtained from limbless animals like the snakes and the earthworms. The vibration-driven system [11,12,13], pioneered by Chernous’ko [14], provides a promising impulsion mechanism to develop new locomotion systems. The forward and backward progression of the system can be obtained in the presence of dry friction combined with a periodically controlled internal mass interacting with the main body. Another earlier model using vibro-impact driven mechanism, proposed by Pavlovskaia et al. [15], has also been widely applied in locomotion systems [7, 16,17,18,19,20]. In both types of the systems, the friction force always has a significant effect. On the one hand, the friction force is considered as a resistance preventing the moving tendency of the both abovementioned systems. On the other hand, the presence of friction plays an important role of external resistance to provide the locomotion of the system in desired direction [11, 21]. In previous studies, the friction force was usually assumed to be isotropic [15, 17, 18, 20, 22,23,24]. Some investigated systems, working under anisotropic friction, i.e. the friction in forward direction is different from that in backward direction, were also examined. However, such system requires a special control of the internal mass motion (See [25] for example) or can only move in the direction with smaller friction (downward of an inclined chute [26]).

The effectiveness of a self-propelled robot has typically been considered by checking with the progression rate and dynamical response of the systems. In vibro-impact systems, the excitation force acting on the internal mass was usually in the sinusoidal form. In several previous studies, the excitation force was treated as a dimensionless number, counted as the ratio between the real amplitude of the excitation force and the Coulomb friction value. The progression rate and/or moving direction of the system was checking as a function of such force ratio (See for example in [15, 17, 18, 23, 24]). In experimental studies, the effect of excitation force was taken into account under a preset and unchanged level of dry friction (See [19, 23, 27,28,29]). The effects of various friction levels on the system response have rarely been experimentally considered ([6, 13]) but not in interaction with the excitation force. Besides, some interesting observations have been reported [23, 30]. For example, when the elastic force acting on the capsule is larger than the threshold of the friction, backward motion of the capsule is observed [30]. At some situations, the average speed of forward progression of the capsule using small amplitude of excitation is much larger than the one with backward progression using large amplitude of excitation. This observation somehow reveals the fact that a large amplitude of excitation cannot improve the performance of the capsule system [23]. However, such interesting observations were only experimentally found at a certain value of friction. Besides, the level of excitation was usually considered as how it is large compared to the friction force. The results of our study revealed that with the same force ratio between the excitation amplitude and the friction threshold, the progression can either move backward or forward, depending how large the friction threshold is. With the same force ratio, different values of friction threshold also provided different average velocities of the progression.

Consequently, this study was made to give deeper insights of the effect of different levels of friction force on the system response. Three levels of friction forces, representing for small, middle and large resistances were examined combined with four different values of the force ratios. The results revealed that with the same force ratio, the system have various behaviors with different levels of frictions. In addition, under the same friction force, varying the force ratio provides different trends of the moving direction of the vibration driven locomotion system. A mathematical model describing the system was developed and experimentally validated. The system response was then scrutinized by mean of bifurcation analysis and basin of attrition, using a new dimensionless model developed from the validated mathematical model.

The paper is organized as below. Basic principle of the vibration driven locomotion system is briefly presented in Sect. 2. The experimental setup is then described in detail in Sect. 3. The results and discussions are given in Sect. 4. Some remarkable conclusions and recommendations are made in the last section.

2 System modeling

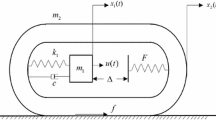
The physical model of a typical vibration-driven locomotion system with impacts is depicted in Fig. 1a. The system is consisted of a body mass, m2 and an inertial mass, m1. A nonlinear elastic spring k and a linear viscous damper, c coupled the two masses. The system body m2 can move along a straight line on a resistive horizontal plane. The internal mass oscillates inside the body along the line parallel to the motion line of the body. A harmonic force Fm with amplitude A and frequency Ω exerts on both masses. The friction force, Fr, occurred at the contact surface between the body and the resistive plane is assumed to obey the Coulomb-Stribeck friction law, as shown in Fig. 1b. When the force acting on the frame body exceeds the threshold of the dry friction force Fs between the body and the slide surface, a bidirectional motion of the body would occur, and then the dynamic friction force, R will be applied. In this study, the friction force is assumed to be isotropic, i.e. Fs+ =|Fs−|= Fs and R+ =|R−|= R.

Fig. 1
figure 1

A vibro-impact locomotion model (a) and Coulomb-Stribeck isotropic friction (b)

Full size image

In Fig. 1a, X1 and X2 represent the absolute displacements of the internal mass and the frame body, respectively. The motion Xi(i = 1, 2) is considered as the forward motion if the value of Xi is positive and vice versa. The two masses are initially positioned with a gap G. When the relative displacement X1− X2 is greater than or equal to the gap G, impact occurs and thus may result in the system moving. The impact characteristics between the two masses were modeled as a linear stiffness k0. The spring connecting the two masses was modeled as a cubic function of the relative displacement of the two masses, as similar to ones in [13, 20], as following:

$$F_{spr} = k_{1} \left( {X_{1} - X_{2} } \right) + k_{2} \left( {X_{1} - X_{2} } \right)^{3}$$
(1)

The friction force plays an important role as a prerequisite condition for movement of the vibration-driven locomotion systems [14, 15]. Naturally, on the one hand, in order to increase the average velocity of motion, the coefficient of friction between the body mass and the environment should be increased and that between the internal mass and the body mass decreased [14]. On the other hand, it was found that the system may either not progress or move in opposite direction if the friction force is excessively small or large.

The system can operate at the time in one of three different stages listed below. The first stage occurs when the mass m1 is not in contact with the obstacle block, i.e. |X1 − X2|< G.

$$\left\{ \begin{gathered} m_{1} \frac{{d^{2} X_{1} }}{{dt^{2} }} = A\sin \left( {\Omega t} \right) - F_{spr} - c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) \hfill \\ m_{2} \frac{{d^{2} X_{2} }}{{dt^{2} }} = - A\sin \left( {\Omega t} \right) + F_{spr} + c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) - F_{r} \hfill \\ \end{gathered} \right.$$
(2)

Once the relative displacement of the two masses is equal to or exceeds the clearance between the mass m1 and the obstacle on the right side, i.e. X1 − X2 ≥ G, an impact of the mass upon the frame occurs. The equations of the system motion of these two stages can be described as

$$\left\{ \begin{gathered} m_{1} \frac{{d^{2} X_{1} }}{{dt^{2} }} = A\sin \left( {\Omega t} \right) - F_{spr} - c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) - k_{0} \left( {X_{1} - X_{2} - G} \right) \hfill \\ m_{2} \frac{{d^{2} X_{2} }}{{dt^{2} }} = - A\sin \left( {\Omega t} \right) + F_{spr} + c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) + k_{0} \left( {X_{1} - X_{2} - G} \right) - F_{r} \hfill \\ \end{gathered} \right.$$
(3)

A comprehensive equation of motion of the system is then expressed by combining Eqs. (2) and (3) as:

$$\left\{ \begin{gathered} m_{1} \frac{{d^{2} X_{1} }}{{dt^{2} }} = A\sin \left( {\Omega t} \right) - F_{spr} - c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) - Hk_{0} \left( {X_{1} - X_{2} - G} \right) \hfill \\ m_{2} \frac{{d^{2} X_{2} }}{{dt^{2} }} = - A\sin \left( {\Omega t} \right) + F_{spr} + c\left( {\frac{{dX_{1} }}{dt} - \frac{{dX_{2} }}{dt}} \right) + Hk_{0} \left( {X_{1} - X_{2} - G} \right) - F_{r} \hfill \\ \end{gathered} \right.$$
(4)

where H(.) is the Heaviside function defined as:

$$\left\{ \begin{gathered} H = 1,\,\,X_{1} - X_{2} - G > 0 \hfill \\ H = 0,\,\,\,X_{1} - X_{2} - G \le 0 \hfill \\ \end{gathered} \right.$$
(5)

Studies on dynamics of mechanical systems have been developed almost exclusively in a non-dimensional form. Typically, the following non-dimensional variables and parameters were used for the system (3) (See [10, 17, 22, 31] for example):

$$\tau = \Omega_{0} t;\,\,x_{1} = \frac{{k_{1} }}{{F_{S} }}X_{1} ;\,x_{2} = \frac{{k_{1} }}{{F_{S} }}X_{2} ;\,\Omega_{0} = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ;\,\omega = \frac{\Omega }{{\Omega_{0} }}; \zeta = \frac{c}{{2m_{1} \Omega_{0} }};\,\alpha = \frac{A}{{F_{S} }};\,\sigma = \frac{{k_{0} }}{{k_{1} }};\,\beta = \frac{{k_{2} }}{{k_{1} }}\left( {\frac{{F_{S} }}{{k_{1} }}} \right)^{2} ;\,\gamma \, = \frac{{k_{1} }}{{F_{S} }}G;\,\mu = \frac{{m_{2} }}{{m_{1} }}$$
(6)

where the friction force FS was a constant. The non-dimensional comprehensive equations of motion for the whole system was then expressed as:

$$\left\{ \begin{gathered} \frac{{d^{2} x_{1} }}{{d\tau^{2} }} = \alpha \sin \left( {\omega \tau } \right) - (x_{1} - x_{2} ) - \beta (x_{1} - x_{2} )^{3} - 2\zeta \left( {\frac{{dx_{1} }}{d\tau } - \frac{{dx_{2} }}{d\tau }} \right) - h\sigma \left( {x_{1} - x_{2} - \gamma } \right) \hfill \\ \frac{{d^{2} x_{2} }}{{d\tau^{2} }} = \left[ { - \alpha \sin \left( {\omega \tau } \right) + (x_{1} - x_{2} ) + \beta (x_{1} - x_{2} )^{3} + 2\zeta \left( {\frac{{dx_{1} }}{d\tau } - \frac{{dx_{2} }}{d\tau }} \right) + h\sigma \left( {x_{1} - x_{2} - \gamma } \right) - {\text{sgn}} \left( {\frac{{dx_{2} }}{d\tau }} \right)} \right]\frac{1}{\mu } \hfill \\ \end{gathered} \right.$$
(7)

was used to examine the system behavior. In Eq. (7), h is the Heaviside function describing the impact conditions in the dimensionless model, i.e.:

$$\left\{ \begin{gathered} h = 1,\,\,x_{1} - x_{2} - \gamma \ge 0 \hfill \\ h = 0,\,\,\,x_{1} - x_{2} - \gamma < 0 \hfill \\ \end{gathered} \right.$$
(8)

In several previous studies, the effect of the excitation force (Fm) on the system behavior were taken into account by varying the value of the force ratio, α (See abovementioned references for example). In those studies, the friction force was usually fixed as a constant level. In such situation, it would be reasonable to examine the system response under different excitation levels by varying the force ratio, α. However, such system responses may be different for other level of the friction force. Our experimental results revealed that, with the same force ratio α but under different values of the friction force, the system can move either forward or backward. Moreover, as shown in Eq. (6), the friction magnitude FS appeared in several other parameters (x1, x2, β, γ), meaning that FS is not independent, causing difficult to examine the system behavior when varying the friction force. Also, using the force ratio, α would lead to a complicated treatment to expand the results using dimensionless model.

In this study, the mathematical model (4) was firstly experimentally validated. The effect of different levels of friction force on the practical system response was then examined. A new non-dimensional model was proposed for more convenient to vary the friction component. Several dynamical responses of the system was then scrutinized using the dimensionless model.

In this study, the friction was adopted in the form of the Coulomb–Stribeck model [23, 32]:

$$F_{r} = \frac{1}{2}F_{s} \left( {1 + e^{{ - \left| {\frac{{dX_{2} }}{dt}} \right|\frac{1}{{V_{S} }}}} } \right){\text{sgn}} \left( {\frac{{dX_{2} }}{dt}} \right)$$
(9)

where Fs is the threshold of the dry friction force for break-away when dX2/dt = 0, and Vs is the Stribeck velocity. In this experimental study, three levels of friction forces Fs, representing for small, middle and large resistances were implemented combined with four different values of the force ratios. The experimental setup and implementing method are presented in the next section.

3 Experimental implementation

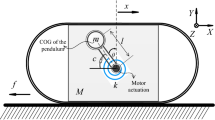
The above model was realized as shown in Fig. 2 [13, 20, 27]. The prototype was made in a large scale to make it convenient to collect the experimental data.

Fig. 2
figure 2

A photograph of the experimental apparatus

Full size image

In Fig. 2, a mini electro-dynamical shaker (1) model MS-20 is placed on a slider of a commercial linear bearing guide (4), providing a tiny rolling friction force. An additional mass (3) was clamped on the shaker shaft with the support of sheet springs (2). Generally, applying a sinusoidal current to the shaker leads to relative linear oscillation of the shaker shaft having the additional mass. Hereafter, the moveable mass, combined by the additional mass and the shaker shaft, is assigned as inertial mass, m1, playing the role of the internal mass of the system. The relative motion of the inertial mass was measured by a non-contact position sensor (9) model Kaman KD-2306. Motion of the shaker body was captured by a linear variable displacement transformer (8). An obstacle block (5) was used to obtain the impact force. In order to vary the friction force when remaining the body mass, a carbon tube (6) is connected with the shaker body by means of a flexible joint, avoiding any misalignment when moving. The body frame, including the shaker body, the position sensor and the carbon tube (6), is referred as the mass m2. The tube is able to slide between two aluminium pieces in the from of a V-block (10). The two V-blocks are fixed on two electromagnets (7), as depicted in more detail on Fig. 3a. Supplying a certain value of electrical current to the coupled electromagnets provides a desired clamping force on the tube and thus a corresponding value of threshold sliding friction. The friction force were measured by pulling the body to move at a steady speed. By adjusting the voltage supplied to the coupled electromagnets, the corresponding friction force can be obtained (See [13] for more detail).

Fig. 3
figure 3

Varying the friction force: a apparatus structure and b the dependency of friction force on the supplied voltage

Full size image

This configuration allows varying the friction force without changing the total weight of the system, including the two masses, and thus can experimentally check with the locomotion capacity in different friction levels.

The shaker is powered by a sinusoidal voltage, generated by a laboratory function generator and then amplified by a commercial amplifier. The application of the sinusoidal current passing the shaker leads to oscillation of the shaker shaft and the mass attached on it. As provided by the shaker supplier, the magnetic force, Fm is solely depended on the current supplied. Adjusting the sinusoidal voltage supplying to the amplifier can provide a desired excitation force. Our pilot experimental data verified that the excitation force is proportional to the current supplied to the shaker (see [20] for detailed information of how to determine this relation). To determine stiffness of the inside spring support which connects the movable shaft and the body of the shaker, a set of tests was carried out when the shaker was switched off. Using a DC geared motor and a screw drive, a slow linear motion (around 0.16 mm/s) of the shaker with respects to its shaft was made. The shaft was fixed with the frame via a load cell. The relative displacements between the shaker and its shaft, which is actually the spring deformation, was measured by the position sensor Kaman KD-2306. The spring force, Fspr was measured by the load cell, and then was plotted as a function of the relative displacement, X1 − X2, denoted as D in Fig. 4a. Here a nonlinear fit, using the cubic function represented in Eq. (1), was applied to carry out the relationship between the spring force and the corresponding deformation. More detailed information of the results are shown in Fig. 4b. As can be seen, a value as high as 0.99242 of the coefficient of determination, R-square, reflected that the determined cubic function for the spring stiffness was well fitted to the experimental data. The values of spring parameters, k1 and k2, are shown in Table 1.

Fig. 4
figure 4

a Function fitting of spring force, Fspr with respect to movement, D and b the detailed results of the fitting process

Full size image
Table 1 Parameters of experiments
Full size table

For operational parameters, three levels of friction force were selected at first. With respect to the total weight of the two masses as 2.336 kg, the threshold friction force were set as 2.3, 6.8 and 13.6 N, corresponding to three levels of the static friction coefficient as approximately 0.1, 0.3 and 0.6. These levels can be respectively considered as low, middle and high friction levels. The minimum magnitude of the excitation force was chosen so as to strong enough to make the mass oscillate and collide to the obstacle block. Consequently, three other levels of the excitation force were selected as strong enough values to make significant differences between the system responses. The overall experimental parameters are given in Table 1.

Twelve sets of experiments were implemented for four levels of the force ratio, α and three levels of the friction magnitude. The excitation frequency of 15 Hz was chosen for analysis in details. It was found that with the given structure parameters, this excitation frequency provided a stable and fast moving stages for the whole system. The results are shown in the next section.

4 Results and discussion

4.1 Numerical and experimental results

Figure 5 shows the comparisons between experiments and numerical simulations by using time histories of displacements which were obtained at α = 0.79 for two levels of friction force, Fs = 2.3 N (Figs. 4a and  5b), and Fs = 13.6 N (Fig. 5c and d). Here α is the ratio between the excitation amplitude and the threshold friction forces. The left-side subplots (Fig. 5a and c) show the simulation results solving Eq. (4), whereas the right-side subplots (Fig. 5b and d) show the corresponding experimental results.

Fig. 5
figure 5

Time histories of the displacement of the internal mass, X1 and of the system body, X2 obtained numerically (a,c) and experimentally (b,d). An excitation frequency of 15 Hz, the force ratio α = 0.79, and friction force of 2.3 N (a,b) and 13.6 N (c,d) were applied

Full size image

As can be seen from Fig. 5, an overall good agreement between numerical and experimental results of the movement direction of the system can be observed. Applying the force ratio of α = 0.79 in both cases of small and large friction (Fs = 2.3 N and Fs = 13.6 N), the moving forward of the whole system was succeeded. Although there is a slight difference between the simulated and experimental displacements, the overall agreements between the mathematical model and experiment can be observed. Also, it can be seen all forward movements of the whole system are linear with respects to time. Moreover, the progression X2 of the system under the high friction force (Fs = 13.6 N on Fig. 5c and d, the moving rate as around + 5 mm/s) is as two times higher than that under the low friction force (Fs = 2.3 N on Fig. 5a and b, the moving rate is as + 2.5 mm/s).

Figure 6 presents other time histories of the system motion corresponding to a higher force ratio, α = 1.19 under two levels of friction force: the low friction, Fs = 2.3 N (Fig. 6a and b) and the high friction, Fs = 13.6 N (Fig. 6c and d). The left-side subplots (Fig. 6a and c) show the simulation results whereas the right-side subplots on the same row (Fig. 5b and d, respectively) show the corresponding experimental results. In overall, in term of the progression rate comparison, it can be seen a good agreement between the simulation and experimental results. The trajectories of the motion of the two masses, X1 and X2, appeared in experiments seem slightly different from that in simulation, which might.

Fig. 6
figure 6

Time histories of the displacement of the internal mass, X1 and of the system body, X2 obtained numerically (a,c) and experimentally (b,d). An excitation frequency of 15 Hz, the force ratio α = 1.19, and friction force of 2.3 N (a,b) and 13.6 N (c,d) were applied

Full size image

be due to the erroneousness of the restoring force modeling or in experimental measurements. Even so, both numerical and experimental results revealed that with the same force ratio α = 1.19, the system moved backward under high friction (Fs = 13.6 N, as shown in Fig. 6c and d), whereas the forward motion was obtained under low friction (Fs = 2.3 N, as shown in Fig. 6a and b).

In order to further examine the moving direction as well as the progression rate of the system under the concurrent effect of the force ratio and the friction level, a set of experimental runs was implemented, including 12 tests, combining three level of the threshold friction (Fs = 2.3 N; 6.8 N and 13.6 N) and four levels of the force ratio (α = 0.59; 0.79; 0.99 and 1.19). As can be seen in Figs. 5 and 6, the displacement of the mass m2, X2 increases linearly with time at all investigated parameters. In order to compare how fast the system can progress at various parameters, the displacement of the system body, X2 after three seconds of operation for each run was defined as the progression rate and denoted as P. Since P was obtained for the same time (three seconds) of running, a higher P reflects a faster progression rate of the system. Also, a negative value of P (P < 0) means to a backward motion of the system. In Fig. 7, the experimental results were then overplot onto the 2-dimension contour plot of the progression rate obtained numerically. The numerical solutions were obtained by varying simultaneously the two parameters with two for loops with steps of 0.5 N for the friction force Fs, and 0.05 for the force ratio, α.

Fig. 7
figure 7

Contour plots of the progression rate, obtained from experiments (represented by star symbols) and from numerical solutions (color fill areas), with respects to friction force, Fs and the force ratio, α. (Color figure online)

Full size image

In Fig. 7, values of the experimental progression rates P (noted by the numeric labels) were placed under the star symbols, corresponding to the two parameters of friction force and the force ratio. The simulated contour plots are color filled corresponding to 5 levels of the progression rate. The areas of backward motion (P ∈ [0..−6]) are represented with grey color, and separated from the area of forward motion (P ∈ [0.. + 6]) by a red-dashed boundary curve. As can be seen from the figure, both forward and backward motions of the system are clearly observed. The highest forward progression appeared at high friction force combined with low force ratio (the red area of the numerical contour). The highest experimental progression rates of 6.392 mm/s were obtained at the combination of the friction force Fs = 13.6 N and the force ratio α = 0.59. The four highest values of experimental forward progression, bounded by yellow rectangles on the figure, are also appeared inside or nearby the highest numerical values (the red-area of contour). These phenomena provided an overall agreement between the numerical solution and experimental results. Hence, the numerical solution of the verified model will be used to examine in more detail the system responses under various condition of friction and the excitation force. Looking as the boundary between forward and backward motion of the system (shown by the red-dashed line in Fig. 7), the system moved backward for α > 1 and Fs < 10 N, and α < 1 under the friction force Fs > 10 N.

Figure 8 present a contour plot of the progression rate with respects to real values of the two parameters. The progression rate of the system here was considered as three large areas: backward motion (the grey area), forward motion (the green area) and fast forward motion (the magenta area). The two bounded lines between those three areas were then extracted and then curve fitted, as shown in Fig. 9. As can be seen in this Figure, with the coefficient of determination R-square of higher than 0.99, each boundary was well fitted by a second order polynomial.

Fig. 8
figure 8

Contour plots with respects to the real values of both friction force, Fs and the excitation force amplitude, A. (Color figure online)

Full size image
Fig. 9
figure 9

Curve fitted for the forward–backward (a) and fast forward (b) boundaries

Full size image

Figure 9a presents the boundary between backward and forward motion, representing by the fitted function:

$$A = 0.71085 + 1.10532F_{s} - 0.0168F_{s}^{2}$$
(10)

For reference, a linear line representing the function A = 1.10532*Fs is also plotted on the figure. It can be remarked that, for each value of the static friction Fs, whenever the excitation amplitude, A, is larger than the value calculated by Eq. (10), the system will move backward and vice versa.

Similarly, the boundary for which the system moved forward with high progression rate (P > 10 mm/s) can be represented by a fitted function as shown in Fig. 9b, which can be expressed as:

$$A_{fast} = - 2.4351 + 0.872F_{s} - 0.0076F_{s}^{2}$$
(11)

For each value of the friction force FS, the system has fast forward motion when the excitation amplitude smaller than the value obtained by Eq. (11).

Using Eqs. (10) and (11), it can be able to check if the system either can move backward or forward, or may have a fast forward motion. It would be mentioned that in similar previous studies [10, 23], the system was examined under one level of the friction force only. For example, the experimental observation of the backward and forward progressions was examined at two values of 1.3 N and 1.4 N for the amplitude excitation force, under a fixed level of friction force with the friction coefficient of 0.6 [23].

4.2 Dynamical analysis

In this section we will carry out a numerical continuation study of the dynamic response of the system under different levels of friction force. At first, a non-dimensional model is developed from the validated model (4) by introducing the following parameters:

$$\tau = \Omega_{0} t;\,\,x_{1} = \frac{{k_{1} }}{{F_{b} }}X_{1} ;\,x_{2} = \frac{{k_{1} }}{{F_{b} }}X_{2} ;\,\Omega_{0} = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ;\,\omega = \frac{\Omega }{{\Omega_{0} }};$$
$$\zeta = \frac{c}{{2m_{1} \Omega_{0} }};\,\chi = \frac{A}{{F_{b} }};\,\sigma = \frac{{k_{0} }}{{k_{1} }};\,\beta = \frac{{k_{2} }}{{k_{1} }}\left( {\frac{{F_{b} }}{{k_{1} }}} \right)^{2} ;\,\gamma \, = \frac{{k_{1} }}{{F_{b} }}G;\,\mu = \frac{{m_{2} }}{{m_{1} }};\,f_{r} = \frac{{F_{S} }}{{F_{b} }}$$
(12)

where Fb is a reference value of force. In practice, this reference force may be determined as a maximum static force providing the allowance stroke of the practical actuator. The new force ratio, χ is introduced replacing the previous force ratio α, making the variation of the excitation force to be independent from the friction force. The dimensionless form of the model (4) is thus expressed as following:

$$\left\{ \begin{gathered} x^{\prime}_{1} = v_{1} \hfill \\ v^{\prime}_{1} = \chi \sin (\omega \tau ) - (x_{1} - x_{2} ) - \beta \left( {x_{1} - x_{2} } \right)^{3} - 2\zeta \left( {\frac{{dx_{1} }}{d\tau } - \frac{{dx_{2} }}{d\tau }} \right) - h\sigma \left( {x_{1} - x_{2} - \gamma } \right) \hfill \\ x^{\prime}_{2} = v_{2} \hfill \\ v^{\prime}_{2} = \left[ { - \chi \cos (\omega \tau ) + (x_{1} - x_{2} ) + \beta (x_{1} - x_{2} )^{3} + 2\zeta \left( {\frac{{dx_{1} }}{d\tau } - \frac{{dx_{2} }}{d\tau }} \right) + h\sigma \left( {x_{1} - x_{2} - \gamma } \right) - f_{r} {\text{sgn}} \left( {\frac{{dx_{2} }}{d\tau }} \right)} \right]\frac{1}{\mu } \hfill \\ \end{gathered} \right.$$
(13)

where the Heaviside function h is defined as similar to Eq. (8).

In order to gain an understanding of the system dynamics, the bifurcation analysis is carried first. Typically, a bifurcation diagram shows the values visited or approached asymptotically of a system as a function of a bifurcation parameter. In this study, the relative velocity between the two masses was chosen as the visited values of the system. We defined the velocity map, V* as the projection of the Poincaré map on the vertical axis of the phase space, constructed from the relative velocity (v1−v2) and the relative position (x1−x2) of the system. We consider the behavior of the system for varying the friction force, fr. Hence, the friction force, fr was chosen as a bifurcation parameter. As a results, the bifurcation diagram will show the plots of the relative velocity map, V*, with respect to the friction force, fr.

It is well known that, a Poincare map is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré section, transversal to the flow of the system. A Poincaré map represents points in the system’s phase space, sampled at equal intervals of time, which denotes the fundamental period of the excitation. If the system is periodic, the Poincaré map will exhibit one dot. If the system has a periodic-2 motion, the Poincaré map will exhibit two dots, and so on. If the system is chaotic, the Poincaré map generally exhibits a random scatter of points.

The plotting process of a bifurcation diagram is described as below. For each value of the bifurcation parameter, fr, the velocity map, V* was calculated from the values of the relative velocity v1−v2, sampled with the frequency of the excitation force. The calculations were applied for 300 cycles of the excited force. The first 100 cycles were considered to be transient and thus were omitted. The steady state of the next 200 points of the map was collected and plotted on the diagram. To make it convenient for reference, the corresponding progression rate of the system with respects to various values of the friction force is plotted beside each bifurcation diagram. The dimensionless progression rate was defined as the displacement of the system, x2 obtained after a dimensionless time τ = 100.

Figure 10a depicts bifurcation diagrams of the Poincaré map of the relative velocity, V* as a function of the friction force, fr ∈ [0, 2]. As can be seen, the bifurcation diagram appeared likely as a single curve for all investigated values of friction levels. This phenomenon revealed that the system always has a period-one response. For reference, the corresponding progression rate of the system was plotted on Fig. 10b. As can be seen, with the excitation amplitude χ = 0.5 and the excitation frequency of ω = 1.56, the system always moved forward for different values of the friction force. The system obtained the highest progression rate at the friction fr≈1.2.

Fig. 10
figure 10

a Bifurcation diagram of the relative velocity maps and b the progression rate for varying friction force, fr ∈ [0, 2]. The calculations obtained for χ = 0.5; ω = 1.56

Full size image

Figure 11 presents the bifurcation diagram (Fig. 11a) and progression rate (Fig. 11b) of the system under the same range of the friction, but with a lower excitation frequency, as ω = 1. As can be seen from Fig. 11, the bifurcation appeared likely as a single curve. This phenomenon reflected that the system has a period-1 motion for all investigated range of the friction force. However, the system moved backward for fr ∈ (0, 0.175]. For higher friction force, fr ∈ [1.75, 2], the system always moves forward, with the highest progression rate observed at fr≈0.9.

Fig. 11
figure 11

a Bifurcation diagram of the relative velocity maps and b the progression rate for varying friction force, fr ∈ [0, 2]. The calculations obtained for χ = 0.5; ω = 1

Full size image

For a higher excitation amplitude, χ = 1, the bifurcation diagram and corresponding progression plot were calculated as shown in Fig. 12. The system has two area of moving trends: moving backward for smaller friction (for fr ∈ (0, 1.18] or having forward motion for higher friction (fr ∈ [1.18, 2].

Fig. 12
figure 12

a Bifurcation diagram of the relative velocity maps and b the progression rate for varying friction force, fr ∈ [0, 2]. The calculations obtained for χ = 1; ω = 1

Full size image

Continuing increase the excitation amplitude to be larger than 1, Fig. 13 depicts the bifurcation diagram and progression rate of the system with χ = 1.5, ω = 1, and fr ∈ [0, 2]. For lower range of the friction force, fr ∈ [0, 1], the bifurcation appeared in narrow bands of the velocity maps, seemed as likely period-1 and period-2 motion. The system always moved backward for this range of friction. For larger range, fr ∈ [1, 2], the system always moved forward. However, the system appeared to have both chaotic motion in some sub-ranges as well as period-1 motion in the other sub-ranges. Dynamics response of the system will be analyzed further by mean of basin of attraction.

Fig. 13
figure 13

a Bifurcation diagram of the relative velocity maps and b the progression rate for varying friction force, fr ∈ [0, 2]. The calculations obtained for χ = 1.5; ω = 1

Full size image

In order to further analysis the qualitative nature of the dynamics responses, basin of attraction plots were built for several sets of the operation parameters. A set of initial conditions of − 0.4 to 0.1 for the relative displacement and − 0.5 to 1 for the relative velocity was remained for all plots.

The first case was examined for the excitation amplitude χ = 1, the excitation frequency ω = 1, combined with a small level of friction force, fr = 0.1. Figure 14 presents the basins of attraction and attractors (Fig. 14a) and two sub-plots (Fig. 14b, c) for phase portraits and Poincaré maps corresponding to such two attractors. As can be seen, the system has period-1 motion for all initial conditions.

Fig. 14
figure 14

a Basin of attraction; b, c trajectories (grey lines) and Poincaré maps (red dots) for the two periodic motions of the system, calculated for χ = 1; ω = 1; fr = 0.1. The first 100 cycles of motion were taken to be transient. (Color figure online)

Full size image

With a higher of friction force, fr = 0.95, the system has a period-1 motion attractor, and two co-attractor of period-2 motion, as shown in Fig. 15. On Fig. 15a, two dominant period-2 orbits were shown by green and red attractors (Fig. 15a), having the cyan and magenta basins, respectively; the period-1 orbit shown in yellow with its grey basin. Figure 15a–c respectively demonstrate the trajectories and Poincaré maps for the coexisting solutions. The first 100 cycles of motion were taken to be transient and not included in the plots.

Fig. 15
figure 15

a Basin of attraction; b,c,d trajectories (grey lines) and Poincaré maps (red dots) for the periodic motion of the system, calculated for χ = 1.5; ω = 1; fr = 0.95. (Color figure online)

Full size image

When the friction force is significantly high, the system has either chaotic or period-1 motion, as already shown in Fig. 13a. The attractor appeared to be chaotic when the friction force is fr = 1.8, as shown in Fig. 16a. Here the chaotic attractor is depicted by a red area, with its basin shown in magenta color. A co-existing attractor of period-1 motion appeared in a green dot, with the basin shown in cyan color. Figure 16b and c respectively presents the phase portrait and Poincaré map of the two such attractors. The first 100 cycles of motion were taken to be transient and not included in the plots.

Fig. 16
figure 16

(color online) a Basin of attraction; b,c trajectories (grey lines) and Poincaré maps (red dots) for the periodic motion of the system, calculated for χ = 1.5; ω = 1; fr = 1.8. (Color figure online)

Full size image

The basin of attraction and Poincaré map confirmed the significant effect of the friction force on the dynamic response of the system.

From the analysis of basin of attraction and Poincaré maps, it can be concluded that the dynamic response of the system varied from period-1, period-2 and chaotic, depending on the levels of the friction force. It would be noted that, the dynamic response of this system have also been examined in several previous studies from other authors [10, 23]. However, the effect of friction force on this system dynamic have not been found. Another study on the dynamic response of this system with different models of friction was made [32]. In that study, the system dynamic response was examined for the varied ratio of the two masses with four different models of friction, but not for the effect of friction magnitude.

5 Conclusions

This paper presented experimental observations and several initial analyses on a vibro-impact driven locomotion system with the effect of friction force. The experimental setup provided a capacity of varying friction force when keeping the weight of the whole system unchanged. A mathematical model was built, experimentally validated and further developed in dimensionless form, providing an ability to expand to different scales of practical systems. Bifurcation analysis and basin of attraction were calculated to scrutinize the effect of friction on the dynamic response of the scaled model. The following remarks would be useful for further studies:

  • For the system working in variable friction force, the force ratio between the excitation magnitude and friction level would not be totally useful to present the excitation effects in modeling the system;

  • The level of friction force would be a significant effect on not only how fast the system move, but also which direction of the progression;

  • Different values of friction force would lead to abundant dynamic response of the system, from period-1, period-2 to chaotic motions.

Further studies would be investigated to carried out the optimal solution of operation parameters for better progression rate as well as more stable dynamics.