On the dynamics of a vibro-driven capsule system

Abstract

This paper studies the nonlinear dynamics of a two-degree-of-freedom vibro-driven capsule system. The capsule is capable of rectilinear locomotion benefiting from the periodic motion of the driving pendulum and the sliding friction between the capsule and the environmental surface in contact. Primary attentions are devoted to the dynamic analysis of the motion and stick-slip effect of the capsule system. Following a modal decoupling procedure, a profile of periodic responses is obtained. Subsequently, this work emphasizes the influences of elasticity and viscosity on the dynamic responses in a mobile system, whose implicit qualitative properties are identified using bifurcation diagrams and Poincaré sections. A locomotion-performance index is proposed and evaluated to identify the optimal viscoelastic parameters. It is found that the dynamic behaviour of the capsule system is mainly periodic, and the desired forward motion of the capsule can be achieved through optimal selection of the elasticity and viscosity coefficients. In view of the stick-slip motion, the critical equilibrium and its dynamic behaviours, different regions of oscillations of the driving pendulum are identified, with the attention focusing on the critical region where linearities are absent and nonlinearities dominate the dynamic behaviour of the pendulum. The conditions for stick-slip motions to achieve a pure forward motion are investigated. The proposed approach can be adopted in designing and selecting of suitable operating parameters for vibro-driven or joint-actuated mechanical systems.

1 Introduction

In recent years, mobile micro-robotic systems which are driven by internally generated force have attracted great attentions from researchers in various communities. These systems have extensive potential applications in engineering diagnosis, medical assistance, pipeline inspection and disaster rescues. This idea is that a mobile system can be propelled rectilinearly utilizing an internally periodically driven mass interacting with the main body, particularly when some resistance forces are acting between the system and the contacting surface. Therefore, a large amount of studies [1,2,3,4,5,6,7,8,9] have been devoted to the systems containing movable internal masses. The main advantage of such systems is the absence of the external driving mechanism, which enables a simple and encapsulated dynamic model of micro-mechanisms working independently in complicated environment. Therefore, such systems are significantly applicable in restricted space and unstructured environment, for instance, robotic inspection in incapacious place and self-propelled human endoscope [10,11,12]. Still, further developments are needed based on the current framework in order to cope with the spring up of new issues in real-life applications.

The dynamical vibration systems containing both the flexible and rigid body modes arise in various practical applications, including robotics and vibro-impact structures. During the past few decades, the practical requirement of engineering applications gives rise to the extensive research interests in vibrational dynamics, aiming to reveal the fundamental natures and exploit the potential applications. Extensive studies on the stability and bifurcation analysis of vibro-impact systems are available in the literature, which can be partly found in [13,14,15,16,17,18].

The harmonically excited mass-spring-damper system is quite well understood, which have complex dynamics in their motion near resonant conditions [19, 20]. Benefiting from the linearity of system dynamics, the vibrational response can be conveniently projected onto the normal mode coordinates and decomposed to analysing treatment of the response of a flexible system or a rigid body system. Luo et al. [21] studied the correlative relationships between the model parameters and dynamic performance. Batako et al. [22] investigated the dynamic response of a friction-driven vibro-impact system with discontinuous nonlinear forces including dry friction and impact. A newly developed three-mass model was analysed and compared with a low-dimensional model by Pavlovskaia et al. [23]. As a practical application, Liu et al. [5] studied the vibro-impact dynamics of a capsule robot, which consists of a capsule main body interacting with an internal mass driven by a harmonic excitation. It is revealed that the system responses are mainly periodic, and the best progression can be determined by a careful choice of the system parameters.

Notably, the dynamic models developed by the aforementioned works have been proved to be useful for uncovering the interactive dynamic performance of such systems in real-world applications. Moreover, the related studies have contributed abundant information of the fundamental characteristics to the non-smooth motions of practical mechanical systems especially with impacts. However, it is noted that most of these researches are, in nature, based on linear motions with the consideration of viscoelastic characteristic. For nonlinear systems, the general modal decoupling procedure is unavailable. Particularly when a pendulum is introduced, its geometric nonlinearity initially coupled with the rotational motion naturally induces the occurrence of quadratic nonlinearities. Extensive investigations were carried out from a perspective of utilizing the pendulum in real environment which needs to be stabilized or neutralized. For instance, effective vibration control of absorbers [24,25,26,27,28], balance control of suspension system [29] and human standing posture [30]. However, the research and design of these mechanisms are mainly restricted to the unforced systems, focusing on the viewpoint of stability. Relatively few efforts have been devoted to the nonlinear dynamic behaviour and suitable design of progressive systems.

In this paper, an encapsulated mobile system with an internally movable pendulum is considered. Two friction models are assumed, including anisotropic Coulomb’s dry friction model acting between the capsule and the sliding surface and the linear viscous friction model induced by the motor at the pivot. It is noted that the nonlinearity and coupling are augmented when confronting with the friction. Therefore, two strongly nonlinear processes (friction and vibration) are combined into the robotic system and a mathematical tool is utilized to coordinate the mutual interaction of these processes. The resulting characteristic of the proposed system is a synchronized motion which has various potential applications, for instance, in pipeline inspection, medical assistance and information acquisition during disaster rescues. It is worth mentioning that the proposed system is capable of bidirectional rectilinear motion in the presence of harmonic excitation. The correlations between dynamic performance and the control parameters (viscosity and elasticity) are studied to find the implicit feasible matching law and to realize steady-state motion. In terms of the stick-slip effect, the critical region dominating the dynamic behaviour of the driving pendulum is identified and the conditions for intermittent forward progression are studied. In this regard, an always forward steady-state progression of the capsule can be achieved.

The organization of this paper is as follows. Section 2 presents the problem formulation and the derivation of the dimensionless dynamics. Section 3 investigates nonlinear dynamics of the proposed capsule system and analyses the dynamic responses under the influences of elasticity and viscosity. The discussion on stick-slip motion is placed in Sect. 4. Finally, conclusion and future work are outlined in Sect. 5.

2 Mechanical model

2.1 Description of the vibro-driven capsule system

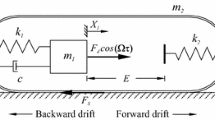
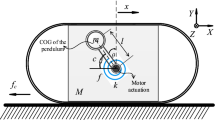
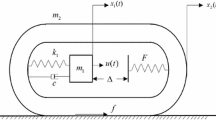
Consider the two-degree-of-freedom vibro-driven capsule system shown in Fig. 1, which consists of a base (merged with a rigid capsule shell) and an inverted pendulum. The movable pendulum is driven by an external harmonic force generated through an actuator at the pivot. The model of the actuator is simplified here, and the interaction between the pendulum and the capsule is represented by a linear viscoelastic pair of torsion spring and viscous damper. The capsule is capable of rectilinear movement. It is assumed that the mass of the pendulum is centralized at the ball, and the centre of mass of the base coincides with the pivot axis. The main difference between the capsule system and the conventional cart-pole system is that the torque is applied at the pivot to rotate the pendulum with no force on the cart, which induces intermittent progression of the capsule.

The capsule is constrained to have one-dimensional movement. The rotating pendulum is driven by an external harmonic force with amplitude A and frequency $\varOmega$. The torsion spring is un-stretched when the inverted pendulum is upright. M and m are the masses of the cart and the ball, respectively. l is the length of the inverted pendulum, $\theta$ and x depict the configuration variables of the rotational and the horizontal movements, i.e. $q=\left[ {q_1\,q_2 } \right] ^{T}=\left[ {\theta \,x} \right] ^{T}$, k and c represent the stiffness and damping coefficients, respectively. T denotes the control input applied to the system and physically describes the torque generated by the motor which exert on the pendulum rotation.

Fig. 1

Two-degree-of-freedom capsule system with an internally driven pendulum

The working principle of the mechanism is as follows. The capsule body is driven over a surface rectilinearly by the force applied on the pendulum and the dry friction between the sliding surface, and the entire body behaves sticking and slipping intermittently. The potential energy is stored and released alternatively in compatible with the compression and extension of the torsion spring.

The motor torque actuation rotates the pendulum back and forth and drives the entire system moving forward through the strongly coupled force. The motion of the capsule starts with static state, and the capsule moves when the magnitude of the resultant force applied on the body in the horizontal direction exceeds the maximal value of the dry friction force at the contact surface. It is termed sticking phase when the above condition is not satisfied. The occurrence of sticking phase is diverse, at the initial static state, during the motion cycle as well as at the end. At the instant when the magnitude of the resultant force exceeds the static resistant force, the sticking phase is annihilated and the capsule body moves progressively, which falls into the fast motion called slipping phase. Extensive investigations have been devoted to the issue of stick-slip phenomenon in the presence of contact and collision with friction [31,32,33,34].

2.2 Geometry and friction models

The ball’s position is uniquely described by two degrees of freedom $x_b$ and $y_b$, chosen as the deflection of the geometric centre of the ball referenced from the medial axis. The position and velocity of the ball are given by

$$\begin{aligned} x_b= & {} x-l\hbox {sin}\theta , \,\,y_b =l\hbox {cos}\theta \end{aligned}$$

(1)

$$\begin{aligned} {\dot{x}_b}= & {} \dot{x} - l\dot{\theta } \hbox {cos}\theta ,\,\,{\dot{y}_b} = - \,l\hbox {sin}\theta \end{aligned}$$

(2)

According to Newton’s law, let F be the resultant force applied on the ball, then we decompose F into the horizontal direction and the vertical direction which is given as

$$\begin{aligned} {F_x}= & {} -\, m\ddot{x} + ml\ddot{\theta } \hbox {cos}\theta - ml{\dot{\theta }^2}\hbox {sin}\theta + \left( {k\theta + c\dot{\theta } } \right) \hbox {cos}\theta /l \end{aligned}$$

(3)

$$\begin{aligned} {F_y}= & {} mg - ml{\dot{\theta } ^2}\hbox {cos}\theta - ml\ddot{\theta } \hbox {sin}\theta - \left( {k\theta + c\dot{\theta } } \right) \hbox {sin}\theta /l \end{aligned}$$

(4)

To mathematically describe the friction force which may induce stick-slip vibrations, two friction models are considered here. For the resistance force between the capsule and the sliding surface, the anisotropic Coulomb’s dry friction model [35] is expressed as

$$\begin{aligned} f = \left\{ {\begin{array}{ll} {\mu _ + }(Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) &{}\quad \hbox {for}\;\dot{x} > 0\\ {f_0},&{}\quad \hbox {for}\;\dot{x} = 0\\ - \,{\mu _ - }(Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) &{}\quad \hbox {for}\;\dot{x} < 0 \end{array}} \right. \end{aligned}$$

(5)

where $\mu _+$ and $\mu _-$ are the friction coefficients. The resistance force does not necessarily turn to zero when the relative velocity of the capsule is zero; thus, $f_0$ falls into the range of $\left[ { -\, {\mu _ - }(Mg + {F_y}} \right) \hbox {Sign}\left( {\dot{x}} \right) ,{\mu _ + }(Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) ]$.

In terms of the viscous friction induced by the motor at the pivot, heuristically, we adopt the anisotropic linear model [36] which is a piecewise-linear function given by

$$\begin{aligned} {f_p} = \left\{ {\begin{array}{l} {{c_ + }\dot{\theta },\quad \dot{\theta } \ge 0}\\ {{c_ - }\dot{\theta },\quad \dot{\theta } < 0} \end{array}} \right. \end{aligned}$$

(6)

where $c_+$ and $c_-$ are coefficients of the motor viscous friction at the pivot.

The sliding friction coefficients $\mu _+$, $\mu _-$ and the resistance coefficients $c_+$, $c_-$ are all positive constants, and in this work, we assume that symmetry exists in the friction model and resistance force, in other words, $\mu _+ =\mu _- =\mu$ and $c_+ =c_- =c$. It is worth mentioning that the contact interface is anisotropic in nature and the asymmetry characteristic may arise in the proposed system due to the physical and structural inconsistency of the system parameters. On the other hand, the friction force at rest $f_0$ is resulting from the sticking motion and largely relying on the magnitudes of the external forces. The non-symmetric friction models and the interconnection between $f_0$ and stick-slip motion are beyond the scope of the work here and will be studied in our future works.

2.3 Mathematical modelling

Based on the aforementioned assumptions and definitions, the governing equations of the vibro-driven system are derived using Euler–Lagrangian approach [37] described as

$$\begin{aligned} \frac{d}{{dt}}\frac{{\partial L\left( {{q_i},{{\dot{q}}_i}} \right) }}{{\partial {{\dot{q}}_i}}} - \frac{{\partial L\left( {{q_i},{{\dot{q}}_i}} \right) }}{{\partial {q_i}}} + f' = {Q_i} \end{aligned}$$

(7)

where $q_i$ are the generalized coordinates, $L\left( {{q_i},{{\dot{q}}_i}} \right) = E\left( {{q_i},{{\dot{q}}_i}} \right) - V\left( {{q_i}} \right)$ is the Lagrangian function, E and V denote the kinetic energy and potential energy, f describes the friction and resistant forces, $Q_i$ is the generalized externally applied force or moment. Applying (7) into the proposed system and letting $q_1 =\theta$, $q_2 =x$, we have

$$\begin{aligned} E= & {} \frac{1}{2}M{\dot{x}^2} + \frac{1}{2}m\left[ {{{\left( {\dot{x} - l\dot{\theta } \hbox {cos}\theta } \right) }^2} + {{\left( { -\, l\dot{\theta } \hbox {sin}\theta } \right) }^2}} \right] \end{aligned}$$

(8)

$$\begin{aligned} V= & {} \frac{1}{2}k\theta ^{2}+mgl\hbox {cos}\theta \end{aligned}$$

(9)

$$\begin{aligned} f^{\prime }= & {} \left[ {{\begin{array}{l} {f_p } \\ f \\ \end{array} }} \right] , Q_i =\left[ {{\begin{array}{l} {Bu} \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(10)

where $B\in R^{n\times n}$ is a constant matrix.

Therefore, taking the derivation of Eqs. (8)–(10) with respect to $\theta$ and x, respectively, the equations of motion of the vibro-driven capsule system yield as

$$\begin{aligned}&m{l^2}\ddot{\theta } - ml\hbox {cos}\theta \ddot{x} - mgl\hbox {sin}\theta + k\theta + c\dot{\theta } = A\hbox {cos}\left( {\varOmega t} \right) \end{aligned}$$

(11)

$$\begin{aligned}&\quad -\, ml\left[ {\hbox {cos}\theta + \mu \hbox {sin}\theta \hbox {Sign}\left( {\dot{x}} \right) } \right] \ddot{\theta } + \left( {M + m} \right) \ddot{x} + ml\left[ {\hbox {sin}\theta - \mu \hbox {cos}\theta \hbox {Sign}\left( {\dot{x}} \right) } \right] {\dot{\theta } ^2} \nonumber \\&\quad +\, \mu \left[ {\left( {M + m} \right) g - \left( {k\theta + c\dot{\theta } } \right) \hbox {sin}\theta /l} \right] \hbox {Sign}\left( {\dot{x}} \right) = 0 \end{aligned}$$

(12)

Defining a set of non-dimensional parameters as follows

$$\begin{aligned} \tau= & {} \omega _n t, X=x/l, \omega _n =\sqrt{g/l}, \omega =\varOmega /\omega _n , \nonumber \\ \lambda= & {} M/m, \rho =k/\left( {ml^{2}\omega _n ^{2}} \right) , \upsilon =c/\left( {ml^{2}\omega _n } \right) , h=A/\left( {ml^{2}\omega _n ^{2}} \right) \end{aligned}$$

(13)

where $\omega _n$ is the natural frequency of the pendulum. This transformation eases the numeric solution and allows for convenient comparison between the dynamic responses at different control parameters.

Adopting Eqs. (13) and (14) into Eqs. (11) and (12) and defining derivatives with respect to $\tau$ through the chain rule lead to the following mass-normalized and reduced form of Eqs. (11) and (12)

$$\begin{aligned}&\ddot{\theta } - \hbox {cos}\theta \ddot{X} - \hbox {sin}\theta + \rho \theta + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(14)

$$\begin{aligned}&\quad -\, \left[ {\hbox {cos}\theta + \mu \hbox {sin}\theta \hbox {Sign}\left( {\dot{X}} \right) } \right] \ddot{\theta } + \left( {\lambda + 1} \right) ~\ddot{X} + \left[ {\hbox {sin}\theta - \mu \hbox {cos}\theta \hbox {Sign}\left( {\dot{X}} \right) } \right] {\dot{\theta } ^2} + \mu \left[ \left( {\lambda + 1} \right) \right. \nonumber \\&\quad \left. -\, \left( {\rho \theta + \upsilon \dot{\theta } } \right) \hbox {sin}\theta \right] \hbox {Sign}\left( {\dot{X}} \right) = 0 \end{aligned}$$

(15)

which represent the motion of the driving pendulum and the base, respectively.

It is noted that the derivations above are conducted with respect to the dimensionless time $\tau$ and accordingly the configuration variables in the dimensionless time coordinate evolved as $\left\{ {\mathfrak {H}} \right\} =\left[ {\xi _1 \xi _2 } \right] ^{T}=\left[ {\theta X} \right] ^{T}$. The above equations of motion are a non-autonomous system consisting of coupled, nonlinear second-order differential equations. The driving force is applied to the pendulum subsystem and transformed to the base subsystem through dynamic coupling, which indicates the underactuated characteristic of the proposed system. Prior to numerical integration and analysis, the scaled governing equations need to be allocated in the state space.

Defining the state vector in an extended phase space as

$$\begin{aligned} S:= & {} \left( {y_1 ,y_2 ,y_3 ,y_4 ,\tau } \right) \in \mathfrak {R}^{4\times 1}\times {\mathcal {S}}^{1\times 1} \nonumber \\:= & {} \left( {\theta ,\dot{\theta } ,X,\dot{X},\tau } \right) \in {\mathfrak {R}^{4 \times 1}} \times {{\mathcal {S}}^{1 \times 1}} \end{aligned}$$

(16)

with the control parameters of the proposed system

$$\begin{aligned} {\mathcal {P}} := \left( {h,\omega ,\lambda ,\rho ,\upsilon } \right) \in {{\mathcal {Q}}^{5 \times 1}} \times {{\mathcal {S}}^{1 \times 1}} \end{aligned}$$

(17)

Decoupling and reorganizing Eqs. (14) and (15), we have a set of four first-order differential equations in compatible with the state vector defined in Eq. (16), which is given as

$$\begin{aligned} \left[ {\begin{array}{c} {{{\dot{y}}_1}\left( \tau \right) }\\ {{{\dot{y}}_2}\left( \tau \right) }\\ {{{\dot{y}}_3}\left( \tau \right) }\\ {{{\dot{y}}_4}\left( \tau \right) } \end{array}} \right] = \left[ {\begin{array}{cccc} 0&{}\quad 1&{}\quad 0&{}\quad 0\\ {{A_{21}}/\Delta }&{}\quad {{A_{22}}/\Delta }&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ {{A_{41}}/\Delta }&{}\quad {{A_{42}}/\Delta }&{}\quad 0&{}\quad 0\\ \end{array}} \right] \left[ {\begin{array}{c} {{y_1}\left( \tau \right) }\\ {{y_2}\left( \tau \right) }\\ {{y_3}\left( \tau \right) }\\ {{y_4}\left( \tau \right) } \end{array}} \right] + \left[ {\begin{array}{c} 0\\ {{B_2}/\Delta }\\ 0\\ {{B_4}/\Delta } \end{array}} \right] \end{aligned}$$

(18)

where

• $A_{21} =-\,\rho \left( {\lambda +1} \right) +\mu \rho \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) \hbox {cos}y_1 ,$

• $A_{22} =-\,\upsilon \left( {\lambda +1} \right) +\left[ {\mu \hbox {cos}y_1 \hbox {Sign}\left( {y_4 } \right) -\hbox {sin}y_1 } \right] y_2 \hbox {cos}y_1 +\mu \upsilon \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) \hbox {cos}y_1 ,$

• $A_{41} =-\,\rho \left[ {\hbox {cos}y_1 +\mu \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) } \right] +\mu \rho \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) ,$

• $A_{42} =\left[ {\mu \hbox {cos}y_1 \hbox {Sign}\left( {y_4 } \right) -\hbox {sin}y_1 } \right] y_2 -\upsilon \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) -\upsilon \left[ {\hbox {cos}y_1 +\mu \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) } \right] ,$

• $B_2 =-\,\mu \left( {\lambda +1} \right) \hbox {Sign}\left( {y_4 } \right) \hbox {cos}y_1 +\left( {\lambda +1} \right) \hbox {sin}y_1 +\left( {\lambda +1} \right) h\hbox {cos}\left( {\omega \tau } \right) ,$

• $B_4 =-\,\mu \left( {\lambda +1} \right) \hbox {Sign}\left( {y_4 } \right) +\left[ {\hbox {cos}y_1 +\mu \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) } \right] \hbox {sin}y_1 +\left[ {\hbox {cos}y_1 +\mu \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) } \right] h\hbox {cos}\left( {\omega \tau } \right) ,$

• $\Delta =\left( {\lambda +1} \right) -\hbox {cos}y_1 \left[ {\hbox {cos}y_1 +\mu \hbox {sin}y_1 \hbox {Sign}\left( {y_4 } \right) } \right]$.

3 Nonlinear dynamic analysis

The definitions of dry frictions given in Sect. 2 reveal that the absence and presence of stick-slip motion are in compatible with the relationship between the values of $F_x$ and the region $\left[ { -\, {\mu _ - }(Mg + {F_y}} \right) \hbox {Sign}\left( {\dot{x}} \right) ,{\mu _ + }(Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) ]$. In this section, we assume that $F_x$ is outside the above region for the situation which the stick-slip effect is absent. Accordingly, the conditions are given by

$$\begin{aligned} {F_x} > \mu (Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) \,\mathrm{{or}}\,{F_x} < - \mu (Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) \end{aligned}$$

(19)

The stick-slip motion of the capsule system will be investigated in Sect. 4. The solutions and their stabilities play a vital role in determining the transient response of the vibro-driven capsule system proposed here. In dynamical systems, bifurcation plays an important role in the creations and annihilations of equilibriums and the periodic solutions. The advantage is that this technique employs a visual interpretation of how the dynamic behaviours are affected by the system parameters and how the stability of solutions changes accompanied by the varying parameters. For problems involving oscillatory motion, the solutions in this section are numerically integrated in MATLAB using the Euler–Cromer method, which conserves energy over each complete period of the motion.

In terms of the behavioural dependence of solutions on the system parameters, the paths should be monitored when parameters vary. Bifurcation analysis is then carried out to achieve traces of the solutions, respectively, against the system parameters. First, for each parameter value, the specific state variable is calculated as a function of dimensionless time $\tau$. To achieve steady-state responses, the first 100 driving periods are discarded so that the initial transients have decayed away, then the state variable is plotted as a function of system parameter. For a set of parameter values which are slightly increased, the bifurcation scenario is studied subject to the selected parameters. Second, the first return Poincaré map is created and projected, respectively, on the reliable axis, considering the boundedness of the state variables. The procedure is then repeated over a reasonably large range of values of parameters in small steps.

3.1 Periodic system responses

For linear systems, the understanding of their solutions is well-established, the affine map from the output to the input is always available based on the linear superposition principles. And the quantitative changes in the system parameters give rise to quantitative changes in the system response. Nevertheless, they lose validity for nonlinear systems. For nonlinear systems, the changes in system parameters lead to qualitative variations like bifurcation phenomena. The aim of this section is to demonstrate that the vibration-driven capsule system results in a variety of responses and identify the most suitable qualitative motion for the forward progression of the capsule system.

The system responses are portrayed through the trajectories on time coordinate and phase plane, and Poincaré sections. Both of the actuated and passive subsystems are taken into consideration. For periodic solutions, the time histories of the driving pendulum and the capsule are repeating with time. Existing as hyper-surface in the state space which is transverse to the dynamic manifold, Poincaré sections present a qualitative evaluation of the dynamic response, which implies that the solution of the dynamic system is sampled for every excitation period.

Parameters employed in the numerical simulation in Sect. 3.1 are provided in Table 1, parameters used in the dynamic analysis of elasticity and viscosity, and the analysis of stick-slip motion are given in Table 2, all as referenced throughout the work. Other parameters which are not provided below can be found in the text.

Table 1 Parameter sets for numerical simulation

Table 2 Parameter sets for influence of elasticity and viscosity and stick-slip motion example

The periodic responses are recorded through numerical integration of Eq. (18) for various combinations of parameters. Figure 2 presents typical periodic responses obtained from parameter set 1 (Table 1). Figure 2a, c, respectively, depicts the motion trajectories of the driving pendulum and the capsule on time coordinate; on the other hand, their counterparts on phase plane are portrayed in Fig. 2b, d. It is noted that the periodic response consists of initial transient and steady-state response as observed in Fig. 2.

Fig. 2

Periodic trajectories on time coordinate and phase plane of the driving pendulum (a, b) and the capsule (c, d)

3.2 Influence of the elasticity $\rho$

The stiffness coefficient is firstly studied as the branching parameter, which essentially gives an index to the influence of elasticity on the dynamic response. The parameter dependence is apparently depicted as bifurcation diagrams in Fig. 3 obtained from parameter set 1 (Table 2). The influence of the elasticity $\rho$ on angular displacement and average capsule progression per period are shown in Fig. 3a, b, respectively. It is also observed from Fig. 3a that a grazing of angular displacement occurs at $\rho =0.25$, and thereafter the angular displacement largely decreases as $\rho$ increases. As a locomotion system, the average locomotion speed is of vital importance; in this regard, the average capsule progression per period of excitation is characterized and shown in Fig. 3b, in which the global maximum and minimum average progressions points are recorded at $\rho =0.9$ and $\rho =0.25$, respectively. A pair of local maximal and minimal points of average progressions is also identified at $\rho =0.65$ and $\rho =0.75$. A sequence of trajectories on the phase plane and Poincaré maps are depicted in Fig. 4. The locations of Poincaré sections $P_b$, $P_c$ and $P_d$ are marked by red dot. Our numerical study shows that after the initial transients have decayed away, the pendulum employs steady-state periodic motions which would repeat subsequently.

Fig. 3

Bifurcation diagrams under varying elasticity: a angular displacement; b average capsule progression per period

Fig. 4

Trajectories of the driving pendulum on phase plane and time histories. a $\rho =0.9$. b $\rho =2.5$. c $\rho =5.0$

Following a similar procedure as the pendulum subsystem, the time contained phase diagram of the capsule motion is shown in Fig. 5, in which the average progressive velocity $y_4$ is plotted as a function of capsule displacement $y_{3}$ and time. The initial transient phases are also plotted here to present the traces of the capsule. It is straightforward to see that for a small stiffness coefficient, not sufficient energy is stored in the spring and injected into the capsule to enhance its progression, and the capsule acts like atypical reciprocating motions and eventually locomote within a certain boundary after initial transient has decayed away. On the other hand, for the parameters within the periodic range, as seen in Fig. 5b, the capsule behaves repeatable steady-state intermittent forward progression.

Fig. 5

Time contained phase diagram of the capsule motion. a $\rho =0.7$. b $\rho =1.0$

The comparison of capsule progression in the presence of varying stiffness coefficient is shown in Figs. 6 and 7. It is observed that at relatively small values of $\rho$ $(\rho =0.5,0.7)$, the capsule behaves undesirable motions (oscillation) after the initial transients decays, which are equivalent to the stiffness coefficients of $0.2001\,({\hbox {N}*\hbox {m}*\hbox {rad}^{-1}})$ and $0.2802\,({\hbox {N}*\hbox {m}*\hbox {rad}^{-1}})$. When the value of stiffness coefficient increases, travelling distance of the capsule increases and then decreases monotonically. The best progression of the capsule is obtained for the periodic response, and the optimal value is recorded at $\rho =0.9$, which is equivalent to the stiffness coefficient of $0.36\,({\hbox {N}*\hbox {m}*\hbox {rad}^{-1}})$.

Fig. 6

Time histories of the displacements of the capsule obtained for varying stiffness coefficient: $\rho =0.9$, $\rho =1.5$ and $\rho =5.0$

Fig. 7

Time histories of the displacements of the capsule obtained for $\rho =0.5$ and $\rho =0.7$, respectively

It is worth mentioning that $\rho$ represents the stiffness coefficient k in un-scaled coordinate and contributes energy effectiveness to the capsule system. The boundaries of steady-state system response are portrayed precisely with respect to the varying stiffness coefficient. Basically, the dependent analysis on varying stiffness shows an optimal parametric selection of the torsion spring to achieve desirable performance and avoid undesirable motions. The undesirable motions are numerically perceived for relatively lower stiffness coefficient. It is illustrated that the system response approaches to smaller stiffness coefficient at atypical instants in time and simultaneously pinpoints higher harmonics during these smaller stiffness values. Replicated motion irregularity is also observed in the undesirable motion region with respect to part of the time history. On the other hand, difference at the steady-state motions exists in the shapes and the Poincaré sections of the limit cycles, which result in varying performance.

3.3 Influence of viscosity $\upsilon$

The influence of viscosity $\upsilon$ is studied as the other branching parameter, which describes, in nature, how the viscous coefficient c affects the system dynamics qualitatively. The bifurcation diagrams are shown in Fig. 8 obtained from parameter set 2 in Table 2. Herein, accompany with the augmentation of damping coefficient, the system response keeps behaving period-one motion for $\upsilon \in \left[ {0.01,5.1} \right]$. From Fig. 8a, it is observed that as $\upsilon$ increases, the angular displacement decreases monotonously. However, it seems insufficient to identify and conclude the effects of $\upsilon$ on the capsule performance through the observation on the pendulum subsystem. Therefore, the average capsule progression per period of excitation is portrayed in Fig. 8b, where the maximum average progression point is recorded at $\upsilon =1.3$. Interestingly from Fig. 8b, it is noted that for value $\upsilon \in \left( {0,1.3} \right]$, the capsule progression increases monotonically as $\upsilon$ augments; on the other hand, for $\upsilon \in \left( {1.3,5.0} \right]$, the viscosity acts negative roles by decreasing the capsule’s forward progression. The identified optimal viscous value is critical for the system and controller design. The trajectories of the pendulum on the phase plane and Poincaré maps are shown in Fig. 9. The locations of Poincaré sections $P_a$, $P_b$, $P_c$ and $P_d$ are marked by red dots. The time histories of the angular displacement in Fig. 9 are important to appreciate the dynamic behaviours illustrated. It is noted that after the initial transients have decayed, the pendulum employs repeatable steady-state periodic motion.

Fig. 8

Bifurcation diagrams of the capsule robot under varying viscosity: a angular displacement; b average capsule progression per period

Fig. 9

Trajectories of the driving pendulum on phase plane and time histories. a $\nu =0.6$. b $\nu =1.5$. c $\nu =2.0$. d $\nu =3.5$

Furthermore, to examine the dynamic behaviour of the entire capsule system, we construct the 3D plotted time contained phase diagram of the capsule motion as shown in Fig. 10. The repeatable steady-state progression is perceived for different damping coefficients after the initial transient. It is illustrated that the larger $\nu$ is employed, the less in progression the capsule performs.

Fig. 10

Time contained phase diagram of the capsule motion. a $\nu =0.6$. b $\nu =3.0$

The comparison of capsule progression in the presence of varying damping coefficient is present in Fig. 11. It is revealed that the proposed system behaves steady-state progression after the initial transient is decayed away, and the capsule progression decreases monotonically accompanied by the augmented damping coefficient. Still, the best progression of the capsule can be obtained for the periodic response and the optimal value is recorded at $\nu =1.3$, which is equivalent to the damping coefficient of $c=0.0923\left( {\hbox {kg}*\hbox {m}^{2}*\hbox {s}^{-1}*\hbox {rad}^{-1}} \right)$.

Fig. 11

Time histories of the displacements of the capsule obtained for: $\nu =0.6,3.5$ and $\nu =5.0$

It is noted that the dependence analysis on varying damping illustrates the effect of the limiting factor on the system dynamics, which heuristically can be adopted to optimize the injection of damping to achieve desired performance and avoid undesired responses. On the other hand, the different shapes of periodic orbits and the locations of Poincaré sections result in varying performance.

It is revealed that complicated interactions exist in the dynamics of the proposed system which are resulted from the coexisting periodic orbits and bifurcations. Moreover, it is noted that the optimal progression of the capsule results from the dynamic behaviour of the periodic response, which is achieved through comparison of the capsule displacements. Consequently, appropriate selection of the control parameters can be determined to achieve the optimal progression of the capsule system.

4 Remarks on stick-slip motions

In this section, the situations that stick-slip effect dominates the system performance are primarily considered. The critical equilibrium and the dynamic behaviours around are identified; the conditions for stick-slip motions in order to achieve a always forward motion of the capsule are studied.

4.1 On the critical equilibrium

As stated, the analysis here is primarily concerned with the dynamics of the proposed system near the regime when the translational mode (slipping phase) of the capsule is resonantly excited, it is natural to firstly identify the local dynamic behaviours of the driving pendulum and scrutinize its equilibrium. This subsection falls into the sticking regime when the force applied in the horizontal direction does not exceed the threshold of the dry friction force and the base keeps stationary. Therefore, the reduced model of the driving pendulum subject to gravity torque, elastic force, viscous damping and harmonic force is considered. Recalling Eq. (14) and letting $\ddot{X} = 0$, we have

$$\begin{aligned} \ddot{\theta } - \,\hbox {sin}\theta + \rho \theta + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(20)

The governing equation is invariant based on the symmetries given by

$$\begin{aligned} \tau\rightarrow & {} \tau +\tau _0 \hbox { (Time translation)} \end{aligned}$$

(21)

$$\begin{aligned} \tau\rightarrow & {} -\,\tau \hbox { (Time reversibility)} \end{aligned}$$

(22)

$$\begin{aligned} \theta\rightarrow & {} -\,\theta \hbox { (Space\, reflection)} \end{aligned}$$

(23)

The dynamics of the driving pendulum assumes that the energy dissipation is increasing in accordance with the growing damping. The spring restoring force can be proved to be quite linear so that the only source of nonlinearity is in the gravitational term.

The approximate steady-state periodic solution for the reduced system can be conveniently achieved by the approach of harmonic balance [38]. Therefore, the solution is assumed as

$$\begin{aligned} \theta =A_1 \hbox {cos}\left( {\omega \tau +\varphi } \right) \end{aligned}$$

(24)

where $A_1$ is the amplitude of the periodic solution.

Furthermore, we introduce the term critical elasticity, which denotes the critical coefficient of the torsion spring subject to elasticity and gravity given by

$$\begin{aligned} k_\mathrm{critical} =mgl \end{aligned}$$

(25)

The notable difference between three types of correlations between k and $k_\mathrm{critical}$ can be perceived from the forms of potential well shown in Fig. 12 which determines the equilibrium and equilibrium angular positions.

Fig. 12

Potential well as a function of angular displacement for $k>mgl$ (red solid line), $k=mgl$ (blue dashed line) and $k<mgl$ (green dotted line). (Color figure online)

The potential energy of the driving pendulum as a function of the angular displacement is a quadratic function given by

$$\begin{aligned} U\left( t \right) =\frac{1}{2}k\theta ^{2}\left( t \right) +mgl\hbox {cos}\theta \left( t \right) \end{aligned}$$

(26)

An arbitrary constant in U can be chosen leading to $U\left( 0 \right) =0$. Using Taylor Series to approximate the equation above yields

$$\begin{aligned} U\left( t \right) =mgl+\frac{1}{2}\left( {k-mgl} \right) \theta ^{2}\left( t \right) +\frac{1}{24}mgl\theta ^{4}\left( t \right) +{\mathcal {O}}\left( {\theta \left( t \right) ^{2}} \right) \end{aligned}$$

(27)

which is the potential for the Duffing oscillator. For $k/mgl>1$, the potential evolved from Eq. (27) is a single well; for $k/mgl<1$, the potential evolved from Eq. (27) is a double well.

4.1.1 Dynamic behaviours around the critical elasticity

Revisiting Eq. (13), the non-dimensionalized stiffness coefficient becomes

$$\begin{aligned} \rho =k/k_\mathrm{critical} \end{aligned}$$

(28)

There are three regions of motion are identified as follows, which are calculated from Eq. (19).

Region I $\rho >1$

In this region, when $\theta \ll 1$, a linear equation for the harmonic motion of the driving pendulum can be easily achieved as

$$\begin{aligned} \ddot{\theta } + \left( {\rho - 1} \right) \theta + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(29)

On the other hand, when $\theta$ falls into other range in this region, the smallest nonlinearities are taken into consideration based on Taylor series expansion; therefore, the motion of the driving pendulum in scaled coordinate is given by

$$\begin{aligned} \ddot{\theta } + {\omega _0}^2\theta + \frac{1}{6}{\theta ^3} + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(30)

where $\omega _0 =\sqrt{\rho -1}$.

Accordantly, a cubic oscillator is achieved, in which the period of motion decreases in accordance with the amplitude due to the positive value of the cubic term.

Region II $\rho <1$

The motion of equation of the driving pendulum in this region is given by

$$\begin{aligned} \ddot{\theta } + {\omega _0}^2\theta + \frac{1}{6}{\theta ^3} + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(31)

where $\omega _0 =\sqrt{1-\rho }$.

The symmetrically placed stable equilibrium angles can be derived as follows

$$\begin{aligned} \theta _e =0,\pm \, \sqrt{6\left( {1-\rho } \right) } \end{aligned}$$

(32)

Revisiting the definition of critical elasticity, the nonzero solutions in Eq. (28) in region III become

$$\begin{aligned} \theta _e =\pm \, \sqrt{6\frac{k_\mathrm{critical} -k}{k_\mathrm{critical} }\approx }\left( {k_\mathrm{critical} -k} \right) ^{1/2} \end{aligned}$$

(33)

which demonstrates the equilibrium close to the bifurcation. The square root exponent is conveniently falling into the Landau mean-field theory for second-order phase transitions [39, 40], which indicates the existence of pitchfork bifurcation.

Region III $\rho =1$

This is a region in which a critical manifold arises and the linearities disappear, which is given as

$$\begin{aligned} \ddot{\theta } + \frac{1}{6}{\theta ^3} + \upsilon \dot{\theta } = h\hbox {cos}\left( {\omega \tau } \right) \end{aligned}$$

(34)

4.1.2 Numerical validation

Different phase portraits are presented to demonstrate the dynamic behaviour identified in the aforementioned three regions. The behaviour of the driving pendulum is portrayed as a function of $\rho$.

The comparison is shown in Fig. 13; it is noted that the trajectories are mostly closed oscillations when the angular displacement is small. For $\rho >1$ in Fig. 13a, there is only one stable equilibrium, the trajectories are mostly oscillations when the angular displacements are small. Figure 13b portrays the equilibrium when $\rho <1$, in this regard, the zero equilibrium is a unstable one, beside this there are two symmetrically stable equilibrium angles; thus, liberations appear between two bifurcated angular position. For the critical situation $\rho =1$, the driving pendulum is wandering between the equilibrium angular positions as shown in Fig. 13c.

Fig. 13

Phase portraits of the driving pendulum. a $\rho >1$. b $\rho <1$. c $\rho =1$

4.2 Conditions for steady-state stick-slip motion

According to the definition of stick-slip motion, it can be elaborately utilized that the capsule has to be remained stationary (sticking) after each cycle of forward motion (slipping) to achieve an always forward progression.

In this regard, the capsule system remains stationary on the ground without any sliding during the return trip in each cycle. Thus, the force of the inverted pendulum applied on the base in the horizontal direction has to be less than the maximal static friction, that is,

$$\begin{aligned} \left| {{F_x}} \right| \le \mu (Mg + {F_y})\hbox {Sign}\left( {\dot{x}} \right) \end{aligned}$$

(35)

which gives a dimensionless inequality condition as

$$\begin{aligned} \left| {\hbox {cos}\theta \ddot{\theta } - \hbox {sin}\theta {{\dot{\theta } }^2} + \rho \theta \hbox {cos}\theta } \right| \le \mu \left[ {\left( {\lambda + 1} \right) - \hbox {sin}\theta \ddot{\theta } - \hbox {cos}\theta {{\dot{\theta } }^2} - \rho \theta \hbox {sin}\theta } \right] \end{aligned}$$

(36)

Furthermore, the interactive force from vertical $F_y$ is implicitly restricted to be non-negative under the constraint above, which essentially in virtue of the unidirectional property of the ground.

Lemma 1

The non-sliding motion for the base will be achieved only if the following inequality is satisfied

$$\begin{aligned} \theta \left( {\ddot{\theta } + {{\dot{\theta } }^2}} \right) \le \varpi \vartheta \end{aligned}$$

(37)

where

$$\begin{aligned} \varpi =\left( {\lambda +1} \right) ^{2}\!/2\rho ,\vartheta =\mu ^{2}/2\left( {\mu ^{2}+1} \right) \end{aligned}$$

Proof

Utilizing the forces in horizontal and vertical directions, removing the absolute value sign and considering one side of the inequality that

$$\begin{aligned} \hbox {cos}\theta \ddot{\theta } - \hbox {sin}\theta {\dot{\theta } ^2} + \rho \theta \hbox {cos}\theta \le \mu \left[ {\left( {\lambda + 1} \right) - \hbox {sin}\theta \ddot{\theta } - \hbox {cos}\theta {{\dot{\theta } }^2} - \rho \theta \hbox {sin}\theta } \right] \end{aligned}$$

(38)

Recombining the elements above gives

$$\begin{aligned} \left( {\mu \hbox {sin}\theta \ddot{\theta } + \hbox {cos}\theta \ddot{\theta } } \right) + \left( {\mu \hbox {cos}\theta {{\dot{\theta } }^2} - \hbox {sin}\theta {{\dot{\theta } }^2}} \right) + \left( {\mu \rho \theta \hbox {sin}\theta + \rho \theta \hbox {cos}\theta } \right) \le \mu \left( {\lambda + 1} \right) \end{aligned}$$

(39)

According to the auxiliary angle formula,

$$\begin{aligned}&\sqrt{{{\left( {\mu sin\theta \ddot{\theta } } \right) }^2} + {{\left( {\hbox {cos}\theta \ddot{\theta } } \right) }^2}} \hbox {sin}\left( {\theta + \alpha '} \right) + \sqrt{{{\left( { - \hbox {sin}\theta {{\dot{\theta } }^2}} \right) }^2} + {{\left( {\mu \hbox {cos}\theta {{\dot{\theta } }^2}} \right) }^2}} \hbox {sin}\left( {\theta + \beta '} \right) \nonumber \\&\quad + \sqrt{{{\left( {\mu \rho \theta \hbox {sin}\theta } \right) }^2} + {{\left( {\rho \theta \hbox {cos}\theta } \right) }^2}} \hbox {sin}\left( {\theta + \gamma '} \right) ) \le \mu \left( {\lambda + 1} \right) \end{aligned}$$

(40)

where

$$\begin{aligned} \alpha ' = \hbox {arctan}1/\mu , \beta ' = \hbox {arctan}\left( { - \,\mu } \right) , \gamma ' = \hbox {arctan}1/\mu \end{aligned}$$

Enlarging the inequality gives a sufficient condition that

$$\begin{aligned} \sqrt{{\mu ^2} + 1} \left( {\ddot{\theta } + {{\dot{\theta } }^2} + \rho \theta } \right) ) \le \mu \left( {\lambda + 1} \right) \end{aligned}$$

(41)

Then, using the Arithmetic geometric inequality theorem gives

$$\begin{aligned} 2\sqrt{{\mu ^2} + 1} \sqrt{\rho \theta \left( {\ddot{\theta } + {{\dot{\theta } }^2}} \right) }\le & {} \mu \left( {\lambda + 1} \right) \end{aligned}$$

(42)

$$\begin{aligned} \theta \left( {\ddot{\theta } + {{\dot{\theta } }^2}} \right)\le & {} \frac{{{{\left[ {\mu \left( {\lambda + 1} \right) } \right] }^2}}}{{4\rho \left( {{\mu ^2} + 1} \right) }} \end{aligned}$$

(43)

$\square$

Remark 1

It is noted that Lemma 1 is proposed to characterize the dynamic constraints for stick-slip forward motions through analytical analysis. The proposed motion strategy generally has two stages: a forward motion stage (slipping) and a resting motion stage (sticking). Equation (43) is derived as a condition that the capsule remains stationary after each cycle of forward motion to obtain an always forward locomotion. This equation is used to optimize and parameterize a prescribed motion trajectory generator, which contains seven motion phases/parameters.

4.3 Numerical example

The numerical example is calculated for the capsule system behaving stick-slip motion. The time histories of the capsule progression for one and ten cycles are shown in Fig. 14 obtained from parameter set 3 in Table 2.

Fig. 14

Time history of the capsule progression for one cycle (a) and ten cycles (b)

Through numerical programme using fourth-order Runge–Kutta algorithm, it is clearly shown in Fig. 14 that one cycle of progressive motion is mainly component with slipping phase and sticking phase. The capsule system performs intermittent forward progression in the presence of the external force and the frictions. One can perceive from Fig. 14 that the capsule moves about 4.2 cm in one cycle with the average velocity about 1.2 cm/s.

It is worth mentioning that there is a time interval for the transition between slipping and sticking, which may induce backward motions and affect the net progression of the capsule. Therefore, reasonably shortening or eliminating the transition time will definitely improve the performance of the capsule system from the energy point of view. This optimization issue is beyond the scope of the work here and will be studied in our future works.

5 Conclusions

In this paper, the nonlinear dynamics of a mobile capsule system with an internally driven pendulum has been studied. As a self-propelled encapsulated micro-mechanism, a coupled translation-rotation model for the micro-actuator has been proposed. Achieving a thorough understanding of the nonlinear phenomena associated with translation-rotation model is essential for condition surveillance and suitable design of vibration-driven (joint-actuated) machinery. Appropriate design is capable of avoiding potentially dangerous and dramatically improving the system performance. Two friction models have been employed to describe the sliding friction and resistance force. The governing equations are non-dimensionalized in time and normalized with respect to mass. Then, a decoupling procedure has been conducted to place the coupled nonlinear differential equations in a state-space representation which is suitable for numeric integration.

Thereafter, a profile of typical periodic responses has been presented for the system studied here. The influences of elasticity and viscosity have been emphasized globally, particularly for the locomotive system. The bifurcation diagrams are with the most represented periodic solutions and demonstrate the thresholds of periodic motions. Our numerical studies have revealed that the behaviour of the system is mainly periodic, and the best progression can be achieved by an optimization of the system parameters. Through the investigation of elasticity $\rho$, a large region of periodic motions have been found. It has been observed from that a grazing of angular displacement occurs at $\rho =0.25$, and thereafter the angular displacement largely decreases as $\rho$ increases. As a locomotion system, the average locomotion speed is of vital importance, in this regard, the average capsule progression per period of excitation has been characterized, in which the global maximum and minimum average progressions points have been recorded at $\rho =0.9$ and $\rho =0.25$, respectively. A pair of local maximal and minimal points of average progressions has also been identified at $\rho =0.65$ and $\rho =0.75$. The bifurcation analysis on the varying damping coefficient $\upsilon$ indicated that the system behaves periodic motion for all the considered set of parameter values, and the maximum average progression point has been recorded at $\upsilon =1.3$. Interestingly, it is noted that for value $\upsilon \in \left( {0,1.3} \right]$, the capsule progression increases monotonically as $\upsilon$ augments; on the other hand, for $\upsilon \in \left( {1.3,5.0} \right]$, the viscosity acts negative roles by decreasing the capsule’s forward progression.

Subsequently, a discussion on stick-slip motion has been presented in order to achieve an always forward progression of the capsule system. Different regions of oscillations of the driving pendulum have been identified, and the attentions were focused on the critical region where linearities are absent and nonlinearities dominate the dynamic behaviour of the pendulum. Additionally, the conditions for stick-slip motion have been investigated. The numerical results have demonstrated the nonlinear dynamics of the proposed system, and the need for future work in developing improved models which consider the non-symmetric anisotropic friction models, impact and uncertainties. Particularly, extensive attentions would focus on the analytical and experimental comparison and investigations, in which the current literature provides relatively few devotions.