Experimental verification of the vibro-impact capsule model

Abstract

In this paper, an experimental verification of the vibro-impact capsule model proposed by Liu et al. in (Int. J. Mech. Sci, 66:2–11; 2013a, Int. J. Mech. Sci, 72:39–54; 2013b, Int. J. Non-Linear Mech., 70, 30–46; 2015) is presented. The capsule dynamics is investigated experimentally by varying the stiffness of the support spring, and the frequency and the amplitude of excitation. The novel design of the experimental set-up is discussed, and comparisons between the experiments and numerical simulations are presented showing a good agreement. The conducted bifurcation analysis indicates that the behaviour of the system is mainly periodic and that a fine tuning of the control parameters can significantly improve the performance of the system. The main findings provide a better insight into the vibro-impact systems subject to nonlinear friction, and the experimental rig can be used to predict the dynamic behaviour of these systems.

1 Introduction

The encapsulated mobile mechanisms driven by autogenous internal force have been the subject of active scientific research in recent years, e.g. [4–6]. The virtue of such systems is that no external driving mechanism is required so that they can move independently in the complex environment. The driving principle of these systems is that the rectilinear motion of the capsule can be obtained by applying a harmonic force to its inner mass which leads to the entire capsule overcoming external resistance. Alternatively, a motion of the inner mass could be designed in order to generate the desired capsule dynamics, see for example [6, 7]. In such cases, the travel distance of the inner mass could be limited leading to complications in practical implementation (e.g. [4]). On the other hand, when the force is applied to the inner mass, the interaction between the capsule and the inner mass needs to be described, and Liu  et al.[1–3] used intrinsic stiffness and damping of the internal connection to consider overall dynamics of the capsule under applied harmonic force. In order to verify this modelling approach, a novel experimental rig was designed and manufactured, and an experimental study of the vibro-impact capsule system is presented in this paper. The capsule dynamics under variation of the stiffness ratio and the frequency and the amplitude of excitation are investigated, and comparisons between the experiments and numerical simulations are given. The bifurcation studies presented in this paper are carried out for a range of system parameters where physical arrangement is feasible. For example, varying the frequency of external excitation in the range of $\omega {\in }(0,0.4)$ allows to validate the results presented in [3] but also to demonstrate some new finding. Also, an ideal secondary linear spring assumption used in previous studies in [1–3] is discussed in this paper, and the implications for the presented experimental set-up are revealed.

The applications of the capsule system are broad ranging from medical inspection, engineering diagnosis to disaster rescues. Capsule endoscopy for gastrointestinal tract diagnosis is one of the core applications which has attracted significant attention from researchers in the past few years, see [8–10]. Self-propulsion using internal/external interactive force is an alternative for active capsule endoscopy. For example, Gao et al. [11] developed a magnetic propulsion system for driving capsule endoscope inside human body through external magnetic fields. A prototype of capsule robot propelled by internal interactive force and external friction was designed by Li et al. [4], and its velocity-dependent frictional resistance inside intestine was investigated in [12]. However, the detailed study of dynamics of the capsule for such an application has not been undertaken, though it would be essential for design and prototyping. Liu et al. [1] studied the dynamics of a vibro-impact capsule system, and it has been found that the best progression could be determined through bifurcation analysis and ensured by a careful choice of the system parameters, e.g. the stiffness ratio, and the frequency and the amplitude of the excitation. In [2], the dynamic analysis of the capsule system in various friction environments was performed, while in [3], forward and backward motion control of the system was investigated using a position feedback controller. This paper provides an experimental verification of the vibro-impact capsule model proposed in [1]. Comparisons between the experiments and numerical simulations show good agreement. The conducted bifurcation analysis indicates that the behaviour of the system is mainly periodic, and a fine tuning of the control parameters can significantly improve the performance of the system. Although the size of the experimental rig here is much larger than the prototypes in [4, 12], the re-scaling could be done using the nondimensionalised parameters of the mathematical model so that the results presented in this paper could be used for prototype design and fabrication.

Vibro-impact system is an interesting subject since it could present very rich and complex dynamical responses. In general, the experimental studies of such systems have been rather limited in the literature. Savi et al. [13] studied a single-degree-of-freedom oscillator with discontinuous support using numerical simulations and experimental validation. A linear oscillator undergoing impact with a secondary elastic support was investigated experimentally and semi-analytically for near-grazing conditions by Ing et al. [14]. In [15], experimental investigation of a vibro-impact system where an elastically mounted hammer impacted inside a cart that vibrated under a prescribed displacement was presented. However, all these experiments were concerned with only one non-smooth nonlinearity, namely impact, and none of them have considered friction as the second non-smooth nonlinearity of the system, though the systems with one-sided friction have been well studied numerically, e.g. [16–18]. In [19], Nguyen et al. studied theoretically and experimentally a vibro-impact moling rig, where both impacts and friction occur. The rig was mounted on a frictional guide rail, where the friction can be adjusted using a clamp bolt. Impacts were realised by placing a obstacle block on the path of the bar. Although both friction and impacts were considered in this work, the motion of the rig was restricted to forward motion and the stiffness during impact was constant. In the current work, the proposed design using a leaf spring allows to investigate the influence of impact stiffness on the system dynamics. In addition, we have investigated complex progression patterns including forward and backward, which have not been reported in the literature before.

The rest of this paper is organised as follows. In Sect. 2, experimental apparatus is introduced, and identification of physical parameters of the experimental rig is presented. In the next section, the mathematical modelling of the vibro-impact capsule system is conducted, which is followed by the experimental investigation of dynamical responses of the system under variations of different control parameters in Sect. 4. Experimental results are then compared with the numerical simulations using the proposed mathematical model. Finally, in Sect. 5, some conclusions are drawn.

Fig. 1

(colour online) a Photograph and b schematics of the experimental set-up showing the novel experimental rig where the internal impacts are controlled by the stiffness of the cantilever beam

2 Experimental apparatus and parameter identification

2.1 Experimental set-up

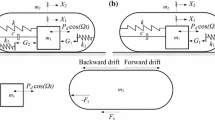
Investigations of the vibro-impact capsule system have been undertaken using a novel experimental rig presented in Fig. 1a, and the schematics of the experimental rig is shown in Fig. 1b. The capsule system consists of a linear DC servomotor mounted on a base frame which also holds a support spring with an adjustable stiffness $k_2$. The motor has a movable internal rod (serving as an inner mass) harmonically excited with the desired frequency and amplitude, ${\varOmega }$ and $P_d$ via the electromagnetic field provided by the coils in the motor. Once the motor is switched on, there is a resistance force keeping the rod in place, which nonlinearly depends on the displacement and velocity of the rod. Assuming that this force could be linearised around the capsule working point, it could be characterised by constant coefficients $k_1$ and c for the displacement and velocity, respectively. A gap, G exists between the rod and the support spring, and the rod contacts with the support spring when their relative displacement is equal to zero. The absolute displacement of the rod is $X_1$, and the absolute displacement of the base frame is $X_2$ which is measured by a linear variable differential transformer (LVDT) displacement transducer. The relative displacement of the rod and the base frame, $X_1-X_2$, is measured through the motor using the hall sensors. The acceleration of the rod, $\ddot{X}_1$, is obtained using an accelerometer mounted directly on the rod. The signals from these devices are captured and observed in real time using the data acquisition system.

2.2 Parameters identification

The combined weight of the rod and the accelerometer provides the value of the inner mass $m_1$, while the weight of the rest body including the motor body, the base frame, and the support spring gives the mass of the capsule $m_2$. They were simply measured by weighting each element and kept constant throughout the experiment. To determine the values of the coefficients $k_1$ and c, the free vibration test was carried out by keeping the switched-on motor stationary, displacing the rod from its equilibrium position and recording the displacement of the oscillating rod. The frequency of the obtained vibrations, ${{\varOmega }}_o$, allows to work out the coefficient $k_1$ with known $m_1$, and the coefficient c was found using the logarithmic decrement method. The stiffness of the support spring, $k_2$, was determined through static tests, and it can be varied by changing the length of the support spring. The current of the motor was measured via motion controller so that the forcing amplitude, $P_d$, can be determined in real time. The gap between the rod and the support spring, G, can be adjusted by setting the initial absolute position of the rod.

Fig. 2

Identified friction coefficients as a function of capsule velocity

Identification of friction coefficient between the capsule and the support surface was carried out by four static and five dynamic tests, and their results are plotted in Fig. 2. The static test was to lift one side of the supporting surface slowly until the stationary capsule started to move, and the static friction coefficient marked by circle in the figure was determined by the angle of the surface slope at that moment. The dynamic friction coefficient was calculated using the energy equivalent equation

$$\begin{aligned} \mu _d(m_1+m_2)gd=\tfrac{1}{2}(m_1+m_2)v^2, \end{aligned}$$

where $\mu _d=\tfrac{v^2}{2gd}$ is the dynamic friction coefficient to be identified, g is the acceleration due to gravity, d is the travel distance of the capsule, and v is the initial velocity of the capsule. The dynamic test was to give the capsule an arbitrary initial speed v by pushing it gently and measure the travel distance of the capsule d subject to dynamic friction. The dynamic friction coefficients are marked by crosses in the figure, and they were found to be well approximated by the Coulomb Stribeck model [2] given by

$$\begin{aligned} F_s=\tfrac{1}{2}\mu \left( 1+e^{-|\dot{X}_2|/{v_s}}\right) \left( m_1+m_2\right) g\cdot \mathrm {sign}\left( \dot{X}_2\right) \end{aligned}$$

(1)

when $\dot{X}_2\ne 0$ and the static friction $F_b=\mu (m_1+m_2)g$ is the threshold of the dry friction force for break-away when $\dot{X}_2=0$, where $\mu$ is the static friction coefficient and $v_s$ is the Stribeck velocity.

The forcing amplitude of excitation applying to the rod was identified using its linear relationship with the current of the motor as shown in Fig. 3. Once the motor is switched on, a predefined external force is applied to the rod from a tension testing machine, and the current reading from the motor is recorded when the external force is balanced by the resistent force. After eight measurements, the proportionality coefficient is determined by applying a linear fit to these data points.

Fig. 3

Motor current as a function of the resistent force on the rod

The identified physical parameters of the capsule system are given in Table 1.

Fig. 4

Sample of the recorded experimental time histories at $k_1=1.42$ kN/m, $k_2=2.42$ kN/m, $m_1=$ $0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=1.2$ N, ${\varOmega }=77.91$ rad/sec, and $G=3$ mm, a the capsule displacement $X_2$, b the relative displacement $X_1-X_2$, c the rod acceleration $\ddot{X}_1$, d the force acting on the rod from the motor

Table 1 Identified physical parameters of the capsule system

2.3 Sample of periodic motion

A sample of the obtained periodic time histories at $k_1=1.42$ kN/m, $k_2=2.42$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=1.2$ N, ${\varOmega }=77.91$ rad/sec, and $G=3$ mm was smoothed by using the Savitzky–Golay algorithm and is presented in Fig. 4, where the signals of the recorded capsule displacement (Fig. 4a), the relative displacement between the rod and the capsule (Fig. 4b), and the rod acceleration (Fig. 4c) are shown together with the processed signal for the force on rod (Fig. 4d). As can be seen from Fig. 4a, the capsule system has backward motion and the impacts are clearly visible in the form of sharp spikes in Fig. 4c. Periodic motion of the system can be determined by observing the relative displacement in Fig. 4b, and differentiation of the relative displacement signal (relative velocity) was used for constructing the trajectories on the phase plane.

Fig. 5

Physical model of the capsule system

3 Mathematical modelling

A physical model of the vibro-impact capsule system is presented in Fig. 5, where a movable internal mass $m_1$ is driven by a harmonic force with amplitude $P_d$ and frequency ${\varOmega }$. The model assumes that the restoring force acting between the inner mass and the capsule could be represented by a nonlinear spring operating near its working point in a linear region with stiffness $k_1$ and a viscous damper with damping coefficient c. A weightless plate is connected to the capsule by a secondary (support) linear spring with stiffness $k_2$. $X_1$ and $X_2$ represent the absolute displacements of the internal mass and the capsule respectively, and the internal mass is in contact with the plate when the relative displacement $X_1-X_2$ is greater or equal to the gap G. When the force acting on the capsule exceeds the threshold of the dry friction force $F_b$ between the capsule and the supporting environmental surface, bidirectional motion of the capsule will occur, and the dynamic friction force $F_\mathrm{s}$ will be applied to the capsule.

The considered system operates in bidirectional stick-slip phases which contain the following four modes: stationary capsule without contact, moving capsule without contact, stationary capsule with contact, and moving capsule with contact. A detailed consideration of these modes can be found in [1]. The comprehensive equations of motion for the vibro-impact capsule system are written as

$$\begin{aligned} \dot{X}_1= & {} Y_1,\nonumber \\ \dot{Y}_1= & {} [P_d\cos ({\varOmega }t)+k_1(X_2-X_1)+c(Y_2-Y_1) \nonumber \\&-\,H_1 k_2(X_1-X_2-G)]/m_1, \nonumber \\ \dot{X}_2= & {} Y_2[H_2(1-H_1)+H_3H_1], \nonumber \\ \dot{Y}_2= & {} [H_2(1-H_1)+H_3H_1][-F_\mathrm{s}-k_1(X_2 -\,X_1)\nonumber \\&{-}c(Y_2-Y_1){+}H_1k_2(X_1{-}X_2{-}G)]/m_2.\nonumber \\ \end{aligned}$$

(2)

The auxiliary functions $H_i, \ i=1,..3$ are given by

$$\begin{aligned} H_1= & {} H(X_1-X_2-G), \\ H_2= & {} H(\,\mid k_1(X_2-X_1)+c(Y_2-Y_1)\mid -F_b), \\ H_3= & {} H(\,\mid k_1(X_2-X_1)+c(Y_2-Y_1) \\&-\,k_2(X_1-X_2-G)\mid -F_b), \end{aligned}$$

where $H(\cdot )$ is the Heaviside function.

4 Numerical and experimental results

This section presents a few different bifurcation scenarios obtained experimentally under variations of the system parameters such as the stiffness of the support spring, and the frequency and the amplitude of excitation. Here, the comparisons of the experimental results with the numerical simulations obtained using the chosen mathematical model are also given. For simplicity, we will use the following abbreviations in bifurcation diagram to describe the periodic motion of the system: P-1-F-2 represents a period-1 forward motion with two impacts per period of external excitation, and P-2-B-1 represents a period-2 backward motion with one impact per period of external excitation.

Fig. 6

(colour online) Bifurcation diagrams obtained numerically (blue dots) and experimentally (red dots) by varying the stiffness of support spring, $k_2$ at $k_1=1.42$ kN/m, $m_1$ $=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=4$ N, ${\varOmega }=34.56$ rad/sec, and $G=1$ mm. Additional windows compare the numerical (in blue) and experimental (in red) trajectories on the phase plane ($X_1-X_2$, $Y_1-Y_2$) obtained for $k_2=3.68$, 18.96, and 51.05 kN/m, respectively. The locations of the impact surface are shown by black lines, and Poincaré sections are marked by green dots

4.1 Variation of the support spring stiffness

A comparison of bifurcation diagrams between numerical simulations and experiments using stiffness of support spring, $k_2$, as a branching parameter is shown in Fig. 6. The variation of stiffness of the support spring was made by changing the length of the support spring, and the bounded relative velocity between the rod and the capsule, $Y_1-Y_2$ was chosen to construct the bifurcation diagram. It can be seen from the figure that period-1 motion of the system is recorded for all the values of stiffness of the support spring $k_2\in [1,\, 55]$ kN/m. In the numerical simulations, period-1 backward motion with one impact is observed for $k_2\in [1,\, 5.87]$ kN/m, and period-1 forward motion with one impact for $k_2\in (5.87,\, 11.7]$ kN/m, followed by a small window of period-1 backward motion with two impacts for $k_2\in (11.7,\, 12.2)$ kN/m. Thereafter, period-1 forward motion with two impacts is recorded for $k_2\in [12.2,\, 55]$ kN/m. In the experiments, period-1 forward motion with one impact is observed for $k_2=3.68$, 4.83, 6.68, and 12.67 kN/m, and period-1 backward motion with two impacts is recorded for $k_2=18.96$, 21.29, and 22.86 kN/m. At $k_2=51.05$ kN/m, period-1 forward motion with two impacts is observed. Additional windows show the trajectories of the system on the phase plane ($X_1-X_2$, $Y_1-Y_2$) obtained both numerically and experimentally for $k_2=3.68$, 18.96, and 51.05 kN/m, where the bifurcation from period-1 forward motion with one impact to period-1 backward motion with two impacts takes place. It should be noted that from the comparison of the trajectories in Fig. 6, the stiffness of the support spring in the experiment seems smaller than the one used in the numerical simulations which might be due to the inaccuracy of the restoring force modelling or in measuring the coefficient $k_1$ and the stiffness of the support spring, $k_2$.

Fig. 7

Time histories of the relative displacement, $X_1-X_2$, and the capsule displacement, $X_2$, obtained experimentally for a $k_2=3.68$ kN/m, b $k_2=18.96$ kN/m, and c $k_2=51.05$ kN/m, and $k_1=1.42$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=4$ N, ${\varOmega }=34.56$ rad/sec, and $G=1$ mm

Figure 7 shows time histories of the relative displacement, $X_1-X_2$, and the capsule displacement, $X_2$, obtained experimentally for $k_2=3.68$, 18.96, and 51.05 kN/m. Figure 7a, b present the change in trajectories when the bifurcation from period-1 forward motion with one impact to period-1 backward motion with two impacts takes place, whereas Figure 7b, c demonstrate the change when period-1 backward motion with two impacts bifurcates into period-1 forward motion with two impacts.

4.2 Variation of the excitation frequency

The comparison of the numerical and experimental bifurcation diagrams constructed by varying the frequency of the excitation was performed in the frequency range $f\in [2.5,\, 6.5]$ Hz (where $f=\tfrac{{\varOmega }}{2\pi }$). As the linear motor can only produce large amplitude of excitation at low frequencies, the conducted study was limited to the low-frequency range. Figure 8 presents the results, where period-1 motion is observed for all the values of excitation frequency. It is worth noting here that the experiments were carried out at $P_d=4$ N using a softer support spring $k_2=18.96$ kN/m with a gap of $G=1.5$ mm. The comparison of trajectories on the phase plane and time histories of displacements is presented in Fig. 9 for the frequency of excitation ${\varOmega }=20.73$ rad/sec. It can be seen from the figure that period-1 forward motion with one impact is recorded in experiment but period-1 forward motion with high-frequency vibro-impact behaviour is obtained by numerical simulations. Comparing the progression of the system, no backward motion is observed in experiment and the capsule has a small backward motion in numerical simulations. However, both overall motions are forward and their total displacements within 2 s are approximately the same.

Figure 10 shows the comparison between experiments and numerical simulations by using time histories of displacements which was obtained at $P_d=2.5$ N in the case of a harder support spring for $k_2=59.41$ kN/m with a gap of $G=1.5$ mm. As can be seen from the figure, period-1 motion with one impact is recorded in experiment and the capsule has forward motion as the frequency of excitation increases. For numerical simulations, period-1 motion with three impacts is observed initially and the response of the system bifurcates into a period-1 motion with two impacts as the frequency of excitation increases leading to the forward motion of the capsule from stationary position.

Fig. 8

(colour online) Bifurcation diagrams constructed numerically (blue dots) and experimentally (red dots) by varying the frequency of excitation, f at $k_1=1.42$ kN/m, $k_2=18.96$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=4$ N, and $G=1.5$ mm

Fig. 9

(colour online) Trajectories on the phase plane and time histories of the relative displacement, $X_1-X_2$ and the capsule displacement, $X_2$ obtained a experimentally and b numerically at $k_1=1.42$ kN/m, $k_2=18.96$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, ${\varOmega }=20.73$ rad/sec, $P_d=4$ N, and $G=1.5$ mm. The locations of the impact surface are shown by red lines, and Poincaré sections are marked by green dots

Fig. 10

(colour online) Time histories of the relative displacement, $X_1-X_2$ and the capsule displacement, $X_2$ obtained experimentally (in red) and numerically (in blue) at a ${\varOmega }=26.58$ rad/sec, b ${\varOmega }=37.33$ rad/sec, c ${\varOmega }=46$ rad/sec, and d ${\varOmega }=54.6$ rad/sec, and $k_1=1.42$ kN/m, $k_2=59.41$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, $P_d=2.5$ N, and $G=1.5$ mm

4.3 Variation of the excitation amplitude

The comparison of the results for varying the amplitude of excitation in the range of $P_d\in [0.6,\, 2.1]$ N is presented in Fig. 11 where the stiffness of support spring is equal to $k_2=56.41$ kN/m, the frequency of excitation is ${\varOmega }=73.58$ rad/sec, and the gap is $G=1$ mm. As can be seen from the figure, chaotic motion is recorded in numerical simulations for $P_d\in [0.6,\, 0.782]$ N, where grazing-induced chaotic motion is observed at $P_d\in [0.728,\, 0.782]$ N followed by a period-1 forward motion with two impacts for $P_d\in (0.782,\, 1.378)$ N. Thereafter, the period-1 forward motion with two impacts bifurcates into a period-2 forward motion with four impacts through a smooth period doubling at $P_d=1.378$ N, and this period-2 motion exists until $P_d=2.04$ N bifurcating into a period-1 forward motion with two impacts via a reverse period doubling. For experimental results, grazing-induced chaotic motion is observed for $P_d=0.7$ and $P_d=0.8$ N followed by a period-1 forward motion with one impact for $P_d=0.9$ N. The bifurcation from the period-1 motion to a period-2 backward motion with one impact is recorded at $P_d=1.4$ N following by another bifurcation into a period-2 backward motion with two impacts at $P_d=1.5$ N. By comparing experimental and numerical results, differences can be found at the number of impacts and the direction of the capsule motion. However, these could be considered as reasonable due to measuring inaccuracies of the support spring stiffness and the approximate estimation of friction coefficient. Overall, it can be concluded that the mathematical model can predict well the grazing-induced chaotic motion and period doubling.

Figure 12 presents the trajectories on the phase plane and time histories of the displacements for the grazing-induced chaotic motion obtained experimentally at $P_d=0.8$ N. The Poincaré sections are marked by green dots on the phase plane ($X_1-X_2$, $Y_1-Y_2$) in Fig. 12a and the location of the impact surface is shown by red line. The intermittent contacts between the rod and the support spring can be observed in Fig. 12b, where the relative displacement of the rod and the capsule is presented. The progression of the capsule is inconsecutive due to grazing as shown in Fig. 12c and the average speed of the capsule is low. Figure 13 shows the experimental result of period doubling from period-1 forward motion with one impact to period-2 backward motion with one impact. Comparing the progression of the capsule in Fig. 13, it can be found that the average speed of forward progression of the capsule using small amplitude of excitation is much larger than the one with backward progression using large amplitude of excitation. This observation somehow reveals the fact that large amplitude of excitation cannot improve the performance of the capsule system and optimal regime exists for different sets of control parameters. Figure 14 demonstrates another bifurcation in experiment which is from period-2 backward motion with one impact to period-2 backward motion with two impacts. Comparing the displacement of the capsule in Fig. 14, it can be observed again that the average speed of the capsule cannot be improved by increasing the amplitude of excitation. In addition, as can be seen from Fig. 14c, large amplitude of excitation may induce extra oscillations for the capsule which will increase the energy consumption of the system.

Fig. 11

(colour online) Bifurcation diagrams constructed numerically (blue dots) and experimentally (red dots) by varying the amplitude of excitation, $P_d$ at $k_1=1.42$ kN/m, $k_2=56.41$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, ${\varOmega }=73.58$ rad/sec, and $G=1$ mm

5 Concluding remarks

This paper presents a verification on a novel experimental rig of the vibro-impact capsule model, which has been studied numerically by Liu et al. in [1–3]. The capsule is excited by the harmonic force applied to the inner mass, and the proposed mathematical model interprets the interactions between the inner mass and the capsule by assuming them as a whole possessing intrinsic stiffness and damping. Since the inner mass is driven by the electromagnetic field provided by the coils of the linear DC servomotor, such an intrinsic stiffness is nonlinear. However, we assumed that the nonlinear stiffness of the inner mass was operated in a linear region of the stiffness in experiment. The Coulomb Stribeck friction model [2] was used to describe the resistant force between the capsule and the supporting surface. The progression of the capsule takes place when the elastic force acting on the capsule exceeds the threshold of the dry friction force.

Fig. 12

(colour online) a Trajectories on the phase plane and time histories of (b) the relative displacement, $X_1-X_2$ and c the capsule displacement, $X_2$ obtained experimentally at $k_1=1.42$ kN/m, $k_2=56.41$ kN/m, $m_1=0.11$ kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, ${\varOmega }=73.58$ rad/sec, $P_d=0.8$ N, and $G=1$ mm. The location of the impact surface is shown by red line, and Poincaré sections are marked by green dots

Fig. 13

Time histories of the relative displacement, $X_1-X_2$ and the capsule displacement, $X_2$ obtained experimentally at a $P_d=1.3$ N, b $P_d=1.4$ N, $k_1=1.42$ kN/m, $k_2=56.41$ kN/m, $m_1=0.11$  kg, $m_2=0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, ${\varOmega }=73.58$ rad/sec, and $G=1$ mm. The experimental results show the period doubling of the capsule system when the response bifurcates from period-1 forward motion with one impact to period-2 backward motion with one impact

Fig. 14

Time histories of the relative displacement, $X_1-X_2$ and the capsule displacement, $X_2$ obtained experimentally at a $P_d=1.4$ N, b $P_d=1.5$ N, c $P_d=1.6$ N, $k_1=1.42$ kN/m, $k_2=56.41$ kN/m, $m_1=0.11$ kg, $m_2=$ $0.53$ kg, $c=3.89$ Ns/m, $\mu =0.66$, $v_\mathrm{s}=0.3$, ${\varOmega }=73.58$ rad/sec, and $G=1$ mm. The experimental results show the bifurcation of the capsule system from period-2 backward motion with one impact to period-2 backward motion with two impacts

Capsule dynamics with different control parameters including support spring stiffness, and frequency and amplitude of excitation was investigated, and comparisons between the experiments and numerical simulations were made using the proposed mathematical model. For all the values of stiffness of the support spring $k_2\in [1,\, 55]$ kN/m, period-1 motion of the system was recorded and the capsule system can be driven forward and backward by varying the stiffness. Experimental results showed that good progression rates of the capsule were observed for a softer support spring for $k_2=18.96$ kN/m. By varying the frequency of excitation at $f\in [2.5,\, 6.5]$ Hz, period-1 motion was observed for all the values of excitation frequency and the overall motion of the capsule system changed from stationary state to forward progression as the frequency of excitation increased. The bifurcation study on the amplitude of excitation for $P_d\in [0.6,\, 2.1]$ N reveals grazing-induced chaotic motion at low amplitudes of excitation. As the amplitude increased, the system response varied from period-1 forward motion with one impact to period-2 backward motion with two impacts. This analysis shows that large amplitude of excitation may not improve the average speed of the capsule system, and optimal regime exists for different sets of control parameters. Therefore, a fine tuning of these control parameters would significantly improve the performance of the capsule system.

Some discrepancies have been observed between experiments and numerical simulations, which could be explained by inaccuracies in measuring the stiffness of the support spring and identifying friction coefficients. However, these inconsistencies were at an acceptable level. Therefore, we can conclude that the proposed mathematical model is able to predict well the main bifurcations in the vibro-impact capsule system.