Dynamical analysis of vibro-impact capsule system with Hertzian contact model and random perturbation excitations

Abstract

In this paper, the modeling and dynamical response of a vibro-impact capsule system with Hertzian contact and random environmental perturbation is studied. The capsule system is modeled as a two-degree-of-freedom dynamical system composed of a rigid capsule and a movable internal mass. The random environmental perturbation is incorporated in the models of the capsule system, which is more realistic working condition of capsule robotic system. The impact between the rigid capsule and the internal mass will occur when the relative displacement is larger than the gap between them. The impact interaction is described by using the Hertzian contact model. The resistance force between the capsule and the sliding face is described by Coulomb friction model. The response of the vibro-impact capsule system is obtained through Monte Carlo simulation. A kind of random stick–slip phenomena can be found in the response of the proposed model, which is consistent with the actual behavior of capsule system. At last, it is worthy noting that stochastic P-bifurcation occurs when the parameters of the system vary.

1 Introduction

The capsule system is quite useful in clinic endoscopy or enteroscope, and the mechanisms of the driven capsule robot have caused extensive study in the past decades [3, 5, 13]. Locomotion is an important aspect that should be considered in capsule robot design. However, the available products generally are passive devices, which is driven by natural peristalsis. The active capsule robot is driven by an actuator, which can drive the capsule to the desired position. Though several kinds of active capsule robot have been developed, it still needs further development and some related problems such as drive, control, power supply need more precise results. The modeling and analysis of the dynamical behavior of capsule robot needs further study. Kim et al. [8, 9] studied a bio-inspired earthworm-like intestine robot with cyclic extension SMA spring actuators based on directional microneedles. Zhang et al show an analytical friction model of the capsule robot and studied the interaction between capsule robot and the intestine [17, 19]. Ciarletta et al. [4] proposed a hyperelastic theory of the layered structure of the intestine to model the mechanical properties of the intestine. Zhang et al. [20] proposed a wireless drive and control method by using rotational magnetic field on a capsule microrobot. The rectilinear motion on a horizontal rough plane of a vibration-driven system is considered by Bolotnik et al. [1]. The working condition of the capsule robot is very complex in actual work condition. The random environmental perturbation is not considered in the modeling of capsule system in the previous studies. However, random perturbations exist broadly in engineering [6] and is an unavoidable part in the modeling of capsule systems. It is more realistic to incorporate the environmental perturbation into the dynamical equations, and the effect of the random noises on the response should be investigated.

A capsule system moving without external driving mechanism is of great use in medicine and engineering. These systems can be used in complex environment such as cleaning robots inside tubes and sensors in human bodies. The capsule system driven by a vibration excitor is originally proposed by Cherousko [2], in which the motion is controlled by internal forces excited by a periodic force. The optimal motion for an internal mass moving inside a capsule is studied by Li et al. [10]. The vibro-impact mechanism as the excitor of capsule system has been proposed and used. Liu et al studied the modeling of the vibro-impact capsule system [12] and further investigated the responses of capsule system with various friction models [11]. The vibro-impact system under random perturbation is an important area of dynamical system and has been studied intensively. The stationary responses of a viscoelastic system with impacts under random excitation are analyzed by Zhao et al. [21]. By using the stochastic averaging method for quasi-Hamiltonian systems, Wu and Zhu studied vibro-impact systems under Poisson white noise excitations [18]. Hertzian contact model is a popular used model in describing the impact interactions between the masses of the system [15, 16]. By using Hertzian contact law, Nayak and Jing studied the stationary response of vibro-impact systems subject to random excitations [7, 14].

In this paper, the modeling and dynamical response of a vibro-impact capsule robot under random environmental perturbation is studied. The impact of the capsule and the internal mass is described by Hertzian contact model with nonlinear elastic force. The average procession of the capsule robot is calculated based on Monte Carlo simulation and the dynamical responses of the capsule robot under random perturbation are derived. By defining the relative displacement and the relative velocity, the stochastic P-bifurcation of the capsule robot system is investigated.

Fig. 1

A sketch of capsule system

2 Dynamical modeling of vibro-impact capsule system

2.1 Preliminary introduction of Vibro-impact capsule system

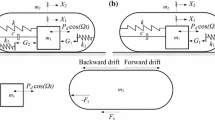
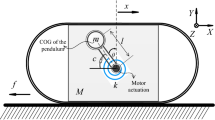
The vibro-impact driven capsule robot can be modeled as a two- degree-of-freedom dynamical system as shown in Fig. 1, which contains a movable internal mass $m_1$ and a rigid capsule $m_2$. The internal mass $m_1$ is connected with the capsule with a linear elastic spring with stiffness $k_1$ and a viscous damper with damping coefficient c. $x_1$ and $x_2$ are the absolute displacements of the internal mass $m_1$ and the rigid capsule $m_2$, respectively. The internal mass is driven by an external force u(t). The external force is composed of two parts: One is the driving harmonic force with amplitude $P_d$, and the other is the random environmental perturbation $\xi _1(t)$, which is modeled by a Gaussian white noise with correlation function $\text {E}(\xi _1(t)\xi _1(t+\tau ))=2D_1\delta (\tau )$.

The impact phenomena between the inner mass and the rigid capsule will occur when the relative displacement $x_1-x_2$ is larger or equals the gap $\varDelta$. The most popular Hertzian contact model is adopted here, which is a nonlinear elastic model. The impact force F is of the following form

$$\begin{aligned} \begin{aligned}&F=0,\quad x_1-x_2\le \varDelta , \\&F=k_h(x_1-x_2-\varDelta )^{3/2},\quad x_1-x_2\ge \varDelta , \end{aligned} \end{aligned}$$

(1)

where $k_h$ is the ratio of the stiffness of the surface, dependent on the elastic properties and the geometry of the colliding bodies. The random environmental excitations on the capsule is modeled by another Gaussian white noise $\xi _2(t)$ with correlation function $\text {E}(\xi _2(t)\xi _2(t+\tau ))=2D_2\delta (\tau )$. The interaction between the sliding surface and the capsule is described by the Coulomb friction model of the following form

$$\begin{aligned} f = \left\{ \begin{array}{ll} 0 ,\quad &{}\dot{x}_2=0, \\ -\,\text {sign}(\dot{x}_2)P_f, \quad &{}\dot{x}_2\ne 0 \end{array} \right. \end{aligned}$$

(2)

The capsule will be static when the sum of the external force on it is smaller than the threshold of the dry friction force ($P_f$), and it will move when the sum of the external force is larger than $P_f$. The driving force is usually added to the inner mass and the capsule can move without external driving mechanism, which is essential in industrial use.

2.2 Dynamical equations

The relative displacement $x_1-x_2$ and the velocity of the capsule $\dot{x}_2$ are essential in the modeling of the dynamical equations of the capsule robot. In light of impact condition (1) and Coulomb friction property (2), the impact condition is determined by $x_1-x_2$ and the movement of the capsule can be judged by the value of $\dot{x}_2$. Thus, there are four possible cases for the dynamical motions of the capsule: stationary capsule without contact between the internal mass and the capsule, Moving capsule without contact, stationary capsule with contact, moving capsule with contact. A detailed discussion for different cases is given next.

Stationary capsule without contact When $x_1-x_2<\varDelta$, the internal mass and the capsule are not in contact. When the force on the capsule is smaller or equal to the threshold of the friction force ($|k_1(x_1-x_2)+c(\dot{x}_2-\dot{x}_1)-\xi _2(t)|\le P_f$), the capsule will be static. In this case, the governing equations of the capsule robot are

$$\begin{aligned} m_1\ddot{x}_1= & {} P_d \cos (\varOmega t)+k_1(x_2-x_1)\nonumber \\&+\,c(\dot{x}_2-\dot{x}_1)+\xi _1(t) \dot{x}_2=0 \end{aligned}$$

(3)

Moving capsule without contact When $x_1-x_2<\varDelta$, the internal mass and the capsule are not in contact. When the force on the capsule is bigger than the threshold of the friction force ($|k_1(x_1-x_2)+c(\dot{x}_2-\dot{x}_1)-\xi _2(t)|>P_f$), the capsule will move. In this case, the governing equations of the capsule robot are

$$\begin{aligned} \begin{aligned} m_1\ddot{x}_1&=P_d \cos (\varOmega t)+k_1(x_2-x_1)\\&\quad +c(\dot{x}_2-\dot{x}_1)+\xi _1(t) \\ m_2\ddot{x}_2&=-\text {sign}(\dot{x}_2)P_f-k_1(x_2-x_1)\\&\quad -c(\dot{x}_2-\dot{x}_1)+\xi _2(t) \end{aligned} \end{aligned}$$

(4)

Stationary capsule with contact When $x_1-x_2\ge \varDelta$, the internal mass and the capsule are in contact. When the force on the capsule is smaller or equal to the threshold of the friction force ($|k_1(x_1-x_2)+c(\dot{x}_2-\dot{x}_1)-k_h(x_1-x_2-\varDelta )^{3/2}-\xi _2(t)|\le P_f$), the capsule will be static. In this case, the governing equations of the capsule robot are

$$\begin{aligned} \begin{aligned} m_1\ddot{x}_1&=P_d \cos (\varOmega t)+k_1(x_2-x_1)+c(\dot{x}_2-\dot{x}_1)\\&\quad -k_h(x_1-x_2-\varDelta )^{3/2}+\xi _1(t) \\ \dot{x}_2&=0 \end{aligned} \end{aligned}$$

(5)

Moving capsule with contact When $x_1-x_2\ge \varDelta$, the internal mass and the capsule are in contact. When the force on the capsule is bigger than the threshold of the friction force ($|k_1(x_1-x_2)+c(\dot{x}_2-\dot{x}_1)-k_h(x_1-x_2-\varDelta )^{3/2}-\xi _2(t)|> P_f$), the capsule will move. In this case, the governing equations of the capsule robot are

$$\begin{aligned} m_1\ddot{x}_1&=P_d \cos (\varOmega t)+k_1(x_2-x_1)+c(\dot{x}_2-\dot{x}_1)\nonumber \\&\quad -k_h(x_1-x_2-\varDelta )^{3/2}+\xi _1(t)\nonumber \\ m_2\ddot{x}_2&=-\text {sign}(\dot{x}_2)P_f-k_1(x_2-x_1)-c(\dot{x}_2-\dot{x}_1)\nonumber \\&\quad +k_h(x_1-x_2-\varDelta )^{3/2}+\xi _2(t) \end{aligned}$$

(6)

2.3 Nondimensional equations

Introduce the dimensionless variables and parameters in according to the following formulas:

$$\begin{aligned} \begin{aligned}&t^*=\varOmega _0t, x_i^*=\frac{k_1}{P_f}x_i,y_i=\frac{dx^*_i}{dt^*}=\frac{k_1}{\varOmega _0P_f}\dot{x}_i,\\&\dot{y}_i=\frac{dy_i}{dt^*}=\frac{k_1}{\varOmega ^2_0P_f}\ddot{x}_i \varOmega _0=\sqrt{\frac{k_1}{m_1}},\omega =\frac{\varOmega }{\varOmega _0}, \\&\alpha =\frac{P_d}{P_f},\zeta =\frac{c}{\sqrt{2m_1\varOmega _0}}, \delta =\frac{k_1}{P_f}\varDelta , \\ {}&\beta =\frac{k_h}{k_1}\sqrt{\frac{P_f}{k_1}}, \gamma =\frac{m_2}{m_1},D_i^*=\frac{D_i}{P_f^2} \end{aligned} \end{aligned}$$

(7)

where $i=1,2$. For simplicity, proceed with the dimensionless variables and parameters in Eq. (7) and omit the asterisks. To incorporate the four kinds of motions into one equation, the following auxiliary functions are adopted

$$\begin{aligned} \begin{aligned} H_1&=H(|(x_2-x_1)+2\zeta (y_2-y_1)-\xi _2(t)|-1) \\ H_2&=H(|(x_2-x_1)+2\zeta (y_2-y_1)\\ {}&\quad -\,\beta (x_1-x_2-\delta )^{3/2}-\xi _2(t)|-1) \\ H_3&=H(x_1-x_2-\delta ) \end{aligned} \end{aligned}$$

(8)

where $H(\cdot )$ is the Heaviside function with the following expression

$$\begin{aligned} H(x) = \left\{ \begin{array}{lll} 0 &{} \text{ when } x < 0, \\ \frac{1}{2} &{} \text{ when } x = 0, \\ 1 &{} \text{ when } x > 0 \end{array} \right. \end{aligned}$$

(9)

The equations of motion for vibro-impact capsule system are

$$\begin{aligned} \begin{aligned} \dot{x}_1&=y_1 \\ \dot{y}_1&=\alpha cos(\omega t)+(x_2-x_1)+2\zeta (y_2-y_1)\\ {}&\quad -H_3\beta (x_1-x_2-\delta )^{3/2}+\xi _1(t) \\ \dot{x}_2&=y_2(H_1(1-H_3)+H_2H_3) \\ \dot{y}_2&=\Bigl (H_1(1-H_3)+H_2H_3)(-sgn(y_2)-(x_2-x_1) \\&\quad -\,2\zeta (y_2-y_1)+H_3\beta (x_1-x_2-\delta )^{3/2}+\xi _2(t)\Bigr )/\gamma \end{aligned} \end{aligned}$$

(10)

3 Dynamical analysis of vibro-impact capsule system

As shown in Eq. (10), the stochastic dynamical equation of capsule robotic system contains nonlinear and nonsmooth terms, which is difficult to derive the analytical results. In this section, numerical results are given for system (10) based on Monte Carlo simulation.

3.1 Dynamical properties of vibro-impact capsule system

Define the following parameter to measure the average progression.

$$\begin{aligned} \begin{aligned} x_{aver}=\mathop {\lim }\limits _{ {t \rightarrow \infty } }\frac{E\bigl (x_2(t)\bigr )}{t} \end{aligned} \end{aligned}$$

(11)

where $E(\cdot )$ denotes the probabilistic average. The average progression $x_{aver}$ is an important index to measure the dynamics of capsule system. As the averaged response of the system can be worked out through Monte Carlo simulation, the expectation can be obtained by the sample of $x_2(t)$ by simulating enough times. The increases of $x_2(t)$ in per exciting period will be a stationary random variable. Thus, the limit in Eq. (11) can be achieved by setting t to be a large value. To make the probabilistic average to be accurate, 400 samples of the orbit are calculated and the accuracy can be guaranteed by the law of large number. Numerical calculation is made with the following parameter values in this section: $\alpha =0.60,\delta =0.02,\zeta =0.05,\omega =1.45,\beta =6.0,\gamma =3.0,D_1=D_2=D$, otherwise mentioned.

Fig. 2

a $x_\mathrm{aver}$ as a function of $\omega$ under noise intensities $D=0.005,0.01,0.02$; b time histories of $x_1$ and $x_2$ for $\omega =0.6$ and $\omega =1.1$ under noise intensities $D=0.005$

Fig. 3

a The sample of the capsule velocity $y_2$ for $\omega =0.6$ under noise intensities $D=0.005$ and b the sample of the capsule velocity $y_2$ for $\omega =1.1$ under noise intensities $D=0.005$

Fig. 4

a $x_\mathrm{aver}$ as a function of $\beta$ under noise intensities $D=0.005,0.01,0.02$; b time histories of $x_1$ and $x_2$ for $\beta =1.2$ and $\beta =3$ under noise intensities $D=0.005$

Fig. 5

a The sample of the capsule velocity $y_2$ for $\beta =1.2$ under noise intensities $D=0.005$ and b the sample of the capsule velocity $y_2$ for $\beta =3$ under noise intensities $D=0.005$

The average progression $x_\mathrm{aver}$ as a function of driven frequency $\omega$ for different noise intensities D ($D=0.005, 0.01, 0.02$) is shown in Fig. 2a. It is seen that the maximum average progression occurred when the driven frequency is close to a critical value $\omega ^*=1.45$ for different values of D. The average progression will increase with the driven frequency $\omega$, while $\omega$ is smaller than $\omega ^*$. The average progression will decrease with the driven frequency $\omega$ while $\omega$ is larger than $\omega ^*$. Generally, the noise intensity D will slightly decrease the average procession, while $\omega$ is small, and it will increase average procession, while $\omega$ is big. From Fig. 2a, we can see, for certain value of $\omega$ , bigger value of D will lead to bigger value of $x_\mathrm{aver}$ , especially in the region near the maximum point, which is of essential use in the design of the capsule system. The time histories of displacements of the mass $x_1$ (solid line) and the capsule $x_2$ (dash red line) for different $\omega$ values ($\omega =0.6,1.1$) are shown in Fig. 2b. From Fig. 2b, it is seen that the capsule will move forward with quasi-periodic behavior. Generally, the capsule system will exhibit stick–slip phenomena due to the Coulomb frictional force. However, the presence of the random perturbation will drive the capsule system with random walk behavior, which can be viewed as random stick–slip phenomena in Fig. 2b. The random stick–slip phenomena can be explained by checking the velocity of the capsule in Fig. 3, where the velocity of the capsule $y_2$ stays near 0 with small random fluctuations in certain segment. Due to the random perturbation excitation, there will be negative values of the velocity ($y_2<0$) in Fig. 3, which means the capsule may even move backward. This phenomenon is called random stick–slip phenomena, which is more real in the actual capsule dynamics.

The average progression $x_\mathrm{aver}$ as a function of parameter $\beta$ for different noise intensities D is shown in Fig. 4a. It is seen that the maximum average progression occurred when $\beta$ is close to a critical value $\beta ^*=2.95$ for different values of D. From Fig. 4a, we can see that bigger value of D will lead to bigger value of $x_\mathrm{aver}$ for different values of $\beta$, which means that D is beneficial in average progression for the selected parameter. The average progression will increase with $\beta$ while $\beta$ is smaller than $\beta ^*$. When $\beta$ is larger than $\beta ^*$, the average progression become flat with slight decrease. This is universal as other parameter changed. Thus, it enable us to find a optimal value of $\beta$ in practical driven capsule system. The time histories of displacements of the mass $x_1$ (solid line) and the capsule $x_2$ (dash red line) for different $\beta$ values ($\beta =1.2,3$) are shown in Fig. 4b. The random stick–slip and backward movement phenomena ($y_2<0$) in Fig. 4 are shown and checked in Fig. 5.

Fig. 6

a The probabilistic density functions $p(x_r,y_r)$ for $\omega =0.65$ and b the probabilistic density functions $p(x_r,y_r)$ for $\omega =1.1$

Fig. 7

a The phase trajectory of $(x_r,y_r)$ for $\omega =0.65$ and b the phase trajectory of $(x_r,y_r)$ for $\omega =1.1$

Fig. 8

a The probabilistic density functions $p(x_r,y_r)$ for $\beta =1.0$ and b the probabilistic density functions $p(x_r,y_r)$ for $\beta =5.5$

Fig. 9

a The phase trajectory of $(x_r,y_r)$ for $\beta =1.0$ and b the phase trajectory of $(x_r,y_r)$ for $\beta =5.5$

3.2 Bifurcation analysis

The capsule system will exhibit various nonlinear phenomena under different parameters. The information derived from the state variable $x_1,x_2$ contains the progression and the fluctuation around the trace of the progression. To get a better view of the statistical information of the system, the following variables are defined

$$\begin{aligned} \begin{aligned}&x_r=x_1-x_2 \\&y_r=y_1-y_2 \end{aligned} \end{aligned}$$

(12)

where $x_r,y_r$ denotes the relative placement and relative velocity. The probabilistic density function (PDF) $p(x_r,y_r)$ of $x_r,y_r$ can be obtained from Monte Carlo simulation. Numerical calculation is made with the following parameter values in this section: $\alpha =0.60,\delta =0.02,\zeta =0.05,\omega =0.7,\beta =4.0,\gamma =3.0,D_1=D_2=D$, otherwise mentioned.

The PDF $p(x_r,y_r)$ of relative displacement $x_r$ and relative velocity $y_r$ for $\omega =0.65$ and $\omega =1.1$ are shown in Fig. 6a, b, respectively. It is seen that the PDF changes from bimodal with two rings to unimodal with one ring. This phenomenon is called stochastic P-bifurcation, which means the shapes of the PDF changed. To better understand this phenomenon, the phase trajectories of $(x_r,y_r)$ for $\omega =0.65$ and $\omega =1.1$ are shown in Fig. 7a, b, respectively. The locations of the impact surface ($x_1-x_2=\delta$) are shown by the red line. From Fig. 7, it is seen that the phase trajectories of $(x_r,y_r)$ change from two random rings to one random ring.

The PDF $p(x_r,y_r)$ of relative displacement $x_r$ and relative velocity $y_r$ for the nonlinear impact coefficients $\beta =1.0$ and $\beta =5.5$ are shown in Fig. 8a, b, respectively. It is seen that the PDF changes from unimodal with one ring to bimodal with two rings, which means that parameter $\beta$ can also induce stochastic P-bifurcation. The phase trajectories of $(x_r,y_r)$ for $\beta =1.0$ and $\beta =5.5$ are shown in Fig. 9a, b, respectively. It is seen from Fig. 7 that the phase trajectory of $(x_r,y_r)$ changes from one random ring to two random rings, and the bifurcation phenomena can be intuitively observed.

4 Conclusion

The modeling and dynamical response of a vibro-impact capsule system is studied in the present paper. The interaction force of the impact is described by Hertzian contact model, and the random environmental perturbation is considered in the established model. The average procession of the capsule system is investigated. It is found that there exists critical value of the driving frequency and the Hertzian contact parameter to maximize the average procession, which can be used in the capsule robot design. Due to the random perturbation, the capsule system will exhibit random stick–slip phenomena and may move backward, which agrees with the actual motion of the capsule system. The probability density function of the relative displacement and the relative velocity is calculated to demonstrate the bifurcation phenomena, and stochastic P-bifurcation occurs, while the driven frequency or the Hertzian contact parameter varies. The model established in the present paper is more realistic in reflecting the actual motion of capsule, and it may be used in medicine such as cleaning robots inside intestine or sensors in human bodies.