1 Introduction

Micro-and nano- machined devices have attracted considerable attention due to their technological applications [1]. Micro-scaled mechanical resonators are the critical components used as sensors, gyro-meters, charge detectors and radio frequency (RF) filters [2]. The scaling property, low energy consumption, low cost, low driving power, large deflection capacity, relative ease of fabrication, etc. make microelectromechanical systems (MEMS) components commercialization attractive [3]. The micro-beams have been widely studied by the MEMS community [4–6] due to their applications ranging from signal filtering to chemical filtering and mass sensing.

Lifshitz and Roukes [7] studied the thermoelastic damping of a beam and found that beyond the Debye peaks, the thermoelastic attenuation get weakened with increasing size. Guo and Rogerson [8] examined the thermoelastic coupling effect on micro-machined beam resonators. Sun et al. [9] presented 2-D analysis of frequency shifts by considering sinusoidal temperature gradients across the thickness of the beam. Sharma [10] derived governing equations of flexural vibrations in a transversely isotropic, thermoelastic beam in closed form based on Euler–Bernoulli theory to study thermoelastic damping (TED) and frequency shift (FS) of vibrations in clamped and simply supported beam structures. Altus [11] calculated the statistical characteristics of heterogeneous microbeams by using probability density and correlation functions to conclude that deflection is load dependent. Abu-Hilal [12] determined the dynamic response of Euler–Bernoulli beams subjected to distributed and concentrated loads. Fang et al. [13] investigated the vibration phenomenon due to laser heating of micro-beams. The frequency spectrum of laser induced vibrations of microbeam resonator has also been analysed. Sun et al. [14] used Laplace transform technique to study the vibration phenomena due to pulsed laser heating of a microbeam under different boundary conditions. Liu et al. [15] studied the mechanical behaviour of a silicon micro-cantilever beam to evaluate the dimension effects on the flexural strength, Young’s modulus and failure strain of MEMS devices. Jia et al. [16] presented an analytical study on the forced vibration of micro-switches under the influence of combined electrostatic and intermolecular forces as well as axial residual stress. Zang and Fu [17] developed a new beam model for a viscoelastic mico-beam based on a modified couple stress theory. Tryland et al. [18] studied the influence of geometry and material variations on the structural response of a beam under patch loading. According to Akgöz and Civalek [19], the classical elasticity theory sufficiently captures accurate response for many engineering problems except where the size effects are prominent in the structure. They explored the bending analysis of micro-sized beams based on Euler–Bernoulli beam theory by using strain gradient elasticity theory. Civalek [20] gave a comparative study of the buckling of thin isotropic plates and elastic columns by using differential quadrature (DQ) and harmonic differential quadrature (HDQ) techniques. Akgöz and Civalek [21] studied the longitudinal free vibrations of strain gradient bars made of functionally graded materials. Belardinelli et al. [22] investigated the dynamic behaviour of an electrically actuated clamped microbeam.

The numerical solutions of engineering and mathematical problems are also possible in a reasonable accuracy with the help of meshless methods developed by researchers [23, 24]. The variational iteration method (VIM) developed by He [23], as a modification of a general Lagrange multiplier method [24], is a powerful technique to obtain approximate solutions of linear as well as non-linear problems. Liu and Gurram [25] employed VIM to solve free vibration problems for elastic Euler–Bernoulli beams. Rezazadeh et al. [26] studied the parametric oscillation of an electrostatically actuated micro-beam by using VIM. Shiekhlou et al. [27] investigated the torsional vibrations and stability of a micro-shaft subjected to an electrostatic parametric excitation with the help of VIM.

Unlike the non-classical (non-Fourier) solution, the classical (Fourier) solution of heat conduction equation shows no distinct wave front and temperature increase starts at the initial time [28]. The difference in the predicted temperature between two theories, Fourier and non-Fourier, is small and only apparent for very small time scales, of the order of picoseconds (ps). However, in certain applications such as non-destructive evaluation (NDE), the time scales are large enough for the solution to be numerically undistinguishable. Moreover, the choice of a specific value for the heat propagation speed in non-Fourier process does not affect the results. However, from the practical point of view, the choice of a value for the heat propagation speed equal to the speed of longitudinal waves in non-classical formulation, presents some numerical advantages. Sharma and Kaur [29] modeled and analysed the forced vibrations in micro-scale anisotropic thermoelastic beams due to time harmonic point load. As per knowledge of the authors, no systematic study on transverse vibrations in a homogeneous, transversely isotropic thin thermoelastic beam under the action of time varying (anharmonic) patch load is available in the literature in the context of generalized (non-Fourier) theory of thermoelasticity.

Keeping in view the above stated facts, the non-Fourier (hyperbolic) model of governing equations developed by Dhaliwal and Sherief [30] has been used to model and study the instant transient problem of dynamic patch load acting on a homogeneous, transversely isotropic thin beam. The double Laplace transform with respect to space and time variables along with calculus of residues has been used to find the analytical solution in the physical domain. The deflection and response ratio in clamped–clamped (CC) and clamped-free (CF) beams have been obtained as functions of axial coordinate and time. The problem has also been solved by employing VIM, being generic and computer friendly, for comparison and validation of the solutions. The expressions for deflection and response ratio have been computed numerically for silicon carbide (SiC) micro-beams by using MATLAB software. The considered material is anisotropic in nature by crystallographic classifications.

2 Mathematical model

We consider a homogenous, transversely isotropic, thermoelastic thin beam with dimensions: length \( L(0 \le x \le L) \), width \( b( - \frac{b}{2} \le y \le \frac{b}{2}) \) and thickness \( h\,( - \frac{h}{2} \le z \le \frac{h}{2}) \) in a Cartesian coordinate system Oxyz. The beam is assumed to be transversely isotropic in the sense that its mechanical and thermal properties are different along the thickness to that in a plane transverse to it. We take x -axis along the length of the beam, y -axis along the width and z -axis along the thickness direction, being also the axis of material symmetry. In equilibrium, the beam is unstrained, unstressed and at uniform temperature T 0. It is assumed that there is no flow of heat across the upper and lower surfaces of the beam. Ignoring the shear deformation and rotary inertia effect, the governing equations of motion and heat conduction equation for transverse vibrations of a homogeneous, transversely isotropic, thermoelastic uniform Euler–Bernoulli beam leads to the beam equation [29]:

$$ c_{11} \,I\frac{{\partial^{4} w}}{{\partial x^{4} }} + \beta_{1} \frac{{\partial^{2} M_{T} }}{{\partial x^{2} }} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} = q(x,t) $$
(1)

where w(x,t) is the transverse deflection at distance \( x \) along the length of the beam at time t, \( c_{11} \,I \), \( I = \frac{{bh^{3} }}{12} \), \( \rho \) and A are the flexural rigidity, moment of inertia of the cross-section, density of the material and the cross-sectional area of the beam respectively. \( \beta_{1} = (c_{11} + c_{12} )\alpha_{1} + c_{13} \alpha_{3} \) is the thermoelastic coupling parameter, \( c_{i\,j} \) are the elastic constants, \( \alpha_{1} \ne \alpha_{3} \), in general, are the coefficients of linear thermal expansion along and perpendicular to the plane of isotropy, \( M_{T} = b\int\limits_{{ - \,\frac{h}{2}}}^{\frac{h}{2}} {Tz} dz \) is the thermal moment of inertia of the beam and \( \beta_{1} M_{T} \) being the thermal moment of the beam, q(x,t) is the load acting in the transverse direction.

We neglect the heat conduction along y-direction [7, 31, 32] and hence the heat conduction equation in this situation takes the form [29]

$$ K_{1} \frac{{\partial^{2} T}}{{\partial x^{2} }} + K_{3} \frac{{\partial^{2} T}}{{\partial z^{2} }} - \rho \,C_{e} (\frac{\partial T}{\partial t} + t_{0} \frac{{\partial^{2} T}}{{\partial t^{2} }}) + \,\,\beta_{1} T_{0} z(\frac{\partial }{\partial t} + t_{0} \frac{{\partial^{2} }}{{\partial t^{2} }})\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0 $$
(2)

where \( T(x,y,z,t) = T_{1} (x,y,z,t) - T_{O} \) is the temperature change, Ce is the specific heat at constant strain, K1 and K3 are the thermal conductivities along and perpendicular to the plane of isotropy and t 0 is the thermal relaxation time. Here, the thermoelastic coupling parameter \( \beta_{3} = 2c_{13} \alpha_{1} + c_{33} \alpha_{3} \) along z-axis does not appear due to Euler–Bernoulli hypothesis.

For mathematical convenience, we define the following non-dimensional quantities:

$$ X = \frac{x}{L},\;Z = \frac{z}{h},\;W = \frac{w}{h},\;\tau = \frac{vt}{L},\;\theta = \frac{T}{{T_{0} }},\;a_{R} = \frac{L}{h},\;M_{\theta } = \frac{{M_{T} }}{{T_{0} Ah}},\;K^{*} = \frac{{K_{3} }}{{K_{1} }}, $$
$$ \Omega ^{*} = \frac{{L\,\omega^{*} }}{v},\tau_{0} = \frac{{vt_{0} }}{L},\beta_{1}^{*} = \frac{{T_{0} \,\beta_{1} }}{{c_{11} }},\varepsilon_{1} = \frac{{\beta_{1}^{2} T_{0} \,}}{{\rho \,C_{e} c_{11} }},q_{1} (X,\tau ) = \frac{{L^{2} }}{{c_{11} Ah}}q(x,t) $$
(3)

where \( \omega^{*} = \frac{{C_{e} c_{11} }}{{K_{1} }} \) and \( v = \sqrt {\frac{{c_{11} }}{\rho }} \) are the thermoelastic characteristic frequency and velocity of longitudinal wave in the beam, respectively.

Upon introducing quantities (3) in Eqs. (1) and (2), we get

$$ \frac{1}{{12\,a_{R}^{2} }}\frac{{\partial^{4} W}}{{\partial X^{4} }} + \beta_{1}^{*} \frac{{\partial^{2} M_{\theta } }}{{\partial X^{2} }} + \frac{{\partial^{2} W}}{{\partial \tau^{2} }} = q_{1} (X,\tau ) $$
(4)
$$ \frac{1}{{K^{*} \,a_{R}^{2} }}\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Z^{2} }} - \frac{{\Omega ^{*} }}{{K^{*} \,a_{R}^{2} }}\left( {\frac{\partial \theta }{\partial \tau } + \tau_{0} \frac{{\partial^{2} \theta }}{{\partial \tau^{2} }}} \right) + \,\,\frac{{\varepsilon_{1}\Omega ^{*} Z}}{{K^{*} \beta_{1}^{*} a_{R}^{4} }}\left( {\frac{\partial }{\partial \tau } + \tau_{0} \frac{{\partial^{2} }}{{\partial \tau^{2} }}} \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} = 0 $$
(5)

where \( M_{\theta } = \int\limits_{{ - \,\frac{1}{2}}}^{\frac{1}{2}} {\theta (X\,,Z,\tau )\,Z} dZ \)

Because the thermal gradients in the plane of cross-section along the thickness direction of the beam are much larger than those along its axis, that is \( \left| {\frac{\partial T}{\partial x}} \right|\, < \left| {\frac{\partial T}{\partial z}} \right| \) [7, 31, 32]. Consequently, \( \left| {\frac{1}{{a_{R}^{2} }}\frac{{\partial^{2} \theta }}{{\partial X^{2} }}} \right|\, < < \left| {\frac{{\partial^{2} \theta }}{{\partial Z^{2} }}} \right| \) and thus the Eq. (5) becomes

$$ \frac{{\partial^{2} \theta }}{{\partial Z^{2} }} - \frac{{\Omega ^{*} }}{{K^{*} \,a_{R}^{2} }}\left( {\frac{\partial \theta }{\partial \tau } + \tau_{0} \frac{{\partial^{2} \theta }}{{\partial \tau^{2} }}} \right) + \,\,\frac{{\varepsilon_{1}\Omega ^{*} Z}}{{K^{*} \beta_{1}^{*} a_{R}^{4} }}\left( {\frac{\partial }{\partial \tau } + \tau_{0} \frac{{\partial^{2} }}{{\partial \tau^{2} }}} \right)\frac{{\partial^{2} W}}{{\partial X^{2} }} = 0 $$
(6)

3 Initial and boundary conditions

Initially, the beam has been assumed to be at rest, undeformed and undisturbed mechanically as well as thermally and at uniform temperature T 0. Thus, the initial conditions are given by:

$$ W(X,0) = 0 = \dot{W}(X,0),\;\theta (X,Z,0) = 0 = \dot{\theta }(X,Z,0) $$
(7)

where superposed dot denotes time differentiation.

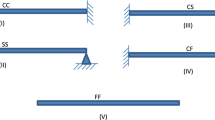
For a thin beam whose ends X = 0 and X = 1 are held either at clamped–clamped (CC) or clamped-free/cantilever (CF) mechanical conditions, the following sets of boundary conditions are satisfied:

Set I: Clamped–Clamped (CC) beam

$$ W = 0,\,\,\,\,\,\,\,\frac{dW}{dX} = 0,\,\,{\text{at}}\;X = 0,\,\,1 $$
(8)

Set II: Clamped-free/Cantilever (CF) beam

$$ \,W = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{\text{d}}W}}{{{\text{d}}X}} = 0,\,\,{\text{at}}\;X = 0 $$
$$ \,\frac{{d^{2} W}}{{dX^{2} }} = 0\,\,\,\,\,,\,\,\,\frac{{{\text{d}}^{3} W}}{{{\text{d}}X^{3} }} = 0,\,\,{\text{at}}\;X = 1 $$
(9)

It is assumed that there is no flow of heat across the upper and lower surfaces of the beam, therefore the following thermal boundary conditions are satisfied on these surfaces:

$$ \frac{\partial \theta }{\partial Z} = 0,{\text{ at}}\;Z = \pm \frac{1}{2}. $$
(10)

4 Temperature field

The Laplace transform with respect to time ‘\( \tau \)’ has been defined as [33]

$$ \bar{W}(X,S) = \int\limits_{0}^{\infty } {e^{ - S\tau } } W(X,\tau )\,{\text{d}}\tau ,\tau > 0 $$
(11)

where \( S = \frac{Ls}{v} \) is non-dimensional Laplace transform parameter. Here ‘s’ is dimensional Laplace transform parameter with respect to time \( \tau \), which may be real or complex.

Applying Laplace transform (11) to Eq. (6) and using initial conditions (7), we get

$$ \frac{{\partial^{2} \bar{\theta }}}{{\partial Z^{2} }} + p^{2} \bar{\theta } - \frac{{\varepsilon_{1} p^{2} Z}}{{\beta_{1}^{*} a_{R}^{2} }}\,\,\frac{{\partial^{2} \bar{W}}}{{\partial X^{2} }} = 0 $$
(12)
$$ {\text{where}}\quad p^{2} = - \frac{{\Omega ^{*} \tau_{0}^{*} S}}{{K^{*} \,a_{R}^{2} }},\;\tau_{0}^{*} = 1 + \tau_{0} S,\;\bar{M}_{\theta } = \int\limits_{{ - \,\frac{1}{2}}}^{\frac{1}{2}} {\bar{\theta }(X,Z,S)Z} \,dZ $$
(13)

The solution of Eq. (12) that satisfies the conditions (10) is obtained as

$$ \bar{\theta }(X,Z,S) = \frac{{\varepsilon_{1} }}{{\beta_{1}^{*} a_{R}^{2} }}\left( {Z - \frac{\sin \,pZ}{{p\,\cos \frac{p}{2}}}} \right)\frac{{\partial^{2} \bar{W}}}{{\partial X^{2} }} $$
(14)

Using (14) in Eq. (13), the thermal moment of inertia has been obtained as:

$$ \bar{M}_{\theta } = \frac{{\varepsilon_{1} }}{{12a_{R}^{2} \beta_{1}^{*} }}\left[ {1 + f(p)} \right]\frac{{\partial^{2} \bar{W}}}{{\partial X^{2} }} $$
(15)
$$ {\text{where}}\;f(p) = \frac{24}{{p^{3} }}\left( {\frac{p}{2} - \tan \frac{p}{2}} \right) $$
(16)

Applying Laplace transform (11) to Eq. (4) and using initial conditions (7), we get

$$ \frac{1}{{12\,a_{R}^{2} }}\frac{{\partial^{4} \bar{W}}}{{\partial X^{4} }} + \beta_{1}^{*} \frac{{\partial^{2} \bar{M}_{\theta } }}{{\partial X^{2} }} + S^{2} \bar{W} = \bar{q}_{1} (X,S) $$
(17)

Eliminating \( \bar{M}_{\theta } \) from Eq. (17) with the help of Eq. (15), we get

$$ \frac{{\partial^{4} \bar{W}}}{{\partial X^{4} }} - \eta^{4} \bar{W} = \frac{1}{{D_{p} }}\bar{q}_{1} (X,S) $$
(18)

where \( \eta^{4} = \frac{{ - S^{2} }}{{D_{p} }} \),

$$ D_{p} = \frac{1}{{12a_{R}^{2} }}[1 + \varepsilon_{1} (1 + f(p))]\, $$
(19)

Here D p is the effective flexural rigidity of the beam.

It is assumed that either of the continuous and exponential decaying patch loads are acting on a segment AB of the beam, where A and B are the points on the axial axis distant a and a * from the origin, respectively. Here \( 0 \le a < a^{*} \le L \) so that \( 0 \le \hat{a} < \hat{b} \le 1 \), where \( \hat{a} = \frac{a}{L}\, \) and\( \,\hat{b} = \frac{{a^{*} }}{L} \). Thus following cases of patch loads in the instant study have been considered:

Case I: Continuous patch load

$$ q_{1} (X,\tau ) = - q_{0}^{*} [H(X - \hat{a}) - H(X - \hat{b})]\,H(\tau - \hat{\tau }) $$

Case II: Exponential decaying patch load

$$ q_{1} (X,\tau ) = - q_{0}^{*} [H(X - \hat{a}) - H(X - \hat{b})]\,[1 - \exp ( -\Omega \tau )] $$
(20)

where \( q_{0}^{*} \) and \( \Omega \) are the magnitude and excitation frequency of the applied patch load, respectively and the quantity H(·) denotes Heaviside function. Here \( \hat{\tau } \) is the time at which the continuous load \( q_{1} (X,\tau ) \) has just been applied to the beam.

Applying Laplace transform (11) to Eq. (20), one gets

$$ {\mathbf{Case}} \, {\mathbf{I}}:\bar{q}_{1} (X,S) = - q_{0}^{*} [H(X - \hat{a}) - H(X - \hat{b})]\,\left[ {\frac{{\exp ( - \hat{\tau }S)}}{S}} \right] $$
$$ {\mathbf{Case}} \, {\mathbf{II}}:\bar{q}_{1} (X,S) = - q_{0}^{*} [H(X - \hat{a}) - H(X - \hat{b})]\,\left[ {\frac{\Omega }{{S(S +\Omega )}}} \right] $$
(21)

The boundary conditions (8) and (9) in the transformed domain became

$$ {\mathbf{Set}} \, {\mathbf{I}}:\bar{W}(X,S)\, = 0\, = \frac{{{\text{d}}\bar{W}(X,S)}}{{{\text{d}}X}},{\text{ at}}\,\,X = 0,1 $$
(22)
$$ {\mathbf{Set}} \, {\mathbf{II}}:\bar{W}(X,S) = 0\, = \frac{{{\text{d}}\bar{W}(X,S)}}{{{\text{d}}X}}, \quad {\text{at}}\,\,X = 0 $$
$$ \frac{{d^{2} \bar{W}(X,S)}}{{dX^{2} }} = 0\,\,\, = \,\,\,\frac{{{\text{d}}^{3} \bar{W}(X,S)}}{{{\text{d}}X^{3} }}, \quad {\text{at}}\,\,X = 1 $$
(23)

The Eq. (18) along conditions (21)–(23) constitutes a mathematical model for the computation of deflection of the thermoelastic thin beam under considered transverse patch loads in cases I and II. The temperature and thermal moment in the transformed domain can also be obtained from Eqs. (14) and (15) with the help of \( \bar{W}(X,S) \).

5 Solution of the model

In order to solve the model Eq. (18), we again employ Laplace transform with respect to X as defined by [33]:

$$ \tilde{\bar{W}}(\xi ,S) = \int\limits_{0}^{\infty } {e^{ - \xi X} } \bar{W}(X,S)\,{\text{d}}X $$
(24)

where \( \xi = L\varsigma \) is non-dimensional Laplace transform parameter. Here ‘\( \varsigma \)’ is dimensional Laplace parameter with respect to X, which may be real or complex. The solution of the model in the light of boundary conditions stated in Set I and Set II will be derived under static and dynamic situations of the thin beam in the following subsections.

5.1 Static analysis

In the static case, the disturbance and load are independent of time. Thus, the load acting on the beam in Case I and II in Eq. (20) becomes

$$ q_{1} (X) = - q_{0}^{*} [H(X - \hat{a}) - H(X - \hat{b})] $$
(25)

Adopting the similar analysis, the model Eq. (18) in this case is replaced by:

$$ \frac{{\partial^{4} W_{stat} (X)}}{{\partial X^{4} }} = \frac{{ - q_{0}^{*} }}{D}[H(X - \hat{a}) - H(X - \hat{b})] $$
(26)

where \( D = \frac{1}{{12a_{R}^{2} }} \) is the flexural rigidity of the elastic beam at isothermal conditions and \( W_{stat} (X) \) denotes the corresponding static deflection of the beam.

Applying Laplace transform (24) to Eq. (26) and using the transformed boundary conditions (22)–(23), the solution \( W_{stat} (X) \), after inversion of the transform, is given by:

$$ {\mathbf{Set}} \, {\mathbf{I}}:W_{stat} (X) = - q_{0}^{*} a_{R}^{2} \left[ {P_{1} X^{3} + Q_{1} X^{2} + \frac{{(X - \hat{a})^{4} }}{2}H(X - \hat{a}) - \frac{{(X - \hat{b})^{4} }}{2}H(X - \hat{b})} \right] $$
(27)
$$ {\mathbf{Set}} \, {\mathbf{II}}:W_{stat} (X) = - q_{0}^{*} a_{R}^{2} \left[ {3Q_{2} X^{2} - 2P_{2} X^{3} + \frac{{(X - \hat{a})^{4} }}{2}H(X - \hat{a}) - \frac{{(X - \hat{b})^{4} }}{2}H(X - \hat{b})} \right] $$
(28)

where \( P_{1} = (1 - \hat{b})^{3} (1 + \hat{b}) - (1 - \hat{a})^{3} (1 + \hat{a}) \)

$$ Q_{1} = \frac{1}{2}\left[ {(1 - \hat{a})^{3} (1 + 3\hat{a}) - (1 - \hat{b})^{3} (1 + 3\hat{b})} \right] $$
$$ P_{2} = \hat{b} - \hat{a},\;Q_{2} = \hat{b}^{2} - \hat{a}^{2} $$
(29)

It may be noted here that at adiabatic conditions, the flexural rigidity \( D \) becomes \( D = \frac{{1 + \varepsilon_{1} }}{{12\,a_{R}^{2} }} \) and consequently, the deflections at adiabatic conditions can be written from Eqs. (27) and (28) by replacing \( a_{R}^{2} \) with \( \frac{{a_{R}^{2} }}{{\,1 + \varepsilon_{1} }} \). This completes the solution of the model equation at static situation and under considered boundary and loading conditions.

5.2 Dynamic analysis

This subsection is devoted to explore the response of the beam under the action of time varying patch loads as under:

Case I: Continuous Patch Load

Upon applying Laplace transform (24) to Eq. (18), along with boundary conditions (22)–(23) at \( X = 0 \) and load \( \bar{q}_{1} (X,S) \) in Eq. (21) and simplifying, one get

Set I:

$$ \begin{gathered} \tilde{\bar{W}}(\xi ,S) = \frac{{c_{1} }}{{2\eta^{2} }}\left( {\frac{\xi }{{\xi^{2} - \eta^{2} }} - \frac{\xi }{{\xi^{2} + \eta^{2} }}} \right) + \frac{{c_{2} }}{{2\eta^{2} }}\left( {\frac{1}{{\xi^{2} - \eta^{2} }} - \frac{1}{{\xi^{2} + \eta^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{q_{0}^{*} e^{{ - \hat{\tau }S}} }}{{S^{3} }}\left[ {\left( {e^{{ - \hat{a}\xi }} - e^{{ - \hat{b}\xi }} } \right)\left\{ { - \frac{1}{\xi } + \frac{1}{2}\left( {\frac{\xi }{{\xi^{2} + \eta^{2} }}} \right) + \frac{1}{2}\left( {\frac{\xi }{{\xi^{2} - \eta^{2} }}} \right)} \right\}} \right] \hfill \\ \end{gathered} $$
(30)

where \( c_{1} = \bar{W}^{''} (0,S),\,\,\,c_{2} = \bar{W}^{''''} (0,S) \)

Set II:

$$ \begin{gathered} \tilde{\bar{W}}(\xi ,S) = \frac{{c_{1} }}{{2\eta^{2} }}\left( {\frac{\xi }{{\xi^{2} - \eta^{2} }} - \frac{\xi }{{\xi^{2} + \eta^{2} }}} \right) + \frac{{c_{2} }}{{2\eta^{2} }}\left( {\frac{1}{{\xi^{2} - \eta^{2} }} - \frac{1}{{\xi^{2} + \eta^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{q_{0}^{*} e^{{ - \hat{\tau }S}} }}{{S^{3} }}\left[ {\left( {e^{{ - \hat{a}\xi }} - e^{{ - \hat{b}\xi }} } \right)\left\{ { - \frac{1}{\xi } + \frac{1}{2}\left( {\frac{\xi }{{\xi^{2} + \eta^{2} }}} \right) + \frac{1}{2}\left( {\frac{\xi }{{\xi^{2} - \eta^{2} }}} \right)} \right\}} \right] \hfill \\ \end{gathered} $$
(31)

Taking inverse of Laplace transforms in Eqs. (30) and (31) with respect to \( \xi \) and employing the boundary conditions (22)–(23) at the end X = 1 of the beam, the constants c j, (j = 1, 2) can be evaluated and used in Eqs. (30) and (31) to obtain the expressions for deflection in the beam. We have

Set I:

$$ \begin{gathered} \bar{W}(X,S) = \frac{{q_{0}^{*} e^{{ - \hat{\tau }S}} }}{{2S^{3}\Delta _{1} }}[A_{1} C(\eta X) - B_{1} S^{*} (\eta X) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\Delta _{1} \{ C(X - \hat{a})H(\,X - \hat{a}) - C(X - \hat{b})H(\,X - \hat{b})\} ] \hfill \\ \end{gathered} $$
(32)

Set II:

$$ \begin{gathered} \bar{W}(X,S) = \frac{{q_{0}^{*} e^{{ - \hat{\tau }S}} }}{{2S^{3}\Delta _{2} }}[A_{2} C(\eta X) - B_{2} S^{*} (\eta X) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\Delta _{2} \{ C(X - \hat{a})H(\,X - \hat{a}) - C(X - \hat{b})H(\,X - \hat{b})\} ] \hfill \\ \end{gathered} $$
(33)

where \( \Delta _{1} = 1 - \cos \,\eta \,\,\cosh \,\eta \),\( \Delta _{2} = 1 + \cos \,\eta \,\,\cosh \,\eta \)

$$ C(\eta \,X) = \cosh \,\eta \,X - \cos \,\eta \,X,\;S^{*} (\eta \,X) = \sinh \,\eta \,X - \sin \,\eta \,X $$
$$ C(X - \hat{a}) = - 1 + \frac{1}{2}\,\cos \,\eta \,(X - \hat{a})\, + \frac{1}{2}\,\cosh \,\eta \,(X - \hat{a}) $$
$$ C(X - \hat{b}) = - 1 + \frac{1}{2}\,\cos \,\eta \,(X - \hat{b})\, + \frac{1}{2}\,\cosh \,\eta \,(X - \hat{b}) $$
(34)

The quantities A i and B i (i = 1,2) have been defined by equations (76)–(79) in the Appendix.

6 Deflection in the physical domain

In order to obtain deflection in the physical domain, we employed the Laplace inversion formula defined by [33]:

$$ W(X,\tau ) = \frac{1}{2\pi i}\,\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {e^{S\tau } } \bar{W}(X,S)dS $$
(35)

where \( \gamma \) is a constant greater than the real parts of all the singularities of \( \bar{W}(X,S) \). Upon using formula (35) in Eqs. (32)–(33), we get

$$ {\mathbf{Set}} \, {\mathbf{I}}:W(X,\tau ) = \frac{1}{2\pi i}\,\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{{q_{0}^{*} e^{{S(\tau - \hat{\tau })}} }}{{2S^{3} }}} \,\,\,\frac{{F{}_{1}(\eta )}}{{\Delta _{1} }}\,dS $$
(36)
$$ {\mathbf{Set}} \, {\mathbf{II}}:W(X,\tau ) = \frac{1}{2\pi i}\,\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{{q_{0}^{*} e^{{S(\tau - \hat{\tau })}} }}{{2S^{3} }}} \,\,\,\frac{{F{}_{2}(\eta )}}{{\Delta _{2} }}\,dS $$
(37)

where

$$ \begin{gathered} F_{1} (\eta ) = A_{1} C(\eta X) - B_{1} S^{*} (\eta X) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\Delta _{1} \,[C(X - \hat{a})H(\,X - \hat{a}) - C(X - \hat{b})H(\,X - \hat{b})]\, \hfill \\ \end{gathered} $$
(38)
$$ \begin{gathered} F_{2} (\eta ) = A_{2} C(\eta X) - B_{2} S^{*} (\eta X) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\Delta _{2} \,[C(X - \hat{a})H(\,X - \hat{a}) - C(X - \hat{b})H(\,X - \hat{b})]\, \hfill \\ \end{gathered} $$
(39)

The integrals (36)–(37) will be evaluated by using calculus of residues, the procedure of which is described below:

The singular points of the integrand in expressions (36) and (37) are given by

$$ S = 0\,\,\,\,,\Delta _{1} = 0; $$
$$ S = 0\,\,\,\,,\;\Delta _{2} = 0 $$
(40)

respectively. These singular points are simple poles of the integrands for Set I and Set II, respectively.

The roots of the equations \( \Delta _{1} = 0 \) and \( \Delta _{2} = 0 \) are given as [34]:

$$ \eta {}_{n} = 4.73,\,7.8532,\left( {n + \frac{1}{2}} \right)\pi ;\;n \ge 3 $$
(41)
$$ \eta {}_{n} = 1.8751,\,4.6941,\left( {n - \frac{1}{2}} \right)\pi ;\;n \ge 3 $$
(42)

respectively. Using Cauchy residue theorem [33], we get

$$ W(X,\tau ) = \,\sum {{\text{Residues at the isolated singularities of}}\;e^{S\tau } \bar{W}(X,S)} $$
(43)

for Set I and Set II. The residue at S = 0 is given by

$$ \text{Re} s[e^{S\tau } \bar{W}(X,S),S = 0] = W_{stat} $$
(44)

Now, the Eq. (19) provides us

$$ S_{n} = i\sqrt {D_{p} } \,\eta_{n}^{2} \, $$
(45)

where \( \eta_{n}^{2} \) is given by Eqs. (41)–(42) in the respective cases. Using the expression (13) for \( p^{2} \) and adopting the procedure of Sharma and Kaur [29], the expression (45) for S n can be written as

$$ S_{n} \, = \,i\,S_{n}^{*} [1 + \frac{{\varepsilon_{1} }}{2}(1 + f(p_{1} ))] $$
(46)
$$ {\text{where}}\;S_{n}^{*} = \frac{{\eta_{n}^{2} }}{{\sqrt {12} \,a_{R} }},\;f(p_{1} ) = \frac{ - 12}{{p^{*2} }} + \frac{24\,}{{p^{*3} }}\,\tanh \,\left( {\frac{{p^{*} }}{2}} \right),\;p^{*} = \sqrt {\frac{{\Omega ^{*} S_{n}^{*} (1 + \tau_{0} S_{n}^{*} )}}{{K^{*} a_{R}^{2} }}} $$
(47)

Therefore, the residues of the integrands at S = S n are given by

$$ {\mathbf{Set}} \, {\mathbf{I}}:\text{Re} s[e^{S\tau } \bar{W}(X,S),S = S_{n} ] = \frac{{q_{0}^{*} \exp \{ S_{n} (\tau - \hat{\tau })\} }}{{2S_{n}^{3} }}\,\frac{{F_{1} (\eta_{n} )}}{{\frac{{d\Delta _{1} }}{dS}\left| {_{{S = S_{n} }} } \right.}},\;n = 1,\,\,2,\,\,3, \ldots \ldots \ldots $$
(48)
$$ {\mathbf{Set}} \, {\mathbf{II}}:\text{Re} s[e^{S\tau } \bar{W}(X,S),S = S_{n} ] = \frac{{q_{0}^{*} \exp \{ S_{n} (\tau - \hat{\tau })\} }}{{2S_{n}^{3} }}\,\frac{{F_{2} (\eta_{n} )}}{{\frac{{d\Delta _{2} }}{dS}\left| {_{{S = S_{n} }} } \right.}},\;n = 1,\,\,2,\,\,3, \ldots \ldots \ldots $$
(49)

The expression (43) with the help of Eqs. (44), (48) and (49) becomes:

$$ {\mathbf{Set}} \, {\mathbf{I}}:W_{dyn} (X,\tau ) = W_{stat} + \sum\limits_{n = 1}^{\infty } {\frac{{q_{0}^{*} \exp \{ S_{n} (\tau - \hat{\tau })\} }}{{2S_{n}^{3} }}\,\frac{{F_{1} (\eta_{n} )}}{{\frac{{d\Delta _{1} }}{dS}\left| {_{{S = S_{n} }} } \right.}}} $$
(50)
$$ {\mathbf{Set}} \, {\mathbf{II}}:W_{dyn} (X,\tau ) = W_{stat} + \sum\limits_{n = 1}^{\infty } {\frac{{q_{0}^{*} \exp \{ S_{n} (\tau - \hat{\tau })\} }}{{2S_{n}^{3} }}\,\frac{{F_{2} (\eta_{n} )}}{{\frac{{d\Delta _{2} }}{dS}\left| {_{{S = S_{n} }} } \right.}}} $$
(51)

The expressions (50) and (51) give us the dynamic deflection in clamped–clamped and cantilever thermoelastic thin beams due to continuous patch load (Case I).

Case II: Exponential-decaying patch load

Proceeding in a similar manner, the expressions for deflection in case of exponential decaying patch load can be obtained and are given below:

Set I: Clamped–Clamped (CC) Beam

$$ W_{dyn} (X,\tau ) = W_{stat} + \frac{{q_{0}^{*} }}{2}\left[ {\sum\limits_{n = 1}^{\infty } {\frac{{\Omega \exp (S_{n} \tau )}}{{S_{n}^{3} (S_{n} +\Omega )}}\,\frac{{F_{1} (\eta_{n} )}}{{\frac{{d\Delta _{1} }}{dS}\left| {_{{S = S_{n} }} } \right.}} - \frac{{\exp ( -\Omega \tau )}}{{\Omega ^{2} }}\,\frac{{F_{1} (\eta_{2} )}}{{\Delta _{1} (\eta_{2} )}}} } \right] $$
(52)

Set II: Clamped-Free (CF) Beam

$$ W_{dyn} (X,\tau ) = W_{stat} + \frac{{q_{0}^{*} }}{2}\left[ {\sum\limits_{n = 1}^{\infty } {\frac{{\Omega \exp (S_{n} \tau )}}{{S_{n}^{3} (S_{n} +\Omega )}}\,\frac{{F_{2} (\eta_{n} )}}{{\frac{{d\Delta _{2} }}{dS}\left| {_{{S = S_{n} }} } \right.}} - \frac{{\exp ( -\Omega \tau )}}{{\Omega ^{2} }}\,\frac{{F_{2} (\eta_{2} )}}{{\Delta _{2} (\eta_{2} )}}} } \right] $$
(53)
$$ {\text{where}}\;\eta_{2} = \sqrt[4]{3}\,(1 + i)\sqrt {a_{R}\Omega } \,[1 - \frac{{\varepsilon_{1} }}{4}(1 + f(p_{2} ))],\;p_{2} = \sqrt {\frac{{{\varOmega \varOmega }^{*} (1 - \tau_{0}\Omega )}}{{K^{*} a_{R}^{2} }}} $$
(54)

This determines the solution of the model equation in dynamic situation under considered boundary and loading conditions.

7 Response and frequency ratios

Here we can also explore the response and frequency ratios of the clamped–clamped (CC) and clamped-free (CF) beams. The response and frequency ratios of the beam have been defined as [35]:

$$ R(\tau ) = \frac{{W_{dyn} }}{{W_{stat} }} $$
(55)

and

$$ \Gamma = \frac{\varOmega }{{S_{n}^{*} }} $$
(56)

respectively. Here the quantities \( W_{stat} \), \( W_{dyn} \), \( S_{n}^{*} \) have been defined in Eqs. (27)–(28), (50)–(53), (47) and \( \Omega \) is the excitation frequency of the applied load.

This completes the analytical study of the transverse vibrations in clamped–clamped and cantilever thermoelastic thin beam under the action of a time varying patch loads acting within the region AB of the beam.

8 Variational iteration method (VIM)

This section is devoted to study the transverse deflection of thermoelastic thin beam under considered transverse patch loads in cases I and II by using variational iteration method (VIM). The basic concept of He’s variational iteration method [23] is briefly introduced as under:Consider a non-linear differential equation

$$ L\,[u(x)] + N[u(x)] = g(x) $$
(57)

where \( L \) is a linear operator, \( N \) is a non-linear operator and g(x) is a source inhomogeneous term.

According to VIM, a correction functional can be written as:

$$ u_{n + 1} (x) = u_{n} (x) + \int\limits_{0}^{x} {\lambda (\zeta )\{ Lu_{n} } (\zeta ) + N\tilde{u}_{n} (\zeta ) - g(\zeta )\} d\zeta ,\;n \ge 0 $$
(58)

where \( \lambda \) is a Lagrange multiplier that can be determined optimally via variational theory. The subscript n indicates the nth approximation and \( \tilde{u}_{n} \) is considered as a restricted variation (\( \delta (\tilde{u}{}_{n}) = 0 \)).

The successive approximations \( u_{n + 1} (x) \) of the solution \( u(x) \) are obtained with the help of Lagrange multiplier \( \lambda \) and the trial function u 0. Consequently, the solution u(x) is given by

$$ u(x) = \mathop {\lim }\limits_{n \to \infty } \,u_{n + 1} (x) $$
(59)

The convergence of the variational iteration method has been investigated by the authors [36, 37].

Employing variational iteration technique to model Eq. (18) along with boundary conditions (22)–(23), the correctional functional is given by

$$ \bar{W}_{n + 1} (X,S) = \bar{W}_{n} (X,S) + \int\limits_{0}^{X} {\lambda (\zeta )\,\left[ {\frac{{d^{4} \bar{W}_{n} (\zeta ,S)}}{{d\zeta^{4} }} - \eta^{4} \tilde{\bar{W}}_{n} (\zeta ,S) - \frac{1}{{D_{p} }}\bar{q}_{1} (\zeta ,S)} \right] } \,d\zeta $$
(60)

where \( \bar{q}_{1} (\zeta ,S) \) can be written from Eq. (20) for Case I and Case II and \( \tilde{\bar{W}}_{n} \) is a restricted variation.

Taking variation on both sides of Eq. (60) with respect to \( \bar{W}_{n} \) and integrating by parts, one can obtain

$$ \begin{aligned} \delta \bar{W}_{n + 1} (X,S) & = \delta \bar{W}_{n} (X,S) + \lambda (X)\delta \bar{W}_{n}^{'''} (X,S) - \lambda^{'} (X)\delta \bar{W}_{n}^{''} (X,S) + \lambda^{''} (X)\delta \bar{W}_{n}^{'} (X,S) \\ & \quad - \lambda^{'''} (X)\delta \bar{W}_{n} (X,S) + \int\limits_{0}^{X} {\lambda^{''''} } (\zeta )d\zeta \\ \end{aligned} $$
(61)

For stationary conditions (\( \delta (\bar{W}_{n + 1} ) = 0 \)), the Eq. (61) provides us

$$ \left. {\lambda (\zeta )} \right|_{\zeta = X} = 0 $$
$$ \left. {\lambda^{'} (\zeta )} \right|_{\zeta = X} = 0 $$
$$ \left. {\lambda^{''} (\zeta )} \right|_{\zeta = X} = 0 $$
$$ \left. {1 - \lambda {}^{'''}(\zeta )} \right|_{\zeta = X} = 0 $$
$$ \lambda^{''''} = 0 $$
(62)

Upon solving Eq. (62), the Lagrange multiplier \( \lambda \) is obtained as

$$ \lambda = \frac{{(\zeta - X)^{3} }}{6} $$
(63)

Substituting \( \lambda \) from Eq. (63), the iteration formula (60) becomes:

$$ \bar{W}_{n + 1} (X,S) = \bar{W}_{n} (X,S) + \int\limits_{0}^{X} {\frac{{(\zeta - X)^{3} }}{6}\,\left[ {\frac{{d^{4} \bar{W}_{n} (\zeta ,S)}}{{d\zeta^{4} }} - \eta^{4} \bar{W}_{n} (\zeta ,S) - \frac{1}{{D_{p} }}\bar{q}_{1} (\zeta ,S)} \right]} \,d\zeta $$
(64)

The initial solution satisfying the boundary conditions at X = 0 is given by

$$ \bar{W}_{0} (X,S) = A\,\{ \cosh (\eta X) - \cos (\eta X)\} + B\,\{ \sinh (\eta X) - \sin (\eta X)\} $$
(65)

where A and B are the arbitrary constants to be determined. Using solution (65) in Eq. (64), the successive iterative approximations to solution for \( n = 1,2,3, \ldots ,k \) are obtained as under:

$$ \bar{W}_{1} (X,S) = \bar{W}_{0} (X,S) + \int\limits_{0}^{X} {\frac{{(\zeta - X)^{3} }}{6}\,\left[ {\frac{{{\text{d}}^{4} \bar{W}_{0} (\zeta ,S)}}{{{\text{d}}\zeta^{4} }} - \eta^{4} \bar{W}_{0} (\zeta ,S) - \frac{1}{{D_{p} }}\bar{q}_{1} (\zeta ,S)} \right]} \,{\text{d}}\zeta $$
(66)

Thus the solution of Eq. (18) for transverse deflection of thin thermoelastic beam under patch load, after evaluating the unknown constants A and B with the help of appropriate boundary conditions at X = 1, is given by

$$ \bar{W}(X,S) = \mathop {\lim }\limits_{k \to \infty } \,\bar{W}_{k} (X,S) $$
(69)

8.1 Evaluation of the eigenvalues

The eigenvalues are computed by dropping the non-homogeneous source term, so that the iteration formula (64) becomes

$$ \bar{W}_{n + 1} (X,S) = \bar{W}_{n} (X,S) + \int\limits_{0}^{X} {\frac{{(\zeta - X)^{3} }}{6}\,\left[ {\frac{{{\text{d}}^{4} \bar{W}_{n} (\zeta ,S)}}{{{\text{d}}\zeta^{4} }} - \eta^{4} \bar{W}_{n} (\zeta ,S)} \right]} \,{\text{d}}\zeta $$
(70)

The approximate solution that satisfies the boundary conditions at the end X = 0 will have the general form

$$ \bar{W}_{n} (X,S,\eta ) = cg_{n} (X,S,\eta ) + d\,h_{n} (X,S,\eta ),\;n > 0 $$
(71)

The Eq. (71) when subjected to the boundary conditions at the other end X = 1 of the beam leads to the following system of equations

$$ cg_{n}^{[k]} (1,S,\eta ) + {\text{d}}\,h_{n}^{[k]} (1,S,\eta ) = 0,\;k \in N $$
$$ cg_{n}^{[l]} (1,S,\eta ) + {\text{d}}\,h_{n}^{[l]} (1,S,\eta ) = 0,\;l \in N,\;l \ne k $$
(72)

For the existence of non-trivial solution of the system of Eq. (72), one must have

$$ D(\eta ,S) = \det \,\left( \begin{gathered} g_{n}^{[k]} (1,S,\eta )\,\,\,\,\,\,h_{n}^{[k]} (1,S,\eta ) \hfill \\ g_{n}^{[l]} (1,S,\eta )\,\,\,\,\,\,\,h_{n}^{[l]} (1,S,\eta ) \hfill \\ \end{gathered} \right) = 0 $$
(73)

The real roots of Eq. (73) give the eigenvalues of Eq. (18). Here the number of iterations (\( n \)) is decided by the equation:

$$ \left| {\eta_{i}^{n} - \eta_{i}^{n - 1} } \right| \le \varepsilon $$
(74)

where \( \varepsilon \) is a small value preset according to the desired accuracy, called tolerance parameter. Once the Eq. (74) is satisfied then \( \eta_{i} \) will be the ith eigenvalue of Eq. (18). Substituting \( \eta_{i} \) into Eq. (68), the transformed deflection \( \bar{W}(X,S) \) can be evaluated.

It is difficult to find the inverse Laplace transform of the expressions representing the transformed deflection of the thermoelastic thin beam obtained by using VIM in the Laplace domain analytically, a numerical inversion technique given by Durbin [38] based on Fourier series approximations for this purpose has been used. Adopting the Durbin’s formulation for inverse Laplace transform, the deflection in the physical domain is given by:

$$ W(X,\tau ) = \frac{{e^{\gamma \tau } }}{\Im }\left[ {\frac{1}{2}\text{Re} \{ \bar{W}(X,\gamma )\} + \sum\limits_{k = 1}^{\infty } {\text{Re} \{ \bar{W}(X,\gamma + i\frac{k\pi }{\Im })\} \cos \,\frac{k\pi }{\Im }t} } \right. $$
$$ - \left. {\sum\limits_{k = 0}^{\infty } {\text{Im} \{ \bar{W}(X,\gamma + i\frac{k\pi }{\Im })\} \sin \,\frac{k\pi }{\Im }t} } \right] $$
(75)

where \( \gamma > 0 \) is arbitrary, but greater than the real parts of all the singularities of \( \bar{W}(X,S) \). The Eq. (75) is the Fourier series representation of the function \( W(X,\tau ) \) in the interval \( [0,\Im ] \). According to Durbin [38], the Eq. (75) provides us the most suitable value for the interval \( 5 \le \gamma \,\Im \le 10 \) and \( k \) ranging from 50 to 5,000.

Equation (75) is a required expression in the physical domain for transverse deflection in the clamped–clamped and cantilever thermoelastic thin beams under the action of a time varying patch load.

9 Numerical results and discussion

With the aim to study the effects of dimensions, size and loadings on the deflection of the thermoelastic micro-beam at different positions and times during the vibrations, we present some numerical results in this section. The material of the beam for this purpose has been chosen as silicon carbide (SiC), as a representative of transversely isotropic materials, whose physical properties are given in Table 1. For the purpose of computations, a micro-beam having length \( L = 60\,\mu m \), width \( b = 5\,\mu m \) and thickness \( h = 1\,\mu m \) with fixed aspect ratio (\( a{}_{R} = 60 \)) has been considered. A patch load of intensity \( q_{0}^{*} = 1 \times 10^{ - 5} \, \) has been assumed to act on the region \( 0.25L \le x \le 0.75L \) of the beam so that \( \hat{a} = 0.25 \) and \( \hat{b} = 0.75 \).

Table 1 Physical data of silicon carbide (SiC) [39, 40]
Full size table

The non-dimensional values of the characteristic time in case of CC and CF beams have been estimated from the relation \( \tau_{c} = (S_{n}^{*} )^{ - 1} \) and are given as \( \tau_{c} \) = 9.29 and 59.17, respectively. The computations of non-dimensional dynamic deflections and response ratios have been carried out for the fundamental mode of vibrations with the help of MATLAB software. The deflection-time response history has been performed at the points X = 0.1, 0.5 on the axial axis. The numerically computed results in respect of deflection and response ratio have been presented graphically in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 in case of LS model, \( \tau_{0} = 9.29 \) for C–C beam and \( \tau_{0} = 59.17 \) for CF beam. For CT model, \( \tau_{0} = 0 \) and the deflection profiles have been noticed to follow similar trends and behaviour except some small variations in their magnitudes. For VIM, we have taken \( \varepsilon = 0.0001 \) and calculated some of the eigenvalues (\( \eta_{i} \)) for CC and CF as given in Table 2. Because the authors are interested to investigate and compare the deflection profiles for the fundamental mode of vibrations, so only first eigenvalue has been evaluated. For the CC beam, the first dimensionless eigenvalue \( \eta_{1}^{5} \) is obtained in the sixth iteration whereas \( \eta_{1}^{3} \) for CF beam is achieved in the third iteration. The other eigenvalues can also be evaluated with repeated iterations. These eigenvalues are exactly the same as those obtained in Ref [29] and those in Eqs. (41) and (42).

Table 2 Eigen values for CC and CF beam
Full size table
Table 3 Deflection of elastic (E) and thermoelastic (TE) micro-beams
Full size table
Fig. 1
figure 1

Deflection (W) of CC micro-beam versus X (Case I)

Full size image
Fig. 2
figure 2

Analytical and numerical solution profiles of deflection (W) in CC micro-beam (Case I)

Full size image
Fig. 3
figure 3

Deflection (W) of CC micro-beam versus time (τ) for given delay time (\( \hat{\tau } \)) (Case I)

Full size image
Fig. 4
figure 4

Deflection (W) of CF micro-beam versus X (Case I)

Full size image
Fig. 5
figure 5

Deflection (W) of CF micro-beam versus time (\( \tau \)) for given delay time (\( \hat{\tau } \)) (Case I)

Full size image
Fig. 6
figure 6

Deflection-time history of micro-beams for given X (Case I)

Full size image
Fig. 7
figure 7

Response ratio (\( R_{{}} (\tau ) \)) versus time (τ) (Case I)

Full size image
Fig. 8
figure 8

Maximum deflection (\( W_{\hbox{max} } \)) of CF micro-beam versus X (Case II)

Full size image
Fig. 9
figure 9

Maximum deflection (\( W_{\hbox{max} } \)) of CC micro-beam versus X (Case II)

Full size image
Fig. 10
figure 10

Analytical and numerical solution profiles of deflection (\( W_{\hbox{max} } \)) in CC micro-beam (Case II)

Full size image
Fig. 11
figure 11

Deflection-time history of CC and CF micro-beams for given X (Case II)

Full size image
Fig. 12
figure 12

Maximum deflection (\( W_{\hbox{max} } \))—frequency ratio (Г) curves of CC & CF micro-beams (Case II)

Full size image
Fig. 13
figure 13

Response ratio (\( R_{\hbox{max} } (\tau ) \)) versus time (τ) (Case II)

Full size image

The effect of temperature change and thermal parameters on the deflection profiles of CC and CF micro-beams at their characteristic times under continuous and exponential decaying patch loads is clearly visible from the computed data presented in Table 3. It is observed that the magnitude of deflection of thermoelastic micro-beam is greater than that of elastic micro-beam. This is attributed to the fact that in the presence of thermal variations, the molecular bonds get loose and material particles are sparsely distributed in comparison to that in the absence of temperature change. Therefore, heating or cooling significantly affects the flexural vibration characteristics of the thin beams under study.

Case I: Continuous patch load

Figures 1, 2, 3, 4, 5, 6 depict the variations of normalised dynamic deflection of micro-beam with X and time (\( \tau \)) due to continuous patch load. Figure 1 shows the dimensionless deflection of CC beam, as a function of X for \( \tau = 1,\,5,\,9.29\, \) and 15 at \( \hat{\tau } = 0 \). It is observed that the deflection profiles of the micro-beam decreases with the increasing time under the given load. Strong reactions have been noticed at the constrained ends of the beam. It is also noticed that the deflection profiles are symmetrical about the mid-point (X = 0.5) of the beam. Figure 2 is the deflection of CC micro-beam at time \( \tau = 1 \) and \( \hat{\tau } = 0 \) obtained by Laplace transform (analytical) and VIM—Durbin (numerical) techniques. The value of \( \gamma \,\Im \) is chosen as 5 with the summation of 1,000 terms in the later method. Numerical computations for both the approaches have almost the same values, which indicate that both analytical and numerical solutions exhibit good agreement and provide us accurate results.

Figure 3 displays the deflection of CC beam with time at X = 0.5 for \( \hat{\tau } = 0,\,50,\,100 \). It is noticed that as the value of \( \hat{\tau } \) increases, the peaks and dips of vibrations shift towards the left. Figure 4 depicts the dimensionless deflection of CF beam versus X for different values of time (\( \tau = 1,\,30,\,59.17,\,70 \)) at \( \hat{\tau } = 0 \). It is seen that the transverse deflection of cantilever beam decreases as time increases. The effect of the conditions prevailing at both axial ends is clearly visible from the profiles. Figure 5 illustrates the deflection of CF beam with time at X = 0.5 for various values of delay time (\( \hat{\tau } \)). It is noticed that the peaks and dips of vibrations shift towards the right as the value of \( \hat{\tau } \) increases. Figure 6 demonstrates the deflection-time response history of CC and CF micro-beams at \( \hat{\tau } = 0 \). Here the profiles of CF (X = 0.5) have been extrapolated (0.2 times) in magnitude to have variations of deflection on the same scale. It is observed that the deflection profiles of CC beam follow oscillatory behaviour with dimensionless time in contrast to CF beam for which it follows sinusoidal trends of variations. The magnitude of deflection is noticed to be maximum at the mid of the beam which decreases as one moves away from this point. The deflection profiles are seen to be symmetrical about the mid-point of the beam. It is also noticed that the magnitude of deflection in case of CF beam is larger than that of CC beam under same loading conditions. Figure 7 demonstrates the dynamic response ratio of CC and CF micro-beams due to continuous patch load. It is observed that the response ratio follows oscillatory behaviour for CC beam and sinusoidal behaviour for CF beam with time (\( \tau \)) under continuous patch loading. It is also noticed that the magnitude of response ratio is almost same for both CC and CF micro-beams.

From the comparison of Figs. 1, 2, 3, 4, 5, 6, 7, it is noticed that the deflection with respect to axial distance (X) in the CC beam is small as compared to that in CF (cantilever) beam. The time period of oscillation of cantilever beam has been noticed to be twice in magnitude as compared to that in CC beam. Both the micro-beams, CC and CF observe oscillatory behaviour of variations, though the beam under CF conditions obeys sinusoidal trends. The peaks and dips of vibrations shift towards the left for CF micro-beam with increasing values of \( \hat{\tau } \) in contrast to that CC beam in which case these shift towards the right. The magnitude of response ratio has been noticed to be almost equal for both the micro-beams. Results obtained both by Laplace transform and VIM techniques are found to be in good agreement with each other.

Case II: Exponential decaying patch load

Figures 8 and 9 demonstrate the relation between \( W_{\hbox{max} } \) versus X in CF and CC micro-beams. It is predicted that the maximum deflection increases with time and becomes steady and stable at large values of time (\( \tau \)). For CC beam, the deflection profiles are noticed to be symmetrical about the mid-point of the beam. The impact of boundary conditions prevailing at the axial ends is clearly visible from the graphs. Figure 10 depicts the comparison of the maximum deflection in CC micro-beam resonator obtained by Laplace transform (analytical) technique and by VIM-Durbin (numerical) method. The Durbin’s parameter \( \gamma \,\Im \) and k are chosen to be 9 and 1,000, respectively for the latter technique. From the profiles in this figure, one can conclude that both analytical and numerical solutions give close results as anticipated.

Figure 11 demonstrates the deflection-time history of the CC and CF micro-beam resonators. The profiles of CF (X = 0.5) have been extrapolated (0.2 times) to that of CC beam in order to be on the same scale. It is seen that the deflection profiles of CC beam vary linearly for \( 0 < \tau \le 60 \), and follow sinusoidal trend of variations for \( \tau > 60 \). However for CF beam, the deflection profiles vary linearly for \( 0 < \tau \le 120 \), and follow sinusoidal trend of variations for \( \tau > 120 \). The magnitude of deflection for CF is noticed to be greater than that of CC beam. The relation between deflection and frequency ratio (Г) for different times has been presented in Fig. 12 on log-linear scales. The deflection profiles of CF (X = 0.1) and CF (X = 0.5) have been extrapolated (0.2 times) to that of C–C beam for the discussion purpose. It is predicted that the deflection profiles of both CC and CF micro-beam resonators remains steady and stable up to the frequency ratio \( \Gamma \le 10^{ - 2} \). The deflection initially increases for \( 10^{ - 2} <\Gamma < 1 \), may be due to numerical approximation in curve fitting, and then decreases abruptly to reach its peak value in the neighbourhood of \( \Gamma = 1 \) (\( 10^{ - 1} \le\Gamma < 10 \)). This shows the occurrence of resonance in deflection of the micro-beams. The deflection in the beams varies linearly in a horizontal fashion for \( \Gamma \ge 10 \). The deflection in CF beam experiences more deflection than that of CC beam under same intensity of load. Figure 13 illustrates the dynamic response ratio of CC and CF beam resonators due to exponential decaying patch load. It is noticed that for CC beam the response ratio varies linearly with time for \( 0 < \tau \le 60 \) and becomes almost constant after attaining the values close to \( R_{\hbox{max} } (\tau ) = 1 \) for \( \tau > 60 \). However for CF beam, the response ratio varies linearly with time for \( 0 < \tau \le 120 \) and becomes almost constant after remaining close to \( R_{\hbox{max} } (\tau ) = 1 \) for \( \tau > 120 \). The aperiodic nature of the load has been clearly depicted from the dynamic response profiles of CC and CF beams.

From the comparison of Figs. 8, 9, 10, 11, 12, 13, it is observed that the maximum deflection (\( W_{\hbox{max} } \)) increases with time and becomes steady and asymptotic at large time. The deflection profiles of CC beam are symmetrical about the mid-point of the beam. The impact of non-periodicity of the load has been clearly observed on the phenomenon of resonance. The time period of oscillation of the micro-beam is twice in case of CF conditions than that for CC one. The magnitude of response ratio has been noticed to be almost same for the CC and CF micro-beams. Both the Laplace transform (analytical) and VIM—Durbin (numerical) results are found to be close to each other.

10 Conclusions

The transverse vibrations of homogeneous, transversely isotropic, thermoelastic thin beams subjected to time varying (anharminic) patch loads have been investigated by using Laplace transform and variational iteration method (VIM)—Durbin techniques. The deflection in case of fundamental mode has been observed to be maximum at the time of application of the load. For CC micro-beam, the deflection profiles are noticed to be symmetrical about the midpoint of the beam. The clamped-free (CF) beam experiences more deflection than that of clamped–clamped (CC) one. The time period of oscillations of CF beam is noticed to be larger than that for CC micro-beam. The time history suggests that the micro-beam observe oscillatory behaviour of vibration under CC and CF conditions though it is sinusoidal in the later one. The phenomenon of resonance is observed in the micro-beams under both mechanical conditions (CC and CF) when load and structural frequencies match each other. The influence of the dynamic character on the CC and CF micro-beams has been noticed to be almost same in case of considered patch load (Case I and Case II). The relaxation time (t 0) has meagre effect on the deflection of the micro-beams due to patch loading. The results obtained by VIM and analytical method compare well and agree to reasonable accuracy. It is verified that VIM is accurate, simple and a systematic powerful mathematical tool for solving the vibrations problems of uniform Euler–Bernoulli beams. The study may find applications in design and improvement of micro-devices such as micro-resonators, micro-switches, micro-gyroscopes and accelerometers under patch loading.