1 Introduction

Parametric excitation is a class of oscillation problems in which one parameter of the system varies alternatively by time. First time Faraday (1831) observed this phenomenon while studying the vibration of fluid filled container [1]. Then Rayleigh [2] studied a systematic mathematical analysis and provided a theoretical basis for these observations. The differential equations of motion for these systems are linear second-order ones with periodically time-varying coefficients. There are many techniques in the literature that have been proposed for obtaining approximate solutions to these equations and defining regions of stability and instability in certain parameter range. For example, Hsu [3–5] solved the Mathieus equation with different boundary conditions analytically and obtained the instability regions.

Boston [6] investigated the response of a nonlinear form of the Mathieu equation with cubic nonlinearity in the first unstable region using the method of harmonic balance. Zavodney et al. [7] studied the response of a single-degree-of-freedom system with quadratic and cubic nonlinearities to a principal parametric resonance. They used the method of multiple scales to determine the fixed points and their stability. Szamplinska-Stupnicka et al. [8] investigated Period doubling and chaos in un-symmetric structures under parametric excitation. They modeled a shallow arch or buckled mechanism by a single-degree-of-freedom and studied nonlinear oscillations of the parametrically-excited system with quadratic and cubic nonlinearities. El-Dib [9] studied nonlinear Mathieu equation and coupled resonance mechanism utilizing the method of multiple-scales to determine a third-order solution for a cubic nonlinear Mathieu equation. Zounes and Rand [10] used Lie transform perturbation theory and elliptic functions to study subharmonic resonances in the nonlinear Mathieu equation. Ng and Rand [11, 12] used a combination of the averaging and perturbation methods to investigate the classical form of the Mathieu equation with the cubic nonlinearities. Insperger and Stepan [13] studied on the stability of the damped Mathieu equation with time delay using Hill’s infinite determinant method. Jazar [14] determined stability chart of parametric vibrating systems using energy-rate method. Younesian et al. [15] studied the nonlinear generalized Mathieu equation, with cubic and quadratic nonlinearities using the two-dimensional Lindstedt–Poincaré method. Morrison and Rand [16] investigated resonance in the delayed nonlinear Mathieu equation with a general delay period using the averaging method to determine stability charts and find the associated bifurcations. Younesian et al. [17] obtained asymptotic solutions for the generalized form of the non-homogeneous Mathieu equation using the strained parameter technique and determined transition curves using the multiple scales method. Cveticanin and Kovacic [18] studied the parametrically excited vibrations of an oscillator with strong cubic negative nonlinearity using the two-dimensional Lindstedt–Poincare perturbation method. Gogu [19] studied bifurcation in constraint singularities in connection with structural parameters of parallel mechanisms and demonstrated the relation between these singularities and the structural parameters of the parallel robots. Amer and Hegazy [20] investigated the nonlinear behavior of a string-beam coupled system subjected to parametric excitation using the method of multiple scales. Zhang et al. [21] studied the nonlinear oscillations and chaotic dynamics of a simply supported rectangular plate made of functionally graded materials (FGMs) subjected to a through-thickness temperature field together with parametric and external excitations using the asymptotic perturbation method based on the Fourier expansion and the temporal rescaling.

There are many physical systems in which parametric oscillations are observed. These systems are: columns made of nonlinear elastic material [22], beams with a harmonically variable length [23], flexible disk rotating at periodically varying angular speed [24] parametrically excited two degrees of freedom vibrating systems [25], axially moving belts [26, 27], parametrically excited pendulums [28, 29], floating offshore structures [30], and so on.

Parametrically excited vibrations in micro-electromechanical systems (MEMS) were demonstrated in [31], and recently it has become an active area of research and extensively has been utilized in MEMS devices, for example, Hu et al. [32] presented an analytical approach to the static, dynamic, and stability analysis of the microstructures subjected to electrostatic forces and they analyzed an electrically actuated micro-cantilever beam as a case study using the analytical approach. Krylov et al. [33] investigated the stabilization of electrostatically actuated microstructures using parametric excitation. Gallacher et al. [34] used combined parametric excitation and harmonic forcing to excite a MEMS electrostatic resonant gyroscope in order to improve its rate resolution performance. Rhoads et al. [35] studied the nonlinear response of resonant micro-beam systems with purely-parametric electrostatic actuation. Zhang and Meng [36] studied nonlinear responses and dynamics of the electrostatically actuated MEMS resonant sensors under two-frequency parametric and external excitations. Harish et al. [37] investigated the simple parametric resonance in an electrostatically actuated micro-electromechanical gyroscope theoretically and experimentally. Krylov et al. [38] reported an approach which allows the efficient parametric excitation of large-amplitude stable oscillations of a microstructure operated by a parallel-plate electrode. Hu et al. [39] performed an experimental study of high gain parametric amplification in an electrostatically actuated and sensed gyroscopic resonant MEMS sensor. Recently Rezazadeh et al. [40] investigated parametric oscillation of an electrostatically actuated micro-beam which suspended between two conductive micro-plates and subjected to a same actuation voltage, Azizi et al. [41] studied mechanical behavior of a parametrically actuated functionally graded piezoelectric (FGP) clamped–clamped micro-beam and Fu et al. [42] used the energy balance method to study a nonlinear oscillator arising in the microbeam-based micro-electromechanical system. The literature interested reader is referred to the existing review articles [43–45]. It can be expressed that the electrostatic actuation is one of the common methods of excitation because of the position-dependent nature of electrostatic forces and extensively is used in MEMS devices. MEMS devices can be implemented as a sensor to measure different properties of materials. As fluids have inertial and dissipative effects on vibrations, Rezazadeh et al. used a piezoelectrically actuated micro-sensor for simultaneous measurement of fluids viscosity and density [46].

In this paper, the stability of a two step micro-shaft suspended between arrayed electrostatic actuators and located in a Newtonian fluid is studied. The device can be used as a fluid viscosity sensor. The static stability of the system is studied and the fixed points of the micro-shaft are determined. Consequently the stability of the fixed points is studied by plotting the micro-shaft phase diagrams for different initial conditions. Subsequently it is shown that the dynamic behavior of the first mode of system is described by Mathieu–Hill equation. The corresponding transition curves and the solution of the governing equation are determined by utilizing variation iteration method. Finally obtained solutions from iteration method are examined by using the fourth-order Runge–Kutta method.

2 Mathematical modeling

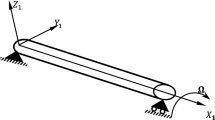
As shown in Fig. 1 the model is a two step clamped-free shaft subjected to an electrostatic excitation at the end of the first step, the second step of the shaft is located in a concentric stationary cylinder and the distance is filled with a Newtonian fluid. The system is modeled with isothermal, incompressible and steady state flow assumptions for fluid. The velocity profile for flow of a Newtonian fluid between two concentric cylinders assumed to be as [47]

(1)

where c 1 and c 2 are constant coefficients calculated satisfying boundary conditions \({u}_{\theta} ({r}_{2},{t})={r}_{2}\dot{\theta} ({L}_{1},{t})\) and u θ (r 3,t)=0. Hence the velocity profile of Eq. (1) gives

(2)

The shear stress for the Newtonian fluid can be written as

(3)

The electrostatic excitation is produced by using plate capacitors placed at end of the first step of the shaft and the outer cylinder, which are parallel to the radial and axial directions of the shaft. The stored energy in a parallel-plate capacitor is given as [48]

(4)

where C is the charge of the capacitor, V is the voltage applied to its terminals, A is the plate area, g is the separation distance between the plates and ε is the permittivity of free space. The produced electric force between the plates caused by the applied voltage is obtained by differentiating W with respect to g as

(5)

As shown in Fig. 2 for a differential element of area (dA=bdr) in the plate (a), the distance between two surfaces on plates (a) and (b) can be expressed as g=r(θ 0−θ), where θ 0 is the initial angular gap between plates and θ is the rotation angle of the shaft at the end of first step. The electric force of a differential element obtains as

(6)

The electrostatic torque between plates (a) and (b) is derived integrating contributions of all the plate elements as

(7)

In the same manner the electrostatic torque between plates (b) and (c) can be obtained substituting g=r(θ 0−θ) in Eq. (6) and repeating above operation. Hence the total electrostatic torque due to the rotation from the static equilibrium state can be obtained as

(8)

In order to improve the performance of the actuation capacitors, arrays of micro-plates consist of a multitude of coupled elements are used where their collective behavior enables a prominent improvement that is not achievable with the individual element performance. It is assumed the effects of the sets are gathered together and the effects of the sets on each other are neglected. Hence the total electrostatic torque can be expressed as

(9)

where n is the number of sets and θ 0=π/n. Equation of vibration of the shaft can be written as

(10)

where \({D}=2\pi\int_{0}^{{r}_{1}}{G}{r}^{3}{dr}\) and \({I}=2\pi\int_{0}^{{r}_{1}}\rho{r}^{3}{dr}\) are the torsional rigidity and moment of inertia of the first step of the shaft, G is the modulus of rigidity and ρ is the density of the shaft. The boundary conditions of the shaft can be expressed as

(11)

Homogenizing boundary conditions of the differential equation of vibration yields [46]

(12)

Substituting Eq. (2) and Eq. (3) into Eq. (12) yields

(13)

By expanding the total electrostatic torque using Calculus of Variation Theory and Taylor expansion about the static equilibrium position up to second order, total electrostatic torque is obtained as

(14)

where δV is the time varying alternating voltage having an amplitude V ac and a frequency Ω, δV=V accos(Ωt), and V dc is the constant bias or tuning voltage. Substituting the total electrostatic torque from Eq. (14) into Eq. (13) takes the following form

(15)

Introducing non-dimensional variables as \(\tilde{z}=\frac{{z}}{{L}_{1}}\), \(\tilde{{t}}=\frac{{t}}{{t}^{*}} \), \(\tilde{\theta} =\frac{\theta}{\theta_{0}}\) and substituting into Eq. (15) gives

(16)

where \(\tilde{b}=\frac{2{nb}\varepsilon {L}_{1}^{2}}{{D}\theta_{0}^{3}}\ln(\frac{{r}_{1}+{h}}{{r}_{1}})\), \(\tilde{{c}}=4\pi\mu\frac{{L}_{1}^{2}{L}_{2}}{{D}{t}^{*}} (\frac{{r}_{2}^{2}{r}_{3}^{2}}{{r}_{3}^{2}-{r}_{2}^{2}})\), \(\tilde{\varOmega} =\varOmega{t}^{*}\), \(\tilde{{a}}=\frac{{I}_{2}}{{I}}\) and \({t}^{*}=\sqrt{{{I}{L}_{1}^{2}}/{{D}}}\).

Fig. 1
figure 1

Schematic view of the system

Full size image
Fig. 2
figure 2

Schematic view of a set of capacitor plates

Full size image

3 Numerical solution

In order to solve Eq. (16) by using the Galerkin’s Weighted Residual Method, the solution approximated to be a product of functions of the independent variables

(17)

Substituting Eq. (17) into Eq. (16) and multiplying the obtained residual by \(\emptyset_{{k}}(\tilde{z})\) as a weight function in Galerkin method and integrating the outcome from \(\tilde{z}=0\) to 1 gives

(18)

where the equivalent mass, viscous damping factor, mechanical stiffness and electrical stiffness matrices respectively are given by:

(19)

In order to obtain an approximate solution with assumption of one degree-of-freedom model n is considered to be one (n=1). Hence Eq. (18) yields

(20)

By applying the transformation \(\tau =\frac{\tilde{\varOmega} \tilde{t}}{2}\) to Eq. (20) a classic damped Mathieu type equation with time varying periodic coefficients is obtained as following

(21)

where \(\gamma =\frac{4{K}_{11}+4{F}_{11}{V}_{\mathrm{dc}}^{2}}{{M}_{11} \tilde{\varOmega}^{2}},\epsilon =\frac{4{F}_{11}{V}_{\mathrm{dc}}{V}_{\mathrm{ac}}}{{M}_{11} \tilde{\varOmega}^{2}}\) and \(\xi\omega_{{n}}=\frac{{C}_{11}}{{M}_{11}\tilde{\varOmega}}\) are constant coefficients. By defining new variable \({q}_{1}=\psi{e}^{-\xi \omega _{{n}}\tau}\) an un-damped form of Mathieu equation is obtained from Eq. (21) as

(22)

where δ=γ−(ξω n )2.

4 Stability analysis

In this section the stability of the micro-shaft near and beyond the static pull-in voltage (pitch fork bifurcation point) is studied by imposing an AC voltage to DC one.

4.1 Static stability

The equilibrium between the applied electrostatic torque T e (V,θ) and the mechanical elastic torque is the static stability condition of the micro-shaft therefore at the equilibrium position the following relationship must be satisfied

(23)

where \({k}_{{eq}}=\frac{{D}}{{L}_{1}}\) is equivalent torsional stiffness of the micro-shaft. The tip rotation angle of the micro-shaft can be obtained by solving the nonlinear Equation (23) at a given applied DC voltage.

4.2 Dynamic stability related to parametric excitations

In order to obtain the transition curves which are the boundaries of the stable and unstable regions, the strained parameter technique is used. It is assumed that δ represented by an expansion having the form

(24)

where δ i are constants that should be determined such that the secular terms are not appeared in results.

Substituting Eq. (24) into Eq. (22) gives the following equation

(25)

For the values of δ 0=k 2 where k is a nonnegative integer and small values of ϵ solution of Eq. (25) is stable.

4.2.1 Let δ 0 be zero

The iteration formula for solving Eq. (25) using VIM [49], while δ 0 is equal to zero, caned be written as

(26)

In the first step, ψ 0(τ)=α is obtained as solution of Eq. (25) considering δ 0=0 and ϵ=0, where α is a constant belong to arbitrary initial conditions. In the second step, in order to attain the first-order approximate solution, it is assumed that δ is reduced to the first-order power expansion. The first-order approximate solution of Eq. (25), considering iteration formula of Eq. (26) can be written as

(27)

Simplifying Eq. (27) gives the first-order approximate solution as

(28)

In order to prevent secular term δ 1 must be equal to zero, hence Eq. (28) yields

(29)

With the aim of achieving the second-order approximate solution, Eq. (29) and the second-order reduced power expansion of δ is used in iteration procedure.

(30)

Simplifying Eq. (30) and eliminating the higher orders of ϵ gives

(31)

Setting \(\delta_{2}=-\frac{1}{2}\), eliminates the secular term in approximate solution. Therefore the second-order approximate solution can be obtained as

(32)

Hence the equation of transition curve which commences from δ=0 can be written as

(33)

4.2.2 Let δ 0 be one

The iteration formula for solving Eq. (25) using VIM [48] considering δ 0=1 can be written as

(34)

Beginning with ψ 0(τ)=βsin(τ) and using iteration formula of Eq. (34) and first-order reduction of δ the first-order approximate solution can be obtained as

(35)

Eliminating secular term in Eq. (35) by taking (δ 1=1) and utilizing second-order reduction of δ in iteration procedure the second-order approximate solution can be obtained as

(36)

It should be taken \(\delta_{2}=-\frac{1}{8}\) in order to eliminate the secular term in Eq. (36). Hence the equation of transition curve which commences from δ=1 can be written as

(37)

Simply can be shown that by beginning with ψ 0(τ)=αcos(τ) and using iteration formula of Eq. (34), the second transition curve which commences from δ=1 can be obtained as

(38)

So it can be shown that by beginning with ψ 0(τ)=βsin(2τ) and ψ 0(τ)=αcos(2τ) respectively transition curves which commence from δ=4 can be obtained as

(39)

As a verification the obtained transition curves using variational method coincides with those obtained by perturbation method [50].

5 Solution of equation

Beginning with ψ 0(τ)=αcos(ωτ)+βsin(ωτ) and using iteration formula of Eq. (34), the first approximate solution of Eq. (22) can be obtained as

(40)

where \(\omega =\sqrt{\delta}\), α=ψ(0) and \(\beta ={\dot{\psi} (0)}/{\omega}\). Using Eq. (40) in iteration procedure, the second approximate solution can be expressed as

(41)

where

(42)

Using Eq. (41) in iteration procedure, the third approximate solution can be obtained as

(43)

where

(44)

Equation (43) gives a third approximate solution using applying direct VIM, in which exist secular terms, therefore the obtained results are valid only for small time. Of course in the stable regions by combining VIM with the method of strained parameter as same as Lindstedt-Poincare method it is possible to obtain periodic solutions.

6 Numerical results

In order to validate this approach, numerical results are calculated for a two-stage micro-shaft which is made of polycrystalline silicon and its characteristics are shown in Table 1.

Table 1 Geometrical and material properties of the micro-shaft
Full size table

6.1 DC voltage excitation

Fixed points of the micro-shaft are obtained by solving Eq. (23). The fixed points of the micro-shaft versus applied DC voltage are depicted in Fig. 3. As shown in Fig. 3 when the applied voltage is low, the system has three fixed points which one of them is stable and the others are unstable. As voltage crosses through the Pitchfork bifurcation point, the pull-in phenomenon is occurred and only one unstable fixed point is emerged.

Fig. 3
figure 3

Micro-shaft tip dimensionless rotation angle versus applied DC voltage

Full size image

In order to investigate the stability of fixed points, the dynamic governing equation is solved by using fourth-order Runge–Kutta numerical integration method for the DC excitation voltage. The results for various initial conditions are depicted in phase diagrams.

There is only one stable center at \(\tilde{\theta} =0\) while no voltage is applied (V=0 V); as shown in Fig. 4a. But when applied voltage is under static pull-in value (V sp) two other unstable saddle nodes are emerged, as shown in Fig. 4b, There are a basin of attraction of stable center which is bounded by a homoclinic orbit and two basin of repulsion of unstable saddle nodes, in this situation depending on the initial conditions, the system can be stable or unstable. When the applied voltage approaches the static pull-in voltage, the stable and unstable branches of the fixed points approach and meet each other in bifurcation diagram. This point is known as pitchfork bifurcation point. The basin of attraction of stable attractor is vanished when the applied voltage approaches or crosses through the pull-in value and the micro-shaft is unstable for any set of initial conditions, Figs. 4c and 4d show this states.

Fig. 4
figure 4

Phase diagrams of the micro-shaft with different initial conditions and various excitation voltages V. (a) V=0 V, (b) V=0.5 V, (c) V sp=0.684 V, (d) V=1 V

Full size image

6.2 Parametric excitations

The functions φ i are taken to be the mode shapes of the clamped-free micro-shaft, namely

(45)

which satisfies the homogenized boundary conditions. The transition curves which are obtained analytically are depicted in Fig. 5, in fact transition curves separate the stable and unstable regions and along them there exists periodic solutions. For the values in the shaded regions the solution is unbounded. For the values in the non-shaded regions it is bounded.

Fig. 5
figure 5

Stable and unstable (shaded) regions in the parameter plane for the Mathieu equation

Full size image

The stable and unstable regions in terms of AC voltage versus DC voltage for given excitation frequencies are depicted in Figs. 6 and 7. The shaded regions are translated to the right by increasing the parameter \(\tilde{\varOmega}\).

Fig. 6
figure 6

Amplitude of V ac versus V dc for \(\tilde{\varOmega} =0.01\)

Full size image
Fig. 7
figure 7

Amplitude of V ac versus V dc for \(\tilde{\varOmega} =0.02\)

Full size image

With the aim of examination of precision of the transition curves, numerical solutions of Mathieu equation for five particular points A–E in parameter (ϵ–δ) plane are carried out. Figure 8 shows solutions for point A (V dc=103 V, V ac=28 V, \(\tilde{\varOmega} =0.01\)), which is located in the unstable region at the ϵ–δ plane and the obtained solution is unbounded and its amplitude increases by increasing time.

Fig. 8
figure 8

Time history and phase diagram for point A (δ=4.03, ϵ=0.37)

Full size image

It can be seen from Fig. 9, the solutions at point B (V dc=95 V, V ac=25 V, \(\tilde{\varOmega} =0.01\)) located in stable region is bounded and oscillatory.

Fig. 9
figure 9

Time history and phase diagram for point B (δ=3.83, ϵ=0.31)

Full size image

As illustrated in Fig. 10 solutions at point C (V dc=90 V, V ac=30 V, \(\tilde{\varOmega} =0.02\)) located in unstable region is unbounded.

Fig. 10
figure 10

Time history and phase diagram for point C (δ=0.93, ϵ=0.09)

Full size image

Solutions at point D (V dc=60 V, V ac=30 V, \(\tilde{\varOmega} =0.02\)) located in stable region is bounded and oscillatory and illustrated in Fig. 11.

Fig. 11
figure 11

Time history and phase diagram for point D (δ=0.78, ϵ=0.06)

Full size image

It can be seen from Fig. 12 the response at point E (V dc=122 V, V ac=27 V, \(\tilde{\varOmega} =0.02\)) located in stable region is bounded and oscillatory.

Fig. 12
figure 12

Time history and phase diagram for point E (δ=1.14, ϵ=0.11)

Full size image

In order to verify the accuracy of the asymptotic analytical procedure, Eq. (22) is re-written in the form of the system of two first-order linear ordinary differential equations and integrated using fourth-order Runge–Kutta method, and the result of VIM equation (43) is compared to those of the Runge–Kutta method for the initial conditions ψ(0)=0.001, \(\dot{\psi} (0)=0\). The time histories ψ(t) for various values of the parameters (ϵ=0.2 and ϵ=0.1) are shown in Figs. 13 and 14. These figures show obviously that during the initial time period the difference between the asymptotic analytical and numerical solutions is negligible.

Fig. 13
figure 13

Comparing VIM and RKM time histories for point (δ=0.2, ϵ=0.2)

Full size image
Fig. 14
figure 14

Comparing VIM and RKM time histories for point (δ=0.2, ϵ=0.1)

Full size image

7 Conclusions

The torsional vibration of a two stage micro-shaft located in a Newtonian fluid and subjected to electrostatic parametric excitations is investigated. The static stability of the system is studied and the fixed points of the micro-shaft are determined and the stability of the fixed points is studied by plotting the micro-shaft phase diagrams for different initial conditions. Subsequently the dynamic governing equation of motion is linearized about static equilibrium situation using calculus of variation theory and discretized using the Galerkin’s procedure. Then the device is modeled as a single-degree-of-freedom system and a Mathieu type equation is obtained. Then the stability regions of the system and solution of differential equation are obtained by using the variation iteration method. The effect of the parameters of system including the excitation frequency and applied DC voltage on the instability regions are discussed. The results obtained from this method have been compared with those obtained from fourth-order Runge–Kutta numerical integration method and excellent agreement observed between these methods. In addition, the results show that using a parametric excitation with an appropriate frequency and amplitude the system can be stabilized in the vicinity of the pitch fork bifurcation point. The obtained results can be useful in design of MEMS sensors especially in viscosity sensors.