Introduction

Extensive usage of different types of fluids in various industrial and engineering applications makes the study of heat and mass transfer for these fluids more desirable [1,2,3,4,5,6,7]. Micropolar fluids are subclass of microfluids [8]. In these fluids, randomly oriented rigid spherical particles having their own spins and microrotation where the deformation of fluid particles is not allowed are suspended in a viscous medium [9]. Some classic examples of micropolar fluids are human and animal blood, salty water, dusty fluids, polymeric fluids, liquid crystals, lubricants, colloidal suspension, and dilute solutions with long-chain atomic structures. Fluid flow due to stretching sheet can be seen in a variety of industry and engineering applications, such as a chemical engineering plant’s polymer processing unit, aerodynamic extrusion of plastic sheets, annealing of copper wires, hot rolling, fiber glass, drawing of plastic films, and paper production. Wide applications of this type of flow make researchers more interested in their study. Sakiadis [10,11,12] presented the theoretical analysis of boundary layer flow over a continuous solid surface moving at constant speed in 1961. Crane [13] expanded further Sakiadis’ work in 1970, exploring at fluid flow caused by stretching sheets. Bachok et al. [14] investigated the unsteady laminar flow of an incompressible micropolar fluid across a stretching sheet in 2011. The stagnation point flow of an incompressible micropolar fluid over a stretching sheet was studied by Nazar et al. [15] in 2004. Mohanty et al. [16] published a numerical study on the heat and mass transfer effect of a micropolar fluid across a stretching sheet through porous medium in 2015. In 2019, Mandal and Mukhopadhyay analyzed [17] behavior of boundary layer flow under the influence of nonlinear convection. Jain and Gupta [18] performed entropy generation analysis of micropolar fluid flow with radiation and thermal slip in 2019. In 2020, Ramadevi et al. [19] numerically studied 2D magnetohydrodynamic nonlinear radiative flow of micropolar fluid. Some more study for the micropolar fluids can be found easily in the literature [20,21,22,23,24,25,26].

Darcy law, which is applicable for flow with a small velocity or Reynolds number, is used to formulate viscous flow into porous media. Porous medium is a solid body that contains small void spaces (pores), which are distributed more or less throughout the body. In the study of viscous flow of micropolar fluids through porous media, many analytical and numerical techniques have been used previously. In [27], variation of parameters technique was used to find analytical solutions of laminar viscous flow in non-Darcy porous medium of micropolar fluid encountering uniform suction/injection. In [28], homotopy analysis method has been applied for the study of micropolar fluid flow. Quasi-linearization technique is applied to study fluid flow of micropolar fluid in [29,30,31]. In [32], finite difference method along with successive over relaxation method has been used for numerical investigation of micropolar fluid flow with porous medium. Fourier sine transform technique [33], Adomian decomposition method [34], homotopy perturbation method [35], Nachtsheim–Swigert iteration method [36], coupling of Runge–Kutta technique and shooting method [37,38,39], etc., are some techniques which were used in the study of fluid flow of micropolar fluids through porous media.

Most of the methods used in the study of micropolar fluid previously are cumbersome due to their semi-analytical nature. In addition, many methods depend on a very accurate initial solution. Due to these difficulties in the previously used methods, one needs to use a more simple and effective method for the study of fluid flow and thermal behavior of the micropolar fluids. Considering the simplicity and effectiveness of the finite difference approximation and classical Newton’s method, we have selected this combination for the current study. The key objective of this study is to investigate the effect of various flow parameters on the fluid flow, microrotation of microstructures present in the fluid, and thermal behavior of micropolar fluids. A detailed description of the present method is given in the method of solution section. In addition, a detailed investigation of the main objective of the current work is presented in the result and discussion section.

The numerical results obtained by the nonstandard finite difference approximation on a quasi-uniform mesh were compared with those obtained by the Runge–Kutta method. The numerical results obtained by both methods are in excellent agreement that validates our findings. The effect of various flow parameters on velocity, microrotation, and temperature distribution is demonstrated graphically in the result and discussion section. Finally, the work is concluded in the conclusion section.

Mathematical model

The theory of micropolar fluids are formulated by considering the principle of conservation of local angular momentum along with principle of conservation of mass and momentum [9]. The governing field equations of the motion are given as [8, 9]: Conservation of mass:

$$\begin{aligned} \frac{\partial {\rho }}{\partial {t}}+\nabla {\cdot }(\rho {\mathbf {U}}) = 0, \end{aligned}$$
(1)

Conservation of momentum:

$$\begin{aligned}&(\lambda _{{\mathrm{c}}}+2\mu _{{\mathrm{c}}}+\kappa _{{\mathrm{c}}})\nabla (\nabla \cdot {\mathbf {U}}) +\kappa _{{\mathrm{c}}}\nabla \times {\mathbf {W}}-\nabla {P}\nonumber \\&\quad -(\mu _{{\mathrm{ c}}}+\kappa _{{\mathrm{ c}}})\nabla \times \nabla \times {\mathbf {U}}+\rho \mathbf {f_{{\mathrm{ b}}}}\nonumber \\&=\rho \frac{D{\mathbf {U}}}{Dt}, \end{aligned}$$
(2)

local angular momentum conservation:

$$\begin{aligned}&(\alpha _{{\mathrm{ c}}}+\beta _{{\mathrm{ c}}}+\gamma _{{\mathrm{ c}}})\nabla (\nabla \cdot {\mathbf {W}}) - \gamma _{{\mathrm{ c}}}\nabla \times \nabla \times {\mathbf {W}} \nonumber \\&\quad + \kappa _{{\mathrm{ c}}}\nabla \times {\mathbf {U}} - 2\kappa _{{\mathrm{ c}}}{\mathbf {W}} + \rho {\mathbf {1}}\nonumber \\&=\rho j\frac{D{\mathbf {W}}}{Dt}, \end{aligned}$$
(3)

here, \({\mathbf {U}}, {\mathbf {W}}, \rho , \mathbf {f_{{\mathrm{ b}}}}, {\mathbf {1}}, P, j\) are velocity vector, microrotation vector, density, body force, body couple per unit mass, pressure, micro-inertia, respectively, and \(\lambda _{{\mathrm{ c}}},\) \(\mu _{{\mathrm{ c}}},\) \( \kappa _{{\mathrm{ c}}},\) \(\gamma _{{\mathrm{ c}}}\) are Stokes viscosity, dynamic viscosity, vortex viscosity, spin gradient viscosity, respectively. \(\alpha _{{\mathrm{ c}}}\) and \(\beta _{{\mathrm{ c}}}\) are material constants.

Consider the steady, 2−D incompressible flow of a micropolar fluid. Flow is considered across a homogeneous porous medium over a porous stretching sheet, assuming that the body force and the body couple are negligible. The permeability of porous medium is K. Fluid flow is affected due to linear stretching of a permeable sheet of length L along the \(x-\)axis. Flow linear velocity is \(U_{{\mathrm{ w}}}=U_0x/L\) in the direction of \(x-\)axis (along with the sheet). Under these assumptions Eqs. (1)–(3) gives:

$$\begin{aligned}&\frac{\partial {u}}{\partial {x}} + \frac{\partial {\nu }}{\partial {y}} = 0, \end{aligned}$$
(4)
$$\begin{aligned}&(\mu _{{\mathrm{ c}}}+\kappa _{{\mathrm{ c}}})\left( \frac{\partial ^2{u}}{\partial {x^2}} + \frac{\partial ^2{u}}{\partial {y^2}}\right) + \kappa _{{\mathrm{ c}}} \frac{\partial {\omega _3}}{\partial {y}} - \frac{\mu _{{\mathrm{ c}}}}{K}u \nonumber \\&\quad = \rho \left( u \frac{\partial {u}}{\partial {x}} + \nu \frac{\partial {u}}{\partial {y}}\right) , \end{aligned}$$
(5)
$$\begin{aligned}&\gamma _{{\mathrm{ c}}} \frac{\partial ^2{\omega _3}}{\partial {y^2}} - 2 \kappa _{ {\mathrm{c}}} \omega _3 + \kappa _{ {\mathrm{c}}} \frac{\partial {u}}{\partial {x}} = \rho j \nu \frac{\partial {\omega _3}}{\partial {y}}, \end{aligned}$$
(6)

where u and \(\nu \) are horizontal and vertical velocity components in the directions of \(x-\)axis and \(y-\)axis. \(\omega _3\) is the the microrotation’s component perpendicular to \(xy-\)plane.

The energy equation is:

$$\begin{aligned} u \frac{\partial {T}}{\partial {x}} + \nu \frac{\partial {T}}{\partial {y}} = \alpha _{{\mathrm{ eff}}} \frac{\partial ^2{T}}{\partial {y^2}}, \end{aligned}$$
(7)

where T is the fluid temperature and \(\alpha _{{\mathrm{ eff}}}\) is the effective thermal diffusivity.

The hydrodynamic boundary conditions are:

$$\begin{aligned} \left. \begin{array}{cccc} u(x^*,0)=U_0x^*, ~\nu (x^*,0)=\nu _{{\mathrm{ w}}}, ~\omega _3(x^*,0)=-m\dfrac{\partial {u}}{\partial {y}},\\ u(x^*,\infty )=0, ~-\omega _3(x^*,\infty )=0, \end{array} \right. \end{aligned}$$
(8)

where \(x^*=x/L\) is the nondimensional \(x-\)coordinate with permeable sheet’s length L, \(U_0\) is wall velocity coefficient which is constant, \(\nu _{{\mathrm{ w}}}\) is injection velocity and m is constant such that \(0\le m\le 1\). \(m=0\) case is called a strong concentration [40]. The concentrated particle flows in this situation, preventing the microelements adjacent to the wall surface from rotating [41]. The case \(m=0.5\) denotes weak concentrations and in this case the stress tensor’s antisymmetric part vanishes [42].The turbulent boundary layer flows are modeled using the \(m=1\) case [43]. The thermal boundary conditions considered are:

$$\begin{aligned} \left. \begin{array}{cccc} T(x^*,0)=T_{\infty } + T_0(x^*)^s, ~T(x^*,\infty )=T_{\infty } ~~ \text {Power-law temperature},\\ -\tau \left. \dfrac{\partial {T}}{\partial {y}}\right| _{(x^*,0)}=q_0(x^*)^s, ~T(x^*,\infty )=T_\infty ~~ \text {Power-law heat flux}, \end{array} \right. \end{aligned}$$
(9)

where \(T_0\) is wall temperature coefficient, \(T_\infty \) temperature far away from the sheet, \(q_0\) is wall heat flux coefficient, \(\tau \) is the medium’s effective thermal conductivity and s is power law index.

The following similarity transformation is used to generate the dimensionless form of the aforementioned equations:

$$\begin{aligned} \left. \begin{array}{cccc} \eta =\dfrac{y}{\sqrt{K}}, ~\psi =U_0x^*\sqrt{K}f(\eta ),\\ u=U_0x^*f'(\eta ), ~\nu =-\dfrac{U_0}{L}\sqrt{K}f(\eta ), ~\omega _3=\dfrac{U_0x^*}{\sqrt{K}}H(\eta ) \end{array} \right. \end{aligned}$$
(10)

where \(\psi \) is stream function, \(\partial {\psi }/\partial {y}=u\), \(-\partial {\psi }/\partial {x}=\nu \) and \(f'=\text{d}f/\text{d}\eta \). Under the similarity transformation (10), (5)–(7) are transformed into following coupled nonlinear ordinary differential equations:

$$\begin{aligned}&(1+c_1)f''' + R_\text{e}(ff''-{f'}^2) -f' +c_1H' = 0, \end{aligned}$$
(11)
$$\begin{aligned}&H'' - c_1c_2(f''- 2H) - c_3(f'H - fH') = 0, \end{aligned}$$
(12)
$$\begin{aligned}&\theta '' + P_{{\mathrm{ r}}}R_{{\mathrm{ e}}}(f\theta '- sf'\theta ) = 0, \end{aligned}$$
(13)

where prime denotes the differentiation with respect to \(\eta \), \(P_{{\mathrm{ r}}}\) is the Prandtl number, \(R_{{\mathrm{ e}}}=\rho U_0 K/L\mu _{{\mathrm{ c}}}\) is the Reynolds number, \(c_1=\kappa _{{\mathrm{ c}}}/\mu _{{\mathrm{ c}}}, c_2=\kappa _{{\mathrm{ c}}}\mu _{{\mathrm{ c}}}/\gamma _{{\mathrm{ c}}}, c_3=\rho j \kappa _{{\mathrm{ c}}}\mu _{{\mathrm{ c}}}/\gamma _{{\mathrm{ c}}}\) are dimensionless material constants.

Equations (8) and (9) give:

$$\begin{aligned} \left. \begin{array}{cccc} f(0)=\lambda , ~f'(0)=1, ~f'(\infty )=0,&\\ H(0)=0, ~H(\infty )=0,&\\ \theta (0)=1, ~\theta (\infty )=0,& (\text {Isothermal}),\\ \theta '(0)=-1, ~\theta '(\infty )=0,&(\text {Isoflux}), \end{array} \right. \end{aligned}$$
(14)

where \(\lambda =-\nu _{{\mathrm{ w}}}L/U_0\sqrt{K}\) is the mass suction/injection parameter. Positive \(\lambda \) is called mass suction parameter and negative \(\lambda \) is called mass injection parameter.

The physical quantities of interest are the local wall shear stress \(\tau _{{\mathrm{ w}}}\), the wall couple stress \(m_{{\mathrm{ w}}}\) and the heat transfer from sheet surface \(q_{{\mathrm{ w}}}\) which are defined as [44]:

$$\begin{aligned} \left. \begin{array}{cccc} \tau _{{\mathrm{ w}}}=\left[ (\mu _{{\mathrm{ c}}} + \kappa _{{\mathrm{ c}}})\dfrac{\partial {u}}{\partial {y}} + \kappa _{{\mathrm{ c}}}H\right] _{y=0},\\ m_{{\mathrm{ w}}}=\gamma _{{\mathrm{ c}}}\left[ \dfrac{\partial {H}}{\partial {y}}\right] _{y=0}, ~q_{{\mathrm{ w}}}=-\left[ \tau \dfrac{\partial {T}}{\partial {y}}\right] _{y=0}. \end{array} \right. \end{aligned}$$

Method of solution

The nonstandard finite difference approximation has been used to solve the boundary value problem (11)–(14). Quasi-uniform mesh is used to discretized BVP (11)–(14). The isothermal and isoflux boundary conditions considered separately in the solution procedure. To apply proposed method, we transformed the BVP (11)–(14) into a system of ordinary differential equations of first order as follows:

$$\begin{aligned} \left. \begin{array}{llll} \dfrac{{\mathrm {d}}g_1}{{\mathrm {d}}\eta }&=&g_2,\\ \dfrac{{\mathrm {d}}g_2}{{\mathrm {d}}\eta }&=&g_3,\\ \dfrac{{\mathrm {d}}g_3}{{\mathrm {d}}\eta }&=&\dfrac{1}{(1+c_1)}\left[ -R_e\left( g_1g_3-g_{2}^{2}\right) + g_2 - c_1g_5\right] ,\\ \dfrac{{\mathrm {d}}g_4}{{\mathrm {d}}\eta }&=&g_5,\\ \dfrac{{\mathrm {d}}g_5}{{\mathrm {d}}\eta }&=&c_1c_2\left( g_3-2g_4\right) +c_3\left( g_2g_4-g_1g_5\right) ,\\ \dfrac{{\mathrm {d}}g_6}{{\mathrm {d}}\eta }&=&g_7,\\ \dfrac{{\mathrm {d}}g_7}{{\mathrm {d}}\eta }&=&-P_{{\mathrm{ r}}}R_{ {\mathrm{e}}}\left( g_1g_7-sg_2g_6\right) , \end{array} \right. \end{aligned}$$
(15)

with boundary conditions

$$\begin{aligned} \left. \begin{array}{cccc} g_1(0)=\lambda , ~g_2(0)=1, ~g_2(\infty )=0,&\\ g_4(0)=0, ~g_4(\infty )=0,&\\ g_6(0)=1, ~g_6(\infty )=0,& (\text {Isothermal}),\\ g_7(0)=-1, ~g_7(\infty )=0,&(\text {Isoflux}), \end{array} \right. \end{aligned}$$
(16)

where \(g_1=f, g_2=f', g_3=f'', g_4=H, g_5=H', g_6=\theta \) and \(g_7=\theta '\).

In the present method, strictly monotone smooth quasi-uniform map \(\eta =\eta (\xi )\) has been considered. This quasi-uniform map is called grid generating function and defined as [45]:

$$\begin{aligned} \eta =-cp\cdot \text {ln}(1-\xi ), \end{aligned}$$
(17)

where \(\xi \in [0,1], \eta \in [0,\infty ]\) and cp is a control parameter. The uniform grids \(\xi _{{\mathrm{ n}}}=n/N; ~n = 0,1,2,\ldots ,N\) defined on interval [0, 1] with \(\xi _0=0\) and \(\xi _{{\mathrm{ n}}+1}=\xi _{{\mathrm{ n}}} + h\) with \(h = 1/N\) generated a quasi-uniform grids \(\eta _{{\mathrm{ n}}}=\eta (\xi _{{\mathrm{ n}}})\) on the interval \([0,\infty ]\). The last interval \([\eta _{ {\mathrm{N}}-1}, \eta _{ {\mathrm{N}}}]\) is infinite. The midpoint \(\eta _{{\mathrm{ N}}-1/2}\) of interval \([\eta _{{\mathrm{N}}-1}, \eta _{{\mathrm{ N}}}]\) is finite, because at the non-integer nodes the quasi uniform grids are defined as

$$\begin{aligned} \eta _{ {\mathrm{n}}+\delta }=\eta \left( \xi =\dfrac{n+\delta }{N}\right) , \end{aligned}$$

with \(n \in \{0,1,2,\ldots ,N-1\}\) and \(\delta \in (0,1)\). The infinite domain is represented by the finite number of intervals using the quasi-uniform map. The last node \(\eta _{ {\mathrm{N}}}\) of this mesh is placed at infinity so that the right-side boundary condition is taken into account properly.

The scalar function \(g(\eta )\) and its first derivative \(g'(\eta )\) at midpoints \(\eta _{{\mathrm{n}}+\frac{1}{2}}\), \(n=0,1,2,\ldots ,N-1\), applying nonstandard finite difference approximation are approximated as [46]:

$$\begin{aligned} g_{ {\mathrm{n}}+\frac{1}{2}} \approx \dfrac{\eta _{{\mathrm{ n}}+\frac{3}{4}}-\eta _{{\mathrm{ n}}+\frac{1}{2}}}{\eta _{{\mathrm{ n}}+\frac{3}{4}}-\eta _{{\mathrm{n}}+\frac{1}{4}}}g_{{\mathrm{ n}}} + \dfrac{\eta _{ {\mathrm{n}}+\frac{1}{2}}-\eta _{ {\mathrm{n}}+\frac{1}{4}}}{\eta _{{\mathrm{ n}}+\frac{3}{4}}-\eta _{{\mathrm{n}}+\frac{1}{4}}}g_{{\mathrm{n}}+1}, \end{aligned}$$
(18)
$$\begin{aligned} \left. \dfrac{{\mathrm {d}}g}{{\mathrm {d}}\eta }\right| _{{\mathrm{n}}+\frac{1}{2}} \approx \dfrac{g_{{\mathrm{n}}+1}-g_{{\mathrm{ n}}}}{2\left( \eta _{ {\mathrm{n}}+\frac{3}{4}}-\eta _{{\mathrm{n}}+\frac{1}{4}}\right) }, \end{aligned}$$
(19)

where \(g_{{\mathrm{ n}}}=g(\eta _{{\mathrm{ n}}})\). Formulae (18)–(19) use the value \(g_{{\mathrm{ N}}}=g_\infty \) without using last grid point \(\eta _{{\mathrm{ N}}}=\infty \). The order of accuracy of the approximation formulae (18) and (19) are \(O\left( N^{-2}\right) \).

Using nonstandard finite difference approximations (18) and (19) into system (15)–(16), we get a nonlinear system of equations with \(7\cdot (N+1)\) equations and \(7\cdot (N+1)\) unknowns namely \(g_{ {\mathrm{i}}}^{\text[n]}\) for \(i=1,2,\ldots ,7\) and \(n=0,1,2,\ldots ,N\), where \(g_{ {\mathrm{i}}}^{\text[n]}=g_{{\mathrm{ i}}}(\eta _{ {\mathrm{n}}})\).

Newton’s method is used for the solution of obtained nonlinear system of \(7\cdot (N+1)\) equations. In the solution by Newton’s method, the following simple termination criterion has been used

$$\begin{aligned} \left| \Delta g_{ {\mathrm{i}}}^{\text[n]}\right| \le \text {TOL} ~~\text {for}~~ i=1,2,\ldots ,7 ~~\text {and}~~ n=0,1,2,\ldots ,N, \end{aligned}$$

where \(\Delta g_{ {\mathrm{i}}}^{[n]}\) is the difference of two successive iterations of \(g_{{\mathrm{i}}}^{\text[n]}\) and \(\text {TOL}\) represents a fixed tolerance. In the next section, all the numerical computations were performed by fixing \(\text {TOL}=1\text {E}-8\). The initial guess in Newton’s method for isothermal wall temperature condition and isofux boundary condition are taken as:

Isothermal: \(g_1(\eta ) = \lambda , g_2(\eta )=1, g_3(\eta )=0, g_4(\eta )=0, g_5(\eta )=0, g_6(\eta )=1, g_7(\eta )=0\).

Isoflux: \(g_1(\eta ) = \lambda , g_2(\eta )=1, g_3(\eta )=0, g_4(\eta )=0, g_5(\eta )=0, g_6(\eta )=0, g_7(\eta )=-1\).

Results and discussion

Here, the numerical study of fluid flow and heat transfer in micropolar fluids through porous medium due to a permeable stretching sheet has been performed using nonstandard finite difference approximation. Isothermal wall temperature condition and isoflux boundary condition are considered in this investigation. The influence of the various physical parameters, namely the Reynolds number, Prandtl number, micropolar material parameters, injection/suction parameter, heat index parameter on flow speed, temperature distribution, and spin behavior of microstructures are presented graphically. The good agreement of the numerical results obtained by the current method with the Runge–Kutta method demonstrates the validity of our findings. The fixed values of the various physical parameters considered in this study are taken as: \(c_1=0.5\), \(c_2=0.1\), \(c_3=0.5\), \(\lambda =0\), \(P_r=1\), \(R_\text{e}=1\). For isothermal and isoflux boundary conditions \(s=0\) and \(s=1\) have been taken. Tables 1 and 3 show the comparison of flow speed obtained by the current method and Runge–Kutta technique with isothermal and isoflux boundary conditions, respectively. Tables 2 and 4 show a comparison of microrotation and temperature distribution by the present method and Runge–Kutta method with isothermal and isoflux boundary conditions, respectively. The numerical results by both the methods have an excellent agreement in Tables 1–4, which validates our study.

Table 1 Results by Runge–Kutta method (RKM) and present method with \(N=201\) (Isothermal)
Full size table
Table 2 Results by Runge–Kutta method (RKM) and present method with \(N=201\) (Isothermal)
Full size table
Table 3 Results by Runge–Kutta method (RKM) and present method with \(N=201\) (Isoflux)
Full size table
Table 4 Results by Runge–Kutta method (RKM) and present method with \(N=201\) (Isoflux)
Full size table

The effect of injection/suction parameter \((\lambda )\) on flow speed \(f'(\eta )\) under isothermal boundary condition has been shown in Fig. 1. The increasing value of \(\lambda \) reduces the boundary layer thickness, i.e., it decreases the flow speed.

Fig. 1
figure 1

Effect of \(\lambda \) on \(f'\) under isothermal condition

Full size image

Figure 2 shows effect of \(\lambda \) on dimensionless microrotation \(H(\eta )\). The microrotation decreases with an increasing value of \(\lambda \). It rises near the boundary and then starts decreasing gradually away from it.

Fig. 2
figure 2

Effect of \(\lambda \) on H under isothermal condition

Full size image

The influence of Prandtl number \((P_\text{r})\) with isothermal boundary condition on temperature profile is depicted in Fig. 3. The thickness of the thermal boundary layer reduces with an increasing value of Prandtl number \((P_\text{r})\).

Fig. 3
figure 3

Effect of \((P_\text{r})\) on \(\theta \) under isothermal condition

Full size image

Figure 4 shows that increasing value of Reynolds number \((R_\text{e})\) decreases value of flow speed \((f'(\eta ))\), i.e., boundary layer thickness reduces with increasing value of \((R_\text{e})\) under isothermal boundary condition.

Fig. 4
figure 4

Effect of \((R_\text{e})\) on \(f'\) under isothermal condition

Full size image

Figure 5 shows effect of Reynolds number \(R_\text{e}\) on dimensionless microrotation \(H(\eta )\). The microrotation increases near the boundary with an increasing value of \(R_\text{e}\). It decreases gradually away from the boundary.

Fig. 5
figure 5

Effect of \((R_\text{e})\) on H under isothermal condition

Full size image

Figure 6 represents temperature distribution \(\theta (\eta )\) for fluid flow with isothermal boundary condition under the influence of heat index parameter s. The thermal boundary layer of fluid flow decreases with an increasing value of s.

Fig. 6
figure 6

Effect of s on \(\theta \) under isothermal condition

Full size image

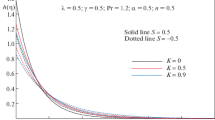
Figure 7 shows increment in boundary layer thickness of fluid flow with an increment in micropolar parameter \(c_1\), i.e., under isothermal boundary condition, with an increasing value of \(c_1\) flow speed \(f'(\eta )\) increases.

Fig. 7
figure 7

Effect of \(c_1\) on \(f'\) under isothermal condition

Full size image

Figure 8 demonstrates the thermal behavior of the fluid under the influence of micropolar parameter \(c_1\). The thermal boundary layer decreases with the increasing value of micropolar parameter \(c_1\). Figures 7 and 8 show that the effect of \(c_1\) on flow speed and temperature distribution are opposite.

Fig. 8
figure 8

Effect of \(c_1\) on \(\theta \) under isothermal condition

Full size image

The effect of injection/suction parameter \(\lambda \) on flow speed \(f'(\eta )\) with isoflux boundary condition is shown in Fig. 9. Figure 9 shows that flow speed reduces with an increasing value of \(\lambda \). Hence, from Figs. 1 and 9, it is remarkable that for isothermal as well as isoflux boundary conditions, the effect of \(\lambda \) on flow speed is the same.

Fig. 9
figure 9

Effect of \(\lambda \) on \(f'\) under isoflux condition

Full size image

Figure 10 displays the effect of \(\lambda \) on dimensionless microrotation \(H(\eta )\) under isoflux boundary condition. The microrotation decreases with an increasing value of \(\lambda \). It increases near the boundary then starts decreasing gradually away from the boundary. From Figs. 10 and 2, it is found that the influence of the injection/suction parameter on microrotation is the same for isothermal and isoflux boundary conditions.

Fig. 10
figure 10

Effect of \(\lambda \) on H under isoflux condition

Full size image

In Fig. 11, effect of Prandtl number \((P_\text{r})\) on temperature profile under isoflux boundary condition is presented. The thickness of thermal boundary layer reduces with an increasing value of Prandtl number \((P_\text{r})\), which is the same as in the isothermal boundary condition.

Fig. 11
figure 11

Effect of \(P_\text{r}\) on \(\theta \) under isoflux condition

Full size image

The effect of Reynolds number \((R_\text{e})\) on flow speed \(f'(\eta )\) under isoflux boundary condition is shown in Fig. 12. The boundary layer thickness reduces with an increasing value of \(R_\text{e}\). The effect of Reynolds number on the boundary layer thickness for both types of boundary conditions is the same.

Fig. 12
figure 12

Effect of \(R_\text{e}\) on \(f'\) under isoflux condition

Full size image

Figure 13 represents influence of the Reynolds number \((R_\text{e})\) on dimensionless microrotation \(H(\eta )\) under isoflux boundary condition. The microrotation increases near the boundary with an increasing value of \(R_\text{e}\). Figure 13 shows gradual decrease in \(H(\eta )\) away from the boundary.

Fig. 13
figure 13

Effect of \(R_\text{e}\) on H under isoflux condition

Full size image

The influence of the heat index s on temperature profile \(\theta (\eta )\) under isoflux boundary condition is depicted in Fig. 14. The thermal boundary layer of fluid flow reduces with an increasing value of s.

Fig. 14
figure 14

Effect of s on \(\theta \) under isoflux condition

Full size image

Figure 15 shows increment in boundary layer thickness of fluid flow with an increment in micropolar parameter \(c_1\), i.e., under isoflux boundary condition, with an increasing value of \(c_1\) flow speed \(f'(\eta )\) increases.

Fig. 15
figure 15

Effect of \(c_1\) on \(f'\) under isoflux condition

Full size image

Figure 16 demonstrates the thermal behavior of the fluid under the influence of micropolar parameter \(c_1\). The thermal boundary layer decreases with the increasing value of micropolar parameter \(c_1\). Figures 15 and 16 show that the effect of \(c_1\) on flow speed and temperature distribution are opposite. Hence, from Figs. 7, 8, 15, and 16, it is clear that the effect of micropolar parameter \(c_1\) on boundary layer thickness and thermal boundary layer thickness remains the same for the isothermal as well as the isoflux boundary conditions.

Fig. 16
figure 16

Effect of \(c_1\) on \(\theta \) under isoflux condition

Full size image

Conclusions

In this work, fluid flow, heat transfer, and microrotation of micropolar fluids with isothermal and isoflux boundary conditions have been studied using nonstandard finite difference approximation. The validity of our numerical results has been proved by comparing these with those obtained by the Runge–Kutta method. The findings of this study are concluded as follows:

  • The increasing value of the injection/suction parameter (negative to positive) reduces the thickness of boundary layer.

  • The increasing value of the injection/suction parameter (negative to positive) increases microrotation of the microstructures near the boundary.

  • For isothermal as well as isoflux boundary conditions, increasing the Reynolds number reduces the thickness of the fluid flow boundary layer.

  • The increasing value of the micropolar parameter reduces the thermal boundary layer thickness for both types of boundary conditions (isothermal and isoflux).

  • The increasing value of the micropolar parameter increases the boundary layer thickness of flow under isothermal as well as isoflux boundary conditions.

  • The thickness of the thermal boundary layer reduces with the increasing value of Prandtl number and heat index parameter for both types of boundary conditions (isothermal and isoflux).