Introduction

Dense motile agents, such as microorganism, cause bioconvection to occur. This happens upon their migration against gravity within a bulk fluid in response to stimuli. These self-propelled motile agents are basically a bit denser as compared to water. Hence, their upward migration creates a combination of asymmetric mass transfer and surface instability in the bulk fluid. All in all, the upward-downhill movement of microorganism produces a current, which is described as bioconvection. The steady boundary layer flow and heat transfer over a stretching sheet has attracted great interest of several researchers because of its many practical applications including wire drawing, rubber sheets, melt–spinning and plastic production. The initiated work of Sakiadis [1, 2] in expressing the laminar and turbulent boundary layer flow issue along with a constantly moving flat plate is so required because it is beneficial in the polymer engineering. Crane [3] reviewed the study of Sakiadis [1, 2] by changing the surface velocity according to the length of the fluid flow.

In the meantime, Carragher and Crane [4] carried out a series of investigation on similar studies, which focuses on gyrotactic bioconvection. Further, established the existence of stability for gyrotactic microorganism using the continuum assumption at the surface of the fluid. Moreover, conclusively proved the existence of strong hydrodynamic interaction between motile cellular organism and bulk fluid. They utilized about 85,000 microparticle beads in the effort to experimentally demonstrate the upward swimming of motile agents and bioconvection. Essentially, the upward swimming of the microorganism in the search of oxygen creates a torque balance. This have been mostly considered for utilization in nanofluids for passive control and thermal mixing [4].

Here is the modern literature that depicts the boundary layer flow over a moving surface with several impacts (see [5,6,7,8,9,10,11,12,13]). The boundary layer flow and heat transfer in the porous medium can be found in some practical applications like radioactive nuclear waste materials, separation procedure in chemical manufacturing, ground water pollution and filtration [14]. Ranganathan and Viskanta [14] initiated the issue of mixed convection flow over a vertical flat plate in a porous medium, and then extended by researchers in various setting [15] and in the bioconvection flow under different circumstances [16,17,18]. However, problems of the non-Newtonian bioconvection fluid flow and heat transfer received less attention from the researchers. Most works induced the nanofluids to enhance the performance of the heat transfer properties. Thus, the current problematic devoted to checking the behaviour of heat transfer characteristics of the micropolar fluid in a porous medium along with the presences of the microorganisms under the influences of heat generation/absorption and viscous dissipation, which is new to the scope of the bioconvection flow. The present work is essential as the biophysical properties of the fluid, distribution of motile constituents of the fluid and permeability features of the porous media may possess a crucial role in process control, involving bioreactors using fluid-containing microorganism embedded in a porous medium.

Active microorganism starts a collective natural process named bioconvection that is influenced by biochemical elements like temperature or light. It is related to the characteristics of the atmosphere [19]. Among its distinctive manner to exhibit its sensitivity is by responding fast and recognized as “taxis,” which represents the motion of the microorganisms away from the stimulus source (negative taxis) or to the stimulus source (positive taxis). Reaction of microorganisms to gravity is recognized as gravi-taxis [20]. The bioconvection procedure happened once the response of the microorganisms, that are slightly denser than water upswimming. As soon as further microorganisms gather at the superior area, that part turns out to be denser until at one point the suspensions become unbalanced and provoke the density reversal. Therefore, the microorganisms fell and made the bioconvection. The microorganisms can survive without the existence of water. They can be found in soil and vegetation [21]. The bioconvection phenomenon is useful in different applications in the bio-microsystems like enzyme biosensors [22], production of biodiesel, synthesis of other products in photobioreactors, and grey water treatment [23]. Both common kinds are usually exploited during the bioconvection experimentations, and diverse sorts of microorganisms have the particular direction of the system [23]. In the hypothetical investigation, the conservative mathematical model relied on oxytactic bacteria and bottom-heavy alga. Researcher progress concerning bioconvection was theoretically clarified in the subsequent literature: [24,25,26,27,28,29,30,31,32,33]. Concerning the boundary layer flow, Kuznetsov [34] focused on the issue of bioconvection flow along a horizontal surface in a nanofluid comprising a gyrotactic microorganism and described the perturbation solutions. Then, many researchers studied the bioconvection boundary layer flow and heat transfer under various settings and effects. One of them is by examining the phenomena of the bioconvection flow and its heat transfer properties in the micropolar fluid.

The micropolar fluid is a sort of non-Newtonian fluid that has rotating microstructures [35] and accentuates the confined impacts from the microstructure and the intrinsic motion of its fluid components [36]. This unique micropolar fluid has many practical applications in the industrial sectors such as clean and polluted engine lubricant, colloids and polymeric suspensions, thrust bearing technologies and radial diffusion paint rheology [36]. Eringen [37] established the model for the micropolar fluid, and then Peddieson and McNitt [38] examined the behaviour of the micropolar fluid within the vicinity of the boundary layer flow. Subsequently, many studies have been conducted to enhance the theoretical work of the micropolar fluid, for instance, in squeezing flow [39, 40], dusty fluid [41] and nanofluid [42,43,44]. The biophysical properties of the fluid, distribution of motile constituents of the fluid and permeability features of the porous media may possess a crucial role in process control, involving bioreactors using fluid-containing microorganism embedded in a porous medium. Thus, this study scrutinizes the free bioconvection transport of motile microorganism flowing in a micropolar fluid enclosed in a porous microstructure past a stretching/shrinking surface. The present study investigates the micropolar parameter effect on the transport of momentum, microorganism and mass in a micropolar fluid immersed in the porous media. The Darcian model is implemented in the investigation of the variable permeability impact on the distribution of microorganism within the fluid domain. Some process conditions such as suction and injection, stretching/shrinking state were selected and considered in the bulk of micropolar fluid flow. Then, the scaling group of transformation was utilised to obtain its impact on velocity, temperature and concentration fields. Not only that, the scaling group of transformation was solved numerically by introducing the Runge–Kutta procedure, assisted by the shooting method. The procedure has been explored to study the nano-bioconvectional transport of microorganism in nanofluid [37,38,39,40].

Ziabakhsh et al. [45] is the first work which had discovered the analytical solution for the problem of the boundary layer flow along with the effect of heat generation past a permeable stationery sheet in the micropolar fluid. Then, Uddin et al. [46] probed the boundary layer backward flow and heat transfer past an exponentially permeable sheet in a micropolar fluid and managed to obtain the non-uniqueness solutions when the act of suction dominates the surface of the sheet. El-Aziz [47] explored the impact of the viscous dissipation in mixed convection flow of the micropolar fluid past a stretching surface and determined that an increment of the viscous dissipation effect reduces the rate of convective heat transfer. Mutlag et al. [48] analysed the problem of the free convection micropolar fluid flow over a stretching vertical flat surface in a porous medium with the slip effects and concluded that the sheet permeability reduces the fluid temperature. It has been found that the impacts of the heat generation/absorption and viscous dissipation have not been considered in the free convection bioconvection micropolar fluid flow past a permeable stretching surface in a porous medium. Therefore, the present work extends the work of Mutlag et al. [48] by including the influences of heat generation/absorption and viscous dissipation while eliminating the slip effects. Moreover, new similarity variables are presented in this work, and the numerical solutions are generated by the finite difference scheme in the shooting technique. These efforts are the main contribution of the present work. The effects of the pertinent parameters are presented graphically and discussed in detail.

Mathematical model

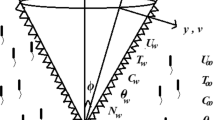
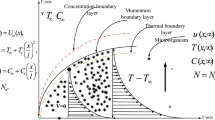
Figure 1 shows a steady two-dimensional free convective boundary layer flow of a micropolar fluid past a moving impermeable stretching/shrinking plate embedded in a Darcy porous medium with gyrotactic microorganisms. This study utilizes assumptions involving boundary layer such as (1) continuity equation (Eq. 1), (2) angular momentum boundary layer (Eq. 2), (3) thermal boundary layer (Eq. 3), concentration boundary layer (Eq. 4), and microorganism boundary layer (Eq. 5). Inside the boundary layer, the fluid temperature, the concentration, angular momentum and the density of motile microorganisms are expressed by \( T,\,C,\,N \) and \( n \), respectively. These assumptions aim to understand the dynamics of micropolar fluid flow for the given physical problem. The micropolar fluid moves with a constant velocity and flows under no-slip boundary conditions. The viscous dissipation and heat generation are also incorporated. According to these conditions and rules, the governing boundary layer equations can be expressed as [45, 46]:

$$ \nabla \cdot \,\vec{V} = 0, $$
(1)
$$ \rho \left( {\frac{{D\vec{V}}}{{D\bar{t}}}} \right) = - \nabla p + \left( {\mu + \kappa } \right)\,\,\nabla^{2} \overrightarrow {V\,} + \kappa \left( {\nabla N} \right) + \rho \vec{g} - \frac{\mu }{{k_{p} }}\vec{V}, $$
(2)
$$ \rho j\left( {\frac{{{\text{D}}N}}{{{\text{D}}\bar{t}}}} \right) = \gamma \,\nabla^{2} N + \kappa \left( { - 2N + \nabla \times \vec{V}} \right), $$
(3)
$$ \frac{{{\text{D}}T}}{{{\text{D}}\bar{t}}} = \alpha \,\nabla^{2} T + \left( {\frac{\mu + \kappa }{{\rho c_{\text{p}} }}} \right)\left( {\nabla \vec{V}} \right)^{2} + \frac{{Q\left( {\frac{{\bar{x}}}{L}} \right)}}{{\rho c_{\text{p}} }}\left( {T - T_{\infty } } \right), $$
(4)
$$ \frac{{{\text{D}}C}}{{{\text{D}}\bar{t}}} = D_{\text{m}} \left( {\nabla^{2} C} \right)\, - K\left( {\frac{{\bar{x}}}{L}} \right)\left( {C - C_{\infty } } \right), $$
(5)
$$ \frac{{{\text{D}}n}}{{{\text{D}}\bar{t}}} + \frac{{\tilde{b}W_{\text{c}} }}{{\Delta C}}\left( {\nabla n \cdot \,\nabla C} \right) = D_{\text{n}} \nabla^{2} n, $$
(6)

where \( \frac{\text{D}}{{{\text{D}}\bar{t}}} = \frac{\partial }{{\partial \bar{t}}} + \vec{V} \cdot \,\nabla \) is the material derivative, \( \nabla = \frac{\partial }{\partial x}\vec{i} + \frac{\partial }{\partial y}\vec{j}, \, \nabla^{2} \) is the Laplacian operator, \( \bar{t} \) is the dimensional time, \( \vec{V} = \left\langle {\vec{u},\vec{v}} \right\rangle \) is the velocity vector, p is the pressure, \( \vec{g} \) is the vector of gravity acceleration applied to the flow, \( k_{\text{p}} \) is the permeability of the porous media, \( \mu \) is the dynamic viscosity, \( \rho \) denotes the fluid density, \( \alpha \) denotes the thermal diffusivity of the fluid, \( \kappa \) is the microrotation viscosity coefficient, \( j \) symbolizes the micro-inertia density, \( \gamma \) is the spin gradient viscosity, \( c_{\text{p}} \) denotes the specific heat at a constant pressure, \( Q\left( {\frac{{\bar{x}}}{L}} \right) \) is the variable heat generation/absorption, and \( K\left( {\frac{{\bar{x}}}{L}} \right) \) is the variable reaction rate. In Eq. (6), \( \tilde{b} \) is the chemo taxis constant, and \( W_{\text{c}} \):maximum cell swimming speed.

Fig. 1
figure 1

Schematic diagram of the present model

Full size image

By applying the Oberbeck–Boussinesq approximation:

$$ \frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\partial \bar{v}}}{{\partial \bar{y}}} = 0, $$
(7)
$$ \begin{aligned} \bar{u}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{y}}} & = \left( {\frac{\mu + \kappa }{\rho }} \right)\frac{{\partial^{2} \bar{u}}}{{\partial \bar{y}^{2} }} + g\beta_{\text{T}} \left( {T - T_{\infty } } \right) + g\beta_{\text{C}} \left( {C - C_{\infty } } \right) + g\beta_{\text{n}} \left( {n - n_{\infty } } \right) \\ & \quad + \frac{\kappa }{\rho }\frac{{\partial \bar{N}}}{{\partial \bar{y}}} - \frac{\nu }{{{\text{k}}_{\text{p}} }}\left( {\bar{u}} \right), \\ \end{aligned} $$
(8)
$$ \bar{u}\frac{{\partial \bar{N}}}{{\partial \bar{x}}} + \bar{v}\frac{{\partial \bar{N}}}{{\partial \bar{y}}} = \frac{\gamma }{\rho j}\frac{{\partial^{2} \bar{N}}}{{\partial \bar{y}^{2} }} - \frac{\kappa }{\rho j}\left( {2\bar{N} + \frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right), $$
(9)
$$ \bar{u}\frac{\partial T}{{\partial \bar{x}}} + \bar{v}\frac{\partial T}{{\partial \bar{y}}} = \alpha \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }} + \left( {\frac{\mu + \kappa }{{\rho c_{\text{p}} }}} \right)\left( {\frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right)^{2} + \frac{{Q\left( {\frac{{\bar{x}}}{L}} \right)}}{{\rho c_{\text{p}} }}\left( {T - T_{\infty } } \right), $$
(10)
$$ \bar{u}\frac{\partial C}{{\partial \bar{x}}} + \bar{v}\frac{\partial C}{{\partial \bar{y}}} = D_{\text{m}} \frac{\partial C}{{\partial \bar{y}}} - K\left( {\frac{{\bar{x}}}{L}} \right)\left( {C - C_{\infty } } \right), $$
(11)
$$ \bar{u}\frac{\partial n}{{\partial \bar{x}}} + \bar{v}\frac{\partial n}{{\partial \bar{y}}} + \frac{{\tilde{b}W_{\text{c}} }}{{\bar{C}_{\text{w}} - \bar{C}_{\infty } }}\left[ {\frac{\partial }{{\partial \bar{y}}}\left( {n\frac{\partial C}{{\partial \bar{y}}}} \right)} \right] = D_{\text{n}} \left( {\frac{{\partial^{2} n}}{{\partial \bar{y}^{2} }}} \right), $$
(12)

where \( \beta_{\text{n}} \) is the coefficient of microorganism expansion, \( \beta_{\text{T}} \) is the coefficient of thermal volume expansion, g is the acceleration due to gravity. The corresponding boundary conditions are given as follows:

$$ \begin{aligned} \bar{u} &= \lambda U_{\text{w}} ,\,\,\,\bar{v} = V_{\text{w}} \left( {\frac{{\bar{x}}}{L}} \right),\,\,\,\, \hfill \\ \bar{N} &= - n_{1} \frac{{\partial \bar{u}}}{{\partial \bar{y}}},\,\,\,T = T_{\text{w}} ,\,\,\,C = C_{\text{w}} \,,\,\,\,n = n_{\text{w}} \quad \,{\text{at}}\,\,\,\bar{y} = 0, \hfill \\ \bar{u} &= 0, \,\,\,\bar{N} = 0,\,\,\,T \to T_{\infty } , \,\,\,C \to C_{\infty } , \,\,\,n \to n_{\infty } = 0 \,\,\,\,\,\,{\text{as }}\,\,\,\bar{y} \to \infty . \hfill \\ \end{aligned} . $$
(13)

Here \( U_{\text{w}} \) is the velocity of the moving plate, \( \lambda \) is the dimensionless stretching/shrinking parameter, and \( V_{\text{w}} \left( {\frac{{\bar{x}}}{L}} \right) \) is the suction/injection slip factor. The boundary conditions in Eq. (13) convey the state at the surface of the moving surface \( \left( {\bar{y} = 0} \right) \) and the setting far from the moving sheet \( \left( {\bar{y} \to \infty } \right) \). For example, the state of moving sheet is expressed with \( \bar{u} = \lambda U_{\text{w}} \), the sheet permeability signified by \( \bar{v} = V_{\text{w}} \left( {\frac{{\bar{x}}}{L}} \right) \), the state of spin condition of the micropolar fluid is given by \( \bar{N} = - n_{1} \frac{{\partial \bar{u}}}{{\partial \bar{y}}} \), where \( n_{1} \) is the boundary parameter and when \( n_{1} = 0 \), the microstructures near the moving surface does not rotate, while \( n_{1} = 0.5 \) elucidates weak rotation of the microstructures, and \( n_{1} = 0.5 \) is suitable for turbulent boundary layer flow. At the wall, surface temperature, volume fraction, and density of motile microorganisms are denoted by \( T_{\text{w}} ,\,C_{\text{w}} \) and \( n_{\text{w}} , \), respectively, and in the distance far from the wall (free stream) they are, respectively, denoted by \( T_{\infty } ,\,C_{\infty } \) and \( n_{\infty } , \), respectively. These conditions are essential to investigate the bioconvection flow of a micropolar fluid past a permeable moving surface.

Non-dimensionalisation of the governing equations

The conversion of the governing equations into dimensionless form is achieved via the subsequent dimensionless variables [48, 49]:

$$ \begin{aligned} & x = \frac{{\bar{x}}}{L},\,\quad \,\,y = \frac{{\bar{y}}}{L}\sqrt {\text{Re} } ,\,\,\quad \,u = \frac{{\bar{u}}}{{U_{\text{w}} }},\,\,\,\quad v = \frac{{\bar{v}}}{{U_{\text{w}} }}\sqrt {\text{Re} } ,\quad N = \frac{{\bar{N}L}}{{U_{\text{w}} \sqrt {\text{Re} } }},\,\quad \,\theta = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\,\,\, \\ & \phi = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }},\,\,\quad \,\chi = \frac{n}{{n_{\text{w}} }},\,\,\quad \text{Re} = \frac{{U_{\text{w}} L}}{\nu }, \\ \end{aligned} $$
(14)

where L is the characteristics length of the plate and Re is the Reynolds number. The stream function is signified by \( \psi \) and defined as \( u = \frac{\partial \psi }{\partial y} \) and \( v = - \frac{\partial \psi }{\partial x}. \) Next, substitute Eq. (14) into Eqs. (7)–(12) to decrease the equation number and independent variables. This substitution satisfied the continuity equation, while other equations can be expressed as follows:

$$ \begin{aligned} & \frac{\partial \psi }{\partial y}\frac{{\partial^{2} \psi }}{\partial x\partial y} - \frac{\partial \psi }{\partial x}\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = \left( {\frac{\mu + \kappa }{\rho }} \right)\frac{\text{Re}}{{U_{\text{w}} L}}\frac{{\partial^{3} \psi }}{{\partial y^{3} }} + \frac{{g\beta_{\text{T}} \left( {\theta \left( {T_{\text{w}} - T_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} \\ & \quad + \frac{{g\beta_{\text{C}} \left( {\phi \left( {C_{\text{w}} - C_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} + \frac{{g\beta_{\text{n}} \left( {\chi \left( {n_{\text{w}} - n_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} + \frac{{\kappa \text{Re} }}{{\rho U_{\text{w}} L}}\frac{\partial N}{\partial y} - \frac{\nu L}{{k_{\text{p}} U_{\text{w}} }}\left( {\frac{\partial \psi }{\partial y}} \right), \\ \end{aligned} $$
(15)
$$ \frac{\partial \psi }{\partial y}\frac{\partial N}{\partial y} - \frac{\partial \psi }{\partial x}\frac{\partial N}{\partial y} = \frac{{\gamma \text{Re} }}{{\rho jU_{\text{w}} L}}\frac{{\partial^{2} N}}{{\partial y^{2} }} - \frac{\kappa L}{{\rho jU_{\text{w}} }}\left( {2N + \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) $$
(16)
$$ \frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y} = \frac{{\alpha \text{Re} }}{{U_{\text{w}} L}}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \left( {\frac{\mu + \kappa }{{\rho c_{\text{p}} }}} \right)\frac{{U_{\text{w}} \text{Re} }}{L\Delta T}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + \frac{L}{{U_{\text{w}} \rho c_{\text{p}} }}Q(x)\theta , $$
(17)
$$ \frac{\partial \psi }{\partial y}\frac{\partial \phi }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial \phi }{\partial y} = \frac{{D_{\text{m}} }}{\nu }\frac{{\partial^{2} \phi }}{{\partial y^{2} }} - \frac{L}{{U_{\text{w}} }}K(x)\phi , $$
(18)
$$ \frac{\partial \psi }{\partial y}\frac{\partial \chi }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial \chi }{\partial y} + \frac{{\tilde{b}W_{\text{c}} }}{\nu }\left[ {\chi \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{\partial \phi }{\partial y}\frac{\partial \chi }{\partial y}} \right] = \frac{{D_{\text{n}} }}{\nu }\frac{{\partial^{2} \chi }}{{\partial y^{2} }}. $$
(19)

The boundary conditions in Eq. (13) become

$$ \begin{aligned} \frac{\partial \psi }{\partial y} = \lambda ,\,\quad \,\,\frac{\partial \psi }{\partial x} = \frac{{V_{\text{w}} \left( x \right)\sqrt {\text{Re} } }}{{U_{\text{w}} }},\,\,\quad \,\theta = 1,\,\,\quad \,\phi = 1,\,\,\,\chi = 1\,,\quad N = - n_{1} \,\frac{{\partial^{2} \psi }}{{\partial y^{2} }}\quad \quad {\text{at}} y = 0 \hfill \\ \frac{\partial \psi }{\partial y} = 0,\,\quad \,N = 0,\quad \, \theta \to 0, \,\,\,\,\,\phi \to 0, \,\,\,\,\,\chi \to 0 \,\,\,\,{\text{as }} \,\,\,\, y \to \infty . \hfill \\ \end{aligned} $$
(20)

Applications of the scaling group of transformations

The solution to the partial differential equations (PDEs) (15)–(19) subject to the boundary condition (20) is quite strenuous to be achieved directly due to its complexity and the solution being computationally expensive. This reason motivates us to employ the scaling group transformation. It is also a structured procedure to convert PDEs into the ordinary differential equations (ODEs). The scaling group transformation method premised on the invariance of the PDEs and the associated boundary conditions. First and foremost, the independent and dependent variables must be scaled out to find the invariant solution, as follows:

$$ \begin{aligned} \varGamma{:}\,x^{*} & = xe^{{\varepsilon \alpha_{1} }} ,y^{*} = ye^{{\varepsilon \alpha_{2} }} ,\psi^{*} = \psi e^{{\varepsilon \alpha_{3} }} ,\theta^{*} = \theta e^{{\varepsilon \alpha_{4} }} ,\phi^{*} = \phi e^{{\varepsilon \alpha_{5} }} ,\chi^{*} = \chi e^{{\varepsilon \alpha_{6} }} , \\ N^{*} & = Ne^{{\varepsilon \alpha_{7} }} ,k_{\text{p}}^{*} = k_{\text{p}} e^{{\varepsilon \alpha_{8} }} ,Q^{*} = Qe^{{\varepsilon \alpha_{9} }} ,K^{*} = Ke^{{\varepsilon \alpha_{10} }} ,j^{*} = je^{{\varepsilon \alpha_{11} }} , \\ \gamma^{*} & = \gamma e^{{\varepsilon \alpha_{12} }} ,V_{\text{w}}^{*} = V_{\text{w}} e^{{\varepsilon \alpha_{13} }} ,\,\,\beta_{\text{T}}^{*} = \beta_{\text{T}} e^{{\varepsilon \alpha_{14} }} ,\beta_{\text{c}}^{*} = \beta_{\text{c}} e^{{\varepsilon \alpha_{15} }} ,\beta_{\text{n}}^{*} = \beta_{\text{n}} e^{{\varepsilon \alpha_{16} }} . \\ \end{aligned} $$
(21)

In this case, \( \varepsilon \) is a parameter, while \( \alpha_{\text{i}} (i = 1,2, \ldots 16) \) are arbitrary real numbers with not all zero concomitantly at the same time. Therefore, transforming Eqs. (15)–(19) and boundary conditions Eq. (20) in (*) form,

$$ \begin{aligned} & \frac{{\partial \psi^{*} }}{{\partial y^{*} }}\frac{{\partial^{2} \psi^{*} }}{{\partial x^{*} \partial y^{*} }} - \frac{{\partial \psi^{*} }}{{\partial x^{*} }}\frac{{\partial^{2} \psi^{*} }}{{\partial y^{*2} }} = \left( {\frac{\mu + \kappa }{\rho }} \right)\frac{\text{Re}}{{U_{\text{w}} L}}\frac{{\partial^{3} \psi^{*} }}{{\partial y^{*3} }} + \frac{{g\beta^{*}_{\text{T}} \left( {\theta^{*} \left( {T_{\text{w}} - T_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} \\ & \quad + \frac{{g\beta^{*}_{\text{C}} \left( {\phi^{*} \left( {C_{\text{w}} - C_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} + \frac{{g\beta^{*}_{\text{n}} \left( {\chi^{*} \left( {n_{\text{w}} - n_{\infty } } \right)} \right)L}}{{U_{\text{w}}^{2} }} + \frac{{\kappa \text{Re} }}{{\rho U_{\text{w}} L}}\frac{{\partial N^{*} }}{{\partial y^{*} }} - \frac{\nu L}{{k_{\text{p}}^{*} U_{\text{w}} }}\left( {\frac{{\partial \psi^{*} }}{{\partial y^{*} }}} \right), \\ \end{aligned} $$
(22)
$$ \frac{{\partial \psi^{*} }}{{\partial y^{*} }}\frac{{\partial N^{*} }}{{\partial x^{*} }} - \frac{{\partial \psi^{*} }}{{\partial x^{*} }}\frac{{\partial N^{*} }}{{\partial y^{*} }} = \frac{{\gamma^{*} \text{Re} }}{{\rho j^{*} U_{\text{w}} L}}\frac{{\partial^{2} N^{*} }}{{\partial y^{*2} }} - \frac{\kappa L}{{\rho j^{*} U_{\text{w}} }}\left( {2N^{*} + \frac{{\partial^{2} \psi^{*} }}{{\partial y^{*2} }}} \right), $$
(23)
$$ \frac{{\partial \psi^{*} }}{{\partial y^{*} }}\frac{{\partial \theta^{*} }}{{\partial x^{*} }} - \frac{{\partial \psi^{*} }}{{\partial x^{*} }}\frac{{\partial \theta^{*} }}{{\partial y^{*} }} = \frac{{\alpha \text{Re} }}{{U_{\text{w}} L}}\frac{{\partial^{2} \theta^{*} }}{{\partial y^{*2} }} + \left( {\frac{\mu + \kappa }{{\rho c_{\text{p}} }}} \right)\frac{{U_{\text{w}} \text{Re} }}{{L\Delta T}}\left( {\frac{{\partial^{2} \psi^{*} }}{{\partial y^{*2} }}} \right)^{2} + \frac{L}{{U_{\text{w}} \rho c_{\text{p}} }}Q^{*} (x)\,\theta^{*} = 0, $$
(24)
$$ \frac{{\partial \psi^{*} }}{{\partial y^{*} }}\frac{{\partial \phi^{*} }}{{\partial x^{*} }} - \frac{{\partial \psi^{*} }}{{\partial x^{*} }}\frac{{\partial \phi^{*} }}{{\partial y^{*} }} = \frac{{D_{\text{m}} }}{\nu }\frac{{\partial^{2} \phi^{*} }}{{\partial y^{*2} }} - \frac{L}{{U_{\text{w}} }}K^{*} (x)\phi , $$
(25)
$$ \frac{{\partial \psi^{*} }}{{\partial y^{*} }}\frac{{\partial \chi^{*} }}{{\partial x^{*} }} - \frac{{\partial \psi^{*} }}{{\partial x^{*} }}\frac{{\partial \chi^{*} }}{{\partial y^{*} }} + \frac{{\tilde{b}W_{\text{c}} }}{\nu }\left[ {\chi^{*} \frac{{\partial^{2} \phi^{*} }}{{\partial y^{*2} }} + \frac{{\partial \phi^{*} }}{{\partial y^{*} }}\frac{{\partial \chi^{*} }}{{\partial y^{*} }}} \right] = \frac{{D_{\text{n}} }}{\nu }\frac{{\partial^{2} \chi^{*} }}{{\partial y^{*2} }}, $$
(26)

With respect to the boundary conditions from (20) in the following (*) form:

$$ \begin{aligned} & \frac{{\partial \psi^{*} }}{{\partial y^{*} }} = \lambda ,\,\,\,\,\frac{{\partial \psi^{*} }}{{\partial x^{*} }} = \frac{{V_{\text{w}}^{*} \left( x \right)\sqrt {\text{Re} } }}{{U_{\text{w}} }},\,\,\, \\ & \theta^{*} = 1,\,\,\,\phi^{*} = 1,\,\,\,\chi^{*} = 1 \,,N^{*} = - n_{1} \,\frac{{\partial^{2} \psi^{*} }}{{\partial y^{*2} }}\,\,\,\,\,\,\,\,\,{\text{at}}\,\,\,\, y = 0, \\ \frac{{\partial \psi^{*} }}{{\partial y^{*} }} = 0,\,N^{*} = 0,\,\,\,\theta^{*} \to 0,\,\,\,\,\phi^{*} \to 0,\,\,\,\,\chi^{*} \to 0 \quad {\text{as }} y \to \infty . \\ \end{aligned} $$
(27)

The system (22)–(27) remain invariant after applying the scaling group transformation in Eq. (21) if \( \alpha_{i} \)’s is correlated such as follows:

$$ \begin{aligned} & - \alpha_{1} - 2\alpha_{2} + 2\alpha_{3} = \alpha_{3} - 3\alpha_{2} = \alpha_{4} + \alpha_{14} = \alpha_{5} + \alpha_{15} = \alpha_{6} + \alpha_{16} = \alpha_{7} - \alpha_{2} = \alpha_{3} - \alpha_{8} - \alpha_{2} , \\ & - \alpha_{2} - \alpha_{1} + \alpha_{3} + \alpha_{7} = \alpha_{12} + \alpha_{7} - \alpha_{11} - 2\alpha_{2} = \alpha_{7} - \alpha_{11} = \alpha_{3} - \alpha_{11} - 2\alpha_{2} , \\ & - \alpha_{1} - \alpha_{2} + \alpha_{3} + \alpha_{4} = - 2\alpha_{2} + \alpha_{4} = 2\alpha_{3} - 4\alpha_{2} = \alpha_{9} + \alpha_{4} , \\ & - \alpha_{1} - \alpha_{2} + \alpha_{3} + \alpha_{5} = - 2\alpha_{2} + \alpha_{5} = \alpha_{10} + \alpha_{5} , \\ & - \alpha_{1} - \alpha_{2} + \alpha_{3} + \alpha_{6} = - 2\alpha_{2} + \alpha_{5} + \alpha_{6} = - 2\alpha_{2} + \alpha_{5} + \alpha_{6} = \alpha_{6} - 2\alpha_{2} , \\ \end{aligned} $$
(28)

and the boundary conditions (27) become

$$ \begin{aligned} & \alpha_{3} - \alpha_{2} = 0,\,\,\,\alpha_{3} - \alpha_{1} = \alpha_{13} ,\,\,\,\alpha_{4} = 0, \\ & \alpha_{5} = \alpha_{6} = 0,\,\,\alpha_{7} = \alpha_{3} - 2\alpha_{2} , \\ & \alpha_{3} - \alpha_{2} = 0,\alpha_{4} = \alpha_{5} = \alpha_{6} = \alpha_{7} = 0. \\ \end{aligned} $$
(29)

The linear system in Eqs. (28) and (29) are resolved and thus produced the following expression:

$$ \begin{aligned} & \alpha_{1} = 2\alpha_{2} ,\,\,\,\alpha_{2} = \alpha_{3} ,\,\,\alpha_{4} = \alpha_{5} = \alpha_{6} = 0,\,\,\,\alpha_{7} = \,\alpha_{13} = \alpha_{17} = - \alpha_{2} ,\,\,\, \\ & \alpha_{8} = \alpha_{11} = \,\alpha_{12} = 2\alpha_{2} ,\,\,\alpha_{9} = \alpha_{10} = \alpha_{14} = \alpha_{15} = \alpha_{16} - 2\alpha_{2} .\,\, \\ \end{aligned} $$
(30)

The group of conversions in Eq. (21) can be expressed in the form of \( \alpha_{2} \) when relying on Eq. (30),

$$ \begin{aligned} & \varGamma :x^{*} = xe^{{2\varepsilon \alpha_{2} }} ,y^{*} = ye^{{\varepsilon \alpha_{2} }} ,\psi^{*} = \psi e^{{\varepsilon \alpha_{2} }} ,\theta^{*} = \theta ,\phi^{*} = \phi ,\chi^{*} = \chi , \\ & N^{*} = Ne^{{ - \varepsilon \alpha_{2} }} ,k_{\text{p}}^{*} = k_{\text{p}} e^{{2\varepsilon \alpha_{2} }} ,Q^{*} = Qe^{{ - 2\varepsilon \alpha_{2} }} ,K^{*} = Ke^{{ - 2\varepsilon \alpha_{2} }} ,j^{*} = je^{{2\varepsilon \alpha_{2} }} , \\ & \gamma^{*} = \gamma e^{{2\varepsilon \alpha_{2} }} ,V_{\text{w}}^{*} = V_{\text{w}} e^{{ - \varepsilon \alpha_{2} }} ,\beta_{\text{T}}^{*} = \beta_{\text{T}} e^{{ - 2\varepsilon \alpha_{2} }} ,\beta_{\text{c}}^{*} = \beta_{\text{c}} e^{{ - 2\varepsilon \alpha_{2} }} ,\beta_{\text{n}}^{*} = \beta_{\text{n}} e^{{ - 2\varepsilon \alpha_{2} }} . \\ \end{aligned} $$
(31)

Expanding (31) via the Taylor’s series in power of \( \varepsilon \) and by ignoring the greater power of \( \varepsilon , \) the resulting formulation can be attained:

$$ \begin{aligned} & x^{*} = x(1 + 2\varepsilon \alpha_{2} ),\,\,\,y^{*} = y(1 + \varepsilon \alpha_{2} ),\,\,\,\psi^{*} = \psi (1 + \varepsilon \alpha_{2} ),\,\,\,\theta^{*} = \theta (1 + 0),\,\,\,\phi^{*} = \phi (1 + 0), \\ & \chi^{*} = \chi (1 + 0),\,\,\,N^{*} = N(1 - \varepsilon \alpha_{2} ),\,k_{\text{p}}^{*} = k_{\text{p}} (1 + 2\varepsilon \alpha_{2} ),\,\,\,Q^{*} = Q(1 - 2\varepsilon \alpha_{2} ),\,\,\,K^{*} = K(1 - 2\varepsilon \alpha_{2} ), \\ & j^{*} = j(1 + 2\varepsilon \alpha_{2} ),\,\gamma^{*} = \gamma (1 + 2\varepsilon \alpha_{2} ),\,\,\beta_{\text{T}}^{*} = \beta_{\text{T}} (1 - 2\varepsilon \alpha_{2} ),\,\beta_{\text{C}}^{*} = \beta_{\text{C}} (1 - 2\varepsilon \alpha_{2} ),\, \\ & \beta_{\text{n}}^{*} = \beta_{\text{n}} (1 - 2\varepsilon \alpha_{2} ),\;\;V_{\text{w}}^{*} = V_{\text{w}} (1 - \varepsilon \alpha_{2} ). \\ \end{aligned} $$
(32)

When the variances between the novel and the original variables are identified as differentials while equating every word, the subsequent formulations can be achieved:

$$ \begin{aligned} \frac{1}{2}\frac{{{\text{d}}x}}{x} & = \frac{{{\text{d}}y}}{y} = \frac{\partial \psi }{\psi } = - \frac{{{\text{d}}N}}{N} = \frac{1}{2}\frac{{{\text{d}}k_{\text{p}} }}{{k_{\text{p}} }} = \frac{1}{2}\frac{{{\text{d}}j}}{j} = \frac{1}{2}\frac{{{\text{d}}\gamma }}{\gamma } \\ & = - \frac{{{\text{d}}V_{\text{w}} }}{{V_{\text{w}} }} = - \frac{1}{2}\frac{{{\text{d}}\beta_{\text{T}} }}{{\beta_{\text{T}} }} = - \frac{1}{2}\frac{{{\text{d}}\beta_{\text{C}} }}{{\beta_{\text{C}} }} = - \frac{1}{2}\frac{{{\text{d}}\beta_{\text{n}} }}{{\beta_{\text{n}} }} = - \frac{1}{2}\frac{{{\text{d}}Q(x)}}{Q(x)} = - \frac{1}{2}\frac{{{\text{d}}K(x)}}{K(x)}. \\ \end{aligned} $$
(33)

Resolving each consequently from Eq. (18) leads to the next similarity conversion:

$$ \begin{aligned} & \eta = \frac{1}{\sqrt 2 }x^{{ - \frac{1}{2}}} y,\,\,\,\psi = \sqrt 2 f(\eta )x^{{\frac{1}{2}}} ,\,\,\,\theta = \theta (\eta ),\,\,\,\phi = \phi (\eta ),\,\,\,\chi = \chi (\eta ),\,\,\,N = \frac{1}{\sqrt 2 }h(\eta )x^{{ - \frac{1}{2}}} ,\, \\ & Q(x) = x^{ - 1} Q_{^\circ } ,\,\,\,\,\,\,\,K(x) = x^{ - 1} K_{^\circ } ,\,\quad k_{\text{p}} = xk_{{{\text{p}}^\circ }} ,\,\,\,\,\,\,\,\,j = xj_{^\circ } ,\,\,\,\,\,\,\,\,\gamma = x\gamma_{^\circ } , \\ & \beta_{\text{T}} = x^{ - 1} \beta_{{{\text{T}}^\circ }} ,\,\,\,\,\,\,\,\,\beta_{\text{C}} = x^{ - 1} \beta_{{{\text{C}}^\circ }} ,\,\,\,\,\,\,\,\beta_{\text{n}} = x^{ - 1} \beta_{{{\text{n}}^\circ }} ,\,\,\,\,\,\,\,V_{\text{w}} = x^{{ - \frac{1}{2}}} V_{{{\text{w}}^\circ }} , \\ \end{aligned} $$
(34)

The thermal volume expansion is symbolised by \( \beta_{{{\text{T}}_{{_{^\circ } }} }} \), \( \beta_{{{\text{C}}_{{_{^\circ } }} }} \) is the concentration expansion, \( \beta_{{{\text{n}}_{{_{^\circ } }} }} \) is the microorganism expansion, \( V_{{{\text{w}}_{{_{^\circ } }} }} \) is the suction/injection slip factor, \( j_{^\circ } \) is the micro-inertia density, \( \gamma_{^\circ } \) is the micropolar spin gradient viscosity, \( k_{{{\text{p}}_{^\circ } }} \) is the permeability of the porous media, \( Q_{{_{^\circ } }} \) is the constant heat generation/absorption, and \( K_{{_{^\circ } }} \) is the constant reaction rate. The substitution of (35) into (15)–(20) leads to the resulting system of ordinary differential equations:

$$ \left( {1 + A_{1} } \right)f^{\prime\prime\prime} + f\,f^{\prime\prime} + {\text{Gr}}\,\theta + {\text{Gr}}_{\text{n}} \phi + {\text{Gr}}_{\text{m}} \chi + A_{1} h^{\prime} - \frac{2}{\text{Da}}f^{\prime} = 0, $$
(35)
$$ \lambda_{0} \,h^{\prime\prime} + h\,f^{\prime} + f\,h^{\prime} - 2I_{0} \left( {2h + f^{\prime\prime}} \right) = 0, $$
(36)
$$ \theta^{\prime\prime} + \Pr f\theta^{\prime} + \Pr {\text{Ec}}\left( {1 + A_{1} } \right)f^{{{\prime \prime }2}} + \Pr Q_{\text{c}} \theta = 0, $$
(37)
$$ \phi^{\prime\prime} + { \Pr }\,{\text{Le}}\,f\phi^{\prime} - { \Pr }\,{\text{Le}}\,K_{\text{c}} \phi = 0, $$
(38)
$$ \chi^{\prime\prime} + { \Pr }\,{\text{Lb}}\chi^{\prime}f - {\text{Pe}}\left( {\chi \,\phi^{\prime\prime} + \phi^{\prime}\chi^{\prime}} \right) = 0. $$
(39)

Here \( A_{1} = \frac{\kappa }{\mu } \) is the micropolar parameter, \( {\text{Gr}} = \frac{{2{\text{Lg}}\beta_{{{\text{T}}_{0} }}\Delta T}}{{U_{\text{w}}^{2} }} \) is the Grashof number,\( {\text{Gr}}_{\text{n}} = \frac{{2Lg\beta_{{{\text{C}}_{0} }} \Delta C}}{{U_{\text{w}}^{2} }} \) is the Grashof number for the mass transfer parameter, \( {\text{Gr}}_{\text{m}} = \frac{{2{\text{Lg}}\beta_{{{\text{n}}_{0} }} n_{\text{w}} }}{{U_{\text{w}}^{2} }} \) is the Grashof number for the microorganism transfer parameter, \( {\text{Da}} = \frac{{k_{{p_{0} }} U_{\text{w}} }}{\nu L} \) is the Darcy number (permeability parameter), \( \lambda_{0} = \frac{{\gamma_{0} }}{{\rho_{{}} j_{0} \nu }} \) is the microrotational density parameter, \( I_{0} = \frac{2L\kappa }{{\rho j_{0} U_{\text{w}} }} \) is the vortex viscosity parameter, \( {\text{Ec}} = \frac{{U_{\text{w}}^{2} }}{{c_{\text{p}}\Delta T}} \) is the Eckert number [50], \( Q_{\text{c}} = \frac{{2Q_{0} L}}{{U_{\text{w}} \rho c_{\text{p}} }} \) is the heat generation or absorption parameter, \( { \Pr } = \frac{\nu }{\alpha } \) is the Prandtl number [50], \( {\text{Le}} = \frac{\alpha }{{D_{\text{m}} }} \) is the Lewis number, \( K_{\text{c}} = \frac{{2LK_{0} }}{{U_{\text{w}} }} \) is the chemical reaction parameter, \( {\text{Pe}} = \frac{{\tilde{b}W_{\text{c}} }}{{D_{\text{n}} }} \) is the Peclet number, and \( {\text{Lb}} = \frac{\alpha }{{D_{\text{n}} }} \) is the bioconvection Lewis number. The boundary conditions (20) can be stated as

$$ \begin{aligned} & f\left( 0 \right) = f_{\text{w}} ,\quad f^{\prime}\left( 0 \right) = \lambda ,\quad h\left( 0 \right) = - n_{1} f^{\prime\prime}\left( 0 \right),\quad \theta \left( 0 \right) = 1,\quad \phi \left( 0 \right) = 1,\quad \chi \left( 0 \right) = 1, \\ & f^{\prime}\left( \infty \right) = h\left( \infty \right) = \theta \left( \infty \right) = \phi \left( \infty \right) = \chi \left( \infty \right) = 0. \\ \end{aligned} $$
(40)

The notation \( (\,\,'\,) \) denotes differentiation with respect to \( \eta ,\,\,f_{\text{w}} = \frac{{\sqrt 2 \left( {V_{\text{w}} } \right)_{0} \sqrt {\text{Re} } }}{{U_{\text{w}} }} \) is the suction/injection slip parameter where \( f_{\text{w}} < 0 \) implies injection, while \( f_{\text{w}} > 0 \) connotes suction. The physical quantities which are highly considered in this investigation are the local Nusselt number \( \left( {{\text{Nu}}_{{{\bar{\text{x}}}}} } \right) \), that can be identified as follows:

$$ C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} = \frac{{\tau_{{{\bar{\text{x}}}}} }}{{\rho U_{\text{w}}^{2} }},\quad {\text{Nu}}_{{{\bar{\text{x}}}}} = \frac{{\bar{x}q_{\text{x}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}},\quad {\text{Sh}}_{{{\bar{\text{x}}}}} = \frac{{\bar{x}q_{\text{m}} }}{{D\left( {C_{\text{w}} - C_{\infty } } \right)}},\quad {\text{Nn}}_{{{\bar{\text{x}}}}} = \frac{{\bar{x}q_{\text{n}} }}{{D_{\text{n}} \left( {n_{\text{w}} } \right)}}. $$
(41)

The skin friction \( \left( {\tau_{{{\bar{\text{x}}}}} } \right), \) the heat flux \( \left( {q_{\text{x}} } \right) \), the mass flux \( \left( {q_{\text{m}} } \right), \) and the motile microorganisms flux \( \left( {q_{\text{n}} } \right) \) along with the stretching surface are given by

$$ \begin{aligned} \tau_{{{\bar{\text{x}}}}} = \left[ {\left( {\mu + \kappa } \right)\frac{{\partial \bar{u}}}{{\partial \bar{y}}} + \kappa \bar{N}} \right]_{{{\bar{\text{y}}} = 0}} ,\quad q_{\text{x}} = - k\left( {\frac{\partial T}{{\partial \bar{y}}}} \right)_{{{\bar{\text{y}}} = 0}} ,\quad \hfill \\ q_{\text{m}} = - D\left( {\frac{\partial C}{{\partial \bar{y}}}} \right)_{{{\bar{\text{y}}} = 0}} ,\quad q_{\text{n}} = - D_{\text{n}} \left( {\frac{\partial n}{{\partial \bar{y}}}} \right)_{{{\bar{\text{y}}} = 0}} . \hfill \\ \end{aligned} $$
(42)

By using (34) and the dimensionless expressions in Eqs. (41) and (42), the related physical quantities can be defined as follows:

$$ \begin{aligned} C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } &= \frac{1}{\sqrt 2 }\left( {1 + A_{1} \left( {1 - n_{1} } \right)} \right)f^{\prime\prime}\left( 0 \right), \, \frac{{{\text{Nu}}_{{{\bar{\text{x}}}}} }}{{\sqrt {\text{Re}_{{{\bar{\text{x}}}}} } }} = - \frac{1}{\sqrt 2 }\theta^{\prime}\left( 0 \right), \hfill \\ & \frac{{Sh_{{{\bar{\text{x}}}}} }}{{\sqrt {\text{Re}_{{{\bar{\text{x}}}}} } }} = - \frac{1}{\sqrt 2 }\phi^{\prime}\left( 0 \right), \, \frac{{{\text{Nn}}_{{{\bar{\text{x}}}}} }}{{\sqrt {\text{Re}_{{{\bar{\text{x}}}}} } }} = - \frac{1}{\sqrt 2 }\chi^{\prime}\left( 0 \right), \hfill \\ \end{aligned} $$
(43)

where the local Reynolds number is denoted by \( \text{Re}_{{{\bar{\text{x}}}}} = \frac{{U_{\text{w}} \bar{x}}}{\nu }. \)

Solving approach and validation

The shooting method in the Maple software resolves the mathematical model in the form of the system of nonlinear ODE’s (35)–(40). This numerical approach capable in solving non-Newtonian fluid transport problems, for instance see Thumma and Mishra [51]. The first procedure in applying the shooting method begins with the step of transforming the reduced mathematical model (35)–(40) into a system of first-order ODE’s as is shown in the following expression:

$$ \begin{aligned} & f^{\prime}\left( \eta \right) = p,\,\,h^{\prime}\left( \eta \right) = r,\,\,\theta^{\prime}\left( \eta \right) = s,\,\,\,\varphi^{\prime}\left( \eta \right) = t,\,\,\,\chi^{\prime}\left( \eta \right) = l,\,\,\,p^{\prime}\left( \eta \right) = q, \\ & q^{\prime}\left( \eta \right) = \frac{1}{{(1 + A_{1} )}}\left[ {(2/{\text{Da}})p - A_{1} r - {\text{Gr}}_{\text{n}} \varphi - {\text{Gr}}_{\text{m}} \chi - Gr\theta - fq} \right], \\ & r^{\prime} = (1/\lambda_{0} )\left[ {2I_{0} (2h + q) - fr - hp} \right], \\ & s^{\prime} = - \Pr \left[ {sf + Ec\left( {1 + A_{1} } \right)q^{2} + Q_{\text{c}} \theta } \right], \\ & t^{\prime} = \Pr {\text{Le}}\;{\text{Kc}}\varphi - f\,t\Pr \;{\text{Le}}, \\ & l^{\prime} = {\text{Pe}}\left( {\chi \Pr \;{\text{Le}}\;{\text{Kc}}\,\varphi - \chi f\,t\Pr \;{\text{Le}} + t\,l} \right) - \Pr \;{\text{Lb}}\,l\,f, \\ & f\left( 0 \right) = f_{\text{w}} ,\quad p\left( 0 \right) = \lambda ,\quad h\left( 0 \right) = - n_{1} q\left( 0 \right),\quad \theta \left( 0 \right) = 1,\quad \varphi \left( 0 \right) = 1,\quad \chi \left( 0 \right) = 1, \\ & p\left( \infty \right) = h\left( \infty \right) = \theta \left( \infty \right) = \varphi \left( \infty \right) = \chi \left( \infty \right) \to 0. \\ \end{aligned} $$
(44)

Next, designating an iterative scheme with the convergence criterion (when the difference of two consecutive approximations is \( \le 10^{ - 5} \)) assist in determining the right numerical solutions. The competence of the shooting method is then validated by comparing several values of the skin friction coefficient \( \left( { - f^{\prime\prime}\left( 0 \right)} \right) \) reported by Ishak et al. [52] and is presented in Table 1. Table 1 shows that the present numerical output is in perfect agreement with the numerical results produced by Ishak et al. [52] which is numerically resolved by using the Keller-box technique with the convergence of 0.00001. Thus, the shooting method is a reliable approach to solve boundary value problems.

Table 1 Comparison values of the skin friction coefficient, \( - f^{\prime\prime}\left( 0 \right) \) for different values of \( A_{1} \) when \( {\text{Gr}} = 0, \)\( {\text{Da}} = 1,\;n_{1} = 0.5,\;{ \Pr } = 0.71,\;I_{0} = \lambda_{0} = \lambda = {\text{Ec}} = 1,\;f_{\text{w}} = 0 \)
Full size table

Results and discussion

Throughout the computation process, the values of the governing parameters are fixed initially as follows:

$$ A_{1} = 0.2,I_{0} = 0.001,\Pr = 0.71,\lambda_{0} = Q_{\text{c}} = {\text{Ec}} = 0.1,{\text{Le}} = {\text{Lb}} = 1,n_{1} = 0.5,{\text{Da}} = 0.5, $$

and \( {\text{Gr}} = {\text{Gr}}_{\text{n}} = {\text{Gr}}_{\text{m}} = 0.5. \) The value for \( A_{1} ,\lambda_{0} \) and \( I_{0} \) is set as 0, 0.1 and 0.001, respectively, so that the fluid is able to reflect the micropolar feature in the laminar boundary layer flow. Moreover, the current work attempts to examine the behaviour of a nitrogen gas containing polymers [15] and hence \( \Pr \) is set to 0.71 at 500 K [53]. \( Q_{\text{c}} \) and \( {\text{Ec}} \) are fixed as 0.1, respectively, so that the influence of the heat generation and dissipation is present in the fluid flow. Table 2 displays the decrement of the reduced skin friction coefficient \( \left( {C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } } \right) \) as the micropolar parameter \( \left( {A_{1} } \right) \) increases past the permeable stretching sheet. The increment in \( A_{1} \) enhances the microrotation viscosity coefficient which then decreases the wall shear stress past a stretching sheet in the porous media, which then reduces the value of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \). The negative values of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) signify that the stretching flat plate inflict the drag force on the micropolar fluid. Next, the increment in \( A_{1} \) enhances the value of \( {\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} . \) The increment in \( A_{1} \) reduces the thermal conductivity of the micropolar fluid, which upsurges the heat flux past a permeable stretching sheet. Eventually, the rate of heat transfer augments. Table 2 also exhibits the rise of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) when Da increases from 0.4 to 0.6. The increment of Da indicates the enhancement of the permeability of the porous medium. This state contributes to the increment in the fluid velocity in the porous medium, which is communicated by the velocity profiles in Fig. 2a. The momentum boundary layer thickness increases and affects the wall shear stress to increase when Da elevate. Thus, the values of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) increase. The increment in Da depreciates the fluid temperature (see Fig. 2b) and increases the temperature gradient. The steeper thermal profile implies the increment in convective heat transfer along the moving surface. Therefore, an improvement in the heat transfer rate when Da increases is underlined. Table 2 exhibits the decrement in the value of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) as \( f_{\text{w}} \) increases. The increment of \( f_{\text{w}} \) from 0.2 to 0.4 explains the dominance of suction at the surface of permeable moving sheet. Physically, the act of suction traps the slowing down molecules in the fluid regime and improves the slow fluid flow on the moving sheet. However, in the porous medium, the increment in \( f_{\text{w}} \) is found to reduce local wall shear stress and the fluid velocity declines in conjunction with the stretching surface. The momentum boundary layer thickness becomes thinner as the suction intensity augments, which then results in the reduction of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } . \) In terms of the heat transfer characteristics, a rise in \( f_{\text{w}} \) reduces the temperature of the micropolar fluid past the stretching surface. The temperature profiles in Fig. 3b display that the stronger influence of suction on the moving plate is noted in a thinner thermal boundary layer thickness and increases the thermal gradient. These outcomes then rise the wall heat flux and encourage \( {\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) to rise.

Table 2 Numerical values of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) and \( {\text{Nn}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) for various values of \( A_{1} ,{\text{Da}},f_{\text{w}} ,\lambda ,{\text{Gr}},{\text{Pe}} \) and Lb
Full size table
Fig. 2
figure 2

a Effect of Da over the velocity distributions and b thermal distributions

Full size image
Fig. 3
figure 3

a Effect of \( f_{\text{w}} \) over the velocity distributions and b thermal distributions

Full size image

Table 2 exposes the decrement in \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } \) when \( \lambda \) increases. The addition in the value of \( \lambda \) implies that the rate of stretching increases and the characteristic length of the sheet become more extensive than before. Now, when the sheet stretches in the porous medium, the velocity of the micropolar fluid close to the wall increases before it declines as the fluid flow gets farer from the stretching sheet (see Fig. 4a). When the velocity profiles converge at \( \eta = 15, \) the micropolar fluid velocity decreases as \( \lambda \) increases. Eventually, the momentum boundary layer thickness turns out to be thicker and thus lessening the values of \( C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } . \) Moreover, numerical results in Table 2 pose the enhancement in the value of \( {\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) when \( \lambda \) increases. The increment in \( \lambda \) increases the surface area of the permeable sheet, and it stimulates the micropolar fluid temperature to decrease (see Fig. 4a). The thermal gradient increases and reduces the thermal conductivity of the fluid, which then provokes better rate of heat transfer past the permeable sheet. However, Table 3 illustrates a significant convective heat transfer enhancement when \( {\text{Ec}} \) increases. Normally, \( {\text{Ec}} \) is used to determine the dissipation effects in the fluid flow, and when the value of \( {\text{Ec}} \) increases, some changes will take place in the fluid regime. Firstly, it raises the fluid velocity and reduces the thermal capacity of the fluid. This is factually true as when \( {\text{Ec}} \) increases, the micropolar fluid temperature increases and reduces the thermal gradient (see Fig. 5a). The wall heat flux at the surface of the stretching surface decreases since the thermal conductivity of the fluid increases. Hence the rate of convective heat transfer decreases.

Fig. 4
figure 4

a Impact of \( \lambda \) over the velocity distributions and b thermal distributions

Full size image
Table 3 Numerical values of the local Nusselt number and the local Sherwood number for when the pertinent parameters vary
Full size table
Fig. 5
figure 5

a Effect of Ec over the thermal distributions and b Impact of \( Q_{\text{c}} \) over the thermal distributions

Full size image

Figure 5b demonstrates the thermal profiles when \( Q_{\text{c}} \) varies from negative to positive values (increase). When the value of \( Q_{\text{c}} \) is less than zero, it suggests the heat absorption situation to the fluid flow, and when it occurs, the temperature of the micropolar fluid decreases (see Fig. 5b), and this increases the wall heat flux along with the stretching surface. Conversely, when the value of \( Q_{\text{c}} \) is more than zero, it indicates the situation where the heat is generated to the fluid regime. The rise in positive values of \( Q_{\text{c}} \) results in the rise in the micropolar fluid temperature, and this is shown in Fig. 5b. The thermal boundary layer thickness increases and enhances the rate of heat transfer. Figure 6a views the increment in the concentration as \( K_{\text{c}} \) varies from the negative to positive values. The negative value of \( K_{\text{c}} \) entails the non-destructive chemical reactions, while positive values of \( K_{\text{c}} \) denote the situation of destructive chemical reaction. Based on the concentration profile in Fig. 6a, it is apparent that the dominance of the non-destructive chemical reaction reduces the concentration of the micropolar fluid and its boundary layer thickness reduces. Consequently, the mass flux past the permeable stretching sheet increases and enhances the value of \( {\text{Sh}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) or the rate of mass transfer along the surface of the sheet. Meanwhile, also from Fig. 6a, the increment of \( K_{\text{c}} > 0 \) results in the increment in the fluid concentration, which then later induces the concentration boundary layer thickness to be thicker. This state then affects the wall mass flux to decrease and induce the value of \( {\text{Sh}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) to decrease (see Table 3).

Fig. 6
figure 6

a Effect of \( K_{\text{c}} \) over the concentration distributions and b Impact of \( {\text{Da}} \) over the density of motile microorganisms distributions

Full size image

Figure 6b displays the decrement in the density of motile microorganisms when Da increases. The increment in Da reduces the characteristics length of the moving sheet, and this affects the density of the motile microorganisms to decrease. The density of motile microorganisms’ boundary layer thickness decreases (see Fig. 6b) and increases the motile microorganisms’ flux over the stretching sheet. Hence, the local density of the motile microorganisms or \( {\text{Nn}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) increases when Da increases (see Table 2).

Conclusions

This study is devoted to contribute the theoretical work in the scope of bioconvection micropolar fluid in a porous medium past a stretching permeable surface. The effects of chemical reactions, heat generation/absorption and dissipation have been evaluated in this model. The present work may be tested under the influence of the nanoparticles (see [54]) and under different shape of surface.

Some of the important deductions can be highlighted from the generated numerical findings as follows:

  • The reduced skin friction coefficient \( \left( {C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } } \right) \) decreases but the local Nusselt number \( \left( {{\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \) increases when the micropolar parameter \( \left( {A_{1} } \right) \) rises past the permeable stretching sheet.

  • The reduced skin friction coefficient \( \left( {C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } } \right) \) and the local Nusselt number \( \left( {{\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \) augments when the permeability parameter \( \left( {\text{Da}} \right) \) increases past the permeable stretching sheet.

  • The reduced skin friction coefficient \( \left( {C_{{{\text{f}}_{{{\bar{\text{x}}}}} }} \sqrt {\text{Re}_{{{\bar{\text{x}}}}} } } \right) \) decreases but the local Nusselt number \( \left( {{\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \) increases when the suction parameter \( \left( {f_{\text{w}} } \right) \) increases.

  • The increment in Ec affects he local Nusselt number \( \left( {{\text{Nu}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \) to increase.

  • The strong impact of the destructive chemical reaction reduces the local Sherwood number \( \left( {{\text{Sh}}_{{{\bar{\text{x}}}}} \text{Re}_{{_{{{\bar{\text{x}}}}} }}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right). \)