Entropy Generation Analysis of MHD Viscoelasticity-Based Micropolar Fluid Flow Past a Stretching Sheet with Thermal Slip and Porous Media

Abstract

Entropy generation analysis of MHD Maxwell visco elasticity-based micropolar fluid flow past a stretching sheet through porous media with radiation and thermal slip has been investigated. Using suitable similarity transformations the coupled non-linear partial differential equations of motion and energy have been converted into a set of non-linear ordinary differential equations. The solutions of reduced equations are computed numerically by RK-4 method with shooting technique. The effects of non-dimensional relevant parameters on velocity distribution, temperature distribution, microrotation, entropy and Bejan have been computed and presented graphically. Also, numeric values of flow and heat transfer, friction factor have been deliberated and presented through tables.

Introduction

The non-Newtonian micropolar fluid model is a microstructure model. It offers great resistance to fluid motion compared to the Newtonian fluid. Also, it explains the characteristics of the fluid flows containing suspended micro particles. The collective microrotation impacts of suspended particles of micropolar fluid in a shear flow can be modelled by an additional equation of conservation of local angular momentum with spin gradient and material parameter which clarify the characteristic of non-Newtonian property. Micropolar fluids are widely used in different industrial processes, like animal blood, solidification of liquid crystal, exotic lubricants, colloidal and suspension solution, extrusion of polymer fluids and cooling of material plates in bath.

In this study, we have considered micropolar fluid with the Maxwell viscoelastic behaviour, resultant Maxwell viscoelasticity based micropolar fluid can show the relaxation as same degree of non-Newtonian property arising from micro-rotaion effect. The MVMF not only demonstrates the relaxation appearances in a shear flow, but also the collective impacts of micro-rotation of particles, i.e., the micropolar behaviour. Erigen [1] studied flow and heat transfer of micropolar fluid have attracted several researchers due to its wide applications, for example suspension solutions, measure of colloidal illuminations and body fluid flows etc. Sui et al. [2] studied thermophoresis charactererized soret number in shear flow of MVMF over a sheet with slip. Mohanty et al. [3] discussed heat and mass transfer impacts of micropolar fluid through a sheet embedded in porous media. Aurangzaib et al. [4] discussed partial slip effect on MHD 2D mixed convection unsteady stagnation point flow of electrically conducting MF through a sheet. Sandeep and Sulochana [5] studied MHD mixed convection MF flow through a shrinking/stretching sheet with heat source/sink. Aurangzaib et al. [6] studied heat transfer influence of micropolar fluid flowpast a permeable exponentially shrinking sheet. Mostafa et al. [7] studied heat generation and slip velocity effect for MF over a stretching surface through MHD. Sarojamma et al. [8] deliberated dual stratification on double diffusion convective mass and heat transfer of a MF induced by a stretched sheet. Shaheen et al. [9] investigated flow and heat transfer of MF with porous media between two stretchable disk and has solved using quasi linearization method. Khalid et al. [10] discussed wall couple stress impacts in MHD flow of MF through porous media with heat and concentration transfer. Mishra et al. [11] studied energy equation and free convection MF flow past a shrinking sheet through heat source. Abbas et al. [12] studied heat transfer impact of micropolar fluid flow over a cylinder. Rehman et al. [13] studied flow and heat transfer of micropolar fluid over an exponentially stretched cylinder.

Radiative flow over stretching sheet has extensive pragamatic applications in engineering industries and technology. Some of such applications are drawing of plastic sheets, glass fiber production, wire drawing, artificial fibers, crystal growing, applicability in extrusion of plastic sheets, paper production. Crane [14] discussed exact solution in closed analytic form for boundary flow. Jain and Bohra [15] studied radiation effects in flow over a rotating disk in the presence of variable fluid properties and porous media. Hayat et al. [16] studied the ferromagnetic Williamson radiative fluid flow with the magnetic dipole. Mustafa et al. [17] discussed water based magnetite nanofluid rotating flow over a stretching surface by nonlinear thermal radiation. Jain and Choudhary [18] studiedsunction/injection on MHD boundary Layer flow over a permeable cylinder with radiation. Many researchers Naramgari and Sulochana [19], Zaimi et al. [20] and Chen [21] discussed fluid flow over a stretching/shrinking sheet.

According to, second law of thermodynamics flow and heat transfer procedures undergo fluctuations that are irreversible caused by energy damages during the processes. Such impacts cannot be entirely eliminated from system and these results in loss of energy. In thermodynamics, irreversibility is measured by entropy generation rate. In thermal engineering, entropy generation minimization is applicable such as air separators, reactors, chillers, fuel cells and thermal solar. Bejan [22] discussed entropy generation analysis in detailed. Jangili et al. [23] studied entropy analysis in the presence of an internal heat generation in magnetized micropolar fluid flow in b/w co-rotating cylinders. Srinivasacharya and Bindu [24] studied second law analysis in the presence of convective condition and slip effect due to micropolar flow between concentric cylinders. Srinivas and Murthy [25] studied thermodynamic effect of two immiscible MF flow between two MHD parallel plates. Khan et al. [26] discussed entropy effect on MF due to rotating disk through slip condition. Many researchers Rashidi et al. [27], Rehman et al. [28], Das et al. [29], Bhatti et al. [30], Khan et al. [31] and Afridi et al. [32] investigated second law analysis through different geometries and fluids.

The aim of this study is to analyze entropy generation minimization of 2D MHD boundary layer flow of Maxwell viscoelasticity based micropolar fluid over stretching sheet withtemperature slip, radiation through porous media. The angular momentum equation is also taken into consideration. Fluid velocity, micro angular velocity, temperature distribution and entropy have been analyzed and depicted through graph.

Mathematical Formulation

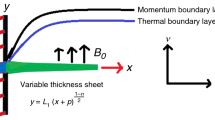
Entropy analysis of MHD Maxwell viscoelasticity based micropolar fluid flow past a horizontal stretching sheet with slip condition and radiationthrough porous media. The slipping nature has been seen for the complex viscoelastic fluids passes through a forced shear flow in the direction of stretching of the surface. The sheet has linear velocity $U_{W} = \omega x.$ Figure 1 shows the physical schematic diagram beyond the boundary layer MVMF with suspended nonrotating micro particles is at rest, while there would be higher gradient phenomena in boundary layer e.g. thermal and viscosity diffusion layers.

Fig. 1

Schematic diagram of the problem

The flow equations including the continuity and momentum equations are written as:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$

(1)

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \left( {\frac{\mu + \kappa }{\rho }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} - \lambda_{v} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) + \frac{\kappa }{\rho }\frac{\partial N}{\partial y} - \frac{{\sigma B_{0}^{2} }}{\rho }u - \frac{\upsilon }{{k_{p} }}u, $$

(2)

$$ u\frac{\partial N}{\partial x} + v\frac{\partial N}{\partial y} = \frac{{\gamma_{m} }}{\rho J}\frac{{\partial^{2} N}}{{\partial y^{2} }} - \frac{\kappa }{\rho J}\left( {2N + \frac{\partial u}{\partial y}} \right), $$

(3)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \frac{\mu + \kappa }{{\rho c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} - \frac{1}{{\rho C_{p} }}\frac{{\partial q_{r} }}{\partial y}, $$

(4)

The boundary conditions at stretching sheet

$$ \begin{array}{l} u = U_{w} ,\;v = 0,\;N = - m\left( {\frac{\partial u}{\partial y}} \right),\;T = T_{W} + L_{1} \left( {\frac{\partial T}{\partial y}} \right), \;{\text{at}}\quad y = 0, \hfill \\ u \to 0,\;N \to 0,\;T \to T_{\infty } ,\; {\text{at}}\quad y \to \infty \hfill \\ \end{array} $$

(5)

here, $\left( {u,v} \right)$ are the velocity component in the $\left( {x,y} \right)$ direction respectively, $\rho$ is the density, $\mu$ and $\kappa$ are the dynamic and vortex viscosity, $N$ is the micro angular velocity in $x - y$ plane corresponding to micro-rotation of particles, $J$ is micro-inertia per unit mass, $\gamma_{m}$ is the spin gradient viscosity written as

$$ \gamma_{m} = \left( {\mu + \frac{\kappa }{2}} \right)J = \mu J\left( {1 + \frac{{K_{m} }}{2}} \right) $$

where, $K_{m} = \frac{\kappa }{\mu }$ signifies the non-dimensional viscosity ratio and is simply named material parameter of MVMF. $m$ is constant range between $0 \le m \le 1$ in which $m = 0$ relatesto a concentrated MVMF and $m = 1$ designates the turbulent flow circumstance. Here we apply $m = \frac{1}{2}$ to describe a dilute MVMF. $c_{p}$ is the specific heat. $T,T_{W}$ and $T_{\infty }$ are the fluid temperature, surface temperature and ambient temperature (Table 1).

Table 1 The comparison of the values of $- \theta ^{\prime}(0)$ with that of Chen et al. [21], Zaimi et al. [20] and Naramgari et al. [19] when $K_{m} = \delta_{m} = K = Ec = B1 = 0$

The Rosseland approximation is expressed as

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial z}, $$

where, $\sigma^{*}$ is the Stefan–Boltzmann constant and $k^{*}$ is the mean absorption coefficient. The temperature difference has been considered very small, so that $T^{4}$ may be expressed as a linear function of temperature.

$$ T^{4} \approx 4T^{3}_{\infty } T - 3T^{4}_{\infty } , $$

The PDE’s are converted into ODE’s by using following transformations:

$$ \eta = \left( {\frac{\omega }{\upsilon }} \right)^{{\frac{1}{2}}} y,\psi = \left( {\omega \upsilon } \right)^{{\frac{1}{2}}} xf\left( \eta \right),N = \left( {\frac{{\omega^{3} }}{\upsilon }} \right)^{{\frac{1}{2}}} xR,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{W} - T_{\infty } }}, $$

(6)

where, $\psi$ is the stream function to describe the velocity components as $u = \frac{\partial \psi }{\partial y}$ and $v = - \frac{\partial \psi }{\partial x}$. $R$ is the non-dimensionallocal micro angular velocity. Eq. (1) is identical satisfied, now substituting Eq. (6) into Eqs. (2)–(4) we get the following nonlinear equations:

$$ \left( {1 + K_{m} } \right)f^{\prime\prime\prime} + ff^{\prime\prime} - f^{\prime 2} - \delta_{m} \left( {f^{\prime\prime\prime}f^{2} - 2ff^{\prime}f^{\prime\prime}} \right) + K_{m} R^{\prime} - \left( {K + M} \right)f^{\prime} = 0 $$

(7)

$$ \left( {1 + \frac{{K_{m} }}{2}} \right)R^{\prime\prime} + fR^{\prime} - Rf^{\prime} - BK_{m} \left( {2R + f^{\prime\prime}} \right) = 0 $$

(8)

$$ \left( {1 + \frac{4}{3}R_{a} } \right)\theta ^{\prime\prime} + \Pr \left[ {f\theta ^{\prime} + Ec(1 + K_{m} )f^{\prime\prime^2} } \right] = 0, $$

(9)

using Eqs. (6) in (5), the related boundary conditions become

$$ \begin{array}{l} f^{\prime}(\eta ) = 1,f\left( \eta \right) = 0,R\left( \eta \right) = - mf^{\prime\prime}(\eta ),\theta \left( \eta \right) = 1 + B1\theta ^{\prime},\; {\text{at}}\quad \eta = 0, \hfill \\ f^{\prime}\left( \eta \right) \to 0,R\left( \eta \right) \to 0,\theta \left( \eta \right) \to 0,\;{\text{at}}\quad \eta \to \infty , \hfill \\ \end{array} $$

(10)

where, $\delta_{m} = \lambda_{v} \omega ,$ is the viscoelastic parameter, $\frac{\kappa }{\mu } = K_{m}$, is the material parameter of MVMF, $K = \frac{\upsilon }{{k_{p} \omega }},$ is the permeability parameter, $M = \frac{{\sigma B_{0}^{2} }}{\rho \omega },$ is the magnetic parameter, $B1 = L_{1} \left( {\frac{\omega }{\upsilon }} \right)^{{\frac{1}{2}}} ,$ is the temperature slip parameter, $\Pr = \frac{{\mu C_{p} }}{k},$ is the Prandtl number, $Ec = \frac{{U_{w}^{2} }}{{c_{p} \left( {T_{w} - T_{\infty } } \right)}},$ is the Eckert number.

Validation of Result

The skin friction coefficient $C_{f} ,$ and the local Nusselt number for heat transfer $Nu_{x} ,$ are defined as $C_{f} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }},$ $Nu_{x} = \frac{{xq_{w} }}{{k(T_{w} - T_{\infty } )}},$ here, the wall shear stress $\tau_{w}$ for the MVMF, wall mass current $J_{w}$ and wall heat transfer $q_{w}$ are as follows

$$ \tau_{w} = - \mu \left( {1 + \delta_{m} } \right)\left\{ {\left( {1 + K_{m} } \right)\frac{\partial u}{\partial y} + K_{m} N} \right\}_{y = 0} ,\;q_{w} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} , $$

by using similarity transformation, we obtain dimensionless parameters

$$ \text{Re}^{{\frac{1}{2}}} C_{f} = - \left( {1 + \delta_{m} } \right)\left( {1 + \frac{{K_{m} }}{2}} \right)f^{\prime\prime}\left( 0 \right),\;\text{Re}^{{\frac{ - 1}{2}}} Nu_{x} = - \theta ^{\prime}\left( 0 \right), $$

Numerical Method

The Eqs. (7)–(9) under the boundary conditions (10) solved numerically by RK-4 order method with shooting technique. The RK method needs a finite domain $0 \le \eta \le \eta_{\infty }$. In this study, we have taken $\eta_{\infty } = 10.$ The boundary value problem has been changed into initial value problems, defined as:

$$ f_{3} ^{\prime} = \frac{ - 1}{{\left( {1 + K_{m} + \delta_{m} f_{1}^{2} } \right)}}\left\{ {f_{1} f_{3} - f_{2}^{2} + 2f_{1} f_{2} f_{3} + K_{m} f_{5} - Kf_{2} } \right\}, $$

$$ f_{5} ^{\prime} = \frac{ - 1}{{\left( {1 + \frac{{K_{m} }}{2}} \right)}}\left\{ {f_{1} f_{5} - f_{4} f_{2} - BK_{m} \left( {2f_{4} + f_{3} } \right)} \right\}, $$

$$ f_{7} ^{\prime} = - \Pr \left[ {f_{1} f_{7} + Ec(1 + K_{m} )f_{3}^{2} } \right], $$

under the boundary condition

$$ \begin{aligned} f_{2} = 1,f_{1} = 0,f_{4} = - mf_{3} ,f_{6} = 1 + B1f_{7} , \,{\text{at}}\quad \eta = 0, \hfill \\ f_{2} = 0,f_{4} = 0,f_{6} = 0,\;{\text{at}}\quad \eta \to \infty , \hfill \\ f_{3} (0) = r_{1} ,f_{5} (0) = r_{2} \,,f_{7} (0) = r_{3.} , \hfill \\ \end{aligned} $$

where, $r_{1} ,\,r_{2} ,r_{3}$ are the initial guesses.

Entropy Analysis

The local volumetric entropy equation rate of the viscoelasticity based micropolar fluid with porous medium is written as

$$ S^{\prime\prime\prime}_{gen} = \frac{k*}{{T_{\infty }^{2} }}\left( {1 + \frac{4}{3}R_{a} } \right)\left( {\frac{\partial T}{\partial y}} \right)^{2} + \frac{\mu + \kappa }{{T_{\infty } }}\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\mu }{{k_{p} T_{\infty } }} + \frac{{\sigma B_{0}^{2} }}{{T_{\infty } }}} \right)u^{2} $$

(11)

The non-dimensional form of characteristic entropy generation rate is

$$ S^{\prime\prime\prime}_{0} = \frac{{k^{*} \left( {T_{w} - T_{\infty } } \right)^{2} }}{{T_{\infty }^{2} x^{2} }}, $$

(12)

hence, the entropy generation is

$$ N_{G} = \frac{{S^{\prime\prime\prime}_{gen} }}{{S^{\prime\prime\prime}_{0} }}, $$

(13)

on using Eqs. (11) and (12) in Eq. (13), we get

$$ N_{G} = \text{Re}_{L} \left( {1 + \frac{4}{3}R_{a} } \right)\theta ^{\prime 2} + \left( {\frac{{\text{Re}_{L} Br}}{\varOmega }} \right)\left( {1 + K_{m} } \right)f^{\prime\prime 2} + \left( {\frac{{\text{Re}_{L} Br}}{\varOmega }} \right)\left( {K + M} \right)f^{\prime 2} $$

(14)

where, $Br,\varOmega$ and $\text{Re}_{L}$ denotes the Brinkman number, dimensionless temperature differenceand local Reynolds number respectively. These parameters are:

$$ Br = \frac{{\mu \omega^{2} x^{2} }}{{k*\left( {T_{W} - T_{\infty } } \right)}},\varOmega = \frac{{T_{W} - T_{\infty } }}{{T_{\infty } }},\text{Re}_{L} = \frac{{U_{w} x}}{\upsilon }, $$

(15)

Bejan number is the ratio of heat transfer irreversibility to entropy generation given as:

$$ Be = \frac{{\text{Re}_{L} \left( {1 + \frac{4}{3}R_{a} } \right)\theta ^{\prime 2} }}{{\left\{ {\text{Re}_{L} \left( {1 + \frac{4}{3}R_{a} } \right)\theta ^{\prime 2} + \left( {\frac{{\text{Re}_{L} Br}}{\varOmega }} \right)\left( {1 + K_{m} } \right)f^{\prime\prime^2} + \left( {\frac{{\text{Re}_{L} Br}}{\varOmega }} \right)\left( {K + M} \right)f^{\prime 2} } \right\}}} $$

(16)

Results and Discussion

The numerical results have been obtained for non-Newtonian micropolar fluid flow through sheet is presented graphically. Effects of pertinent parameters like viscoelastic parameter, material parameter of MVMF, permeability parameter, magnetic parameter, temperature slip parameter, radiation parameter, Prandtl number, Eckert number, Brinkman number, dimensionless temperature difference, on velocity, temperature, microrotation and entropy has been analysed and depicted graphically for fix values.

$K_{m} = 0.5,M = 0,K = 0.1,\delta_{m} = 0.5,B = 0.1,B1 = 0,m = (1/2),\Pr = 0.71,Ec = 0.3,Br = 1,R_{a} = 0,\varOmega = 1,Re = 1,$ Table 2 shows that the influences of different non-dimensional parameters on skin friction coefficient $\left( {\text{Re}^{{\frac{1}{2}}} C_{f} } \right)$ and angular momentum $\left\{ { - R^{\prime}(0)} \right\}$. Skin friction coefficient increases with enhancing values of $K_{m} ,K,\delta_{m} ,B$ and $m$ while values angular momentum increases with increasing value of $K,\delta_{m} ,B,m,$ while reverse impact shows with increasing value of $K_{m} .$

Table 2 Variation of $\text{Re}^{{\frac{1}{2}}} C_{f}$ and $- R^{\prime}(0)$ for viscoelasticity based micropolar fluid

Table 3 shows that the influences of different non-dimensional parameters on $\left\{ { - \theta ^{\prime}(0)} \right\}$. Temperature profile enhances with increasing values of $B,\Pr$ while reverse impact shows with increasing value of $K_{m} ,K,\delta_{m} ,B1,m,Ec.$

Table 3 Variation of $- \theta ^{\prime}(0)$ for viscoelasticity based micropolar fluid

Figure 2 shows that the fluid velocity enhances as the material parameter increases. It is due to the reason that for high values of material parameter, fluid viscosity decreases, as a result flow accelerated. Figure 3 reveals that the velocity diminishes with increasing value of permeability parameter.

Fig. 2

Fluid velocity profile for $K_{m}$

Fig. 3

Fluid velocity profile for $K$

Figure 4 shows that the influences of viscoelastic parameter on fluid velocity. The enhancing values of viscoelastic parameter will lead to reduce fluid velocity field across the boundary layer. In MVMF the delay reaction of strain layer by layer, caused by relaxation behaviour, means the viscoelastic parameter is contributed to decline the fluid velocity field in shear flow. So that velocity on sheet surface diminishes with viscoelastic parameter. Figure 5 influence that the micro-angular velocity enhances with enhancing value of viscoelastic parameter.

Fig. 4

Fluid velocity profile for $\delta_{m}$

Fig. 5

Micro-angular velocity profile for $\delta_{m}$

Figure 6 depicts that the impacts of magnetic parameter on fluid velocity and micro-angular velocity. The enhancing values of magnetic parameter will lead to reduced fluid velocity field across the boundary layer, because transverse magnetic field created a Lorentz force, which opposes the velocity gradient and fluid motion. Figure 7 shows that the micro-angular velocity increases with increasing values of magnetic parameter.

Fig. 6

Fluid velocity profile for $M$

Fig. 7

Micro-angular velocity profile for $M$

Figure 8 indicates that the influences of the material parameter on micro-angular velocity. The micro-rotation indicates an initial decline near the boundary and then proceeding further away from the surface the micro-rotation $R$ boosts up in rest of region. It may be determined that higher values of micro-angular velocity when material parameter is incremented. This is due to reduction of viscosity of the material parameter which leads to enhancement of micro angular velocity. Figure 9 indicates the effect of permeability parameter on micro-angular velocity profile. Micro-angular velocity increases with enhancing value of permeability parameter.

Fig. 8

Micro-angular velocity profile for $K_{m}$

Fig. 9

Micro-angular velocity profile for $K$

Figures 10 and 11 shows the effect of thermal slip and viscoelastic parameter on temperature profile. Temperature profile decreases with the rises value of thermal slip parameter. Temperature profile increases with the increasing value of viscoelastic parameter, i.e., resultant boundary layer is thick.

Fig. 10

Temperature profile for $B1$

Fig. 11

Temperature profile for $\delta_{m}$

Figure 12 shows the influences of Prandtl number on temperature profile. These graphs show that the effect of increasing values of Prandtl number resultant decrease in the temperature. Physically, smaller values of Prandtl number enhance the thermal conductivity of fluid velocity, therefore heat is capable to diffuse away more rapidly for higher values of Prandtl number from heated surface. Figure 13 elucidates the effect of Eckert number on temperature profile. Temperature profile enhances with the enhancing values of Eckert number. By the definition of Eckert number, a positive Eckert number corresponding to fluid heating, whereasthe negative Eckert number means fluid is being cooled.

Fig. 12

Temperature profile for $\Pr$

Fig. 13

Temperature profile for $Ec$

Figures 14 and 15 indicate the influence of material parameter and permeability parameter on temperature profile. Increasing values of material parameter reduces with the temperature profile, while permeability parameter increases with the temperature profile. Due to circumstance that an enhancement in micropolar parameter increases the boundary layer thickness.

Fig. 14

Temperature profile for $K_{m}$

Fig. 15

Temperature profile for $K$

Figures 16 and 17 indicate the influence of radiation parameter and magnetic parameter on temperature profile. Rising values of radiation parameter and magnetic parameter increases with the temperature profile.

Fig. 16

Temperature profile for $R_{a}$

Fig. 17

Temperature profile for $M$

Figures 18 and 19 show the effect of material parameter and Eckert parameter on the entropy generation number. Entropy generation number enhances with the enhancing value of material parameter, while Eckert number decreases near the wall, but far away from the wall Eckert number increases with the entropy generation number.

Fig. 18

Entropy number for $K_{m}$

Fig. 19

Entropy number for $Ec$

Figures 20, 21 and 22 show the effect of permeability parameter,$Br\varOmega^{ - 1}$ and Prandtl number on the entropy generation number. Increasing value of $Br\varOmega^{ - 1}$ enhances with the entropy generation number, while permeability parameter and Prandtl enhances near the wall but far away from the wall permeability parameter and Prandtl number decreases with the entropy generation number.

Fig. 20

Entropy number for $K$

Fig. 21

Entropy number for $Br\varOmega^{ - 1}$

Fig. 22

Entropy number for $\Pr$

Figures 23, 24 and 25 indicate the influences of $Br\varOmega^{ - 1}$, material parameter and permeability parameter, on the Bejan number. Bejan number increases with the increasing value of $Br\varOmega^{ - 1}$ and material parameter, while permeability parameter enhances near the wall but far away from the wall permeability parameter reduces with Bejan number.

Fig. 23

Bejan number for $Br\varOmega^{ - 1}$

Fig. 24

Bejan number for $K_{m}$

Fig. 25

Bejan number for $K$

Conclusion

Entropy generation analysis on viscoelasticity-based micropolar non-Newtonian fluid flow through a sheet with temperature slip and porous medium has been investigated. Significant results of our study are summarized below:

• The effect of viscoelastic parameter, magnetic parameter and permeability parameter decelerate the fluid velocity decrease, whereas material parameter shows the reverse behaviour.

• For large values of material parameter, magnetic parameter, viscoelastic parameter and permeability parameter, the microangular velocity distribution enhances.

• Viscous dissipation produces heat due to drag between the fluid particles, which causes an increase in fluid temperature.

• Viscoelastic parameter, Eckert number, magnetic parameter, radiation parameter and permeability parameter increase the temperature profile, whereas Prandtl number, material parameter shows the reverse behaviour.

• Entropy profile increases for increasing value of dimensionless $Br\varOmega^{ - 1}$, material parameter and permeability parameter.

• Entropy generation number enhances near the wall but far away from the wall diminishes with increasing value of Prandtl number.

• Bejan number rises for rising value of dimensionless material parameter, $Br\varOmega^{ - 1}$ and permeability parameter.