Influence of Velocity Slip on the MHD Flow of a Micropolar Fluid Over a Stretching Surface

Abstract

Free convection of an electrically conducting micropolar fluid past a permeable stretching surface is considered in the present analysis. The crux of the investigation is the study of velocity slip boundary condition that affects the flow behavior. In addition to that the temperature profile enhances with the inclusion of dissipative heat energy, thermal radiation and the heat generation/absorption parameter. Employing suitable similarity variables, the governing equations are transformed to nonlinear ODEs and numerical treatment such as fourth-order Runge-Kutta method in conjunction with shooting technique. Physical behavior of several contributing parameters for the flow phenomena, local skin-friction coefficient, the wall couple stress, and the local Nusselt number are presented via graphs and further described in the results and discussion section.

1 Introduction

In recent days, a considerable interest among the researchers is found for the study of flow phenomena through a stretching sheet. The fact is the extensive application in both engineering and industries. As a pioneer work, Crane [1] presented his study for the laminar boundary flow of an incompressible, time-independent flow through a stretching surface. Further, Gupta and Gupta [2] extended the work of [1] for the influence of suction/injection in the boundary layer over a stretching surface. Vajravelu and Rollins [3] and Pavlov [4] have investigated the heat transfer properties in an electrically conducting fluid in conjunction with internal heat generation or absorption. Baag et al. [5] studied numerically by using the fourth-order Runge-Kutta method with shooting technique to compare their result with previous study. They confirmed the accuracy of their study. Ayano et al. [6] reported that the flow of micro-rotation components will be in opposite direction and one of these components is not rotating.

Das [7] investigated the chemical reaction and thermal radiation effect of MHD micropolar fluid by considering a rotating frame of reference. An analytical treatment by using least square method (LSM) has been carried out to investigate the effects of Reynolds number and Peclet number on a micropolar fluid flow by Fakour et al. [8]. Shamshuddin and Narayana [9] have considered an unsteady case of MHD micropolar fluid whose flow past an inclined plate with reference to a rotating system. They observed the regular behavior of micropolar fluid in their study. Ishak et al. [10] considered the MHD micropolar fluid flow in presence of magnetic field which is applied normal to the plate and thermal buouyancy in their study. They observed the dual behavior of solutions which exist for the assisting flow. Nazeer et al. [11] have considered a micropolar fluid in porous medium with uniform and non-uniform heated bottom wall. A study of micropolar fluid flow in porous medium over a stretchable disk by considering all the profiles like axial velocity, radial velocity, micro-rotation, temperature, and concentrations profiles have been carried out by Rauf et al. [12]. Sheikholeslami et al. [13] in their study of micropolar fluid used an analytical method (Homotopy Analysis Method) to investigate the behavior of Reynolds number and Pecelet number on all the used profiles. They observed the inter link of both these said numbers with Nusselt and Sherwood numbers.Viscous dissipation taken into consideration on the study of a MHD micropolar fluid flow is to investigate the behavior of translation velocity, micro-rotation, and temperature profiles. It has been observed that all these profiles showed the decreasing behavior for increasing values of viscous dissipation (see [14]). Srivastava [15] in his research paper considered the flow of MHD micropolar fluid in between two eccentrically rotating disks to study the effects of the micropolar parameter and Hartmann number on the velocity and micro-rotation profiles. Mishra et al. [16, 17] used the uniform magnetic field strengths along the flow direction to check the behavior of all the profiles considered in the work in presence of heat source and radiation parameter. Ashmawy [18] considered a convective micropolar fluid in between two vertical uniformly heated channels with velocity slip condition applied. Ferdows and Liu [19] used magnetic field and thermal buoyancy parameters in momentum equation, non-uniform heat source parameter in energy equation to investigate the behavior of magneto-micropolar fluid flow in a vertical plate.

In view of aforesaid discussion it is important to describe the physical significance of heat generation and absorption. Though it is difficult to model the exact internal heat generation or absorption, a mathematical model, following Foraboschi and Federico [20], can be expressed as $S = \left\{ \begin{gathered} Q_{0} (T - T_{\infty } ),\,\,T \ge T_{\infty } \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,T < T_{\infty } \hfill \\ \end{gathered} \right.$ which is valid for the state of some exothermic processes. We have extended the work of Mahmoud et al. [21] by incorporating thermal buoyancy parameter in momentum equation, thermal radiation, and viscous dissipation term in energy equation and also boundary condition of micropolar profile has been modified.

2 Mathematical Formulation

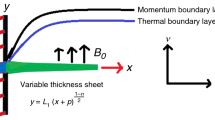
Two-dimensional free convective flow of an electrically conducting micropolar fluid past a porous stretching surface is considered in the present investigation. The plate is along the plane $y = 0$, the flow takes place in the region $y > 0$. Applied uniform magnetic field of strength $B_{0}$ is imposed along the normal direction of the flow. Variable surface heat flux $q_{s} (x) = bx^{m}$ (where b, m are constants) as well as the slip velocity boundary conditions are also assumed. Based upon the aforesaid assumptions the basic governing equations for the flow are

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$

(1)

$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \left( {\frac{\mu + k}{\rho }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{k}{\rho }\frac{\partial N}{{\partial y}} + g\beta_{T} (T - T_{\infty } ) - \frac{{\sigma B_{0}^{2} }}{\rho }u$$

(2)

$$u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} = \frac{\gamma }{\rho j}\frac{{\partial^{2} N}}{{\partial y^{2} }} - \frac{k}{\rho j}\left( {2N + \frac{\partial u}{{\partial y}}} \right)$$

(3)

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{k}{\rho Cp}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{\rho Cp}\left( {T - T_{\infty } } \right) - \frac{1}{\rho Cp}\frac{{\partial q_{r} }}{\partial y} + \frac{\mu }{\rho Cp}\left( {\frac{\partial u}{{\partial y}}} \right)^{2}$$

(4)

The boundary conditions are

$$\left. \begin{gathered} u = ax + \alpha^{*} \left[ {(\mu + k)\frac{\partial u}{{\partial y}} + kN} \right],\,v = v_{w} ,\,N = - n\frac{\partial u}{{\partial y}},\,\frac{\partial T}{{\partial y}} = - \frac{{bx^{m} }}{k},\,at\,y\, = 0 \hfill \\ u \to 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,N \to 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,T \to T_{\infty } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,as\,y \to \infty \hfill \\ \end{gathered} \right\}$$

(5)

Jena and Matkur [22] considered the case $(n = 0)$ of concentrated particle flows in which they observed that micro-elements close to the wall are unable to rotate. But Ahmadi [23] examined the case $(n = 1/2)$ of weak concentrations and indicates the vanishing of antisymmetric part where as the case for $(n = 1)$ turbulent boundary layer flows suggested by Peddieson [24]. The radiative heat flux term by using the Rosseland approximation [25] is given by

$$q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}$$

(6)

where $\sigma^{*}$ Stefan–Boltzmann constant and $k^{*}$ mean absorption coefficient. We have assumed that the temperature differences are very small within the fluid. We have expanded $T^{4}$ by Taylor series expansion about $T_{\infty }$ and neglecting higher order terms to express as a linear function. So $q_{r}$ can be written as

$$q_{r} = - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{\partial T}{{\partial y}}$$

Equation (4) takes the form:

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \left( {\frac{k}{\rho Cp} + \frac{1}{\rho Cp}\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{\rho Cp}\left( {T - T_{\infty } } \right) + \frac{\mu }{\rho Cp}\left( {\frac{\partial u}{{\partial y}}} \right)^{2}$$

(7)

3 Method of Solution

The equation of continuity (1) is satisfied by introducing the stream function $\psi$ such that

$$u = \frac{\partial \psi }{{\partial y}},\,\,\,v = - \frac{\partial \psi }{{\partial x}}$$

(8)

and with the following dimensionless variables:

$$\eta = \sqrt {\frac{a}{\upsilon }} \,y,\psi = \sqrt {a\upsilon \,} xf(\eta ),\,N = ax\sqrt {\frac{a}{\upsilon }} \,\omega (\eta ),T = T_{\infty } + \frac{{q_{s} (x)}}{k}\sqrt {\frac{\upsilon }{a}} \theta (\eta )$$

(9)

So the modified equations of the flow can be written as

$$(1 + K)f^{\prime\prime\prime} + ff^{\prime\prime} - \left( {f^{\prime}} \right)^{2} + K\omega^{\prime} - Mf^{\prime} + \lambda \theta = 0$$

(10)

$$G\omega^{\prime\prime} + f\omega^{\prime} - f^{\prime}\omega - K\left( {2\omega + f^{\prime\prime}} \right) = 0$$

(11)

$$\frac{1}{\Pr }\left( {1 + \frac{4}{3}R} \right)\theta^{\prime\prime} + f\theta^{\prime} - mf^{\prime}\theta + S\theta + Ec\,(f^{\prime\prime})^{2} = 0$$

(12)

$$\left. \begin{gathered} f = f_{w} ,\,f^{\prime} = 1 + \alpha (1 + K)f^{\prime\prime}\,,\,\omega = - nf^{\prime\prime},\theta^{\prime} = - 1\,\,\,{\text{at}}\,\,\eta = 0 \hfill \\ f^{\prime} \to 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\omega \to 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta \to 0\,\,\,{\text{as}}\,\,\eta \to \infty \hfill \\ \end{gathered} \right\}$$

(13)

$$\begin{gathered} K = \frac{k}{\mu },M = \frac{{\sigma B_{0}^{2} }}{a\rho },\lambda = \frac{{g\beta_{T} q_{s} \sqrt \upsilon }}{{ka^{3/2} }},G = \frac{\gamma }{j\mu },j = \frac{\upsilon }{a},\Pr = \frac{{\mu c_{p} }}{k} \hfill \\ R = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{kk^{*} }},S = \frac{{Q_{0} }}{{a\rho c_{p} }},Ec = \frac{{\sqrt \upsilon ka^{3/2} x^{2} }}{{c_{p} q_{s} }},\alpha = \,\mu \alpha^{*} \sqrt {\frac{a}{\upsilon }} \hfill \\ \end{gathered}$$

(14)

The physical quantities of interest are the local skin-friction coefficient $C_{fx}$, the dimensionless wall couple stress $M_{x}$, and the local Nusselt number $Nu_{x}$, which are defined as

$$C_{fx} = \frac{{2\tau_{w} }}{{\rho (ax)^{2} }},\,M_{x} = \frac{{m_{w} }}{{\rho a\upsilon x^{3} }},Nu_{x} = \frac{{xq_{w} }}{{\kappa (T_{w} - T_{\infty } )}}$$

(15)

where the local wall shear stress $\tau_{W}$, the wall couple stress $m_{w}$, and the heat transfer from the plate $q_{w}$ are defined by

$$\tau_{W} = \left[ {\left( {\mu + k} \right)\frac{\partial u}{{\partial y}} + kN} \right]_{y = 0} ,m_{w} = \gamma_{0} \left[ {\frac{\partial N}{{\partial y}}} \right]_{y = 0} ,q_{w} = - k\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}$$

(16)

Using the similarity variables (10), we get

$$C_{fx} {\text{Re}}_{x}^{1/2} = - 2(1 + K)f^{\prime\prime}(0),M_{x} {\text{Re}}_{x} = KG\omega^{\prime}(0),Nu_{x} {\text{Re}}_{x}^{ - 1/2} = - \theta^{\prime}(0)$$

(17)

where ${\text{Re}}_{x} = \frac{{ax^{2} }}{\upsilon }$ is the local Reynolds number.

4 Results and Discussion

Free convection of an electrically conducting micropolar fluid past a stretching surface is considered in the current investigation. The characteristics of the energy equation are enhanced by incorporating the heat generation/absorption parameter as well as the viscous dissipation. In an addition, the slip boundary condition for the velocity is considered which affects the flow phenomena. The physical significance of the contributing parameters are obtained and presented via graphs. The rate coefficients for all the profiles are also displayed through graphs. The variation of several parameters on the profiles is presented in the corresponding figures. Figure 1 depicts the validation of the transverse velocity, longitudinal velocity, micro-rotation, and the temperature profiles in the absence of magnetic field, thermal buoyancy, and the thermal radiation. However, the result coincides with the work of Mahmoud et al. [21] showing the conformity of the convergence procedure of the current methodology. Figure 2 exhibits the behavior of the suction/injection parameter for various values of slip factor on the velocity distribution. The partial vacuum exerts upon a liquid is caused by the suction. Reduction in pressure is marked due to the removal of air from the space resulted to enter the fluid into the space. Therefore, the fluid exerts from the higher pressure region to lower pressure region. In comparison to suction and injection, it is seen that the suction lowers down the velocity profiles irrespective of the slip or no slip region. However, in case of no slip condition, the maximum velocity is rendered within the boundary layer and reduction in the profile is observed with increasing slip. Pick in the micro-rotation profiles is marked near the surface up to the region $\eta \le 1$ and afterwards sudden fall is marked in Fig. 3. Moreover, suction produces higher pressure to reduce the profiles than that of injection. Similar observation is rendered in case of slip parameter as described in the Fig. 2. Figure 4 exhibits the distribution of temperature profiles for the variation of the suction/injection and slip parameters. It is observed that increasing slip enhances the fluid temperature in the entire region of the thermal boundary layer and injection also favorable to increase the temperature as well. The values of the material parameter ($K$) indicates the Newtonian and non-Newtonian characteristics of the fluid. $K$ = 0 represents the Newtonian case and the $K \ne 0$ shows the non-Newtonian nature. However, in the present case we have considered the non-Newtonian behavior of the fluid. Figure 5 illustrates the profiles of micro-rotation in conjunction with suction/injection. An increase in the material parameter enhances the micro-rotation profiles with pick near the surface and further it decelerates. The case of injection is also favorable to enhance it significantly. Figure 6 portrays the wall surface condition parameter (n) with suction/injection parameter on the micro-rotation distribution. The micro-rotation profile enhances rapidly near the surface with increasing the wall surface condition parameter. However, the injection is now favorable to enhance the profile for lower values of n but effect is reversed for higher values. Irrespective of values of suction/injection parameter, buoyancy parameter enriches the velocity profiles that exhibit in Fig. 7. The pressure difference results in a net upward force on the object. Figures 8 and 9 describe the impact of thermal radiation and heat source on the temperature profiles in conjunction with suction/injection parameter. Thermal radiation is one of the characteristics that depends on the various properties of the surface. Thermal enhancement occurs in the entire domain due to increase in the thermal radiation and heat source parameter. The coupling of temperature and velocity profile occurs due to the inclusion of coupling parameter, i.e., the Eckert number. Figure 10 describes the temperature distribution for the various values of Eckert number. From the mathematical definition, it is clear that increasing Eckert number enhances the fluid temperature. Finally, Figs. 11, 12, 13 display the computational results of shear stress, rate of heat transfer, and the couple stress for various values of suction/injection versus the slip parameter. The trend of the graph shows the decelerating effect, whereas increasing suction increases the rate coefficients with increasing slip.

Fig. 1

Validation of stream function $f(\eta )$, Velocity $f^{\prime}(\eta )$, Micro-rotation $\omega (\eta )$, and Temperature $\theta (\eta )$ profile

Fig. 2

Variation of Velocity Profile with $\alpha$ and ${\text{f}}_{{\text{w}}}$

Fig. 3

Variation of Micro-rotation Profile with $\alpha$ and ${\text{f}}_{{\text{w}}}$

Fig. 4

Variation of Temperature Profile with $\alpha$ and ${\text{f}}_{{\text{w}}}$

Fig. 5

Variation of Micro-rotation Profile with $K$ and ${\text{f}}_{{\text{w}}}$

Fig. 6

Variation of Micro-rotation Profile with $n$ and ${\text{f}}_{{\text{w}}}$

Fig. 7

Variation of Velocity Profile with $\lambda$ and ${\text{f}}_{{\text{w}}}$

Fig. 8

Variation of Temperature Profile with $R$ and ${\text{f}}_{{\text{w}}}$

Fig. 9

Variation of Temperature Profile with $S$ and ${\text{f}}_{{\text{w}}}$

Fig. 10

Variation of Temperature Profile with $Ec$ and ${\text{f}}_{{\text{w}}}$

Fig. 11

Variation of Skin Friction Coefficient $\alpha$ and ${\text{f}}_{{\text{w}}}$

Fig. 12

Variation of Nusselt Number $\alpha$ and ${\text{f}}_{{\text{w}}}$

Fig. 13

Variation of Wall Couple Stress Coefficient $\alpha$ and ${\text{f}}_{{\text{w}}}$

5 Conclusive Remarks

Free convection of micropolar fluid in conjunction with slip parameter and the effect of heat source are exhibited in the present investigation. The behavior of characterizing parameter on the flow phenomena is displayed and discussed. However, the major contributions are laid down as

• The validation of present result with earlier established result shows the conformity of the convergence procedure of the methodology employed.

• Retardation in the velocity profiles is marked due to increase in suction regardless with the increase of slip parameter.

• The rate coefficients enhance with increasing suction with respect to the slip parameter.