Introduction

Significant applications are made on shrinking sheet in manufacturing and technological processes. Fang and Zhang [1] found the particular solution for the flow over a shrinking sheet. Bhattacharyya [2] and Mukhopadhyay [3] established the dual solutions past an exponentially shrinking sheet. Nadeem et al. [4] have examined the flow behavior of water-based nanofluid. Swain et al. [5] have studied the viscoelastic nanofluid flow over an elongating sheet. Numerical simulation was made by Motsumi and Makinde [6] to study the dissipation on chemically reactive nanofluid. Naramgari and Sulochana [7] illustrated a numerical solution to study the impact of suction/injection on MHD nanofluid flow over a permeable elongating/shrinking sheet. The slip flow investigation on stretching sheet was carried out by Swain et al. [8].

Nanofluid is used to augment the heat transfer rate of base fluids. The nanoparticles are emerged in base fluid to enhance the thermal conductivity which allows more heat transfer. Hady et al. [9] have considered the nanofluid over a non-linearly extending sheet. Sheikholeslami et al. [10] obtained a numerical simulation of MHD nanofluid flow considering viscous dissipation. Mahanthesh et al. [11] explored the three dimensional flow of nanofluid over a non-linearly elongating sheet by taking water as base fluid. Ghosh and Mukhopadhyay [12] studied the slip flow analysis of two kinds of nanofluids over an exponentially enlarging sheet. Mebarek-Oudina [13] examined the nanofluid flow using different base fluids. Kolsi et al. [14] have numerical investigated the aggregation effects on MWCNT–water nanofluid. Ghosh and Mukhopadhyay [15] have obtained a stability analysis for nanofluid flow with slip boundary conditions. Various recent researches are carried out using analytical and numerical methods to treat heat transfer and nanofluids in thermal and energy systems [16,17,18,19,20,21,22,23,24,25,26].

Hybrid nanofluid is a mixture of two types of nanoparticles suspended in regular fluid and applied in all fields of heat transfer such as manufacturing, electro- and biosensors, and acoustics. Hayat and Nadeem [27] have studied the impact of heat transfer of Ag–CuO/water hybrid nanofluid over an extending sheet. Ghadikolaei et al. [28] have considered nanoparticles shape factor to study the behavior of TiO2–CuO/ethylene glycol–water hybrid nanofluid over rotating cone. Waini et al. [29] have numerically examined the hybrid nanofluid flow over a nonlinear permeable enlarging/shrinking sheet. Bagheri et al. [30] have analyzed the sensitive analysis of hybrid nanofluids with consideration of heat flux. The effect of viscous dissipation on Cu–Al2O3–H2O hybrid nanofluid over a shrinking surface with stability analysis is considered by Lund et al. [31]. Aziz et al. [32] and Lund et al. [33] have investigated the hybrid nanofluid over a widening sheet. Some related investigations can be found in the articles [34,35,36,37,38,39,40].

Sundar et al. [41] studied the heat transfer and friction factor of MWCNT–Fe3O4/water hybrid nanofluids. Sohail et al. [42, 43] have studied the 3D flow of nanofluid over a stretching sheet with thermal radiation. Further, Sohail et al. [44,45,46] examined the flow of nanofluid by using different fluid model in the presence of bio-convective gyrotactic microorganisms and variable thermal conductivity. Shah et al. [47] studied the effect of Lorentz force on solidification of NEPCM. Moreover, Shah et al. [48] and Wakif [49] investigated the influences of chemical reaction on MHD Casson nanofluid over a stretching sheet. Shah et al. [50, 51] studied the micropolar Casson fluid over a stretching/shrinking sheet and between two rotating parallel plates, respectively. Deebani et al. [52] examined the Hall current effect on radiative Casson fluid with chemical reaction. Senapati et al. [53] numerical studied the three-dimensional flow of Casson nanofluid past an exponentially stretching sheet. Wakif et al. [54, 55] studied the influence of uniform transverse magnetic field on water-based nanofluids with metallic nanoparticles using Buongiorno’s model. Further, Wakif et al. [56] examined the dissipative flow of Stokes second problem. Wakif et al. [57] carried out the numerical solution of unsteady Couette nanofluid flow in the existence of thermal radiation.

To the authors information, no studies have been done for flow, heat, and mass transfer characteristics of MWCNT/Fe3O4–water hybrid nanofluid over an exponentially shrinking in presence of porous matrix with slip boundary conditions. Further, the influences of thermal radiation and heat generation on chemically reactive species hybrid nanofluid are highly affected with heat transfer development theory. The efficient shooting technique is applied to solve the nonlinear ordinary differential equations (ODEs). The effects of various relevant parameters are shown through graphs and tables. It is concluded that the external new parameters such as slip parameters, Schmidt number, chemical reaction, Prandtl number, and thermal radiation make a significant impact on the hybridity which improves the temperature and concentration profiles.

Mathematical formulation

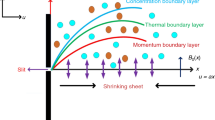
Consider two dimensional (2D) flow of MWCNT/Fe3O4–water hybrid nanoliquid over an exponentially shrinking sheet embedded in a porous matrix. The plate is placed along x-axis, and a variable magnetic field \(B = B_{0} {\text{e}}^{{\frac{x}{L}}}\) is induced in the flow (Fig. 1). The gravitational effect and viscous dissipative heat are also neglected. The leading equations of flow, heat, and mass transport following Ghosh and Mukhopadhyay [15] and Waini et al. [59] are written as

$$\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \upsilon_{\text{hnf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma_{\text{hnf}} B^{2} u}}{{\rho_{\text{hnf}} }} - \frac{{\mu_{\text{hnf}} u}}{{\rho_{\text{hnf}} Kp^{ * } }},$$
(2)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{\text{hnf}} }}{{\left( {\rho c_{p} } \right)_{\text{hnf}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } \left( {\rho c_{\text{p}} } \right)_{\text{hnf}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{Q}{{\left( {\rho c_{\text{p}} } \right)_{\text{hnf}} }}\left( {T - T_{\infty } } \right),$$
(3)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} - Kc^{ * } \left( {C - C_{\infty } } \right),$$
(4)

with the corresponding boundary conditions as:

$$\begin{aligned} & u = - U_{\text{w}} + B^{\prime}\upsilon_{\text{f}} \frac{\partial u}{\partial y},v = - v_{\text{w}} = - v_{0} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}} ,T = T_{\text{w}} + D^{\prime}\frac{\partial T}{\partial y},C = C_{\text{w}} + E'\frac{\partial C}{\partial y}\;{\text{at}}\;y = 0, \\ & u \to 0,T \to T_{\infty } ,C \to C_{\infty } \;{\text{at}}\;y \to \infty , \\ \end{aligned}$$
(5)

where \( U_{\text{W}} = - c{\text{e}}^{\frac{\rm x}{\rm L}}\) is the shrinking velocity with shrinking constant \(c > 0\), and \(v_{\text{w}} = v_{0} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}}\) where \(v_{0}\) is a constant (\(v_{0} > 0\) indicates suction and \(v_{0} < 0\) indicates injection), \(T_{\text{w}} = T_{\infty } + T_{0} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}}\) (\(T_{0}\) is a constant), \(C_{w} = C_{\infty } + C_{0} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}}\) (\(C_{0}\) is a constant), \(Q = Q_{0} {\text{e}}^\frac{\rm x}{\rm L}\) are, respectively, the variable temperature, concentration and heat source/sink. Here \(B^{\prime} = B_{1} {\text{e}}^{ - \frac{{\text{x}}}{2{\text{L}}}}\), \(D^{\prime} = D_{1} {\text{e}}^{ - \frac{\text{x}}{2{\text{L}}}}\), and \(E^{\prime} = E_{1} {\text{e}}^{ - \frac{\text{x}}{2{\text{L}}}}\) are the velocity, thermal, and solutal slip factors, respectively.

Fig. 1
figure 1

Flow geometry

Full size image

The effective nanofluid properties are given by

$$\begin{aligned} & \mu_{\text{hnf}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)^{2.5} }},\,\rho_{\text{hnf}} = \left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)\rho_{\text{f}} + \phi_{\text{MWCNT}} \rho_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} \rho_{{{\text{Fe}}_{3} {\text{O}}_{4} }} ,\, \\ & \left( {\rho c_{\text{p}} } \right)_{\text{hnf}} = \left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \phi_{\text{MWCNT}} \left( {\rho c_{\text{p}} } \right)_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} \left( {\rho c_{\text{p}} } \right)_{{{\text{Fe}}_{3} {\text{O}}_{4} }} , \\ & \frac{{\sigma_{\text{hnf}} }}{{\sigma_{\text{f}} }} = \left[ {1 + \frac{{3\left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} - 1} \right)\left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)}}{{\left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} + 2} \right) - \left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} - 1} \right)\left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)}}} \right], \\ & \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} = \frac{{\left[ {\frac{{\phi_{\text{MWCNT}} k_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} k_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }} + 2k_{\text{f}} + 2\left( {\phi_{\text{MWCNT}} k_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} k_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right) - 2\left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)k_{\text{f}} } \right]}}{{\left[ {\frac{{\phi_{\text{MWCNT}} k_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} k_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }} + 2k_{\text{f}} - \left( {\phi_{\text{MWCNT}} k_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} k_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right) + \left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)k_{\text{f}} } \right]}} \\ \end{aligned}$$

where \(\phi\) is the solid volume fraction, \(\mu_{\text{f}}\) and \(\mu_{\text{hnf}}\) are the dynamic viscosities, \(\upsilon_{\text{f}}\) and \(\upsilon_{\text{hnf}}\) are the kinematic viscosities, \(\rho_{\text{f}}\) and \(\rho_{\text{hnf}}\) are the densities, \(\left( {\rho c_{\text{p}} } \right)_{\text{f}}\) and \(\left( {\rho c_{\text{p}} } \right)_{\text{hnf}}\) are the heat capacitances, \(k_{\text{f}}\) and \(k_{\text{hnf}}\) are the thermal conductivities, and \(\sigma_{\text{f}}\) and \(\sigma_{\text{hnf}}\) are the electrically conductivities of the base fluid and hybrid nanofluid, respectively.

Similarity transformations

Consider the following similarity transformation

$$\psi = \sqrt {2\upsilon_{\text{f}} cL} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}} f(\eta ),\eta = y\sqrt {\frac{c}{{2\upsilon_{\text{f}} L}}} {\text{e}}^{\frac{\text{x}}{2{\text{L}}}} ,\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\varPhi (n) = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}.$$
(6)

In view of (6), Eqs. (1)–(5) become

$$\zeta_{1} \zeta_{2} f''' + ff'' - 2f'^{2} - \zeta_{2} \zeta_{3} Mf^{\prime} - \zeta_{1} \zeta_{2} Kpf^{\prime} = 0,$$
(7)
$$\zeta_{4} \left\{ {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + \frac{4}{3}R} \right\}\theta '' + { \Pr }\left\{ {f\theta ' - f'\theta + q\zeta_{4} \theta } \right\} = 0,$$
(8)
$$\Phi^{\prime\prime} + {\text{Sc}}\left\{ {f\Phi^{\prime} - f^{\prime}\Phi - {\text{Kc}}\Phi } \right\} = 0.$$
(9)
$$\begin{aligned} & f(\eta ) = S,\,\,\,f^{\prime}(\eta ) = - 1 + Bf^{\prime\prime}(\eta ),\,\,\,\theta (\eta ) = 1 + D\theta^{\prime}(\eta ),\,\,\,\,\varPhi \left( \eta \right) = 1 + E\varPhi^{\prime}\left( \eta \right)\,\,{\text{at}}\,\,\eta = 0 \\ & f^{\prime}(\eta ) \to 0,\,\,\theta (\eta ) \to 0,\,\,\varPhi (\eta ) \to 0\,\,{\text{as}}\,\,\eta \to \infty \\ \end{aligned}$$
(10)

where

$$\begin{aligned} & \zeta_{1} = \frac{1}{{\left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)^{2.5} }},\,\,\zeta_{2} = \frac{1}{{\left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right) + \phi_{\text{MWCNT}} \left( {\frac{{\rho_{\text{MWCNT}} }}{{\rho_{\text{f}} }}} \right) + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} \left( {\frac{{\rho_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\rho_{\text{f}} }}} \right)}}, \\ & \zeta_{3} = 1 + \frac{{3\left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} - 1} \right)\left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)}}{{\left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} + 2} \right) - \left( {\frac{{\sigma_{\text{MWCNT}} + \sigma_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\sigma_{\text{f}} }} - 1} \right)\left( {\phi_{\text{MWCNT}} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)}},\,M = \frac{{2LB_{0}^{2} \sigma_{\text{f}} }}{{c\rho_{\text{f}} }},Kp = \frac{{2L\upsilon_{\text{f}} }}{{cKp^{ * } }}, \\ & \zeta_{4} = \frac{1}{{\left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right) + \phi_{\text{MWCNT}} \frac{{\left( {\rho c_{\text{p}} } \right)_{\text{MWCNT}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }} + \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} \frac{{\left( {\rho c_{\text{p}} } \right)_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}}}\,,S = - \frac{{v_{0} }}{{\sqrt {{\raise0.7ex\hbox{${\left( {v_{\text{f}} c} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {v_{\text{f}} c} \right)} {2L}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2L}$}}} }},B = B_{1} \sqrt {\frac{{c\upsilon_{\text{f}} }}{2L}} , \\ & D = D_{1} \sqrt {\frac{c}{{2\upsilon_{\text{f}} L}}} ,E = E_{1} \sqrt {\frac{c}{{2\upsilon_{\text{f}} L}}} ,R = \frac{{4\sigma^{ * } T_{\infty }^{3} }}{{3k_{\text{f}} k^{ * } }},Q = \frac{{2LQ^{ * } }}{{c\left( {\rho C_{\text{p}} } \right)_{\text{f}} }},\Pr = \frac{{\upsilon_{\text{f}} \left( {\rho C_{\text{p}} } \right)_{\text{f}} }}{{k_{\text{f}} }},{\text{Sc}} = \frac{{\upsilon_{\text{f}} }}{{D_{\text{B}} }}. \\ \end{aligned}$$

The surface conditions of practical interest such as the skin friction coefficient \((C_{\text{f}} )\), Nusselt number \(\left( {{\text{Nu}}_{\text{x}} } \right)\), and Sherwood number \(\left( {{\text{Sh}}_{\text{x}} } \right)\) are given by

$$\begin{aligned} & C_{\text{f}} = \frac{{\mu_{{{\text{h}}\eta {\text{f}}}} }}{{\rho_{\text{f}} U_{\text{w}}^{2} {\text{e}}^{{\frac{2x}{L}}} }}\left. {\frac{\partial u}{\partial y}} \right|_{y = 0} ,{\text{Nu}}_{\text{x}} = - \frac{{xk_{\text{hnf}} }}{{k_{\text{f}} (T_{\text{w}} - T_{\infty } )}}\left. {\frac{\partial T}{\partial y}} \right|_{y = 0} \;{\text{and}}\;{\text{Sh}}_{\text{x}} = - \frac{{xk_{\text{hnf}} }}{{k_{\text{f}} \left( {C_{\text{w}} - C_{\infty } } \right)}}\left. {\frac{\partial C}{\partial y}} \right|_{y = 0} \\ & C_{\text{fx}} \text{Re}_{\text{x}}^{\frac{1}{2}} = \frac{1}{{\left( {1 - \phi_{\text{MWCNT}} - \phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} } \right)^{2.5} }}f''(0),{\text{Nu}}_{\text{x}} \text{Re}_{\text{x}}^{\frac{1}{2}} = - \left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + \frac{4}{3}R} \right)\theta '(0),{\text{Sh}}_{\text{x}} \text{Re}_{\text{x}}^{\frac{1}{2}} = - \left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}} \right)\varPhi^{\prime}(0) \\ \end{aligned}$$

Numerical solution

The nonlinear ODEs (7)–(10) are solved numerically by employing Runge–Kutta fourth-order method along with shooting technique. In this process, boundary value problem (BVP) is transformed to initial value problem (IVP). At first, the highest order terms can be written in the remaining lower-order terms as follows:

$$f^{\prime \prime \prime } = \frac{1}{{\zeta_{1} \zeta_{2} }}\left[ { - ff^{\prime \prime } + 2f^{\prime 2} + \zeta_{2} \zeta_{3} Mf^{\prime } + \zeta_{1} \zeta_{2} Kpf^{\prime } } \right],$$
(11)
$$\theta^{\prime\prime} = \frac{ - \Pr }{{\zeta_{4} \left\{ {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + \frac{4}{3}R} \right\}}}\left[ {f\theta^{\prime} - f^{\prime}\theta + \zeta_{4} q\theta } \right],$$
(12)
$$\varPhi^{\prime\prime} = - {\text{Sc}}\left[ {f\varPhi^{\prime} - f^{\prime}\varPhi - {\text{Kc}}\varPhi } \right].$$
(13)

Then, the governing equations are transformed to a set of following first ODEs by presenting the new variables as:

$$f = y_{1} ,\,f^{\prime} = y_{2} ,f^{\prime\prime} = y_{3} ,\theta = y_{4} ,\,\theta^{\prime} = y_{5} ,\varPhi = y_{6} ,\,\varPhi^{\prime} = y_{7} .$$
(14)

Let \(y = \left[ {f\,\,f^{\prime}\,\,f^{\prime\prime}\,\,\theta \,\,\theta^{\prime}\,\,\varPhi \,\,\varPhi^{\prime}\,} \right]^{\text{T}}\) which gives

$$\frac{\text{d}}{{{\text{d}}\eta }}\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {y_{3} } \\ {y_{4} } \\ {y_{5} } \\ {y_{6} } \\ {y_{7} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{2} } \\ {y_{3} } \\ {\frac{1}{{\zeta_{1} \zeta_{2} }}\left[ { - y_{1} y_{3} + 2y_{2}^{2} + \zeta_{2} \zeta_{3} My_{2} + \zeta_{1} \zeta_{2} Kpy_{2} } \right]} \\ {y_{4} } \\ {\frac{ - \Pr }{{\zeta_{4} \left\{ {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + \frac{4}{3}R} \right\}}}\left[ {y_{1} y_{5} - y_{2} y_{4} + \zeta_{4} qy_{4} } \right]} \\ {y_{6} } \\ { - {\text{Sc}}\left[ {y_{1} y_{7} - y_{2} y_{6} - {\text{Kc}}y_{6} } \right]} \\ \end{array} } \right],$$
(15)

subject to the initial conditions

$$\begin{aligned} & y_{1} \left( 0 \right) = S,\,y_{2} \left( 0 \right) = - 1 + By_{3} \left( 0 \right),\,\,y_{2} \left( \infty \right) \to 0,\,y_{3} \left( 0 \right) = l_{1} , \\ & y_{4} \left( 0 \right) = 1 + Dy_{5} ,\,\,y_{4} \left( \infty \right) \to 0,y_{5} \left( 0 \right) = l_{2} ,\,y_{6} \left( 0 \right) = 1 + Ey_{7} ,\,\,y_{6} \left( \infty \right) \to 0,\,y_{7} \left( 0 \right) = l_{3} , \\ \end{aligned}$$
(16)

with some initial guess values of \(l_{1} ,\,l_{2} ,\,\) and \(l_{3}\), we apply Runge–Kutta method of fourth order to solve the above IVP. There is an inbuilt self-corrective procedure in the MATLAB coding to correct the unknown guess values. Once the corrected values are attended, then the step-by-step integration by Runge–Kutta scheme is executed and the solution is attained within the prescribed error limit. The reduced Nusselt number \(\left\{ { - \theta^{\prime}\left( 0 \right)} \right\}\) is compared with the works of Devi and Devi [58] and Waini et al. [59] in the absence of nanoparticles for different values of Pr, and results are in good agreement as shown in Table 1.

Table 1 Comparison of \(- \theta^{\prime}\left( 0 \right)\) for base fluid \(\left( {\phi_{\text{MWCNT}} = 0,\phi_{{{\text{Fe}}_{3} {\text{O}}_{4} }} = 0} \right)\) for various values of Pr
Full size table

Numerical results and discussion

The system of nonlinear ODEs (7)–(10) are solved numerically using the bvp4c scheme from MATLAB software to observe the influences of the related operating parameters in the flow domain. The impacts of such parameters are depicted clearly in Figs. 2–11. Table 2 provides the thermo-physical properties of base fluid and nanofluid at 25 °C. In the present study, we consider \(\phi_{1} = \phi_{2} = 0\) for base fluid and \(\phi_{1} = \phi_{2} = 0.05\) for hybrid nanofluid. During numerical simulations, we fixed the values of the parameters as \(M = q = B = D = E = \, 0.1,\Pr = 6.2,{\text{Sc}} = 0.6,{\text{Kp}} = R = {\text{Kc}} = 0.5\) and \(S = 3\), unless otherwise the values are mentioned.

Fig. 2
figure 2

Variation in \(f^{\prime}\left( \eta \right)\) with \(M\) and \(B\)

Full size image
Fig. 3
figure 3

Variation in \(f^{\prime}\left( \eta \right)\) with \(S\)

Full size image
Fig. 4
figure 4

Variation in \(f^{\prime}\left( \eta \right)\) with \(M\)

Full size image
Fig. 5
figure 5

Variation in \(f^{\prime}\left( \eta \right)\) with Kp

Full size image
Fig. 6
figure 6

Variation in \(\theta \left( \eta \right)\) with \(R\)

Full size image
Fig. 7
figure 7

Variation in \(\theta \left( \eta \right)\) with \(q\)

Full size image
Fig. 8
figure 8

Variation in \(\theta \left( \eta \right)\) with \(D\)

Full size image
Fig. 9
figure 9

Variation in \(\varPhi \left( \eta \right)\) with \({\text{Sc}}\)

Full size image
Fig. 10
figure 10

Variation in \(\varPhi \left( \eta \right)\) with \(Kc\)

Full size image
Fig. 11
figure 11

Variation in \(\varPhi \left( \eta \right)\) with \(E\)

Full size image
Table 2 Thermo-physical properties of \({\text{MWCNT}}\) and \({\text{Fe}}_{3} {\text{O}}_{4}\) [29]
Full size table

Figure 2 depicts the effects of magnetic parameter (M) and velocity slip parameter (B). It is seen that the velocity profiles \(\left( {f^{\prime}\left( \eta \right)} \right)\) increase due to rise in M and B. Therefore, the velocity boundary layer thickness declines. Figure 3 presents the comparison of \(f^{\prime}\left( \eta \right)\) for H2O, MWCNT–water and MWCNT-Fe3O4/water for various values of suction parameter \(\left( S \right)\). It is observed that \(f^{\prime}\left( \eta \right)\) increases for all types of fluids taken into consideration because suction reduces the drag on bodies in an external flow. Moreover, in a porous medium, the continuous suction is more effective than in a non-porous medium. This is the practical importance of combined effect of suction and porous medium. Further, it is seen that velocity of MWCNT-Fe3O4/water is lower than MWCNT-water and H2O. Figure 4 depicts the comparison of velocity profiles due to absence and presence of magnetic parameter (M). When M = 0, the velocity of the all fluids is less than that of M = 1. Close analysis reveals that the velocity of the hybrid nanofluid is less than other fluids when M = 0. Figure 5 displays the effect of resistive force caused by the porous medium. A comparison study is made to analyze the effect of permeability parameter (Kp) on \(f^{\prime}\left( \eta \right)\) for H2O, MWCNT–water and MWCNT-Fe3O4/water. It is perceived that \(f^{\prime}\left( \eta \right)\) of hybrid nanofluid is less in the absence of porous matrix.

Figure 6 represents the comparison of temperature profiles \(\theta \left( \eta \right)\) between hybrid nanofluid (MWCNT-Fe3O4/water), nanofluid (MWCNT–water) and base fluid (water) by the inspiration of radiation parameter (R). It is perceived that under same conditions, the hybrid nanofluid achieves higher temperature than nanofluid and regular fluid. In general, \(\theta \left( \eta \right)\) is an increasing function of \(R\). For higher values of \(R\) (i.e., thermal radiation is dominate over conduction), an excessive amount of heat energy is released due to radiation which increases \(\theta \left( \eta \right)\). Figure 7 reveals that heat source/sink parameter (q) enhances \(\theta \left( \eta \right)\). From Fig. 8, it is found that the thermal slip parameter (D) causes a decline in \(\theta \left( \eta \right)\). Moreover, temperature of MWCNT–Fe3O4/water is more higher than that of MWCNT–water and water.

Figure 9 shows the effect of Schmidt number \(\left( {\text{Sc}} \right)\) on concentration distribution \(\varPhi \left( \eta \right)\). Since \({\text{Sc}}\) is the ratio of momentum diffusivity and mass diffusivity, heavier species leads to reduce \(\varPhi \left( \eta \right)\). Further,\(\varPhi \left( \eta \right)\) for hybrid nanofluid (MWCNT–Fe3O4/water), nanofluid (MWCNT/water) and base fluid (water) are almost same. Figure 10 depicts the effects of Kc on concentration profiles \(\varPhi \left( \eta \right)\). Here Kc > 0 relates to constructive and Kc < 0 for destructive chemical reaction. It is seen that higher values of Kc diminish the concentration level in all the layers. Figure 11 shows the effect of solutal slip parameter (E) on \(\varPhi \left( \eta \right)\). It is observed that the higher values of E decrease \(\varPhi \left( \eta \right)\) for both nanofluid and hybrid nanofluid.

Table 3 is computed to observe the impact of M, Kp, B and S on skin friction coefficients for nanofluid (MWCNT/water) and hybrid nanofluid (MWCNT–Fe3O4/water). It is seen that M, Kp and S enhance the skin friction coefficients, but reverse effect is seen for \(B\). Table 4 is calculated to get the impact of operating parameters such as D, E, Pr, R, Sc, and Kc on local Nusselt number and local Sherwood number for nanofluid and hybrid nanofluid. It is perceived that D, Pr, and R are responsible for heat transfer rate, whereas E, Sc, and Kc are responsible for mass transfer. Greater values of Pr and R boost the local Nusselt number, but D reduces it. In similar way, Sc and Kc increase the local Sherwood number and E decreases it. It is interesting to note that E, Sc, and Kc have no impact on local Nusselt number and D, Pr, and R have no inspiration on local Sherwood number.

Table 3 Computation of \(f''(0)\) for nanofluid (MWCNT–water) and hybrid nanofluid (MWCNT-Fe3O4/water) when D = E = q = 0.1, Pr = 6.2, Sc= 0.6, R = Kc = 0.5
Full size table
Table 4 Computation of \(- \theta '(0)\) and \(- \varPhi^{\prime}(0)\) for nanofluid (MWCNT–water) and hybrid nanofluid (MWCNT–Fe3O4/water) when M = B = q = 0.1, Kp = 0.5, S = 3
Full size table

Conclusions

The key findings of the current study are:

  • Hybridity enhances the temperature profiles as well as concentration profiles.

  • Slip parameters are responsible to decrease their respective profiles.

  • Sc and Kc boost the mass transfer rate, whereas Pr and R enhance the heat transfer rate.

  • There is an improvement in shearing stress at the wall by augmenting the values of M, Kp, and S.

Finally, it is concluded that the external new parameters such as Slip parameters, Schmidt number, chemical reaction, Prandtl number, and radiation make a significant impact on the hybridity which enriches the temperature and concentration profiles.