Mixed Convective Magneto Flow of SiO₂–MoS₂/C₂H₆O₂ Hybrid Nanoliquids Through a Vertical Stretching/Shrinking Wedge: Stability Analysis

Abstract

Hybrid nanoliquid as an expansion of nanoliquid is acquired by scattering combination of nano-powder or numerous distinct nanomaterials in the regular liquid. Hybrid nanofluids are impeding fluids which furnish better performance of heat transport and thermo-physical properties than convectional heat transport fluids (ethylene glycol, water and oil) and nanofluids with single material. At this juncture, a sort of hybrid nanofluid comprising nano-size materials through an ethylene glycol as a regular liquid is modeled to expand the magnetic impact on the mixed convection flow through a shrinking/stretched wedge. The impacts of Joule heating and viscous dissipation are also revealed. The PDEs which governed the flow problem with heat transport are changed into a dimensionless ODEs system through a similarity technique. Then these equations are numerically exercised by utilizing bvp4c solver. The impact of emerging constraints on the flow field with heat transport is discussed with the aid of plots. Also, the stability analysis is implemented to classify which result is physically reliable and stable.

1 Introduction

In the current era, nanoliquids are renowned smartly engineer liquids completed of a regular liquid and nanomaterials (1.00–100.00 nm). Such kinds of liquids have superior thermal conductivity and heat transport coefficients of single phase as compared to conventional liquids. A novel type of nanoliquid be constructed by mixing two distinct types of nanomaterials named nano-composite or hybrid particles in the regular liquid, is known hybrid or nano-composite liquid. The hybrid nanomaterial is a material which merges chemical and physical characteristics of distinct nanomaterials simultaneously and offers the homogenous phase properties. These given hybrid nanoliquids are realistically a novel class of nanoliquids which has several imaginable applications in entirely heat transport fields, e.g. acoustics, manufacturing, defense, micro fluidics, transportation, naval structures, etc. Improvement of hybrid nanoliquids with superiority stability and thermal conductivity augmented is significant and can guide to optimization and sustainability of energy, since it enhances the thermal system efficiency [1]. Sarkar et al. [2] and Sidik et al. [3] have précised the earlier and current research and improvement correlated to preparation techniques of hybrid nanoliquids, the properties of thermophysical of hybrid nanoliquids and recent applications of hybrid nanoliquids. Senthilraja et al. [4] experimentally scrutinized water based Al₂O₃/CuO nanoparticles and Al₂O₃-CuO hybrid nanoliquid. Toghraiel et al. [5] explored the thermal properties of ethylene glycol based ZnO-TiO₂ hybrid nanoliquid and the temperature fluctuated from 25 to 50 °C and volume fraction particle from 0 to 3.5%. Also, it was monitored that at a lower temperature enhancement of thermal conductivity was less contrasted to a higher temperature. The impact of water based hybrid nanoliquid through mixing nanoparticles (TiO₂, SiO₂ and Al₂O₃) with distinct viscosity was estimated by Adriana et al. [6]. Maraj et al. [7] scrutinized the influence of shape factor by utilizing the carrying of hybrid MoS₂–SiO₂/H₂O nanoparticles through an isothermal porous vertical cone. They also considered the viscous dissipation and magnetic impacts. Rostami et al. [8] scrutinized the influence of magnetic field on forced and free convection flow of hybrid SiO₂–Al₂O₃–H₂O nanofluids from a porous vertical surface. The nonlinear radiative time dependent flow water based Cu-Al₂O₃ hybrid micropolar nanofluid suspended in polar materials was explored by Mackolil and Mahanthesh [9]. The data of linear regression for the friction factor and Nusselt number are also analyzed. Shruthy and Mahanthesh [10] investigated Casson liquid containing hybrid nanoliquid with thermal Rayleigh–Bénard convection and obtained the analytic solution. They observed that the hybrid nanoliquid stoppages the convection. Ghadikolaei et al. [11] explored the 3D magneto impact on the free convective flow comprising hybrid MoS₂-Ag nanomaterials mixed in water based C₂H₆O₂ nanoparticle with radiation effect. Mackolil and Mahanthesh [12] inspected the impact of heat absorption on the radiative flow of Casson nanofluid with diffusion-thermo effect and applied sensitivity analysis to obtain the solution. The impact of magnetic function on the flow of hybrid nanoliquid suspended in water and ethylene glycol base fluid was examined Mahanthesh [13]. Ashlin and Mahanthesh [14] investigated water based alumina nanofluid as well as copper/alumina hybrid nanoliquid through a vertical plate owing to co-axial rotation with five different shapes. They utilized the Laplace technique to find the exact solution. Recently, Thriveni and Mahanthesh [15] applied the sensitivity analysis to study the magneto radiative flow of hybrid nanoliquid with mixed convective.

Owing to applications of shrinking and stretching sheets in the majority of the modern techniques, researchers have been eager to investigate the flows containing shrinking/stretching sheets. These include heating or cooling of films, polymer processes, conveyor belts, insulating materials, etc. From the family of the boundary-layer flow, Falkner and Skan [16] discovered the similarity results of flow through a stationary wedge. Hartree [17], Koh and Hartnett [18] implemented the boundary-layer assumptions to investigate the flow problem through a wedge by taking different engaged factors. Postelnicu and Pop [19] discussed the Falker–Skan flow comprising power law liquid from a stretched wedge. They found the multiple solutions for some fixed value of m, n and f₀. The impacts of magnetic and radiation parameters on forced and free convective 2D flow with heat transport from a stretched porous wedge with Joule heating were scrutinized by Su et al. [20] and obtained the solutions using an innovative technique named as DTM-BF. Yang and Machado [21] addressed the operator of new fractional-order of the erratic order first time and also presented the Fourier and Laplace transforms. The impact of bio-convection flow of a nanoliquid involving microorganism from a fixed wedge in a Darcy medium is studied by Zaib et al. [22]. Yang [23] reported the new results of the general fractional calculus and also proposed new special functions. Yang and Gao [24] proposed Sumudu transform to solve the heat and diffusion equations. Yang [25] addressed the fractional derivatives of variables as well as of constant orders applied in different kinds of the problems in heat transfer. He applies the derivative in the form of Caputo type derivative. Yang and coauthors [26,27,28] suggested the fundamental results of the anomalous and general fractional order diffusion equation with singular, negative Prabhakar, non-singular and exponential decay kernels. The impact of the induced magnetic field of steady 2D flow containing nanofluid through a moving as well as fixed wedge was monitored by Nadeem et al. [29]. Recently, various studies on nanofluids are carried out in refs.[30,31,32,33,34,35].

The foregoing literature review discloses that the general problem of mixed convection containing hybrid nanofluids particularly stretching/shrinking wedge with Joule heating and dissipation has been underlined as mostly unexplored fields. Thus, the current work aims to scrutinize the hybrid nanoliquid magneto flow through a shrinking/stretching wedge with mixed convection by utilizing the mathematical model of hybrid nanoliquids suggested by the Devi and Devi [36], and Hayat and Nadeem [37]. In addition, the Joule heating and viscous dissipation impacts are also captivating. Here, hybrid nanoliquid is formed by mixing two distinct nanoparticles that are SiO₂ (silicon dioxide) and MoS₂ (Molybdenum disulfide) in the regular liquid (ethylene glycol). MoS₂ has a structure in layered form and it is utilized as a catalyst and lubricant due to its distinctive properties like chemical inertness, anisotropy and resistance of photo corrosion. In addition, MoS₂ nanomaterials product may be employed as nanocatalyses hydrogenation. The leading PDEs are transmuting into nonlinear ODEs through an appropriate transformation and then these ODEs are tackled via bvp4c. Influences of the pertinent constraints are investigated and portrayed via the plots.

2 Problem Statement

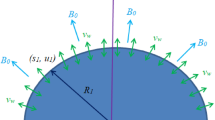
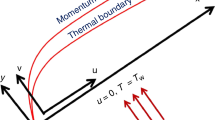
Consider the 2D steady mixed convective flow with heat transport containing hybrid nanoparticles through a porous wedge as portrayed in Fig. 1. The viscous dissipation with Joule heating also invoked here. The ethylene glycol based SiO₂–MoS₂ nanoparticles have been taken in this investigation. In this model, initially SiO₂ scattered into the regular liquid (ethylene glycol), and then to develop the marked hybrid nanoliquid SiO₂–MoS₂/C₂H₆O₂, MoS₂ is diffused in nanoliquid SiO₂/ethylene glycol. In extra assumption, the variable magnetic field is applied normal to wedge walls. It is supposed that moving wedge and the ambient velocity flow are respectively $u_{w} (x)$ and $u_{\infty } (x)$, whereas the walls temperature and the ambient temperature are respectively, $T_{{\text{w}}} (x)$ and $T_{\infty }$ with $T_{{\text{w}}} (x) > T_{\infty }$ utilized for the assisting flow (heated surface) and $T_{{\text{w}}} (x) < T_{\infty }$ consumed for the opposing flow (cooled surface). Applying the Boussinesq with boundary layer approximations, the steady leading equations are

$$ \frac{\partial v}{{\partial y}} + \frac{\partial u}{{\partial x}} = 0, $$

(1)

$$ \begin{aligned} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} &= u_{\infty } \frac{{du_{\infty } }}{dx} + \frac{{\mu_{{{\text{hbnf}}}} }}{{\rho_{{{\text{hbnf}}}} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\sigma_{{{\text{hbnf}}}} B^{2} (x)}}{{\rho_{{{\text{hbnf}}}} }}\left( {u_{\infty } - u} \right) \\ &\quad+ \frac{{g\left( {\rho \beta } \right)_{{{\text{hbnf}}}} }}{{\rho_{{{\text{hbnf}}}} }}\left( {T - T_{\infty } } \right)\cos \left( {\frac{\Omega }{2}} \right), \end{aligned} $$

(2)

$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{{k_{{{\text{hbnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hbnf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\sigma_{{{\text{hbnf}}}} B^{2} \left( x \right)}}{{\left( {\rho c_{p} } \right)_{{{\text{hbnf}}}} }}u^{2} + \frac{{\mu_{{{\text{hbnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hbnf}}}} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} . $$

(3)

Fig. 1

Physical diagram of the problem

The physical boundary conditions are

$$ \begin{gathered} u = u_{{\text{w}}} (x), \, v = v_{{\text{w}}} ,T = T_{{\text{w}}} (x){\text{ at }}y = 0,\,\,\, \hfill \\ u = u_{\infty } (x), \, T \to T_{\infty } {\text{ as }}y \to \infty , \hfill \\ \end{gathered} $$

(4)

in which $v$ and $u$ are components of velocity respectively in $y{ - }$ and x-directions. Moreover, these symbols $\rho_{{{\text{hbnf}}}} ,\mu_{{{\text{hbnf}}}} ,\sigma_{{{\text{hbnf}}}} ,g,\left( {\rho \beta } \right)_{{{\text{hbnf}}}} ,v_{{\text{w}}}$ are called density, dynamic viscosity, electrical conductivity, gravitational acceleration, coefficient of thermal expansion, suction of hybrid nanoliquids, respectively.

2.1 Thermophysical Properties of Hybrid Nanofluid

The combination of hybrid nanoliquid comprising SiO₂ $\left( {\phi_{1} } \right)$ and MoS₂ $\left( {\phi_{2} } \right)$ nanoparticles in ethylene glycol considered as a regular liquid. Furthermore, volume fractions of nanoparticle SiO₂ has been set to 1% and of MoS₂ vary from 1 to 5%. Following Xie et al. [38], the volume fraction of hybrid nanoliquid is suggested as

$$ \phi_{{{\text{hnf}}}} = \frac{{V_{{{\text{SiO}}_{{2}} }} + V_{{{\text{MoS}}_{{2}} }} }}{{V_{{{\text{Total}}}} }} = \phi_{1} + \phi_{2} . $$

Moreover, Table 1 is prepared to show the thermophysical attributes of the hybrid nanoliquid.

Table 1 Thermophysical characteristics of hybrid nanofluid

Following Deswita et al. [39]; Ishak et al. [40], the values of $u_{{\text{w}}} (x)$,$u_{\infty } (x)$, $T_{{\text{w}}} (x)$ and $B(x)$ are invoked in the text are given below as

$$ \begin{aligned} u_{{\text{w}}} (x) &= U_{0} x^{m} ,u_{\infty } (x) = U_{\infty } x^{m} ,T_{{\text{w}}} (x) - bx^{(5m - 1)/2} \\ &= T_{\infty } ,B(x) = B_{0} x^{{\frac{m - 1}{2}}} , \end{aligned} $$

(5)

where $U_{0}$, $U_{\infty }$ are constant velocities and $m = \frac{{ - \beta_{1} }}{{\left( {\beta_{1} - 2} \right)}}$ with $\beta_{1}$ is called the parameter named as Hartree of pressure slope which joins to $\beta_{1} = \Omega /\pi$ for a wedge material angle, $B_{0}$ called the strength of magnetic.

One would take the following similarity variables:

$$ \begin{gathered} u = u_{\infty } (x)F^{\prime } (\eta ), \, v = - \left( {\frac{{\left( {1 + m} \right)\nu_{{\text{f}}} u_{\infty } (x)}}{2x}} \right)^{\frac{1}{2}} \left[ {F(\eta ) + \left( {\frac{m - 1}{{m + 1}}} \right)\eta F^{\prime } (\eta )} \right], \, \hfill \\ \eta = y\left( {\frac{{\left( {1 + m} \right)u_{\infty } (x)}}{{2\nu_{f} x}}} \right)^{\frac{1}{2}} , \, \theta (\eta )\left( {T_{{\text{w}}} - T_{\infty } } \right) + T_{\infty } = T. \hfill \\ \end{gathered} $$

(6)

Implementation of the transformations above into Eqs. (2)–(5) and to get consistent transmuted ODEs via the well-known equation (6) become as

$$ \begin{aligned} &F^{\prime \prime \prime } {\rm X}_{1}^{ - 1} + {\rm X}_{2} \left( {\frac{2m}{{m + 1}}\left( {1 - \left( {F^{\prime } } \right)^{2} } \right) + FF^{\prime \prime } } \right) \\ &\quad+ \left( {\frac{2}{m + 1}} \right)M{\rm X}_{3} (1 - F^{\prime } ) \\ &\quad+ \left( {\frac{2}{m + 1}} \right)\lambda_{1} \cos \left( {\frac{\Omega }{2}} \right){\rm X}_{4} \theta = 0, \end{aligned} $$

(7)

$$ \begin{aligned} &{\rm X}_{5} \theta^{\prime \prime } + \Pr {\rm X}_{6} \left( {F\theta^{\prime } - \left( {\frac{5m - 1}{{m + 1}}} \right)\theta F^{\prime } } \right) \\ &\quad+ \Pr EcM\left( {\frac{2}{m + 1}} \right)F^{\prime 2} + \frac{\Pr Ec}{{{\rm X}_{1} }}\left( {F^{\prime \prime } } \right)^{2} = 0, \end{aligned} $$

(8)

with the dimensional form of boundary restriction is

$$ \begin{gathered} F(0) - s = 0,F^{\prime } (0) - \lambda = 0,\theta (0) - 1 = 0, \hfill \\ F^{\prime}(\infty ) - 1 \to 0,\theta (\infty ) \to 0, \hfill \\ \end{gathered} $$

(9)

in which

$$ \begin{aligned} {\rm X}_{1} &= \left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} , \hfill \\ {\rm X}_{2} &= \left( {\left( {1 - \phi_{2} } \right)\left\{ {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\rho_{{s_{1} }} }}{{\rho_{{\text{f}}} }}} \right\} + \phi_{2} \frac{{\rho_{{s_{2} }} }}{{\rho_{{\text{f}}} }}} \right), \hfill \\ {\rm X}_{3} &= \left( {\frac{{\sigma_{{s_{2} }} \left( {1 + 2\phi_{2} } \right) + 2\sigma_{{{\text{bf}}}} \left( {1 - \phi_{2} } \right)}}{{\sigma_{{s_{2} }} \left( {1 - \phi_{2} } \right) + \sigma_{{{\text{bf}}}} \left( {2 + \phi_{2} } \right)}}} \right)\\ &\quad\left( {\frac{{\sigma_{{s_{1} }} \left( {1 + 2\phi_{1} } \right) + 2\sigma_{{\text{f}}} \left( {1 - \phi_{1} } \right)}}{{\sigma_{{s_{1} }} \left( {1 - \phi_{1} } \right) + \sigma_{{\text{f}}} \left( {2 + \phi_{1} } \right)}}} \right), \hfill \\ {\rm X}_{4} &= \left( {\left( {1 - \phi_{2} } \right)\left[ {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho \beta } \right)_{{s_{1} }} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }}} \right] + \phi_{2} \frac{{\left( {\rho \beta } \right)_{{s_{2} }} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }}} \right), \hfill \\ {\rm X}_{5} &= \left[ {\left( {\frac{{k_{{s_{2} }} + 2k_{{{\text{nf}}}} - 2\phi_{2} \left( {k_{{{\text{nf}}}} - k_{{s_{2} }} } \right)}}{{k_{{s_{2} }} + 2k_{{{\text{nf}}}} + \phi_{2} \left( {k_{{{\text{nf}}}} - k_{{s_{2} }} } \right)}}} \right)}\right. \\ &\quad \left.{\left( {\frac{{\left( {k_{{s_{1} }} + 2k_{{\text{f}}} } \right) - 2\phi_{1} \left( {k_{{\text{f}}} - k_{{s_{1} }} } \right)}}{{\left( {k_{{s_{1} }} + 2k_{{\text{f}}} } \right) + \phi_{1} \left( {k_{{\text{f}}} - k_{{s_{1} }} } \right)}}} \right)} \right], \hfill \\ X_{6} &= \left( {\left( {1 - \phi_{2} } \right)\left[ {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{s_{1} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right] + \phi_{2} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{s_{2} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right). \hfill \\ \end{aligned} $$

(9A)

The non-dimensional patent parameters in Eqs. (7) and (8) which are expressed as mathematically

$$ \begin{aligned} \lambda_{1} &= \frac{{{\text{Gr}}_{x} }}{{{\text{Re}}_{x}^{2} }},M = \frac{{\sigma_{{\text{f}}} B_{0}^{2} }}{{\rho_{{\text{f}}} U_{\infty } }},{\text{Re}}_{x} = \frac{{xu_{\infty } \left( x \right)}}{{\nu_{{\text{f}}} }},\\ \Pr &= \frac{{\nu_{{\text{f}}} }}{{\alpha_{{\text{f}}} }},{\text{Gr}}_{x} = \frac{{g\beta_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)x^{3} }}{{\nu_{{\text{f}}}^{2} }}, \hfill \\ \lambda &= \frac{{U_{{\text{w}}} }}{{U_{\infty } }},{\text{Ec}} = \frac{{u_{\infty }^{2} }}{{\left( {c_{{\text{p}}} } \right)_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}. \hfill \\ \end{aligned} $$

(9B)

While these parameters namely called the mixed convective parameter $\left( {\lambda_{1} } \right)$ (where it is defined as $\lambda_{1} = \frac{{{\text{Gr}}_{x} }}{{{\text{Re}}_{x}^{2} }}$ called the fraction of $\left( {{\text{Gr}}_{x} } \right)$ Grashof number and the Reynolds number $\left( {{\text{Re}}_{x} } \right)$, magnetic parameter $\left( M \right)$, Prandtl number $\left( {\Pr } \right)$, Eckert number $\left( {{\text{Ec}}} \right)$ and the stretching/ shrinking parameter $\left( \lambda \right)$, respectively.

The local rate of heat transfer (Nusselt number) and the skin friction factor are the physical significant quantities concerning on the flow with heat transport. These quantities in the ODEs form are

$$ Nu_{x} = \frac{{ - k_{{{\text{hbnf}}}} x}}{{k_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} , $$

(10)

$$ C_{{\text{F}}} = \frac{{\mu_{{{\text{hbnf}}}} }}{{\rho u_{\infty }^{2} \left( x \right)}}\left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} . $$

(11)

Applying (6), we get

$$ \left( {{\text{Re}}_{x} } \right)^{{\frac{ - 1}{2}}} {\text{Nu}}_{x} = \frac{{ - k_{{{\text{hbnf}}}} \theta^{\prime } (0)}}{{k_{{\text{f}}} }}\left\{ {\frac{m + 1}{2}} \right\}^{\frac{1}{2}} , $$

(12)

$$ \sqrt {{\text{Re}}_{x} } C_{{\text{F}}} = \frac{{F^{\prime \prime } (0)}}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\left\{ {\frac{m + 1}{2}} \right\}^{\frac{1}{2}} . $$

(13)

3 Numerical Process

There are several techniques for solving nonlinear problems such as [41,42,43,44,45,46]. Prior utilizing the bvp4c solver based on 3-stage Lobatto technique which is handy to hold the 1st-order initial value problem. In general, Lobatto IIIA techniques have been used for the BVP owing to their extremely excellent properties of stability and contain accuracy of fourth-order over the entire interval. First the leading differential equations are transmuted into the first order group of ODEs. To achieve this, assume the new variables:

$$ F = R_{1}^{*} ,F^{\prime } = R_{2}^{*} ,F^{\prime \prime } = R_{3}^{*} ,\theta = R_{4}^{*} ,\theta^{\prime } = R_{5}^{*} . $$

(14)

The dependent first-order system is obtained as

$$ \left( {\begin{array}{*{20}c} {R_{1}^{*\prime } } \\ {R_{2}^{*\prime } } \\ {R_{3}^{*\prime } } \\ \begin{gathered} R_{4}^{*\prime } \hfill \\ R_{5}^{*\prime } \hfill \\ \end{gathered} \\ \end{array} } \right) = \left( \begin{gathered} R_{2}^{*} \hfill \\ R_{3}^{*} \hfill \\ - {\rm X}_{1} {\rm X}_{2} \left( {R_{1}^{*} R_{3}^{*} + \frac{2m}{{m + 1}}\left( {1 - \left( {R_{2}^{*} } \right)^{2} } \right)} \right) - {\rm X}_{1} {\rm X}_{3} M\left( {\frac{2}{m + 1}\left( {1 - R_{2}^{*} } \right)} \right) - \hfill \\ {\rm X}_{1} {\rm X}_{4} \lambda_{1} \left( {\frac{2}{m + 1}\cos \left( {\frac{\Omega }{2}} \right)R_{4}^{*} } \right) \hfill \\ R_{5}^{*} \hfill \\ \frac{{\left( { - M\Pr Ec\left( {\frac{2}{m + 1}\left( {R_{2}^{*} } \right)^{2} } \right) - \Pr {\rm X}_{6} \left( {R_{1}^{*} R_{5}^{*} - \left( {\frac{5m - 1}{{m + 1}}} \right)R_{2}^{*} R_{4}^{*} } \right) - \frac{{\Pr {\text{Ec}}\left( {R_{3}^{*} } \right)^{2} }}{{{\rm X}_{1} }}} \right)}}{{{\rm X}_{5} }} \hfill \\ \end{gathered} \right), $$

(15)

and the reformed initial conditions are

$$ \left( {\begin{array}{*{20}c} {R_{1}^{*} (0)} \\ {R_{2}^{*} (0)} \\ {R_{2}^{*} (\infty )} \\ \begin{gathered} R_{4}^{*} (0) \hfill \\ R_{4}^{*} (\infty ) \hfill \\ \end{gathered} \\ \end{array} } \right) = \left( \begin{gathered} s \hfill \\ \lambda \hfill \\ 1 \hfill \\ 1 \hfill \\ 0 \hfill \\ \end{gathered} \right). $$

(16)

Throughout this exploration, the set of up non-linear ODEs is numerically attempted by utilizing the bvp4c solver. The above problem may possibly have dual results; thus the assumed numerical method needs distinct early guesses to accomplish the conditions (9). In addition, the early value is relatively easy and simple to obtain the first solution (FS). Meanwhile, it is relatively difficult to obtain the precise initial guess for the second solution (SS). The numerical integration range is taken to be $\eta_{\max } = 3$ in the computation that is sufficient for the graphical outcomes to accomplish the two point condition asymptotically. The size of step is taken as $\Delta \eta = \frac{1}{100}$. The iteratively procedure is replicated awaiting the obligatory results are achieved up to accuracy level 10⁻⁵ to fit the convergence criterion.

4 Stability Analysis of the Solution

When one does the stability analysis, it is done with the primary objective to obtain the result of the aforementioned problem to check that the physical realization of the first branches in practice and to what extent and as well as for the (SS) that is not physically realizable. The unsteady equation would be taken in a specific order to determine their physical significance is given as under

$$ \frac{\partial v}{{\partial y}} + \frac{\partial u}{{\partial x}} = 0, $$

(17)

$$ \begin{gathered} \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = u_{\infty } \frac{{du_{\infty } }}{dx} + \frac{{\mu_{{{\text{hbnf}}}} }}{{\rho_{{{\text{hbnf}}}} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\sigma_{{{\text{hbnf}}}} B^{2} (x)}}{{\rho_{{{\text{hbnf}}}} }}\left( {u_{\infty } - u} \right) \hfill \\ + \frac{{g\left( {\rho \beta } \right)_{{{\text{hbnf}}}} }}{{\rho_{{{\text{hbnf}}}} }}\left( {T - T_{\infty } } \right)\cos \left( {\frac{\Omega }{2}} \right), \hfill \\ \end{gathered} $$

(18)

$$ \begin{aligned} \frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} &= \frac{{k_{{{\text{hbnf}}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{hbnf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\sigma_{{{\text{hbnf}}}} B^{2} \left( x \right)}}{{\left( {\rho c_{p} } \right)_{{{\text{hbnf}}}} }}u^{2} \\ &\quad+ \frac{{\mu_{{{\text{hbnf}}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{hbnf}}}} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} . \end{aligned} $$

(19)

Aforementioned model of stability, declare the fresh time variable that is dimensionless $\tau$. For this stability model the similarity transformation has now become as

$$ \begin{aligned} u &= U_{\infty } x^{m} F^{\prime } (\eta ), \, \\ v &= - \sqrt {\frac{{\left( {1 + m} \right)\nu_{{\text{f}}} U_{\infty } }}{2}} x^{{\frac{m - 1}{2}}} \left[ {\left( {\frac{m - 1}{{m + 1}}} \right)\eta F^{\prime } (\eta ) + F(\eta )} \right], \, \hfill \\ \eta &= y\sqrt {\frac{{\left( {1 + m} \right)U_{\infty } }}{{2\nu_{{\text{f}}} }}} x^{{\frac{m - 1}{2}}} , \, \theta (\eta )\left( {T_{{\text{w}}} - T_{\infty } } \right) + T_{\infty } = T, \, \\ \tau &{ = }\frac{{\text{m } + \text{ 1}}}{{2}}\left( {\frac{{u_{\infty } \left( x \right)}}{x}} \right)t. \hfill \\ \end{aligned} $$

(20)

By plugging Eq. (20) into Eqs. (18) and (19), we get

$$ \begin{aligned}& \frac{{\partial^{3} F}}{{\partial \eta^{3} }}{\rm X}_{1}^{ - 1} + {\rm X}_{2} \left( {F\frac{{\partial^{2} F}}{{\partial \eta^{2} }} + \frac{2m}{{m + 1}}\left( {1 - \left( {\frac{\partial F}{{\partial \eta }}} \right)^{2} } \right) - \frac{{\partial^{2} F}}{\partial \eta \partial \tau }} \right) \hfill \\&\quad+ \left( {\frac{2}{m + 1}} \right)M{\rm X}_{3} \left( {1 - \frac{\partial F}{{\partial \eta }}} \right) + \left( {\frac{2}{m + 1}} \right)\lambda_{1} \cos \left( {\frac{\Omega }{2}} \right){\rm X}_{4} \theta = 0 \hfill \\ \end{aligned} $$

(21)

$$ \begin{aligned} &\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }}{\rm X}_{5} + \Pr {\text{Ec}}M\left( {\frac{2}{m + 1}} \right)\left( {\frac{\partial F}{{\partial \eta }}} \right)^{2} \\ &\quad+ \Pr {\rm X}_{6} \left( {F\frac{\partial \theta }{{\partial \eta }} - \left( {\frac{5m - 1}{{m + 1}}} \right)\theta \frac{\partial F}{{\partial \eta }} - \frac{\partial \theta }{{\partial \tau }}} \right) \hfill \\&\quad + \frac{{\Pr {\text{Ec}}}}{{{\rm X}_{1} }}\left( {\frac{{\partial^{2} F}}{{\partial \eta^{2} }}} \right)^{2} = 0, \hfill \\ \end{aligned} $$

(22)

and the subjected conditions are

$$ \begin{gathered} F(0,\tau ) = s,\frac{\partial F(0,\tau )}{{\partial \eta }} = \lambda , \, \theta (0,\tau ) = 1,{\text{ at }}\eta = 0 \hfill \\ \frac{\partial F(\eta ,\tau )}{{\partial \eta }} \to 1, \, \theta (\eta ,\tau ) \to 0{\text{ as }}\eta \to \infty . \hfill \\ \end{gathered} $$

(23)

To check the time independent flow solution stability, let us have $\left( {F(\eta ) = f_{0} (\eta )} \right)$ $f\left( \eta \right) = f_{0} \left( \eta \right)$ and $\left( {\theta (\eta ) = \theta_{0} (\eta )} \right)$ gratifying the BVP (2)–(5), it implements (Merkin [47], Sharma et al. [48] and Weidman et al. [49]).

Let

$$ \begin{gathered} F(\eta ,\tau ) = f_{0} (\eta ) + e^{ - \varsigma \tau } G(\eta ,\tau ) \hfill \\ \theta (\eta ,\tau ) = \theta_{0} (\eta ) + e^{ - \varsigma \tau } S(\eta ,\tau ), \hfill \\ \end{gathered} $$

(24)

where $\varsigma$ is a value that is not known (growth and decay distribution) eigenvalue and $G(\eta ,\tau )$ and $S(\eta ,\tau )$ are too small to be letting $f_{0} (\eta )$ and $\theta_{0} (\eta )$, respectively.

Now, plugging Eq. (24) into Eqs. (21) and (22), one infers the subsequent equations:

$$ \begin{gathered} \frac{{\left( {\frac{{\partial^{3} f_{0} }}{{\partial \eta^{3} }} + e^{ - \varsigma \tau } \frac{{\partial^{3} G}}{{\partial \eta^{3} }}} \right)}}{{{\rm X}_{1} }} + {\rm X}_{2} \left( {\left\{ {f_{0} + e^{ - \varsigma \tau } G} \right\}\left\{ {\frac{{\partial^{2} f_{0} }}{{\partial \eta^{2} }} + e^{ - \varsigma \tau } \frac{{\partial^{2} G}}{{\partial \eta^{2} }}} \right\} + \frac{2m}{{m + 1}}\left( {1 - \left( {\frac{{\partial f_{0} }}{\partial \eta } + e^{ - \varsigma \tau } \frac{\partial G}{{\partial \eta }}} \right)^{2} } \right) + \varsigma e^{ - \varsigma \tau } \frac{\partial G}{{\partial \eta }} - e^{ - \varsigma \tau } \frac{{\partial^{2} G}}{\partial \eta \partial \tau }} \right) \hfill \\ + \left( {\frac{2}{m + 1}} \right)M{\rm X}_{3} \left( {1 - \frac{{\partial f_{0} }}{\partial \eta } - e^{ - \varsigma \tau } \frac{\partial G}{{\partial \eta }}} \right) + \left( {\frac{2}{m + 1}} \right)\lambda_{1} \cos \left( {\frac{\Omega }{2}} \right){\rm X}_{4} \left( {\theta_{0} + e^{ - \varsigma \tau } S} \right) = 0, \hfill \\ \end{gathered} $$

(25)

$$ \begin{gathered} \left\{ {\frac{{\partial^{2} \theta_{0} }}{{\partial \eta^{2} }} + e^{ - \varsigma \tau } \frac{{\partial^{2} S}}{{\partial \eta^{2} }}} \right\}{\rm X}_{5} + \left( {\frac{2}{m + 1}} \right)M\Pr {\text{Ec}}\left( { - e^{ - \varsigma \tau } \frac{\partial G}{{\partial \eta }} - \frac{{\partial f_{0} }}{\partial \eta }} \right)^{2} \hfill \\ + \Pr {\rm X}_{6} \left( {\left\{ {f_{0} + e^{ - \varsigma \tau } G} \right\}\left\{ {\frac{{\partial \theta_{0} }}{\partial \eta } + e^{ - \varsigma \tau } \frac{\partial S}{{\partial \eta }}} \right\} - \left( {\frac{5m - 1}{{m + 1}}} \right)\left\{ {e^{ - \varsigma \tau } S + \theta_{0} } \right\}\left\{ {\frac{{\partial f_{0} }}{\partial \eta } + e^{ - \varsigma \tau } \frac{\partial G}{{\partial \eta }}} \right\} + \varsigma e^{ - \varsigma \tau } S - e^{ - \varsigma \tau } \frac{\partial \theta }{{\partial \tau }}} \right) \hfill \\ + \frac{\Pr Ec}{{{\rm X}_{1} }}\left( {\frac{{\partial^{2} f_{0} }}{{\partial \eta^{2} }} + e^{ - \varsigma \tau } \frac{{\partial^{2} G}}{{\partial \eta^{2} }}} \right)^{2} = 0 \hfill \\ \end{gathered} $$

(26)

with the conditions are given as:

$$ \begin{gathered} G(0,\tau ) = 0{ ,}\frac{\partial G(0,\tau )}{{\partial \eta }} = 0,S(0,\tau ) = 0,{\text{ at }}\eta = 0 \hfill \\ \frac{\partial G(\eta ,\tau )}{{\partial \eta }} \to 0, \, S(\eta ,\tau ) \to 0{\text{ as }}\eta \to \infty . \hfill \\ \end{gathered} $$

(27)

Following Weidman et al. [49], it is investigated the stable solution for the phenomenon of steady flow $f_{0} (\eta )$ with heat transfer solution $\theta_{0} (\eta )$ through site $\tau = 0$ and; therefore ,$G = G_{0} (\eta )$ and $S = S_{0} (\eta )$ in (25) and (26) to classify early increase/deterioration of the result. Therefore, we explain the subsequent problem linear eigenvalue:

$$ \begin{gathered} \frac{{G_{0}^{\prime \prime \prime } }}{{{\rm X}_{1} }} + {\rm X}_{2} \left( {f_{0} G_{0}^{\prime \prime } + Gf_{0}^{\prime \prime } - \left( {\frac{4m}{{m + 1}}} \right)f_{0}^{\prime } G_{0}^{\prime } + \varsigma G_{0}^{\prime } } \right) + \left( {\frac{2}{m + 1}} \right)M{\rm X}_{3} G_{0}^{\prime } \hfill \\ + \left( {\frac{2}{m + 1}} \right)\lambda_{1} \cos \left( {\frac{\Omega }{2}} \right){\rm X}_{4} S_{0} = 0, \hfill \\ \end{gathered} $$

(28)

$$ \begin{aligned} & S_{0}^{\prime \prime } {\rm X}_{5} + \left( {\frac{4}{m + 1}} \right)M\Pr {\text{Ec}}f_{0}^{\prime } G_{0}^{\prime } + \Pr {\rm X}_{6} \left( {f_{0} S_{0}^{\prime } + G_{0} \theta_{0}^{\prime } }\right. \hfill \\&\quad \left.{- \left( {\frac{5m - 1}{{m + 1}}} \right)\left\{ {\theta_{0} G_{0}^{\prime } + S_{0} f_{0}^{\prime } } \right\} + \varsigma S_{0} } \right) + \frac{{2\Pr {\text{Ec}}}}{{{\rm X}_{1} }}f_{0}^{\prime \prime } G_{0}^{\prime \prime } = 0 \hfill \\ \end{aligned} $$

(29)

with conditions pertaining at boundary is

$$ \begin{gathered} G_{0} (0) = 0, \, S_{0} \left( 0 \right) = 0{ ,}G_{0}^{\prime } \left( 0 \right) = 0,{\text{ at }}\eta = 0 \hfill \\ G_{0}^{\prime } \to 0, \, S_{0} \to 0{\text{ as }}\eta \to \infty . \hfill \\ \end{gathered} $$

(30)

In this research, the linear eigenvalue equations of IVP (28) and (29) with a new boundary condition (30) is explained by relaxing the condition $G_{0} (\eta )$ and $S_{0} (\eta )$. So for here the condition $S_{0} \to 0{\text{ as }}\eta \to \infty$ is relaxed and for unchanged number of $\varsigma$, Eqs. (28) and (29) in conjunction with the fresh boundary restriction $G_{0} ^{\prime\prime}(0) = 1$ are worked out.

5 Results and Discussion

The system consisting of ODEs (7) and (8) with boundary restriction (9) has been executed numerically through bvp4c solver. The analysis of graphical results of the physical parameters like hybrid nanoparticles $\left( {\phi_{1} ,\phi_{2} } \right)$, mixed convective parameter $\left( {\lambda_{1} } \right)$, Eckert number $\left( {{\text{Ec}}} \right)$, magnetic parameter $\left( M \right)$ and shrinking/ stretching parameter $\left( \lambda \right)$ are precisely explored on the temperature and velocity profiles together with the heat transfer rate and friction factor in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19. The thermo physical features of hybrid nanofluid are depicted in Table 2. Also, check the accuracy of our result’s precision, we compare our outcomes in limiting cases with previously published articles [50, 51] and results displayed a tremendous harmony (see Table 3).

Fig. 2

Influence of $\phi_{1} ,\phi_{2}$ on $F^{\prime } (\eta )$

Fig. 3

Influence of $\phi_{1} ,\phi_{2}$ on $\theta (\eta )$

Fig. 4

Influence of $m$ on $F^{\prime } (\eta )$

Fig. 5

Influence of $m$ on $\theta (\eta )$

Fig. 6

Influence of $M$ on $F^{\prime } (\eta )$

Fig. 7

Influence of $M$ on $\theta (\eta )$

Fig. 8

Influence of $s$ on $F^{\prime } (\eta )$

Fig. 9

Influence of $s$ on $\theta (\eta )$

Fig. 10

Influence of $\lambda$ on $F^{\prime } (\eta )$

Fig. 11

Effect of $\lambda$ on $\theta (\eta )$

Fig. 12

Influence of $\lambda_{1}$ on $F^{\prime}(\eta )$

Fig. 13

Effect of $\lambda_{1}$ on $\theta (\eta )$

Fig. 14

Effect of ${\text{Ec}}$ on $\theta (\eta )$

Fig. 15

Impact of $s$ versus $\lambda$ on $C_{{\text{F}}} {\text{Re}}_{x}^{1/2}$

Fig. 16

Impact of $s$ versus $\lambda$ on $Nu_{x} {\text{Re}}_{x}^{ - 1/2}$

Fig. 17

Impact of $M$ versus $\lambda$ on $C_{{\text{F}}} {\text{Re}}_{x}^{1/2}$

Fig. 18

Impact of $M$ versus $\lambda$ on ${\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2}$

Fig. 19

Influence of ${\text{Ec}}$ versus $\lambda$ on ${\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2}$

Table 2 Thermo physical properties of the base fluid and hybrid nanoparticles [7, 8, 11]

Table 3 Comparison of $C_{fx} {\text{Re}}_{x}^{1/2}$ through different $m$ with $M = 0,\lambda = 0,\phi_{1} = \phi_{2} = 0$

5.1 Variation in the Velocity and Temperature Profiles

In Figs. 2 and 3, the impact of alters in increasing amount of hybrid nanoparticles is portrayed on velocity and temperature distribution, respectively. Enhancing hybrid nanoparticles causes a decrease in the fluid velocity (Fig. 2) in the FS, while in the SS, the fluid velocity enhances. In Fig. 3, the temperature distribution augments due to hybrid nanoparticles in the result of the first branch, while in the result of second branch, it declines. Physically, the hybrid nanomaterials scattering augments the thermal energy in the hybrid nanofluid layer which upsurges the temperature. Therefore, the present findings demonstrate that the exploitation of hybrid nanomaterials can help us to develop improved heat circulation in particular heat transfer equipment and can accumulate energy through chemical processes. It is fascinating to perceive that the rise in the profile initially and then asymptotically converge due to the greater value of Prandtl number (Pr = 204). Figures 4 and 5 demonstrate the stimulation of $m$ or $\Omega$ on the fluid velocity and fluid temperature, respectively. Furthermore, Fig. 4 describes that the momentum boundary layer decelerate due to wedge angle in first and second results. Figure 5 displays that the temperature of fluid accelerates with augmenting wedge angle in both solutions. The reason behind this that the buoyancy factor owing to thermal diffusion declines due to $\cos \, \Omega /2$ and thus the driving force of the nanoliquid declines and consequently, the temperature enhances. Growing the inclination angle crafts it difficult for the fluid to move along the surface of the wedge and causes it to grow to be warmer due to nanoliquid density is greater. The decline of nanofluid velocity and temperature distribution in the FS by enhancing the magnetic parameter is illustrated in Figs. 6 and 7, respectively, whilst, the opposite trend are captured in the second solution. Physically, the creation of Lorentz force through the augment in the magnetic constraint caused the retardation to flow and declined the temperature and velocity of nanoliquid. The mass suction impact on the profiles of temperature and velocity is inspected in Figs. 9 and 8, respectively. Figure 8 elucidates that the velocity boosts up due to suction in the FS and failures in the SS. Whereas, the temperature of hybrid nanoliquid declines in the FS and augments in the SS as shown in Fig. 9. Physically, the animated liquid is pressed towards a convective wedge wall where the forces of buoyancy can proceed to delay the liquid because of the greater impact of hybrid nanofluid viscosity. Figures 10 and 11 are drawn to see the stretching/shrinking impact on the profiles of velocity and temperature. However, Figs. 10 and 11 reveal that the velocity of nanofluid declines and temperature augments due to stretching/shrinking parameter in the FS, whilst the opposing conduct is analyzed for the second solution. These figures confirm that the broad boundary constraints of the field (9) are met asymptotically, which strengthens the numerical results obtained for the bvp (7) and (8). In addition, it is apparent that profile of velocity boundary-layer develops to be thicker and thicker for the FS as compared to the SS, while the opposite behavior is monitored for the thermal boundary-layer. Figures 12 and 13 are ready to watch the impact of mixed convective parameter on velocity and temperature profiles. In fact, the mixed convective parameter is a combination of buoyancy and viscosity forces. The contrary connection between viscous forces and λ which declines the nanofluid velocity (Fig. 12) and enhance the temperature (Fig. 13) in the branch of FS, whilst the change behavior is scrutinized in the branch of SS. The temperature of the hybrid nanoliquid within the boundary-layer augments with growing Eckert number as depicted in Fig. 14 in the both solutions. Physically, due to rising the liquid friction amid the neighboring layers of liquid rises which consecutively change the kinetic energy into heat energy, and therefore, the liquid temperature goes up.

5.2 Variation in the Skin Friction and the Nusselt Number

Figures 15 and 16 highlight the deviation of the skin factor and the Nusselt number verses parameter $\lambda$ for different $s$. It is spotlighted here to investigate the existence of the multiple solutions for shrinking wedge $\lambda$ up to a certain domain of parameter. Also, these multiple results are acknowledged as the FS (the upper branch) and the SS (the lower branch). The FS is symbolized through solid line and the SS is confined by dotted lines. Since our investigation, it is pragmatic that it can attain the results up to a certain range of $\lambda$. In addition, a hurrying drift is monitored for the skin friction factor of the FS, whilst devaluation for the SS is scrutinized with the superior strength of suction as shown in Fig. 15. Also, the diagram in Fig. 16 verifies the aforementioned restriction on $\lambda$ of existence of dual solutions. It is apparent from this graph that the heat transfer declines for the both solutions by enhancing the suction parameter. Thus more than one solution is obtained for both the heated surface and as well as for the cooled surface up to a certain range of varying parameter lambda as seen in the figures while the solid and dotted line are merged at a point in the aforementioned pictures called the critical points and is denoted by $\lambda = \lambda_{c}$ whose values are $\left( { - {2}{\text{.88470,}} - {2}{\text{.66586,}} - {2}{\text{.32992}}} \right).$ Figures 17 and 18 are revealed to monitor the variation of the skin factor and heat transfer with stretching/shrinking parameter for distinct magnetic number. In these graphs the multiple solutions were found for both phenomena of $\lambda < 0$ and $\lambda > 0$ while the critical points at which the boundary layer is separated and whose count number are $\left( { - {2}{\text{.32992,}} - {2}{\text{.3350,}} - {2}{\text{.35670}}} \right).$ Figure 17 explains that the amount of the friction factor augment owing to magnetic number in the first solution and decline in the second solution. Figure 18 reveals that the rate of heat transfer decelerates due to $M$ in both results. The impact of the Eckert number on the heat transfer rate versus $\lambda$ is shown in Fig. 19. This graph suggests that the values of heat transfer diminish with the augmenting Eckert number in both solutions.

6 Final Remarks

In this work, the impact of magnetic field on mixed convection involving ethylene glycol (C₂H₆O₂) based SiO₂–MoS₂ hybrid nanoliquid through a shrinking/stretching wedge is scrutinized. The transmuted ODEs have been examined numerically through bvp4c solver. The essence of the problem is as follows:

• The liquid velocity declines and temperature augments due to hybrid nanoparticle in the result of first branch and contrary trend is seen in the result of the second branch.

• The angle of wedge enhances the profiles of velocity and temperature in both branches of results.

• The magnetic number decelerates the velocity and temperature distribution in the FS, whilst the opposite behavior is noticed in the SS.

• The velocity increases and temperature declines due to the suction in the first solution.

• The momentum and thermal boundary layers enhance due to shrinking parameter in the FS and shrink in the SS.

• Mixed convection parameter decays the velocity and expands the temperature in the FS, whereas the opposite trend is scrutinized in the SS.

• The temperature augments due to Eckert number in both solutions.

• The friction factor increases due to suction and magnetic parameters in the branch of FS, whereas the rate of heat transfer declines.