Introduction

Free heat convection of fluids inside enclosures has attracted a great deal of attention from researchers because of its vast applications, including double-glass windows, oil cargo in ship tanks, solar collectors, electronics cooling systems, etc [1,2,3,4]. Thanks to technological advancements, controlling natural convection leads systems to be smaller, lighter, and more efficient because of low cost, low noise, and regeneration features of this mode of heat convection [4,5,6]. In many problems, an unwanted inevitable magnetic field is assigned to the enclosure in a direction sometimes to intensify the flow circulation and sometimes to suppress it. For both situations, designing the best enclosure to maximize or minimize the heat transfer is a necessity [7,8,9]. In this regard, there has been an increasing attention paid to the understanding of the flow pattern and the heat transfer mechanism of rectangular enclosures filled with an electrically conducting fluid subjected to a magnetic field [10,11,12,13].

The natural convection of pure fluids inside enclosures was studied by lots of researchers [10,11,12,13,14,15,16,17,18,19]. The impact of Grashof number, aspect ratio, and magnetic field intensity on the unsteady MHD flow was numerically studied by Venkatachalappa and Subbaraya [10] in two different aspect ratios of 1 and 2. They assigned prescribed heat fluxes uniformly to the vertical walls while keeping the top and bottom walls insulated. According to the results, streamlines are elongated at the center of the enclosure at high Hartmann numbers and low Grashof numbers; also, isothermal lines form a roughly parallel position perpendicular to the horizontal walls, which show that the conduction heat transfer was dominated. They reported no significant changes in the structure of streamlines and isotherms for the cases of long and square enclosures. In many studies, the enclosure was considered as a rectangular cavity confined by cold and hot sidewalls and insulated top and bottom walls [11,12,13,14,15,16,17,18,19,20,21,22]. Teamah [11] investigated double-diffusive free convection of heat absorbing/generating fluid. Hartmann, and Rayleigh numbers effects on flow pattern and thermal performance of the long enclosure with an aspect ratio of two was studied. They found that the heat sink intensifies the heat transfer so that the lower the heat generation and tending to sink condition leads to change the sign of the Nusselt number from negative to positive. Also, the imposed magnetic field suppresses the flow circulation and has a decreasing effect on the Nusselt number. Such a damping effect of magnetic field, which depends on the orientation of action, was reported by Refs. [12,13,14,15,16] for pure fluids and Refs. [20,21,22,23,24] for nanofluids. A magnetic field applied to the enclosure in the parallel direction of the gravitational acceleration was studied by Rudraiah et al. [13]. They indicated that the circulating currents became weakened when the magnetic field was intensified and subsequently caused the temperature stratification became predominant horizontally in the core region and heat transfer disruption. Xu et al. [12] experimentally examined the thermal behavior of natural heat convection of molten gallium with and without a magnetic field inside a confined cell and underlined the suppression effect of the magnetic field. Four different locations of heat source-sink pair were compared while imposing a magnetic field on a square enclosure filled with liquid gallium by Mahmoodia et al. [25]. For cases wherein magnetic field has a negative effect by hindering the heat transfer, they proposed placing the hot heat source on top wall and cold heat source to the bottom. Mehryan et al. [14] studied the unsteady MHD natural convection of water as the working fluid inside the typical enclosure subparted by a flexible membrane while considering the interaction of water and solid membrane. They clearly reported that the flow circulation might be intensified or suppressed by a magnetic field depends on the direction of effect. Karimipour et al. [26,27,28] systematically have focused their studies on the effect a magnetic field effect of a laminar flow within microchannel while considering slip flow condition. On that case, Hartmann number causes a reduction in velocity near walls and leads fluid to flow more uniformely along the microchannel. It was indicated that the thermally developing region is highly affected by imposing the magnetic field. So that the Nu number increases with increasing Hartmann number. Besides, heat transfer from the fully developed region was shown to be almost independent of the magnetic field.

Attaching fin as a passive route to enhance the heat transfer has attracted many attentions [15, 16]. Hydrodynamic effects of oscillating pins were studied by Ghalambaz et al. [15] simulating a Fluid–Structure Interaction (FSI) model of a flexible cantilever thin fin attached to the left wall oscillating sinusoidally on its free end. Increasing the amplitude of oscillation was found to increase the Nusselt number, with a higher thermal performance for short oscillating fins. Ismael and Jasim [16] conducted a similar study to examine how much the heat transfer from a vented enclosure improves by attaching a flexible fin to the bottom. About 230% improvement in heat transfer was reported for the case with an elastic fin compared to the enclosure without a fin, although the flexible attachment showed a better thermal performance compared to the rigid one. The effect of the radius of a cylinderical heater inside a square enclosure was investigated by Hemmat et al. [29]. The effects of adding nanoadditives become negligible for needle-like heaters.

Interestingly, some of the researchers [30,31,32] addressed situations wherein the increasing Nusselt number with an increase in magnetic field occurs. For the case of double-diffusive MHD natural convection inside a porous enclosure, Shekar et al. [30] showed that the weakening of flow cell resulted from increasing the imposed magnetic field is not always associated with the heat transfer deterioration for the typical enclosure. The local Nusselt number along the hot wall is increased with an increase in magnetic strength. The effect of temperature-dependent properties of natural convection of kerosene solution suspended by Mn–Zn nanoparticles inside a cube-shaped enclosure was examined by Yamaguchi et al. [31]. An upward uniform magnetic field was imposed to the enclosure, while a square cylinder heat generator was placed at the center of the enclosure. Their results showed that although the bigger the heater size causes flow obstruction by reducing the flow space, magnetic field enhances the heat transfer characteristics.

A large number of papers and books on nano/microscale systems have been released to underline the fact that heat transfer rate increases by increasing fluid thermal conductivity originated from adding particles in nanoscale into a base fluid such as ethylene glycol, oil, and water [9, 20,21,22, 24, 32]. Khanafer et al. [9] analyzed free heat convection of water–Cu nanofluid within an enclosure. They revealed that the heat transfer rate increases by increasing volumetric fraction of nanoparticles. About 25% Nusselt number enhancement was reported by adding just 2% Cu nanoparticles into water [9]. While Mahian et al. [33] experimentally and numerically investigated three different configurations of enclosures, vertical, tilted, and right triangular. The volume fraction of SiO2 nanoparticles was found that has a decreasing impact on the Nusselt number. The effect of a heat-generating source numerically explored by Teamah and El-Maghlany [20] in various magnetic field intensities. A comparison of heat transfer efficiency for three different nanoparticles of Cupper, Titanium, and Alumina was carried out. Their results showed that at low Hartmann numbers, heat transfer rate was in a direct relation with nanoparticles volume fraction. Besides, at low Rayleigh number, in which heat transfer strongly depends on thermal conductivity of the working fluid, water-Cu nanofluid showed a higher potential for using in heat exchanger devices than water-TiO2 and water–Al2O3. A similar enclosure filled with water–Al2O3 nanofluid was used in the study of Ghasemi et al. [21]. They showed that heat transfer rate has a direct relation with Rayleigh number due to convection intensification. Moreover, the Nusselt number inversely related to the Hartmann number since increasing the Lorentz force leads to the weakening of the vortices strength. They also indicated that the higher the volume fraction of nanoparticles is the more efficient the thermal performance is. The same results were also reported by Esfandiary et al. [34] for the case of an inclined cavity filled with water–Al2O3 nanofluid. They also reported that the Nusselt number increases with the inclination angle. Karimipour et al. [35] examined the effects of inclination angle and Richardson number on a shallow tilted lid driven cavity. It was found that the effect of inclination angle is negligible for low Richardson numbers. Using Boltzmann grid, Mahmoudi et al. [22] investigated how the position of two insulated obstacles attached to the top and bottom walls could control the thermal behavior of the enclosure. According to their findings, the Nusselt number highly depends on their positions. They also demonstrated that both the Rayleigh number and the nanoparticles volume fraction have increasing effects on the Nusselt number. This method was also employed by Sheikholeslami and Ellahi [23] to investigate the effect of a magnetic field on water–Al2O3 nanofluid free convection inside a cubic enclosure. It was heated from below and cooled from the top with two different constant temperatures while other walls were held insulated. They took Brownian motion into account in their model in order for the conductivity and viscosity of the nanofluid to be estimated more accurately. They demonstrated that magnetic field has a noticeable impact on natural convection heat transfer, especially for high Rayleigh numbers. In detail, the convection is suppressed by increasing the Hartmann number and the sensitivity of heat transfer rate to the magnetic strength becomes stronger by increasing Rayleigh number. Sheikholeslami et al. [32] reported the same results for the problem with magnetic-dependent viscosity for low values of viscosity parameter. In fact, they showed that increasing in an unwanted magnetic strength increases the Nusselt number for a rectangular container.

Various types of Dirichlet boundary condition, including constant, linear, and sinusoidal wall temperature distribution, and Neumann boundary condition, including constant and variants heat flux were used by researchers [36,37,38]. Assigning sinusoidal temperature distribution to the vertical walls, Mejri et al. [36] numerically studied the effect of sinusoidal phase deviation through the use of Lattice Boltzmann Method (LBM). According to their results, the heat transfer rate is enhanced by increasing the Rayleigh number. A similar study was performed by Hajatzadeh Pordanjani et al. [37] to numerically examine the impact of magnetic field angle and aspect ratio on flow pattern and heat transfer characteristics. Two obstacles at the center were assumed warmer than the two isotherm vertical walls. Whatever the aspect ratio of the two heaters decreases the Nusselt number is intensified, especially from the top of the side walls. Mahmoudi et al. [38] examined the effect of imposing a linear temperature distribution on the side walls. The Nusselt number was found to be in a direct relation to the Rayleigh number, whereas it was in an inverse relation to the Hartmann number.

The literature review showed that the natural heat convection rate could be enhanced by introducing the Lorentz force originated from applying a magnetic field. Up to now, there have been only a few works carried out dealing with the effects of geometrical variations of a heat-generating fin attached to the bottom of an enclosure in the presence of a magnetic field. The cross-linking effects of the side walls thickness of an enclosure filled with the water–Al2O3 nanofluid and two geometrical variables of the heater remain unstudied. Therefore, a second order polynomial correlation was made for Nusselt number as a function of the side walls thickness and the fin size. In order to present practical points for designers of such heat transfer devices, a sensitivity analysis was carried out to evaluate how much the Nusselt number is affected by the aforementioned factors. An optimization was then accomplished to attain the maximum heat transfer rate. Useful guidelines were provided as initial data for the fabrication of enclosures.

Mathematical formulation

Physical model

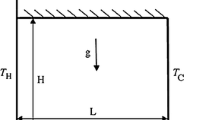
As shown in Fig. 1, a 2D square enclosure, with a heat source located at the bottom of it, was studied in the present study. The height and width of the heat source are \(H\) and \(W\), respectively, and its distance from the side walls are the same. The enclosure filled with water–Al2O3 nanofluid with the properties tabulated in Table 1 is bounded by two thick isothermal vertical walls at temperature \(T_{\text{c}}\) and by two horizontal adiabatic walls. The generated heat by the fin is assumed to be transferred via the heater surfaces to the surrounding nanofluid. All the walls are exposed to no-slip conditions. Two external body forces originated from the magnetic field (with the strength of \(B_{0}\)) and gravity are imposed to the nanofluid. They are assigned in the positive and the negative directions of y-axis, respectively.

Fig. 1
figure 1

A schematic representation of the problem

Full size image
Table 1 Thermophysical properties of water and nanoparticles [24]
Full size table

Governing equations

It was assumed that Al2O3 nanoparticles and water were in thermal equilibrium, and the nanofluid is Newtonian and incompressible. The flow is considered steady, two dimensional and laminar, and the radiation effects are negligible. The governing equations were derived in the nondimensional form for a two-dimensional, laminar, Newtonian and incompressible flow inside the enclosure. In order to take the hydrodynamic and thermal interaction into account, Boussinesq approximation was employed. The derived equations are as follows [37, 38]:

  • Mass continuity

    $$\frac{{{\text{d}}U}}{{{\text{d}}X}} + \frac{\partial V}{\partial Y} = 0$$
    (1)

  • Momentum equations

    $$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} \alpha_{\text{f}} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) + \frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}Pr\,Ha^{2} \left( {V\sin \gamma \cos \gamma - U\sin^{2} \gamma } \right)$$
    (2)
    $$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} \alpha_{\text{f}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + \frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}Pr\,Ha^{2} \left( {U\sin \gamma \cos \gamma - V\cos^{2} \gamma } \right) + \frac{{\beta_{\text{nf}} }}{{\beta_{\text{f}} }}Ra\,Pr\,\theta$$
    (3)

  • Energy equation

    $$\left( {U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} } \right) = \frac{{\alpha_{\text{nf}} }}{{\alpha_{\text{f}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
    (4)

    For the fin, the energy equation is reduced to:

    $$\frac{\partial }{\partial x}\left( {K^{*} \frac{\partial \theta }{\partial X}} \right) + \frac{\partial }{\partial x}\left( {K^{*} \frac{\partial \theta }{\partial Y}} \right) = 0$$
    (5)

  • Dimensionless parameters

    In the above equations, the following non-dimensional parameters are used.

    $$X = \frac{x}{l}, Y = \frac{y}{l}, U = \frac{ul}{{\alpha_{\text{f}} }}, V = \frac{vl}{{\alpha_{\text{f}} }}, K^{*} = \frac{{k_{\text{s}} }}{{k_{\text{f}} }}, P = \frac{{\bar{P}l^{2} }}{{\rho_{\text{nf}} \alpha_{\text{f}}^{2} }}, \theta = \frac{{T - T_{\text{c}} }}{{\frac{{q^{\prime \prime \prime } l}}{{k_{\text{f}} }}}}$$
    (6)
    $$Pr = \frac{{\vartheta_{\text{f}} }}{{\alpha_{\text{f}} }}, Ra = \frac{{g\beta_{\text{f}} l^{3} q^{\prime \prime \prime } l}}{{\alpha_{\text{f}} \vartheta_{\text{f}} k_{\text{f}} }}, Ha = B_{0} l\sqrt {\frac{{\sigma_{\text{f}} }}{{\rho_{\text{f}} \vartheta_{\text{f}} }}}$$
    (7)

Boundary conditions

According to the physical model described before, Eqs. (1–5) must satisfy the following boundary conditions:

$$k_{\text{s}} \left. {\frac{\partial \theta }{\partial n}} \right|_{\text{s}} = k_{\text{nf}} \left. {\frac{\partial \theta }{\partial n}} \right|_{\text{nf}} ,\;\;\theta_{\text{s}} = \theta_{\text{nf}} ,\;\;U = {\text{V}} = 0\quad {\text{Heat}}\;{\text{source}}\;{\text{surfaces}}$$
$$0 \le Y \le 1,\;\;X = 0,\;\;X = 1:\theta \left( Y \right) = 0,\;\;U = V = 0\quad {\text{Side}}\;{\text{walls}}$$
$$0 \le X \le 1,\;\;Y = 0,\;\;Y = 1:\frac{\partial \theta }{\partial y} = 0,\;\;U = V = 0\quad {\text{Horizontal}}\;{\text{walls}}$$

Thermophysical properties of the nanofluid

The properties of nanofluid, including effective electrical conductivity, effective density, effective volumetric thermal expansion, effective thermal capacity, and nanofluid thermal diffusivity coefficient were obtained as follows:

$$\sigma_{\text{nf}} = \left( {1 - \varphi } \right)\sigma_{\text{f}} + \varphi \sigma_{\text{s}}$$
(8)
$$\rho_{\text{nf}} = \left( {1 - \varphi } \right)\rho_{\text{f}} + \varphi \rho_{\text{s}}$$
(9)
$$(\rho \beta )_{\text{nf}} = \left( {1 - \varphi } \right)(\rho \beta )_{\text{f}} + \varphi (\rho \beta )_{\text{p}}$$
(10)
$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \varphi } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi \left( {\rho c_{\text{p}} } \right)_{\text{s}}$$
(11)
$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }}$$
(12)

In the equations proposed for nanofluid properties, the indices f and s denote the properties of pure fluid and Al2O3 nanoparticles, respectively. Many equations have been presented by researchers for calculating the thermal conductivity and viscosity of the nanofluid. In the current study, the effective thermal conductivity and viscosity of nanofluids were calculated through the use of modified models suggested by Vajjha [39]. As seen from the following equations, Brownian motion effect was considered in both models. Maxwell and Brinkman’s models were used for the term \(k_{\text{static}}\) and \(\mu_{\text{static}}\), respectively [40, 41].

$$\begin{aligned} k_{\text{nf}} & = k_{\text{static}} + k_{\text{Brownian}} \\ & = \frac{{k_{\text{s}} + 2k_{\text{f}} - 2(k_{\text{f}} - k_{\text{s}} )}}{{k_{\text{s}} + 2k_{\text{f}} + (k_{\text{f}} - k_{\text{s}} )\varphi }}k_{\text{f}} + 5 \times 10^{4} \beta \varphi \rho (c_{\text{p}} )_{\text{f}} \sqrt {\frac{{k_{\text{b}} T}}{{\rho_{\text{s}} d_{\text{s}} }}} f(T,\varphi ) \\ \end{aligned}$$
(13)
$$\mu_{\text{nf}} = \mu_{\text{static}} + \mu_{\text{Brownian}} = \frac{{\mu_{\text{f}} }}{{(1 - \varphi )^{2.5} }} + 5 \times 10^{4} \beta \varphi \rho_{\text{f}} (c_{\text{p}} )_{\text{f}} \frac{{\mu_{\text{f}} }}{{k_{\text{f}} \Pr }}\sqrt {\frac{{k_{\text{b}} T}}{{\rho_{\text{s}} d_{\text{s}} }}} f(T,\varphi )$$
(14)

In above equations, the terms \(\beta\) and \(f(T.\varphi\)) are obtained through the following equations for the water-Al2O3 nanofluid [41].

$$f(T,\varphi ) = (2.8217 \times 10^{ - 2} \varphi + 3.917 \times 10^{ - 3} )\left( {\frac{T}{{T_{0} }}} \right) + ( - 3.0669 \times 10^{ - 2} \varphi - 3.91123 \times 10^{ - 3} )$$
(15)
$$\beta = 8.4407\left( {100\varphi } \right)^{ - 1.07304}$$
(16)

Auxiliary equations

In order to analyze the thermal performance of the enclosure and how it is affected by different parameters, the Nusselt number is selected. The local Nusselt number is expressed as follows:

$$Nu_{\text{s}} = \frac{hL}{{k_{\text{nf}} }}$$
(17)

The convection heat transfer coefficient is expressed as follows:

$$h = \frac{{q_{\omega }^{{\prime \prime }} }}{{T_{\text{h}} - T_{\text{c}} }}$$
(18)

Heat flux is calculated by the following equation.

$$q_{\omega }^{\prime \prime } = k_{\text{nf}} \left( {\frac{\partial T}{\partial x}} \right)$$
(19)

Using Eqs. (6, 18, 19) and manipulating Eq. (17), the local Nusselt number is derived as follows:

$$Nu_{\text{s}} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {\frac{\partial \theta }{\partial X}} \right)$$
(20)

The average Nusselt number is then obtained by integrating the above equation over the cold walls of the enclosure:

$$Nu_{\text{ave}} = \frac{1}{L}\mathop \int \limits_{0}^{L} Nu_{{\left( {x = 0 , 1} \right)}} {\text{d}}Y = - \frac{1}{L}\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\mathop \int \limits_{0}^{L} \left( {\frac{\partial \theta }{\partial X}} \right)_{{\left( {x = 0 , 1} \right)}} {\text{d}}Y$$
(21)

Numerical approach

Using finite volume method over the staggered grid, the governing equations of mass, momentum, and energy have been discretized. Also, a SIMPLE algorithm was used to solve the coupling between pressure and velocity [42]. The convection and diffusion terms were discretized by using power-law scheme and a FORTRAN code was developed to solve the discretized equations iteratively by tri-diagonal matrix algorithm. The convergence criterion of the summation residual was assumed to be less than 10−8.

Grid study and validation

A uniform structured mesh was generated for use in the FVM solver. To this end, the effect of mesh size on \(Nu_{\text{ave}}\) and \(\varPsi_{ \hbox{max} }\) was evaluated. A sample of the results is tabulated in Table 2. The results are roughly independent from the mesh size for grids finer than \(120 \times 120\).

Table 2 Grid independence study in the case of \(Ha = 20\), \(\gamma = 90^\circ\), \(\varphi = 0.03\), \(K^{*} = 20\), \(Ra = 10^{5}\), \(W = 0.3\), \(L_{\text{b}} = 0.125\) and \(H = 0.45\)
Full size table

In order to validate the results of the program written in FORTRAN, the obtained results of \(Nu_{\text{ave}}\) was compared with both experimental and numerical studies of other researchers [21, 24, 43]. \(Nu_{\text{ave}}\) was compared with the work of Ghasemi et al. [21] to evaluate the effect of magnetic field on nanofluid flow behavior inside an enclosure with cold and hot side walls and insulated top and bottom walls. It was done for different nanoparticle volume fractions and Hartmann numbers at \(Ra = 10^{5}\) and the results are tabulated in Table 3. Further evaluations were done by comparing \(Nu_{\text{ave}}\) with the work of Aminossadati and Ghasemi [24] for natural convection in a partially heated enclosure filled with water-Cu nanofluid at different \(Ra\) numbers. The present numerical code was also validated against the experimental results of Krane and Jessee [43] for natural convection in an enclosure filled with air as shown in Fig. 3. Table 3, Figs. 2 and 3 all indicate that the developed CFD-code works well.

Table 3 A comparison of the mean Nusselt number for water-Al2O3 nanofluid at different Hartmann numbers and nanoparticle volume fractions with the results reported by Ghasemi et al. [21]
Full size table
Fig. 2
figure 2

A comparison of the average Nusselt number for water–Cu nanofluid at different values of Ra number and heater length with the results reported by Aminossadati and Ghasemi [24]

Full size image
Fig. 3
figure 3

Validation of the present code for the natural convection in an enclosure filled with air against the experimental results reported by Krane and Jessee [43]

Full size image

CFD simulation

Effect of fin width

In order to study merely the effect of the heat source width on flow pattern and thermal behavior, all of the other effective parameters were held constant and the width was changed from 0.1 to 0.5. So that, magnetic field angle, Ra number, heat source position, nanofluid properties and etc. were kept constant. The effect of heat source width on streamlines and isotherms are depicted in Fig. 4. It can be seen that the two counter-rotating circulating cells appear both sides of the heat source. The fluid became warmer in the middle of the obstacle and goes toward the vertical walls and then descends from both low-temperature side walls. Circulation is completed by means of buoyant forces.

Fig. 4
figure 4

Streamlines (right) and isotherms (left) for low (top) and high (bottom) levels of the heat source width in the middle level of \(H\) and \(L_{\text{b}}\)

Full size image

Comparing the streamlines, increasing the width of the heat source is associated with an increase and a decrease in the power of circulating flows respectively from top and side walls of the heat source which is originated from the compactness of streamlines against the side walls. This observation is supported by the fact that the effect of buoyancy force on circulating flows from both sides is declined while its effect is heightened from the top. Subsequently, it can be concluded that the compactness of isotherms to the wall leads the heat transfer to increase.

Effect of fin height

The heat transfer is highly affected by the height of the heat source. As shown in Fig. 5, the higher the heat source height is, the lower the power of flow circulation is. Roughly speaking, the enclosure is divided into two sub enclosures and the fin is blocking the vortex in the surrounding area when the fin height is increased. As a result, it reduces the flow circulation and the subsequent buoyancy force. The regions of low isotherms concentration are the regions of low heat transfer. Comparing the isotherms show that the isotherms at the top of the heat source became more compacted as the heat source height decreases. Therefore, one could state that the large heater promotes thermal stratification against the side walls vertically due to the weakness of the flow circulation.

Fig. 5
figure 5

Streamlines (right) and isotherms (left) for low (top) and high (bottom) levels of the heat source height in the middle level of \(W\) and \(L_{\text{b}}\)

Full size image

Effect of side walls thickness

The streamlines and isotherms are depicted in Fig. 6 to show the effect of side walls thickness on flow pattern and thermal performance. The rotating circulating cells became weaker by increasing side walls thickness. In the case of the thickest side walls, the regions close to the vertical walls are almost inactive and no fluid flows there, while in the case of the thinnest side walls the fluid flows almost throughout the enclosure. As a matter of fact, the buoyancy force is intensified for the thinnest side walls originated from the lowest ability of the side walls to gain heat. In other words, the upward flow is concentrated at a close distance to the obstacle in high values of \(L_{\text{b}}\). As a result, the conduction mode plays the dominant role in heat transfer at the thickest vertical walls, while a mixed convection-diffusion heat transfer is responsible for heat transfer at the thinnest side walls. This fact is also supported by focusing on the isotherms. Generally speaking, the more regular and vertical shape of the isotherms next to the vertical walls implies on the more important the conduction mode.

Fig. 6
figure 6

Streamlines (right) and isotherms (left) for low (top) and high (bottom) levels of the side walls thickness in the middle level of \(W\) and \(H\)

Full size image

Optimization part

Application of response surface methodology

The response surface methodology is a mathematical-statistical approach which could make a relation between some independent parameters and some responses with minimum resources and quantitative data [44, 45]. The procedure that RSM follows has been illustrated in Fig. 7.

Fig. 7
figure 7

Flow chart of response surface methodology procedure

Full size image

In the current study, \(W\), \(H\) and \(L_{\text{b}}\) are input parameters and \(Nu_{\text{ave}}\) is the response. This method uses a sequential plan to find the best correlations based on least squares error fitting [46]. The multivariate model of \(Nu_{\text{ave}}\) in terms of factors can be written as follows:

$$Nu_{\text{ave}} = \alpha_{0} + \mathop \sum \limits_{i = 1}^{3} \alpha_{\text{i}} x_{\text{i}} + \mathop \sum \limits_{i = 1}^{3} \alpha_{\text{ii}} x_{\text{i}} x_{\text{i}} + \mathop \sum \limits_{i = 1}^{3} \mathop \sum \limits_{j = 1, j \ne i}^{3} \alpha_{{i{\text{j}}}} x_{\text{i}} x_{\text{j}}$$
(22)

where \(\alpha_{0}\) is the intercept, \(\alpha_{\text{i}}\) and \(\alpha_{\text{ii}}\) respectively are the linear and quadratic regression coefficients of \(i{\text{th}}\) factor, and \(\alpha_{\text{ij}}\) is the interaction of \(i{\text{th}}\) and \(j{\text{th}}\) factors. Central Composite Design (CCD) is one of the most well-known RSM-based models to find the above unknown function [46, 47]. According to the literature and the presented CFD simulations three-factor three-levels face-centered CCD-RSM, with complete replication is considered. Table 4 shows the low, middle, and high levels of the investigated factors. A Design of Experiment (DoE) resulted from CCD is necessary in order to perform the RSM analysis. Each design composed of 2k factorial points, 2k axial points and several center points. k is the number of independent factors. In order to fit linear and interaction terms, factorial points are necessary; also the estimation of curvature provided by axial points. Center points are repetitive for determination of the existence noise of system, which are suggested six for three factors CCD. Thus, twenty values for \(Nu_{\text{ave}}\) have to be collected in Table 5.

Table 4 The three levels of factors based on CCD-RSM
Full size table
Table 5 The CCD based DoE matrix
Full size table

Statistical analysis

The response, \(Nu_{\text{ave}}\), was computed on the basis of numerical experiment with respect to Table 5. The mathematical correlation was determined by using multiple regression. Regression models have to pass several statistical performance tests in order to check their accuracy. ANOVA introduced by Fisher is a collection of standard statistical indicators to identify the best fitted model by omitting the insignificant terms [48]. All of the statistical estimators, including Sum of Squares (SS), Degree Of Freedom (DOF), Mean Squares (MS), F value, P value, R2 and, adj-R2, are computed in ANOVA procedure and gathered in Table 6. Each term of the regression model has a distinct F value which indicated whether it remains or leaves the regression model. F value shows the data variance around the mean. The insignificant terms which crossed out from the model are the ones that have F values smaller than the unity [48]. Consequently, the quadratic term of C (\(L_{\text{b}}\)) was eliminated from \(Nu_{\text{ave}}\). After manipulations and using a power transformation, the ANOVA is changed. The regression coefficients and P-values of each term in the reduced model of \(Nu_{\text{ave}}\) were listed in Table 7. The statistical indicators of the updated models shows the model is appropriate to calculate the values of the average Nusselt number.

Table 6 ANOVA for \(Nu_{\text{ave}}\)
Full size table
Table 7 Regression coefficients for \(Nu_{\text{ave}}^{ - 0.96}\)
Full size table

Regression models of responses

The reduced regression model for \(Nu_{\text{ave}}\) which is valid in the range of \(0.1 < W < 0.5\), \(0.1 < H < 0.8\) and \(0.05 < L_{\text{b}} < 0.2\) is given as follows:

  • Statistical model:

    $$Nu_{\text{ave}} = \left( {0.6 - 0.64A - 0.036B - 1.29 \times 10^{ - 3} C - 4.981 \times 10^{ - 3} WH - 8.667 \times 10^{ - 3} WL_{\text{b}} - 1.213 \times 10^{ - 3} HL_{\text{b}} + 0.41W^{2} + 0.037H^{2} } \right)^{{\frac{ - 1}{0.96}}}$$
    (23)

  • Technological model:

    $$Nu_{\text{ave}} = \left( {2.551 - 9.197W - 0.3441H + 0.177L_{\text{b}} - 0.071WH - 0.578WL_{\text{b}} - 0.046HL_{\text{b}} + 10.139W^{2} + 0.298H^{2} } \right)^{{\frac{ - 1}{0.96}}}$$
    (24)

Residual plots for \(Nu_{\text{ave}}^{ - 0.96}\) are plotted in Fig. 8 to determine the accuracy of the obtained correlation. Normal probability is depicted in Fig. 8a. Since the residuals are lied down on a straight line, the errors are normally distributed. Figures 8b, d respectively show the studentized residuals versus predicted values and versus run numbers for \(Nu_{\text{ave}}^{ - 0.96}\). According to these two figures, the maximum error for \(Nu_{\text{ave}}^{ - 0.96}\) is something neat to 2 among all the responses. Predicted values from the regression model versus actual values, which indicate the goodness of fit and subsequently the model accuracy, have been shown in Fig. 8b. Since the residuals are falling on or near the straight line, regression model is well fitted with the actual values [49].

Fig. 8
figure 8

Residual plots for \(Nu_{\text{ave}}^{ - 0.96}\), a normal probability, b goodness of fit, c studentized residuals versus predicted, d studentized residuals versus run number

Full size image

R2 and adj-R2, which are the two indicators for showing the better fitting, both are 99.99% for this model, as depicted in Table 5. The closer the two aforementioned values to 100% the better the regression model fitting. For instance, 99.99% indicates that the model could be implemented with 0.01% of uncertainty. Thus, the model is able to predict the Nusselt number with an excellent accuracy [50].

Response surface analysis

Figure 9 shows the 3D surfaces and contour plots of Eq. (24). The interaction between the height and width of the fin has been investigated simultaneously and plotted in Fig. 9a while the \(L_{\text{b}}\) kept in its middle level (C=0). Both of the height and width of the fin have increasing effects on \(Nu_{\text{ave}}\), except for the region corresponds to middle and high levels of both \(W\) (A = 0 and A = + 1) and \(H\) (B = 0 and B = + 1). In other words, such an increasing trend is preserved until \(Nu_{\text{ave}}\) reaches to its maximum value somewhere within the aforementioned region. Another important result would be appeared by focusing on Fig. 9a. If the \(Nu_{\text{ave}}\) always increased by increasing the fin height, then \(Nu_{\text{ave}}\) must be reached to its maximum at high level of \(H\). However, Fig. 9a shows a negative fact, it indicates that the maximum value of \(Nu_{\text{ave}}\) occurred somewhere between 0.6 cm and 0.7 cm, while keeping \(L_{\text{b}}\) at the middle level. This result is also supported by Fig. 9b, which shows the interaction of \(L_{\text{b}}\) and \(W\) at the same time on \(Nu_{\text{ave}}\). As depicted in Figs. 9b and 9c, \(L_{\text{b}}\) always has an increasing impact on \(Nu_{\text{ave}}\) at any fixed value of \(W\) and \(H\). Therefore, it could be inferred that the maximum of \(Nu_{\text{ave}}\) happens at the thickest sidewalls.

Fig. 9
figure 9

Three-dimensional surfaces and contour plots of the effect of, a heat source width and height, b heat source height and side walls thickness, c heat source width and side walls thickness

Full size image

Sensitivity Analysis and Optimization

To determine the effects of factors, the sensitivity of the model to the factors was carried out based on CCD-RSM and presented in Table 8. The increasing or decreasing rate of \(Nu_{\text{ave}}\) with A, B and C, which described by sensitivity function, can be obtained by differentiating the regression model of \(Nu_{\text{ave}}\) in coded form, Eq. (23), with respect to A, B, and C, respectively, as follows:

$$S_{1} = - \frac{1}{0.96}\left( { - 0.64 - 4.98 \times 10^{ - 3} B - 8.667 \times 10^{ - 3} C + 0.8A} \right)\left( {Nu_{\text{ave}} } \right)^{ + 1.96}$$
(25)
$$S_{2} = - \frac{1}{0.96}\left( { - 0.036 - 4.98 \times 10^{ - 3} A - 1.213 \times 10^{ - 3} C + 0.074B} \right)\left( {Nu_{\text{ave}} } \right)^{ + 1.96}$$
(26)
$$S_{3} = - \frac{1}{0.96}\left( { - 1.29 \times 10^{ - 3} - 8.667 \times 10^{ - 3} {\text{A}} - 1.213 \times 10^{ - 3} {\text{B}}} \right)\left( {Nu_{\text{ave}} } \right)^{ + 1.96}$$
(27)

where \(S_{1}\), \(S_{2}\), and \(S_{3}\) are sensitivity functions. Sensitivity of \(Nu_{\text{ave}}\) to factors are performed for the three levels of \(W\), \(H\) and \(L_{\text{b}}\). Consequently, 27 values for each sensitivity functions will be calculated and collected in Table 8. The magnitude of the values regardless of their sign demonstrates the amount of sensitivity between the response and the investigated factor. In addition, positive sign depicts that, the response increases with increasing the investigated factor [51].

Table 8 The sensitivity analysis of the \(Nu_{\text{ave}}\)
Full size table

According to Table 8, since the amount of the values for \(S_{1}\) are larger than those of the two columns, the averaged Nusselt number is very sensitive to a change in fin width rather than fin height and side walls thickness. Moreover, In the middle level of \(A\), one could state that the larger the fin height, the more sensitive the \(Nu_{\text{ave}}\) to fin width. The results also reveal that, around the low and middle levels of fin width, the Nusselt number increases by an increase in fin width, while the trend is inverted in high level of fin width. Consequently, no doubt, a maximum point is existed somewhere between the middle and high levels of \(A\).

It can be seen from the column of \(S_{2}\) that, in all values of the three factors, the sensitivity of Nusselt number to fin height is increased by increasing the fin width. Focusing on the column of \(S_{2}\) shows that \(S_{2}\) experienced a slight change by changing the \(L_{\text{b}}\), especially in lower values of \(L_{\text{b}}\). Morover, the averaged Nusselt number first increases as fin height increases, reaches to a maximum value, then it decreases. So, the trend obviously shows that there is a maximum point between the middle and high levels of \(B\), where the \(S_{2}\) became zero.

Relatively, the lowest value of sensitivity is for the sensitivity of \(Nu_{\text{ave}}\) to \(L_{\text{b}}\). The results show that Nusselt number is in an inverse relation with \(L_{\text{b}}\) for thin fin, but the trend is inversed by inceasing in \(W\), namely, at high level of \(W\), the Nusselt number is increased by a rise in \(L_{\text{b}}\). Furthermore, the thicker the side walls always intensify the effect of side walls thickness on heat transfer. Besides, the intensity of \(S_{3}\) is decreased by increasing \(H\) in low level of \(A\), while the trend is inversed in the middle and high levels of \(A\). As a result, it can be inferred that, the minimum of \(Nu_{\text{ave}}\) occurs somewhere between the low and middle levels of \(A\). The results also reveal that, compared to the interaction of \(L_{\text{b}}\) with \(W\), the interactions of \(L_{\text{b}}\) with itself as well as with \(H\) are not noticeable.

The influence of the individual main effects of factors on the heat transfer was further elucidated using the perturbation plot shown in Fig. 10. The figure illustrates how Nuave varies as each factor changes from the reference point while other two factors held constant at the middle level (coded zero level). It is evident that the most influencing process parameter is fin width (A) followed by fin length (B) which has a moderate effect on Nuave followed by side walls thickness (C) which produces a minor effect as it changes from the reference point. It can be also observed that the profiles of A and B are curved because of the quadratic terms of Eqs. (23, 24). The curvature of the profile of fin width (A) is more noticable compared to the figure for fin length (B). This is due to the fact that its coefficient for the quadratic term of fin width is larger than that of the quadratic term of fin length. Fin width (A) showed negative quadratic effect and hence, there is a continous heat transfer enhancement up to an optimal point, than decreased with further increase in fin width. Side walls thickness (C) confirmed little contribution on heat transfer and its effect is almost negligible.

Fig. 10
figure 10

Perturbation plot comparing Nuave number to changes in factors

Full size image

Optimal point happens at the peak point, if exist any, or happens at the fringes, if a monotonic trend was preserved in perturbation plot. Therefore, it can be simply infered from the perturbation plot that the minimum heat transfer occures at the lowest levels of the factors, at the fringes, and the maximum heat transfer happens at the peak point. Capturing the exact position of the peak point is difficult without using an optimization technique because of the interactions between factors. In fact, the position of the peak point varies as the factors position changes. Thus, it should be necessary to select an efficient method.

The objective of RSM is providing the optimum solution to reduce the cost of expensive analysis methods [51]. After trying to fit the best regression models to one or more responses, RSM provides the best set of factor levels to minimize or maximize the responses. To this end, a hill climbing technique was used with a set of random points to check whether a more desirable solution exists or not [52]. It is an iterative mathematical optimization method, which searches the best solution locally. It starts with an arbitrary solution, and then tries to find a better solution comparing with the previous solution. Desirability value was selected as the criterion for the present work. The general desirability objective function is expressed as follows:

$$D = \left( {\mathop \prod \limits_{i = 1}^{n} d_{\text{i}}^{{r_{1} }} } \right)^{{\frac{1}{{\sum r_{\text{i}} }}}}$$
(28)

where, n is the number of responses and \(r_{i}\) is the importance value. This approach is limitless for the number of investigated responses. In fact, all goals are combined into a single desirability function in multi-objective optimization. The importance varies from 1 (the least important) to 5 (the most important). From the above equation, \(d_{\text{i}}\) is the desirability of i-th response, which reflects the desirable ranges for each response. Its calculation depends on the goal of maximizing or minimizing as follows:

$$d_{\text{i}} = \left\{ {\begin{array}{*{20}l} {\left[ {\frac{{Y_{i} - Y_{L, i} }}{{Y_{H, i} - Y_{L, i} }}} \right],} \hfill & {{\text{for}}\;{\text{maximization}}} \hfill \\ {\left[ {\frac{{Y_{H, i} - Y_{i} }}{{Y_{H, i} - Y_{L, i} }}} \right],} \hfill & {{\text{for}}\;{\text{minimization}}} \hfill \\ \end{array} } \right.$$
(29)

where, \(Y_{\text{i}}\), \(Y_{\text{L, i}}\), and \(Y_{\text{H, i}}\) are the predicted, the lowest, and the highest values of the ith response, respectively. So that, \(d_{\text{i}}\) has a value in the range of 0 to 1. The closer the value of \(d_{\text{i}}\) to the unity, the candidate point is closer to the goal and the optimal solution is reachable. Zero indicates that the Nusselt number is outside the acceptable limit and one corresponds to the ideal solution. As expressed previously, the lowest and the highest values of the responses individually happen at the two axial points especified in Fig. 10. The first experiment number of Table 5 is associated to the lowest values of the response, and the eighth experiment number is associated to the highest value. The minimum heat transfer occurs when \(W\), \(H\) and \(L_{\text{b}}\) respectively being equal to 0.1, 0.1 and 0.05 with the desirability of 0.9975. \(Nu_{\text{ave}}\) is predicted as 0.57298 while its actual value is 0.56690 at this point. Exploring the maximum of \(Nu_{\text{ave}}\) needs more efforts. All of the points within the circled region of Fig. 10 have the desirability value of unity. Hill climing tecnique provides a set of maximum points (not displayed) need to be screen to select the best one. The maximum heat transfer occurs when \(W\), \(H\) and \(L_{\text{b}}\) respectively being equal to 0.4615, 0.6467 and 0.2 with the desirability of unity. The predicted maximum Nusselt number by the RSM regression model, Eq. (24), is calculated as 3.2120 while the figure resulted from the CFD model is 3.16814. Figure 11 shows the streamlines and isotherms of the maximum heat transfer.

Fig. 11
figure 11

Optimal solution for the maximum heat transfer (Left: Isotherms, Right: Streamlines)

Full size image

Conclusions

In the present work, flow and natural heat convection of water-Al2O3 nanofluid resulted from a heat generating fin attached to the bottom of a square enclosure has been studied. The effects of fin geometry and side walls thickness variations on flow pattern and heat transfer characteristics have been studied while a magnetic field assigned to the enclosure. The highlights of the paper are listed as follows:

  • The two counter-rotating circulating cells become stronger as the heat source width and height increases and decreases, respectively. The thinner the side walls intensify their influence too.

  • The heat transfer from the top of the heat source is reduced in the case of the thinnest heat source and side walls and the longest heat source.

  • Increasing side walls thickness always enhances the heat transfer rate, except for thin fin.

  • The average Nusselt number, which is the heat transfer characteristic, increases with increasing width and height of the heat source, reaches its peak, then decreases. So, there is a peak point somewhere in the considered ranges of the two investigated factors.

  • The effect of fin length is secondary compared to fin width and side walls thickness has the lowest effect on fin effectiveness.

  • Optimizing the Nusselt number to attain the maximum heat transfer between the heat source and the two vertical walls, the maximum Nusselt number takes place at \(W = 0.4615\), \(H = 0.6467\) and \(L_{\text{b}} = 0.2\).