The effect of fins and wavy geometry on natural convection heat transfer of $\hbox {TiO}_{{2}}$–water nanofluid in trash bin-shaped cavity

Abstract

This paper studies the effect of fins number and size and wavy wall of a trash bin-shaped cavity on the natural convection heat transfer (NC) of a $\hbox {TiO}_{2}$–water nanofluid. The flow is considered buoyancy driven, which is under thermal radiation. The effects of Rayleigh number ($10^{3}-10^{5})$, thermal radiation (0.1$-$0.3), nanoparticle concentration (0.02$-$0.04), and geometry are investigated. Non-dimensional mode of NS equations would be governing equations, and the finite element technique is utilized to discrete them. Two plans are examined: firstly, the effects of thermal parameters on the enclosure with no fin are studied. Secondly, the effects of the fins length and number, and also the wavy geometry on Nusselt number (Nu) and flow distribution are investigated. The findings of the present paper are that increasing the fin number around the inner cylinder increases $\hbox {Nu}_{\mathrm{avg}}$ up to 54%, and reduces the local entropy generation (EG) and enhances the Bejan number. Moreover, if the wavy wall amplitude changes from 0.05 to 0.1, $\hbox {Nu}_{\mathrm{avg}}$ reduces by 31%, and if the Ra changes from $10^{3}$ to $10^{5}$, $\hbox {Nu}_{\mathrm{avg}}$ increases up to 36%.

1 Introduction

Adding nanoparticles laden in base fluids is a novel method for enhancing heat transfer. This idea was firstly introduced by Choi and Eastman [1]. This method is applicable in different branches of science and engineering such as HVAC [2], heat exchangers [3, 4], solar energy [5], heat pipe [6, 7], blood flow [8, 9], and composites [10, 11]. The effects of various parameters, namely, Rayleigh number, Hartmann number, radiation, and also different shapes of cavities, are investigated by researchers.

The effect of geometry is one of the most critical factors in natural convection (NC) analysis. Disparate structures of chamber, i.e., rectangular [12], triangle-shaped [13], trapezoid-shaped [14], and unusual forms are perused. Bahiraei et al. studied hybrid nanofluid of graphene and silver in a microchannel heat sink with ribs which directed the flow toward secondary channels. They concluded that the average convective heat transfer coefficient has a direct relation with Reynolds number and the concentration of nanoparticles [15]. Sun and pop analyzed NC in a triangle-shaped cavity. Three types of nanomaterials were applied to explore the mean Nusselt number and temperature features [16]. Ashorynejad and Hoseinpour studied NC in a porous chamber. They used lattice Boltzmann method (LBM) to calculate entropy generation and average Nusselt number [17]. Eshaghi et al. [18] studied FEM simulation of double-diffusive NC in an H-shaped chamber. Besides, they investigated the effect of varying configuration of fin on the flow. Bahmani et al. [19] studied turbulent heat transfer of a water–alumina nanofluid in a double pipe heat exchanger. They solved the governing equations by the finite volume method and studied the effects of Reynolds number, nanoparticle volume fraction, and flow direction on Nusselt number and thermal efficiency. They reached 32.7% enhancement in Nusselt number by changing the mentioned parameters. Hatami et al. studied NC heat transfer in circular and wavy cavity. They used RSM to detect the best geometry for the wavy wall and also RSM and FEM for optimizing the results. The best case (between the tested cases) is when the number of the undulations is 12 and the amplitude value is 0.3. Their proposed method had a widespread application in time-efficient optimization of heat transfer in irregular geometries [20]. The effect of wavy wall is another interesting parameter studied in literature. Few studies conducted this issue in their analysis. Abdelkaber et al. [21] studied the effect of different aspect ratios of the wavy wall on Nusselt number in various Ra numbers. Nguyen et al. [22] did the numerical study about the interaction of wavy nanofluid and porous media enclosure on the NC for Cu–water nanofluid. They used the ISPH method to solve their governing equations. Various ranges of Rayleigh number ($10^{3}-10^{6})$, Darcy ($10^{-6}-10^{-1})$, and porous medium height (0.25$-$0.75), amplitude (0$-$0.25), and undulation number (1–3) were considered in their work. Waqas et al. [23] studied the theoretical analysis of the SWCNT–MWCNT in a rotating disk using von Karman approach. Rao et al. [24] studied the NC of a heat source which was embedded in a wavy cavity. The effect of various parameters such as heater’s non-dimensional length and waviness of the right wall were investigated. They concluded that non-dimensional length reduces the rate of convection. Dogonchi et al. [25] did a numerical investigation on NC of Cu–water nanofluid in a square wavy cavity. They used CVFEM to solve the governing equations, and their most important finding was that wavy contraction ratio has a negative impact on NC heat transfer. The effect of the shape of the nanoparticles was also considered by Dogonchi et al. [26]. They used irregular triangular enclosure for their analysis. Other related works can be found in Refs. [27,28,29,30,31,32,33,34,35].

The effect of fin’s number and shape on the heat transfer is an ongoing topic that is popular among researchers in the field of heat transfer. Feng et al. [36] studied two series of fins in a new cross-fin heat sink: perpendicular short fins and long fins. Their ultimate goal was to enhance natural convection heat transfer by considering both NC and radiation. They concluded that heat sink enhances both NC and radiation by 11% and 15%, respectively. It is vital to mention that they used both numerical and experimental analysis to validate their results. Saleh et al. [37] numerically studied the effect of flexible fin on NC in a square cavity by putting the fin on the left wall. They used Brinkman–Forchheimer extended Darcy flow model and searched the effects of fin oscillation and elasticity on the overall intensity of heat transfer and concluded that both oscillation and elasticity of fin have a positive impact up to 3.4% on heat transfer rate. The effect of fin’s length and location in a wavy enclosure with Galerkin weighted residual finite element technique was studied by Asad et al. [38]. The lower and upper walls were considered to be wavy and the most important finding was that the fin length causes an increase in $\hbox {Nu}_{\mathrm{avg}}$. Khetib et al. [39] studied the effect of curved, inclined, and straight fins on NC and entropy of the nanofluid in a square cavity. They found that increasing the fin’s angle and curvature have a positive impact on heat transfer rate and entropy generation. Alfarhani et al. [40] considered porous enclosure with two fins attached to the hot wall to see the changes in NC of $\hbox {Al}_{2}\hbox {O}_{3}$–water nanofluid. They studied the effect of Hartman number, magnetic field, Ra, and length of the fins and concluded that the fin’s length is in direct relation with heat transfer rate. Other works on the effect of fin can be found in [41, 42].

Entropy generation (S) demonstrates the irreversibility of the fluid flow. S in cavities with nanofluids is due to friction, fluid flow, porous media, and magnetic field. Tayebi et al. [43] studied the entropy production of a hybrid nanofluid in an elliptical cavity. One of their important findings was that the maximum amount of entropy was achieved for higher Rayleigh numbers and nanoparticle concentration. Li et al. [44] studied entropy generation in a square cavity exposed to constant magnetic field. Their results showed that radiation and nanoparticle concentration increase the entropy generation. The entropy generation of hybrid nanofluid [45], entropy generation of simple fluids [46, 47], and the effect of geometry on S [48] are the hot topics for this parameter. Chamkha et al. [49] investigated the thorough effect of magnetohydrodynamic mixed convection on the parameter of entropy generation. They used finite volume technique to numerically analyze the effect of constant magnetic field on entropy generation in a gamma-shaped cavity. They concluded that the main factor which causes considerable change in entropy generation is nanoparticle volume fraction. Tilehnoee et al. [50] studied the entropy generation in an incinerator cavity with wavy heater. They considered the effect of different parameters in two flow regimes: laminar and turbulent flow. They demonstrated that Ra and Da enhance the entropy generation in laminar flow; however, the Da has a negative impact on $\hbox {Nu}_{\mathrm{avg}}$ when the flow is turbulent. Tilehnoee et al. [51] measured the entropy generation of NEPCMs in a porous cavity. They used four different channels with three configurations for cooling purpose. Their findings include the direct impact of Ha on Bejan number, and also the negative impact of Ra on Bejan number. Other works on entropy generation can be found in [52,53,54,55,56].

Fig. 1

Geometry of enclosure

According to the aforesaid published papers, there may be a lack of investigations of the simultaneous effect of wavy wall geometry and the number and shape of the fins on NC and S in cavities. There is a gap in the investigation of the simultaneous effect of wavy wall and fins on such a geometry which is applicable mostly in heat exchangers, valley due to sun radiator which is applied in studying the mechanism of fog, cooling appliances, building thermal elements, and thermal storage tanks. The present paper aims to investigate the effect of thermal parameters (Ra, Rd, and $\phi$), and geometry on Nusselt number and S of $\hbox {TiO}_{2}$–water nanofluid in a wavy crown enclosure with a cylindrical obstacle inside. This is the first time that the effect of thermal and geometrical parameters on the NC and S is perused in this especial wavy container. This examination may be suitable in heat exchangers and their wavy walls, HVAC, and renewable energy systems such as solar energy systems with radiation effects.

2 Problem description

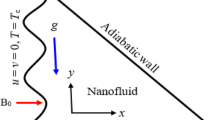
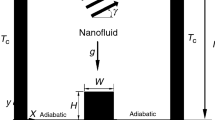
The geometry of the trash bin-shaped enclosure with a cylindrical obstacle inside may be depicted in Fig. 1. The mesh size and structure of the mesh is also shown in this figure. The boundary conditions are as follows: the right and left adiabatic walls, constant heat flux from the bottom wall, the cold top wavy wall, and the cold cylinder at the middle of the cavity. Boussinesq approximation is used for density changes, and there may be no slip condition among $\hbox {TiO}_{2}$ nanomaterials and water. Besides, the flow is at thermal equilibrium. Table 1 demonstrates the properties of $\hbox {TiO}_{2}$ and water.

Table 1 Thermo-physical features of $\hbox {H}_{2}\hbox {O}$ and $\hbox {TiO}_{2}$ [52]

Table 2 Comparison of $\hbox {Nu}_{\mathrm{avg}}$ of the present work and Oztop [66]

The flow in this study is assumed incompressible, laminar, and steady. So, the governing equations would be [57, 58]:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho _{nf} }\frac{\partial p}{\partial x}+\upsilon _{nf} \left( \frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}\right) , \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} =-\frac{1}{\rho _{nf} }\frac{\partial p}{\partial y}+\upsilon _{nf} \left( \frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}\right) \nonumber \\&\qquad \qquad \qquad \quad +\frac{(\rho \beta )_{nf} }{\rho _{nf} }g(\mathrm{T}-\mathrm{T}_{c} ), \end{aligned}$$

(3)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{K_{nf} }{(\rho \mathrm{C}_{p} )_{nf} }\left( \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}\right) -\frac{1}{(\rho \mathrm{C}_{p} )_{nf} }\frac{\partial q_{r} }{\partial y},\nonumber \\ \end{aligned}$$

(4)

where $q_{r} =-\frac{4\sigma _{r} }{3\chi _{r} }\frac{\partial T^{4}}{\partial y}$ and $T^{4}\cong -3T_{c}^{4}+4T_{c}^{3}T.$

The following terms are introduced to make dimensionless mode of the above equations:

$$\begin{aligned}&X=\frac{x}{L},U=\frac{uL}{\alpha },P=\frac{L^{2}p}{\alpha _{f}^{2}\rho _{f} },\nonumber \\&Y=\frac{y}{L},V=\frac{vL}{\alpha },\theta =\frac{(\mathrm{T}-\mathrm{T}_{c} )}{\Delta T}. \end{aligned}$$

(5)

Fig. 2

Comparison of the streamline between the current results with those of [64] and [65] at $\hbox {Ra}=1.78\times 105$

Fig. 3

U-velocity distribution for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

Fig. 4

V-velocity distribution for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

Hence, Eqs. (1)–(4) may follow the following form:

$$\begin{aligned}&U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}\nonumber \\&\quad =-\frac{\rho _{f} }{\rho _{nf} }\frac{\partial P}{\partial X}+\Pr \frac{(\mu _{nf} /\mu _{f} )}{(\rho _{nf} /\rho _{f} )}\left( \frac{\partial ^{2}U}{\partial X^{2}}+\frac{\partial ^{2}U}{\partial Y^{2}}\right) , \end{aligned}$$

(6)

$$\begin{aligned}&U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\rho _{f} }{\rho _{nf} }\frac{\partial P}{\partial X}+\Pr \frac{(\mu _{nf} /\mu _{f} )}{(\rho _{nf} /\rho _{f} )}\left( \frac{\partial ^{2}V}{\partial X^{2}}+\frac{\partial ^{2}V}{\partial Y^{2}}\right) \nonumber \\&\qquad \qquad \qquad \qquad +\frac{(\rho \beta )_{nf} }{\rho _{nf} \beta _{f} }\Pr Ra\theta , \end{aligned}$$

(7)

$$\begin{aligned}&U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y} =\frac{(\mathrm{k}_{nf} /\mathrm{k}_{f} )}{((\rho C_{p} )_{nf} /(\rho C_{p} )_{f} )}\left( \frac{\partial ^{2}\theta }{\partial X^{2}}+\frac{\partial ^{2}\theta }{\partial Y^{2}}\right) \nonumber \\&\quad \qquad \qquad \qquad +\frac{4}{3}\frac{1}{((\rho C_{p} )_{nf} /(\rho C_{p} )_{f} )}Rd\frac{\partial ^{2}\theta }{\partial Y^{2}}, \end{aligned}$$

(8)

where

$$\begin{aligned} \Pr =\frac{\upsilon _{f} }{\alpha _{f} },Ra=g\beta _{f} (T_{h} -T_{c} )\mathrm{L}^{3},Rd=\frac{4\sigma _{r} T_{c}^{3}}{\chi _{r} k_{f} }. \end{aligned}$$

(9)

With the boundary conditions:

$$\begin{aligned}&\hbox {Left wall:}\,\frac{\partial \theta }{\partial n}=0,\mathrm{V}=0\, \mathrm{U}=0\nonumber \\&\hbox {Right wall:}\, V=0,U=0,\frac{\partial \theta }{\partial n}=0\nonumber \\&\hbox {Bottom wall }(\hbox {Y}=0)\,:V=0,U=0,\frac{\partial \theta }{\partial Y}=-1\nonumber \\&\hbox {Cylinder and Wavy wall: }\theta =0,V=0,U=0.\nonumber \\ \end{aligned}$$

(10)

Fig. 5

Streamline distribution for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

Fig. 6

Isotherm distribution for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

The n may be a vector normal to the surfaces of the enclosure at every point. The Nusselt number (local as well as average), on the other hand, would be specified as:

$$\begin{aligned} \text {Nu}= & {} \left( 1+\frac{4}{3}\frac{k_{f} }{k_{nf} }\mathrm{Rd}\right) \left( \frac{k_{nf} }{k_{f} }\right) \left( {\frac{1}{\theta }} \right) , \end{aligned}$$

(11)

$$\begin{aligned} \text {Nu}_{\text {avg}}= & {} \frac{1}{2\pi }\int \limits _0^{2\pi } {\text {Nu}d\xi }. \end{aligned}$$

(12)

The thermo-physical correlations of $\hbox {TiO}_{2}$-$\hbox {H}_{2}\hbox {O}$ would be defined as:

$$\begin{aligned} \rho _{nf}= & {} \phi \rho _{s} +(1-\phi )\rho _{f}, \end{aligned}$$

(13)

$$\begin{aligned} (\rho C_{p} )_{nf}= & {} (\rho C_{p} )_{f} (1-\phi )+(\rho C_{p} )_{s} \phi , \end{aligned}$$

(14)

$$\begin{aligned} (\rho \beta )_{nf}= & {} (\rho \beta )_{f} (1-\phi )+(\rho \beta )_{s} \phi , \end{aligned}$$

(15)

$$\begin{aligned} \alpha _{nf}= & {} \frac{k_{nf} }{(\rho \mathrm{C}_{p} )_{nf} }. \end{aligned}$$

(16)

The nano-suspension thermal conductivity is defined as:

$$\begin{aligned} \frac{K_{nf} }{K_{f} }=\frac{(\mathrm{K}_{\text {eq}} -2K_{f} )-2(\mathrm{K}_{\text {eq}} -\mathrm{K}_{f} )(1-\gamma )^{3}\phi }{(\mathrm{K}_{\text {eq}} +2\mathrm{K}_{f} )-(\mathrm{K}_{\text {eq}} -\mathrm{K}_{f} )(1-\gamma )^{3}\phi }, \nonumber \\ \end{aligned}$$

(17)

where $\gamma =\frac{h_{nl} }{r_{p} }$, and the equivalent thermal conductivity of the nanoparticles ($\hbox {K}_{\mathrm{eq}}$) is:

$$\begin{aligned} \frac{K_{\text {eq}} }{K_{s} }=\zeta \frac{2(1-\zeta )+(1-\gamma )^{3}(1+2\zeta )}{-(1-\zeta )+(1-\gamma )^{3}(1+2\zeta )}, \end{aligned}$$

(18)

in which $\zeta =\frac{K_{\text {nl}} }{K_{p} }$. For the present study, the assumptions are as follows: ${K}_{\mathrm{nl}}=100{K}_{{f}}$, ${r}_{{p}}=3\,\hbox {nm}$, and $\hbox {h}_{\mathrm{nl}}=2\,\,\hbox {nm}$ [59].

The equations for entropy generation (S) would be [60]:

$$\begin{aligned} S_{\text {gen}} =S_{\text {HT}} +S_{\text {FF}}, \end{aligned}$$

(19)

$\hbox {S}_{\mathrm{HT}}$ and $\hbox {S}_{\mathrm{FF}}$ are the local S in which heat transfer and fluid friction are, respectively, responsible and are expressed as:

$$\begin{aligned} S_{\text {HT}}= & {} \frac{k_{nf} }{k_{f} }\left[ {\left( {\frac{\partial \theta }{\partial X}} \right) ^{2}+\left( {\frac{\partial \theta }{\partial Y}} \right) ^{2}} \right] , \end{aligned}$$

(20)

$$\begin{aligned} S_{FF}= & {} \phi _{n} \frac{\mu _{nf} }{\mu _{f} }\left( 2\left( \left( \frac{\partial V}{\partial Y}\right) ^{2}+\left( \frac{\partial U}{\partial X}\right) ^{2}\right) \right. \nonumber \\&\left. +\left( \frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right) ^{2}\right) . \end{aligned}$$

(21)

The Bejan number is:

$$\begin{aligned} \text {Be}=\frac{S_{\text {HT}} }{S_{\text {gen}} }. \end{aligned}$$

(22)

Fig. 7

Local entropy generation for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

Fig. 8

Bejan number distribution for different Ra and $\hbox {R}_{\mathrm{d}}$ ($\phi =0.01)$

3 Validation and numerical analysis

A Finite element method (FEM) is used to solve the conservation equations [20]. This method is in terms of Galerkin method and divides the domain into subdomains and then combines the elements again. The conditions in a two-way coordinate in the FEM method in a specific point are related to the upstream and downstream of that point. Based on the mentioned points, the Flex-PDE software is used to solve the governing equations. This software solves the continuity, momentum, and energy equations with the defined boundary conditions by Galerkin finite element method (GFEM). For solving momentum and continuity, the $\hbox {P}_{2}$-$\hbox {P}_{1}$ Lagrange finite element is used, and for energy equation, the Lagrange-quadratic finite element is considered [61]. Besides, the convergence criterion for this solution is when the error of the residuals is less than $10^{-5}$. The following solutions for velocities (U, V) and temperature ($\theta$) are introduced based on Galerkin finite element method [62, 63]:

$$\begin{aligned} U&\cong \sum \limits _{n=1}^N {U_{n} } \gamma _{n} ({ X,Y}),V\cong \sum \limits _{n=1}^N {V_{n} } \gamma _{n} ({X,Y}),\nonumber \\&\theta \cong \sum \limits _{n=1}^N {\theta _{n} } \gamma _{n} ({X,Y}). \end{aligned}$$

(23)

If one incorporates these equations to 6–8, then the nonlinear residual equations at all nodes of the internal domain on the trash bin cavity will be:

$$\begin{aligned} R_{K}^{U}= & {} \sum \limits _{n=1}^N U_{n} \int \limits _\Omega \left[ \left( {\sum \limits _{n=1}^N {U_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial X}\right. \nonumber \\&\left. +\left( {\sum \limits _{n=1}^N {V_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial Y} \right] \gamma _{k} dXdY \nonumber \\&+\Upsilon \left[ \sum \limits _{n=1}^N U_{n} \int \limits _\Omega \frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial X}dXdY\right. \nonumber \\&\left. +\sum \limits _{n=1}^N {V_{n} \int \limits _\Omega {\frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial Y}dXdY} } \right] \nonumber \\&+\Pr \sum \limits _{n=1}^N {U_{n} \int \limits _\Omega {\left[ {\frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial X}+\frac{\partial \gamma _{k} }{\partial Y}\frac{\partial \gamma _{n} }{\partial Y}} \right] dXdY} }, \end{aligned}$$

(24)

$$\begin{aligned} R_{K}^{V}= & {} \sum \limits _{n=1}^N U_{n} \int \limits _\Omega \left[ \left( {\sum \limits _{n=1}^N {U_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial X}\right. \nonumber \\&\left. +\left( {\sum \limits _{n=1}^N {V_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial Y} \right] \gamma _{k} dXdY \nonumber \\&+\Upsilon \left[ \sum \limits _{n=1}^N U_{n} \int \limits _\Omega \frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial X}dXdY\right. \nonumber \\&\left. +\sum \limits _{n=1}^N {V_{n} \int \limits _\Omega {\frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial Y}dXdY} } \right] \nonumber \\&+\Pr \sum \limits _{n=1}^N {U_{n} \int \limits _\Omega {\left[ {\frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial X}+\frac{\partial \gamma _{k} }{\partial Y}\frac{\partial \gamma _{n} }{\partial Y}} \right] dXdY} } \nonumber \\&-\Pr Ra\left( {\sum \limits _{n=1}^N {\theta _{n} \int \limits _\Omega {\gamma _{n} \gamma _{k} dXdY} } } \right) , \end{aligned}$$

(25)

$$\begin{aligned} R_{K}^{\theta }= & {} \sum \limits _{n=1}^N \theta _{n} \int \limits _\Omega \left[ \left( {\sum \limits _{n=1}^N {U_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial X}\right. \nonumber \\&\left. +\left( {\sum \limits _{n=1}^N {V_{n} \gamma _{n} } } \right) \frac{\partial \gamma _{n} }{\partial Y} \right] \gamma _{k} dXdY \nonumber \\&+\left( 1+\frac{4}{3}\mathrm{Rd}\right) \sum \limits _{n=1}^N {\theta _{n} \int \limits _\Omega {\left[ {\frac{\partial \gamma _{k} }{\partial X}\frac{\partial \gamma _{n} }{\partial X}+\frac{\partial \gamma _{k} }{\partial Y}\frac{\partial \gamma _{n} }{\partial Y}} \right] dXdY} } \nonumber \\&-\lambda \left( {\sum \limits _{n=1}^N {\theta _{n} \int \limits _\Omega {\gamma _{n} \gamma _{k} dXdY} } } \right) . \end{aligned}$$

(26)

Fig. 9

a The effect of nanoparticle concentration on $\hbox {Nu}_{\mathrm{avg}}$ ($\hbox {Rd}=0.1$). b The effect of radiation parameter on $\hbox {Nu}_{\mathrm{avg}}\,(\phi =0.01$)

Fig. 10

Streamline distribution for variable numbers of fins ($\phi =0.01$, $\hbox {Rd}=0.1$)

The case with no fins has the best isotherm distribution among the other cases (Fig. 11). The range of temperature change is minimum for this case and when $\hbox {Ra}=10^{5}$.

Fig. 11

Isotherm distribution for variable number of fins ($\phi =0.01$, $\hbox {Rd}=0.1$)

Fig. 12

Local entropy distribution for different number of fins ($\phi =0.01$, $\hbox {Rd}=0.1$)

Fig. 13

Bejan number for different number of fins ($\phi =0.01$, $\hbox {Rd}=0.1$)

The Eqs. (24–26) are scrutinized by the reduced integration method and Newton Raphson approach. Then, the 4N*4N system of equations at each iteration will be:

$$\begin{aligned} J(\mathrm{a}^{n})\left[ {\mathrm{a}^{n}-\mathrm{a}^{n+1}} \right] =R(\mathrm{a}^{n}), \end{aligned}$$

(27)

where the Jacobian matrix is $\hbox {J}(\hbox {a}^{\mathrm{n}})$, and $\hbox {R}(\hbox {a}^{\mathrm{n}})$ is the residual vector.

Moreover, the results of [64] and also [65] are used to validate the present code. The results show that there is a negligible difference between these analyses and the code is valid.

Moreover, to validate the results of the present work with the wavy wall geometries studied before, the results are compared with those of Oztop et al. [66] in Table 2. Again, the results are in good agreement with Ref. [66].

4 Results

4.1 Geometry with no fin

The outcomes of the present study are introduced and analyzed in two plans: first of all, the thermal parameters’ impact on the Nu and S is studied when there is no fin attached to the middle circle. Figure 3 shows the contours of U-velocity for varying Rd and Ra. There may be four counter-rotating cells that exist owing to density diversity. These cells will be more potent if Ra goes up from $10^{3}$ to $10^{5}$. Besides, the maximum value of U-velocity goes up from 0.03 to 12 if Ra increases. On the other hand, the radiation has a negative impact on the maximum amount of U-velocity. V-velocity has also the same attitude toward changes in Ra and Rd. Figure 4 depicts the contours of V-velocity. One is able to see that Ra has a positive and Rd has a reverse impact on this parameter. This is because higher Ra means better buoyancy-driven flow and better movement of nanofluid. However, Higher Rd means more contribution of conduction heat transfer to thermal radiation. Based on Figs. 3 and  4, one can conclude that the radiation parameter can be used as a tool to control the power of fluid flow within the thermal systems.

The distribution of streamlines is depicted in Fig. 5. There are two main and big counter-rotating cells with high intensity around the circle. The main reason is the difference between the density of the hot flow coming from the bottom wall and the cold wall of the circle. For the cases in which the intensity of the streamline is important such as pipes and the force of the fluid flow on them, this behavior is of interest. Moreover, the highest amount of streamline happens when $\hbox {Ra}=10^{5}$ and $\hbox {Rd}=0.1$.

The isotherm distribution which is responsible for temperature distribution inside the cavity is shown in Fig. 6. The isotherms are distributed uniformly due to constant heat flux of the bottom wall. The lower sections of the cavity have higher amount of isotherms and by coming up to the wavy wall this amount reduces. The maximum amount of isotherm is seen for the case with $\hbox {Ra}=10^{3}$ and $\hbox {Rd}=0.1$. However, the distribution of isotherms is smoother for the case with $\hbox {Ra}=10^{5}$ and $\hbox {Rd}=0.3$.

Local S and Bejan number are other interesting parameters in this study. The entropy generation here is due to heat transfer and friction between the base fluid and nanoparticles. This factor increases by going up the Rayleigh number (Fig. 7). Furthermore, the maximum value of local S takes place at the lower section of the circle. This is the place where the hot and cold flows are intertwined to each other rigorously which means there is more loss of energy at this point. Increasing the Rayleigh number is responsible for a decrease in Bejan number (Fig. 8). Bejan number is defined as the ratio of irreversibility due to heat transfer to the total irreversibility. When the Ra increases, the buoyancy-driven flow is enhanced and the natural convection heat transfer also becomes better. This means lower irreversibility in heat transfer and accordingly lower Bejan number. Radiation has a very slight positive impact on Bejan number, especially for the case ($\hbox {Ra}=10^{5})$. The increase in Be due to increasing radiation parameter clearly shows that Rd has a negative impact on the stability of energy systems.

Nanoparticle concentration and radiation parameter are the two factors which affect the $\hbox {Nu}_{\mathrm{avg}}$. Figure 9a shows that increasing $\phi$ enhances the average Nusselt number for the case $\hbox {Ra}=10^{5}$. This increase is 19%. For the two other cases, there is no change in $\hbox {Nu}_{\mathrm{avg}}$. On the other hand, the radiation parameter enhances $\hbox {Nu}_{\mathrm{avg}}$ for all the cases of Ra (Fig. 9b). This behavior shows that Rd is a positive factor as one of the procedures for heat transfer enhancement.

4.2 The geometry with fin

In the second plan, the geometry’s impact on heat transfer is perused. The number of fins, the shape of the fin, and the geometry of wavy wall are the geometrical parameters changed to see the effects on Nu and S. The effect of fin number of streamline distribution reveals that the case with two fins has the minimum intensity of rotating vortices below the cylinder and has the best streamline distribution (Fig. 10). Besides, adding two fins reduces the intensity of maximum streamlines up to 94% due to the fact that the fins block the flow from moving around the cylinder.

The effect of fin number on local S and Bejan number is depicted in Figs. 12 and 13, respectively. S due to fluid friction and heat transfer increases by increasing the number of the fins. For the case with four fins, this increase in very noticeable, which means increasing the fins causes a huge irreversibility of flow in the cavity. Interestingly, the best distribution of the Bejan number is for the case with four fins. This means that the irreversibility due to heat transfer is the lowest for the case for four fins (Fig. 13). These two figures reveal that increasing the fin number is the main cause for increasing the friction loss; however, it reduces the irreversibility due to heat transfer.

The effect of fin number on $\hbox {Nu}_{\mathrm{avg}}$ is obtained for different parameters in Table 3. Overall, the fin number has a useful influence on $\hbox {Nu}_{\mathrm{avg}}$. This means that increasing the number of fins enhances the overall NC heat transfer of the bottom wall. The maximum increase in $\hbox {Nu}_{\mathrm{avg}}$ is obtained for the case with $\hbox {Ra}=10^{4}$. Accordingly, if one wants to enhance heat transfer in industrial applications, increasing the number of the fins is one solution. Furthermore, $\hbox {Nu}_{\mathrm{avg}}$ will be enhanced by 30% for the case with $\hbox {Ra}=10^{3}$, 29% for the case with $\hbox {Ra}=10^{4}$, and 54% for the case with $\hbox {Ra}=10^{5}$, when the number of fins increases from zero to four. So, it can be concluded that the effect of fin’s number is superior for the case with $\hbox {Ra}=10^{5}$.

The effect of fin size is also studied in this research. Three different fin sizes are considered ($\hbox {L}=\hbox {r}$, $\hbox {L}=\hbox {r}/2$, $\hbox {L}=\hbox {r}/4$), in which r is the radius of the circle. The intensity of the cells increases by increasing the length of the fin; however, the area of the cells reduces (Fig. 14a). Besides, the isotherms are more uniform for the last case with the largest fin size (Fig. 14b), and the Bejan number reduces at the upper side of the cavity for the case with $\hbox {L}=\hbox {r}$ (Fig. 14c).

Table 3 The effect of fin number on $\hbox {Nu}_{\mathrm{avg}}$

Fig. 14

a Streamline distribution for different fin sizes ($\phi = 0.01, \hbox {Rd}=0.1, \hbox {Ra}=104$). b Isotherm distribution for different fin sizes ($\phi = 0.01, \hbox {Rd}=0.1, \hbox {Ra}=104$). c Bejan number for different fin sizes ($\phi =0.01, \hbox {Rd}=0.1, \hbox {Ra}=10^{4}$)

The effect of wavy wall is studied in Fig. 15. Three shapes of wavy wall with different amplitudes (0.05, 0.075, and 0.1) and fixed undulation (2) are considered. The average fin size ($\hbox {L}=\hbox {r}/2$) is used for this simulation. The intensity of vortices is reduced by increasing the amplitude. Besides, the Bejan number increases by increasing the amplitude from 0.05 to 0.1. Moreover, Table 4 shows the amount of $\hbox {Nu}_{\mathrm{avg}}$ for these three cases. The amplitude of wavy wall has a reverse influence on $\hbox {Nu}_{\mathrm{avg}}$. The $\hbox {Nu}_{\mathrm{avg}}$ lessens by 22% when the amplitude is increased from 0.05 to 0.075.

Fig. 15

a Streamline distribution for different wavy sizes ($\phi =0.03, \hbox {Rd}=0.1, \hbox {Ra}=105$). b Isotherm distribution for different wavy sizes ($\phi =0.03, \hbox {Rd}=0.1, \hbox {Ra}=105$). c Bejan number for different wavy sizes ($\phi =0.03, \hbox {Rd}=0.1, \hbox {Ra}=10^{5}$)

5 Conclusion

Natural convection (NC) and entropy generation (S) of the $\hbox {TiO}_{2}$-$\hbox {H}_{2}\hbox {O}$ nanofluid is studied in a trash bin-shaped wavy wall cavity. Two scenarios are considered: in the first scenario, the effects of thermal parameters on the enclosure with bare cylinder inside are examined. In the second plan, the geometry of the wavy wall (amplitude of wavy wall) and fins of the cylinder’s impact on NC and S are considered. Some of the most important findings are:

• Increasing Ra causes an increase in streamlines and velocity and decrease in Bejan number.

• Changes in Rd (from 0.1 to 0.3) enhances $\hbox {Nu}_{\mathrm{avg}}$ up to 90%.

• Increasing the number of the fins is responsible for reducing the heat transfer irreversibility and increasing the friction irreversibility.

• Increasing the fin number from 0 to 4 enhances the $\hbox {Nu}_{\mathrm{avg}}$ by 29%, 31%, and 54% for the cases with $\hbox {Ra}=10^{3}$, $\hbox {Ra}=10^{4}$, and $\hbox {Ra}=10^{5}$, respectively.

• Increasing the length of the fin reduces the irreversibility due to heat transfer. On the other hand, it increases the irreversibility due to friction.

• The best $\hbox {Nu}_{\mathrm{avg}}$ is obtained for the wavy wall with the least amplitude (0.05), and if the amplitude is increased from 0.05 to 0.1, the $\hbox {Nu}_{\mathrm{avg}}$ reduces by 31%.

• The Bejan number increases by increasing the amplitude of the wavy wall.

Table 4 The wavy wall amplitude’s impact on $\hbox {Nu}_{\mathrm{avg}}$ ($\phi =0.03, \hbox {Rd}=0.1, \hbox {Ra}=10^{5})$